MODEL-BASED IMAGE RECONSTRUCTION FOR MRI

Abstract

Magnetic resonance imaging (MRI) is a sophisticated and versatile medical imaging modality. Traditionally, MR images are reconstructed from the raw measurements by a simple inverse 2D or 3D fast Fourier transform (FFT). However, there are a growing number of MRI applications where a simple inverse FFT is inadequate, e.g., due to non-Cartesian sampling patterns, non-Fourier physical effects, nonlinear magnetic fields, or deliberate under-sampling to reduce scan times. Such considerations have led to increasing interest in methods for model-based image reconstruction in MRI.

1. INTRODUCTION

The inverse fast Fourier transform (FFT) has served the MR community very well as the conventional image reconstruction method for k-space data with full Cartesian sampling. And for well sampled non-Cartesian data, the gridding method [1] with appropriate density compensation factors [2] is fast and effective. But when only under-sampled data is available, or when non-Fourier physical effects like field inhomogeneity are important, then gridding/FFT methods for image reconstruction are suboptimal, and iterative algorithms based on appropriate models can improve image quality, at the price of increased computation. This paper reviews the use of iterative algorithms for model-based MR image reconstruction. The references give pointers to some recent work but are by no means a comprehensive survey^★.

2. MRI BACKGROUND

Any signal processing method aimed at forming images from measurement devices such as MRI scanners must consider the relevant physics. A survey in this magazine [3] and a book written from a signal processing perspective [4] have described MRI physics well. Here we review the physics in a somewhat unconventional way that facilitates describing some of the “non-Fourier” aspects of MRI.

2.1. MRI physics

Standard MRI scanners use a large static magnetic field

$${\overrightarrow{B}}_0(\overrightarrow{r})=B_0(\overrightarrow{r})\overrightarrow{k}$$ (1)

to induce a net magnetization M⃗ = M_xi⃗ + M_y j⃗+ M_z k⃗ at each point in space in the body being imaged, where i⃗, j⃗, k⃗ denote the unit vectors along the x, y and z axes respectively, and r⃗ = (x, y, z) denotes 3D spatial coordinates. Ideally the static field strength B₀(r⃗) would be spatially uniform, i.e., a single constant B₀. In practice it is never perfectly uniform, due to the unavoidable nonuniformities of all practical coil designs and due to the field strength variations that are induced by the nonuniform magnetic susceptibilities of different tissue types[5] [6]. The electron distributions in different molecules also influence the local magnetic environment experienced by an atom’s nucleus, called chemical shift. Some types of MRI scans are robust to such spatial variations of B₀; others are sensitive to nonuniformities, necessitating correction methods[7].

At equilibrium (which is established within a few seconds for a stationary object), the magnetization M⃗ is aligned with the applied static field and its magnitude is proportional to the product of B₀(r⃗) and the object-dependent local density of (predominately) hydrogen protons or “spins.” This proton density alone is of only modest interest in MRI; in practice one applies time-varying magnetic fields B⃗ (r⃗, t) that induce time-varying changes in the magnetization

$$\overrightarrow{M}(\overrightarrow{r},t)=M_{\text{x}}(\overrightarrow{r},t)\overrightarrow{\iota }+M_{\text{y}}(\overrightarrow{r},t)\overrightarrow{j}+M_{\text{z}}(\overrightarrow{r},t)\overrightarrow{k}.$$ (2)

These changes depend on time constants (tissue-dependent relaxation parameters) and other factors, and the goal in MRI is to form images of aspects of this magnetization. By manipulating the applied field B⃗₀(r⃗, t) appropriately, sometimes in conjunction with injected or inhaled contrast agents, one can examine a multitude of different tissue properties.

An MRI scan consists of one or more alternations between two stages: excitation and readout. During the excitation stage, the applied magnetic field B⃗ (r⃗, t) is designed to tip the magnetization vectors M⃗ within some slice or slab away from equilibrium, so that they have a component in the transverse plane, i.e., the (x, y) plane. It is convenient to represent this transverse component mathematically using a complex function defined as follows:

$$\text{M}(\overrightarrow{r},t)\triangleq M_{\text{x}}(\overrightarrow{r},t)+\iota M_{\text{y}}(\overrightarrow{r},t),$$ (3)

where $\iota \triangleq \sqrt{-1}$. Note that the field components M_x and M_y are real physical quantities; the “transverse magnetization” M(r⃗, t) is complex solely by definition. The excitation process can be quite complicated to model and is beyond the scope of this paper. See [3] for an introduction to the role that signal processing plays in the design of excitation pulses, and [8] [9] [10] for some recent model-based RF pulse design methods.

During the readout stage, the applied field B⃗ (r⃗, t) is manipulated in ways that help elucidate the transverse magnetization M(r⃗, t). For image reconstruction, it is essential to model the effects of the applied field on the transverse magnetization. The precise relationship is governed by the Bloch equation [11] [3]. For most image reconstruction purposes, it suffices to consider just two aspects of the full relationship: precession and transverse relaxation. The most important equation in MRI is the Larmor relation: ω = γ|B⃗|, which states that the magnetization precesses (around the axis of the applied field) at a frequency ω that is proportional to the magnitude of the applied field. The constant of proportionality γ is called the gyromagnetic ratio and is about 42.6 MHz per Tesla for hydrogen protons. During a readout, only the longitudinal component of B⃗ is varied usually, i.e.,

$$\overrightarrow{B}(\overrightarrow{r},t)=B_{\text{z}}(\overrightarrow{r},t)\overrightarrow{k},$$ (4)

so the magnetization precesses around k⃗, i.e., within the transverse plane. This property is why the complex representation (3) is convenient, because precession can be expressed using a complex phase in this form. In general the applied longitudinal field strength B_z(r⃗, t) varies both spatially and temporally, so the Larmor relationship describes the instantaneous frequency at a given spatial location:

$$\omega (\overrightarrow{r},t)=\gamma B_{\text{z}}(\overrightarrow{r},t).$$ (5)

Without loss of generality, let t = 0 be the time when the excitation pulse is completed, and consider some time point t > 0 during the readout. The precession of the transverse magnetization between time 0 and time t corresponds to a net phase that is the integral of the instantaneous frequency (5), i.e., ideally we would have

$$\text{M}(\overrightarrow{r},t)=\text{M}(\overrightarrow{r},0)exp\left(-\iota {\int }_0^t\omega (\overrightarrow{r},t^{\prime })\text{d}{t}^{\prime }\right).$$

In practice, microscopic variations in the magnetic field cause the spins within a given voxel to become out of phase over time. So the transverse magnetization vector’s magnitude decreases approximately exponentially with a time constant $T_2^{\ast }$. Accounting for this decay, an accurate model for the temporal evolution of the transverse magnetization during a readout is

$$\text{M}(\overrightarrow{r},t)=f(\overrightarrow{r}){\text{e}}^{-t/T_2^{\ast }(\overrightarrow{r})}exp\left(-\iota \gamma {\int }_0^t{B}_{\text{z}}(\overrightarrow{r},t^{\prime })\text{d}{t}^{\prime }\right),$$ (6)

where f(r⃗) ≜ M(r⃗,0) denotes the object’s transverse magnetization immediately after excitation. A typical goal in MRI is to form an image of f(r⃗). The properties of f(r⃗) depend not only on spin density, but also on the type of excitation used. Note that for simplicity of exposition, we focus here on the case where the object is static so that f(r⃗) is not a function of time t. Generalizations to dynamic imaging are very active research areas in MR image reconstruction[12].

The relaxation factor $T_2^{\ast }$ varies spatially, and often is on the order of 10 ms. This relatively rapid decay is a significant limitation in MRI. If $T_2^{\ast }$ were longer, then a signal excitation stage followed by a (lengthy) readout stage could be sufficient to form a high-resolution image of f(r⃗). In practice, the rapid decay limits how much spatial information can be recorded in a single readout stage, so such “single shot” imaging, such as echo-planar imaging (EPI) [13], provides only modest spatial resolution. Therefore, high-resolution imaging uses multiple alternations between excitation stages and readout stages, each with different variations of the applied field B_z(r⃗, t).

2.2. Data acquisition: the MR signal

By Faraday’s law the time-varying magnetization M(r⃗, t) will induce an electromotive force (emf) in a nearby coil. The emf will be proportional to the volume integral of the time derivative of the magnetization M(r⃗, t) multiplied by the coil response pattern c(r⃗). The resulting electrical potential v(t) across the receive coil is

$$v(t)=\text{real}\left(\int c(\overrightarrow{r})\frac{\text{d}}{\text{d}t}\text{M}(\overrightarrow{r},t)\text{d}\overrightarrow{r}\right),$$ (7)

where real(·) denotes the real part of a complex number. The coil response c(r⃗) generally decreases with distance from the coil. If uncorrected, this nonuniformity causes spatial variations in signal strength that can be a challenge for image processing methods like segmentation algorithms. Numerous correction methods have been developed[14] [15] [16] [17] [18].

Because the time constant $T_2^{\ast }$ is on the order of milliseconds whereas the phase variations in (6) are many MHz, it is very reasonable to use a narrow-band approximation when evaluating the time derivative of M(r⃗, t) as needed in (7). The time derivative of a narrow-band signal is well approximated by a constant scaling factor: $\frac{\text{d}}{\text{d}t}\text{M}(\overrightarrow{r},t)\approx c_0\text{M}(\overrightarrow{r},t)$. We absorb this constant into the coil response pattern and rewrite (7) as

$$v(t)=\text{real}\left(\int c(\overrightarrow{r})\text{M}(\overrightarrow{r},t)\text{d}\overrightarrow{r}\right).$$ (8)

The receive coil’s signal is amplified and demodulated using some center frequency ω₀. Ideally one would use ω₀ = γB₀ if the static magnetic field had uniform strength B₀. Usually quadrature demodulation is used, yielding separate in-phase I(t) and quadrature Q(t) baseband signals. In the literature, the demodulated “MR signal” s(t) is defined (implicitly) as

$$\begin{array}{l}s(t)\triangleq I(t)+\iota Q(t)\\ =\text{lowpass}(e^{\iota {\omega }_{0}t}v(t))\\ =e^{\iota {\omega }_{0}t}\int c(\overrightarrow{r})\text{M}(\overrightarrow{r},t)\text{d}\overrightarrow{r},\end{array}$$ (9)

where the lowpass operation selects the baseband component of the demodulated signal. This complex analog signal is just a mathematical definition; in practice, the I(t) and Q(t) signals are each sampled and digitized yielding two digital signals. (One can use two separate A/D converters, or a single A/D converter running at twice the normal rate to avoid I/Q imbalance.) Digitally, these two signals can be combined and stored as complex values, i.e., we record samples

$$I(m{\mathrm{\Delta }}_{\text{T}})+\iota Q(m{\mathrm{\Delta }}_{\text{T}}),m=1,\dots ,n_{\text{d}},$$

where Δ_T denotes the sampling rate (typically around 1 μs) and n_d denotes the number of recorded samples, typically 64-512 for a given readout stage. Again, the physical quantities are real, but complex quantities are defined in terms of those physical quantities for convenience. (In some systems, digital demodulation is used, but the modeling remains identical.)

2.3. Signal model

To improve signal to noise ratio (SNR) and reduce acquisition times, the use of multiple receive coils has become increasingly popular in MRI. Although originally called phased array imaging [19], a term that resonates with other signal processing applications involving multiple receivers, today the use of multiple receive coils in MRI is usually called parallel imaging [20] [21] [22].

Let c_l(r⃗) denote the sensitivity (response pattern) of the lth coil, for l = 1, …, L, where L denotes the number of coils. Let s_l(t) denote the demodulated “MR signal” associated with the lth coil, defined as in (9). Substituting (6) into (9) and simplifying yields the following general forward model for the MR signal associated with the lth coil:

$$s_l(t)=\int c_l(\overrightarrow{r})f(\overrightarrow{r}){\text{e}}^{-t/T_2^{\ast }(\overrightarrow{r})}{\text{e}}^{-\iota \phi (\overrightarrow{r},t)}\text{d}\overrightarrow{r},$$ (10)

where the space- and time-varying phase is

$$\phi (\overrightarrow{r},t)\triangleq {\int }_0^t(\gamma B_{\text{z}}(\overrightarrow{r},t^{\prime })-{\omega }_0)\text{d}{t}^{\prime }.$$ (11)

In practice multiple such signals are recorded, one for each excitation/readout pair (“shots”). For simplicity of notation we consider “single shot” imaging; the extension to multiple shots is conceptually straightforward but notationally cumbersome. Note that the phase variations (11) are common to all receive coils; only the coil response patterns {c_l(r⃗)} differ between coils.

2.4. Measurement model

The recorded measurements in a MR scan consist of noisy samples of the MR signal (10)

$$y_{li}=s_l(t_i)+{\epsilon }_{li},i=1,\dots ,n_{\text{d}},l=1,\dots ,L,$$ (12)

where y_li denotes the ith sample of the lth coil’s signal at time t_i and n_d denotes the number of time samples. Usually the t_i values are equally spaced, and often there are one or more time values where the signal is particularly strong due to alignment of the magnetization’s phases; these values are called echo times. The measurement errors ε_li are very well modeled by additive, complex, zero-mean, temporally white gaussian noise [23] [24] [25]. However, there can be coupling of the noise values between different coils for the same time points, i.e.,

$$\text{Cov}\{{\epsilon }_{li},{\epsilon }_{kj}\}={\sum }_{lk}\delta [i-j],$$ (13)

where δ denotes the Kronecker impulse, and the L × L matrix Σ characterizes the noise covariance between coils [26] [22].

3. LINEAR RECONSTRUCTION PROBLEM

Using the measurement model (12) and the signal model (10), the “typical” image reconstruction problem in MRI is to estimate the object f(r⃗) from the measurement vector y = (y₁, …, y_L), where y_l = (y_l1, …, y_l,nd). (All vectors are column vectors here.) We first consider model-based image reconstruction for this “basic” linear formulation. Because parallel imaging is of considerable interest, we continue to consider the general case of L receive coils. A standard single receive coil is a simple special case.

This is an ill-posed problem because the given measurements y are discrete whereas the object f(r⃗) is an unknown continuous-space function. To facilitate parametric estimation, we approximate the object f(r⃗) using a “finite series expansion” as follows:

$$f(\overrightarrow{r})=\sum _{j=1}^N{f}_{j}b(\overrightarrow{r}-{\overrightarrow{r}}_j),$$ (14)

where b(·) denotes the object basis function, r⃗_j denotes the center of the jth translated basis function, and N is the number of parameters. Such approximations are classic in the tomographic image reconstruction literature [27] and are slowly taking root in the MR community. Minimum 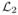norm methods [28] can postpone the discretization (14) until the final step of displaying the image, but it is unclear if this approach provides image quality benefits that outweigh its computational requirements. For simplicity, hereafter we use rect basis functions b(r⃗) = rect(r⃗/Δ), i.e., square pixels of dimension Δ, so N is the number of pixels, or voxels in 3D scans. Many other possible basis function choices can be considered, all of which are imperfect because the true object never satisfies the parametric model (14) exactly. Nevertheless simple basis functions can provide useful approximations.

Substituting the basis expansion (14) into the signal model (10) and simplifying leads to the discrete forward model

$$s_l(t_i)=\sum _{j=1}^N{a}_{\mathit{lij}}{f}_j$$ (15)

where the elements {a_lij} of the system matrix A_l associated with the lth coil are given by

$$a_{\mathit{lij}}=\int b(\overrightarrow{r}-{\overrightarrow{r}}_j)c_l(\overrightarrow{r}){\text{e}}^{-t_i/T_2^{\ast }(\overrightarrow{r})}{\text{e}}^{-\iota \phi (\overrightarrow{r},t_i)}\text{d}\overrightarrow{r}.$$ (16)

In practice the basis functions are usually highly localized (e.g., voxels), so “center of voxel” approximations like the following are nearly always used, often implicitly:

$$a_{\mathit{lij}}\approx c_l({\overrightarrow{r}}_j){\text{e}}^{-t_i/T_2^{\ast }({\overrightarrow{r}}_j)}{\text{e}}^{-\iota \phi ({\overrightarrow{r}}_j,t_i)}.$$ (17)

For exceptions, see [29] [30].

Typically the decay due to $T_2^{\ast }$ is ignored, or it is assumed implicitly that the total readout time t_nd− t₁ is small relative to $T_2^{\ast }$ in which case one can make the approximation ${\text{e}}^{-t_i/T_2^{\ast }(\overrightarrow{r})}\approx {\text{e}}^{-t_1/T_2^{\ast }(\overrightarrow{r})}$. Under this approximation, we can absorb the $T_2^{\ast }$-weighting effect of ${\text{e}}^{-t_1/T_2^{\ast }(\overrightarrow{r})}$ into the unknown image f(r⃗).

Combining (12) and (15) in matrix-vector form yields:

$${\mathit{y}}_l={\mathit{A}}_l\mathit{f}+{\mathit{\epsilon }}_l,$$

where f = (f₁, …, f_N) is the vector of parameters (pixel values) that we wish to estimate from the data y. Stacking up all L measurement vectors as y = (y₁, …, y_L) and defining the (n_dL) × N system matrix A = (A₁, …, A_L) yields the linear model

$$\mathit{y}=\mathit{Af}+\mathit{\epsilon }.$$ (18)

At first glance this linear model appears amenable to a variety of iterative solution methods. However, a significant challenge that arises is that in general the elements of A can be quite complicated in the form above, yet A is too large to store for typical problem sizes. Most iterative algorithms require matrix-vector multiplication by A and its transpose; there are fast algorithms for these operations (without storing A explicitly) in many special cases of interest [31] [30] [7].

Thus far we have allowed the phase function φ(r⃗_j, t_i) to be quite general, without the traditional focus on “Fourier encoding.” Recently there has been interest in investigating nonlinear magnetic field variations B_z(r⃗, t) in (4), and reconstruction algorithms have been proposed that use much of the generality in (16) [32] [33]. These are currently specialized research topics, so we now focus on the more common case of linear field gradients.

3.1. Fourier encoding

In typical MR scanners, the longitudinal component of the applied field B_z(r⃗, t) in (4) consists of three components:

$$B_{\text{z}}(\overrightarrow{r},t)=B_0+\mathrm{\Delta }{B}_0(\overrightarrow{r})+\overrightarrow{G}(t)·\overrightarrow{r}.$$ (19)

The constant B₀ denotes the advertised field strength of the main static field. The function ΔB₀(r⃗) denotes the spatial deviations of the field strength from this nominal value. This function is often called a field map, and in general it is unknown, but it can be estimated by suitable types of acquisitions and data processing methods [34] [35]. The field gradients G⃗(t) = G⃗_x(t)j⃗ + G⃗_y(t)j⃗ + G⃗_z(t)j⃗ consist of three user-controlled functions that are the historical key to providing spatial information in standard MR imaging[36]. Many different types of MR scans are possible by changing G⃗ (t).

Substituting (19) into (11) using ω₀ ≜ γ B₀ and simplifying yields

$$\phi (\overrightarrow{r},t)={\int }_0^t\gamma \mathrm{\Delta }{B}_0(\overrightarrow{r})+\gamma \overrightarrow{G}(t)·\overrightarrow{r}\text{d}t$$

or equivalently

$${\text{e}}^{-\iota \phi (\overrightarrow{r},t)}={\text{e}}^{-\iota \mathrm{\Delta }{\omega }_0(\overrightarrow{r})t}{\text{e}}^{-\iota 2\pi \overrightarrow{k}(t)·\overrightarrow{r}}$$ (20)

where Δω₀(r⃗) ≜ γ ΔB₀(r⃗) denotes the off-resonance frequency and the k-space trajectory is defined by

$$\overrightarrow{k}(t)\triangleq \frac{1}{2\pi }{\int }_0^t\gamma \overrightarrow{G}(t)\text{d}t.$$ (21)

Usually the phase accrual e^{−i Δ ω₀(r⃗)t} due to off resonance is undesirable and can distort reconstructed images if ignored[37]. Therefore some image reconstruction methods, particularly in fMRI, account for its effects [38] [30]. In some cases the map Δω₀(r⃗) is found from a separate “pre-scan;” in other cases it is estimated jointly with f [39] [40] [41]. In chemical shift imaging, e.g., to separate fat and water components, the term Δω₀(r⃗) includes both useful information about the chemical shift effect as well as the undesirable variations due to field inhomogeneity [42] [43].

For the linear field gradients (19), substituting (20) into (17) yields simpler expressions for the system matrix:

$$a_{\mathit{lij}}\approx c_l({\overrightarrow{r}}_j){\text{e}}^{-z({\overrightarrow{r}}_j)t_i}{\text{e}}^{-\iota 2\pi \overrightarrow{k}(t_i)·{\overrightarrow{r}}_j},$$ (22)

where we define the “rate map” z(r⃗) by combining the relaxation and field maps:

$$z(\overrightarrow{r})\triangleq 1/T_2^{\ast }(\overrightarrow{r})+\iota \mathrm{\Delta }{\omega }_0(\overrightarrow{r}).$$ (23)

When this rate map is assumed to be zero, i.e., if relaxation and off resonance are ignored, then a_lij is the product of a Fourier encoding matrix having elements e^{−i2πk⃗(t_i) ·r⃗_j} with a diagonal sensitivity encoding matrix having elements c_l(r⃗_j).

If the k-space sample locations k⃗(t_i) lie on an appropriate subset of a Cartesian grid, then FFT operations provide efficient multiplication by A and its transpose. If non-Cartesian k-space sampling is used, then a nonuniform FFT (NUFFT) is needed [44].

When z(r⃗) in (22) is nonzero, then the elements (22) no longer correspond to a standard Fourier transform. Approximations are needed to provide fast computation of matrix-vector products. In particular, often one can approximate the exponentials in (17) using an additively separable form:

$${\text{e}}^{-z({\overrightarrow{r}}_j)t_i}\approx \sum _k{b}_{ik}{c}_{kj}$$

for various choices for the basis functions b_ik and coefficients c_kj [7]. With this type of approximation, we can rewrite matrix-vector multiplication as follows:

$${[{\mathit{A}}_l\mathit{f}]}_i\approx \sum _k{b}_{ik}\sum _{j=1}^N(c_{kj}{c}_l({\overrightarrow{r}}_j)f_j){\text{e}}^{-\iota 2\pi \overrightarrow{k}(t_i)·{\overrightarrow{r}}_j}.$$

The inner sum is simply a FFT or NUFFT so this approach is relatively fast. Free software for this is available [45].

3.2. Reconstruction cost function

Having specified the linear model (18), we now turn to solution methods. Because the noise in MRI measurements is gaussian, a natural approach is to estimate f by minimizing a regularized least-squares cost function:

$$\widehat{\mathit{f}}=\underset{\mathit{f}}{argmin}\mathrm{\Psi }(\mathit{f}),\mathrm{\Psi }(\mathit{f})\triangleq {\left|\right|\mathit{y}-\mathit{Af}\left|\right|}^2+\beta \text{R}(\mathit{f}).$$ (24)

For a single coil, the noise variance in the k-space data is white (uncorrelated with uniform variance), so the usual Euclidian norm ||·|| is appropriate. For parallel MRI, noise is stationary across time samples (i), but the norm should include the inverse of the L × L covariance matrix Σ in (13) that describes the noise correlation between receive coils [26] [22].

If the k-space samples lie on an equally-spaced grid (Cartesian sampling) with appropriate sample spacings relative to the object field of view, and if the rate map z(r⃗) is zero (i.e., we ignore relaxation and field inhomogeneity), and if we consider just a single coil (L = 1) and treat the sensitivity pattern as uniform, i.e., c₁(r⃗) = 1, then the system matrix A_l is orthogonal. In this special case, no regularization is needed and ${\mathit{A}}^{-1}=\frac{1}{N}{\mathit{A}}^{\prime }$ and the solution is simply $\widehat{\mathit{f}}=\frac{1}{N}{\mathit{A}}^{\prime }\mathit{y}$, which can be evaluated by an inverse FFT. This is the most common MR image reconstruction method. However, if any of these conditions do not hold, then typically the system matrix A is not well conditioned, and the unregularized LS solution can lead to undesirable noise amplification. To avoid this problem, some form of regularization is needed.

3.3. Regularization

An open problem in most image reconstruction problems, including MRI, is how to best choose the regularizer R(f). If this term is not included, then the image estimate f̂ will suffer from noise and artifacts for under-sampled and/or non-Cartesian data, because this inverse problem is ill-conditioned. The approach for iterative reconstruction that has been adopted in commercial PET scanners is to use an unregularized algorithm[46], initialize it with a uniform image, stop iterating just as the image gets unacceptably noisy, and then perhaps apply a bit of post-filtering to reduce the noise. One could adopt a similar approach for MR imaging[47]. However, introducing regularization can ensure that the iterative algorithm converges to a stable image, and can enforce prior information that improves image quality particularly for under-sampled data.

The simplest choice is Tikhonov regularization R(f) = ||f||² or R(f) = ||f − f̄|^|2, where f̄ is some prior or reference image (possibly zero). The disadvantage of this choice is that it biases the estimate towards the reference image f̄. In particular, if the reference image is zero, then all pixel values in f̂ are diminished towards zero, possibly reducing contrast.

Another choice is a quadratic roughness penalty function, which in 1D would be written

$$\text{R}(\mathit{f})=\sum _{j=2}^N\mid f_j-f_{j-1}{\mid }^2.$$ (25)

This choice biases the reconstruction towards a smooth image where neighboring pixel values are similar. It is convenient for minimization [30], but it has the drawback of smoothing image edges, particularly if the regularization parameter β in (24) is too large. One can prove that using (25) guarantees that the cost function (24) has a unique minimizer.

More recently, total variation methods have been investigated for MR image reconstruction [48]. In 1D, these methods replace the squared differences between neighboring pixels above with absolute differences:

$$\text{R}(\mathit{f})=\sum _{j=2}^N\mid f_j-f_{j-1}\mid .$$ (26)

In 2D continuous space, the analogous functional is

$$\int \left|\right|\nabla f\left|\right|\text{d}\overrightarrow{r}=\int \int \sqrt{{\left|\frac{\partial }{\partial x}f(\overrightarrow{r})\right|}^2+{\left|\frac{\partial }{\partial y}f(\overrightarrow{r})\right|}^2}\text{d}x\text{d}y.$$

The advantage of this type of regularization is that it biases the reconstructed image towards a piecewise smooth image, instead of a globally smooth image, thereby better preserving image edges. However it is harder to minimize and can lead to the appearance of “blocky” texture in images[49]. Numerous alternatives of the form

$$\text{R}(\mathit{f})=\sum _{j=2}^N\psi (f_j-f_{j-1})$$

for various choices of the “potential function” ψ(·) have been proposed in the imaging literature. Many of these compromise between the quadratic case (25) and the absolute difference case (26), for example the hyperbola

$$\psi (t)=\sqrt{1+\mid t/\delta {\mid }^2}-1$$ (27)

is approximately quadratic near 0, which aids noise reduction, yet approximately linear away from 0, which helps preserve edges[50].

3.4. Algorithms

Iterative algorithms are needed to minimize (24). For differentiable regularizers such as (25), the conjugate gradient algorithm is a natural choice [26] [30]. For nondifferentiable regularizers like (26), more sophisticated algorithms are needed and this is an active research area[51, 52] [12].

4. RECONSTRUCTION CHALLENGES

Although a variety of useful problems can be solved in MRI using the formulation (24), there are numerous challenges that provide research opportunities.

4.1. Regularization parameter selection

A practical challenge with regularized methods is selection of the regularization parameter β in (24). For quadratic regularization, there is a well-developed theory for choosing β in terms of the desired spatial resolution properties of the reconstructed image [53] [54]. This theory extends readily to MR imaging with reasonably well sampled trajectories (and to parallel imaging with reasonable acceleration factors) for which the point spread function (PSF) of the reconstructed image is relatively close to a Kronecker impulse so that simple measures like full width at half maximum (FWHM) are reasonable resolution metrics[55]. For highly under-sampled trajectories the PSF can have “heavy tails” due to aliasing effects, and more investigation is needed to extend the above methods to MR applications.

For nonquadratic regularization such as the total variation method (26), the analysis in [53] [54] is inapplicable so one must resort to other methods for choosing β. Statisticians often use cross validation [56] [57] for choosing regularization parameters, with a goal of finding the parameter that minimizes the mean-squared error (MSE) between f̂ and the unknown f. However, MSE is the sum of variance and bias squared, and where bias is related to spatial resolution and artifacts, and it is unclear whether an equal weighting of noise variance and bias (squared) is optimal from an image quality perspective in medical imaging.

Another method for choosing β is the “L-curve” method[58] [59]. This method is expensive because it requires evaluating f̂ for several values of β, and it has some theoretical deficiencies [60].

In summary, choosing β for nonquadratic regularization remains a nontrivial issue in most ill-posed imaging problems including MRI, and remains an active research area [61] [62].

4.2. Partial k-space methods

If the object f(r⃗) were real, then its Fourier transform would be Hermitian symmetric so in principle only half of k-space would need to be sampled. In practice the magnetization (3) is complex due to a variety of physical effects. However, in many cases the phase of M(r⃗, t) can be assumed to be a smooth function. This property has led to a variety of partial k-space methods where one samples a bit more than half of k-space, then estimates the phase from the central portion of k-space (corresponding to low spatial frequencies), and then uses this estimated phase to reconstruct the entire image [63] [64] [65] [66]. Such methods are used routinely in many types of MR scans.

4.3. Under-sampled k-space data

The need for some type of regularization is essential when the k-space data is under sampled, i.e., when the number of measurements Ln_d is less than the number of unknown voxels N. In MRI, the scan time is roughly proportional to the number of measurements, so collecting fewer samples can reduce scan time, which is particularly desirable in dynamic imaging.

In the broader field of tomographic image reconstruction, there is a long history of using prior information, such as assuming objects are piecewise smooth, to reconstruct images from an under-sampled set of projection views, e.g., [67] [68] [69] [70] [71]. Many of these methods involve cost functions of the form (24) with a suitable system matrix A for the application and appropriate regularizers R(f) that capture prior information about the object.

Recently it has become very popular to express prior information in terms of some type of sparsity of the object. Notions of sparsity have deep roots in statistical signal processing [72] [73] [74] [75]. Sparsity is especially apparent in MR angiography [76]. The moniker of compressed sensing or compressive sampling has become widespread for such techniques, and recently entire sessions at MR conferences are devoted to this topic [77] [12]. Some compressed sensing formulations ignore the noise in the data. In the presence of noise, a typical formulation is

$$\underset{\mathit{f}}{argmin}{\left|\right|\mathbf{\Psi }\mathit{f}\left|\right|}_1\text{s}.\text{t}.{\left|\right|\mathit{y}-\mathit{Af}\left|\right|}_2\le \epsilon ,$$

where Ψ transforms the image f into a domain (such as wavelet coefficients) where one postulates that the signal is sparse.

Often this optimization problem is solved using a Lagrange multiplier approach:

$$\underset{\mathit{f}}{argmin}{\left|\right|\mathit{y}-\mathit{Af}\left|\right|}_2^2+\beta {\left|\right|\mathit{\Psi }\mathit{f}\left|\right|}_1,$$

which corresponds to a particular regularizer in (24). Rarely is the ℓ₁ norm implemented exactly; in practice usually a continuously differentiable approximation is used, such as:

$${\left|\right|\mathit{v}\left|\right|}_1\approx \sum _i\left(\sqrt{\mid v_i{\mid }^2+{\delta }^2}-\delta \right)$$ (28)

for some small value of δ > 0. This approximation is equivalent to the hyperbola (27) used frequently for edge-preserving image reconstruction. Non-convex methods that enforce sparsity even more strongly are also under investigation[78]. In the usual case where A corresponds to an under-sampled discrete Fourier transform (DFT), a variety of algorithms are available that have numerous potential applications in MR [12]. Challenges with this approach include choosing the sparsifying transform Ψ and regularization parameters β and δ appropriately. Furthermore, when δ is small, the regularizer (28) has very high curvature near 0, which can slow convergence. Choice of the k-space sampling pattern is also important. Nonuniform sampling has a long history in MRI, e.g., [79].

5. NONLINEAR RECONSTRUCTION PROBLEMS

The linear image reconstruction problem (24) is just one of many estimation problems of interest in MRI. Returning to the elements of the system matrix (22), there has been research on estimating essentially every component therein, as summarized below.

5.1. Field map estimation

For scans with long readout times, the effect of field inhomogeneity Δω₀ in (22) is important. In practice the field map ω(r⃗) is not known a priori but rather it must be estimated from noisy MR scans. One can examine the phase differences between two scans having different echo times to determine Δω₀. If these two scans have short readouts, then there are simple image-domain methods for estimating Δω₀, which is known as B₀ field mapping [80] [35]. Errors in the field map estimates may cause artifacts in reconstructed images that are based on models like (22).

In addition, object motion that occurs between the field map scans and subsequent scans of interest, e.g., in fMRI, will lead to an inconsistency between the actual scan data and the assumed model (22) used by the reconstruction algorithm. This possibility has motivated the development of dynamic field mapping methods that estimate the field map separately for each frame in a dynamic study, e.g., [38] [81] [82] [41]. For scans with long readout durations, the appearance of Δω₀ in a complex exponential in (22) makes this a somewhat complicated nonlinear estimation problem.

5.2. Relaxation map estimation

In some MR applications, it is useful to estimate tissue relaxation parameters, particularly T₂ or $T_2^{\ast }$, on a pixel-by-pixel basis[83] [84] [85] [86]. One approach to measuring such relaxation parameters is to acquire a “baseline” scan of the object and then acquire one or more additional scans having different echo times. One then reconstructs images from each of those scans, and then performs linear regression on a voxel-by-voxel basis using the logarithm of the image voxel values. This approach can be adequate if the readout durations are sufficiently small. But for acquisitions with long readouts, the effect of time t_i in the e^{− z(r⃗_j) t_i} in (22) should be considered, i.e., we should account for relaxation during the signal readout[86]. This requires methods that estimate the relaxation map directly from the k-space data. These are more challenging nonlinear estimation problems because $T_2^{\ast }$ appears in an exponent in (22). Several methods for jointly estimating $T_2^{\ast }$, Δω₀, and f (r⃗) have been investigated [87] [88] [40] [89] [82].

5.3. Sensitivity map estimation

The coil sensitivity patterns c_l(r⃗) in (22) also must be determined for parallel imaging based on sensitivity encoding. Normally this is done by acquiring well-sampled data both with local receive coils and with a reference body coil and dividing the two [22]. Acquiring the extra reference data can be inconvenient, so normalizing by the square root of the sum of squares of the local receive coils is also used[90]. A variety of other estimation methods have been proposed[91] [92] [93], including methods that jointly estimate the sensitivity maps {c_l(r⃗)} and the image f(r⃗) [94] [95] [96]. Note that if f(r⃗) were known, then the problem of estimating c_l(r⃗) would be a linear estimation problem because c_l(r⃗) appears as a linear scaling in (22). But when both f(r⃗) and c_l(r⃗) are to be estimated, the model is bilinear because f(r⃗) and c_l(r⃗) appear as a product in (10). This complicates joint estimation.

5.4. Trajectory mapping

The k-space trajectory k⃗(t_i), defined as an integral of the gradient waveforms in (21), should be calibrated carefully to ensure that the system model (22) is accurate. In practice, the field gradients induced by the gradient coils in the scanner are not exactly proportional to the waveforms applied to those coils due to eddy currents. Therefore the physical k-space trajectory realized in the system can depart somewhat from the desired k-space trajectory. These differences can degrade the reconstructed image, particularly for non-Cartesian trajectories with long readout durations. Therefore, a variety of techniques have been developed for mapping the actual k-space trajectory experimentally[97] [98] [99] [100] [101] [102] [103].

5.5. Within-voxel gradients

The model (23) treats the field inhomogeneity within each voxel as being a constant, ignoring within-voxel gradients of the off-resonance map. However, these gradients can be significant in functional magnetic resonance imaging (fMRI) based on the BOLD effect [104]. Accurate reconstruction of signals near air-tissue interfaces requires compensation for these within-voxel gradients, which complicates the reconstruction method [105] [106] [29] [107].

6. EXAMPLE

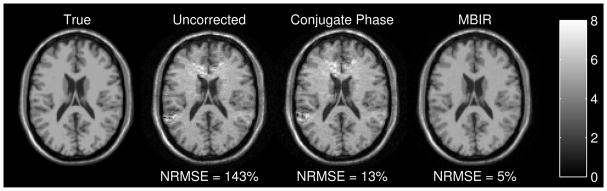
To illustrate the capabilities of model-based image reconstruction methods for MRI, we simulated k-space data for a 4-shot EPI sequence with matrix size 128 × 128 and 5 μsec sampling so the readout duration was 27.3 msec per shot. The field map ΔB₀(r⃗) appears in Fig. 2 of [35] and is based on a brain slice above the sinuses and ear canals where susceptibility effects occur. Fig. 1 shows the true image used in the simulations and images from three different reconstruction methods. The “uncorrected” reconstruction simply uses an inverse 2D FFT, with no consideration of field inhomogeneity. The field inhomogeneity causes spatial distortion in the read-out (vertical) direction (that increases NRMSE dramatically), as well as significant intensity artifacts above the ears and sinuses where the susceptibility effects are largest. The classical conjugate phase reconstruction method, which corresponds to A′y in this single-coil case, reduces the spatial distortion but the intensity artifacts persist. Applying 15 iterations of a conjugate gradient algorithm with a monotonic line search [108] [7] to the cost function (24) with the edge-preserving hyperbola (27) yields the right-most image in Fig. 1. This model-based image reconstruction method yields the lowest RMS error, but it requires about 30 × more computation than the noniterative conjugate phase method [7] because each iteration requires multiplication by A and A′. The software that generated this figure is available online [45].

Fig. 1.

Comparison of model-based image reconstruction with conventional methods.

7. SUMMARY

Image reconstruction is not a single problem in MRI, but rather is a wide family of problems depending on what physical effects are included in the signal model. The most widely studied case, particularly in the signal processing community, is when nearly all physical effects are disregarded and the system model consists solely of sampled of the Fourier transform of the object. This basic model is amenable to familiar signal processing tools and is applicable to many MR scans. But there are also many interesting applications where other physical effects are relevant, and model-based methods that account for those effects are proving to be beneficial for improving image quality. Model-based methods themselves depend on estimates of a variety of model parameters, leading to interesting problems where those parameters are determined either by separate calibration scans or by jointly estimating the image and those parameters. Despite over 3 decades of MR research, there remain challenging and intriguing problems in MR image reconstruction.

The published version of this paper (with a short bibliography) is [109].