Weighted Distance Weighted Discrimination and Its Asymptotic Properties

Abstract

While Distance Weighted Discrimination (DWD) is an appealing approach to classification in high dimensions, it was designed for balanced datasets. In the case of unequal costs, biased sampling, or unbalanced data, there are major improvements available, using appropriately weighted versions of DWD (wDWD). A major contribution of this paper is the development of optimal weighting schemes for various nonstandard classification problems. In addition, we discuss several alternative criteria and propose an adaptive weighting scheme (awDWD) and demonstrate its advantages over nonadaptive weighting schemes under some situations. The second major contribution is a theoretical study of weighted DWD. Both high-dimensional low sample-size asymptotics and Fisher consistency of DWD are studied. The performance of weighted DWD is evaluated using simulated examples and two real data examples. The theoretical results are also confirmed by simulations.

1. INTRODUCTION

The Support Vector Machine (SVM) (Vapnik 1995) is a powerful classification tool. Distance Weighted Discrimination (DWD; Marron, Todd, and Ahn 2007) is an improved classification method for high-dimensional, low sample-size (HDLSS) data settings, where the dimension d is greater than the sample size n.

In the separable case, SVM seeks the separating hyperplane maximizing the minimum of the distances, r_i, from each data point to the hyperplane. SVM has a good performance record, but it may suffer from a loss of generalizability in HDLSS settings, as noted in Marron, Todd, and Ahn (2007) (see figure 1 of that paper), due to the data-piling property. That is, the support vectors tend to pile up on top of each other at the boundaries of the margin when projected on the normal vector of the separating hyperplane. Data-piling generally leads to loss of generalizability because it is driven by small-scale noise artifacts of the particular realization of the data. DWD overcomes this issue by finding the hyperplane that minimizes the sum of the reciprocals of $r_i(min{\sum }_i{r}_i^{-1})$. DWD allows all data vectors to have influence on the separating hyperplane, instead of only the support vectors as in the SVM.

Figure 1.

High-dimensional simulated example: Projection plots of data points on the stdDWD (top) and wDWD (bottom) directions. The separating hyperplanes intersect the wDWD and stdDWD directions at the two dashed vertical lines respectively. These plots show much better performance of wDWD in this unbalanced HDLSS setting. A color version of this figure is available in the electronic version of this article.

Standard DWD (hereafter labeled as stdDWD) was originally designed for balanced data, that is, the case where the sample proportions for the two classes are similar. It has inefficient generalizability under nonstandard situations, for example, unequal costs or biased sampling (addressed for SVM by Lin, Lee, and Wahba 2002), or when the two populations are seriously unbalanced (Qiao and Liu 2009). In particular, uneven class proportions can lead to a classifier which is poor in the sense that it ignores the minority class. In this paper, we propose weighted DWD (wDWD) to incorporate class proportions as well as prior costs to improve upon standard DWD. In particular, wDWD uses the new objective function, $min{\sum }_i{w}_i{r}_i^{-1}$, where w_i is the weight for the ith training data point. Note that weighted DWD is more flexible than standard DWD by allowing flexible choices of weights. This leads to better generalizability of weighted DWD under nonstandard situations.

Figure 1 studies classification for a high-dimensional simulated example (d = 1000; this is the constant signal case in Section 3.1.1). In the projection plot of all data points on the std-DWD direction (top panel of Figure 1), the stdDWD boundary (the vertical dashed line) works well for the training set (shown as triangles). However, a potential problem is that it is too close to the positive class (on the right) because of the unbalanced class proportions. The test data (the + and × signs) in Figure 1 show that stdDWD does not have good generalizability. In the bottom panel of Figure 1, note that the wDWD boundary provides a dramatic improvement over stdDWD for the test set.

Section 2 develops optimal weighting schemes under the Overall Misclassification (OM) criterion. In strongly unbalanced cases, OM may ignore the minority class. Thus we also study several alternative criteria. To implement some of them, we propose an adaptive weighting scheme, which leads to adaptive wDWD (awDWD). In our simulation studies, we show that adaptive weighting greatly improves performance.

Section 4.1 develops asymptotic properties of wDWD in HDLSS settings. Ge and Simpson (1998) analyzed the high-dimensional asymptotics of some classifiers. Bickel and Levina (2004) and Fan and Fan (2008) also studied the impact of high dimensionality on various modifications of linear classifiers. Hall, Marron, and Neeman (2005) found conditions where there exists a geometric representation of HDLSS data, a special structure which gives insight into the classification problem. The results in Hall, Marron, and Neeman (2005) assume the entries of each data vector to be nearly independent, in a mixing conditional sense. Ahn et al. (2007) extended their work by showing that the conditions can be relaxed to asymptotic properties of the sample covariance matrix and its eigenvalues, assuming Gaussianity. A much broader set of assumptions for geometric representation has been developed in Jung and Marron (2009). In this article, our theory makes use of this broader framework.

To study asymptotic properties of wDWD, Section 4.1.2 develops a geometric representation for two data samples from two classes as in Hall, Marron, and Neeman (2005) but under milder assumptions. Using this representation, we study two aspects of the wDWD asymptotic properties as d → ∞ with n fixed. Both properties follow from the geometric representation described above. First, we study the classification error of wDWD. Second, we explore the relationship between the wDWD direction and the optimal linear classification direction. Both aspects are driven by appropriate notions of signal-to-noise ratios, defined in terms of class means and within-class variances. Furthermore, we show Fisher consistency for wDWD in Section 4.3.

As observed in many applications, in high-dimensional settings, linear classifiers such as the SVM and DWD often give better performance than their nonlinear extensions (cf. El Karoui 2007). Though nonlinear methods are known to be more flexible than linear ones, they may be more prone to overfit than linear classifiers when the simple size is small. Furthermore, the geometric representation theory in Hall, Marron, and Neeman (2005) and this article can shed some light on this issue. As discussed in Section 4.2.1, when d ≫ n, two classes of points will form two simplicies asymptotically under certain conditions, which makes linear classifiers a natural choice. In this paper, we only use linear classifiers for high-dimensional examples.

The rest of this article is organized as follows. We propose wDWD in Section 2.1, and focus on optimal weighting schemes in Section 2.2. Alternative criteria, and their implementations by adaptive weighting schemes, are developed in Section 2.3. Numerical studies are given in Section 3 based on simulated and real-data examples. In Section 4.1, we provide the geometric representation of two HDLSS data samples from two classes and study the HDLSS asymptotic properties of wDWD, followed by a simulation confirmation in Section 4.2. Fisher consistency of wDWD is provided in Section 4.3. Some concluding remarks are given in Section 5. Proofs of the theoretical results are included in the Appendix.

2. WEIGHTED DWD

Consider the problem of classifying subjects associated with the covariate vector X ∈ ⊆ ℝ^d (d predictors) into one of two classes with the class label Y ∈ {±1}. Assume the target population has an unknown probability distribution P(X, Y), and the examples are independently generated from P(X, Y). Let the marginal class probabilities of the populations be π⁺ = Pr(Y = +1) and π⁻ = Pr(Y = −1), and g⁺(x) and g⁻(x) the conditional densities of X given Y = +1 and Y = −1, respectively. Then the conditional probability of a subject belonging to Class “+1” given X = x is

$$p(\mathbf{x})=Pr(Y=+1\mid \mathbf{X}=\mathbf{x})=\frac{{\pi }^{+}{g}^{+}(\mathbf{x})}{{\pi }^{+}{g}^{+}(\mathbf{x})+{\pi }^{-}{g}^{-}(\mathbf{x})}.$$ (1)

A linear classifier φ (x) can be obtained from φ (x) = sign(f(x)), where $f({\mathbf{x}}_i)=f_i={\mathbf{x}}_i^{\prime }\mathit{\omega }+b$, ω ∈ ℝ^d, b ∈ ℝ. The data vector with covariate x_i is classified to Class “+1” if sign(f_i) = +1 and Class “−1” otherwise.

2.1 Formulation for Weighted DWD

Suppose the classification boundary is represented as a separating hyperplane, x′ω+ b = 0. The standard DWD proposed in Marron, Todd, and Ahn (2007) seeks to find a separating hyperplane minimizing a notion of inverse distance between each point and the hyperplane (details below). As mentioned in Section 1, standard DWD has some limitations for unbalanced data. For example, in Figure 1, the stdDWD classification boundary is pushed towards the positive class, mainly caused by the dramatic difference between two class proportions. Our proposed weighted DWD aims to address this problem by allowing flexible weights for data points from different classes. In particular, wDWD solves (ω, b) via the following optimization problem:

$$\underset{\mathit{\omega },b,\mathit{\xi }}{min}\sum _{i=1}^{n}W(y_i)\left(\frac{1}{r_i}+C{\xi }_i\right),$$ (2)

$$\begin{array}{l}\text{s}.\text{t}.r_i=y_i({\mathbf{x}}_i^{\prime }\mathit{\omega }+b)+{\xi }_i,{\mathit{\omega }}^{\prime }\mathit{\omega }\le 1,\\ r_i\ge 0,{\xi }_i\ge 0\text{for}i=1,2,\dots ,n.\end{array}$$ (3)

Here we assign different weights to data vectors from different classes. Note that the solution to (2) is totally determined by the ratio of W(+1) and W(−1), instead of the exact values of the two weights. The standard DWD is a special case of the weighted DWD with equal weights, W(+1) = W(−1).

To have a better understanding of (2), we first consider a simple separable setting with a choice of C where all ξ_i’s are 0. Then wDWD minimizes the total weighted inverse distances of all points to the decision boundary. When the perfect separation is not possible, (2) allows violation with amount ξ_i for training data point i.

The constant parameter C in (2) controls the penalty on the variable ξ_i, the amount of violation of classification. Note that C plays the similar role as the tuning parameter in the SVM [see equation (54) in Chen, Lin, and Schölkopf 2005; also see Vapnik 1995 and Schölkopf and Smola 2002]. This optimization problem in (2) can be reformulated as a second-order cone programming (SOCP) problem (Alizadeh and Goldfarb 2003), as shown in Marron, Todd, and Ahn (2007).

Marron, Todd, and Ahn (2007) discussed the choice of C and suggested that C should be a large constant (e.g., 100 in their work) divided by a notion of typical squared distance of the training points (e.g., squared median of the pairwise interclass Euclidean distances). The usage of typical squared distance will result in a choice of C that is essentially “scale-invariant.” From the simulation results in Section 3.1, where we tune for the best parameter C using a grid search on the tuning set, we find that the tuned C values are reasonably close to their suggestion.

It is worth noting that careful tuning needs to be done for DWD when the data are unbalanced and the signal (denoted by the distance between the two population means) is small. In particular, a small C should be avoided. For unbalanced data, a small value of C tends to yield undesired results for stdDWD, with most data vectors classified into the majority class. This is because DWD optimization avoids large values of reciprocal distances 1/r_i by sacrificing the data from the minority class. Thus C needs to be large enough to increase the misclassification cost. Weighted DWD, on the other hand, alleviates this problem in tuning since the adverse effect of the unbalanced proportion ratio on stdDWD can be greatly reduced if the weighting scheme is appropriately chosen.

2.2 Optimal Weighting Schemes

Define W(−1)I[y = −1]I[φ (x) = +1] + W(+1)I[y = +1] × I[φ(x) = −1] as the weighted 0–1 loss function corresponding to problem (2). The Bayes decision rule for this weighted 0–1 loss is given in (4) as follows

$${\phi }^{\ast }(\mathbf{x})=\text{sign}\left[p(\mathbf{x})-\frac{W(-1)}{W(-1)+W(+1)}\right].$$ (4)

In this section, we discuss two nonstandard classification situations which are commonly encountered in practice, and study the choices of optimal weights for each situation. We consider the situation of unequal costs in Section 2.2.1 and the biased sampling situation in Section 2.2.2. The optimal weights are given for both Overall Misclassification (OM) criterion and Mean Within Group Error (MWGE) criterion.

2.2.1 Unequal Costs

For some real applications, it is more proper to use different costs for different types of misclassification, say, classifying a “+1” subject as “−1” represents a more serious error than classifying a “−1” subject as “+1.” For example, failing to diagnose a potentially fatal illness may be viewed as substantially more costly than concluding that the disease is present when it is not. We use c⁺ for the false-positive cost and c⁻ for the false-negative cost. Table 1 shows these costs.

Table 1.

Unequal costs for different types of misclassification

		Classify as
		+1	−1
True population:	+1	0	c−
	−1	c+	0

Using the OM criterion, for any classifier φ, where either φ (x) = +1 or φ (x) = −1, its loss function for classifying a pair (x, y) is defined as L[φ] = c⁺I[y = −1]I[φ (x) = +1] + c⁻I[y = +1]I[φ (x) = −1]. Given x, the risk, that is, the expected loss of φ given X = x, is E[L(φ)|X = x] = c⁺[1 − p(x)]I[φ (x) = +1] + c⁻p(x)I[φ (x) = −1]. The Bayes optimal decision rule φ^* for this loss function minimizes the risk and is given by

$$\begin{array}{l}{\phi }^{\ast }(\mathbf{x})=\{\begin{array}{ll}+1\hfill & \text{if}\frac{p(\mathbf{x})}{1-p(\mathbf{x})}>\frac{c^{+}}{c^{-}}\hfill \\ -1\hfill & \text{if}\frac{p(\mathbf{x})}{1-p(\mathbf{x})}<\frac{c^{+}}{c^{-}}\hfill \end{array}\text{or}\\ {\phi }^{\ast }(\mathbf{x})=\text{sign}\left[p(\mathbf{x})-\frac{c^{+}}{c^{+}+c^{-}}\right].\end{array}$$ (5)

Comparing this to (4), by defining W(+1) = c⁻ and W(−1) = c⁺, we have the two Bayes rules identical to each other.

Our discussions so far assume the traditional OM criterion. This criterion has some limitations. For example, if the two classes are extremely unbalanced, a naive classifier, which classifies all the data vectors to the majority class, can still be regarded as a good one by this criterion. Alternatively, one can use the MWGE criterion (Qiao and Liu 2009), which considers the average of the within-class errors. Under MWGE, the modified 0–1 loss function becomes $\frac{c^{+}}{{\pi }^{-}}I[y=-1]I[\phi (\mathbf{x})=+1]+\frac{c^{-}}{{\pi }^{+}}I[y=+1]I[\phi (\mathbf{x})=-1]$. The corresponding Bayes rule φ_* is given by ${\phi }_{\ast }(\mathbf{x})=\text{sign}[p(\mathbf{x})-\frac{c^{+}/{\pi }^{-}}{c^{+}/{\pi }^{-}+c^{-}/{\pi }^{+}}]$, which implies that the optimal weighting scheme under MWGE is $W(+1)=\frac{c^{-}}{{\pi }^{+}},W(-1)=\frac{c^{+}}{{\pi }^{-}}$. Discussion on several other alternative criteria will be given in Section 2.3.

2.2.2 Biased Sampling

In some real situations, the proportions in the sample may not reflect those in the target population due to sampling bias. For example, if the two classes have very different proportions in the population, the smaller class may be oversampled, while the larger class may be undersampled in order to achieve more balance in the sample. Because we build the classification model on the sample while we predict a future data vector from the population, the discrepancy of the class proportion ratios between the sample and the population could lead to a problematic classifier. Lin, Lee, and Wahba (2002) discussed nonstandard situations for the SVM.

Assume the proportions are labeled as in Table 2. Let (X_s, Y_s) be a random pair that has the same distribution as the sample. Note that the conditional densities $g_s^{+}$ and $g_s^{-}$ are the same as g⁺ and g⁻. Then the conditional probability of a case from the sample belonging to the +1 class given that X_s = x is

Table 2.

Proportions in the target population and the sample

Proportions	+1 class	−1 class
In population	π+	π−
In sample	${\pi }_s^{+}$	${\pi }_s^{-}$

$$\begin{array}{l}{p}_s(\mathbf{x})=\text{Pr}(Y_s=+1\mid {\mathbf{X}}_s=\mathbf{x})=\frac{{\pi }_s^{+}{g}_s^{+}({\mathbf{x}}_s)}{{\pi }_s^{+}{g}_s^{+}({\mathbf{x}}_s)+{\pi }_s^{-}{g}_s^{-}({\mathbf{x}}_s)}\\ =\frac{{\pi }_s^{+}{g}^{+}(\mathbf{x})}{{\pi }_s^{+}{g}^{+}(\mathbf{x})+{\pi }_s^{-}{g}^{-}(\mathbf{x})}.\end{array}$$ (6)

Comparing (1) and (6), the relationship of the odds ratio of p(x) from the population and that of p_s(x) from the sample is

$$\frac{p(\mathbf{x})}{1-p(\mathbf{x})}=\frac{{\pi }^{+}{g}^{+}(\mathbf{x})}{{\pi }^{-}{g}^{-}(\mathbf{x})}=\frac{{\pi }_s^{+}{g}^{+}(\mathbf{x})}{{\pi }_s^{-}{g}^{-}(\mathbf{x})}\frac{{\pi }^{+}{\pi }_s^{-}}{{\pi }^{-}{\pi }_s^{+}}=\frac{p_s(\mathbf{x})}{1-p_s(\mathbf{x})}\frac{{\pi }^{+}{\pi }_s^{-}}{{\pi }^{-}{\pi }_s^{+}}.$$

Then the Bayes rule in (5) can be expressed in terms of p_s(x) as

$$\begin{array}{l}{\phi }^{\ast }(\mathbf{x})=\{\begin{array}{ll}+1\hfill & \text{if}\frac{p_s(\mathbf{x})}{1-p_s(\mathbf{x})}>\frac{c^{+}{\pi }_s^{+}{\pi }^{-}}{c^{-}{\pi }_s^{-}{\pi }^{+}}\hfill \\ -1\hfill & \text{if}\frac{p_s(\mathbf{x})}{1-p_s(\mathbf{x})}<\frac{c^{+}{\pi }_s^{+}{\pi }^{-}}{c^{-}{\pi }_s^{-}{\pi }^{+}}\hfill \end{array}\text{or}\\ {\phi }^{\ast }(\mathbf{x})=\text{sign}\left[p_s(\mathbf{x})-\frac{c^{+}{\pi }^{-}/{\pi }_s^{+}}{c^{+}{\pi }^{-}/{\pi }_s^{+}+c^{-}{\pi }^{+}/{\pi }_s^{+}}\right].\end{array}$$

Note that because the calculation of a classifier is based on the sample, instead of the population, when biased sampling exists, p_s(x) should be used in the classification rule φ(x) whereas p(x) in (5) is not useful, since p(x) ≠ p_s(x). Again, using the formulation in (4), we can see that the choice of weights becomes $W(+1)=\frac{c^{-}{\pi }^{+}}{{\pi }_s^{+}}$ and $W(-1)=\frac{c^{+}{\pi }^{-}}{{\pi }_s^{-}}$.

Now we consider the situation where the MWGE criterion is used. The Bayes rule φ_* under MWGE is then given by

$${\phi }_{\ast }(\mathbf{x})=\{\begin{array}{ll}+1\hfill & \text{if}\frac{p_s(\mathbf{x})}{1-p_s(\mathbf{x})}>\frac{c^{+}{\pi }_s^{+}}{c^{-}{\pi }_s^{-}}\hfill \\ -1\hfill & \text{if}\frac{p_s(\mathbf{x})}{1-p_s(\mathbf{x})}<\frac{c^{+}{\pi }_s^{+}}{c^{-}{\pi }_s^{-}}.\hfill \end{array}$$

Accordingly, we can define the weights $W(+1)=\frac{c^{-}}{{\pi }_s^{+}},W(-1)=\frac{c^{+}}{{\pi }_s^{-}}$.

In summary, the optimal weighting scheme is displayed in Table 3.

Table 3.

Optimal weighting schemes for biased sampling under two criteria

Criterion	OM	MWGE
W(+1)	$\frac{c^{-}{\pi }^{+}}{{\pi }_s^{+}}$	$\frac{c^{-}}{{\pi }_s^{+}}$
W(−1)	$\frac{c^{+}{\pi }^{-}}{{\pi }_s^{-}}$	$\frac{c^{+}}{{\pi }_s^{-}}$

2.3 Alternative Criteria and Adaptive Weighting Schemes

In Section 2.2, we introduced the optimal weighting schemes under the OM and MWGE criteria (Table 3). Recall that the OM criterion aims to minimize the OM cost. Qiao and Liu (2009) pointed out that this criterion may result in a high error for the minority class when the proportions are unbalanced. In addition to MWGE, they introduced Mean Square Within Group Error (MSWGE). In this paper, we also consider the criterion of Maximal Within Group Error (MaxWGE). Let e_j = E[I(φ (X) ≠ j)|Y = j] be the conditional error for class j. We reformulate the minimization of these criteria equivalently as follows:

1. OM:

   $$arg\underset{\phi }{min}{\pi }^{+}{e}_{+}+{\pi }^{-}{e}_{-}$$
2. the alternatives:

   $$arg\underset{\phi }{min}{(e_{+}^p+e_{-}^p)}^{1/p}=\{\begin{array}{ll}arg\underset{\phi }{min}\frac{1}{2}(e_{+}+e_{-})(\text{MWGE})\hfill & \text{if}p=1\hfill \\ arg\underset{\phi }{min}\sqrt{\frac{1}{2}(e_{+}^2+e_{-}^2)}(\text{MSWGE})\hfill & \text{if}p=2\hfill \\ arg\underset{\phi }{min}max(e_{+},e_{-})(\text{MaxWGE})\hfill & \text{if}p=\infty .\hfill \end{array}$$ (7)

The alternative criteria can be simply expressed as |e|_p, the L_p norm of the within-class error vector e = [e₊, e₋]^T. One important feature of the alternative criteria (MWGE, MSWGE, and MaxWGE) is that they do not require knowledge of, or even specification of, the prior proportions π⁺ and π⁻. Thus, these criteria overcome the severe limitations of OM in the unbalanced case. The three alternative criteria provide different summaries of the error. The MWGE (L₁) criterion tends to minimize the mean of the within-class errors while the MSWGE (L₂) criterion minimizes the mean and variation at the same time. The MaxWGE (L_∞) criterion controls the worse class error. Choice among these will depend on the statistical context at hand.

To demonstrate the relative performance of these criteria, we consider a one-dimensional toy example with two classes, the density curves of which are two triangles as shown in Figure 2. Note that the OM Bayes rule is sensitive to the change of the class proportions and is not desirable when the class proportions are unknown. On the other hand, the Bayes rules for the alternative criteria do not change with proportions. Different alternative criteria provide different Bayes cut-off points in this example.

Figure 2.

One-dimensional density curves for two populations and the Bayes rules for OM (dotted), MWGE (dashed), MSWGE (solid), and MaxWGE (dot-dashed) criteria when the population proportion ratio is 5 : 1, 1 : 1, or 1 : 5. Shows OM is very sensitive to class proportions, and compares the three alternative criteria. A color version of this figure is available in the electronic version of this article.

Qiao and Liu (2009) showed that there exist closed forms for the OM and MWGE Bayes rules, which lead to the optimal DWD weighting schemes introduced in Section 2.2. However, the Bayes rules under the other two alternative criteria (MSWGE and MaxWGE) do not seem to have simple closed forms. Therefore, in order to achieve better results based on the alternative criteria, we propose a two-step procedure to adaptively choose the weights using the sample within-class errors. The proposed adaptive procedure is implemented as follows:

• Step 1. Train wDWD with the MWGE optimal weights W(±1), from the right column (MWGE) in Table 3. Calculate the within-class errors ê₊ and ê₋ for the combined dataset including both training and tuning sets.

• Step 2. Update weights for class j as W(j) · exp(max(ê_j, η)), for j ∈ {+, −}, and calculate wDWD using the new weights.

We call the resulting classifier the adaptive weighted DWD (awDWD). The adaptive weighting adjustment at the second step gives a bigger weight to the class with larger error. The threshold η is added to avoid adversely decreasing the weight for the nearly perfectly classified class. We set η to 0.1 in the simulation. For the updating rule, we use an exponential form: this provides a simple weight adjustment with less potential for overweighting compared to alternative forms such as a linear form, as discussed in Qiao and Liu (2009). Simulation there also showed better performance for the exponential updating rule. To reduce the computational cost, we use a simple two-step procedure, instead of an iterative version. We will show in Section 3.1.2 that awDWD can provide additional improvements over wDWD.

3. NUMERICAL STUDY

In this section, we compare wDWD with stdDWD and several other classification methods, based on two high-dimensional simulated examples (independent predictors and correlated predictors) in Section 3.1 and two real data examples in Section 3.2.

We consider L₁ SVM (Fung and Mangasarian 2004), weighted SVM (wSVM), standard SVM (stdSVM), the L₁ penalized logistic regression (L₁ PLR; Lokhorst 1999; Shevade and Keerthi 2003) and the L₂ penalized logistic regression (L₂ PLR; Lee and Silvapulle 1988; Le Cessie and Van Houwelingen 1992). L₁ SVM and L₁ PLR use the L₁ penalty for variable selection. Weighted SVM is the weighted version of standard SVM, where we use the same weights as that of wDWD. In Section 3.1.1, we also implement awDWD to show its performance. For comparison purpose, we apply the same adaptive weights for wSVM, namely awSVM. As a remark, we note that the results for the L₁ and L₂ PLR are not available for some examples due to numerical difficulties.

3.1 Simulation

Let the dimension d = 1000, and the sample size of the training data n = 200. Assume that the data are balanced with π⁺ = π⁻ = 50% and equal costs c⁻ = c⁺, but with a biased sampling, ${\pi }_s^{+}=20\%$ and ${\pi }_s^{-}=80\%$. For simplicity, we denote w₊ and w₋ as the two weights W(+1) and W(−1). The weights for this dataset are w₊ = 2.5 and w₋ = 0.625. Note that because π⁺ = π⁻, the two weighting schemes given by Table 3 and the two Bayes rules for the two criteria (OM and MWGE) are the same.

3.1.1 Independent Predictors

We consider three settings of high-dimensional simulated data, namely constant signal, proportional signal, and sparse signal. In the constant signal setting, the variable-wise mean differences are equal for all 1000 variables, while in the sparse signal setting, only the first 10 variables have nonzero mean differences. One intermediate setting is the proportional signal where the squared mean difference for each variable is proportional to the variable index ({1,…, 1000}). The data vectors from the positive class follow d-dimensional normal distributions N_d(u₁1_d,0.75² I_d), N_d(u₂(1, 2,…, d)^T, 0.75² I_d) and ${\text{N}}_d(u_3{({\mathbf{1}}_{10}^T,0,\dots ,0)}^T,{0.75}^2{\mathbf{I}}_d)$ corresponding to the three settings, where 1_k = [1, 1,…, 1]^T is the k-dimensional vector of 1’s. The negative data vectors are generated in a similar manner except with negative means −u₁1_d, −u₂(1, 2,…, d)^T and $-u_3{({\mathbf{1}}_{10}^T,0,\dots ,0)}^T$ in the normal distributions. The positive constants u₁, u₂ and u₃ are chosen so that the Euclidean distances of the two population means for the three settings are all equal to 3. For tuning and testing purposes, we generate a tuning set with size 200 and a test set with size 600. We replicate this simulation 100 times.

From Table 4, we first compare the nonadaptive methods for the three settings. In each setting, wDWD works much better than stdDWD. In addition, wDWD works better than all the other nonadaptive methods in the constant signal and proportional signal settings. For the sparse signal case, both L₁ SVM and L₁ PLR are better than wDWD. This is expected since our current wDWD does not attempt to handle sparsity by variable selection. A potential approach to improving wDWD for the sparse signal setting is to design a classification algorithm combining wDWD and some sparse penalty such as the L₁ (Tibshirani 1996) or SCAD (Fan and Li 2001) penalty to implement variable selection.

Table 4.

Summary statistics of the simulation results for the three simulation settings: Averaged OM/MWGE, MSWGE, and MaxWGE (in percentage) over 100 runs. The numbers reported in the parentheses are the standard error

Data (%)	Constant			Proportional			Sparse
	OM/MWGE	MSWGE	MaxWGE	OM/MWGE	MSWGE	MaxWGE	OM/MWGE	MSWGE	MaxWGE
Bayes	2.22 (0.06)	2.3 (0.07)	2.71 (0.08)	2.27 (0.06)	2.34 (0.06)	2.74 (0.08)	2.26 (0.06)	2.33 (0.06)	2.73 (0.08)
wDWD	16.3 (0.68)	19.66 (1.08)	26.36 (1.61)	16.39 (0.69)	20.03 (1.08)	27.02 (1.62)	16.28 (0.68)	19.85 (1.06)	26.95 (1.57)
awDWD	13.05 (0.21)	13.76 (0.3)	16.42 (0.51)	13.04 (0.22)	13.85 (0.34)	16.81 (0.56)	13.2 (0.18)	13.97 (0.25)	17.02 (0.44)
stdDWD	45.72 (0.11)	64.65 (0.15)	91.42 (0.22)	45.69 (0.12)	64.6 (0.17)	91.36 (0.24)	45.4 (0.12)	64.19 (0.17)	90.78 (0.24)
L1 SVM	36.35 (0.32)	36.77 (0.32)	40.49 (0.46)	32.64 (0.26)	38.47 (0.56)	52.03 (0.98)	7.24 (0.13)	9.05 (0.18)	12.63 (0.25)
wSVM	21 (0.48)	28.09 (0.77)	39.52 (1.12)	20.97 (0.49)	28 (0.79)	39.38 (1.14)	21.4 (0.43)	28.73 (0.69)	40.48 (0.99)
awSVM	15.48 (0.28)	18.53 (0.47)	25.15 (0.75)	15.2 (0.31)	18.18 (0.51)	24.67 (0.8)	15.42 (0.24)	18.57 (0.41)	25.39 (0.65)
stdSVM	30.65 (0.23)	42.82 (0.32)	60.54 (0.46)	30.58 (0.22)	42.75 (0.31)	60.45 (0.44)	30.44 (0.25)	42.48 (0.36)	60.07 (0.51)
L1 PLR	39.07 (0.23)	50.85 (0.35)	71.59 (0.5)	37.94 (0.19)	49.45 (0.29)	69.62 (0.42)	6.72 (0.16)	8.81 (0.22)	12.39 (0.31)
L2 PLR	34.03 (0.22)	47.89 (0.32)	67.72 (0.45)	33.88 (0.21)	47.68 (0.3)	67.43 (0.42)	33.54 (0.24)	47.16 (0.34)	66.69 (0.48)

Table 4 also indicates that adaptive weighted DWD introduced in Section 2.3 works very well. In all three signal settings, awDWD dominates all the other methods except L₁ SVM and L₁ PLR in the sparse setting. It seems that the advantage of awDWD comes from the fact that it prevents wDWD from overweighting by incorporating both class proportions and within-class performance in the weights. Moreover, both adaptive weighting methods (awDWD and awSVM) provide further improvement on wDWD and wSVM in these examples, in terms of the MSWGE and MaxWGE criteria, in addition to the MWGE criterion.

Furthermore, we note that for the nonadaptive weighting methods, even though their OM error or MWGE seem to be fine, their MSWGE and MaxWGE are not satisfactory (e.g., wDWD for proportional signal has MaxWGE of 27.02%). Adaptive weighting methods usually lead to lower MSWGE and MaxWGE as shown in Table 4.

Among these different methods, L₁ SVM performs much better than wDWD under the sparse signal setting. To further compare them, we consider their classification directions. Figure 3 contains four projection plots which study the angles between the optimal linear classification direction and the classification direction from wDWD (in the left panel) or from L₁ SVM (in the right panel) for the constant signal setting (in the first row) or the sparse signal setting (in the second row). We can see that the angles for wDWD are comparable between the two settings, whereas the angles for L₁ SVM are larger than those for wDWD in the constant signal setting but smaller in the sparse signal setting. These angles help to explain the difference between classification performances of these two methods. Note that there is severe data-piling for L₁ SVM, as shown in the right column of Figure 3.

Figure 3.

Projection plots of all the data vectors to the two-dimensional space spanned by the Bayes optimal classification direction (Bayes drn) and the wDWD direction (in the left panels) or the L₁ SVM direction (in the right panels) for simulated data from the constant signal setting (the first row) and the sparse signal setting (the second row). A color version of this figure is available in the electronic version of this article.

3.1.2 Correlated Predictors

We modify the high-dimensional example in Section 3.1.1 by adding correlations among the predictors. Instead of assuming iid Gaussian noise, we let the noise term be an autoregressive process of order 1 [AR(1)] with marginal variance 0.75². We use several choices of the autocorrelation parameter, ρ = 0.05, 0.35, 0.65, and 0.95. Before adding the three types of variablewise mean difference (which was chosen for each case to give good separation between the classifiers, while conveying the challenge of highly correlated errors), we permute the order of the variables to break down the AR structure.

In Figure 4, we plot the OM test errors for various methods in three signal settings: constant, proportional, sparse. For all three settings, wDWD works the best when ρ = 0.05 and 0.35, except for L₁ SVM in the sparse setting. For larger ρ, such as 0.65 and 0.95, wDWD and wSVM are comparable. In the sparse setting, L₁ SVM is the best as expected. One important observation we have is that wDWD is less efficient in the highly correlated case, which was also noted by Ahn and Marron (2010), who showed more data-piling is actually better in this type of very nonstandard case.

Figure 4.

Simulation results of wDWD (solid), stdDWD (wide-dotted), wSVM (dashed), stdSVM (dotted), and L₁ SVM (dot-dashed) for three 1000-dimensional settings (constant, proportional, and sparse signals) with AR(1) noise where ρ = 0.05, 0.35, 0.65, and 0.95. (a) Constant, (b) proportional, (c) sparse. A color version of this figure is available in the electronic version of this article.

In these studies, we choose the tuning parameter C based on a search grid of 10^{{−4,−3.5,…,3.5,4}}. In all the three settings, we observe that our tuning parameter search procedure tends to choose 10^−1.5 for weighted DWD, while the recommendation of C by Marron, Todd, and Ahn (2007) turns out to be about 10^−1.05. Based on our limited experience, their recommendation appears to work reasonably well.

3.2 Real Data Examples

In this section we demonstrate the performance of various classifiers including stdDWD, wDWD, stdSVM, wSVM, and L₁ SVM on two real examples: the Human Lung Carcinomas Microarrays Dataset (lung cancer data) (Bhattacharjee et al. 2001; http://www.broad.mit.edu/mpr/lung/) and the Gisette data (http://www.nipsfsc.ecs.soton.ac.uk/).

The Lung cancer dataset has six classes: adenocarcinoma, squamous, pulmonary carcinoid, colon, normal, and small cell carcinoma, with sample sizes of 128, 21, 20, 13, 17, and 6, respectively. Liu et al. (2008) used this data as a test set to demonstrate their proposed significance analysis of clustering. We combine the last four and the first two subclasses to form the positive and negative classes respectively. We randomly split the data into training (n₊ = 100 and n₋ = 40) and test (49 + 16) sets. In order to reduce the computational cost, we first screen the variables according to the cluster indices (the within-class sums of squares about the mean, divided by the total sum of squares about the overall mean), on each variable (Dudoit, Fridlyand, and Speed 2002). The 500 variables with the lowest cluster indices are kept.

The context of the Gisette dataset is a handwritten digit recognition problem to separate the highly confusable digits “4” and “9.” The original dataset has 6000 (3000 + 3000) cases in the training set and 1000 (500 + 500) in a separate test set. We randomly choose 600 and 200 cases for each class from the original training set, and equally split them to form the new training and tuning set. There are 5000 predictors in all, where 2500 predictors have true predictive power and the rest of them are deliberately irrelevant.

For the choice of the tuning parameter C, we use 5-fold cross validation for the lung cancer data and use the tuning set for the Gisette data. For computational simplicity, we use the MWGE weighting scheme in Table 3.

We run the random splitting 100 times and report the mean of the errors for the test data, and the associated standard error, in Table 5. For both data, weighted DWD appears to be better than stdDWD, L₁ SVM and stdSVM for all types of criteria. For the lung cancer data, the weighted DWD works better than wSVM in terms of the MWGE, MSWGE, and MaxWGE, although not for the OM error. For the Gisette data, the weighted DWD works better than weighted SVM for all criteria.

Table 5.

Summary statistics of the classification errors in the lung cancer data and the Gisette data: Mean classification errors (OM, MWGE, MSWGE, and MaxWGE) for the test sets over 100 random splitting of training and test sets. The numbers reported in the parentheses are the standard error

Data (%)	Lung cancer data				Gisette data
	OM	MWGE	MSWGE	MaxWGE	OM/MWGE	MSWGE	MaxWGE
wDWD	5.11 (0.25)	4.88 (0.28)	5.66 (0.29)	7.26 (0.38)	8.29 (0.11)	10.28 (0.17)	14.31 (0.25)
stdDWD	7.49 (0.26)	10.93 (0.43)	13.21 (0.57)	18.03 (0.83)	13.98 (0.14)	19.39 (0.21)	27.41 (0.29)
L1 SVM	7.88 (0.25)	9.43 (0.39)	10.68 (0.46)	13.87 (0.66)	9.14 (0.1)	11.21 (0.14)	15.61 (0.19)
wSVM	4.91 (0.25)	5 (0.29)	5.75 (0.3)	7.4 (0.39)	8.34 (0.11)	10.53 (0.17)	14.73 (0.24)
stdSVM	6.03 (0.25)	7.64 (0.41)	8.94 (0.51)	11.78 (0.72)	9.4 (0.12)	12.53 (0.18)	17.68 (0.26)

4. THEORETICAL RESULTS

In this section, we study several theoretical aspects of wDWD. HDLSS asymptotics are discussed in Section 4.1, followed by simulation validation in Section 4.2. Fisher consistency for wDWD is discussed in Section 4.3.

4.1 HDLSS Asymptotics for Weighted DWD

In this section, we explore the HDLSS asymptotics of wDWD. The geometric representation by Hall, Marron, and Neeman (2005) implies that the pairwise distances between the n⁺ (n⁻, resp.) data points from the same “+1” (“−1,” resp.) class are approximately constant as d → ∞ with n⁺ (n⁻, resp.) fixed. As a consequence, each sample from one class (of size n⁺ or n⁻) can be viewed as a regular (n⁺ − 1) ((n⁻ − 1), resp.)-simplex. The results in Hall, Marron, and Neeman (2005) assume that when the entries of each data vector are viewed as a time series with the time index d, these entries must satisfy a ρ-mixing condition. Ahn et al. (2007) relaxed this condition. We will first improve the theory of Ahn et al. (2007) using a much broader set of assumptions. In addition, we geometrically represent two data samples under the new assumption.

4.1.1 Geometric Representation for One Sample Under Mild Conditions

First consider the positive class ${\mathcal{X}}^{+}(d)=\{{\mathbf{x}}_1^{+}(d),{\mathbf{x}}_2^{+}(d),\dots ,{\mathbf{x}}_{n^{+}}^{+}(d)\}$ with n⁺ data vectors and d variables. We have a d × n⁺ data matrix ${\mathbf{X}}_d^{+}=[{\mathbf{x}}_1^2,{\mathbf{x}}_2^{+},\dots ,{\mathbf{x}}_{n^{+}}^{+}]$ with d > n⁺, where ${\mathbf{x}}_j^{+}={(x_{1j}^{+},x_{2j}^{+},\dots ,x_{dj}^{+})}^T\in {\mathbb{R}}^d$, j = 1, 2,…, n⁺, are independent and identically distributed from a d-dimensional multivariate distribution with positive definite covariance matrix ${\mathbf{\sum }}_d^{+}$. Without loss of generality, we assume that each ${\mathbf{x}}_j^{+}$ has zero mean. Denote the d × d sample covariance matrix of ${\mathbf{X}}_d^{+}$ as ${\mathbf{S}}_d^{+}=n_{+}^{-1}{\mathbf{X}}_d^{+}{{\mathbf{X}}_d^{+}}^T$. The eigenvalue decomposition of ${\mathbf{\sum }}_d^{+}$ is ${\mathbf{\sum }}_d^{+}={\mathbf{V}}_d^{+}{\mathbf{\Lambda }}_d^{+}{{\mathbf{V}}_d^{+}}^T$, where ${\mathbf{\Lambda }}_d^{+}=\text{diag}\{{\lambda }_1^{+},\dots ,{\lambda }_d^{+}\}$ is the diagonal matrix of eigenvalues. Furthermore, we define the average of the eigenvalues ${\sigma }_d^2=\frac{1}{d}{\sum }_{i=1}^d{\lambda }_{i,d}^{+}$. We can write ${\mathbf{X}}_d^{+}={\mathbf{V}}_d^{+}{{\mathbf{\Lambda }}_d^{+}}^{1/2}{\mathbf{Z}}_d^{+}$, where ${\mathbf{Z}}_d^{+}={{\mathbf{\Lambda }}_d^{+}}^{-1/2}{{\mathbf{V}}_d^{+}}^T{\mathbf{X}}_d^{+}$ is a d × n⁺ random data matrix from a distribution with zero mean and identity covariance matrix. The n⁺ × n⁺ dual sample covariance matrix is defined as ${\mathbf{S}}_{D,d}^{+}=d^{-1}{{\mathbf{X}}_d^{+}}^T{\mathbf{X}}_d^{+}$, reversing the roles of rows and columns in the data matrix. Denote the n⁺ × n⁺ matrix ${\mathbf{W}}_{i,d}^{+}$ as ${({\mathbf{Z}}_{i,d}^2)}^T{\mathbf{Z}}_{i,d}^{+}$, where ${\mathbf{Z}}_{i,d}^{+}$, i = 1, 2,…, d, are the row vectors of ${\mathbf{Z}}_d^{+}$. It was noted in Ahn et al. (2007) that $d{\mathbf{S}}_{D,d}^{+}$ has a simple Wishart representation,

$$d{\mathbf{S}}_{D,d}^{+}=\sum _{i=1}^d{\lambda }_{i,d}^{+}{\mathbf{W}}_{i,d}^{+}.$$ (8)

Note that if ${\mathbf{X}}_d^{+}$ is Gaussian, then each ${\mathbf{W}}_{i,d}^{+}$ follows the Wishart distribution 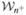(1, I_n+) independently.

Assumption 1

For a fixed n⁺, consider a sequence of random data matrices ${\mathbf{X}}_1^{+}$,…, ${\mathbf{X}}_d^{+}$,…, indexed by the number of rows d. Assume each ${\mathbf{X}}_d^{+}$ comes from a multivariate distribution with dimension d. Let ${\lambda }_{1,d}^{+}\ge \cdots \ge {\lambda }_{d,d}^{+}$ be the eigenvalues of the covariance matrix ${\mathbf{\sum }}_d^{+}$, and let ${\mathbf{S}}_{D,d}^{+}$ be the corresponding n⁺ × n⁺ dual sample covariance matrix. We assume the following,

1. Each column of ${\mathbf{X}}_d^{+}$ has zero mean and positive definite covariance matrix ${\mathbf{\sum }}_d^{+}$.

2. The fourth moment of each entry of each column is uniformly bounded by M⁺ > 0 and also the representation in (8) holds for each ${\mathbf{X}}_d^{+}$.

3. Entries of ${\mathbf{Z}}_d^{+}={{\mathbf{\sum }}_d^{+}}^{-1/2}{\mathbf{X}}_d^{+}={{\mathbf{\Lambda }}_d^{+}}^{-1/2}{{\mathbf{V}}_d^{+}}^T{\mathbf{X}}_d^{+}$ (as defined above) are independent.

4. The eigenvalues of ${\mathbf{\sum }}_d^{+}$ are sufficiently diffused, in the sense that

   $${\epsilon }_d^{+}=\frac{{\sum }_{i=1}^d{({\lambda }_{i,d}^{+})}^2}{{({\sum }_{i=1}^d{\lambda }_{i,d}^{+})}^2}\to 0\text{as}d\to \infty .$$ (9)

5. The sum of the eigenvalues of ${\mathbf{\sum }}_d^{+}$ is the same order as d, in the sense that ${\sigma }_d^2=O(1)$ and $1/{\sigma }_d^2=O(1)$.

Condition (9) can be viewed as a measure of the sphericity of the data matrix. This restricts the underlying distribution to be not too close to the extreme case of a few dominant eigenvalues. The spherical Gaussian is an example which has perfect sphericity, that is, ${\epsilon }_d=\frac{1}{d}$. As mentioned in Ahn et al. (2007), the ρ-mixing condition in Hall, Marron, and Neeman (2005) is also a special case that satisfies Assumption 1.

One main result of Ahn et al. (2007) is that under their weaker version of Assumption 1 [in particular, condition (iii) did not appear there], the sample eigenvalues behave as if they follow an identity covariance matrix, in the sense that $\frac{1}{{\sigma }^2}{\mathbf{S}}_{D,d}\to {\mathbf{I}}_n$, as d → ∞. Based on this theory they claim that the pairwise squared distance between the data vectors from (d), rescaled by $\frac{1}{d}$, is approximately constant. However, John Kent pointed out that an additional assumption is needed, using a counter-example. Kent’s example is a mixture of normals, which is N_d(0, I_d) with probability 1/2 and N_d(0, 10I_d) also with probability 1/2. This example satisfies conditions (i), (ii), (iv), and (v). But the pairwise distances have a nondegenerate discrete limiting distribution.

The theory in Ahn et al. (2007) goes through if additional assumptions are added. A simple strengthening is to assume Gaussianity. Our (iii) is weaker than Gaussianity, assuming only a set of underlying independent entries, ${\mathbf{Z}}_d^{+}$. We restate the theorem as follows.

Theorem 1

Under Assumption 1, the dual sample covariance matrix, rescaled by ${\sigma }_d^2$, becomes approximately the identity matrix I_n, as d → ∞.

$$\frac{1}{{\sigma }_d^2}{\mathbf{S}}_{D,d}\to {\mathbf{I}}_n\text{in}\text{probability},\text{as}d\to \infty .$$

A direct consequence of Theorem 1 is that the pairwise squared distance rescaled by d⁻¹ is approximately constant as d → ∞.

Corollary 2

Under Assumption 1, the pairwise distances between the n⁺ data vectors are approximately the same. In particular, scaled by $1/d{\sigma }_d^2$, the squared distance satisfies

$$\frac{1}{d{\sigma }_d^2}{\left|\right|{\mathbf{x}}_k^{+}-{\mathbf{x}}_l^{+}\left|\right|}^2\to 2\text{in}\text{probability},\text{as}d\to \infty .$$

Thus these n⁺ data vectors form a regular (n⁺ − 1)-simplex in ℝ^d.

4.1.2 Geometric Representation for Two Samples

The n⁻-point sample ${\mathcal{X}}^{-}(d)=\{{\mathbf{x}}_1^{-}(d),{\mathbf{x}}_2^{-}(d),\dots ,{\mathbf{x}}_{n^{-}}^{-}(d)\}$ is defined similarly to (d). In particular, the average of the eigenvalues is defined as ${\tau }_d^2=\frac{1}{d}{\sum }_{i=1}^d{\lambda }_{i,d}^{-}$. When the eigenvalues for the negative class data matrix are sufficiently diffused, that is, ${\epsilon }_d^{-}=\frac{{\sum }_{i=1}^d{({\lambda }_{i,d}^{-})}^2}{{({\sum }_{i=1}^d{\lambda }_{i,d}^{-})}^2}\to 0$ as d → ∞, in the same manner, the pair-wise squared distances between the n⁻ data vectors are approximately the same,

$$\frac{1}{d{\tau }_d^2}{\left|\right|{\mathbf{x}}_k^{-}-{\mathbf{x}}_l^{-}\left|\right|}^2\to 2,\text{as}d\to \infty .$$ (10)

Now we generalize the two classes to allow different means. We assume that the squared distance between the population means, rescaled by 1/d, is a constant μ²,

$$\frac{1}{d}{\left|\right|E({\mathbf{x}}^{+})-E({\mathbf{x}}^{-})\left|\right|}^2\to {\mu }^2.$$ (11)

For convenience, we assume that the limiting average eigenvalues exist,

$${\sigma }_d^2\to {\sigma }^2\text{and}{\tau }_d^2\to {\tau }^2\text{as}d\to \infty .$$ (12)

Theorem 3

Assume two independent data samples (d) and (d) satisfy Assumption 1, (11), and (12). Then the squared distance between a data vector in (d) and a data vector in (d), divided by d, converges in probability to l²:= σ² + τ² + μ², that is,

$$Pr\left[\left|\frac{1}{d}{\left|\right|{\mathbf{x}}_k^{+}-{\mathbf{x}}_l^{-}\left|\right|}^2-l^2\right|\ge \epsilon \right]\to 0,\text{as}d\to \infty ,\text{for}\text{any}\epsilon >0.$$

Theorem 3 says that, if both samples satisfy Assumption 1, then the pairwise rescaled distance between all pairs of data vectors from the two samples is approximately constant. Theorem 3 gives the interclass distances in the d-limit, while Corollary 2 and (10) give the intraclass distances. From these results, one can organize the linear discrimination possibilities as follows.

1. If μ² is so large that σ² + τ² + μ² is significantly greater than 2σ² and 2τ², then the two simplices are far from each other, and thus as discussed in Section 4.1.3 and Section 4.1.4, there is a natural separating hyperplane, that will give good classification, that is, good generalizability.

2. If μ² is so small that σ² + τ² + μ² < 2 max(σ², τ²), then it is much harder than above to classify by linear discrimination as shown in Section 4.1.3 and the generalizability is weak as discussed in Section 4.1.4.

4.1.3 Asymptotic Properties of the wDWD Intercept

In this section, we illustrate the asymptotic properties of the wDWD intercept in the HDLSS data settings. Let O⁺ be the centroid of the (n⁺ − 1)-simplex (d) and O⁻ the centroid of the (n⁻ − 1)-simplex (d). As noted in Hall, Marron, and Neeman (2005), an important corollary of Corollary 2 and Theorem 3 is:

Corollary 4

In the d-asymptotic limit, the DWD hyperplane is orthogonal to the line O⁺O⁻ joining the two centroids.

Let P be any point on the interval O⁺O⁻. In Figure 5, let α and β be the distances from P to the centroids. P lies on the weighted DWD hyperplane only when

Figure 5.

Simplex centroids O⁺, O⁻ and the candidate DWD cut-off point P.

$$\frac{\alpha }{\beta }={\left(\frac{w_{+}{n}^{+}}{w_{-}{n}^{-}}\right)}^{1/2}.$$ (13)

This determines the DWD hyperplane, which is orthogonal to the line O⁺O⁻ and passes through the point P which satisfies condition (13). The larger $\frac{w_{+}{n}^{+}}{w_{-}{n}^{-}}$ is, the closer the cut-off point P will be to O⁻, and thus it will be more likely that a new data point will be classified to . Theorem 5 shows the conditions under which a future data point is always correctly classified or misclassified.

Theorem 5

Assume that ${\sigma }^2/[n_{+}^{3/2}{w}_{+}^{1/2}]\ge {\tau }^2/[n_{-}^{3/2}{w}_{-}^{1/2}]$; if needed, interchange and to satisfy this assumption.

• For a new data point ${\mathbf{x}}_0^{+}$ from the -population,

  1. If μ² > (n⁻w₋/n⁺w₊)^1/2σ²/n⁺ − τ²/n⁻, then

     $$Pr({\mathbf{x}}_0^{+}\text{is}\text{correctly}\text{classified}\text{by}\text{weighted}\text{DWD})\to 1,$$

     as d → ∞.

  2. If μ² < (n⁻w₋/n⁺w₊)^1/2σ²/n⁺ − τ²/n⁻, then

     $$Pr({\mathbf{x}}_0^{+}\text{is}\text{wrongly}\text{classified}\text{by}\text{weighted}\text{DWD})\to 1,$$

     as d → ∞.

• For a new data point ${\mathbf{x}}_0^{-}$ from the -population, for any μ > 0,

  $$Pr({\mathbf{x}}_0^{-}\text{is}\text{correctly}\text{classified}\text{by}\text{weighted}\text{DWD})\to 1,$$

  as d → ∞.

An intuitive interpretation of Theorem 5 is that the intraclass average variances σ² and τ², the sizes n⁺ and n⁻ and the interclass squared distances μ², jointly control the ability to classify the new data point from and . Large interclass distance will lead to better accuracy in general. When one class has a smaller intraclass variance or a larger sample size, standard DWD will give a more accurate classification rule. This comes at a cost of worse classification performance for the other class. Weighted DWD helps to offset the effect of unbalanced sample size to some extent.

Theorem 5 is the weighted extension to theorem 3 in Hall, Marron, and Neeman (2005). Compared to its original version, Theorem 5 extends DWD by the introduction of w₊ and w₋ into the assumptions. For example, in the case of unbalanced data with equal cost and unbiased sampling, for relatively small n⁻ and large n⁺, we have the weight ratio $\frac{w^{+}}{w^{-}}=\frac{n^{-}}{n^{+}}$ under MWGE. In Theorem 5, the main condition in Hall, Marron, and Neeman (2005), ${\sigma }^2/n_{+}^{3/2}\ge {\tau }^2/n_{-}^{3/2}$, is relaxed to σ²/n⁺ = τ²/n⁻. This condition is more easily satisfied so that, as shown in Theorem 5, one can classify a new data point from correctly by weighted DWD in contrast to standard DWD. However, the condition in Hall, Marron, and Neeman (2005), under which the data point from is correctly classified, μ² > (n⁻/n⁺)^1/2σ²/n⁺ − τ²/n⁻, becomes μ² > σ²/n⁺ − τ²/n⁻ now, which is not as easily attained as before.

To summarize, for standard DWD in the asymptotic setting of Theorem 5, misclassifying some future points is unavoidable, because this is totally controlled by the relative magnitudes of μ², n⁺, n⁻, σ², τ², which are all aspects of the underlying distributions. However for weighted DWD, we can adaptively choose the weights to adjust those relevant quantities, which can reduce the misclassified region and lead to better classification accuracy. In the ideal (but unrealistic) case, where the values μ², n⁺, n⁻, σ², τ² are known in advance, we can choose the weights intelligently such that the scenario 2. in Theorem 5 can be avoided as much as possible.

4.1.4 Asymptotic Properties of the wDWD Direction

Theorem 5 gives a sufficient condition under which new data are correctly classified. However, it holds under the assumption that the intraclass average variances σ² and τ², that is, the noise levels, are not very large. When the noise level is not negligible with respect to the signal (the interclass distance μ²), Theorem 5 does not indicate the performance of wDWD. Instead, in this case, the relationship between the wDWD direction (the vector orthogonal to the separating hyperplane) and the direction of the line joining the two population means is more useful. If the angle between the above two directions is close to 0, the classification can be generalizable, in the sense of performing well for new data.

Theorem 6

Assume that (d) and (d) satisfy Assumption 1. As d → ∞, with probability converging to 1, the angle between the direction joining the two population means and the direction joining the centroids of the two simplices becomes $\theta ={cos}^{-1}{(\frac{{\mu }^2}{{\mu }^2+{\sigma }^2/n^{+}+{\tau }^2/n^{-}})}^{1/2}$.

Recall from Corollary 4, the weighted DWD direction coincides with the direction which joins the two centroids d-asymptotically. The asymptotic property of the angle θ between the wDWD direction and the optimal linear classification direction is then implied by Theorem 6. In particular,

$$\theta \approx \{\begin{array}{ll}90°\hfill & \text{if}{\mu }^2\ll \frac{{\sigma }^2}{n^{+}}+\frac{{\tau }^2}{n^{-}}\hfill \\ 0°\hfill & \text{if}\frac{{\sigma }^2}{n^{+}}+\frac{{\tau }^2}{n^{-}}\ll {\mu }^2,\hfill \end{array}$$ (14)

in the sense that lim_{γ→ 0} θ = 90° and lim_{γ→ ∞} θ = 0° for $\gamma ={\mu }^2/(\frac{{\sigma }^2}{n^{+}}+\frac{{\tau }^2}{n^{-}})$. Theorem 6 and (14) imply that wDWD tends to give the optimal linear classification direction when the signal level μ² is much higher than the noise levels σ² and τ², and on the other hand tends to give a direction which is orthogonal to the desired direction, that is, is strongly inconsistent, when the noise is significantly greater than the signal. The second implication of Theorem 6 is that the angle goes to 0 if n⁺ and n⁻ → ∞, giving another notion of consistency of wDWD from the d-asymptotic point of view.

4.2 Simulation Confirmation

In this section, we verify the asymptotic results for weighted DWD by simulations. To verify Theorem 1, Corollary 2, and Theorem 3, which provide the interclass and intraclass pairwise distances, in Section 4.2.1, we calculate the corresponding distances for the high-dimensional simulated example discussed in Section 3.1.1. To verify Theorem 5 and Theorem 6, we perform a new simulation study in Section 4.2.2.

4.2.1 Pairwise Distances

We calculate the pairwise squared distances (scaled by d⁻¹) within each class and between classes for the constant signal simulation described in Section 3.1.1. Table 6 shows the summary statistics. In Table 6, note that all three of the mean rescaled squared distances fall reasonably close to the theoretical predictions. Moreover, the small standard deviation of the observed distance is consistent with Theorem 1 and Theorem 3, which imply that the distance should be constant in the large d-limit.

Table 6.

Summary statistics for the rescaled pairwise squared distances. The standard deviation of the distance is small relative to the mean

	# of pairs	Mean	SD	Theoretical	Formula
Within positive class	72,010	1.1241	0.0489	1.1250	2σ2
Within negative class	191,890	1.1242	0.0491	1.1250	2τ2
Between classes	235,600	1.1339	0.0491	1.1340	σ2 + τ2 + μ2

4.2.2 DWD Classification Performance

To verify Theorem 5 and Theorem 6, we consider three simulated examples similar to the constant signal setting in Section 3.1.1. Here we fix the same noise level (σ² = τ² = 1) and the sample sizes (n⁺ = 60, n⁻ = 150), but assign different signal levels (μ²) over the three examples. With the assumption of equal costs and equal class proportions, the optimal weights from Table 3 are $w_{+}=\frac{1}{n^{+}}$ and $w_{-}=\frac{1}{n^{-}}$. Standard DWD is a special case of weighted DWD with w₊ = w₋ = 1. Theorem 5 gives a threshold for μ²,

$${(n^{-}{w}_{-}/n^{+}{w}_{+})}^{1/2}{\sigma }^2/n^{+}-{\tau }^2/n^{-}.$$ (15)

According to the theorem, standard/weighted DWD correctly classifies ${\mathbf{x}}_0^{+}$ with probability 1 if μ² is greater than the threshold. Here, the value of (15) for standard DWD is (n⁻/n⁺)^1/2σ²/n⁺ − τ²/n⁻ = 0.020, and that for weighted DWD it is σ²/n⁺ − τ²/n⁻ = 0.010. We explore the possible cases, by choosing:

• μ² = 0.005, where neither correct classification probability takes to 1

• μ² = 0.011, where only the wDWD correct classification probability takes to 1

• μ² = 0.059, where both wDWD and stdDWD correct classification probabilities take to 1.

In Table 7, note that when the signal is weak enough (μ² = 0.005), both weighted and standard DWD fail to classify future data vectors from the population. However, when the signal is strong enough (μ² = 0.059), both methods succeed. If the data have intermediate signal strength (μ² = 0.011), then weighted DWD works reasonably well (error < 30%) while the standard DWD does not (error > 60%). These observations are consistent with Theorem 5. Secondly, we find that the observed angles in the simulation for both weighted and standard DWD are in line with the theoretical angles based on the d-asymptotic results given by Theorem 6. Note that the angle between the optimal direction and the weighted DWD direction will often be closer to the theoretical angle (from Theorem 6), than that of the standard DWD.

Table 7.

Simulation results for theorem verification: The top rows investigate Theorem 5; they display the average misclassification errors for both classes over 100 simulations and the standard error (in parentheses). The bottom rows validate Theorem 6, by showing that the theoretical angle between the DWD direction and the optimal classification direction given by the theorem, and the average observed angles for both wDWD and stdDWD together with the standard error (in parentheses)

	Case 1 weak		Case 2 intermediate		Case 3 strong
	μ2 = 0.005 < 0.01		0.01 < μ2 = 0.011 < 0.02		μ2 = 0.059 > 0.02
	Class +	Class −	Class +	Class −	Class +	Class −
Error wDWD	43.91 (1.714)	33.76 (1.674)	29.41 (1.368)	25.3 (1.244)	2.4 (0.148)	0.71 (0.078)
Error stdDWD	78.04 (0.381)	8.63 (0.233)	67.06 (0.432)	4.67 (0.148)	13.17 (0.291)	0.05 (0.015)
Theoretical angle	65.16		55.43		32.15
Obs. angle wDWD	65.41 (0.208)		55.59 (0.189)		32.56 (0.139)
Obs. angle stdDWD	66.86 (0.193)		57.5 (0.189)		34.06 (0.127)

4.3 Fisher Consistency of DWD

This section studies Fisher consistency of weighted DWD. As noted in Bartlett, Jordan, and McAuliffe (2006), many of the classification algorithms developed in the machine learning literature can be viewed as minimum contrast methods that minimize a convex surrogate of the 0–1 loss function. The weighted DWD (2) minimizes a surrogate of the corresponding weighted 0–1 loss function, W(−1)I[y = −1]I[φ(x) = +1] + W(+1) × I[y = +1]I[φ(x) = −1]. We first demonstrate the convex surrogate loss function for DWD (Section 2.1). This is similar to the hinge loss function for SVM (Wahba 1999) through an equivalent formulation of the DWD optimization. A binary classifier with loss V(yf (x)) is Fisher consistent if the minimizer of E[W(Y_s)V(Y_Sf(X_s))] has the same sign as $p_s(\mathbf{x})-\frac{W(-1)}{W(-1)+W(+1)}$. Liu (2007) studied Fisher consistency for multi-categorical SVM and its various extensions. To our knowledge, Fisher consistency of DWD has not been studied.

4.3.1 Equivalent Formulation

For each i = 1, …, n, we define $f_i=f({\mathbf{x}}_i\mid \mathit{\omega },b)={\mathbf{x}}_i^{\prime }\mathit{\omega }+b$. The weighted DWD optimization problem (2) can be shown to be equivalent to the following problem

$$\underset{\{\mathit{\omega },b:{\mathit{\omega }}^{\prime }\mathit{\omega }\le 1\}}{min}\underset{\mathit{\xi }\ge 0}{min}\sum _{i=1}^{n}W(y_i)\left(\frac{1}{y_i{f}_i+{\xi }_i}+C{\xi }_i\right).$$ (16)

It can be shown that the optimal solution for the inside optimization part of (16) is given by ${\mathit{\xi }}^{\ast }={({\xi }_1^{\ast },\dots ,{\xi }_n^{\ast })}^T$, where ${\xi }_1^{\ast }=\frac{1}{\sqrt{C}}-y_i{f}_i$ if $y_i{f}_i\le \frac{1}{\sqrt{C}};{\xi }_i^{\ast }=0$ otherwise. Then the DWD optimization problem amounts to

$$\underset{\mathit{\omega },b}{min}\sum _{i=1}^{n}W(y_i)\left([2\sqrt{C}-C·y_i{f}_i]I\left[y_i{f}_i\le \frac{1}{\sqrt{C}}\right]+\frac{1}{y_i{f}_i}I\left[y_i{f}_i>\frac{1}{\sqrt{C}}\right]\right),\text{s}.\text{t}.{\mathit{\omega }}^{\prime }\mathit{\omega }\le 1.$$

If we define the DWD loss function as

$$V(yf)=\{\begin{array}{ll}2\sqrt{C}-C·yf\hfill & \text{if}yf\le \frac{1}{\sqrt{C}}\hfill \\ \frac{1}{yf}\hfill & \text{otherwise},\hfill \end{array}$$ (17)

then the weighted DWD optimization is ${min}_{\mathit{\omega },b}{\sum }_{i=1}^{n}W(y_i)\times V(y_i{f}_i(\mathit{\omega },b))$, s.t. ω′ω ≤ 1. This representation provides some insights into DWD as a modification of the hinge loss of SVM, H(yf) = (1 − yf)₊. Actually, the first expression for the DWD loss is similar to the hinge loss, while the second expression $\frac{1}{yf}$ is positive, in contrast to being 0 for the hinge loss when yf > 1. The statistical insight is that all the points correctly classified by $\text{DWD}(yf>\frac{1}{\sqrt{C}})$ have some impact on the optimization (i.e., $\frac{1}{yf}>0$), while those for SVM (yf > 1) do not.

4.3.2 Fisher Consistency

For any classification function f, the expected DWD loss, that is, the risk, is R(f) = E[W(Y_s) × V(Y_sf (X_s))]. Fisher consistency of the classifier f can be proved by showing that the sign of the global minimizer of the unconditional risk arg min_f R(f), is equal to the Bayes optimal decision rule φ^* given in (4). Theorem 7 proves this relationship and thus shows Fisher consistency of weighted DWD under the OM criterion.

Theorem 7

Let f^* be the global minimizer of E[W(Y_s) × V(Y_sf (X_s))], where V(·) is the DWD loss function given in (17). Then sign[f ^*(x)] = φ^*(x), where φ^*(x) is the Bayes decision rule under the OM criterion given in (4), or equivalently, $\text{sign}[f^{\ast }(\mathbf{x})]=\text{sign}[p_s(\mathbf{x})-\frac{W(-1)}{W(+1)+W(-1)}]$.

Similarly, under the MWGE criterion, with the weighting scheme W(·) given by Table 3, weighted DWD can also be shown to be Fisher consistent.

5. CONCLUSION

In this article, we have proposed weighted DWD to improve standard DWD for unbalanced data and various nonstandard situations. We have made the following contributions. First, we have provided the optimal weighting schemes for several nonstandard situations, using one of the two criteria, OM error and MWGE. Second, we propose an adaptive weighting scheme to improve one of the two alternative criteria, MSWGE and MaxWGE. Third, we represent datasets from two classes geometrically in HDLSS settings. Fourth, we develop the HDLSS asymptotic properties of weighted DWD. Lastly, we show Fisher consistency for wDWD. Our numerical studies demonstrate the effectiveness of weighted DWD and verify the asymptotic results.

The results on the tuning parameter C from our simulations suggest that the recommendation for the tuning parameter C = 100/(dt)² proposed by Marron, Todd, and Ahn (2007), which was originally designed for balanced data, also works well in unbalanced and nonstandard situations as long as we use weighted DWD instead of standard DWD. Thus their recommendation of tuning parameter C can be used for weighted DWD as a simple alternative of cross validation.

The simulation results show that in the sparse signal setting, our current version of weighted DWD does not work as well as some sparse methods, for example, L₁ SVM. One possible future research direction is to study weighted DWD with builtin sparse penalty for variable selection.

APPENDIX

For Theorem 1, Corollary 2, and Theorem 5, we only outline the main steps of the proofs. Readers can refer to Qiao et al. (2008) for technical details.

Proof of Theorem 1

Let ${\mathbf{Z}}_d^{+}={{\mathbf{\Lambda }}_d^{+}}^{-1/2}{{\mathbf{V}}_d^{+}}^T{\mathbf{X}}_d^{+}=[{\mathbf{z}}_1^{+},\dots ,{\mathbf{z}}_{n^{+}}^{+}]$, where ${\mathbf{z}}_k^{+}={[z_{1k}^{+},\dots ,z_{dk}^{+}]}^T$ is the kth column. Each column of ${\mathbf{Z}}_d^{+}$ is independently and identically distributed as an underlying d-dimensional distribution with identity covariance matrix I_d, where ${\mathbf{\Lambda }}_d^{+}$ and ${\mathbf{V}}_d^{+}$ form the eigenvalue-decomposition of the covariance matrix, ${\mathbf{\sum }}_d^{+}={\mathbf{V}}_d^{+}\times {\mathbf{\Lambda }}_d^{+}{{\mathbf{V}}_d^{+}}^T$. Define the relative eigenvalue by ${\stackrel{\sim }{\lambda }}_{i,d}^{+}={\lambda }_{i,d}^{+}/({\sum }_{i=1}^d{\lambda }_{i,d}^{+})$. The sphericity condition in Assumption 1 is equivalent to ${\sum }_{i=1}^d{({\stackrel{\sim }{\lambda }}_{i,d}^{+})}^2\to 0$, as d → ∞. Note that relative eigenvalues sum up to 1, that is, ${\sum }_{i=1}^d{\stackrel{\sim }{\lambda }}_{i,d}^{+}=1$.

From the representation in (8), $\frac{1}{{\sigma }_d^2}{\mathbf{S}}_{D,d}^{+}=\frac{1}{{\sum }_{i=1}^d{\lambda }_{i,d}^{+}}{\sum }_{i=1}^d({\lambda }_{i,d}^{+}\times {\mathbf{W}}_{i,d}^{+})={\sum }_{i=1}^d({\stackrel{\sim }{\lambda }}_{i,d}^{+}{\mathbf{W}}_{i,d}^{+})$. The kth diagonal element of $\frac{1}{{\sigma }^2}{\mathbf{S}}_{D,d}^{+}$ can be expressed as ${\sum }_{i=1}^d{\stackrel{\sim }{\lambda }}_{i,d}^{+}{(z_{ik}^{+})}^2$, where the $z_{ik}^{+}$’s (i = 1, …, d) are independent distributed with mean 0 and unit variance. And the (k, l)th off-diagonal element of $\frac{1}{{\sigma }_d^2}{\mathbf{S}}_{D,d}^{+}$ can be expressed as ${\sum }_{i=1}^d{\stackrel{\sim }{\lambda }}_{i,d}^{+}(z_{ik}^{+}{z}_{il}^{+})$, where all $z_{ik}^{+}$’s and $z_{il}^{+}$’s are independent (i = 1, …, d), with mean 0 and unit variance.

Chebyshev’s inequality is then used twice (one for the diagonal elements, one for the off-diagonal elements) to show that each element of $\frac{1}{{\sigma }_d^2}{\mathbf{S}}_{D,d}^{+}$ converges to the counterpart of the identity matrix I_n in probability as d → ∞.

Note that when each column of ${\mathbf{X}}_d^{+}$ follows the multivariate Gaussian distribution, so does ${\mathbf{z}}_k^{+}$, the kth column of ${\mathbf{Z}}_d^{+}$. Hence, with identity covariance matrix of ${\mathbf{z}}_k^{+}$, its entries, $z_{ik}^{+}$ (i = 1, …, d), are independent, which satisfies the independence condition.

Proof of Corollary 2

Let ${\mathbf{x}}_j^{+}={(x_{1j}^{+},\dots ,x_{dj}^{+})}^T$, j = 1, …, n⁺, be the jth column of the data matrix X⁺. Let ${\mathbf{x}}_j^{-}={(x_{1j}^{-},\dots ,x_{dj}^{-})}^T$, j = 1, …, n⁻, be the jth column of the data matrix X⁻. The squared distance between ${\mathbf{x}}_k^{+}$ and ${\mathbf{x}}_l^{+}$, rescaled by ${(d{\sigma }_d^2)}^{-1}$ is $\frac{1}{d{\sigma }_d^2}{\left|\right|{\mathbf{x}}_k^{+}-{\mathbf{x}}_l^{+}\left|\right|}^2=\frac{1}{d{\sigma }_d^2}{\sum }_{i=1}^d{(x_{ik}^{+}-x_{il}^{+})}^2=\frac{1}{d{\sigma }_d^2}{\sum }_{i=1}^d{(x_{ik}^{+})}^2+\frac{1}{d{\sigma }_d^2}{\sum }_{i=1}^d{(x_{il}^{+})}^2-\frac{2}{d{\sigma }_d^2}{\sum }_{i=1}^d{x}_{ik}{x}_{il}$. The first and second terms on the right-hand side are the kth and lth diagonal elements of $\frac{1}{{\sigma }_d^2}{\mathbf{S}}_{D,d}^{+}$, respectively, which were proved to converge to 1 in probability as d → ∞ in Theorem 1. The third term is the (k, l)th off-diagonal element of $\frac{1}{{\sigma }_d^2}{\mathbf{S}}_{D,d}^{+}$, which converges to 0 in probability as d → ∞. Thus $\frac{1}{d{\sigma }_d^2}\left|\right|{\mathbf{x}}_k^{+}-{\mathbf{x}}_l^{+}\left|\right|\to 2$, in probability as d → ∞.

Lemma A.1

Assume that ${\sum }_{i=1}^d{({\lambda }_{i,d}^{+})}^2,{\sum }_{i=1}^d{({\lambda }_{i,d}^{-})}^2\to 0$, as d → ∞ and that ${\sum }_{i=1}^d{\lambda }_{i,d}^{+}={\sum }_{j=1}^d{\lambda }_{j,d}^{-}=1$. Denote by U = [u_ij]_i,j=1,…,d as an arbitrary d × d orthogonal matrix. Then it holds that ${\sum }_{i=1}^d{\sum }_{j=1}^d{u}_{i,j}^2{\lambda }_{i,d}^{+}{\lambda }_{j,d}^{-}\to 0$, as d → ∞.

Note that sum of squared entries in each column and row of U is 1. Lemma A.1 can be proved using the Cauchy–Schwarz inequality.

Proof of Theorem 3

Let ${\mathbf{x}}_j^{+}={(x_{1j}^{+},\dots ,x_{dj}^{+})}^T$, j = 1, …, n⁺, be the jth column of the data matrix X⁺. Let ${\mathbf{x}}_j^{-}={(x_{1j}^{-},\dots ,x_{dj}^{-})}^T$, j = 1, …, n⁻, be the jth column of the data matrix X⁻. The squared distance between ${\mathbf{x}}_k^{+}$ and ${\mathbf{x}}_l^{-}$ is

$${\left|\right|{\mathbf{x}}_k^{+}-{\mathbf{x}}_l^{-}\left|\right|}^2=\sum _{i=1}^d{\{[x_{ik}^{+}-E(x_{i·}^{+})]-[x_{il}^{-}-E(x_{i·}^{-})]+[E(x_{i·}^{+})-E(x_{i·}^{-})]\}}^2$$ (A.1)

$$=\sum _{i=1}^d{({\stackrel{.}{x}}_{ik}^{+})}^2+\sum _{i=1}^d{({\stackrel{.}{x}}_{il}^{-})}^2-2\sum _{i=1}^d{({\stackrel{.}{x}}_{ik}^{+})}^2({\stackrel{.}{x}}_{il}^{-})+\sum _{i=1}^d{[E(x_{i·}^{+})-E(x_{i·}^{-})]}^2$$ (A.2)

$$+2\sum _{i=1}^d[E(x_{i·}^{+})-E(x_{i·}^{-})][{\stackrel{.}{x}}_{ik}^{+}-{\stackrel{.}{x}}_{il}^{-}].$$ (A.3)

Here ${\stackrel{.}{x}}_{ik}^{+}=x_{ik}^{+}-E(x_{i·}^{+})$ and ${\stackrel{.}{x}}_{il}^{-}=x_{il}^{-}-E(x_{i·}^{-})$ are the ith entries on the kth and lth columns of the demeaned data matrices Ẋ⁺ and Ẋ⁻.

The first two terms in (A.2), rescaled by ${(d{\sigma }_d^2)}^{-1}$ and ${(d{\tau }_d^2)}^{-1}$, respectively, are the kth and lth diagonal entries of $\frac{1}{{\sigma }_d^2}{\mathbf{S}}_D^{+}$ and $\frac{1}{{\tau }_d^2}{\mathbf{S}}_D^{-}$. By the proof of Theorem 1, both converge to 1 in probability as d → ∞. Thus, for any ε > 0, $Pr(\mid \frac{1}{d}{\sum }_{i=1}^d{({\stackrel{.}{x}}_{ik}^{+})}^2-{\sigma }^2\mid \ge \epsilon )\to 0$, as d → ∞ and $Pr(\mid \frac{1}{d}{\sum }_{i=1}^d{({\stackrel{.}{x}}_{il}^{-})}^2-{\tau }^2\mid \ge \epsilon )\to 0$, as d → ∞.

The third term, ${\sum }_{i=1}^d({\stackrel{.}{x}}_{ik}^{+})({\stackrel{.}{x}}_{il}^{-})$, is the inner product of ${\stackrel{.}{\mathit{x}}}_k^{+}$ and ${\stackrel{.}{\mathbf{x}}}_l^{-}$, the kth column of the demeaned data matrix Ẋ⁺, and the lth column of the demeaned data matrix Ẋ⁻. Recall that we can write ${\stackrel{.}{\mathbf{x}}}_k^{+}={\mathbf{V}}^{+}{{\mathbf{\Lambda }}^{+}}^{1/2}{\mathbf{z}}_k^{+}$, where ${\mathbf{z}}_k^{+}={(z_1^{+},\dots ,z_d^{+})}^T$ is a d dimensional vector from a distribution with the identity covariance matrix and zero mean. So is ${\stackrel{.}{\mathbf{x}}}_l^{-}={\mathbf{V}}^{-}{({\mathbf{\Lambda }}^{-})}^{1/2}{\mathbf{z}}_l^{-}$, where ${\mathbf{z}}_l^{-}={(z_1^{-},\dots ,z_d^{-})}^T$. Let U = [u_ij]_i,j=1,…,d = V^+T V⁻. Define the relative eigenvalues by ${\stackrel{\sim }{\lambda }}_{i,d}^{+}={\lambda }_{i,d}^{+}/{\sum }_{i=1}^d{\lambda }_{i,d}^{+}$ and ${\stackrel{\sim }{\lambda }}_{j,d}^{-}={\lambda }_{j,d}^{-}/{\sum }_{j=1}^d{\lambda }_{j,d}^{-}$. Then ${(d{\sigma }_d{\tau }_d)}^{-1}{\sum }_{i=1}^d({\stackrel{.}{x}}_{ik}^{+})({\stackrel{.}{x}}_{il}^{-})$ becomes

$$\begin{array}{l}{(d{\sigma }_d{\tau }_d)}^{-1}[z_1^{+},\dots ,z_d^{+}]{({\mathbf{\Lambda }}^{+})}^{1/2}{{\mathbf{V}}^{+}}^T{\mathbf{V}}^{-}{({\mathbf{\Lambda }}^{-})}^{1/2}{[z_1^{-},\dots ,z_d^{-}]}^T={\left(\sum _{i=1}^d{\lambda }_{i,d}^{+}\right)}^{-1/2}{\left(\sum _{j=1}^d{\lambda }_{j,d}^{-}\right)}^{-1/2}\sum _{s=1}^d\sum _{t=1}^d{u}_{s,t}{z}_s^{+}{z}_t^{-}\sqrt{{\lambda }_{s,d}^{+}{\lambda }_{t,d}^{-}}\\ =\sum _{s=1}^d\sum _{t=1}^d{u}_{s,t}{z}_s^{+}{z}_t^{-}\sqrt{{\stackrel{\sim }{\lambda }}_{s,d}^{+}{\stackrel{\sim }{\lambda }}_{t,d}^{-}}.\end{array}$$

The expectation of ${\sum }_{s=1}^d{\sum }_{t=1}^d{u}_{s,t}{z}_s^{+}{z}_t^{-}\sqrt{{\stackrel{\sim }{\lambda }}_{s,d}^{+}{\stackrel{\sim }{\lambda }}_{t,d}^{-}}$ is 0. Thus by Chebyshev’s inequality,

$$\begin{array}{l}Pr\left[\left|\sum _{s=1}^d\sum _{t=1}^d{u}_{s,t}{z}_s^{+}{z}_t^{-}\sqrt{{\stackrel{\sim }{\lambda }}_{s,d}^{+}{\stackrel{\sim }{\lambda }}_{t,d}^{-}}\right|\ge \epsilon \right]\le {\epsilon }^{-2}E{\left(\sum _{s=1}^d\sum _{t=1}^d{u}_{s,t}{z}_s^{+}{z}_s^{-}\sqrt{{\stackrel{\sim }{\lambda }}_{s,d}^{+}{\stackrel{\sim }{\lambda }}_{t,d}^{-}}\right)}^2\\ ={\epsilon }^{-2}\sum _{s=1}^d\sum _{t=1}^d{u}_{s,t}^2{\stackrel{\sim }{\lambda }}_{s,d}^{+}{\stackrel{\sim }{\lambda }}_{t,d}^{-}.\end{array}$$

Since U is the product of two orthogonal matrix U = V^+T V⁻, U is itself orthogonal. The relative eigenvalues satisfy the condition in Lemma A.1. Thus by Lemma A.1, $Pr[\mid {\sum }_{s=1}^d{\sum }_{t=1}^d{u}_{s,t}{z}_s^{+}{z}_s^{-}\times \sqrt{{\stackrel{\sim }{\lambda }}_{s,d}^{+}{\stackrel{\sim }{\lambda }}_{t,d}^{-}}\mid \ge \epsilon ]\to 0$, as d → ∞. Thus ${(d{\sigma }_d{\tau }_d)}^{-1}{\sum }_{i=1}^d({\stackrel{.}{x}}_{ik}^{+})({\stackrel{.}{x}}_{il}^{-})$ converges to 0 in probability as d → ∞. Further, since ${\sigma }_d^2\to {\sigma }^2<\infty$ and ${\tau }_d^2\to {\tau }^2<\infty ,\frac{1}{d}{\sum }_{i=1}^d({\stackrel{.}{x}}_{ik}^{+})({\stackrel{.}{x}}_{il}^{-})\to 0$ in probability as d → ∞.

The fourth term is the squared distance between means, which is defined as dμ².

The last term can be decomposed into two components: ${\sum }_{i=1}^d[E(x_{i·}^{+})-E(x_{i·}^{-})]{\stackrel{.}{x}}_{ik}^{+}$ and ${\sum }_{i=1}^d[E(x_{i·}^{+})-E(x_{i·}^{-})]{\stackrel{.}{x}}_{il}^{-}$. Let ${\delta }_i=E(x_{i·}^{+})-E(x_{i·}^{-})$. Note that ${\sum }_{i=1}^d{\delta }_i^2=d{\mu }^2$. Each component, after being rescaled by d⁻¹, can be shown to converge to 0 in probability as d → ∞. For example, the first component, rescaled by (dσ_d)⁻¹, becomes $\frac{1}{d{\sigma }_d}{\sum }_{i=1}^d[E(x_{i·}^{+})-E(x_{i·}^{-})]{\stackrel{.}{x}}_{ik}^{+}=\frac{1}{d^{1/2}}\sqrt{\frac{1}{d{\sigma }_d^2}}{\sum }_{i=1}^d{\delta }_i{\stackrel{.}{x}}_{ik}^{+}=\frac{1}{d^{1/2}}{\sum }_{i=1}^d{\delta }_i{\sum }_{s=1}^d{v}_{i,s}^{+}\sqrt{{\stackrel{\sim }{\lambda }}_{s,d}^{+}}{z}_s^{+}$. By Chebychev’s inequality,

$$\begin{array}{l}Pr\left(\left|\frac{1}{d^{1/2}}\sum _{i=1}^d{\delta }_i\sum _{s=1}^d{v}_{i,s}^{+}\sqrt{{\stackrel{\sim }{\lambda }}_{s,d}^{+}}{z}_s^{+}\right|>\epsilon \right)\le {\epsilon }^{-2}E{\left(\frac{1}{d^{1/2}}\sum _{i=1}^d{\delta }_i\sum _{s=1}^d{v}_{i,s}^{+}\sqrt{{\stackrel{\sim }{\lambda }}_{s,d}^{+}}{z}_s^{+}\right)}^2\\ ={\epsilon }^{-2}\frac{1}{d}E{\left(\sum _{s=1}^d\sum _{i=1}^d{\delta }_i{v}_{i,s}^{+}\sqrt{{\stackrel{\sim }{\lambda }}_{s,d}^{+}}{z}_s^{+}\right)}^2\\ ={\epsilon }^{-2}\frac{1}{d}\sum _{s=1}^d{\left(\sum _{i=1}^d{\delta }_i{v}_{i,s}^{+}\right)}^2{\stackrel{\sim }{\lambda }}_{s,d}^{+}E{(z_s^{+})}^2\\ ={\epsilon }^{-2}\frac{1}{d}\sum _{s=1}^d{\left(\sum _{i=1}^d{\delta }_i{v}_{i,s}^{+}\right)}^2{\stackrel{\sim }{\lambda }}_{s,d}^{+}\\ \le {\epsilon }^{-2}\frac{1}{d}\sum _{s=1}^d{\left(\sum _{i=1}^d{\delta }_i{v}_{i,s}^{+}\right)}^2\underset{i}{max}({\stackrel{\sim }{\lambda }}_{i,d}^{+})\\ ={\epsilon }^{-2}{\mu }^2\underset{i}{max}({\stackrel{\sim }{\lambda }}_{i,d}^{+})\to 0,\text{as}d\to \infty .\end{array}$$

Note that ${\sum }_{s=1}^d({\sum }_{i=1}^d{\delta }_i{v}_{i,s}^{+})={\sum }_{i=1}^d{\delta }_i^2=d{\mu }^2$ because V⁺ is an orthogonal matrix, which keeps the norm of δ after transformation. Hence the first component ${\sum }_{i=1}^d[E(x_{i·}^{+})-E(x_{i·}^{-})]{\stackrel{.}{x}}_{ik}^{+}$, rescaled by d⁻¹ converges to 0 in probability as d → ∞. And so does the second component ${\sum }_{i=1}^d[E(x_{i·}^{+})-E(x_{i·}^{-})]{\stackrel{.}{x}}_{il}^{-}$.

To summarize the analysis above, $\frac{1}{d}{\left|\right|{\mathbf{x}}_k^{+}-{\mathbf{x}}_l^{-}\left|\right|}^2\to {\sigma }^2+{\tau }^2+{\mu }^2$, in probability, as d → ∞.

Proof of Theorem 5

Recall that the DWD hyperplane cut-off point P^* satisfies (13): $\frac{{\alpha }^{\ast }}{{\beta }^{\ast }}={(\frac{w_{+}{n}^{+}}{w_{-}{n}^{-}})}^{1/2}$. Let ${\mathbf{x}}_0^{+}$ be a new data point from the -population. It was shown in Hall, Marron, and Neeman (2005) that the rescaled squared distance of ${\mathbf{x}}_0^{+}$ from O⁺ and O⁻ are ${\sigma }^2(1+n_{+}^{-1})$ and μ² + σ² + τ²/n⁻, respectively, and it was known that the squared distance between O⁺ and O⁻ was μ² + σ²/n⁺ + τ²/n⁻. Let P be the projection of ${\mathbf{x}}_0^{+}$ to the line O⁺O⁻, with distances to the two centroids being α and β. It was shown by a series of geometric calculations in Hall, Marron, and Neeman (2005) that $\frac{\alpha }{\beta }=\frac{{\sigma }^2/n^{+}}{{\mu }^2+{\tau }^2/n^{-}}$.

The point ${\mathbf{x}}_0^{+}$ will be correctly classified as type if it lies on the same side of the DWD hyperplane as O⁺, that is, if $\frac{{\sigma }^2/n^{+}}{{\mu }^2+{\tau }^2/n^{-}}<{(\frac{w_{+}{n}^{+}}{w_{-}{n}^{-}})}^{1/2}$. It will be wrongly classified as if $\frac{{\sigma }^2/n^{+}}{{\mu }^2+{\tau }^2/n^{-}}>{(\frac{w_{+}{n}^{+}}{w_{-}{n}^{-}})}^{1/2}$.

The first and second parts of Theorem 5 follows from the two inequalities above immediately. Now assume that ${\sigma }^2/[n_{+}^{3/2}{w}_{+}^{1/2}]\ge {\tau }^2/[n_{-}^{3/2}{w}_{-}^{1/2}]$. This ensures the nonnegativity of (n⁻w₋/n⁺w₊)^1/2σ²/n⁺ − τ²/n⁻, the right-hand side of the inequality in the first and second parts. Furthermore, suppose that we have a data point ${\mathbf{x}}_0^{+}$ from the -population. By the inequality above, $\frac{{\tau }^2/n^{-}}{{\sigma }^2/n^{+}}\le {(\frac{w_{-}{n}^{-}}{w_{+}{n}^{+}})}^{1/2}$. Then for any positive μ² we have $\frac{{\tau }^2/n^{-}}{{\mu }^2/{\sigma }^2/n^{+}}<\frac{{\tau }^2/n^{-}}{{\sigma }^2/n^{+}}\le {(\frac{w_{-}{n}^{-}}{w_{+}{n}^{+}})}^{1/2}$, that is, ${\mathbf{x}}_0^{+}$ will always be classified as belonging to . Theorem 5 simply combines the analysis above.

Proof of Theorem 6

Denote the centroids of the (n⁺ − 1)-simplex from as $O_{+}^{n^{+}}$ and the (n⁻ − 1)-simplex from X⁻ as $O_{-}^{n^{-}}$. Also denote the population means of and as $O_{+}^{\infty }$ and $O_{-}^{\infty }$, respectively. In the large d-limit, the expected squared distance, rescaled by d⁻¹, between $O_{+}^{n^{+}}$ and $O_{-}^{n^{-}}$ is μ² + σ²/n⁺ + τ²/n⁻. If we consider k more data vectors from , the expected squared distance, rescaled by d⁻¹, between the centroids $O_{+}^{(n^{+}+k)}$, of the new (n⁺ + k − 1)-simplex, and the centroid $O_{-}^{n^{-}}$, of the (n⁻ − 1)-simplex is μ² + σ²/(n⁺ + k) + τ²/n⁻. Also the expected squared distance, rescaled by d⁻¹, between $O_{+}^{n^{+}}$ and $O_{+}^{(n^{+}+k)}$ is $(\frac{k}{n^{+}(n^{+}+k)}){\sigma }^2$. This can be shown by calculating the distance between the two (n⁺ + k)-dimensional vectors,

$$\sqrt{d\sigma }{(\underset{n^{+}}{\underbrace{n_{+}^{-1}+n_{+}^{-1},\dots ,n_{+}^{-1}}},\underset{k}{\underbrace{0,0,\dots ,0}})}^T$$

and

$$\sqrt{d\sigma }{(\underset{n^{+}+k}{\underbrace{{(n^{+}+k)}^{-1},{(n^{+}+k)}^{-1},\dots ,{(n^{+}+k)}^{-1}}})}^T,$$

which are the centroids of the (n⁺ − 1)-simplex

$$\{\sqrt{d}(\underset{n^{+}}{\underbrace{1,0,\dots ,0}},\underset{k}{\underbrace{0,\dots ,0}}),\dots ,\sqrt{d}(\underset{n^{+}}{\underbrace{0,\dots ,0,1}},\underset{k}{\underbrace{0,\dots ,0}})\}$$

and the (n⁺ − 1 + k)-simplex

$$\{\sqrt{d}(\underset{n^{+}+k}{\underbrace{1,0,\dots ,0}}),\dots ,\sqrt{d}(\underset{n^{+}+k}{\underbrace{0,\dots ,0,1}})\},$$

respectively.

Thus by the Pythagorean theorem, $O_{+}^{n^{+}}{O}_{+}^{(n^{+}+k)},O_{+}^{n^{+}}{O}_{-}^{n^{-}}$, and $O_{+}^{(n^{+}+k)}{O}_{-}^{n^{-}}$ form a right triangle, with $O_{+}^{n^{+}}{O}_{-}^{n^{-}}$ being the hypotenuse. And it follows that the angle between $O_{+}^{(n^{+}+k)}{O}_{-}^{n^{-}}$ and $O_{+}^{n^{+}}{O}_{-}^{n^{-}}$ becomes approximately ${cos}^{-1}{(\frac{{\mu }^2+{\sigma }^2/(n^{+}+k)+{\tau }^2/n^{-}}{{\mu }^2+{\sigma }^2/n^{+}+{\tau }^2/n^{-}})}^{1/2}$. Let k → ∞. $O_{+}^{(n^{+}+k)}$ converges to $O_{+}^{\infty }$. Thus the angle between $O_{+}^{\infty }{O}_{-}^{n^{-}}$ and $O_{+}^{n^{+}}{O}_{-}^{n^{-}}$ becomes ${cos}^{-1}{(\frac{{\mu }^2+{\tau }^2/n^{-}}{{\mu }^2+{\sigma }^2/n^{+}+{\tau }^2/n^{-}})}^{1/2}$.

In the same manner, consider l more data vectors from , and let l → ∞. Then the angle between $O_{+}^{\infty }{O}_{-}^{\infty }$ and $O_{+}^{n^{+}}{O}_{-}^{n^{-}}$ is ${cos}^{-1}{(\frac{{\mu }^2}{{\mu }^2+{\sigma }^2/n^{+}+{\tau }^2/n^{-}})}^{1/2}$, that is, the angle between the direction joining the means of two populations and the DWD direction joining the centroids of the (n⁺ − 1)-simplex (d) and the (n⁻ − 1)-simplex (d) becomes $\theta ={cos}^{-1}{(\frac{{\mu }^2}{{\mu }^2+{\sigma }^2/n^{+}+{\tau }^2/n^{-}})}^{1/2}$.

Proof of Theorem 7

For any fixed x, the conditional risk is

$$E[W(Y_s)V(Y_{sf})\mid {\mathbf{X}}_s=\mathbf{x}]=p_s(\mathbf{x})W(+1)V(f(\mathbf{x}))+(1-p_s(\mathbf{x}))W(-1)V(-f(\mathbf{x})).$$

Here the DWD loss V(·) is defined in (17). For simplicity, we write R(f) = p_sW(+1)V(f) + (1 − p_s)W(−1)V(−f). Then f^* is obtained by solving R′(f) = 0, where R′(f) = p_sW(+1)1V′(f) − (1 −p_s)W(−1)V′(−f). Straightforward computations give

$$\begin{array}{l}V(f)=\{\begin{array}{ll}2\sqrt{C}-Cf\hfill & \text{if}f\le \frac{1}{\sqrt{C}}\hfill \\ \frac{1}{f}\hfill & \text{otherwise}\hfill \end{array}\text{and}\\ V(-f)=\{\begin{array}{ll}2\sqrt{C}+Cf\hfill & \text{if}f\ge -\frac{1}{\sqrt{C}}\hfill \\ -\frac{1}{f}\hfill & \text{otherwise.}\hfill \end{array}\end{array}$$

We can show that, for fixed p_s, R(f) is continuous and differentiable everywhere and R(f) is convex in [−∞, ∞], that is, R′(f) is nondecreasing. By directly solving the equation R′(f) = 0, we get f^*, the minimizer of R(f) as

$$f^{\ast }=\frac{1}{\sqrt{C}}·\{\begin{array}{ll}\sqrt{\frac{p_{s}W(+1)}{(1-p_s)W(-1)}}\hfill & \text{if}\frac{p_{s}W(+1)}{(1-p_s)W(-1)}>1\hfill \\ 0\hfill & \text{if}\frac{p_{s}W(+1)}{(1-p_s)W(-1)}=1\hfill \\ -\sqrt{\frac{(1-p_s)W(-1)}{p_{s}W(+1)}}\hfill & \text{if}\frac{p_{s}W(+1)}{(1-p_s)W(-1)}<1.\hfill \end{array}$$

Note when $\frac{p_{s}W(+1)}{(1-p_s)W(-1)}=1$, f^* can take any value in [−(((1 − p_s) W(−1))/(Cp_sW(+1)))^1/2, ((p_sW(+1))/(C(1 − p_s) W(−1)))^1/2]. We choose 0 here for convenience. Therefore, the minimizer of R(f) satisfies $\text{sign}[f^{\ast }]=\text{sign}[\frac{p_{s}W(+1)}{(1-p_s)W(-1)}-1]=\text{sign}[p_{s}W(+1)-(1-p_s)W(-1)]=\text{sign}[p_s\{W(+1)+W(-1)\}-W(-1)]=\text{sign}[p_s>\frac{W(-1)}{W(+1)+W(-1)}]={\phi }^{\ast }$.