Abstract
Objective
When using imaging to predict time to progression from mild cognitive impairment (MCI) to Alzheimer's disease (AD), time-to-event statistical methods account for varying lengths of follow-up times among subjects whereas two-sample t-tests in voxel-based morphometry (VBM) do not. Our objectives were to apply a time-to-event voxel-based analytic method to identify regions on MRI where atrophy is associated with significantly increased risk of future progression to AD in subjects with MCI and to compare it to traditional voxel-level patterns obtained by applying two-sample methods. We also compared the power required to detect an association using time-to-event methods versus two-sample approaches.
Methods
Subjects with MCI at baseline were followed prospectively. The event of interest was clinical diagnosis of AD. Cox proportional hazards models adjusted for age, sex, and education were used to estimate the relative hazard of progression from MCI to AD based on rank-transformed voxel-level gray matter density (GMD) estimates.
Results
The greatest risk of progression to AD was associated with atrophy of the medial temporal lobes. Patients ranked at the 25th percentile of GMD in these regions had more than a doubling of risk of progression to AD at a given time-point compared to patients at the 75th percentile. Power calculations showed the time-to-event approach to be more efficient than the traditional two-sample approach.
Conclusions
We present a new voxel-based analytic method that incorporates time-to-event statistical methods. In the context of a progressive disease like AD, time-to-event VBM seems more appropriate and powerful than traditional two-sample methods.
Keywords: Alzheimer Disease, mild cognitive impairment, magnetic resonance imaging, Cox proportional hazards model
1. Introduction
Mild cognitive impairment (MCI) is considered a transitional stage between normal aging and dementia. Amnestic MCI (aMCI) is a subtype of MCI that primarily involves memory complaints and deficits and is often a prodromal stage of Alzheimer's disease (AD) [1, 2] with about 12%–15% of aMCI subjects annually progressing to AD [2–4]. Diagnostic criteria for AD are currently based on clinical and psychometric assessment. However degenerative histological changes occur long before AD is clinically diagnosed [5]. Therefore neuroimaging can be a useful aid in predicting the future progression of aMCI to AD.
In order to optimally utilize structural Magnetic Resonance Imaging for prediction of future progression to AD, it is important to understand the patterns of 3D structural changes that are associated with this clinical event. The most common study design in this context uses voxel based morphometry (VBM) [6] to perform voxel-wise two-sample comparisons to assess the full 3D topographic gray matter (GM) atrophy patterns in MCI who progress to AD (so-called “progressors”) versus those who do not (so-called “non-progressors” or “stables”) [7–9]. These case-control type studies have identified the medial temporal lobe limbic cortex, inferio-lateral temporal neocortex, and posterior cingulate as the regions with the greatest differences. While informative, this two-sample approach by definition dichotomizes subjects into either progressors or non-progressors after a fixed period of follow-up. Non-progressors who do not reach this follow-up time cannot be included in the study due to insufficient time at risk [10]. Also follow-up information that is available in non-progressors after the fixed follow-up time cannot be used in this type of analysis. Thus, the two-sample approach discards potentially valuable information which is available but cannot be used analytically.
Study designs that use time-to-event based statistical methods such as Cox proportional hazards models are used extensively [11] in the field of biostatistics in part because they allow for variable lengths of follow-up and for incorporating “partial” information in the form of censoring. A subject followed for x years who has not progressed by last follow-up is considered to be stable through x years and to have an unobserved progression time that occurs at some later point. This subject can be said to contribute x years of progression-free follow-up but is not rigidly classified as stable.
Several imaging studies have employed time-to-event methods to demonstrate that atrophy on ROI-based hippocampus and entorhinal cortex volume measurements is associated with increased risk of progressing to AD [12–14]. Quantifying volumes of medial temporal structures such as the hippocampus and entorhinal cortex is logical since AD-related atrophy occurs earliest and most severely in these regions [15, 16]. And employing time-to-event statistical methods in analyses of prediction is fairly straightforward using ROI-based MRI measurements. However using only measures derived from one (or a few) specific pre-selected regions does not make use of all the available information in a 3D MRI data set.
In this study we present a voxel-wise time-to-event analysis examining the increased hazard of progression to AD associated with topographic gray matter atrophy in the brain. Our aims were to (1) identify topographic patterns of anatomic regions on MRI where atrophy is associated with significantly increased risk of future progression using robust time-to-event statistical methods at a voxel level, (2) to quantify the effect size in an interpretable way using hazard ratio estimates, (3) to compare topographic patterns of risk of progression found in a time-to-event analysis to those based on a two-sample study design; (4) to compare the power to detect associations between gray matter atrophy at the voxel level and progression to AD using time-to-event versus two-sample approaches.
2. Materials and methods
2.1 Subjects
This study was approved by the Mayo IRB, and informed consent for participation was obtained from every subject. A total of 296 MCI patients were recruited to the Mayo Clinic AD Research Center (ADRC) /AD Patient Registry (ADPR) [17, 18] and followed through February 2010. Subjects enrolled in the ADPR are recruited from primary care providers in the community; they were referred to the ADPR for further evaluation if a memory complaint came up in the course of the general medical exam. Subjects enrolled in the ADRC were self-referred or referred by their doctors for a cognitive problem, usually memory. Although the recruitment mechanisms differ between the ADPR and the ADRC, once enrolled, the subjects are evaluated using the same protocols and diagnostic criteria. Individuals participating in the ADRC/ADPR studies undergo approximately annual neurological examinations, structural brain MRI, routine laboratory tests, and a battery of neuropsychological tests. At the completion of the evaluation, a consensus committee meeting is held to determine a diagnosis; committee members include behavioral neurologists, neuropsychologists, nurses, and geriatricians who evaluated the subjects. A total of 151 MCI patients agreed to participate in MRI studies, and were followed until February 2010.
The operational definition of MCI was based on clinical judgment through a history from the patient and almost always a collateral source without reference to MRI using the criteria for the broad definition of MCI [2]: Cognitive complaint, cognitive function not normal for age, decline in cognition, essentially normal functional activities, and not demented. Patients with MCI were further classified into one of the two MCI subtypes: aMCI, if the impairment included the memory domain or naMCI if the impairment was in one or more non-memory domains with relative preservation of memory. We included only aMCI subjects in this analysis for purposes of diagnostic uniformity. In general, the aMCI determination is made when the memory measures fall 1.0 to 1.5 standard deviations below the means for age- and education-matched individuals in our community. Rigid cutoffs on psychometric scores were not used to establish the diagnosis of aMCI which was made on clinical grounds by consensus. These well-established criteria have been used by our institution for many years and have been adopted by numerous research programs including the National Institute on Aging (NIA) Alzheimer disease Centers Program and the Alzheimer Disease Neuroimaging Initiative (ADNI) (http://www.adni-info.org/). In all cases the diagnosis of aMCI is made independently of any quantitative MRI findings. Patients were reevaluated approximately annually and the decision of whether subjects had progressed to clinically probable AD was made at a consensus committee meeting as previously described [19]. The diagnosis of dementia was made based on the Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition [20]. The clinical diagnoses of AD, dementia with Lewy bodies (DLB), and frontotemporal lobar degeneration (FTLD) were made using published consensus criteria [21]. Patients with structural abnormalities that could impair cognitive function other than cerebrovascular lesions were excluded. Subjects were not excluded for the presence of infarctions and leukoaraiosis, thus the full range of ischemic cerebrovascular disease was included.
2.2 MRI acquisitions
All MRI studies were performed on fifteen different 1.5 Tesla GE-SIGNA MRI scanners (GE Medical Systems, Waukesha, WI) over a period 5 years (2001–2005) using a standard transmit-receive volume head coil. Since these scanners are all used in clinical practice, they undergo a standardized quality control calibration procedure every morning which monitors geometric fidelity over a 200 mm volume along all 3 cardinal axes, signal to noise ratio, and transmit gain. We did not find evidence of systematic scanner-related differences and therefore do not account for scanner in our analyses. Subject images were obtained using a standardized imaging protocol that included a coronal T1-weighted 3-dimensional volumetric spoiled gradient echo (SPGR) sequence with the following scan parameters: FOV = 24 × 18.5 or 22 × 16.5 cm, in-plane matrix = 256 × 192, 1.6 mm partition thickness and 124 contiguous partitions, flip angle = 25°, TR = 23 ms, min full TE. Prior to processing, all scans were reviewed for artifacts (such as motion) and potential subjects with severe artifacts were removed from the study.
2.3 MRI image pre-processing
SPM5 was used for tissue segmentation and normalization (http://www.fil.ion.ucl.ac.uk/spm) of each scan [22]. In order to reduce any potential normalization and segmentation bias across the subjects, a custom template and tissue probability maps (TPMs) were created in SPM5 using the T1 weighted 3D MRI scans from an earlier study [23]. All the MCI scans are registered to this template. Jacobian modulation was applied to compensate for the effect of spatial normalization and to restore the original absolute gray matter density (GMD) in the segmented gray matter images. These modulated images were then smoothed with an 8 mm FWHM smoothing kernel. These GMD images were down-sampled to an isotropic voxel size of 8 mm by simple averaging to reduce the computational load and provide less noisy voxel-level estimates. This down-sampling resulted in a total of 3410 voxel-level GMD estimates for each subject and constituted the data used for the analysis presented in this paper. Results based on an isotropic voxel size of 4 mm were found to be very similar.
2.4 Statistical methods
2.4.1 Primary analysis
We used Cox proportional hazards models to analyze the data on a per-voxel level [11]. The earliest available MCI visit with a concomitant MRI was defined as the baseline, i.e., time zero. Subjects were followed prospectively from their MRI until the first diagnosis of AD, our event of interest. For those who progressed to AD by last follow-up, the event time was defined as the midpoint between the last MCI diagnosis and the first AD diagnosis. Subjects who were not observed to progress to AD were censored at their last MCI visit, provided they remained stable, or at the midpoint between their last MCI visit and first diagnosis of a neurodegenerative disease other than AD such as DLB. Censoring, rather than excluding, subjects who obtained a non-AD neurodegenerative diagnosis or had died is appropriate because they are considered “at risk” of AD up until their non-AD diagnosis or death. Since these subjects met the inclusion criteria at baseline and also had “AD-free follow-up” until that point, to exclude them would bias our findings. This approach is consistent with a competing risks framework in which subjects may be considered at risk of several competing events: AD, a non-AD dementia, death, etc. The Cox model is appropriate in the competing risk framework with hazard ratios interpreted as “cause-specific”, i.e., AD-specific effects [24]. To estimate the cumulative incidence of progression to AD in the context of competing risks, we used the competing-risks approach rather than the Kaplan-Meier approach [25].
Each Cox model included age at MRI, sex, years of education, and the GMD for a given voxel. Because some voxel GMD distributions were found to be skewed and also to increase the robustness of our models, we rank-transformed all GMD predictors prior to analysis [26]. To quantify the effect of GMD at each voxel in an interpretable way, for each voxel we report age-, sex-, and education-adjusted hazard ratios that represent the relative hazard or instantaneous rate of progression from MCI to AD, for a participant at the 25th percentile of the GMD distribution versus one at the 75th percentile. The 25th percentile can be interpreted as representing a typical value among those with greater-than-average atrophy while the 75th percentile can be interpreted as representing a typical value among those with less-than-average atrophy. For each model, we assessed the proportional hazards assumption by testing for a correlation between the rank-transformed event times and the Schoenfeld partial residuals [11].
We performed 1 degree of freedom likelihood ratio tests to quantify the evidence that the GMD values at that voxel provide additional predictive information regarding time to AD after accounting for age, sex, and education. We report P-values based on a false discovery rate (FDR) correction across all 3410 tests. To display the entire cortical findings, we show cortical surface rendering maps of medial, lateral and ventral surfaces where the intensity is indexed to the hazard ratio [27] and the results are thresholded to an FDR-corrected P-value of 0.05.
2.4.2 Secondary analysis
As a secondary analysis, we performed four separate two-sample analyses using linear regression at each voxel. The first analysis was based on dividing subjects into those who had progressed by 2 years of follow-up versus those who remained stable through 2 years. Subjects with less than two years of follow-up were excluded, as were subjects who had progressed to a non-AD dementia prior to the 2 year follow up time point. At each voxel we fit a linear regression model in which the response was the rank-transformed GMD estimate, the primary predictor was group (progressors vs. non-progressors) while age, sex, and years of education were included as adjustment variables. These models can be considered two-group analysis of covariance (ANCOVA) models. A rank transform was used due to skewness and to increase the robustness of our analyses. We quantify the differences between groups in terms of t statistics and summarize the results over all 3410 voxels using cortical surface rendering heat maps where the intensity is indexed to the t-statistic and the results are thresholded to an FDR-corrected P-value of 0.05. We repeated this two-sample analysis using additional follow-up cut-points of three, four, and five years.
2.4.3 Power comparison of Cox model with two-sample approaches
We used two approaches to compare the statistical power of a time-to-event analysis versus a regression analysis comparing progressors vs. stables. In the first approach we assume a sample size equal to that of the current analysis (n=123) and assess power to detect a voxel-level difference as the effect size, i.e., the strength of the voxel-wise association, is varied. We examined associations ranging from an HR for an interquartile difference (i.e., 25th percentile vs. 75th percentile) of 1.5 up to 3.0 in increments of 0.5. At each HR level we generated 1000 replicate data sets and for each data set we performed a Cox model analysis and a separate two-sample analysis based on comparing progressors vs. non-progressors at 1, 2, 3, 4, and 5 years of follow-up.
The Cox model analysis used a rank-transform of the GMD distribution and a 1 degree of freedom likelihood ratio test. The two-sample analyses were based on linear regression of the rank-transformed GMD values in the form of a simple two-group ANOVA. Power for each test was estimated by the proportion of the 1000 replicate data sets where the P-value was below 0.05. Although in our full analysis we adjust for age, sex, and education, for simplicity these power analyses were all univariate. The simulated data sets were generated from a Weibull distribution using parameters that were realistic given our observed data. For each Weibull-based progression time, we generated a censoring time that was uniformly distributed on the interval 0 to 6 years. The simulated observed time was the minimum of the progression time versus the censor times. A simulated event was observed if the progression time was before the censoring time. Using this approach, our simulations closely matched the observed data set in terms of median follow-up times, number of events, etc.
In the second approach to comparing statistical power, we assume the imaging predictor is normally distributed with mean 0 and SD of 1 and that the hazard ratios for an inter-quartile range (IQR) difference is approximately 2. We then estimate power based on 1000 simulated data sets using the two competing statistical approaches described above for sample sizes of 50, 75, 100, 125, 150, 175, and 200. All power calculations were performed assuming a two-sided alpha level of 0.05.
All statistical analyses were performed using R version 2.8.1 (http://www.R-project.org) and the survival package version 2.35-9. All the results were displayed using Caret software [27].
3. Results
3.1 Clinical findings
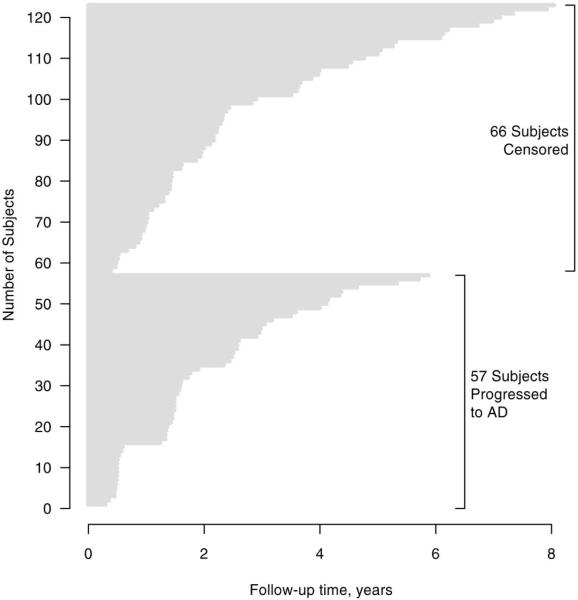
A total of 123 amnestic MCI subjects with a usable MRI scan and at least one follow-up visit were included in this study. We excluded one available patient because of inconsistencies regarding her clinical course. Subject demographic characteristics and cognitive performance at baseline are summarized in Table 1. The hazard ratios for progression to AD associated with each demographic variable are also listed in Table 1. By last follow-up, 57 patients had progressed to clinically diagnosed AD, 11 to DLB, and 2 had progressed to FTD. One subject who progressed to mixed AD plus vascular dementia was censored at this diagnosis (i.e. this was not considered a “progression-to-AD” event in our analyses). The remaining 52 subjects were not demented at last follow-up and were therefore censored. Of these, 16 were known to have died a median of 2.6 years after their last visit (range 8 months to 6.4 years). Another 12 subjects had a visit within the last 18 months while 24 were lost to follow-up. Using the cumulative incidence method in the presence of competing risks, the median time to AD was 3.5 years. The follow-up intervals separated by whether the subject progressed to AD by last follow-up are presented graphically in Fig. 1.
Table 1. Demographics.
Demographic and baseline cognitive characteristics of the 123 subjects in the cohort
| Characteristic | Summary | HR (95% CI)a | Pb |
|---|---|---|---|
| Gender, no. (%) | 0.05 | ||
| Women | 51 (41.5) | 1.8 (1.0, 3.0) | |
| Men | 72 (58.5) | 1.0 | |
| Age at MRI, years | 1.1 (0.9, 1.3) | 0.47 | |
| Median (IQR) | 77 (72, 83) | ||
| Range | 55 to 94 | ||
| Education level, years | 1.0 (0.9, 1.1) | 0.98 | |
| Median (IQR) | 15 (12, 17) | ||
| Range | 7 to 21 | ||
| Apolipoprotein E, no. (%)c | 0.04 | ||
| ε4 carrier | 59 (50.9) | 1.8 (1.0, 3.1) | |
| ε4 non-carrier | 57 (49.1) | 1.0 | |
| White matter hyperintensity | 1.0 (0.8, 1.3) | 0.99 | |
| load, cm3 | |||
| Median (IQR) | 12 (6, 25) | ||
| Range | 1 to 110 | ||
| Cortical infarctions, no. (%) | |||
| Present | 9 (7.3) | 1.2 (0.4, 3.8) | 0.78 |
| Absent | 114 (92.7) | 1.0 | |
| Subcortical infarctions, no. (%) | |||
| Present | 11 (8.9) | 0.47 (0.1, 1.5) | 0.16 |
| Absent | 112 (91.1) | 1 | |
| MMSE at baseline | 1.2 (1.1, 1.3) | 0.002 | |
| Median (IQR) | 27 (25, 28) | ||
| Range | 18 to 30 | ||
| CDR sum of boxes at baseline | 1.5 (1.3, 1.9) | <0.001 | |
| Median (IQR) | 0.5 (0.5, 1.5) | ||
| Range | 0 to 6.5 | ||
| AVLT sum of trials 1–5d | 1.4 (1.2, 1.6) | <0.001 | |
| Median (IQR) | 28 (24, 34) | ||
| Range | 7 to 48 |
Hazard ratios for age based on a 5-year increase, for education based on a 1-year decrease; for white matter hyperintensity load based on a 1-unit increase on the natural log scale; for MMSE based on a 1-unit decrease; for CDR sum of boxes based on a 1-unit increase; for AVLT sum of trials 1–5 based on a 5-unit decrease
P-value based on 1 degree of freedom likelihood ratio test
APOE unavailable in 5 subjects
AVLT unavailable in 1 subject
Abbreviations: HR, hazard ratio; IQR, interquartile range; MMSE, Mini Mental State Exam; CDR, Clinical Dementia Rating; AVLT, Auditory Verbal Learning Test
Fig. 1.
Follow-up times for 123 patients in the study grouped by whether they progressed to AD by last follow-up. The cumulative incidence for progression to AD by 1 year was estimated to be 12%, by 2 years it was 32%, by 3 years 47%, by 4 years 54% and by 5 years 64%.
3.2 Voxel-wise hazard ratio maps
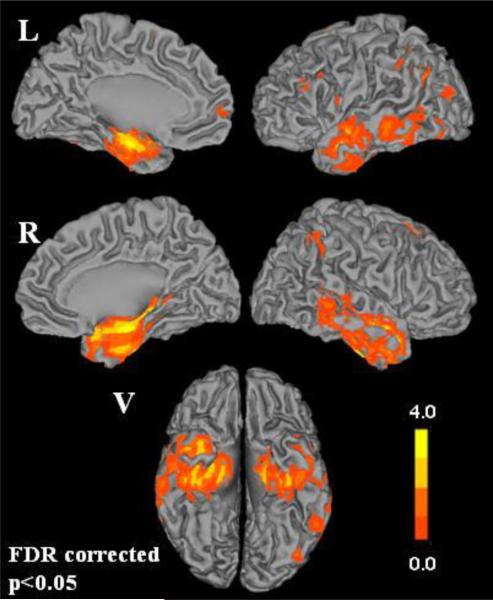
Fig. 2 shows a cortical surface of HRs that are significant at the FDR corrected level of P<0.05 after adjusting for age, sex, and years of education. The intensity of the maps corresponds to HRs based on comparing the 25th percentile of GMD to the 75th percentile of GMD. In other words, an HR of 2 indicates a subject at the 25th percentile of GMD has twice the estimated hazard of progression versus a subject at the 75th percentile of GMD. The greatest risk of progression to AD is associated with atrophy of the medial and inferior temporal lobes including the temporal pole, entorhinal cortex and hippocampus. The MNI coordinates of the two peak HR clusters were in the right hippocampus (34,−10,−20) and left hippocampus (−24,−12,−20) with hazard ratio values of 5.3 and 4.4 respectively.
Fig. 2.
Cortical surface renderings showing the estimated voxel-wise hazard ratios (HRs) for progression from aMCI to AD comparing subjects at 25th percentile to the 75th percentile after adjusting for age, sex, and years of education (FDR corrected p<0.05). Left and right medial, lateral and ventral (V) cortical surfaces are shown.
Based on a global test of proportional hazards, only 4 of 3410 voxel-wise models had evidence of non-proportional hazards based (P<0.05). For the specific test of proportionality associated with the rank-transformed GMD predictor, we found 108/3410 (3.2%) had significant evidence (P < 0.05) of non-proportionality. Since we would expect about 5% just by chance, this was largely consistent with the null hypothesis of proportional hazards. Further, none of the voxels significant at the FDR-corrected threshold of 0.05 had evidence of a non-proportional hazard GMD effect.
3.3 Voxel-wise two-sample t-test maps
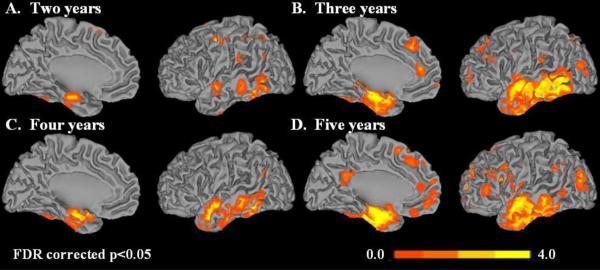
Fig. 3 shows cortical surface maps of voxels that are significantly different between progressors and non-progressors at the FDR-corrected level of P<0.05 after adjusting for age, sex, and years of education. At two years the progressor to non-progressor ratio was 34:60 with 29 excluded because they did not have the minimum required 2 years of follow-up or had progressed to a non-AD dementia. For 3 years the ratio was 45:34 with 44 excluded, for 4 years it was 50:25 with 48 excluded, and for 5 years it was 54:16 with 53 excluded. As indicated above, subjects who were free of AD but followed less than the cutoff were excluded from the respective analysis because of their ambiguous clinical classification for a 2 group analysis. Fig 3A shows regions of atrophy in progressors compared to non-progressors with a cutoff of two years. The greatest atrophy is seen in the hippocampus. With a follow-up cutoff of three years (Fig 3B) atrophy in progressors vs non-progressors involves the entire medial temporal and inferior temporal lobes. For a cutoff of four years the anatomic extent of atrophy in progressors vs non-progressors is less than that seen in at three years. In Fig. 3D with a cutoff of five years, the anatomic extent of atrophy in progressors vs non-progressors is greater than that seen at four years in the medial temporal as well as the frontal lobes. We believe that by five years, subjects that were in the non-progressor group are inherently very stable.
Fig. 3.
Cortical surface renderings showing t-statistics comparing progressors versus non-progressors after adjusting for age, sex, and years of education for four follow-up cutoffs. The cut-offs used were (A) two years, (B) three years (C) four years and (D) five years of follow-up (FDR corrected p<0.05). Left hemisphere medial and lateral cortical surfaces are shown.
3.4 Power and samples sizes required for Cox model vs. two-sample approaches
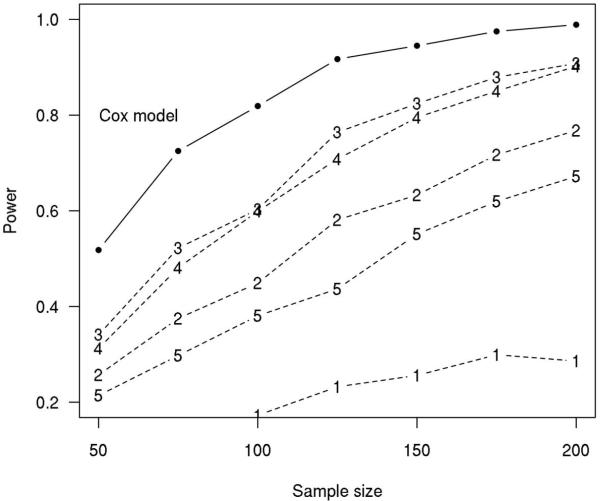
For a sample size of 123, the estimated power to detect an association using the Cox-model approach versus a two-sample approach is compared in Table 2. In terms of power, the Cox model approach is superior to the two-sample approach, although power for the two-sample approach varies with the follow-up cutoff used. The estimated power as a function of sample size for different statistical approaches is shown in Fig. 4. We again see the Cox-model based approach out-performs the traditional two-sample approach (for any of the follow-up times evaluated from 1 to 5 years) in terms of statistical power. We note that Fig. 4 illustrates an interesting phenomenon. The similarity in power for the 2- and 5-year cutoffs was found to be due to quite different characteristics of the samples. On average, the 2-year cutoff allowed more subjects to be included with better balance between stables and progressors. The 5-year cutoff included fewer subjects overall, with few stable MCIs. However, the sample size disadvantage is offset by greatly increased separation in GMD when the 5-year cutoff is used. This sample-size/separation tradeoff was what made the power comparable for the 2-year and 5-year cutoffs.
Table 2. Simulation Results.
Estimated power to detect an association using a Cox-model based approach vs. a two-sample t-test comparing progressors and non-progressors. We assume rank-transformed GMD values, a sample size of n=123, and a two-sided alpha level of 0.05.
| Effect Size Expressed in terms of Hazard Ratioa |
||||
|---|---|---|---|---|
| Analysis Performed | 1.5 | 2.0 | 2.5 | 3.0 |
| Cox model approach | 0.39 | 0.80 | 0.97 | 1.0 |
| Two-sample approach | ||||
| 1 y follow-up cutoff | 0.15 | 0.30 | 0.53 | 0.62 |
| 2 y follow-up cutoff | 0.24 | 0.54 | 0.80 | 0.88 |
| 3 y follow-up cutoff | 0.29 | 0.63 | 0.88 | 0.94 |
| 4 y follow-up cutoff | 0.27 | 0.58 | 0.84 | 0.91 |
| 5 y follow-up cutoff | 0.18 | 0.39 | 0.62 | 0.70 |
Hazard ratio based on comparing the 25th percentile to the 75th percentile
Fig. 4. Simulation Results.
Estimated power as a function of sample size for competing statistical approaches based on Weibull model simulations. The power of the Cox model approach is indicated by the solid black line while the power of the two-sample approaches are indicated by a dashed line with the numeric symbol indicating the follow-up cutoff in years from baseline. Here we assume the predictor x is normally distributed with mean 0 and SD 1 and that the hazard ratio for an increase equivalent to one IQR is approximately 2.
4. Discussion
We applied a time-to-event statistical analysis using age, sex, and education adjusted Cox proportional hazard models to SPM5-derived GMD estimates at the voxel level. Our statistical approach, while commonly applied in biomedical research, to our knowledge has not been used previously in the context of voxel-wise imaging analyses of progression to AD. Our voxel-based analyses found the strongest associations with progression to AD in the medial temporal limbic areas, followed by the inferior and lateral temporal neocortex (Fig. 2). The findings of the present study are consistent with Braak staging topography [28] and also agree with several imaging studies [13, 29–31].
As a secondary analysis, we performed a series of two-sample comparisons based on follow-up cutoffs varying from 2 to 5 years. While the findings were generally similar, there are a number of interrelated drawbacks of a two-sample approach. First, in a two-sample study design based on a cohort study, subjects who have not progressed by last follow-up but also lack the minimum follow-up must be excluded from the analysis because they cannot unambiguously be considered non-progressors. Omitting these subjects plus those who progress to a non-AD dementia reduces sample sizes appreciably as noted above. A second aspect of the two-sample study design is that the spatial distribution of gray matter atrophy that distinguishes progressors from non-progressors has the potential to differ depending on the cut-point selected. Third, two-sample designs ignore the underlying time until progression occurs. As illustrated in Fig. 1, the follow-up time for our 123 MCI patients in the study is quite variable, as is nearly always the case in typical observational studies. Fourth, two-sample designs depend on an arbitrary follow-up cutoff that can separate subjects with very similar clinical courses into different groups depending on which side of the cutoff they fall on. For example, if the two-sample design sets the minimum follow-up at 2 years, a subject who progresses by 23 months could be contrasted with a subject classified as stable who progresses at 25 months, even though these subjects have nearly equivalent times to progression. Finally, two-sample designs suggest a binary classification of subjects rather than facilitating thinking about disease progression on a continuum with some subjects progressing quickly and others progressing slowly.
We empirically found the Cox model approach to be more powerful than the two-sample approach. This has been found in other contexts with power gains coming primarily when there is additional follow-up and consequently additional events, after the cutoff [32]. One possible critique of our power analysis is that by virtue of simulating from a Weibull distribution the simulations were performed assuming the Cox proportional hazards model was “correct.” Specifically, we assumed that MCI subjects progress over time and that when progression was not observed it was due to a censored follow-up time or a competing event and that lower gray matter density at a given voxel increases an MCI subject's hazard of progression and consequently reduces their time to AD. While these assumptions are likely to only be approximately true in real situations, we think they are more reasonable than the assumptions underlying a two-sample approach.
An implied assumption in the two-sample approach is that subjects who progress by x years are qualitatively different from subjects who remain stable through x years. This is difficult to justify when one considers that the composition of the groups is arbitrary because shortening or lengthening the cutoff by even a few months would move subjects from one group to the other. A second but essential assumption is that average gray matter density in the two groups differs. This is a relatively weak assumption, but one that when found to be true may not add a lot of clarity. Do the two groups differ because risk of progression increases as gray matter density decreases? Or do the two groups differ because those who progress by x years are qualitatively different from those who remained stable through x years? Overall, we think that the time-to-event framework better models the nature of the disease and allows for a more straightforward interpretation of the findings.
One interesting aspect of the two-sample approach in our simulations was that power can be thought of as a compromise between number of subjects who are included in an analysis and separation of the distributions of gray matter density. Assuming a significant association between GMD and hazard of progression, the greater the interval from baseline to cutoff the greater the separation between progressors and non-progressors on the baseline scans. However, this separation becomes harder to detect because overall sample size decreases with time due to inevitable attrition. In our simulations, the 3 year cutoff was most powerful because it represented a balance of group-wise separation and sample sizes. At 2 years, the sample sizes were comparable to those at 3 years, but the separation was less pronounced. At 4 years, the separation on the baseline scans between progressors vs non-progressors was appreciably greater, but the number of stable MCI subjects has dropped considerably, taking its toll on power. The similarity of the power for the 2-year and 5-year cutoffs is interesting because the power is achieved in different ways: greater subject numbers at 2 years versus greater baseline separation in gray matter properties between progressors and non-progressors at 5 years.
4.1 Limitations of the Study
There are some limitations to our approach: 1) If everyone was followed for the same length of time then the proposed technique would not have any advantages over two-sample techniques. While this may happen in therapeutic clinical trials, it rarely happens in observational or epidemiological studies and we believe that this data accurately reflects research practice where the follow-up varies across subjects and individual subjects reach the event at different times. 2) We did not compare the proposed approach to a third approach explained in Jagust et al. [33] where we would estimate voxel-wise associations between lower baseline imaging measures and future cognitive decline. However the goal of the paper was to investigate the optimal method to apply when creating maps of a specific clinically definable endpoint – i.e., the clinical diagnosis of Alzheimer's dementia. The regression approach answers a slightly different question of detecting regions that correlate with decline in future cognition [8, 33, 34]. 3) While the Cox model with a rank-transformed predictor can be considered relatively robust in that it is based on the association between the rank ordering of GMD and the rank ordering of event times, it is semi-parametric but not non-parametric. As such, modeling assumptions such as proportional hazards still need to be verified and alternative models used when the assumptions are not met. However, although non-parametric voxel-wise approaches have been advocated [35] analyses based on linear models with little checking of assumptions appear to be the norm. 4) The power to detect group-wise differences using a two-sample test based on simulated data generated from event times which themselves depend on an MRI predictor is a complicated function of many parameters. These parameters include the underlying distribution of the event times, the censoring mechanism, and the distribution of the predictor. We have not shown the Cox model to be more powerful analytically but rather under limited simulations that are realistic given our data. The relative power of the two methods will therefore depend on the actual distributions, the nature of the censoring, and perhaps even the underlying competing risks.
Research Highlights.
New voxel-based analytic method that incorporates time-to-event statistical methods
Empirically Cox model more powerful compared to two-sample approaches
For a progressive disease like AD, time-to-event VBM more appropriate
Greatest risk of progression to AD associated with medial temporal lobe atrophy
Acknowledgments
This work was supported by the NIH grant R01 AG11378; P50 AG16574; U01 AG06786; K23 AG030935; Robert H. Smith Family Foundation Research Fellowship; the Alexander Family Alzheimer's Disease Research Professorship of the Mayo Foundation, U.S.A and Opus building NIH grant C06 RR018898.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Petersen RC, et al. Mild cognitive impairment: clinical characterization and outcome. Arch Neurol. 1999;56(3):303–8. doi: 10.1001/archneur.56.3.303. [DOI] [PubMed] [Google Scholar]
- 2.Petersen RC. Mild cognitive impairment as a diagnostic entity. J Intern Med. 2004;256(3):183–94. doi: 10.1111/j.1365-2796.2004.01388.x. [DOI] [PubMed] [Google Scholar]
- 3.Fischer P, et al. Conversion from subtypes of mild cognitive impairment to Alzheimer dementia. Neurology. 2007;68(4):288–91. doi: 10.1212/01.wnl.0000252358.03285.9d. [DOI] [PubMed] [Google Scholar]
- 4.Petersen RC. Mild cognitive impairment: current research and clinical implications. Semin Neurol. 2007;27(1):22–31. doi: 10.1055/s-2006-956752. [DOI] [PubMed] [Google Scholar]
- 5.Gomez-Isla T, et al. Profound loss of layer II entorhinal cortex neurons occurs in very mild Alzheimer's disease. J Neurosci. 1996;16(14):4491–500. doi: 10.1523/JNEUROSCI.16-14-04491.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ashburner J, Friston KJ. Voxel-based morphometry--the methods. Neuroimage. 2000;11:805–821. doi: 10.1006/nimg.2000.0582. [DOI] [PubMed] [Google Scholar]
- 7.Bozzali M, et al. The contribution of voxel-based morphometry in staging patients with mild cognitive impairment. Neurology. 2006;67(3):453–60. doi: 10.1212/01.wnl.0000228243.56665.c2. [DOI] [PubMed] [Google Scholar]
- 8.Chetelat G, et al. Using voxel-based morphometry to map the structural changes associated with rapid conversion in MCI: a longitudinal MRI study. Neuroimage. 2005;27(4):934–46. doi: 10.1016/j.neuroimage.2005.05.015. [DOI] [PubMed] [Google Scholar]
- 9.Whitwell JL, et al. MRI patterns of atrophy associated with progression to AD in amnestic mild cognitive impairment. Neurology. 2008;70(7):512–20. doi: 10.1212/01.wnl.0000280575.77437.a2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Berkson J, Gage RP. Calculation of survival rates for cancer. Proc Staff Meet Mayo Clinic. 1950;25(11):270–86. [PubMed] [Google Scholar]
- 11.Therneau TM, Grambsch PM. Modeling survival data: extending the Cox model. Springer; New York: 2000. [Google Scholar]
- 12.Devanand DP, et al. Hippocampal and entorhinal atrophy in mild cognitive impairment: prediction of Alzheimer disease. Neurology. 2007;68(11):828–36. doi: 10.1212/01.wnl.0000256697.20968.d7. [DOI] [PubMed] [Google Scholar]
- 13.Jack CR, Jr., et al. Prediction of AD with MRI-based hippocampal volume in mild cognitive impairment. Neurology. 1999;52(7):1397–403. doi: 10.1212/wnl.52.7.1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Stoub TR, et al. MRI predictors of risk of incident Alzheimer disease: a longitudinal study. Neurology. 2005;64(9):1520–4. doi: 10.1212/01.WNL.0000160089.43264.1A. [DOI] [PubMed] [Google Scholar]
- 15.Jack CR, Jr., et al. MR-based hippocampal volumetry in the diagnosis of Alzheimer's disease. Neurology. 1992;42(1):183–8. doi: 10.1212/wnl.42.1.183. [DOI] [PubMed] [Google Scholar]
- 16.Fox NC, et al. Presymptomatic hippocampal atrophy in Alzheimer's disease. A longitudinal MRI study. Brain. 1996;119(Pt 6):2001–7. doi: 10.1093/brain/119.6.2001. [DOI] [PubMed] [Google Scholar]
- 17.Kantarci K, et al. Risk of dementia in MCI: combined effect of cerebrovascular disease, volumetric MRI, and 1H MRS. Neurology. 2009;72(17):1519–25. doi: 10.1212/WNL.0b013e3181a2e864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Petersen RC, et al. Mayo Clinic Alzheimer's Disease Patient Registry. Aging (Milano) 1990;2(4):408–15. doi: 10.1007/BF03323961. [DOI] [PubMed] [Google Scholar]
- 19.Petersen RC, et al. Neuropathologic features of amnestic mild cognitive impairment. Arch Neurol. 2006;63:665–672. doi: 10.1001/archneur.63.5.665. [DOI] [PubMed] [Google Scholar]
- 20.American Psychiatric Association . Diagnostic and Statistical Manual of Mental Disorders (4th Ed) (DSM IV) American Psychiatric Association; Washington DC: 1994. [Google Scholar]
- 21.Knopman DS, et al. Antemortem diagnosis of frontotemporal lobar degeneration. Ann Neurol. 2005;57(4):480–8. doi: 10.1002/ana.20425. [DOI] [PubMed] [Google Scholar]
- 22.Ashburner J, Friston KJ. Unified Segmentation. NeruoImage. 2005;26(3):839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- 23.Vemuri P, et al. Alzheimer's disease diagnosis in individual subjects using structural MR images: validation studies. Neuroimage. 2008;39(3):1186–97. doi: 10.1016/j.neuroimage.2007.09.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Putter H, Fiocco M, Geskus RB. Tutorial in biostatistics: competing risks and multi-state models. Stat Med. 2007;26(11):2389–430. doi: 10.1002/sim.2712. [DOI] [PubMed] [Google Scholar]
- 25.Gray RJ. A class of K-sample tests for comparing the cumulative incidence of a competing risk. Annals of Statistics. 1988;16:1141–1154. [Google Scholar]
- 26.O'Quigley J, Prentice RL. Nonparametric tests of association between survival time and continuously measured covariates: the logit-rank and associated procedures. Biometrics. 1991;47(1):117–27. [PubMed] [Google Scholar]
- 27.Van Essen DC, et al. An integrated software suite for surface-based analyses of cerebral cortex. J Am Med Inform Assoc. 2001;8(5):443–59. doi: 10.1136/jamia.2001.0080443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Braak H, Braak E. Evolution of the neuropathology of Alzheimer's disease. Acta Neurol Scand Suppl. 1996;165:3–12. doi: 10.1111/j.1600-0404.1996.tb05866.x. [DOI] [PubMed] [Google Scholar]
- 29.Bakkour A, Morris JC, Dickerson BC. The cortical signature of prodromal AD: regional thinning predicts mild AD dementia. Neurology. 2009;72(12):1048–55. doi: 10.1212/01.wnl.0000340981.97664.2f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Henneman WJ, et al. Hippocampal atrophy rates in Alzheimer disease: added value over whole brain volume measures. Neurology. 2009;72(11):999–1007. doi: 10.1212/01.wnl.0000344568.09360.31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.McDonald CR, et al. Regional rates of neocortical atrophy from normal aging to early Alzheimer disease. Neurology. 2009;73(6):457–65. doi: 10.1212/WNL.0b013e3181b16431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Annesi I, Moreau T, Lellouch J. Efficiency of the logistic regression and Cox proportional hazards models in longitudinal studies. Stat Med. 1989;8(12):1515–21. doi: 10.1002/sim.4780081211. [DOI] [PubMed] [Google Scholar]
- 33.Jagust W, et al. Brain imaging evidence of preclinical Alzheimer's disease in normal aging. Ann Neurol. 2006;59(4):673–81. doi: 10.1002/ana.20799. [DOI] [PubMed] [Google Scholar]
- 34.Landau SM, et al. Associations between cognitive, functional, and FDG-PET measures of decline in AD and MCI. Neurobiol Aging. 2009 doi: 10.1016/j.neurobiolaging.2009.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nichols TE, Holmes AP. Nonparametric permutation tests for functional neuroimaging: a primer with examples. Hum Brain Mapp. 2002;15(1):1–25. doi: 10.1002/hbm.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]