Abstract
The implementation of the Effective Fragment Potential (EFP) method within the Q-Chem electronic structure package is presented. The EFP method is used to study non-covalent π – π and hydrogen-bonding interactions in DNA strands. Since EFP is a computationally inexpensive alternative to high-level ab initio calculations, it is possible to go beyond the dimers of nucleic acid bases and to investigate the asymptotic behavior of different components of the total interaction energy. The calculations demonstrated that the dispersion energy is a leading component in π-stacked oligomers of all sizes. Exchange-repulsion energy also plays an important role. The contribution of polarization is small in these systems, whereas the magnitude of electrostatics varies. Pairwise fragment interactions (i.e., the sum of dimer binding energies) were found to be a good approximation for the oligomer energy.
1 Introduction
Non-covalent interactions1–4 are at least an order of magnitude weaker than a typical chemical bond energy (100 kcal/mol), yet they govern such important processes as solvation, adsorption, condensation and crystallization. They play a crucial role in many biological processes such as protein folding5 and structure,6–9 enzyme catalysis, drug binding, the function of DNA and RNA, protein-DNA interactions,10–12 self-assembled supramolecular architecture,13,14 and molecular recognition.15–17 For example, the structure of the DNA double helix is determined by hydrogen bonding between the complimentary nucleobases (adenine-thymine and guanine-cytosine) and π-π interactions between the stacked bases (see Fig. 1). Non-covalent interactions also control the structure and function of intercalation compounds in DNA and RNA that are crucial for the understanding of replication and origin of life.10,18–20
Figure 1.

Hydrogen bonding and π-stacking interactions are equally important for the structural integrity of the double helix. The hydrogen bonding is responsible for keeping the strands together, while π-stacking determines the helical shape of the strands. Turning off either one of these interactions, as was done in a computational study of Hobza and coworkers,21 leads to the unfolding of the double helix.
Non-covalent interactions most often involve closed-shell species in which electron sharing between the fragments is negligible (hence, non-covalent), however, they also play a role in weakly-bound systems with some covalent character involving radicals (consider, for example, the (NO) dimer,22 solvated CN radical,23 Al-ethylene complex24).
Non-covalent interactions, such as hydrogen bonding, π-π and van der Waals, consist of electrostatic and dispersion forces. The strongest non-covalent interaction, hydrogen bonding (5–18 kcal/mol), is dominated by electrostatics and also includes partial covalent character (electron sharing between the two fragments). On the other end of the spectrum there are van der Waals interactions, which originate in a correlated motion of electrons, ranging from several Kelvin (e.g., He2) to several kcal/mol. The strength of π-π interactions, which is determined by an interplay between the electrostatics and dispersion, varies from 2–3 kcal/mol (as in the benzene dimer) to more than 10 kcal/mol (e.g., clusters of nucleobases).
Non-covalent interactions pose a challenge for computational methods.1,2 Their small magnitude calls for high accuracy. Dispersion is a purely electron correlation effect, and can only be captured by high-level correlated methods, such as the coupled-cluster with single, double and perturbative triple excitations [CCSD(T)] method. Moreover, large augmented atomic basis sets are needed for an accurate description of the inter-fragment region to mitigate basis set superposition errors (BSSE).
There are several computational strategies for modeling non-covalent interactions. For small systems, highly accurate results can be obtained using reliable ab initio methods.1,25–29 While such calculations are of great value for benchmark purposes, they are not applicable to extended systems due to the steep computational scaling of wave function based methods. Different approaches are being developed to overcome this problem ranging from linear scaling30–33 to energy additivity (ONIOM-like) and fragmentation techniques.2,34–38 Alternatively, weak intermolecular interactions can be treated as perturbations using wave functions (or electron densities) of the fragments, as done in symmetry-adapted perturbation theory (SAPT) and similar methods.26,39,40 More empirical approaches include dispersion-corrected density functional theory (DFT-D).41,42
On another end of the spectrum, there are quantum mechanics/molecular mechanics (QM/MM) approaches using empirical force fields.43–46 The QM/MM methods are very efficient, however, the empirical parameterization of the MM part undermines their predictive power. Moreover, some effects are notoriously difficult to describe by traditional (non-polarizable) force fields.
The effective fragment potential (EFP) method is developed as a non-empirical alternative to force-field based QM/MM.47–50 EFP, which is a QM based potential, is a more sophisticated approach than simple parameterized MM methods. The first variant of EFP (EFP1) was designed to describe aqueous solvent effects. It included Coulombic and polarization terms in the same rigorous fashion as in the general EFP method (see Section 2), however, the remaining terms (mainly exchange-repulsion) were fitted by an exponential function to match the total ab initio energy of the water dimer potential energy surface. Depending on the level of theory used for fitting, there are Hartree-Fock-based51 (EFP1/HF), MP2-based (EFP1/MP2), and DFT-based52 (EFP1/DFT) potentials. The fitted form of the exchange-repulsion term simplifies the coupling between the quantum and the EFP regions, and several QM/EFP1 models, with the quantum part described by HF, MP2, DFT, or MCSCF, have been implemented in GAMESS (General Atomic and Molecular Electronic Structure System).50,53 The functional form of EFP1 is similar to other polarizable embedding models, however, the parameterization is different. Recently, EFP1 has been integrated with configuration interaction singles (CIS),54 time-dependent DFT (TD-DFT),55 and multi-reference perturbation theory (MRPT).56 EFP1 has been employed in studies of chemical reactions in solutions,57,58 clusters,52,59,60 an SN2 reaction,61 amino acid neutral/zwitterion equilibria,62,63 and electronic excitations of chromophores in bulk water.55,64
To extend EFP beyond water, a more general approach with no empirically fitted parameters has been developed.48,65 This general EFP method is a computationally inexpensive way of modeling intermolecular interactions in non-covalently bound systems. The absence of fitted parameters and a natural partitioning of the interaction energy into Coulomb, polarization, dispersion, and exchange-repulsion terms make it an attractive choice for analysis and interpretation of intermolecular forces. Moreover, by construction, it is free from the BSSE that plagues ab initio calculations of weakly bound systems. The EFP Hamiltonian is pairwise, however, leading many-body effects are included through a self-consistent treatment of polarization.
The performance of the general EFP method (referred to as EFP2) has been benchmarked against high-level ab initio data for a variety of non-covalent systems, including those dominated by hydrogen-bonding, π – π, or mixed interactions. For example, in benzene dimers,66 the EFP total interaction energies and the EFP energy components were shown to agree well with the high-level ab initio values computed by CCSD(T) and SAPT.25,67,68 For the three benzene dimer structures (sandwich, parallel-displaced, and T-shaped) the largest discrepancy between EFP and CCSD(T)/aug-cc-pVQZ is 0.4 kcal/-mol in binding energies, and 0.2 Å in the equilibrium structures inter-fragment distances [in Ref. 69, the EFP, SAPT and CCSD(T) potential energy curves for various benzene structures were computed using frozen fragments geometries]. The agreement of the EFP interaction energies with the CCSD(T) values was better than that of MP2. Accurate evaluation of the electrostatic energy was found to be crucial for this system. For example, in the sandwich and parallel-displaced structures, the attractive Coulomb interactions are solely due to the charge-penetration effect, and, therefore, Coulomb damping is essential. Calculations of substituted benzene dimers (OH, CH3, F, and CN substituents) confirmed the high accuracy of EFP in predicting equilibrium structures and binding energies in π-stacked aromatic complexes and describing the trends in binding energies in dimers with electron-withdrawing or electron-donating substituents.70
The structures and energetics of different conformations of the styrene dimer, which feature various π – π, H-bonding, and mixed π-H interacting patterns, are correctly captured by EFP, as demonstrated by comparison against MP2.71
The prediction of structures and binding energies in water-benzene complexes, in which an interplay between π – π and H-π interactions results in unique structural patterns, is a stringent test for any computational technique. In these complexes, π – π and H-π interactions between benzenes and between benzene and water molecules are similar in strength and compete with H-bonds of water. EFP provides reliable results for these complicated systems, as compared to the CCSD(T) and MP2 methods. Interestingly, benzene molecules in a water environment are polarized and participate in the hydrogen-bond network of water.72
EFP has already enabled a number of insightful computational studies of extended systems. Some of the examples are highlighted below.
EFP studies of small water-methanol clusters revealed an incomplete mixing of water and methanol at the molecular level, i.e., heterogeneous structures were found to be consistently lower in energy than the homogeneously mixed structures. For the smallest clusters, these results were confirmed by MP2.73
EFP was also used in a study of the solvation of alanine.74,75 Structures of non-ionized and zwitterionic conformers of alanine in water obtained with Monte Carlo sampling were used for calculation of the free energy difference between the non-ionized and zwitterionic forms at the MP2 and DFT levels of theory in combination with the EFP1 potential for water and the polarizable continuum model (PCM) description of the bulk.
EFP was employed in studies of bulk properties of liquids using molecular dynamics simulations.76 Additionally, coarse-graining of the EFP potential has been explored on the basis of these simulations.77
Coupling the EFP potential to the quantum region through the frozen localized molecular orbital approach78 allowed calculations of pKa of various amino-acids in proteins.79,80
Recently, EFP2 was interfaced with the equation-of-motion coupled-cluster singles and doubles (EOM-CCSD) method to describe electronic excited states of chromophores in solution.81 A number of studies on the electronically excited states of biological chromophores using EFP combined with multi-reference methods have also been reported.82–85
In sum, numerous previous studies conducted with GAMESS50 have demonstrated that EFP is an accurate and robust approach to intermolecular interactions. The present work discusses implementation of the general EFP method in the Q-Chem electronic structure package.86 We apply EFP to investigate the asymptotic behavior of non-covalent interactions in the stacks of DNA bases. As discussed above, the relative contributions to non-covalent interactions have been investigated for a variety of small model systems (dimers and small clusters). The focus of this work is on the asymptotic behavior of different contributions in large systems. Our goal is to understand the physics behind non-covalent interactions, e.g., how the relative importance of different contributions changes with the system size, what is the magnitude of non-additive effects, etc. This knowledge is important for empirical method development, as discussed in a recent study of Sherrill and coworkers.3 We present the results for stacks of thymine and adenine at configurations relevant to the native DNA structure. We analyze the convergence of different components of the interaction energy to their bulk values. In the stacking interactions, the dispersion and exchange-repulsion play a significant role. The contribution of electrostatics varies. Regarding the range of interactions, the exchange-repulsion and dispersion are essentially short range interactions, while polarization and Coulomb terms have a much longer range. A detailed analysis of the interactions of heterocyclic aromatic compounds including DNA bases will appear in a separate publication.87
The structure of this paper is as follows. The next section describes the theory behind EFP and gives general expressions for different components of the interaction energy. Calculation of the EFP parameters is described in Section 3. The EFP calculations of nucleic acid base (NAB) oligomers are presented in Section 4. Programmable expressions and further details of the EFP implementation are given in the Supplementary Materials. Concluding remarks are presented in Section 5.
2 The EFP method
In EFP, one describes (relatively weak) intermolecular interactions using perturbation theory starting from the non-interacting (unperturbed) fragments. The intermolecular interactions can be represented as a series of short- and long-range terms. Long-range interactions, which are proportional to the distance according to 1/Rn, include Coulomb, induction (polarization), and dispersion terms, whereas short-range interactions that depend on the inter-fragment density overlaps consist of exchange-repulsion, charge-transfer, and screening terms.88
The total energy of a system containing both EFP and QM components consists of the interactions between the effective fragments (Eef−ef) and the energy of the QM region in the field of the fragments. The former includes Coulomb, polarization, dispersion and exchange-repulsion contributions (the charge-transfer term, which is important for a description of ionic and highly polar species,89 is omitted here):
| (1) |
The QM-EF interactions are computed as follows. The Coulomb and polarization parts of the EFP potential contribute to the quantum Hamiltonian via one-electron terms:
| (2) |
whereas dispersion and exchange-repulsion QM-EF interactions are treated as additive corrections to the total energy, i.e., similar to the fragment interactions. For fully quantum coupling, these contributions should also be included in the QM Hamiltonian, as, for example, has been done in Ref. 90.
In the present implementations, the fragments are rigid and their potentials can be generated from a set of ab initio calculations on each unique isolated fragment.91
The Q-Chem implementation includes a library of standard fragments with precomputed potentials. The EF potential includes: (i) multipoles (produced by Stone’s Distributed Multipolar Analysis) for Coulomb and polarization terms; (ii) static polarizability tensors centered at localized molecular orbital (LMO) centroids (obtained from coupled-perturbed Hartree-Fock calculations), which are used for calculations of polarization; (iii) dynamic polarizability tensors centered on the LMOs that are generated by time-dependent HF calculations and used for calculations of dispersion; and (iv) the Fock matrix, basis set, and localized orbitals needed for the exchange-repulsion term. In sum, all the EFP parameters are obtained from ab initio calculations on an isolated fragment and contain no empirically fitted parameters.
Below we describe the theoretical background of the different energy terms in the EFP method, followed by the detailed formulation and programmable expressions.
In the long-range perturbation expansion, the zero-order Hamiltonian Ĥ(0) is the Hamiltonian of the non-interacting fragments A and B, and the perturbation Ĥ′ is a particular (e.g., Coulomb) interaction between the fragments:
| (3) |
where |m〉 and |n〉 are the eigenfunctions of ĤA and ĤB, respectively. Following the non-degenerate Rayleigh-Schrödinger perturbation theory, the ground state energies (m = n = 0) of the the closed-shell molecules are:
| (4) |
where EA and EB are the energies of the individual isolated fragments, E(n) are the perturbative corrections of order n, and is the energy of the state |mn〉 for the two non-interacting fragments.
The first order perturbative correction E(1) is the expectation value of the Coulomb interaction Ĥ(0) for the ground state |00〉. EFP describes the Coulomb interaction by a distributed multipole expansion (Section 2.1). The second order perturbative correction consists of polarization (induction) and dispersion terms:
| (5) |
The polarization component of EFP is accounted for by distributed polarizabilities (Section 2.2). The dispersion interaction is expressed as an inverse R dependence:
| (6) |
where coefficients Cn are derived from the frequency-dependent distributed polarizabilities (Section 2.3). The higher order terms in the perturbative expansion, Eq. (4), are expected to have smaller values and are neglected in the current EFP formalism. One of the reasons for the success of EFP69 is that some of the higher-order terms apparently cancel each other. For example, charge-transfer and exchange-induction are similar in magnitude, but have opposite signs and thus cancel out. The exchange-dispersion partially cancels higher order dispersion terms (such as induced dipole-induced quadrupole) that are also omitted in the EFP formalism.69
The perturbative treatment of intermolecular interactions described above works well at large separations between fragments, but breaks down when molecules approach each other such that their electronic densities overlap. EFP accounts for this effect by including short-range terms, i.e., the exchange-repulsion interaction (Section 2.4) and charge-penetration corrections to the long-range terms.69
The exchange-repulsion interaction is derived as an expansion in the intermolecular overlap, truncated at the quadratic term,92,93 which requires that each effective fragment carries a basis set that is used to calculate overlap and kinetic one-electron integrals for each interacting pair of fragments (see Section 2.4).
The long-range terms are modulated by damping (or screening) expressions. The classical point multipole model breaks down when fragments approach too closely, since then the actual electron density on the two fragments is not well approximated by point multipoles. Consequently, at short separations between fragments, the Coulomb interactions become too repulsive, whereas the induction and dispersion interactions become too attractive. Damping terms are discussed in sections 2.1 and 2.3.
2.1 Coulomb energy
The Coulomb component of the EFP energy accounts for Coulombic interactions. In molecular systems with hydrogen bonds or polar molecules, this is the leading contribution to the total intermolecular interaction energy.94
Buckingham94 has shown that the Coulomb potential of a molecule at point x can be expressed using a multipole expansion around point k:
| (7) |
where q, μ, Θ, and Ω are the net charge, dipole, quadrupole, and octopole, respectively, and T, Ta, Tab, and Tabc are the electrostatic tensors of the zero, first, second, and third ranks, respectively. This expression converges to the exact electrostatic potential when a complete (infinite) number of terms is included. However, the convergence is slow95 and a large number of terms is required to achieve reasonable accuracy, even when such expansions are assigned to the individual atoms using a Mulliken population analysis.96 Thus, single point or atomic-based representations of the molecular electrostatic potential are impractical.
An accurate representation of the electrostatic potential, which has been exploited in the EFP approach,47,51 is achieved by using a multipole expansion (obtained from Stone’s distributed multipole analysis) around atomic centers and bond midpoints (i.e., the points with high electronic density) and truncating this expansion at octopoles.95,97 The expansion points for water are shown in Fig. 2.
Figure 2.
The distributed multipole expansion points for a water molecule. The electrostatic potential of an effective fragment is specified by charges, dipoles, quadrupoles and octopoles placed at atomic centers and bond midpoints.
The fragment-fragment Coulomb interactions consist of charge-charge, charge-dipole, charge-quadrupole, charge-octopole, dipole-dipole, dipole-quadrupole, and quadrupole-quadrupole terms, as well as terms describing interactions of multipoles with the nuclei and nuclear repulsion energy. The corresponding equations are given in Supplementary Materials.
The Coulomb interaction between an effective fragment and the QM part is described by a perturbation V̂ of the ab initio Hamiltonian:
| (8) |
The perturbation enters the one-electron part of the Hamiltonian as a sum of contributions from the expansion points k and nuclei I of the effective fragments A:
| (9) |
where p and q are atomic orbitals in the ab initio region, ZI is a nuclear charge, dpq is an element of the atomic density matrix and is the Coulomb potential from the expansion point k.
The one-electron contribution to the Hamiltonian from the individual expansion point k consists of four terms originating from the electrostatic potential of the corresponding multipole:47
| (10) |
where R, a, b and c are the distance and its Cartesian components between the electron and the expansion point k. The first integral in Eq. (10) has the same form as an electron–nucleus attraction integral, however, the remaining terms are not typically encountered in standard electronic structure calculations. Such integrals are readily evaluated in Gaussian basis sets using Obara–Saika recurrence relations,98 which we have implemented within Q-Chem’s general multipole one-electron integral code.
Charge penetration
The multipole representation of the Coulomb density of a fragment breaks down at close separations between the fragments. The multipole interactions become too repulsive due to significant overlap of the electronic densities and the charge-penetration effect. The magnitude of the charge-penetration effect is usually around 15% of the total Coulomb energy in polar systems, however, it can be as large as 200% of the Coulomb energy in systems with weak Coulomb interactions.66 Several electrostatic screening functions have been considered.69,99 In the present implementation, we use the simple exponential damping of the charge-charge term, which was shown to efficiently account for most of the charge-penetration effect.99 Screening of the higher-order multipoles, which can also be important, is not considered here. The charge-charge screened energy between the expansion points k and l is given by the following expression, where αk and αl are the damping parameters associated with the corresponding expansion points:
| (11) |
Generation of the damping parameters is discussed in Section 3.
Ab initio-EFP Coulomb interactions are calculated without damping corrections in the implementation presented here.
2.2 Polarization energy
Polarization (induction) accounts for the intramolecular charge redistribution in response to an external electric field. It is the major component of many-body interactions responsible for cooperative molecular behavior. Since polarization cannot be parameterized by pairwise potentials, it is often neglected in molecular mechanics models. However, in hydrogen bonded systems, up to 20% of the total intermolecular interaction energy is due to polarization.47
The polarization interaction appears in the second order of long-range perturbation theory, see Eq. (4). Expanding the Coulomb potential V in a series and combining terms with the same electric field derivatives yields the following equation:
| (12) |
where Fa and Fab are the first and second electric field derivatives, α is the static dipole polarizability tensor, β is the static dipole hyperpolarizability, and A, B and C are quadrupole polarizability tensors.
The EFP method employs distributed polarizabilities placed at the centers of the valence LMOs. This allows the truncation of the expansion in Eq. (12) after the first term while retaining reasonable accuracy.47 Unlike the isotropic total molecular polarizability tensor, the distributed polarizability tensors are anisotropic. Polarizability points for a water molecule are shown in Fig. 3.
Figure 3.

Distributed polarizabilities for a water molecule described by dipole polarizability tensors, see Eq. (12).
The polarization energy of a system consisting only of effective fragments is:
| (13) |
where are the Cartesian components of the induced dipoles at the distributed point k, and are the Cartesian components of the external field due to static multipoles and nuclei of other fragments. The induced dipoles at each polarizability point are computed as:
| (14) |
where the total field comprises the static field plus the field due to other induced dipoles :
| (15) |
It follows from the above equation that the induced dipoles on fragment A depend on the values of the induced dipoles of all other fragments (B). (R and a,b are the distance and its Cartesian components) is the second-order Coulomb tensor. Therefore, the induced dipoles on fragments should be computed self-consistently. Eq. (15) can be rewritten as:
| (16) |
or
| (17) |
where the tensor is defined as:
| (18) |
Thus, to determine the induced dipoles, one formally needs the inverse of the matrix . A more efficient approach used in the EFP method is based on solving Eq. (17) iteratively.
In a system consisting of effective fragments and an ab initio region, the total electric field Fai total acting on an effective fragment consists of the static and induced fields due to other effective fragments, as well as fields due to the electron density Fai elec and nuclei Fai nuc of the ab initio part:
| (19) |
The field due to the ab initio electron density is expressed through the electric field operator f̂elec as:
| (20) |
Thus, the induced dipoles on the effective fragments depend on the ab initio electron density, which, in turn, is affected by the field created by these induced dipoles through a one-electron contribution to the Hamiltonian:
| (21) |
where R and a are the distance and Cartesian components between an electron and the polarizability point k. is the conjugate induced dipole:
| (22) |
where is the transposed polarizability tensor at the polarization point k.
The total polarization energy is computed self-consistently using a two level iterative procedure illustrated in Fig. 4. The objectives of the higher and lower levels are to converge the wave function, and induced dipoles for a given fixed wave function, respectively.
Figure 4.
Computing the induced dipoles through the two-level self-consistent iterative procedure. Ψ is the ab initio wave function, μ is a set of induced dipoles, FΨ is the field due to the wave function and Fμ is the field due to the induced dipoles.
At every higher-level iteration, the wave function is updated based on the values of the induced dipoles from the previous step. Then the field from this new wave function acting on the polarizability points is recomputed. The convergence criterion is that the wave function parameters (e.g., molecular orbital coefficients) are within a predefined range from their values on the previous iteration.
At the lower level, the values of the induced dipoles are computed at every iteration based on the electric field from the ab initio part (which remains constant during the lower-level iterations), as well as the static and induced fields from the previous lower-level iteration. The convergence criterion is that the difference between the new induced dipoles and those from the previous iteration is within a predefined threshold.
Thus, the lower-level iterative procedure exits when the induced dipoles are self-consistent and are consistent with a frozen ab initio wave function. Convergence of the higher-level iterative procedure yields self-consistent induced dipoles and the ab initio wave function. If the system does not contain the ab initio part, only the lower-level procedure is required.
Once the values of the induced dipoles are obtained, the total polarization energy of the system can be computed as:47
| (23) |
The self-consistent treatment of the polarization accounts for many-body interaction effects. The present implementation does not include damping of the polarization energy.69
2.3 Dispersion
Dispersion provides a leading contribution to stabilization in aromatic π-stacked compounds such as DNA strands. However, an accurate description of dispersion is a difficult task since it arises due to the correlated motion of electrons.
The exact expression for the dispersion energy appears in the second order of long-range perturbation theory. Expanding the electrostatic potential V in the series in Eq. (4), the dispersion energy can be expressed in the so called London series:
| (24) |
where the Cn coefficients correspond to induced dipole—induced dipole (C6), induced dipole—induced quadrupole (C8), induced quadrupole—induced quadrupole and induced dipole—induced octopole (C10) interactions. Additionally, odd power terms (R−7, R−9, etc) appear in the expansion for non-centrosymmetric molecules or LMOs.100
Similarly to the other EFP terms, the dispersion is treated in a distributed fashion, with expansion points located at the LMO centroids, i.e., at the same centers as the polarization expansion points. Reasonable accuracy is achieved by truncating the London expansion, Eq. (24), after the first term and approximating the rest as 1/3 of this term.101
The induced dipole-induced dipole dispersion energy between the expansion points k and l can be computed by using the following equation:
| (25) |
where and are dynamic polarizability tensors, iν is the the imaginary frequency, and are the second-rank electrostatic tensors. The indices k, l refer to LMOs on the two interacting fragments, and the indices a, b, c, d run over x, y, z. The interaction energy described by Eq. (25) is anisotropic, distance-dependent and computationally expensive.101 The approximation used in EFP includes only the trace of the polarizability tensors, which is isotropic and distance-independent.
The total dispersion energy for a system of effective fragments is:
| (26) |
where A and B are effective fragments, k and l are LMO centroids, is the dispersion coefficient, and Rkl is the distance between two LMO centroids.
Intermolecular dispersion coefficients for each pair of expansion points k and l are computed using the 12 point Gauss-Legendre integration formula:
| (27) |
where α−k(iνi) and α−l(iνi) are 1/3 of the traces of the corresponding polarizability tensors.
For small distances between effective fragments, dispersion interactions must be corrected for charge penetration and the electron density overlap effect. This is ensured by the Tang—Toennies damping formula102 with parameter b = 1.5, similarly to the original EFP implementation:
| (28) |
We should note, however, that recent studies revealed that this formula over-damps the dispersion and a more appropriate damping function is based on the intermolecular overlap.69
Ab initio-EFP dispersion interactions in the present implementation are treated as EFP-EFP interactions, i.e., the QM region is represented as a fragment, and the dispersion QM-EFP interaction is evaluated using Eq. (26).
2.4 Exchange-repulsion
Exchange-repulsion originates from the Pauli exclusion principle, which states that the wave function of two identical fermions must be anti-symmetric. In traditional classical force fields, exchange-repulsion is introduced as a positive (repulsive) term, e.g., in the Lennard-Jones potential. However, since the Pauli exclusion principle is intrinsically quantum mechanical, its classical description may not be sufficiently accurate. The EFP method uses a wave function-based formalism to account for the electron exchange.
The EFP exchange-repulsion energy term has been derived from the exact equation for the exchange-repulsion energy of two closed-shell molecules:65,92,93
| (29) |
where A and B are two molecules described by ΨA and ΨB wave functions, V̂AB is the intermolecular Coulomb interaction, and  is the anti-symmetrization operator:
| (30) |
where Pi is a permutation of i electron pairs consisting of one electron from each molecule.
Truncating sequence (30) after the second term and applying an infinite basis set and a spherical gaussian overlap approximation led to the following expression for the exchange-repulsion energy in terms of localized molecular orbitals:65,92
| (31) |
| (32) |
where A and B are the effective fragments, i, j, k and l are the LMOs, I and J are the nuclei, S and T are the intermolecular overlap and kinetic energy integrals, respectively, and F is the Fock matrix element.
The expression for involves overlap and kinetic energy integrals between pairs of localized orbitals. In addition, since equation (32) is derived within an infinite basis set approximation, a reasonably large basis set is required for accuracy, i.e. 6-31+G(d) is considered to be the smallest acceptable basis set, 6-311++G(3df,2p) is recommended. These factors make the exchange-repulsion the most computationally expensive part of EFP energy calculations in moderately sized systems (excluding charge-transfer89).
Large systems require additional considerations. Eq. (31) contains a sum over all fragment pairs and its computational cost formally scales as O(N2) with the number of effective fragments N. However, exchange-repulsion is a short-range interaction because the overlap and kinetic energy integrals decay exponentially with the inter-fragment distance. Therefore, by employing a distance-based screening, the number of essential overlap and kinetic energy integrals scales as O(N). Consequently, for large systems the cost of exchange-repulsion will eventually become smaller than the evaluation of the long-range EFP components (such as Coulomb interactions).
The ab initio-EFP exchange-repulsion energy is currently calculated at the EFP-EFP level, by representing the quantum part as an EFP and using Eq. (32). In this way, the quantum Hamiltonian is not affected by the exchange potential of the fragments. The rigorous quantum coupling between the ab initio and EFP regions has been recently developed, but the computational cost is high.90
3 Generation of the EF potentials and the fragment library
The EF potential consists of the following parameters: coordinates of atoms, coordinates of the multipolar expansion points (typically, atoms and bond mid-points), the distributed multipole moments (up to octopoles), the electrostatic screening parameters, the coordinates of the LMO centroids, the static and dynamic polarizability tensors at the LMO centroids, the wave function and Fock matrix elements in the basis of the localized molecular orbitals, and the atomic labels of the EF atoms.
Coordinates of effective fragments
The position of a fragment is specified in terms of translation coordinates (x, y, z) and rotation by the Euler angles (α, β, γ) relative to the fragment frame, i.e., coordinates of the standard fragment that are provided along with the other fragment parameters (see Fig. 5). The rotation matrix corresponding to these angles is:
| (33) |
Figure 5.
Representing the orientation with the Euler angles. xyz is the fixed system, XYZ is the rotated system, N is the intersection between the xy and XY planes called the line of nodes. Transformation between the xyz and XYZ systems is given by α rotation in the xy plane, followed by β rotation in the new y′z′ plane (around the N axis), followed by γ rotation in the new x″y″ plane.
Coulomb parameters
The distributed multipoles q, μ, Θ, Ω are obtained from an ab initio electronic density of the individual fragment using the distributed multipole analysis (DMA) procedure developed by Stone.95,97 First, a molecular wave function expressed in the basis of N gaussians is computed with an ab initio (typically, HF) method. Then, spherical multipole expansions are calculated at the centers of the gaussian basis function products. These expansions are finite and include multipoles up to order L1 + L2 where L1 and L2 are angular moments of the two gaussians. These multipoles are translated to the EFP expansion points (atomic centers and bond midpoints) as described in Ref. 95, and truncated after the 4th term. This set of spherical multipoles is converted to traceless Buckingham multipoles using the equations provided in the Supplementary Materials.
Coulomb damping parameters
The screening parameters α [Eq. (11)] are computed using a fitting procedure described in details in Refs. 66, 99, once for every type of fragment. This procedure optimizes the screening parameters so that the sum of the differences between the ab initio Coulomb potential (typically, the HF potential) and the EFP Coulomb potential with screening is minimized:
| (34) |
where the sum is taken over all points p of the grid. The screened EFP potential VCoul, damp has the following form:
| (35) |
where the damping function fdamp is:
| (36) |
The grid is constructed such that it includes the regions of space that are important for intermolecular interactions, i.e., between 0.7 and 3.0 van der Waals radii of each atom in the fragment. A projection of such a grid for a water molecule is shown in Fig. 6.
Figure 6.
The shape of the grid (gray area) for fitting the screening parameters of a water molecule.
Polarization parameters
The EF polarization parameters are the centers of LMOs and the polarizability tensors. The LMOs are obtained with the Boys localization procedure based on the ab initio electronic density.103,104 Polarizabilities are obtained as the derivatives of the dipole moment (μ) with respect to electric field (F):
| (37) |
We use a finite difference procedure in which the dipole moment of an LMO is computed with and without an electric field and the polarizability tensor is computed as:
| (38) |
Dispersion parameters
The dispersion parameters for an effective fragment are the coordinates of the LMO centroids and, for each LMO, the sets of traces of the dynamic polarizability tensors obtained at 12 frequencies corresponding to the Gauss-Legendre quadrature intervals. Dynamic polarizabilities can be computed using dynamic time-dependent Hartree-Fock (TDHF) or dynamic TD-DFT as described in Ref. 101.
Exchange-repulsion parameters
The parameters required for evaluation of the exchange-repulsion energy [Eq. (32)] are the elements of the Fock matrix and the LMO information (orbital coefficients, basis set, and the LMO centroids) for each unique fragment. These parameters are extracted from a Hartree-Fock calculation followed by the orbital localization procedure (e.g., Boys localization).93
Effective fragment library
To simplify EFP calculations, a library of standard fragments with precomputed effective fragment potentials has been developed. Currently, the library includes 12 common organic solvents (see Supplementary Materials): acetone, carbon tetrachloride, dichloromethane, methane, methanol, ammonia, acetonitrile, water dimethyl sulfoxide, benzene, phenol, and toluene, as well as fragment potentials for five nucleobases (adenine, thymine, cytosine, guanine, and uracil). The geometries of the solvent molecules were optimized using MP2/cc-pVTZ. Their EFP parameters were obtained using the HF method with the 6-31+G(d) (electrostatic multipoles and damping coefficients) and 6-311++G(3df,2p) (all other parameters) basis sets. For nucleobases, RI-MP2/cc-pVTZ optimized geometries were used. Their EFP parameters were obtained with the 6-31G* (electrostatic multipoles and damping coefficients) and 6-311++G(3df,2p) (all other parameters) bases. The EFP parameters were obtained using the GAMESS program and converted to the Q-Chem format using a set of scripts (see Supplementary Materials for details).
4 Asymptotic behavior of non-covalent interactions in nucleobase oligomers
Nucleic acid base pairs and their stacked structures form the stable double-helical structure of DNA (see Fig. 1). Several factors contribute to the stability of the structure of DNA,21 and their relative importance may depend on the size of the system. Our study addresses the following questions:
How do relative contributions of various energy components (Coulomb, polarization, exchange-repulsion and dispersion) depend on the size of the oligomer?
Which components of the energy give rise to long range interactions and which components consist of only short range interactions?
How do far-field (non-nearest-neighbor) energy components depend on the cluster size? Can the sums of the dimer interaction energies be used to estimate the interaction energies for large oligomers with sufficient accuracy?
The term “fragment interaction energy” (or “interaction energy”) refers to the total EFP energy, which is the energy due to the interaction between the effective fragments.
In this work we follow the analysis of pairwise contributions in benzene oligomers by Sherrill and co-workers27 and Tschumper and co-workers.105 The goal is to investigate whether a simple sum of dimer energies is a good approximation for the interaction energies of the oligomer chains and to analyze the convergence of the different components of the interaction energy to their bulk values.
We begin by calibrating EFP against ab initio calculations using stacked and H-bonded adenine (AA) and thymine dimers (TT) (see Supplementary Materials). The agreement of the EFP stacked dimer and H-bonded dimer energies is within 1.5 kcal/mol and 3.5 kcal/mol, respectively, of the MP2 energies (note that the error bars of MP2 energies are of similar magnitude).106–108 We then proceed to investigate how the interaction energies depend on the relative orientation of the fragments (Section 4.1). The relative contributions of the various components of the EFP energies for adenine and thymine stacked structures are analyzed in Section 4.2. We then investigate the spatial extent of these interactions as well as the far-field component (i.e., the fraction which is not recovered by the energies of the neighboring dimers) of the various components (Sections 4.3 and 4.4) following the analysis in Refs. 27 and 105.
4.1 The effect of fragment rotation on interaction energy in the adenine and thymine dimers
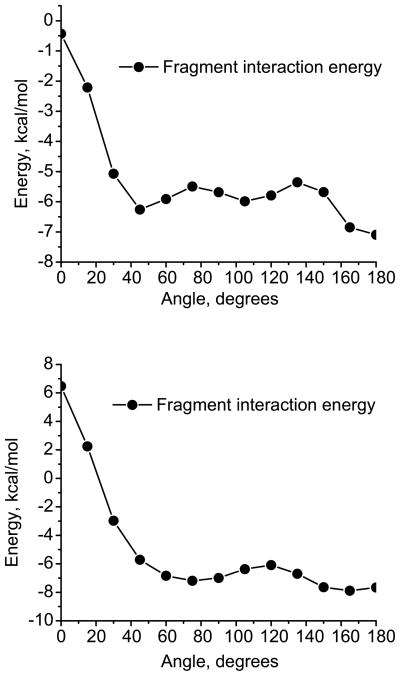
The experimental structure of the B-DNA helix can be described as the stacked AA/TT dimers with the fragments twisted by about 38° and slightly displaced in the XY plane (see Fig. 8). We begin by investigating the dependence of the interaction energy of the stacked dimers on the rotation around adenine or thymine centers of mass (see Fig. 7). Since the distance between the AA/TT dimers in B-DNA is ≈ 3.33 Å, we investigate the effect of relative fragment rotation at the inter-fragment distance of ≈ 3.33 Å. The dependence of the interaction energy and its various components on this rotation angle α is shown in Figs. 9 and 10, respectively.
Figure 8.
The h-twist (Ω), tilt (Θ), and displacement in the DNA helix. (a) The arrow indicates the rotation (h-twist) around the center of the base pair. This scissor-like motion results in a displacement in the XY plane along with a rotation of the adenine/thymine stacked dimers. (b) The arrow indicates the tilt angle between the planes of the adjacent base-pairs. (c) The arrow indicates the lateral displacement of the centers of the adjacent base pairs.
Figure 7.
The rotation angle α in the stacked AA (left) and TT (right) dimers. The angle is defined as a rotation of the adenine or thymine monomer around its center of mass in the XY plane.
Figure 9.
The dependence of the fragment interaction energy (kcal/mol) on the rotation angle α between the fragments in the stacked AA (top) and TT (bottom) dimers. The fragments are parallel and the inter-fragment distance is fixed at 3.33 Å. There is no displacement in the XY plane.
Figure 10.
The dependence of the different energy components (in kcal/mol) on the rotation angle α between the fragments in the stacked AA (top) and TT (bottom) dimers. The fragments are parallel and the inter-fragment distance is fixed at 3.33 Å. There is no displacement in the XY plane.
As follows from Fig. 9, the structure with two parallel stacked adenines with no rotation has low stabilization energy of ≈ 0.5 kcal/mol. The stabilization energy increases monotonically with the α angle increase from 0° to 45°, and then decreases. Inspection of the individual components of the interaction energy (Fig. 10, top) reveals that the maximum change in stabilization is due to the increase in Coulomb stabilization and the reduction of the exchange-repulsion de-stabilization. The dispersion and polarization energies do not significantly contribute to the variations in stability due to the twist in the adenine dimers.
Fig. 9 (bottom) shows the change in the fragment interaction energy with respect to the relative rotation between the thymine monomers in the TT stacked dimer. The trend is similar to that in the adenine dimers. The main difference is observed for the zero twist configuration, where the thymine dimers are not stable (the dimer has a destabilization energy of 6 kcal/mol) due to unfavorable charge-dipole interactions (the charge-dipole interaction in thymine is +1 kcal/mol whereas it is −6 kcal/mol in adenine). The change in energy due to the rotation is also more pronounced in the case of thymine (≈ 14 kcal/mol) than in adenine (≈ 6 kcal/mol) mainly due to a more polar nature of thymine. Therefore, greater stabilization energy is gained due to the alignment of the polar NH and CO bonds at a relative angle of 60°, as discussed in a recent study of TT and AA dimers.109
Fig. 10 (bottom), which summarizes the changes in the energy components due to the fragment rotation in the thymine dimer, shows that the components that exhibit substantial changes are Coulomb and exchange-repulsion. Near the rotation angle of α = 40°, which is close to that of the B-DNA structure, the total fragment interaction energy is ≈ −6 kcal/mol with the Coulomb component being ≈ −2.5 kcal/mol.
However, in addition to the relative rotation, the B-DNA structure also includes a displacement in the XY plane and the angle of rotation in the real B-DNA structure, known as the “h-twist”, is different from the simple rotation angle α discussed above. The effect of the h-twist (see Fig. 8) causes a lateral displacement between the adenine/thymine molecules due to the axis of rotation being in the center of the adenine-thymine base pair. Thus, this scissor-like motion around the center of the base pair, changes the distance between the thymine dimers (in the XY plane) along with the relative angle between the dimers.
Table 1 shows the effect of the h-twist on the interaction energy components of the thymine dimers (see also Supplementary Materials). As one can see, the h-twist affects the exchange-repulsion and dispersion energies much more than a simple rotation around the center of the molecule. The change in the Coulomb energy along the h-twist angle plays a relatively small role compared to the corresponding change in exchange-repulsion.
Table 1.
The effect of the h-twist (Ω, see Fig. 8) on the fragment interaction energies (in kcal/mol) of the stacked thymine dimer.
| Angle | Frag. interaction energy | Coulomb energy | Exch-repulsion energy | Polarization energy | Dispersion energy |
|---|---|---|---|---|---|
| 0 | 5.356 | 1.338 | 17.214 | −0.467 | −12.728 |
| 15 | −1.205 | 2.259 | 6.694 | −0.367 | −9.790 |
| 30 | −3.583 | 0.774 | 2.639 | −0.300 | −6.696 |
| 45 | −3.475 | −0.009 | 1.007 | −0.261 | −4.212 |
4.2 Relative contribution of the components of the interaction energy
Numerous theoretical studies have investigated the nature of non-covalent interactions.2,110–117 Owing to the high cost of ab initio calculations, the bulk of these calculations have been performed for dimers, with a handful of trimer and tetramer studies.1–3 The various components of interaction energy in small model clusters have also been studied.3,25,66 The goal of the present calculations is to understand how the components of the total fragment interaction energy vary with the size of the oligomers.
To understand the effect of long-range interactions of stacked nucleobases in DNA, we consider model oligomers of up to 20 stacked bases. The stacks were constructed by using the twist, tilt and displacements (as shown in Fig. 8) from the crystal structure of B-DNA, i.e., the parameters for AA and TT dimers were extracted from the crystal structure and then 10 such identical dimers were replicated.
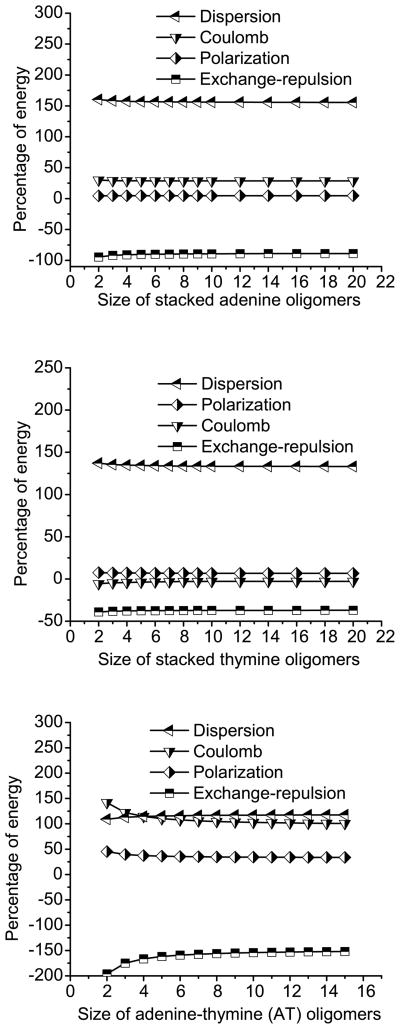
Fig. 11 shows the percentage contribution of the different components of the interaction energy for stacked adenine/thymine oligomers as a function of the oligomer size. The relative contributions are rather insensitive to the length, which is somewhat surprising. Dispersion is the leading component in oligomers of all sizes in both adenine and thymine stacks. The attractive dispersion and Coulomb energies are balanced by the destabilization due to exchange-repulsion. The polarization contribution is relatively small in all of the oligomers. The only difference between the adenine and thymine stacks is the magnitude of the Coulomb component. Unexpectedly, the Coulomb component in the thymine stacks is quite small (almost negligible) due to the combined effect of the displacement in the XY plane and the twist of 38° (as shown in Table 1).
Figure 11.
Percentage contribution of each component to the fragment interaction energy of adenine (top), thymine (middle) and adenine-thymine (bottom) stacked oligomers of various lengths.
In the case of the adenine-thymine oligomers, where a dimer is defined as (AT)2, the Coulomb and dispersion components are comparable to each other and provide the major part of the stabilization energy. This is due to the predominance of Coulomb in the H-bonded interactions in adenine-thymine pairs. The importance of polarization, though smaller than the Coulomb and dispersion terms, is significantly higher than in the case of individual adenine or thymine stacks due to H-bonded nature of the dimers.
These results suggest that the importance of the different components of the fragment interaction energy does not vary significantly with the system size. The dispersion and exchange-repulsion always play the dominant role in these π – π interactions, while the polarization contribution is small. However, the Coulomb part of the interaction energy can vary significantly depending on the system and relative fragment orientation.
4.3 Long-range interaction
To understand the effect of long- and short-range interactions and the relative importance of different components, we examined the same 20 units long oligomer stacks of adenine and thymine. Tables 2 and 3 show the total fragment interaction energies and their components for different oligomers. The absolute values of all energy components increase monotonically with the stack length due to the increasing number of interactions. Intuitively, the most important interactions are between the nearest neighbors. For the stack of N fragments, there are N − 1 such two-body interactions. To quantify the change in energy per interacting pair with the size of the oligomer, we considered a more relevant quantity, that is, the fragment interaction energy scaled by . Fig. 12 shows the scaled components of the fragment interaction energy. As one can see, each of the components scaled per number of the nearest-neighbor two-body interactions is fairly size-independent. This confirms that the leading contribution indeed comes from the nearest-neighbor two-body interactions.
Table 2.
Different components of the fragment interaction energy (in kcal/mol) for stacked adenine oligomers.
| Length of oligomers | Frag. interaction energy | Coulomb energy | Exch-repulsion energy | Polarization energy | Dispersion energy |
|---|---|---|---|---|---|
| 2 | −6.74 | −2.02 | 6.38 | −0.29 | −10.80 |
| 3 | −13.85 | −4.04 | 12.74 | −0.63 | −21.92 |
| 4 | −21.01 | −6.06 | 19.10 | −0.97 | −33.08 |
| 5 | −28.18 | −8.10 | 25.46 | −1.30 | −44.24 |
| 6 | −35.37 | −10.14 | 31.84 | −1.64 | −55.42 |
| 7 | −42.56 | −12.19 | 38.20 | −1.98 | −66.59 |
| 8 | −49.75 | −14.24 | 44.57 | −2.31 | −77.76 |
| 9 | −56.95 | −16.30 | 50.93 | −2.65 | −88.93 |
| 10 | −64.14 | −18.35 | 57.30 | −2.99 | −100.11 |
| 12 | −78.53 | −22.44 | 70.02 | −3.67 | −122.44 |
| 14 | −92.93 | −26.54 | 82.75 | −4.35 | −144.79 |
| 16 | −107.3 | −30.64 | 95.49 | −5.04 | −167.13 |
| 18 | −121.7 | −34.75 | 108.22 | −5.72 | −189.47 |
| 20 | −136.1 | −38.85 | 120.95 | −6.41 | −211.82 |
Table 3.
Different components of the fragment interaction energy (in kcal/mol) for stacked thymine oligomers.
| Length of oligomers | Frag. interaction energy | Coulomb energy | Exch-repulsion energy | Polarization energy | Dispersion energy |
|---|---|---|---|---|---|
| 2 | −3.75 | 0.21 | 1.47 | −0.28 | −5.15 |
| 3 | −7.68 | 0.35 | 2.93 | −0.56 | −10.41 |
| 4 | −11.63 | 0.48 | 4.40 | −0.83 | −15.68 |
| 5 | −15.60 | 0.59 | 5.87 | −1.09 | −20.96 |
| 6 | −19.57 | 0.69 | 7.34 | −1.36 | −26.24 |
| 7 | −23.57 | 0.76 | 8.81 | −1.61 | −31.52 |
| 8 | −27.55 | 0.84 | 10.28 | −1.87 | −36.80 |
| 9 | −31.53 | 0.93 | 11.75 | −2.12 | −42.09 |
| 10 | −35.51 | 1.02 | 13.22 | −2.38 | −47.37 |
| 12 | −43.44 | 1.23 | 16.16 | −2.90 | −57.93 |
| 14 | −51.37 | 1.45 | 19.10 | −3.42 | −68.50 |
| 16 | −59.32 | 1.64 | 22.04 | −3.94 | −79.06 |
| 18 | −67.26 | 1.85 | 24.98 | −4.46 | −89.62 |
| 20 | −75.19 | 2.05 | 27.91 | −4.98 | −100.17 |
Figure 12.
Different components of the interaction energy (in kcal/mol) scaled by the number of the nearest two-body interaction as a function of the oligomer size for adenine (top), thymine (middle) and adenine-thymine (bottom) stacks.
Let us now consider the derivative of the plots from Fig. 12 scaled to the inverse of the component itself, i.e. , where E is the energy component, dE is the change in the energy component and dN is the change in the length of the stacked oligomers (Fig. 13). These plots provide a measure of the rate of change of the energy components with the size of the oligomers. The asymptotic behavior of the derivative plot (insets in Fig. 13) shows the length scales over which each interaction occurs and contributes to the respective component of the energy.
Figure 13.
Derivatives of the interaction energy components per number of the nearest two body interactions scaled to the component as a function of the oligomer length. The inset zooms into the data for largest size oligomers.
For both adenine and thymine, the derivative for the exchange-repulsion energy is nearly zero for all sizes of oligomers, which is consistent with the short-range pair-wise character of this term. At the asymptotic limit, the maximum value in the derivative plots for adenine occurs for polarization followed by Coulomb and dispersion. This is somewhat counter-intuitive since the Coulomb energy includes the charge-charge interactions that scale as and are expected to exhibit the slowest decay. However, the polarization decays more slowly. A closer examination of the different components of the Coulomb energy provides an explanation. The leading contribution to the Coulomb terms is not the charge-charge term but the dipole-dipole and charge-dipole terms. This results in a faster than decay of the Coulomb interaction energy. Overall, the decay holds for charged species only, whereas for neutrals the leading Coulomb term is almost always dipole-dipole and decreases as .
The derivative plots for thymine oligomers are somewhat different — the Coulomb component exhibits very large changes even at longer oligomer sizes, showing the long-range nature of the Coulomb component consistent with intuitive expectations based on decay of the predominant charge-charge term in the Coulomb component. However, due to the small absolute values of the Coulomb component, the long-range nature of Coulomb interactions in the thymine oligomers is of minor importance. The shoulder in the Coulomb component of the derivative plot of the thymine oligomers may possibly be an artifact of the very small Coulomb energy and the sensitive cancellations between the various components of the Coulomb energy.
The derivative plots for the adenine-thymine oligomers show a trend that is very different from the individual adenine and thymine oligomers. The rate of change is much higher than in the pure stacks and so is the order in which the individual components differ. This is mainly due to the fact that in each of the (AT)n oligomers there are varying numbers of different interactions (H-bonded AT, cross H-bonded AT and stacking interactions for AA and TT, as shown in Fig. 14), while we are considering the change with respect to the stacking interactions only.
Figure 14.

Different types of interactions in the adenine-thymine dimer: H-bond between adjacent adenine and thymine (dash), H-bond between the adenine and thymine molecules that are one step away from each other (dot), and stacking interactions between adenines and thymines (dash-dot). In the case of (AT)n, if we consider only nearest neighbor interactions, there are (n − 1) adenine and thymine stacked interactions (dash-dot), n AT H-bonding interactions (dash) and 2n cross H-bonding interactions (dot).
To summarize, the exchange-repulsion energy is a short range interaction that can be accurately approximated by nearest-neighbor energies. The dispersion interaction ( ) has a longer range than exchange-repulsion [∝ exp(−aR)], however, it falls off within a 10-mer. The Coulomb and polarization are the longest-range interactions, however, the actual length scale over which they provide significant contributions is system-specific due to the intricate interplay between different components (i.e., charge-charge, charge-dipole, charge-quadrupole, etc).
4.4 Far-field interactions and their dependence on the size of the oligomers
The next problem that we address is the relative importance of the non-pairwise, or, more precisely, far-field (non-nearest-neighbor) part of the interaction energy and its dependence on the size of the oligomers. This analysis assesses the feasibility and accuracy of representing multiple non-covalent π–π interactions by a sum of pair-wise interactions.
For the simplest example, a trimer, we can define the total two-body energy E2(total) as:
| (39) |
where E2(N; M ) is the interaction energy for the NM dimer. The many-body interaction (i.e., non-pairwise) is defined as the energy that is not accounted for by the sum of these two-body interactions. The many-body interaction for the trimer is:
| (40) |
and in a general case of N oligomers it becomes:
| (41) |
Total pairwise energy, E2(total), can be approximated by considering only the interactions between the nearest neighbors (or next nearest-neighbors), as was done in Refs. 27, 105. Such analysis allows one to quantify non-additive component of the far-field part of the interaction energy.
The many-body energy in Eq. (41) consists only of intrinsic non-pairwise contributions. In EFP, the only non-pairwise term is polarization. One can characterize the importance of the many-body (or non-additive) contribution by considering its percentage fraction to the interaction energy:
| (42) |
Using the EFP interaction energies for the adenine and thymine oligomers, the far-field (non-nearest-neighbor) part of the interaction energy is less than 5% of the total interaction energy. Taking into account the next nearest neighbors decreases this value to less than 1%. Additional details of the analysis are provided in Supplementary Materials.
5 Conclusion
We report the implementation of the EFP method in the Q-Chem electronic structure program.86 EFP,48 an ab initio-based model potential, is an inexpensive alternative to a full ab initio description of non-covalent interactions. EFP can be described as a polarizable force field (or polarizable embedding model) that has no empirically fitted parameters. All parameters are obtained from ab initio calculations on isolated fragments.
We employed the EFP method to investigate non-covalent interaction energies in large oligomers of adenine and thymine representing a simple model of DNA. For the dimers, the EFP energies of π – π and H-bonding interactions are in good agreement with high-level ab initio calculations. The low computational cost of EFP allowed us to go beyond the dimers108,114,118,119 and to investigate asymptotic behavior of different components of interaction energies.
Our calculations demonstrate that the dispersion energy is the leading component in the π – π interaction for all oligomer sizes. The exchange-repulsion energy also plays an important role. The contribution of polarization is small in these systems, whereas the magnitude of the Coulomb term varies. The importance of various components obtained from our calculations can be compared to the results obtained by SAPT calculations2,116 where the dispersion and exchange-repulsion were found to be the major components in the parallel-slipped structures of benzene and substituted benzene dimers. The total interaction energies and the individual components are also in agreement with the results obtained by Leszczynski and co-workers.117
The rate of change of different energy components with the size of oligomers shows that exchange-repulsion has the shortest range followed by the dispersion energy. The polarization and Coulomb are the longest range interactions.
To assess whether a simple sum of the dimer energies can accurately represent the total interaction energy in extended systems, we analyzed the far-field part of the EFP energies. The polarization energy has a high non-additive fraction. Other energy components have a significantly lower percentage of far-field contributions.
The accuracy and low computational cost of the EFP method are very encouraging. However, to take full advantage of EFP, analytic gradients are necessary, and this work is underway.
Supplementary Material
Acknowledgments
This work was supported by an NIH-SBIR grant with Q-Chem, Inc. (AIK and LVS) and by grants from the Basic Energy Science Division of the Department of Energy to the Ames Laboratory Chemical Physics Program (MSG). LVS acknowledges additional support from the NSF-CAREER (CHE-0955419) grant. We thank Dr. Yihan Shao and Dr. Jing Kong for their generous help with the implementation. We are also grateful to Prof. Alexander V. Nemukhin and Dr. Bella Grigorenko for valuable discussions. In addition, we acknowledge contributions of Ilya Kaliman.
Footnotes
Supporting information is available free of charge via the Internet at http://pubs.acs.org. The supporting information contains details of the equations used in the fragment-fragment Coulomb interactions, Buckingham multipoles as well as some notes about the effective fragment library of common solvents. The benchmark results about adenine and thymine dimers to calibrate against ab initio calculations are presented as well as effects of h-twist on the interaction energy in thymine dimer and far-field interactions in stacked adenine and thymine dimers. The geometries of the adenine and thymine monomers and oligomers are reported.
References
- 1.Sherrill CD. In: Reviews in Computational Chemistry. Lipkowitz KB, Cundari TA, editors. Jon Wiley & Sons; 2009. p. 1. [Google Scholar]
- 2.Tschumper GS. In: Reviews in Computational Chemistry. Lipkowitz KB, Cundari TA, editors. Jon Wiley & Sons; 2009. p. 39. [Google Scholar]
- 3.Tauer TP, Sherrill CD. J Phys Chem A. 2005;109:10475. doi: 10.1021/jp0553479. [DOI] [PubMed] [Google Scholar]
- 4.Hunter CA, Sanders JKM. J Am Chem Soc. 1990;112:5525. [Google Scholar]
- 5.Privalov PL, Makhatadze GI. J Mol Biol. 1992;224:715. doi: 10.1016/0022-2836(92)90555-x. [DOI] [PubMed] [Google Scholar]
- 6.Burley SK, Petsko GA. Science. 1985;229:23. doi: 10.1126/science.3892686. [DOI] [PubMed] [Google Scholar]
- 7.Hunter CA, Singh J, Thornton JM. J Mol Biol. 1991;218:837. doi: 10.1016/0022-2836(91)90271-7. [DOI] [PubMed] [Google Scholar]
- 8.Morgan RS, Tatsh CE, Gushard RH, Mcadon JM, Warme PK. Int J Pept Prot Res. 1978;11:209. doi: 10.1111/j.1399-3011.1978.tb02841.x. [DOI] [PubMed] [Google Scholar]
- 9.Zauhar RJ, Colbert CL, Morgan RS, Welsh WJ. Biopolymer. 2000;53:233. doi: 10.1002/(SICI)1097-0282(200003)53:3<233::AID-BIP3>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- 10.Brana MF, Cacho M, Gradillas A, Pascual-Teresa B, Ramos A. Curr Pharm Des. 2001;7:1745. doi: 10.2174/1381612013397113. [DOI] [PubMed] [Google Scholar]
- 11.Wintjens R, Lievin J, Rooman M, Buisine E. J Mol Biol. 2000;302:395. doi: 10.1006/jmbi.2000.4040. [DOI] [PubMed] [Google Scholar]
- 12.Anbarasu A, Anand S, Babu MM, Sethumadhavan R. Macromol. 2007;41:251. doi: 10.1016/j.ijbiomac.2007.02.013. [DOI] [PubMed] [Google Scholar]
- 13.Claessens CG, Stoddart JF. J Phys Org Chem. 1997;10:254. [Google Scholar]
- 14.Gazit E. Chem Soc Rev. 2007;36:1263. doi: 10.1039/b605536m. [DOI] [PubMed] [Google Scholar]
- 15.Meyer EA, Castellano RK, Diederich F. Angew Chem Int Edit. 2003;42:1210. doi: 10.1002/anie.200390319. [DOI] [PubMed] [Google Scholar]
- 16.Askew B, Ballester P, Buhr C, Jeong KS, Jones S, Parris K, Williams K, Rebek J., Jr J Am Chem Soc. 1989;111:1082. [Google Scholar]
- 17.Hunter CA. Chem Soc Rev. 1994;23:101. [Google Scholar]
- 18.Hud N, Anet FAL. J Theor Biol. 2000;205:543. doi: 10.1006/jtbi.2000.2084. [DOI] [PubMed] [Google Scholar]
- 19.Řeha D, Kabeláč M, Ryjáček F, Šponer J, Šponer JE, Elstner M, Suhai S, Hobza P. J Am Chem Soc. 2002;124:3366. doi: 10.1021/ja011490d. [DOI] [PubMed] [Google Scholar]
- 20.Ferguson LR, Denny WA. Mutation Research. 2007;623:14. doi: 10.1016/j.mrfmmm.2007.03.014. [DOI] [PubMed] [Google Scholar]
- 21.Rezac J, Hobza P, Harris SA. Biophysical Journal. 2010;98:101. doi: 10.1016/j.bpj.2009.08.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gessner O, Lee AMD, Shaffer JP, Reisler H, Levchenko S, Krylov A, Underwood JG, Shi H, East ALL, Wardlaw DM, Chrysostom Et-H, Hayden CC, Stolow A. Science. 2006;311:219. doi: 10.1126/science.1120779. [DOI] [PubMed] [Google Scholar]
- 23.Pieniazek PA, Bradforth SE, Krylov AI. J Phys Chem A. 2006;110:4854. doi: 10.1021/jp0545952. [DOI] [PubMed] [Google Scholar]
- 24.Cristian AMC, Krylov AI. J Chem Phys. 2003;118:10912. [Google Scholar]
- 25.Podeszwa R, Szalewicz K. J Chem Phys. 2007;126:194101. doi: 10.1063/1.2733648. [DOI] [PubMed] [Google Scholar]
- 26.Podeszwa R, Bukowski R, Szalewicz K. J Phys Chem A. 2006;110:10345. doi: 10.1021/jp064095o. [DOI] [PubMed] [Google Scholar]
- 27.Sinnokrot MO, Sherrill CD. J Phys Chem A. 2006;110:10656. doi: 10.1021/jp0610416. [DOI] [PubMed] [Google Scholar]
- 28.Tsuzuki S, Uchimaru T, Matsumura K, Mikami M, Tanabe K. Chem Phys Lett. 2000;319:547. [Google Scholar]
- 29.Ye X, Li Z, Wang W, Fan K, Xu W, Hua Z. Chem Phys Lett. 2004;397:56. [Google Scholar]
- 30.Bowler DR, Miyazaki T, Gillan MJ. J Phys: Condens Matter. 2002;14:2781. [Google Scholar]
- 31.Schütz M, Hetzer G, Werner H. J Chem Phys. 1999;111:5691. [Google Scholar]
- 32.Scuseria GE, Ayala PY. J Chem Phys. 1999;111:8330. [Google Scholar]
- 33.White CA, Johnson BG, Gill PMW, Head-Gordon M. Chem Phys Lett. 1996;253:268. [Google Scholar]
- 34.Deev V, Collins MA. J Chem Phys. 2005;122:154102. doi: 10.1063/1.1879792. [DOI] [PubMed] [Google Scholar]
- 35.Kitaura K, Ikeo E, Asada T, Nakano T, Uebayasi M. Chem Phys Lett. 1999;313:701. [Google Scholar]
- 36.Fedorov DG, Kitaura K. J Phys Chem A. 2007;111:6904. doi: 10.1021/jp0716740. [DOI] [PubMed] [Google Scholar]
- 37.Fedorov DG, Kitaura K. The Fragment Molecular Orbital Method: Practical Applications to Large Molecular Systems. CRC Press; Boca Raton: 2009. [Google Scholar]
- 38.Gordon MS, Mullin JM, Pruitt SR, Roskop LB, Slipchenko LV, Boatz JA. J Phys Chem B. 2009;113:9646. doi: 10.1021/jp811519x. [DOI] [PubMed] [Google Scholar]
- 39.Sanz-Garcia A, Wheatley RJ. Chem Phys Chem. 2003;5:801. [Google Scholar]
- 40.Korona T. J Chem Phys. 2008;128:224104. doi: 10.1063/1.2933312. [DOI] [PubMed] [Google Scholar]
- 41.Grimme S. J Comput Chem. 2004;25:1463. doi: 10.1002/jcc.20078. [DOI] [PubMed] [Google Scholar]
- 42.Chai J-D, Head-Gordon M. Phys Chem Chem Phys. 2008;10:6615. doi: 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
- 43.Allunger NL, Yuh YH, Lii JH. J Am Chem Soc. 1989;111:8551. [Google Scholar]
- 44.Mayo SL, Olafson BD, Goddard WA. J Phys Chem. 1990;94:8897. [Google Scholar]
- 45.Casewit CJ, Colwell KS, Rappe AK. J Am Chem Soc. 1992;114:10035. [Google Scholar]
- 46.MacKerell AD, Bashford D, Bellott Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. J Phys Chem B. 1998;102:3586. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 47.Day PN, Jensen JH, Gordon MS, Webb SP, Stevens WJ, Krauss M, Garmer D, Basch H, Cohen D. J Chem Phys. 1996;105:1968. [Google Scholar]
- 48.Gordon MS, Slipchenko L, Li H, Jensen JH. Annual Reports in Computational Chemistry. In: Spellmeyer DC, Wheeler R, editors. Annual Reports in Computational Chemistry. Vol. 3. Elsevier; 2007. p. 177. [Google Scholar]
- 49.Gordon MS, Freitag MA, Bandyopadhyay P, Jensen JH, Kairys V, Stevens WJ. J Phys Chem A. 2001;105:293. [Google Scholar]
- 50.Schmidt MW, Baldridge KK, Boatz JA, Elbert ST, Gordon MS, Jensen JH, Koseki S, Mastunaga N, Nguyen KA, Su S, Windus TL, Dupuis M, Montgomery JA. J Comput Chem. 1993;14:1347. [Google Scholar]
- 51.Gordon MS, Freitag MA, Bandyopadhyay P, Jensen JH, Kairys V, Stevens WJ. J Phys Chem A. 2001;105:293. [Google Scholar]
- 52.Adamovic I, Freitag MA, Gordon MS. J Chem Phys. 2003;118:6725. [Google Scholar]
- 53.Gordon MS, Schmidt MW. jcc. 1993;14:1347. [Google Scholar]
- 54.Arora P, Slipchenko LV, Webb SP, Defusco A, Gordon MS. J Phys Chem A. 2010;114:6742. doi: 10.1021/jp101780r. [DOI] [PubMed] [Google Scholar]
- 55.Yoo S, Zahariev F, Sok S, Gordon MS. J Chem Phys. 2008;129:8. doi: 10.1063/1.2992049. [DOI] [PubMed] [Google Scholar]
- 56.DeFusco AA, III, Gordon MS. Proceedings of 238th ACS National Meeting; Washington D.C. 2009. [Google Scholar]
- 57.Chen W, Gordon MS. J Chem Phys. 1996;105:11081. [Google Scholar]
- 58.Webb SP, Gordon MS. J Phys Chem A. 1999;103:1265. [Google Scholar]
- 59.Merrill GN, Gordon MS. J Phys Chem A. 1998;102:2650. [Google Scholar]
- 60.Day PN, Pachter R, Gordon MS, Merrill GN. J Chem Phys. 2000;112:2063. [Google Scholar]
- 61.Adamovic I, Gordon MS. J Phys Chem A. 2005;109:1629. doi: 10.1021/jp040665d. [DOI] [PubMed] [Google Scholar]
- 62.Bandyopadhyay P, Gordon MS. J Chem Phys. 2000;113:1104. [Google Scholar]
- 63.Bandyopadhyay P, Gordon MS, Mennucci B, Tomasi J. J Chem Phys. 2002;116:5023. [Google Scholar]
- 64.Kina D, Nakayama A, Noro T, Taketsugu T, Gordon MS. J Phys Chem A. 2008;112:9675. doi: 10.1021/jp804368p. [DOI] [PubMed] [Google Scholar]
- 65.Jensen JH. J Chem Phys. 1996;104:7795. [Google Scholar]
- 66.Slipchenko LV, Gordon MS. J Comput Chem. 2007;28:276. doi: 10.1002/jcc.20520. [DOI] [PubMed] [Google Scholar]
- 67.Sinnokrot MO, Sherrill CD. J Am Chem Soc. 2004;126:7690. doi: 10.1021/ja049434a. [DOI] [PubMed] [Google Scholar]
- 68.Podeszwa R, Bukowski R, Szalewicz K. J Phys Chem A. 2006;110:10345. doi: 10.1021/jp064095o. [DOI] [PubMed] [Google Scholar]
- 69.Slipchenko LV, Gordon MS. Mol Phys. 2009;107:999. [Google Scholar]
- 70.Smith T, Slipchenko LV, Gordon MS. J Phys Chem A. 2008;112:5286. doi: 10.1021/jp800107z. [DOI] [PubMed] [Google Scholar]
- 71.Adamovic I, Li H, Lamm MH, Gordon MS. J Phys Chem A. 2006;110:519. doi: 10.1021/jp058140o. [DOI] [PubMed] [Google Scholar]
- 72.Slipchenko LV, Gordon MS. J Phys Chem A. 2009;113:2092. doi: 10.1021/jp808845b. [DOI] [PubMed] [Google Scholar]
- 73.Adamovic I, Gordon MS. J Phys Chem A. 2006;110:10267. doi: 10.1021/jp060607n. [DOI] [PubMed] [Google Scholar]
- 74.Mullin JM, Gordon MS. J Phys Chem B. 2009;113:8657. doi: 10.1021/jp901459y. [DOI] [PubMed] [Google Scholar]
- 75.Mullin JM, Gordon MS. J Phys Chem B. 2009;113:14413. doi: 10.1021/jp904826v. [DOI] [PubMed] [Google Scholar]
- 76.Mullin JM. PhD Thesis. Iowa State University; 2009. [Google Scholar]
- 77.Pranami G, Slipchenko LV, Lamm NH, Gordon MS. Multi-scale Quantum Models for Biocatalysis. In: Lee T-S, York DM, editors. Challenges and Advances in Computational Chemistry and Physics. Springer; Netherlands: 2009. [Google Scholar]
- 78.Kairys V, Jensen JH. J Phys Chem A. 2000;104:6656. [Google Scholar]
- 79.Li H, Hains AW, Everts JE, Robertson AD, Jensen JH. J Phys Chem B. 2002;106:3486. [Google Scholar]
- 80.Jensen JH, Li H, Robertson AD, Molina A. J Phys Chem A. 2005;109:6634. doi: 10.1021/jp051922x. [DOI] [PubMed] [Google Scholar]
- 81.Slipchenko LV. J Phys Chem A. 2010 doi: 10.1021/jp101797a. in press. [DOI] [PubMed] [Google Scholar]
- 82.Polyakov I, Epifanovsky E, Grigorenko BL, Krylov AI, Nemukhin AV. J Chem Theory Comput. 2009;5:1907. doi: 10.1021/ct9001448. [DOI] [PubMed] [Google Scholar]
- 83.Nemukhin AV, Grigorenko BL, Rogov AV, Topol IA, Burt SK. Theor Chem Acc. 2004;111:36. [Google Scholar]
- 84.Grigorenko BL, Nemukhin AV, Topol IA, Burt SK. J Phys Chem A. 2002;106:10663. [Google Scholar]
- 85.Nemukhin AV, Grigorenko BL, Bochenkova AV, Topol IA, Burt SK. J Molec Struct (Theochem) 2002;581:167. [Google Scholar]
- 86.Shao Y, Molnar LF, Jung Y, Kussmann J, Ochsenfeld C, Brown S, Gilbert ATB, Slipchenko LV, Levchenko SV, O’Neil DP, Distasio RA, Jr, Lochan RC, Wang T, Beran GJO, Besley NA, Herbert JM, Lin CY, Van Voorhis T, Chien SH, Sodt A, Steele RP, Rassolov VA, Maslen P, Korambath PP, Adamson RD, Austin B, Baker J, Bird EFC, Daschel H, Doerksen RJ, Drew A, Dunietz BD, Dutoi AD, Furlani TR, Gwaltney SR, Heyden A, Hirata S, Hsu C-P, Kedziora GS, Khalliulin RZ, Klunziger P, Lee AM, Liang WZ, Lotan I, Nair N, Peters B, Proynov EI, Pieniazek PA, Rhee YM, Ritchie J, Rosta E, Sherrill CD, Simmonett AC, Subotnik JE, Woodcock HL, III, Zhang W, Bell AT, Chakraborty AK, Chipman DM, Keil FJ, Warshel A, Herhe WJ, Schaefer HF, III, Kong J, Krylov AI, Gill PMW, Head-Gordon M. Phys Chem Chem Phys. 2006;8:3172. doi: 10.1039/b517914a. [DOI] [PubMed] [Google Scholar]
- 87.Smith T, Slipchenko LV, Gordon MS. Proceedings of 239th ACS National Meeting; San Francisco, CA. 2010. [Google Scholar]
- 88.Stone AJ. The Theory of Intermolecular Forces. Oxford University Press; 1997. p. 50. [Google Scholar]
- 89.Li H, Gordon MS, Jensen JH. J Chem Phys. 2006;124 doi: 10.1063/1.2196884. [DOI] [PubMed] [Google Scholar]
- 90.Kemp DD, Rintelman JM, Gordon MS, Jensen JH. Theor Chim Acta. 2010;125:481. [Google Scholar]
- 91.E.g., the “makefp” run in the GAMESS suite of programs performs this task.
- 92.Jensen JH, Gordon MS. Mol Phys. 1996;89:1313. [Google Scholar]
- 93.Jensen JH, Gordon MS. J Chem Phys. 1998;108:4772. [Google Scholar]
- 94.Buckingham AD. Q Rev Chem Soc. 1959;13:183. [Google Scholar]
- 95.Stone AJ. Chem Phys Lett. 1981;83:233. [Google Scholar]
- 96.Mulliken RS. J Chem Phys. 1955;23:1833. [Google Scholar]
- 97.Stone AJ, Alderton M. Mol Phys. 1985;56:1047. [Google Scholar]
- 98.Obara S, Saika A. J Chem Phys. 1986;84:3963. [Google Scholar]
- 99.Freitag MA, Gordon MS, Jensen JH, Stevens WJ. J Chem Phys. 2000;112:7300. [Google Scholar]
- 100.Magnasco V, Costa C, Figari G. J Molec Struct (Theochem) 1990;206:235. [Google Scholar]
- 101.Adamovic I, Gordon MS. Mol Phys. 2005;103:379. [Google Scholar]
- 102.Tang KT, Toennies JP. J Chem Phys. 1984;80:3726. [Google Scholar]
- 103.Boys SF. Rev Mod Phys. 1960;32:296. [Google Scholar]
- 104.Boys SF. Quantum Science of Atoms, Molecules, and Solids. Academic Press; 1966. p. 253. [Google Scholar]
- 105.Hopkins BW, Tschumper GS. Chem Phys Lett. 2005;407:362. [Google Scholar]
- 106.Sponer J, Leszczynski J, Hobza P. Biopolymers. 2002;61:3. doi: 10.1002/1097-0282(2001)61:1<3::AID-BIP10048>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- 107.Sponer J, Leszczynski J, Hobza P. J Phys Chem. 1996;100:5590. [Google Scholar]
- 108.Jurečka P, Hobza P. J Am Chem Soc. 2003;125:15608. doi: 10.1021/ja036611j. [DOI] [PubMed] [Google Scholar]
- 109.Bravaya KB, Kostko O, Ahmed M, Krylov AI. Phys Chem Chem Phys. 2010;12:2292. doi: 10.1039/b919930f. [DOI] [PubMed] [Google Scholar]
- 110.Černý J, Hobza P. Phys Chem Chem Phys. 2007;9:5291. doi: 10.1039/b704781a. [DOI] [PubMed] [Google Scholar]
- 111.Rappé AK, Bernstein ER. J Phys Chem A. 2000;104:6117. [Google Scholar]
- 112.Müller-Dethlefs K, Hobza P. Chem Rev. 2000;100:143. doi: 10.1021/cr9900331. [DOI] [PubMed] [Google Scholar]
- 113.Engkvist O, Hobza P, Selzle HL, Schlag EW. J Chem Phys. 1999;110:5758. [Google Scholar]
- 114.Sinnokrot MO, Sherrill CD. J Phys Chem A. 2004;108:10200. [Google Scholar]
- 115.Sinnokrot MO, Sherrill CD. J Phys Chem A. 2006;110:10656. doi: 10.1021/jp0610416. [DOI] [PubMed] [Google Scholar]
- 116.Bates DM, Anderson JA, Oloyede P, Tschumper GS. Phys Chem Chem Phys. 2008;10:2775. doi: 10.1039/b718720c. [DOI] [PubMed] [Google Scholar]
- 117.Hill G, Forde G, Hill N, Lester WA, Jr, Sokalski WA, Leszczynski J. Chem Phys Lett. 2003;381:729. [Google Scholar]
- 118.Hobza P, Zahradnik R, Müller-Dethlefs K. Collect Czech Chem Commun. 2006;71:443. [Google Scholar]
- 119.Hobza P, Selzle HL, Schlag EW. J Phys Chem. 1996;100:18790. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.