Enhanced ICBM Diffusion Tensor Template of the Human Brain

Abstract

Development of a diffusion tensor (DT) template that is representative of the micro-architecture of the human brain is crucial for comparisons of neuronal structural integrity and brain connectivity across populations, as well as for the generation of a detailed white matter atlas. Furthermore, a DT template in ICBM space may simplify consolidation of information from DT, anatomical and functional MRI studies. The previously developed “IIT DT brain template” was produced in ICBM-152 space, based on a large number of subjects from a limited age-range, using data with minimal image artifacts, and non-linear registration. That template was characterized by higher image sharpness, provided the ability to distinguish smaller white matter fiber structures, and contained fewer image artifacts, than several previously published DT templates. However, low-dimensional registration was used in the development of that template, which led to a mismatch of DT information across subjects, eventually manifested as loss of local diffusion information and errors in the final tensors. Also, low-dimensional registration led to a mismatch of the anatomy in the IIT and ICBM-152 templates. In this work, a significantly improved DT brain template in ICBM-152 space was developed, using high-dimensional non-linear registration and the raw data collected for the purposes of the IIT template. The accuracy of inter-subject DT matching was significantly increased compared to that achieved for the development of the IIT template. Consequently, the new template contained DT information that was more representative of single-subject human brain data, and was characterized by higher image sharpness than the IIT template. Furthermore, a bootstrap approach demonstrated that the variance of tensor characteristics was lower in the new template. Additionally, compared to the IIT template, brain anatomy in the new template more accurately matched ICBM-152 space. Finally, spatial normalization of a number of DT datasets through registration to the new and existing IIT templates was improved when using the new template.

Introduction

Diffusion tensor imaging (DTI) is unique in providing a wealth of information regarding the microstructure of brain tissue in vivo (Basser et al., 1994; Basser and Pierpaoli, 1996). However, in the vast majority of DTI studies, comparisons across subjects have primarily focused only on scalar quantities derived from the diffusion tensor (Lim et al., 1999, Bruno et al., 2008, Pfefferbaum et al., 2005, van Gelderen et al., 1994, Bammer et al., 2000, Klingberg et al., 2000, Ellis et al., 1999, Arfanakis et al., 2002). The remaining important structural information contained in the tensor, such as the primary diffusion direction, which can be used to infer estimates of brain connectivity, is simply overlooked. Comprehensive comparison of diffusion tensors between populations of patients and healthy controls requires spatial normalization of DTI data across subjects and appropriate tensor reorientation (Alexander et al., 2001). The accuracy of the registration and subsequent comparisons is contingent upon the use of a DTI template representative of the human brain. Furthermore, development of a DTI template that is representative of the healthy human brain is also important for the generation of a detailed white matter atlas (Mori et al., 2008).

Several DTI brain templates have been developed to date (Ardekani and Sinha, 2006; Chiang et al., 2008; Goodlett et al., 2006; Jones et al., 2002; Mori et al., 2008; Muller et al., 2007; Park et al., 2003; van Hecke et al., 2008; Xu et al., 2003; Yap et al., 2009; Zhang et al., 2006; Zhang et al., 2007). However, a combination of several sources of error reduced the accuracy of these templates (Peng et al., 2009): a) image artifacts in individual DTI datasets contaminated the final template, b) suboptimal diffusion-encoding schemes, or imaging protocols, reduced the quality of DTI information in the final template, c) ineffective registration techniques lead to averaging of information from different types of tissue and to a template with unrealistic diffusion characteristics, d) use of a limited number of subjects resulted in a template heavily influenced by the characteristics of individual subjects, and e) averaging data across age-groups with different macro- and micro-structural properties resulted in an unrealistic template, not representative of any age-group. In order to address these shortcomings, Peng et al. imaged a large cohort of human subjects from a limited age-range (67 subjects, 20-40 years of age), using Turboprop-DTI (Arfanakis et al., 2005; Pipe and Zwart, 2006; Arfanakis et al., 2007), which provides images with significantly fewer image artifacts than conventional DTI acquisition techniques, combined with an appropriate imaging protocol, and produced a DTI brain template in ICBM-152 (International Consortium for Brain Mapping) space (Mazziotta et al., 1995). That template, named the IIT DTI brain template: a) was characterized by higher image sharpness, b) provided the ability to distinguish smaller white matter structures, c) contained fewer image artifacts, than previously published DTI templates (Peng et al., 2009). However, for its development, low-dimensional non-linear registration based on the SPM5 software (Wellcome Department of Imaging and Neuroscience, London, UK) was used to, first, produce a temporary DTI template in ICBM-152 space, and then, to register fractional anisotropy (FA) and mean diffusion-weighted (DW) volumes from each subject to the temporary template (Peng et al., 2009). The average transformations were then applied on the diffusion tensor (DT) volume of individual subjects, and the resulting tensors were averaged across subjects to generate the IIT DTI brain template. Due to the low-dimensional registration approach used, DT information from different subjects was not accurately matched in 3D space, which led to loss of local diffusion information and errors in the final tensors. Also, low-dimensional registration led to a mismatch of the anatomical information in certain brain structures of the IIT and ICBM-152 templates.

The purpose of this study was to address the limitations of previous efforts and develop a DTI template in ICBM-152 space that is more representative of the micro-architecture of the human brain. The new template was developed using data acquired for the purposes of the previously published IIT template, consisting of 67 DT datasets with minimal artifacts, collected on 67 subjects with a limited age-range. In contrast to the process followed for the development of that template, high-dimensional non-linear registration was employed. The accuracy of inter-subject DT matching achieved with high-dimensional registration was evaluated using a number of similarity metrics, and was compared to that achieved for the development of the previously published IIT template. The new template was compared to the existing IIT template in terms of image sharpness, DT properties, variance of DT characteristics (estimated with a bootstrap approach), and accuracy in matching brain anatomy to ICBM-152 space. Both mean and median tensors were used in the new template to summarize the DT information from the 67 subjects. The new mean and median DT templates, as well as the corresponding maps of the variance of tensor characteristics, were made publicly available. Finally, the accuracy of spatial normalization when using the new compared to the existing IIT template was assessed.

Methods

DTI data

Turboprop-DTI data from forty female (27.2±5.4 years of age, 20–39 years of age) and twenty-seven male (31.7±5.6 years of age, 22–40 years of age) healthy human subjects, acquired for the development of the previously published IIT template (Peng et al., 2009), were used in this study for the development of the new template. The diffusion properties of the brain are shown to be relatively similar across subjects from this age-range (Hasan et al., 2008; Sullivan and Pfefferbaum, 2006). Additional Turboprop-DTI data from nine male (32.8±5.8 years of age, 20-40 years of age) and thirteen female (28.8±4.8 years of age, 21-36 years of age) subjects were acquired for assessing the accuracy of spatial normalization when using the new and existing IIT templates. Written informed consent was provided by all participants according to procedures approved by the institutional committee for the protection of human subjects. All datasets were collected on a 3 Tesla General Electric MRI scanner (GE, Waukesha, WI) with the following parameters: TR=5800 ms, TE=94 ms, 8 spin-echoes per TR, 5 k-space lines per spin-echo, 128 samples per line, 16 blades per image, field-of-view 24 cm×24 cm, 45 contiguous oblique axial slices, 3 mm slice thickness, 256×256 final image matrix, b=900 s/mm² for 12 diffusion directions uniformly distributed in 3D space (minimum energy scheme) (Hasan et al., 2001), and two b=0 s/mm² images of each slice.

Pre-processing

Head motion was in general minimal in the Turboprop-DTI data included in this work (Peng et al., 2009). Any residual motion between DW or b=0 s/mm² volumes was corrected for each dataset as described in (Peng et al., 2009). Brain extraction, tensor estimation, generation of fractional anisotropy (FA), trace, primary eigenvalue and eigenvector volumes was completed with FSL (Oxford, UK) (Peng et al., 2009; Smith, 2002). The average b=0 s/mm² volume of each subject from the first group mentioned above (67 subjects), was smoothed with a Gaussian kernel with full width at half maximum (FWHM) of 8 mm, and was registered to the ICBM-152 template using rigid-body registration (FSL, Oxford, UK). Subsequently, all b=0 s/mm² volumes from the first group were normalized to the ICBM-152 template using the Automatic Registration Toolbox (ART) (Ardekani et al., 2005). ART was recently shown to be among the most accurate high-dimensional non-linear registration tools for inter-subject normalization of anatomical MRI data (Klein et al., 2009). An affine registration step preceded non-linear registration with ART. The number of iterations for non-linear registration was set to 6, and a search window size of 9 voxels was chosen. The subject with the lowest total deformation was identified. The original averaged b=0 s/mm² volume from that subject was smoothed with a Gaussian kernel with FWHM = 8 mm, and was registered to the ICBM-152 template using ART. The same spatial transformation was applied to the DW data from that subject. Trilinear interpolation was used. The diffusion tensors throughout the brain of that subject were then calculated using DTIFIT (FSL, Oxford, UK). The resulting DTI dataset in ICBM-152 space contained 181×217×181 voxels, with a voxel size of 1 mm × 1 mm × 1 mm, and was used as a temporary DTI brain template.

DTI registration to the temporary template

The white matter, grey matter and cerebrospinal fluid (CSF) were segmented for each subject from the first group based on the FA and trace maps of the pre-processed DTI data (Yang et al., 2008b). The different tissue components were then registered to those of the temporary template using a high-dimensional elastic registration method (Shen and Davatzikos, 2002) (HAMMER, Section of Biomedical Image Analysis, University of Pennsylvania, PA, USA). The resulting deformation for each subject was applied on the corresponding pre-processed DTI data. The diffusion tensor in each voxel of a DTI dataset was reoriented using the rotational component of the deformation field, and a statistical estimate of the fiber orientation from the voxel’s neighborhood (Xu et al., 2003). All steps of the process used to register the 67 DTI datasets to the temporary DTI template were completed using DTIGUI (Yang et al., 2008b) (Section of Biomedical Image Analysis, University of Pennsylvania, PA, USA).

Assessment of the accuracy of inter-subject spatial normalization achieved for the DTI datasets used in the development of the template

A number of similarity metrics were used to assess the accuracy of tensor matching achieved with the high-dimensional non-linear registration method described above, for the 67 DTI datasets. Due to the wealth of information contained in the diffusion tensor, and in order to better characterize the accuracy of tensor matching, the metrics used in this step included those designed to explore similarity of whole tensors (see (a) below), as well as others exploring similarity in portions of the diffusion tensor contents (see (b-e) below).

1. The Euclidean distance of tensors from two datasets (DTED) was estimated using:

   $$\mathrm{DTED}=\sqrt{\mathrm{trace}({({\mathbf{D}}_1-{\mathbf{D}}_2)}^2)},$$ [1]

   where D₁ and D₂ are two diffusion tensors (Alexander and Gee, 2000). The average Euclidean distance for all possible pairs of subjects was estimated in each voxel. Maps of the average Euclidean distance of tensors were produced.
2. Similarly, the Euclidean distance of the deviatoric tensors from different datasets (DVED) was estimated by substituting D in Equation 1, with the deviatoric tensor D_an:

   $${\mathbf{D}}_{\mathrm{an}}=\mathbf{D}-[\mathrm{trace}(\mathbf{D})/3]\ast \mathbf{I},$$ [2]

   where I is the identity matrix. Maps of the average Euclidean distance of deviatoric tensors over all pairs of subjects were produced.
3. The cross-correlation of FA values between two datasets was estimated using:

   $${\mathrm{corr}}_{\mathrm{FA}}=\frac{{\sum }_{{\mathrm{x}}_{\mathrm{i}}}{\mathrm{FA}}_1({\mathrm{x}}_{\mathrm{i}}){\mathrm{FA}}_2({\mathrm{x}}_{\mathrm{i}})}{{\left({\sum }_{{\mathrm{x}}_{\mathrm{i}}}{\mathrm{FA}}_1({\mathrm{x}}_{\mathrm{i}}){\mathrm{FA}}_1({\mathrm{x}}_{\mathrm{i}}){\sum }_{{\mathrm{x}}_{\mathrm{i}}}{\mathrm{FA}}_2({\mathrm{x}}_{\mathrm{i}}){\mathrm{FA}}_2({\mathrm{x}}_{\mathrm{i}})\right)}^{1/2}},$$ [3]

   where FA₁(x_i), FA₂(x_i) are the FA values at voxel location x_i from two different DTI datasets. The average cross-correlation of FA values was then estimated for all possible pairs of subjects. Similarly, the average cross-correlation of trace values (corr_trace) was estimated for all pairs of subjects.
4. The overlap of eigenvalue-eigenvector pairs between tensors from different datasets was estimated using:

   $$\mathrm{OVL}=\frac{{\displaystyle \sum _{\mathrm{j}=1}^3\left({\mathrm{\lambda }}_{\mathrm{j}}{\mathrm{\lambda }}_{\mathrm{j}}^{+}\cdot {\left({\mathbf{\epsilon }}_{\mathrm{j}}\cdot {\mathbf{\epsilon }}_{\mathrm{j}}^{+}\right)}^2\right)}}{{\displaystyle \sum _{\mathrm{j}=1}^3{\mathrm{\lambda }}_{\mathrm{j}}{\mathrm{\lambda }}_{\mathrm{j}}^{+}}},$$ [4]

   where λ_j, ε_j, and λ_j ⁺, ε_j ⁺ are the eigenvalue-eigenvector pairs from two different tensors (Basser and Pajevic, 2000). The average OVL for all possible pairs of subjects was estimated in each voxel. Maps of the average OVL were produced.
5. The coherence of primary eigenvectors from multiple co-registered tensors was estimated using:

   $$\mathrm{COH}=1-\sqrt{\frac{{\mathrm{\beta }}_2+{\mathrm{\beta }}_3}{2{\mathrm{\beta }}_1}},$$ [5]

   where β₁, β₂, β₃ are the primary, secondary and tertiary eigenvalues of the mean dyadic tensor given by:

   $$\langle {{\mathbf{\epsilon }}_1{\mathbf{\epsilon }}_1}^{\mathrm{T}}\rangle =\langle \left(\begin{array}{ccc}{\mathrm{\epsilon }}_{1\mathrm{x}}^2& {\mathrm{\epsilon }}_{1\mathrm{x}}{\mathrm{\epsilon }}_{1\mathrm{y}}& {\mathrm{\epsilon }}_{1\mathrm{x}}{\mathrm{\epsilon }}_{1\mathrm{z}}\\ {\mathrm{\epsilon }}_{1\mathrm{x}}{\mathrm{\epsilon }}_{1\mathrm{y}}& {\mathrm{\epsilon }}_{1\mathrm{y}}^2& {\mathrm{\epsilon }}_{1\mathrm{y}}{\mathrm{\epsilon }}_{1\mathrm{z}}\\ {\mathrm{\epsilon }}_{1\mathrm{x}}{\mathrm{\epsilon }}_{1\mathrm{z}}& {\mathrm{\epsilon }}_{1\mathrm{y}}{\mathrm{\epsilon }}_{1\mathrm{z}}& {\mathrm{\epsilon }}_{1\mathrm{z}}^2\end{array}\right)\rangle =\frac{{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathbf{\epsilon }}_1^{\mathrm{i}}{\mathbf{\epsilon }}_1^{{\mathrm{i}}^{\mathrm{T}}}}}{\mathrm{N}},$$ [6]

   where ε₁ ⁱ is the primary eigenvector of the i^th subject, ε_1x, ε_1y, ε_1z are the three components of the primary eigenvector, and N is the total number of subjects (N=67) (Basser and Pajevic, 2000; Jones et al., 2002). Maps of the coherence of primary eigenvectors were produced.

The accuracy of tensor matching achieved for the 67 DTI datasets using the high-dimensional non-linear registration method described above, was compared to that achieved in the development of the previously published IIT DTI brain template (Peng et al., 2009). The average corr_FA and corr_trace over all pairs of subjects was compared between methods. Furthermore, the following regions of interest (ROI) were selected in white matter, based on FA maps derived from the mean tensors estimated from the 67 datasets: genu of the corpus callosum (gcc), splenium of the corpus callosum (scc), cingulum (cg), anterior limb of the internal capsule (alic), posterior limb of the internal capsule (plic), external capsule (ec), and corticospinal tract (cst). All ROIs were drawn in the central portion of these structures to avoid partial volume effects. The average DTED, DVED, and OVL over all pairs of subjects were compared in the selected ROIs between registration methods. The average COH in the selected ROIs was also compared between registration techniques. In all cases, a two-tailed Student’s t-test was used to assess the significance of any differences. Only differences with p<0.01, corrected for multiple comparisons with the Bonferroni approach, were considered significant.

Development and evaluation of the DTI human brain template

Following registration of all 67 DT datasets to the temporary template, the mean and median diffusion tensors were estimated in each voxel (Peng et al., 2009). The template containing mean tensors was named “IIT2_mean DTI template”, and the one containing median tensors was named “IIT2_median DTI template”. Maps of FA and trace were also produced from the mean and median tensors. The IIT2_mean and IIT2_median DTI templates were compared on a voxel-by-voxel basis by subtracting corresponding maps of FA and trace.

The IIT2_mean template was compared to the previously published IIT_mean DTI template (Peng et al., 2009). Diffusion anisotropy color maps were compared based on level of artifacts, smoothness, and ability to identify certain small brain structures. Differences in image sharpness of FA maps derived from the IIT_mean and IIT2_mean templates were assessed by means of the normalized power spectra. FA values in the ROIs selected in the previous section were also compared between the IIT_mean and IIT2_mean templates. A two-tailed Student’s t-test was used to assess the significance of any differences. Only differences with p<0.01, corrected for multiple comparisons with the Bonferroni approach, were considered significant. To test if the FA values of the mean tensor templates were representative of single subject FA values, FA maps derived from the IIT_mean and IIT2_mean templates were subtracted from the mean of the 67 FA maps (after registration).

A bootstrap approach was used to estimate the total variance of the diffusion tensor (TVDT) (sum of the variances of the tensor elements) (Papadakis et al., 1999), the standard deviation of FA (FA_std) and trace (trace_std), as well as the uncertainty in the principal diffusion direction of mean tensors in the IIT_mean and IIT2_mean templates. For that purpose, 67 co-registered datasets from the group of 67 subjects were randomly selected with replacement. A template T_k, containing mean tensors D_k, was produced, and the corresponding ε_1k, FA_k, trace_k were estimated in each voxel. The same procedure was repeated 100 times. Maps of the TVDT, FA_std, trace_std, and the 95% cone of uncertainty (COU) (Jones, 2003) were produced from the 100 templates. Histograms of the TVDT, FA_std, trace_std, considering all brain voxels, were compared between the IIT_mean and IIT2_mean templates. The COU was compared in the ROIs selected in the previous section between the IIT_mean and IIT2_mean templates. Similarly, the TVDT, FA_std, trace_std, and COU were compared between the IIT2_mean and IIT2_median templates.

The accuracy in matching the anatomical information of the IIT2 and ICBM-152 templates was assessed. For that purpose, the b=0 sec/mm² volumes from all 67 co-registered DT datasets were averaged. The cross-correlation between the average b=0 sec/mm² images and the T₂-weighted images of the ICBM-152 template was estimated. The same procedure was repeated for the previously published IIT template, and the cross correlation values were compared for the two DTI templates.

Assessment of the accuracy of inter-subject DTI spatial normalization through registration to the mean tensor template

The Turboprop-DTI datasets from the second group scanned (22 subjects) were registered to the IIT_mean and IIT2_mean templates, separately, and the accuracy of inter-subject tensor matching was compared for the two templates. The registration techniques used to build the two templates were not used in this step in order to avoid any potential bias. Instead, registration to the two templates was performed using a piecewise affine algorithm based on diffusion tensor information (DTI-TK) (Zhang et al., 2006). Tensor orientation was explicitly optimized (Zhang et al., 2006). Also, during registration, tensor reorientation was conducted using the finite strain strategy, and for the final re-slicing, using the preservation of principal direction (PPD) approach (Alexander et al., 2001). The COU and the metrics described in equations 1-6 were used to assess the accuracy of spatial normalization of the 22 DTI datasets through registration to the IIT_mean and IIT2_mean templates. Histograms of the COU, OVL, COH, DTED, DVED, considering all white matter voxels (FA>0.2 in mean FA maps), were generated for registration of the 22 DTI datasets to the two templates. The procedure described in this section was then repeated for 50 different combinations of the DTI datasets, following a bootstrap approach. This process generated 50 copies of each histogram, which allowed estimation of the 95% confidence intervals of the histograms. Finally, the statistical analysis of corr_FA and corr_trace results was described earlier in the methods.

Results

Assessment of the accuracy of inter-subject spatial normalization achieved for the DTI datasets used in the development of the template

The average corr_FA for the 67 DT datasets used for the development of the IIT2 template was significantly higher (0.901±0.006) than that achieved for the development of the IIT template (0.874±0.009) (p<10^-10). Similarly, the average corr_trace was significantly higher for the IIT2 (0.946±0.006) than the IIT (0.928±0.01) template (p<10^-10). Tables 1-4 present results of the average DTED, DVED, and OVL over all pairs of subjects, as well as the average COH, achieved in selected ROIs, for the datasets used for the development of the IIT2 and IIT templates. It was shown that the DTED and DVED were significantly lower, and the OVL and COH significantly higher, in all ROIs, for the spatially normalized data used in the construction of the IIT2 compared to the IIT template (Fig.1).

Table 1.

Average Euclidean distance of tensors over all pairs of datasets used in the development of the IIT and IIT2 templates. Statistically significant differences (after correction for multiple comparisons with the Bonferroni approach) are marked with an asterisk (*).

Brain structures	IITmean DTED × 103 s/mm2	IIT2mean DTED × 103 s/mm2	Number of voxels	P-value
gcc	0.72±0.09	0.54±0.06	50	<10-15 *
scc	0.67±0.07	0.60±0.06	102	1.3×10-13 *
cg	0.48±0.03	0.42±0.03	157	<10-15 *
alic	0.40±0.02	0.35±0.03	71	<10-15 *
plic	0.35±0.02	0.32±0.02	81	1.3×10-13 *
ec	0.33±0.03	0.29±0.03	126	<10-15 *
cst	0.45±0.02	0.41±0.02	79	<10-15 *

Table 4.

Coherence of primary eigenvectors of the datasets used in the development of the IIT and IIT2 templates. Statistically significant differences (after correction for multiple comparisons with the Bonferroni approach) are marked with an asterisk (*).

Brain structures	IITmean COH	IIT2mean COH	Number of voxels	P-value
gcc	0.87±0.02	0.88±0.01	50	7×10-5 *
scc	0.91±0.01	0.92±0.01	102	<10-15 *
cg	0.81±0.04	0.87±0.03	157	<10-15 *
alic	0.895±0.006	0.923±0.009	71	<10-15 *
plic	0.91±0.01	0.925±0.009	81	2.3×10-11 *
ec	0.83±0.05	0.87 ±0.05	126	1.1×10-7 *
cst	0.83±0.03	0.85±0.02	79	2.4×10-6 *

Figure 1.

Maps of the average DTED (A), DVED (B), OVL (C) over all pairs of subjects, as well as the average COH (D) for the datasets used in the development of the IIT (left image in each image-pair) and IIT2 (right image in each image-pair) templates. Only one slice through each volume is shown.

Development and evaluation of the DTI human brain template

Diffusion anisotropy color maps and trace maps derived from the IIT2_mean and IIT2_median templates are presented in Figure 2. Images derived from the IIT2_median template appeared to be noisier than the corresponding images from the IIT2_mean template, especially in regions near the surface of the brain (Fig.2). In white matter tissue, FA of mean tensors was lower on average than that of median tensors (Fig.3A,B). Furthermore, near the interface of brain tissue and CSF-filled spaces, the eigenvalues and trace were increased, and the FA was in many cases decreased for mean compared to median tensors (Fig.3).

Figure 2.

Axial diffusion anisotropy color maps and trace maps derived from the IIT2_mean (A, C) and IIT2_median (B, D) templates.

Figure 3.

(A) Maps of white matter voxels in which the FA of the median tensor is higher than that of the mean tensor. (B) Maps of white matter voxels in which the FA of the mean tensor is higher than that of the median tensor. The different grey scale levels represent the absolute value of the FA difference between mean and median tensors. (C) Map of voxels in which the trace of the median tensor is higher than that of the mean tensor. (D) Map of voxels in which the trace of the mean tensor is higher than that of the median tensor. The different grey scale levels represent the absolute value of the difference in trace between the mean and median tensors.

FA and trace maps derived from the IIT_mean and IIT2_mean templates are compared in Figure 4. No visible artifacts (e.g. eddy-current or susceptibility-induced artifacts) were present in either of the two templates, in contrast to several previously published templates (Ardekani and Sinha., 2006; Chiang et al., 2008; Mori et al., 2008; Zhang et al., 2006). FA and trace maps derived from the IIT2_mean template appeared sharper than those of the IIT_mean template (Fig.4). The energy at high spatial frequencies was higher in the normalized power spectra of FA maps from the IIT2_mean than the IIT_mean template (Fig.5). Additionally, FA values in several white matter ROIs were significantly higher (Table 5), and more similar to those of individual subjects (Fig.6), in the IIT2_mean compared to the IIT_mean template. FA values of the IIT2_mean template were also comparable to those published elsewhere for individual subjects from similar age-groups (Bisdas et al., 2008; Pierpaoli et al., 1996).

Figure 4.

FA (A, B) and trace (C, D) maps derived from the IIT2_mean (A, C) and IIT_mean (B, D) templates.

Figure 5.

Normalized power spectra for the same FA slice (shown in the 2^nd column of Figure 2) derived from the IIT_mean (grey curve) and IIT2_mean (black curve) templates.

Table 5.

Mean and standard deviation of FA values in selected white matter ROIs of the IIT_mean and IIT2_mean templates.

Brain structures	IITmean FA	IIT2mean FA	Number of voxels	P-value
gcc	0.66±0.08	0.72±0.06	50	6.9×10-4
scc	0.84±0.03	0.86±0.03	102	2.7×10-4
cg	0.59±0.05	0.63±0.05	157	7.1×10-12
fornix	0.59±0.11	0.73±0.11	25	2.3×10-4
ec	0.44±0.06	0.49±0.6	126	1.8×10-9

Figure 6.

Maps of the reduction in FA in the IIT_mean (A-D) and IIT2_mean (E-H) templates compared to the mean of the 67 individual FA maps.

Maps of the TVDT, FA_std, and trace_std showed reduced noise in the IIT2_mean compared to the IIT_mean template (Fig.7). The difference in FA_std was most visible at the edges of white matter structures (Fig.7A,B), and in trace_std, at the interface between brain tissue and CSF-filled spaces. Histograms of the TVDT, FA_std, and trace_std, considering all brain voxels, demonstrated that, in the IIT2_mean template, a larger percentage of voxels corresponded to lower noise levels compared to the IIT_mean template (Fig.8). Also, the COU in selected ROIs was significantly lower in the IIT2_mean compared to the IIT_mean template (Table 6). Finally, the TVDT, FA_std, trace_std, and COU were significantly higher in the IIT2_median than the IIT2_mean template (Fig.9).

Figure 7.

Maps of FA_std (A, B) and trace_std (C, D) from the same axial slice of the IIT_mean (A, C) and IIT2_mean (B, D) templates.

Figure 8.

Histograms of the relative number of brain voxels corresponding to different values of the TVDT (A), FA_std (B), and trace_std (C), for the IIT_mean (grey curve) and IIT2_mean (black curve) templates.

Table 6.

COU in selected white matter ROIs of the IIT_mean and IIT2_mean templates.

Brain structures	IITmean COU (°)	IIT2mean COU (°)	Number of voxels	P-value
gcc	2.07±0.28	1.91±0.26	50	4×10-3
scc	1.50±0.21	1.24±0.17	102	<10-15
cg	2.6±0.3	2.1±0.4	157	<10-15
alic	1.90±0.14	1.30±0.19	71	<10-15
plic	1.5±0.3	1.26±0.21	81	<10-15
fx	1.6±0.4	1.17±0.28	25	<10-15
cst	2.3±0.5	1.9±0.4	79	<10-15

Figure 9.

Maps of the TVDT from the same axial slice of the IIT2_mean (A) and IIT2_median (B) templates.

The cross-correlation between the average b=0 sec/mm² images of the IIT2 template and the T₂-weighted images of the ICBM-152 template was equal to 0.9784. The cross-correlation between the same images of the previously published IIT and ICBM-152 templates was slightly lower, at 0.9730. Although the difference in cross-correlation values was small, the matching of anatomical information was visibly improved between the IIT2 and ICBM-152 templates, compared to the IIT and ICBM-152 templates, especially in medial white matter structures such as the corpus callosum (Fig.10).

Figure 10.

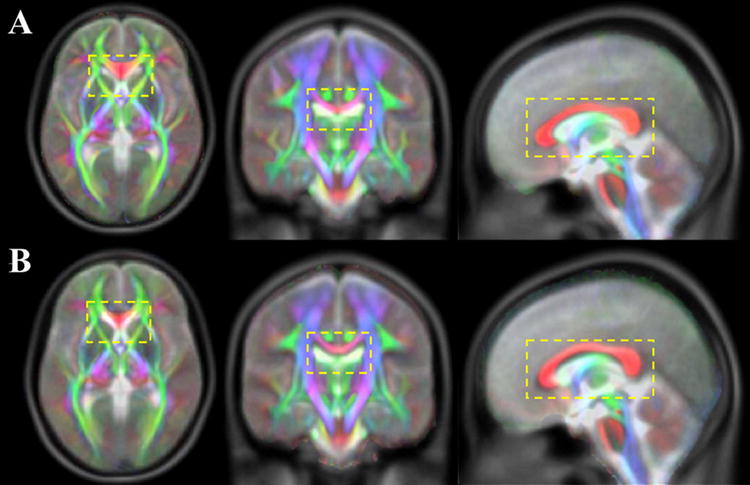
Diffusion anisotropy color maps from the IIT2 (A) and IIT (B) templates overlaid on the corresponding T₂-weighted images of the ICBM-152 template.

Assessment of the accuracy of inter-subject DTI spatial normalization through registration to the mean tensor template

Histograms of the COU, OVL, COH considering all white matter voxels (FA>0.2 in mean FA maps) demonstrated that, when registering the 22 datasets to the IIT2_mean template, a larger percentage of voxels were characterized by low COU (Fig.11A: left peak), high OVL (Fig.11B: right peak), and high COH (Fig.11C: right peak) values, and a smaller percentage of voxels were characterized by high COU (Fig.11A: right peak), low OVL (Fig.11B: left peak), and low COH (Fig.11C: left peak) values, compared to registration of the same 22 datasets to the IIT_mean template (Fig.11). The multiple copies of the histograms generated with the bootstrap approach were used to perform a paired t-test for the peaks of the histograms of Figure 11 (Table 7). As shown in Table 7, the differences in the relative number of white matter voxels corresponding to the peaks of the histograms obtained for registration to the IIT_mean and IIT2_mean templates were statistically significant (p<10^-8). Furthermore, the 95% confidence intervals of the histograms presented in Figure 11 were very narrow and practically indistinguishable from the histograms themselves. Also, according to a Kolmogorov-Smirnov test, the histograms of the COU, OVL, COH were significantly different when comparing registration to the IIT_mean and IIT2_mean templates (p<10^-8). Similar but smaller improvement when registering to the IIT2_mean template was observed with DTED and DVED. Finally, the average whole brain corr_FA for the 22 DT datasets after registration to the IIT2_mean template was significantly higher (0.916±0.008) than that after registration to the IIT_mean template (0.907±0.007) (p<10^-8). Similarly, the average corr_trace was significantly higher for registration to the IIT2_mean (0.936±0.010) than the IIT_mean template (0.933±0.010) (p=0.0026).

Figure 11.

Histograms of the relative number of white matter voxels corresponding to different values of COU (A), OVL (B), and COH (C), for registration of 22 Turboprop-DTI datasets to the IIT_mean (grey curve) and IIT2_mean (black curve) templates. The 95% confidence intervals are not shown since they were practically indistinguishable from the histograms themselves.

Table 7.

Mean and standard deviation of the relative number of white matter voxels corresponding to the peaks of the histograms of Figure 11, for registration of 22 subjects to the IIT_mean and IIT2_mean templates. The first column contains the range of COU, OVL, COH values under investigation.

	Registration to IITmean (relative # of white matter voxels × 102)	Registration to IIT2mean (relative # of white matter voxels × 102 )	P-value
COU = [12.12°, 13.08°]	2.02±0.01	2.23±0.02	<10-8
COU = [79.42°, 80.38°]	1.56±0.02	1.30±0.02	<10-8
OVL = [0.459, 0.465]	1.32±0.01	1.10±0.02	<10-8
OVL = [0.939, 0.946]	1.46±0.01	1.64±0.02	<10-8
COH = [0.578, 0.588]	1.50±0.02	1.39±0.01	<10-8
COH = [0.908, 0.917]	2.86±0.02	3.13±0.03	<10-8

Discussion

A DTI template that is representative of the micro-architecture of the human brain is crucial for comparisons of neuronal structural integrity and brain connectivity across populations, as well as for the generation of a detailed white matter atlas. A significantly improved DTI human brain template in ICBM-152 space was developed in this work. The new template maintained advantages of the original IIT template over other published templates. In addition, the new template was characterized by: a) higher image sharpness, b) lower noise levels, c) DT information that was more representative of single-subject human brain data, and d) improved matching of its anatomical information to that of the ICBM-152 template, than the existing IIT template. Also, registration of DTI datasets from different subjects to the new template resulted in more accurate inter-subject spatial normalization than registration to the original IIT template.

Accuracy of inter-subject spatial normalization achieved for the DTI datasets used in the development of the template

The algorithm used in this work for registration of the 67 DTI datasets to the temporary template (DTIGUI, Section of Biomedical Image Analysis, University of Pennsylvania, PA, USA) resulted in significantly more accurate spatial normalization (as demonstrated by means of the corr_FA, corr_trace, DTED, DVED, OVL, and COH), than that achieved with the SPM-based approach (SPM5, Wellcome Department of Imaging and Neuroscience, London, UK) used for the development of the previously published IIT template (Fig.1, Tables 1-4). This may be due to the higher-dimensional registration approach employed in DTIGUI, compared to that used in the development of the original IIT template (Peng et al., 2009). Furthermore, the improved inter-subject matching of tensor information achieved in this work may partly be due to the fact that the tensor reorientation method used here has been shown to be less sensitive to noise (Xu et al., 2003) than the one used in the development of the IIT template (preservation of principal direction) (Alexander et al., 2001). However, in both cases, registration was based on scalar quantities derived from the diffusion tensor (FA, trace, mean DW). Tensor matching can be improved when information such as the primary eigenvectors, or the whole tensors are taken into account in the estimation of the transformation (Alexander and Gee, 2000). Several advanced registration algorithms that normalize DTI data based on more information derived from the diffusion tensor than what was used here, or the diffusion tensor itself, have been published (Alexander and Gee, 2000; Avants et al., 2008; Cao et al., 2005; Chiang et al., 2008; Park et al., 2003; Rohde et al., 2004; Ruiz-Alzola et al., 2002; van Hecke et al., 2007; Verma and Davatzikos, 2004; Yang et al., 2008a; Yap et al., 2009; Yeo et al., 2008; Zhang et al., 2006; Zhang et al., 2007; Ziyan et al., 2007). Further research is necessary to compare their accuracy and robustness.

Development and evaluation of the DTI human brain template

It was recently demonstrated that, when the primary eigenvectors of anisotropic tensors with the same shape are misaligned, the FA of the mean tensor is reduced, but the FA of the median tensor is equal to that of the individual anisotropic tensors (Peng et al., 2009). This effect was also observed in this work, where the FA was shown to be higher in more white matter voxels of the IIT2_median than the IIT2_mean template, suggesting a residual mismatch in the primary eigenvectors of white matter tensors (Figs. 3A, B). Furthermore, it was previously shown that when highly anisotropic tensors are assigned to the same location as isotropic tensors with a higher trace due to imperfections in registration, the FA and trace of the mean tensor are reduced and increased, respectively, compared to the FA and trace values of the anisotropic tensors (Peng et al., 2009). In contrast, the median tensor maintains the characteristics of the anisotropic tensors as long as at least 50% of the tensors are anisotropic, and assumes the shape of the isotropic tensors when less than 50% of the tensors are anisotropic. These effects were also observed in this work, where the FA in some edges of the ventricles was higher in the IIT2_median than the IIT2_mean template (Fig.3A), and the trace values along the edges of CSF-filled spaces were higher in the IIT2_mean than the IIT2_median template (Fig.3, C, D). Thus, it was verified that, at the single-voxel level, in the presence of registration inaccuracies, median tensors better represent the characteristics of a group of tensors compared to mean tensors.

Based on the above discussion, when spatially normalizing DTI data from a group of subjects, a mismatch of brain structures across subjects is manifested as blurring in FA and trace maps of the mean tensor template, and misalignment of tensors with the same shape leads to mean tensors that are more isotropic (Peng et al., 2009). When comparing the IIT2_mean to the IIT_mean template, it was shown that the former was characterized by sharper FA and trace maps, and higher FA values in several ROIs, than the latter (Figs.4, 5, Table 5). Furthermore, FA values in white matter were in general more similar to those of individual subjects in the IIT2_mean compared to the IIT_mean template (Fig.6). Since both templates were based on the same raw datasets, these findings are a direct consequence of the improved spatial normalization of the 67 individual datasets achieved in the present study.

In this work, DTI brain templates were evaluated for the first time (to the best of our knowledge) in terms of the variance of tensor characteristics. A bootstrap approach was employed for this purpose, and the results showed that the values of TVDT, FA_std, trace_std, and COU were significantly lower in the IIT2_mean compared to the IIT_mean template, in several brain regions (Figs.7, 8, Table 6). This is also a result of the improved tensor matching achieved in the present study, and suggests higher confidence in the information presented in the IIT2_mean compared to the IIT_mean template.

When comparing the variance of tensor characteristics of the IIT2_mean to those of the IIT2_median template, the latter was shown to be significantly higher than the former (Fig.9). This was due to the fact that the mean of tensors grouped together using a bootstrap procedure is more stable than the median of these tensors. Although this may suggest higher confidence in the information presented in the IIT2_mean compared to the IIT2_median template, as mentioned earlier, at the single-voxel level, median tensors better represent the characteristics of a group of tensors compared to mean tensors. When the accuracy of inter-subject registration is sufficiently high, the mean also provides a good representation of the characteristics of a group of tensors. Further work is necessary to identify strategies for summarizing a group of tensors that a) result in low variance of tensor characteristics, and b) maintain the properties of individual tensors.

Temporary ICBM DTI templates were constructed during the development of both the IIT and IIT2 templates, by spatially normalizing the b=0sec/mm² volumes of a selected dataset to the T₂-weighted ICBM-152 volume. In the present study, this was achieved using a higher dimensional registration algorithm, provided by ART, compared to the algorithm used in the development of the original IIT template. The ability of ART to produce a more accurate inter-subject match of brain MRI images than several other registration techniques was shown recently (Klein et al., 2009). As a result, the temporary ICBM DTI template used in the development of the IIT2 template demonstrated an improved anatomical match with the ICBM-152 template. Consequently, the matching of anatomical information was improved between the IIT2 and ICBM-152 templates, compared to the IIT and ICBM-152 templates, especially in medial white matter structures (e.g. corpus callosum) (Fig.10).

One limitation of the new IIT2 template may be the fact that the DT properties of the single dataset used as a temporary template may have introduced a bias in the properties of the final template. However, this bias was minimized due to: a) the fact that the single dataset was used as a temporary template only after it had first been warped to ICBM-152 space using high dimensional non-linear registration (with ART), and b) a large number of DTI datasets were averaged to produce the final template. Another limitation may be the fact that 12 diffusion directions were used to acquire all DTI data, when it has been shown that at least 30 diffusion directions are required for a robust estimation of tensor-orientation and mean diffusivity (Jones, 2004). However, using 30 diffusion directions would significantly increase the acquisition time for Turboprop-DTI (which was already relatively long), and was therefore avoided. Furthermore, the benefit of increasing the diffusion directions from 12 to 30 would be minimal for the SNR achieved in this study (Jones, 2004), and would be limited to voxels with FA>0.8 (Jones, 2004), which constitute a small percentage of all white matter voxels. Additionally, any minor errors due to the use of 12 directions were further reduced by the averaging of DTI data from 67 subjects. Therefore, it is expected that the quality of information contained in the IIT2 template has not been significantly compromised by either of the two limitations discussed here.

Accuracy of inter-subject DTI spatial normalization through registration to the mean tensor template

Registration of DTI datasets from 22 subjects to the new template resulted in more accurate inter-subject spatial normalization than registration to the original IIT template. Since both templates were developed using DTI data from the same 67 subjects, the improvement in inter-subject spatial normalization when using the new template was due to the significantly improved image quality and tensor characteristics of that template.

Conclusion

In this study, a DTI human brain template for subjects between 20 and 40 years of age was developed in ICBM-152 space. The new template maintained advantages of the original IIT template over other published templates, such as: a) it was based on a relatively large number of subjects with a limited age-range, b) did not contain any visible artifacts, and c) provided the ability to distinguish even small white matter structures. In addition, the new template was characterized by: a) higher image sharpness, b) lower noise levels, c) DT information that was more representative of single-subject human brain data, and d) improved matching of its anatomical information to ICBM-152 space, than the existing IIT template. The main factors that contributed to the significant improvements in the new template were the use of: a) high-dimensional non-linear registration and b) tensor reorientation that is less sensitive to noise. Registration of DTI datasets from different subjects to the new template resulted in more accurate inter-subject spatial normalization than registration to the original IIT template. Other potential uses of the IIT2 template include development of a detailed white matter atlas, and automated segmentation of white matter structures on a subject-by-subject basis through normalization to the IIT2 template. The IIT2_mean and IIT2_median templates, the corresponding FA and trace maps, the mean b=0 s/mm², TVDT, FA_std, trace_std, and COU volumes, are available at www.iit.edu/~mri.

Table 2.

Average Euclidean distance of deviatoric tensors over all pairs of datasets used in the development of the IIT and IIT2 templates. Statistically significant differences (after correction for multiple comparisons with the Bonferroni approach) are marked with an asterisk (*).

Brain structures	IITmean DVED × 103 s/mm2	IIT2mean DVED × 103 s/mm2	Number of voxels	P-value
gcc	0.45±0.03	0.42±0.04	50	2.2×10-6 *
scc	0.53±0.06	0.48±0.06	102	3×10-9 *
cg	0.45±0.03	0.38±0.03	157	<10-15 *
alic	0.34±0.02	0.30±0.02	71	<10-15 *
plic	0.31±0.01	0.29±0.02	81	<10-15 *
ec	0.29±0.03	0.25±0.03	126	<10-15 *
cst	0.40±0.01	0.36±0.01	79	<10-15 *

Table 3.

Average overlap of eigenvalues-eigenvectors over all pairs of datasets used in the development of the IIT and IIT2 templates. Statistically significant differences (after correction for multiple comparisons with the Bonferroni approach) are marked with an asterisk (*).

Brain structures	IITmean OVL	IIT2mean OVL	Number of voxels	P-value
gcc	0.86±0.03	0.88±0.02	50	1.6×10-6 *
scc	0.95±0.01	0.96±0.007	102	<10-15 *
cg	0.83±0.04	0.90±0.02	157	<10-15 *
alic	0.95±0.01	0.96±0.01	71	<10-15 *
plic	0.96±0.01	0.970±0.006	81	3×10-11 *
ec	0.88±0.05	0.90±0.07	126	10-3 *
cst	0.88±0.03	0.91±0.02	79	7×10-9 *