Spatiotemporal dynamics of low frequency BOLD fluctuations in rats and humans

Abstract

Most studies involving spontaneous fluctuations in the BOLD signal extract connectivity patterns that show relationships between brain areas that are maintained over the length of the scanning session. In this study, however, we examine the spatiotemporal dynamics of the BOLD fluctuations to identify common patterns of propagation within a scan. A novel pattern finding algorithm was developed for detecting repeated spatiotemporal patterns in BOLD fMRI data. The algorithm was applied to high temporal resolution T2*-weighted multislice images obtained from rats and humans in the absence of any task or stimulation. In rats, the primary pattern consisted of waves of high signal intensity, propagating in a lateral to medial direction across the cortex, replicating our previous findings (Majeed et al., 2009a). These waves were observed primarily in sensorimotor cortex, but also extended to visual and parietal association areas. A secondary pattern, confined to subcortical regions consisted of an initial increase and subsequent decrease in signal intensity in the caudate-putamen. In humans, the most common spatiotemporal pattern consisted of an alteration between activation of areas comprising the “default-mode” (e.g., posterior cingulate and anterior medial prefrontal cortices) and the “task-positive” (e.g., superior parietal and premotor cortices) networks. Signal propagation from focal starting points was also observed. The pattern finding algorithm was shown to be reasonably insensitive to the variation in user-defined parameters, and the results were consistent within and between subjects. This novel approach for probing the spontaneous network activity of the brain has implications for the interpretation of conventional functional connectivity studies, and may increase the amount of information that can be obtained from neuroimaging data.

1. Introduction

Spontaneous low frequency fluctuations (LFFs)¹ in the blood oxygenation level dependent (BOLD) fMRI signal have become widely used for mapping the functional connectivity of the brain at rest (Biswal et al., 1995). Networks associated with different functional systems including visual, motor, auditory, memory and language have been detected in resting state fMRI studies (Cordes et al., 2000; Vincent et al., 2006). Researchers have also identified two widely-present networks, one containing areas (e.g. posterior cingulate and anterior medial prefrontal cortices) that are typically deactivated during the performance of a task (the “default mode” network) and another, “task-positive network” containing areas (e.g. superior parietal and premotor cortices) that are active during the performance of a wide variety of tasks and that may be related to attention (Fox et al., 2005).

Spontaneous fluctuations in the BOLD signal may contain a wealth of information not captured by most current analysis techniques, which focus on detecting correlations among different brain regions that are assumed to persist over several minutes (Biswal et al., 1995; Cordes et al., 2002; van de Ven et al., 2004). In a recent study using high temporal resolution data obtained from rats, we demonstrated that frame-by-frame visualization of band-pass filtered BOLD time-courses exhibits discrete spatiotemporal events, suggesting that detection of individual events in the data is possible (Majeed et al., 2009a). Waves of high signal intensity propagating from secondary somatosensory cortex (SII) to medial cortical areas were observed in α-chloralose anesthetized rats. These areas are not part of the same network when traditional seed-based cross-correlation techniques are used, indicating that the conventional methods may not extract all the information that can be obtained from functional connectivity data (Williams et al., in press). This opens a new avenue for functional connectivity research. The detection of propagating waves of MRI signal fluctuations that may reflect slow changes in electrical activity naturally leads to speculation about whether other dynamic neural events can be detected with MRI in anesthetized rodents, and whether similar spatiotemporal patterns / events can be found in awake humans. An in-depth study of these patterns may help to elucidate the origin and significance of LFFs. For example, it has been proposed that LFFs in different brain regions may be caused by one or more subcortical sources or “drivers” (Drew et al., 2008). Identification of sources of the high intensity signal can identify possible drivers / regions receiving direct input from the drivers of the LFFs in BOLD. Also, if similar spatiotemporal patterns can be detected in humans, it may be possible to tie these events to behavioral performance data. The presence of such time-varying patterns would suggest that the coherence between the BOLD fluctuations from different areas may change over time. In support of that idea, a recent study reports variability in the coherence between posterior cingulate cortex and task-positive network over time (Chang and Glover, 2009). These studies highlight the need for novel analysis techniques that could capture time-varying features in spontaneous BOLD fluctuations.

Our preliminary exploration of the spatiotemporal patterns of spontaneous BOLD fluctuations was based purely on visual inspection (Majeed et al., 2009a). The amplitude of the low frequency BOLD fluctuations is small, typically ∼1-2%, and visual detection of the patterns is limited by signal to noise ratio (SNR), and thus it is possible that patterns may be obscured in the presence of noise. Therefore, it is desirable to have an automatic method for the detection of such patterns. The previous study examined only single slice data, so that analysis was restricted to a single coronal plane. Three-dimensional data is necessary to characterize the true direction of propagation, which may contain significant through-plane components.

In this paper, we describe a method for the detection of repetitive spatiotemporal patterns in fMRI data, validate it using appropriate controls and test it for robustness. The method is applied to multislice data obtained from humans and rats to characterize reproducible spatiotemporal patterns. The results suggest that BOLD fluctuations propagate temporally over brain areas, and conventional functional connectivity analysis may not reveal such interactions. These findings not only push the limits of information that can be obtained from functional connectivity data, but also open new directions for future research.

2. Materials and Methods

2.1 Animal Preparation

All experiments were performed in compliance with guidelines set by the Emory University Institutional Animal Care and Use Committee (IACUC). Eight rats were initially anesthetized with 5% isoflurane and maintained at 2% isoflurane during preparation for imaging. Optical ointment was applied to the eyes of the animal. Two needle electrodes were inserted just under the skin of each forepaw, one between digits 1 and 2, and the other between digits 2 and 3. The rat was given a bolus of medetomidine (0.5 mg/kg) and isoflurane was discontinued. Anesthesia was maintained with a constant medetomidine infusion rate (0.1 mg/kg/hr). The rat was placed on a heated water pad while in the magnet to maintain rectal temperature at 37° C. Each animal was secured in a head holder with ear bars and a bite bar to prevent head motion and was strapped to a plastic cradle. Heart rate and blood oxygen level were continuously monitored during the experiment using a pulse oximeter, clipped to the left forepaw. A pressure-sensitive respiratory pad placed under the chest was used to continuously monitor breathing. All animals were carefully monitored for any sign of inadequate anesthesia (motion in the MR images, an abrupt rise in heart rate, or uneven respiration), but none were observed in the course of this study.

2.2 Animal Imaging

All images were acquired with a 9.4T / 20 cm horizontal bore BRUKER magnet, interfaced to an AVANCE console (Bruker, Billerica, MA) and equipped with a gradient set capable of providing 20 G/cm with a rise time of 120 μs. A two-coil actively decoupled imaging setup was used (2 cm diameter surface coil for reception and 7 cm diameter volume coil for transmission; Bruker, Billerica, MA) to achieve maximal SNR over the cortical areas of interest. Scout images were acquired in three planes with a FLASH sequence to determine appropriate positioning for the fMRI study. A gradient-echo EPI sequence (64 × 64 matrix, echo time (TE) 15-20 ms, repetition time (TR) 1.5 sec, field of view 2.56 cm × 2.56 cm) was used to acquire a series of images during forepaw stimulation in order to locate the slice containing forepaw region of the primary somatosensory cortex (SI). A block design stimulation paradigm was used, consisting of alternating rest and stimulation blocks (4 mA current, 300 μs pulses repeated at 9 Hz, 30 TRs on, 30 TRs off). The slice containing forepaw region of SI was used as a reference for slice placement for functional connectivity scans. Functional connectivity data were acquired with gradient echo EPI with following parameters: TR 500 ms, TE 20 ms, field of view 1.92 cm × 1.92 cm or 2.56 cm × 2.56 cm, four 2 mm thick slices, 1200 repetitions. No stimulation was given during functional connectivity scans.

2.3 Human Imaging

Two groups of human subjects were scanned for this study. The data from the first group was acquired with short TR (300 ms) to minimize the effects of aliasing and achieve better temporal resolution, while the data from the second group was acquired with long TR (1.5 s) to allow whole brain coverage and inter-subject registration. Imaging was performed on a 3T Siemens scanner using a birdcage head coil. Experiments were conducted according to the Georgia Institute of Technology/Emory University Institutional Review Board (IRB) guidelines. The subjects were asked to lie quietly in the scanner with their eyes closed. Anatomical scout scans were acquired in the three orthogonal planes and were used for placement of the slices for the functional scans.

2.3.1 Group 1 - Six healthy volunteers (19-22 year old; 3 male, 3 female)

Two runs of EPI image series were acquired with the following parameters: 300 ms TR, 30 ms TE, 3.44 mm × 3.44 mm in-plane resolution, 1600 repetitions, four 5 mm thick horizontal slices (parallel to the line joining anterior and posterior commissures).

2.3.2 Group 2- 14 healthy volunteers (32-66 year old, 3 male, 11 female)

A single run of EPI image series was acquired with whole brain coverage, using the following parameters: 1500 ms TR, 30 ms TE, 3 mm × 3 mm in-plane resolution, 276 repetitions, 28 horizontal slices with 4 mm thickness.

2.4 Preprocessing

All analyses were performed using Matlab (MathWorks, Natick, MA) unless otherwise noted. The processing steps described below were performed on all the datasets (humans and rats) unless specified otherwise. Slice-timing correction and motion correction were performed on all the datasets using AFNI (Cox, 1996). For the rat data, the area comprising the brain was segmented using an intensity threshold and manual removal of remaining voxels outside the brain. Gray matter, white matter and cerebrospinal fluid (CSF) masks were obtained for the human data using Statistical Parametric Mapping (SPM8) software (Wellcome Department of Cognitive Neurology, London, UK). Group 2 human datasets (TR = 1.5 s, whole-brain coverage) were spatially normalized to match the MNI template and resampled to the final voxel size of 3 × 3 × 3 mm³ using SPM8. 3D Gaussian kernel (FWHM = 6 mm) was utilized to smooth the Group 2 human data using SPM8. In-plane blurring was performed for the rest of the datasets with a 3 × 3 Gaussian kernel with σ = 2 pixels. The time-course from each voxel was band-pass filtered using FIR filters (0.01-0.08 Hz for humans, 0.08-0.2 Hz for rats). Transient time-points were discarded before and after filtering in order to discard transient effects of data acquisition and filtering respectively. Resultant time-courses were mean subtracted, quadratically detrended and normalized to unit variance. Signals from whole brain, CSF and white matter, as well as motion parameters (translation and rotation in 3 dimensions) were regressed out for human data in order to minimize effects of motion, physiological noise and scanner noise.

2.5 Detection of spatiotemporal patterns

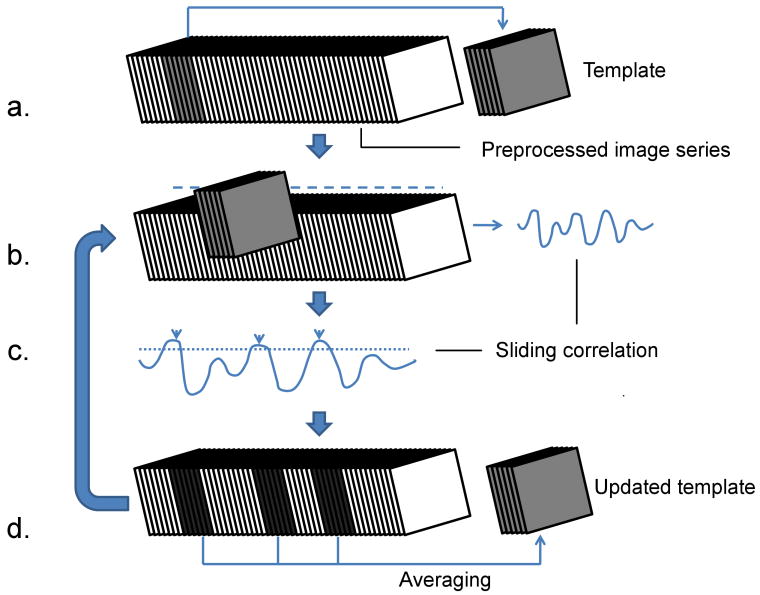
To improve on the original approach of visual inspection described in (Majeed et al., 2009a), we developed an algorithm that identifies recurring spatiotemporal patterns in the data without user input, using a random starting location and an iterative, correlation-based approach (Figure 1). A template, consisting of several consecutive preprocessed images is created with a random starting image. Sliding correlation of the template with the preprocessed image series is obtained in order to locate the segments of images in the image series which are similar to the template. The segments are averaged to obtain a new template and the process is repeated until the further iterations do not result in any modification in the template. If a spatiotemporal pattern occurs repeatedly and is captured by the initial template, it is possible to obtain high SNR approximation of the pattern using this approach. The detailed description of the algorithm is given below (summarized in Figure 1):

Figure 1. Algorithm for automatic detection of dynamic patterns.

a) A chunk of consecutive images starting at a random time is selected from the filtered image series to serve as template. b) Sliding correlation between the filtered image series and the template is obtained. c) Peaks are detected in the thresholded sliding correlation. d) Chunks of images corresponding to the peaks correlation values are averaged in order to obtain updated template. Steps b to d are repeated until the template does not change for two successive iterations (cc > 0.9999).

1. An initial guess about the duration of spatiotemporal patterns to be detected is chosen, termed window length (WL). WL can be based upon the duration of events observed visually. For example, the initial WL for the rats was chosen based on the duration of the patterns seen in our previous work (Majeed et al., 2009a). Alternatively, different experimental values of WL can be used in order to explore spatiotemporal events with different time scales in the data.

2. A random image in the preprocessed image series is chosen as a starting point for the template time-series. The time location corresponding to the starting point is termed q and referred to as the “seed time-point” later in the text. A template is essentially a series of consecutive images, with its duration equal to WL.

   $$T(x,y,z,n)=I(x,y,z,n+q-1)1\le n\le WL$$
3. Sliding correlation r(n) between the preprocessed image series I(x, y, z, k) and template T(x, y, z, k) is obtained using following equation (N_s represents number of voxels in the ROI):

   $$r(n)=\stackrel{1}{}/\underset{K(n)}{}\sum _{m=n}^{n+WL-1}\sum _{(x,y,z)\in s}\left(I(x,y,z,m)-{\mu }_I(n)\right).\left(T(x,y,z,m-n+1)-{\mu }_T\right)$$
   where

   $$\begin{array}{l}{\mu }_T=\stackrel{1}{}/\underset{(N_s.WL)}{}\sum _{m=1}^{WL}{\sum }_{(x,y,z)\in S}T(x,y,z,m),{\mu }_I(n)=\stackrel{1}{}/\underset{(N_S.WL)}{}\sum _{m=n}^{n+WL-1}{\sum }_{(x,y,z)\in S}I(x,y,z,m)\\ K(n)=\sqrt{\sum _{m=1}^{WL}{\sum }_{(x,y,z)\in S}{\left(T(x,y,z,m)-{\mu }_T\right)}^2}\sqrt{\sum _{m=n}^{n+WL-1}{\sum }_{(x,y,z)\in S}{\left(I(x,y,z,m)-{\mu }_I(n)\right)}^2}\end{array}$$

   r(n) represents sliding correlation at temporal delay equal to n images. S is the set of spatial coordinates (x, y, z) belonging to the region of interest (ROI) chosen for spatiotemporal analysis. I(x, y, z, k) and T(x, y, z, k) represent intensity values of the preprocessed image series and template respectively at spatial location (x, y, z) in the k^th image of the corresponding image series.

4. Time values corresponding to local maxima of r(n) are obtained. An array v with length p, consisting of time-values for which local maxima are greater than a correlation threshold, is created.

5. The template is updated by averaging the segments of images corresponding to local maxima, using the following expression:

   $$T(x,y,z,n)=\stackrel{1}{}/\underset{p}{}\sum _{m=1}^{p}I(x,y,z,v(m)+n-1)1\le n\le WL$$

6. Steps 1-5 are repeated until r(n) does not change for two successive iterations (cc (correlation coefficient) > 0.9999).

The value of correlation threshold can be modified during the iterations. For this study, lower threshold value (0.1) was chosen for the initial 3 steps, followed by higher value (0.2) for the subsequent steps.

The final template obtained after convergence is used as the representative spatiotemporal pattern, and peaks in the thresholded final sliding correlation time-course indicate occurrence times for the pattern. After the convergent correlation time-course is obtained, templates with expanded window length (WL′) can be obtained by averaging the segments of images centered on the peaks in the thresholded correlation time-course in order to visualize any significant averaging outside the window chosen for the analysis. Although the voxels outside the ROI are not used for calculating and optimizing the sliding correlation, the final template can be obtained by including the whole image in the final averaging process (Figure 1d).

Rat datasets as well as Group 1 human datasets were analyzed separately for each subject. Human data were analyzed using this algorithm with an ROI comprising the gray matter mask obtained using SPM8. Rat data were analyzed with manually chosen ROIs placed in 1) entire brain, 2) entire cortex, and 3) caudate-putamen (CP). Group analysis was not performed for the Group 1 datasets as well as rat datasets because inter-subject registration was not possible due to limited number of slices. Therefore, qualitative comparison was used for assessing reproducibility across the subjects.

Whole-brain coverage allowed for group analysis for the Group 2 human data. In order to perform group analysis, the preprocessed image series for all the subjects were concatenated together. The template was obtained using the concatenated data (with ROI covering the entire cortex), while ignoring the peaks in the correlation time-course that may have been influenced by the junction between any two datasets. The resultant template was resampled (2 × 2 × 2 mm³). Statistical significance of the template in space and time was computed as follows: Intensity values for each spatial location and time were obtained from the image segments averaged to give the final template. Two-tailed t-test was used in order to identify the voxels with intensity values significantly different from zero at a given time (p < 0.001). Isolated voxels in the significance map were removed by performing erosion followed by dilation (3 × 3 × 3 kernel consisting of ones).

In order to test sensitivity of the algorithm on the pre-defined parameters, the algorithm was repeated with 1) different values of WL and 2) different values of seed-time point q on the rat data as well as Group 1 human data. The results with different initial parameters were compared. In order to compare the templates, sliding correlation was obtained between the templates (WL′ = 3WL, maximum lag = WL) and the maximum value of the sliding correlation was used as the similarity measure between the templates (termed as optimal correlation). Sliding correlation time-courses were compared using the same approach. In addition, the method was applied on phase-randomized data from a living rat. The phase-randomized data consisted of time-courses with magnitude spectra identical to those of the data from a living rat, but randomized phase spectra. The following procedure was applied to individual time-courses from the living rat in order to randomize the phases:

1. The discrete Fourier transformation G was obtained for a given time-course g, where G and g have the same length.

2. A random time-course h was generated using MATLAB with its length equal to the original time-course, and its discrete Fourier transform H was obtained.

3. The Fourier transformation W of the phase-randomized time-course w was obtained using the following expression:

   $$W(u)=\left|G(u)\right|.e^{i\phi (u)},\text{where}\phi (u)=arctan\left(\frac{\mathit{\text{imag}}(H(u)}{\mathit{\text{real}}(H(u)}\right)$$
4. The phase randomized time-course w was obtained by taking the inverse Fourier transformation of W.

   $$w=F^{-1}[W]$$

3. Results

3.1 Rat Data

In all rats, forepaw stimulation resulted in normal activation in the contralateral SI. The slice showing maximum activation was used as a reference for slice placement for the resting state studies. Compared with the data presented in (Majeed et al., 2009a), the propagation of signal intensity was less clear, though waves could still be seen by visual inspection.

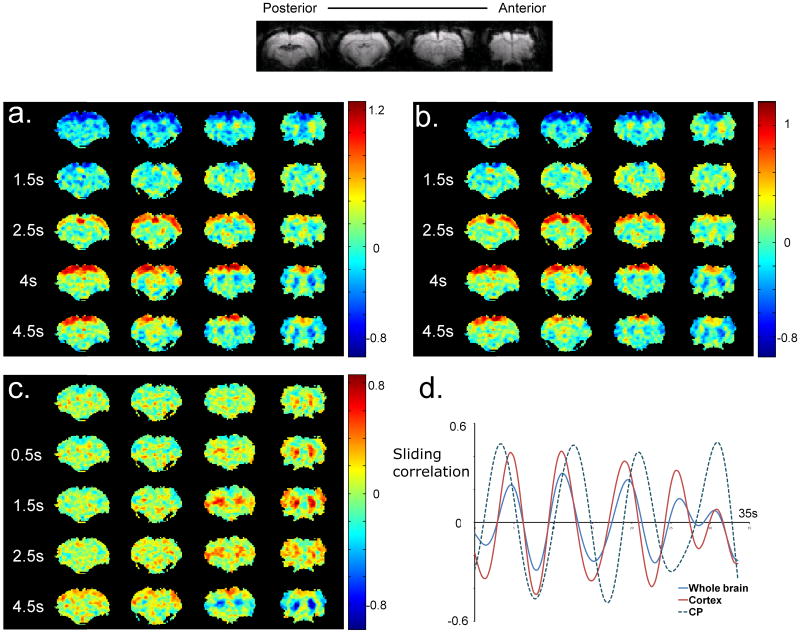
Figure 2a shows five frames of a typical template obtained with the ROI comprising the whole brain from one of the rat datasets. A window length of 9 s was for the rat datasets unless otherwise noted, which is nearly twice the propagation time (4.7 s – defined as the time required for the high intensity signal to travel from SII to primary motor cortex) for the waves reported in (Majeed et al., 2009a), in order to include the negative part of the cycle. Propagation of high intensity from lateral to medial areas is observed in the slices containing sensorimotor cortex (two most anterior slices), confirming the result reported in (Majeed et al., 2009a) with a different type of anesthesia. In addition, similar waves with similar durations are observed in more posterior slices containing parietal association area and visual cortex. The waves can be observed for 7 of 8 rats (Movie 1). The only rat dataset not showing this pattern (Rat 5) shows a pattern caused by an imaging artifact (Movie 1). Time-courses from the template were obtained from manually drawn ROIs in the most lateral and most medial areas in the second most frontal slice, which contains sensorimotor regions. The time gap between the transition from negative to positive signal in the most lateral area and transition from positive to negative in the most medial area was defined as the propagation time of the wave. This time averaged 4.8±0.92 s, which is in agreement with the results reported in (Majeed et al., 2009a). An almost identical pattern (average optimal cc between the templates with either ROI = 0.87±0.11) is detected when an ROI comprising the cortex rather than the whole brain is used for the analysis (Figure 2b, Movie 2). The pattern can be reproducibly observed for all the rats (Movie 2). Half cycle durations (the time between successive positive and negative peaks in the time-course from template for a given region) were recorded to be 3.8±0.42 s and 3.44±0.42 s for ROIs drawn in left and right SI respectively. The speed of propagation of the peak intensity was also measured in the sensorimotor cortex (second most frontal slice). A piecewise linear curve was manually drawn through the middle of the cortex, and the length of the curve was divided by the time-interval between peak intensities in voxels corresponding to the ends of the curve. The average speed of propagation of the intensity peak was measured to be 4.0±1.34 mm/s. High variability in the calculated speed can be attributed to long sampling time (which reduces temporal precision) as well as inaccuracies in the distance computation due to finite voxel size, distortion and manual delineation of the path of travel.

Figure 2. Templates and sliding correlation time-courses for one rat.

a) Five frames from a template obtained with an ROI covering the whole brain are shown. A propagating wave of high intensity can be observed in all the slices, followed by a propagating wave of low intensity in the same direction. The second frame (1.5 s) shows the onset of the waves, marked by increased intensity in the lateral cortical areas. The later frames show the propagation of the high intensity towards the medial areas, followed by a wave of low intensity in the same direction. b) The propagation pattern with an ROI covering just the cortex is almost identical to that obtained with the ROI covering the whole brain. The templates obtained with either ROI are highly correlated (cc = 0.87±0.11, averaged over all the rats). c) The spatiotemporal pattern obtained with CP-based ROI shows alternation of positive and negative signal intensities in CP. The increase in BOLD signal is focal in the beginning (0 s) and expands to fill the entire CP. d) Sliding correlation with respective templates for 3 different ROIs. Peaks in the sliding correlation time-course occur at nearly identical time-points for the ROIs covering whole brain and cortex. The correlation time-courses for CP and the other ROIs are sometimes well-aligned, while at other times they are out of phase.

Figure 2c shows the template obtained from a ROI placed in left and right CP. The main feature of this pattern is an alternation between high and low intensities in bilateral CP. The durations of the half cycle in left and right CP (time between consecutive positive and negative peaks averaged over all the rats for manually defined ROIs in CP) were 3.31±0.26 s and 3.38±0.23 s respectively, similar to the length of the half cycle in SI. Notably, high signal intensity is observed for some cortical areas even though the intensities from the cortex were not used for determining the segments of images that were averaged. In some other cases, the cortex shows low intensity in the averaged template (Movie 3). The pattern was observed in all 8 datasets (Movie 3).

The sliding correlation time-course shows multiple peaks crossing the threshold (0.2) for all the ROIs, which suggests that the spatiotemporal patterns corresponding to their respective template are repeated several times during the length of the scan (Figure 2d). Average peak-to-peak interval values for the ROIs comprising the whole brain, cortex and CP are 10.22±1.45 s, 8.61±1.15 s and 8.02±0.47 s respectively (sub-threshold peaks were not included). As shown in Figure 2d, the correlation patterns for the whole brain and cortical ROI are almost identical, as expected from the similarity between the corresponding templates. However, the timing of occurrence of the peaks is different for the templates with ROIs placed in cortex and CP as shown in Figure 2d. Consequently, the templates obtained with CP-based ROIs show lower optimal correlation with the templates based on the other ROIs (whole brain vs. CP: 0.57±0.14, CP vs. cortex: 0.56±0.13), compared with the correlation between the whole brain and cortex-based templates (0.87±0.11). As can be seen in Figure 2d, the sliding correlation time-courses for cortical ROIs and CP ROIs are sometimes well-aligned, while at other times they are out of phase. The inconsistent synchrony may account for the inclusion of some cortical areas in the CP templates, depending on which part of the cortical cycle is most commonly aligned with the CP cycle over the duration of the scan.

Although it was not possible to register all the brains due to differences in slice geometry, three datasets with the most similar orientations were registered together using AFNI (Cox, 1996), and their templates were aligned in time and displayed as a movie (Movie 4). The visual comparison between the three templates demonstrates consistency of the results across the rats.

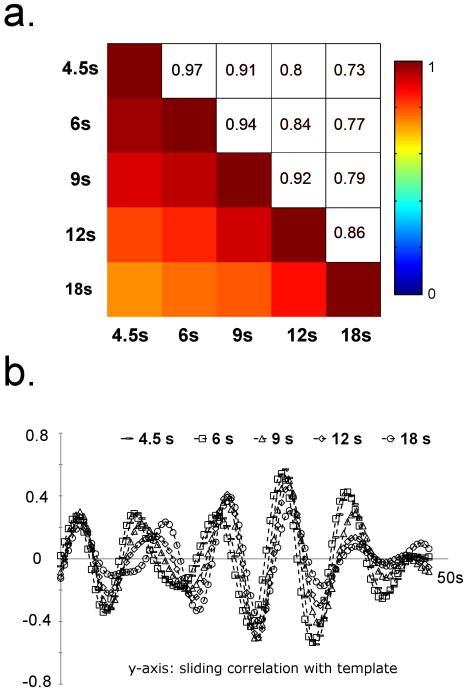
In order to assess the reproducibility of the method, the results obtained with different window lengths and seed time-points were compared. Figure 3a shows the pair-wise optimum correlation between the sliding correlation time-courses obtained with different window lengths, averaged over all the datasets (ROI comprising the cortex). The correlation time-courses were used for comparison instead of the templates due to unequal lengths of the templates. The time-courses are very similar for a wide range of WL (cc > 0.7 for the window lengths ranging from 9 to 36 TRs), implying that the method is relatively insensitive to the variation in WL. Figure 3b shows sliding correlation time-courses for 5 different window lengths for one of the rats. The time-courses are very similar for all 5 window lengths. Pairwise correlation values (between the templates obtained using an ROI covering the whole brain) at optimum delay were obtained for 10 different randomly selected seed time-points for all datasets. The average optimal correlation value of 0.86±0.1 (averaged over all the rats and 40 pairwise comparisons per rat) was obtained, demonstrating the insensitivity of the method to the seed time-point as long as the patterns to be detected occur frequently throughout the course of the scan.

Figure 3. Sensitivity to the initial parameters for rat data.

a) Pairwise optimal correlation between the sliding correlation time-courses with different window lengths (averaged over 8 rats). The time-courses are very similar for a wide range of window lengths as indicated by high correlation values between the templates with different window lengths, suggesting that it is not necessary to have accurate a priori knowledge of the temporal extent of the patterns to be detected. b) Sliding correlation time-courses with different window lengths for one rat. Consistent with figure 3a, the time-courses are very similar for a wide range of window lengths.

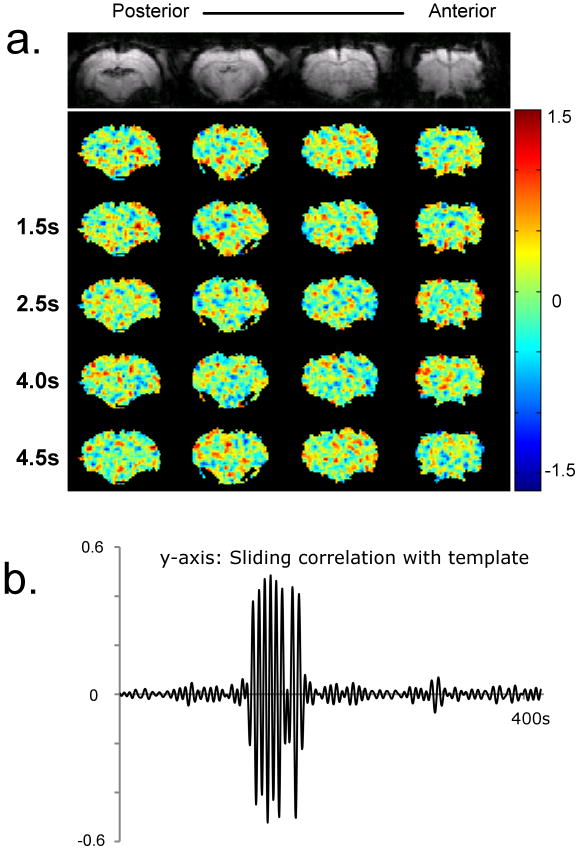
Figure 4 shows a template and plot of sliding correlation for phase-randomized data with the ROI covering the whole brain. No organized patterns can be seen in the template (Figure 4a). The sliding correlation function shows some high peaks in vicinity of the seed time-point (Figure 4b). The amplitude of the peaks rapidly decays to values close to zero (< 0.1), which suggests that no repeated dynamic patterns are present in the phase-randomized data.

Figure 4. Template and sliding correlation obtained from a phase randomized dataset (dataset with same magnitude spectrum as that of a real dataset, but randomized phases).

a) Five frames from the template. No specific patterns can be observed. b) Sliding correlation time-course for the phase-randomized data. The time-course shows high peaks at the time-points only in the vicinity of the seed time-point. Peaks near the seed time-point are expected because the data is temporally smoothed due to filtering. These results suggest that the patterns shown in previous figures are not likely to occur by chance.

3.2 Human Data

3.2.1 Group 1(high temporal resolution)

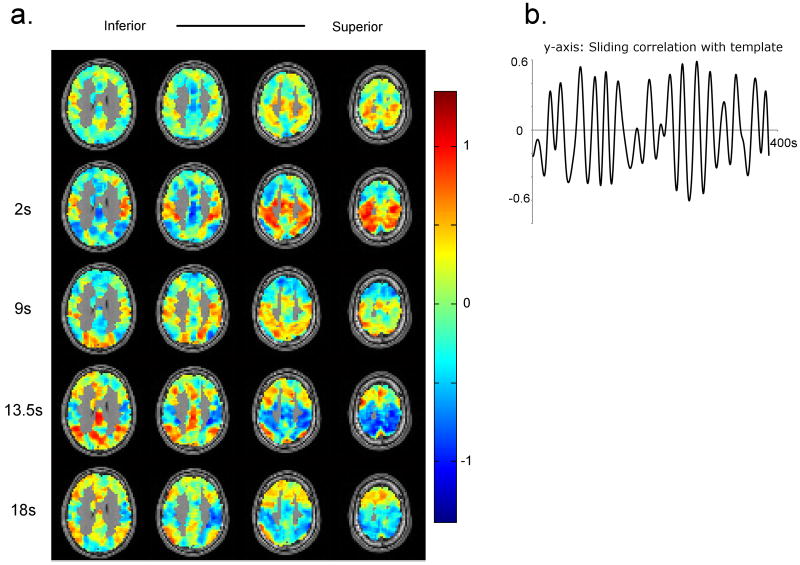
Figure 5a shows five frames for the template obtained for a human dataset (TR = 300 ms, WL = 67 TRs, or ∼20 s). The template shows switching between the two groups of areas: 1) areas comprising default mode network, and 2) sensory and motor areas that have been referred to as the dorsal attention network, or task-positive network. These networks have been reported as consistently being anti-correlated in human resting state data (Buckner et al., 2008; Fox et al., 2005; Fransson, 2006). The pattern occurs several times during the course of the scan, as apparent from the peaks in the sliding correlation function (Figure 5b). However the occurrence pattern is relatively sparse (peak-peak interval = 26.41±4.35 s, averaged over all the subjects and sessions), compared with the patterns observed in rats.

Figure 5. Spatiotemporal patterns and sliding correlation time-courses obtained from a human dataset.

a) The pattern shows alteration between the default mode and task-positive/attention networks. At t = 2 s, the attention network shows high signal and the signal from default mode network is reduced. 3^rd frame (9 s) shows an intermediate stage between positive and negative signal intensitiy in the attention network marked by reduced signal intensity in the attention network. At t = 13.5 s, positive intensity in the default mode network and negative intensity in the attention network are observed. The signal intensity returns to baseline after some time, as seen in the last frame (18 s). b) The sliding correlation time-course shows multiple peaks which are distributed in time, indicating that the pattern occurs repeatedly during the course of scanning

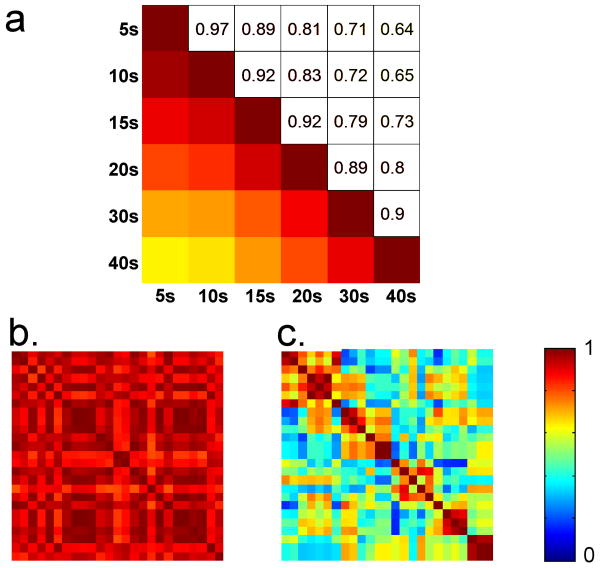
The robustness of the method against initial parameters was tested using the approach used for rats. Correlation time-courses show very little variability for a wide range of window lengths (Figure 6a). However, in contrast with the results obtained for rats, the templates do not always show high correlation for different seed time-points with a fixed window length (Figure 6b and 6c). Therefore the template obtained from a given dataset with a fixed window length is not unique, which complicates the comparison of the patterns within and between the subjects. In order to resolve this issue, templates were obtained from 25 different seed time-points for each dataset (window length = 67 TRs or ∼20 s). The templates were clustered based upon the pairwise optimal correlation values using hierarchical clustering. The seed time-point corresponding to the “most central” template belonging to the biggest cluster was chosen for within and between subject comparison, where the “most central” template is defined as the one with the maximum average correlation with rest of the templates belonging to the biggest cluster. The seed time-point selected using this method resulted in the templates containing the pattern described above. The seed-time point for the template displayed in Figure 5 was chosen using the same approach. Qualitative comparison suggests that the pattern shown in Figure 5 was obtained for 11 out of 12 sessions (Movie 5). Session 1 for the subject 6 is the only session for which this pattern was not observed (Movie 5). Based upon qualitative comparison, the results are reproducible within the subject for 5 out of 6 subjects (subjects 1-5). The average optimal correlation between the templates obtained from the two sessions was 0.3±0.12. Half cycle times for average signals from ROIs drawn in task-positive and default mode were 9.6±1.12 s and 9.95±1.0 s respectively (averaged over the 11 sessions with consistent spatiotemporal pattern). Speed of propagation was not calculated for humans because the propagation path is not clearly defined due to the convoluted cortex. The average switching time (defined as the time between positive peak intensities in the default mode and task-positive networks) was 10.5±1.45 s (calculated using manually drawn ROIs, 11 sessions exhibiting consistent pattern used).

Figure 6. Sensitivity to the initial parameter for human data.

a) Pairwise optimal correlation between the sliding correlation time-courses with different window lengths (averaged over 12 sessions). Correlation time-course for 20 s window length is very similar to those obtained from window lengths ranging from 5 s to 40 s (cc > 0.8). Therefore it is not necessary to have exact knowledge about length of the pattern to be detected. However, relatively low correlation is observed between longest and shortest window lengths. b) Correlation matrix representing pairwise optimal correlation between the templates obtained using 25 random starting points for a human dataset. The templates obtained with different seed time-points are highly correlated for this dataset. c) Correlation matrix obtained from another human dataset (the data points were re-ordered in order to emphasize the clusters of similar templates). For this particular dataset, not all the templates with random seed-points show high correlation. b and c suggest that depending upon the data set, the seed time-point may or may not have an impact on the results.

3.2.2 Group 2 (low temporal resolution)

In order to perform group analysis, the preprocessed image series for all the subjects were concatenated together. Clustering of templates with random seed-points was used to select the seed, as described above. The templates for 50 random seed time-points were obtained (WL = 13 TRs or ∼20 s). The templates thus obtained were clustered as described above and the most central seed time-point in the biggest cluster was used for rest of the analysis. The statistical significance of the template in space and time was computed using a t-test in order to identify voxels which showed statistically significant positive / negative intensity at a given time, as described in the methods section (p < 0.001). Since the data was acquired with whole brain coverage, it was possible to visualize the dynamic pattern for other orientations (Figure 7, Movie 6).

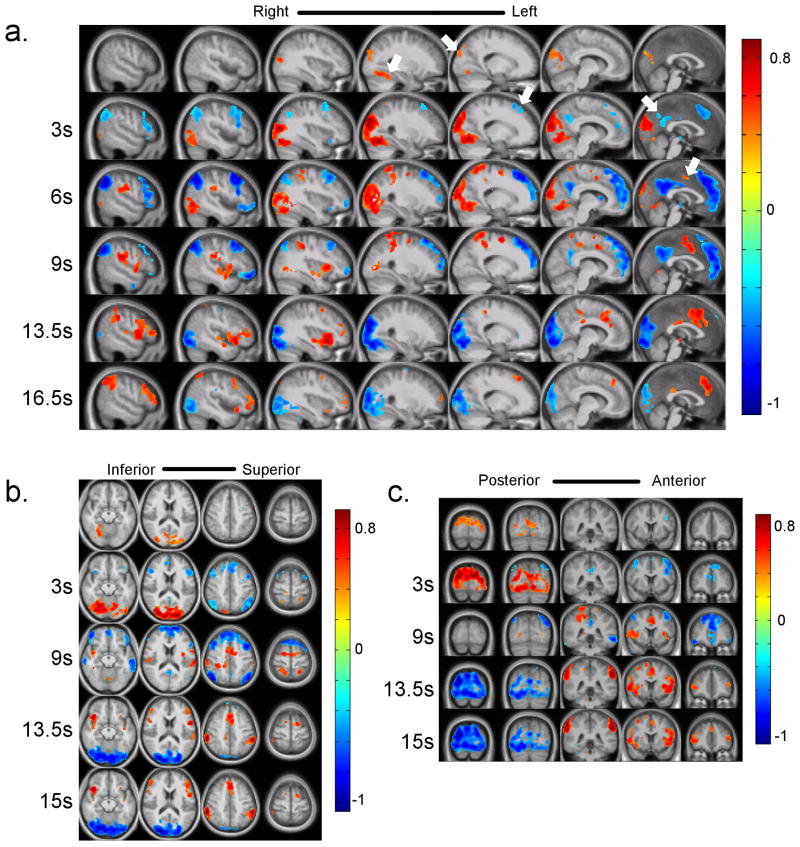
Figure 7. Frames from the template obtained using group analysis in three different planes.

The color bars represent average z-scores for a given voxel at a given time in the template. Switching between the task-positive and default mode networks can be observed in all three orientations (a, b, c). Closer inspection reveals propagation of signal from focal points to the other brain areas (especially in the sagittal plane). The “sources” of the signal propagation are indicated by white arrows on figure 7a. Propagation of positive signal change can be seen starting from fusiform gyrus and parieto-occipital sulcus (0 s, columns 4 and 5) as well as medial premotor cortex (6 s, column 7). The propagation of negative signal change can be seen from the areas including medial prefrontal cortex (column 5, 3 s), posterior cingulate cortex (column 7, 3 s). The propagation can continue for more than 10 s (e.g. the propagation of positive signal change from premotor cortex). A clearer visualization of these propagation patterns can be seen in Movie 6. More investigation into finding the significance of such “sources” can provide us a new insight into the origin of the low frequency fluctuation.

Visual inspection of the template shows alteration between the default mode and anti-correlated task-positive networks. Close examination, however, reveals propagation of intensity from some focal points, especially in the sagittal plane (indicated on Figure 7a using white arrows) over several seconds. The first propagation starts with appearance of high intensity in parieto-occipital sulcus and fusiform gyrus (Figure 7a, 0 s, columns 5 and 4 from the left). The high intensity propagates to other areas including precuneus, cuneus, and visual cortex. The second propagation pattern starts after the first pattern and is marked by propagation of negative signal intensity within the prefrontal cortex towards more frontal areas (column 5, 3 s). Propagation of negative intensity from the posterior cingulate cortex to the adjacent areas is also observed (column 7, 3 s). Another propagation pattern consists of propagation of high intensity from premotor cortex to more anterior parts of the frontal cortex, and probably posterior cingulate cortex (column 7, 6 s). This template is shown with more time-points and slices in Movie 6. ROIs were drawn in the default mode network and task-positive network and the switching time (time between maximum signal intensities in default mode network and task-positive network) was calculated. The switching time obtained for the template for group data was 10.5 s. Half cycle times for default and task-positive networks had the same value of 10.5 s (measured using the approach described earlier). All these measurements are within one standard deviation from those obtained from Group 1 data.

4. Discussion

This study demonstrates that the spatiotemporal patterns of BOLD fluctuations that were previously observed in the anesthetized rodent are a robust phenomenon, occurring in both rats and humans and detectable at a wide range of field strengths. To better characterize the dynamics of the BOLD signal, we present a novel approach to detect repeated spatiotemporal patterns in the fMRI data. The method has been tested for robustness to changes in initial parameters, and can be applied to multislice human and rat data to detect the patterns which are reproducible within and between subjects.

Ideally, a functional imaging modality should be able to provide information about both spatial and temporal aspects of brain activity. In other words, it should be able to provide information about brain function with high spatial and temporal resolution. Compared with other functional modalities, fMRI provides excellent spatial and moderate temporal resolution. However, the amount of information that can be obtained from fMRI data is limited by several factors, SNR being one of them. In order to overcome this limitation, averaging over time is a method used extensively in fMRI studies exploring the response to a task or stimulus. This allows us to identify the areas that, on average, show an increase or decrease in activation under the time-window representing the stimulus or task. Although this averaging does not preserve trial-to-trial variability or ongoing changes in brain activity that might be unrelated to the task, it allows us to effectively increase the SNR, and provides some spatial and temporal information at the cost of details which are averaged out. This approach relies on manipulation of brain activity at known times. (i.e. blocks or events). Improvement of SNR by averaging for functional connectivity data, on the other hand, is non-trivial of the fact that the brain activity is not controlled by any external stimuli. As a result, conventional functional connectivity analysis techniques rely on detecting a relationship between signals from brain regions over the entire length of acquisition. This approach identifies brain areas that show correlated BOLD fluctuations across the session, but compromises precise temporal information. The results discussed in this paper show that averaging is possible for functional connectivity data because the data consists of the repetitive spatiotemporal blocks. We can then study when these blocks occur in time, thereby preserving the temporal information.

4.1 Rat Data

The propagating waves that we detected in rats are identical to those identified previously through visual observation (Majeed et al., 2009a). Additionally, multislice acquisition used in this study made it possible to detect any anterior-posterior component of the wave propagation. Our results suggest that the wave propagation takes place primarily in the lateral to medial direction. Also, the spatiotemporal pattern involves simultaneous propagation in multiple slices ranging from SI to visual cortex. This observation suggests that the underlying neurovascular event for this pattern either involves long range interaction between the functional modalities, or is caused by a common source of input or generator.

Although the frequency range of interest for LFF analysis in humans is fairly well established (Biswal et al., 1995; Fox et al., 2006; Fox et al., 2005; Vincent et al., 2006), different groups have used different frequency ranges for the analysis of rat data (Lu et al., 2007; Majeed et al., 2009a; Pawela et al., 2008; Williams et al., in press; Zhao et al., 2008). Several of these studies have utilized a frequency cutoff of 0.08-0.1 Hz, which matches that used for human data analysis (Lu et al., 2007; Pawela et al., 2008; Zhao et al., 2008). These studies also used longer TRs (1.426-2 seconds), and so a smaller number of image volumes (110-300) was obtained to keep the acquisition time reasonable. The resulting spectral resolution did not allow a detailed analysis of the frequency components in the low frequency range. In our previous study, we used short TR (100ms) data with a large number of image volumes (3600) to examine the spectral structure of the low frequency range (Majeed et al., 2009a). Two low frequency peaks (LF1: f < 0.025 Hz, LF2: 0.12-0.17 Hz) were detected in the data obtained from α-chloralose anesthetized rats. LF1 (isolated using a low-pass filter with 0.05 Hz cutoff) showed global connectivity patterns, suggesting that it may not contain useful information about functional networks. LF2, however, showed specific bilateral connectivity patterns, suggesting that frequency components with f > 0.08-0.1 Hz may carry more information about the functional connectivity networks in rats. However, the relative specificity of the two peaks may hold for only the particular experimental paradigm used by (Majeed et al., 2009a) since specific connectivity patterns have been reported for cutoff frequencies of 0.1 Hz or 0.08 Hz (Lu et al., 2007; Pawela et al., 2008; Zhao et al., 2008). This specificity may be due to the variation in the TRs used, the primary difference between these studies and the work presented in (Majeed et al., 2009a). With a very short TR (100 ms) and single slice acquisition, the signal fluctuations are likely to be heavily influenced by inflow effects. If these fall primarily into the LF1 band, they may contaminate the otherwise functionally specific lower frequency component.

Further work in medetomidine anesthetized rats shows that the higher frequency fluctuations are not merely a consequence of the α-chloralose anesthesia. In contrast with the two distinct peaks seen in at least some of the α-chloralose anesthetized rats, a broad low frequency spectrum (0-0.2 Hz) was observed for medetomidine anesthetized rats (Magnuson et al., 2009; Majeed et al., 2009b; Williams et al., in press). This suggests that the use of different anesthetic agents might result in variation in the relative contribution of different vascular or neural factors to the LFFs and raises the question of whether the band-pass filtered component in the data obtained from medetomidine anesthetized rats is equivalent to LF2 peak as observed in α-chloralose anesthetized rats (Majeed et al., 2009a). We believe that 0.08-0.2 Hz component of LFFs in medetomidine anesthetized rats has a dominant LF2 contribution because the spatiotemporal properties of the 0.08-0.2 Hz component are similar for both types of anesthesia. Additional evidence comes from a study showing a peak at ∼0.2 Hz in the CBV-weighted functional data obtained from medetomidine anesthetized rats (Magnuson et al., 2009), while a broader low frequency spectrum was observed for BOLD weighted images obtained from the same rats. The spatiotemporal properties for the CBV-weighted data were in agreement with those reported for α-chloralose anesthetized BOLD data (data not shown). We have focused on the analysis of LF2 in this study because it allows direct comparison to our previous study (Majeed et al., 2009a) and confirms that similar spatiotemporal dynamics can be observed at a lower field strength and under a different anesthesia. The contribution in the lower frequency range for the medetomidine anesthetized rats will be analyzed separately as part of future work.

Our previous work with rats utilized a 100 ms TR which guaranteed separation of respiratory and cardiac noise in frequency domain (Majeed et al., 2009a). A longer TR (500 ms) was used in this study in order to obtain multislice datasets. Therefore, the first harmonics of respiratory and cardiac noise are aliased into 0-1 Hz range. The typical respiration rate for this study was ∼70-80 cycles/minute. However, even frequencies as high as 100 cycles/minute are aliased no lower than 0.33 Hz in the sampled signal, suggesting that respiratory noise is mostly removed by the low-pass filter. However, cardiac noise has a much higher frequency and may be aliased into 0-0.2 Hz range. Since the propagation patterns observed in this study are identical to those observed in (Majeed et al., 2009a), cardiac noise does not seem to limit the detection of this particular pattern in the data. This is supported by the fact that the cardiac noise is mainly localized to the surface of brains near the draining veins, or base of the brain (Majeed et al., 2009a; Williams et al., in press).

Lateral to medial propagation of intensity was observed for all the rats in this study. However, the propagation was visually detectable only in 3 out of 6 datasets analyzed in our previous study (Majeed et al., 2009a). LF2 did not appear as a distinct peak in the 3 rats which did not show the propagation pattern. We re-analyzed that data using the pattern detection approach used in this study and were able to detect the propagation pattern in the three datasets for which the pattern was not visually detectable (Movie 7). This highlights the improved detection sensitivity achieved by this method, compared with visual detection and suggests the presence of some LF2 contribution in those 3 rats, even though LF2 peak was not clearly observed visually.

4.2 Human Data

The most obvious pattern detected in short TR human data at the individual subject level shows an alteration in signal intensity between default mode and task-positive networks. This result is in agreement with studies that report anti-correlation between these two major networks (Fox et al., 2005). Propagation of intensity from some focal points can be more readily observed in the template obtained from the whole-brain data (Movie 6, Figure 7). The group analysis provides more information due to high SNR achieved by averaging, as well as the possibility of visualization of the pattern in multiple planes. Interestingly, close inspection of the whole-brain human data suggests a possible further division of the anti-correlated task-positive or “attention” network, based on spatiotemporal dynamics. Specifically, frontal eye fields, inferior parietal and occipital regions, largely corresponding to what has been called the dorsal attention system (Corbetta and Shulman, 2002; Fox et al., 2005), appear to show high signal intensity early in the pattern (Figure 7, 3-9 s in red). Subsequently, elements of the ventral attention system come online (Figure 7, 9-16.5 s in red), including anterior cingulate, frontoinsular, lateral prefrontal and lateral parietal cortices. Recent work (Seeley et al., 2007) suggests the ventral attention network can be further subdivided into two networks based on intrinsic connectivity: a salience network, containing dorsal anterior cingulate and frontoinsular cortices, and a right-lateralized executive network, comprised of lateral prefrontal cortex and lateral parietal cortex. This subdivision may also be reflected temporally in our data, as regions within the salience network (Figure 7, 9-13.5 s in red) appear to peak in intensity before those in the executive network (Figure 7, 13.5-16.5 s in red). The temporal relationship between these putative sub-networks may speak to the internal connectivity and “drivers” within these systems, and should be investigated further. Examinations such as these further highlight the utility of approaches that investigate spatiotemporal dynamics of BOLD fluctuations.

The spatiotemporal patterns detected for the short and long TRs show alteration between default and task-positive networks. The switching time between default and attention network obtained using both TRs are in excellent agreement (10.5±1.45 s for individual subjects vs 10.5 s for group template). As removal of primary components of respiratory and cardiac noise was possible with a TR of 300 ms, it can be concluded that the pattern is not caused by aliased components of respiratory or cardiac noise. However, it is possible that physiological noise may alter the spatial spread of the pattern, as suggested by the reduction in spatial extent of correlation caused by regression of respiratory contribution (Birn et al., 2006). Simultaneous acquisition of fMRI and physiological signals will be used in future studies in order to study the effect of removal of these cycles on the spatiotemporal pattern.

While other factors, including vasomotion, can contribute towards the BOLD signal in addition to the local hemodynamics associated with the neural activity, there is mounting evidence suggesting neural and behavioral relevance of the LFFs (Goldman et al., 2002; Gonçalves et al., 2006; Liu et al., 2008; McNamara et al., 2007). Therefore, it is reasonable to hypothesize the neural basis of the patterns presented in this paper. The link between propagation of the BOLD signal and possible propagation of neural activity is yet to be established. The difference in hemodynamic delays between different brain regions can result in the propagation patterns even in the absence of propagating neural activity. A multimodality approach involving fMRI and electroencephalography (EEG) will be needed to establish the neural/non-neural basis of the propagation patterns.

4.3 Pattern detection algorithm

The algorithm developed for detection of spatiotemporal patterns relies on the assumption that the patterns occur several times during the course of data acquisition. Another assumption is that a chunk of consecutive images starting at a random time captures whole or part of a spatiotemporal pattern of interest with fairly high probability. Therefore, this approach for detecting spatiotemporal patterns has certain limitations. First, it can only be used for reproducible patterns, as sufficient averaging may not be achieved for isolated events. However, the validity of isolated events, even if detected, would remain questionable due to SNR limitations. Second, the method uses a pre-specified window length and starting point. Although the examples shown in the present study suggest that the results are not influenced by window length over a wide range of window length, it is conceivable that some patterns might have significantly different duration compared with the window length used, and thus may not be detected. In addition, the seed time-point used for the process might influence the final template obtained by the method, as observed for the human data. These problems can be alleviated by using this method as an exploratory approach. Templates can be obtained for a wide range of window lengths and seed time-points. For a given seed time-point, the templates can be clustered into the groups representing spatiotemporal patterns with different durations. For a given window length, the clusters would represent spatiotemporal patterns with almost the same duration which occur at different times (this approach was used for seed selection for human subjects).

Results obtained from the rats are largely independent of the window length. The same trend is observed for human data. Lack of dependence on the window length may occur for different reasons. Independence of the results on window lengths much higher than the duration of the pattern might indicate the occurrence of the patterns in groups or quasi-periodicity. In that case, the algorithm would consider multiple instances of a pattern as a larger pattern. Another reason would be lack of patterns with the larger time-scale, which might change overall correlation trends if present. Independence on smaller window lengths is conceivable because template comprising a part of the actual pattern would give rise to peak in the sliding correlation at the same location as those obtained using a template with its length equal to the actual pattern. The location of the best match would remain the same in either case.

Although our results suggest that these spatiotemporal patterns can be detected reproducibly with long (1.5 s for humans) as well as short (300 ms for humans, 500 ms for rats) TRs, the selection of optimal TR for such studies is an important issue that warrants further investigation. Longer TRs allow for whole brain coverage, inter-subject registration and group analysis, but result in coarser representation of the spatiotemporal patterns. On the other hand, shorter TRs allow for a more fine-grained temporal visualization of the patterns, and make it possible to detect any patterns with a shorter time-span. The feasibility of the group analysis for the shorter TRs depends upon slice positioning across the subjects. In principle, the TR should not exceed a fraction of the period of interest. Shorter TRs can initially be used in order to characterize the patterns at different time-scales. The optimal TR can then be chosen based upon 1) the time-scale of the patterns of interest and 2) brain coverage required for a particular study.

4.3 Implications for functional connectivity studies

This study has several implications for functional connectivity research. The approach developed in this study provides a way to detect the underlying spatiotemporal patterns that give rise to the LFFs. It would be interesting to explore other patterns in the data and find their relative contribution to the LFFs. It has been suggested that LFFs might be caused by a “neuronal driver”, sending a common input to “functionally connected” areas (Drew et al., 2008). Although this speculation has yet to be confirmed experimentally, our technique to study spatiotemporal propagation provides a promising way to identify potential candidates for the driver (or drivers) of LFFs, or the areas receiving direct input from the drivers. For example, lateral to medial propagation of the signal in rodents might suggest that the lateral areas are either the drivers of the LFFs, or they receive the input from the drivers, which further spreads across the cortex. If these areas act as the starting points for a slow modulation of neural activity, the energy demands of adjacent areas would increase as their activity increased, resulting in an increase in BOLD signal that follows the propagation path of the activity. However, as discussed earlier, difference in hemodynamic delays can induce propagating patters in BOLD signal which may not be related with propagating neural activity. Therefore, further investigation with multiple modalities is needed to test this hypothesis.

4.5 Conclusions

In conclusion, we have identified reproducible spatiotemporal patterns of BOLD fluctuations in human and rodent data using a novel approach. The approach was validated and tested for robustness. The patterns we observed are in agreement with previous studies and are likely to carry important information about brain activity at rest. This method provides a powerful tool to investigate the spatiotemporal patterns of BOLD signal fluctuations that contribute to functional connectivity. Future research will focus on establishing the link between these patterns and behavior/task performance. Further, additional spatiotemporal patterns and their relative contribution towards LFFs will be explored.

Supplementary Material

1. Movie 1: Spatiotemporal pattern detected with an ROI covering the whole brain for 8 rats.

Propagation of signal intensity from lateral to medial cortical areas can be readily observed for 7 out of 8 rats, suggesting that the pattern can be observed reproducibly across the rats. The pattern cannot be observed for rat 5 due to an imaging artifact.

2. Movie 2: Spatiotemporal pattern detected with an ROI covering the cortex for 8 rats.

The spatiotemporal pattern consists of propagation of signal intensity from lateral to medial cortical areas, as seen for the templates with whole brain ROI. The propagation covers all 4 slices except for rat 8 for which the most posterior slice (containing visual cortex) does not show visually detectable propagation.

3. Movie 3: Spatiotemporal pattern detected with an ROI covering the CP for 8 rats.

The spatiotemporal pattern consists of an increase and subsequent decrease in intensity of CP, which can be seen in all 8 rats. The intensity changes in CP show inconsistent phase relationship with the intensity changes in the cortex. For example, the changes in the cortex and CP are in sync for some rats (e.g. rats 7 and 8), but are out of phase for the others (e.g. rats 1 and 2)

4. Movie 4: Temporally aligned templates for 3 different rats for cortex-based ROI (only one slice per rat is shown).

The propagation patterns have comparable timing for all 3 rats, suggesting inter-subject reproducibly of this particular pattern. Individual frames of the movie were interpolated for display purposes.

5. Movie 5: Spatiotemporal pattern obtained from Group 1 (300 ms TR) subjects (6 subjects, 2 sessions per subject).

The pattern shows alteration between the default mode and task-positive networks. This alteration is seen for 11 of 12 sessions (session 1 from the subject 6 does not show this pattern), suggesting that the pattern can be observed reproducibly across the subjects. Registration with the template was not possible for the Group 2 data. Therefore, inter-subject statistical comparison is not possible. The time-aligned templates (for two different sessions) show correlated signal changes in the pattern across the sessions except for the subject 6 (optimal correlation = 0.3±0.12, averaged over all the subjects).

6. Movie 6: Spatiotemporal pattern obtained from Group 2 (1.5 s TR) subjects.

The template was obtained using group analysis, as explained in the methods section. The pattern is shown in sagittal, horizontal and coronal planes. The pattern consists of switching between the task-positive and default mode networks, with propagation of signal intensity from focal brain areas, more readily observed in sagittal plane.

7. Movie 7: Spatiotemporal pattern obtained from data used in (Majeed et al., 2009a).

This movie shows templates obtained with ROI covering the cortex from rats 4-6 used in our previous study (Majeed et al., 2009a). The rats were anesthetized with α-chloralose and 100ms TR was used. LF2 peak (in 0.12-0.17 Hz range) was visually detectable only in three of the 6 rats (rats 1-3). Also, medial to lateral propagation was not visually detectable in rats 4-6. This movie shows that the templates (ROI comprising cortex) obtained from rats 4-6 (used in our previous study) exhibit medial to lateral propagating waves, demonstrating superior sensitivity of our detection algorithm, as compared with visual detection.

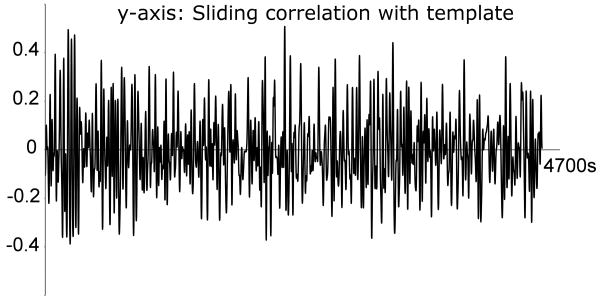
Figure 8. Sliding correlation time-course for the template obtained from the concatenated data.

The occurrence of high peaks is not restricted to a small window in time, suggesting that the template obtained from the concatenated data represents a pattern that occurs reproducibly across the subjects.