Power consequences of linkage disequilibrium variation between populations

Abstract

We quantify the degree to which LD differences exist in the human genome and investigates the consequences that variations in patterns of LD between populations can have on the power of case-control or family-trio association studies. Although only a small proportion of SNPs show significant LD differences (0.8–5%), these can introduce artificial signals of associations and reduce the power to detect true associations in case-control designs, even when meta-analytic approaches are used to account for stratification.We show that combining trios from different populations in the presence of significant LD differences can adversely affect power even though the number of trios has increased. Our results have implications on genetic studies conducted in populations with substantial population structure and show that the use of meta-analytic approaches or family-based designs to protect Type 1 error does not prevent loss of power due to differences in LD across populations.

INTRODUCTION

Population structure has conventionally been defined to take the form of allele frequency differences between populations, and measures for quantifying the extent of population differences typically rely on variations in allele frequencies between populations [Wright, 1943, 1951; Chakraborty and Danker-Hopfe, 1991; Excoffier, 2001; Balding and Nichols, 1995; Nicholson et al., 2002; Balding, 2003; Marchini et al., 2004; Devlin and Roeder, 1999]. It has been systematically reported that the presence of population structure results in inflated test statistics, thus increasing the likelihood of false positives in disease association studies [Marchini et al., 2004; Thomas and Witte, 2002; Ziv and Burchard 2003; Freedman et al., 2004; Helgason et al., 2005; Clayton et al., 2005; Price et al., 2006; Kimmel et al., 2007], particularly in association studies of complex diseases where the magnitude of signals from multiple disease genes may be comparable to confounding signals from population structure. Failure to replicate earlier findings has also been attributed to the presence of unaccounted population structure in the form of differences in allele frequencies [Marchini et al., 2004; Editorial, 1999; Weiss et al., 2001]. However, because of allele frequency differences, population structure can manifest in variations in the patterns of linkage disequilibrium (LD) between populations. Such LD variations may take the form of differences in the length of LD between populations or the existence of different haplotypes between populations [Hanchard et al., 2007].

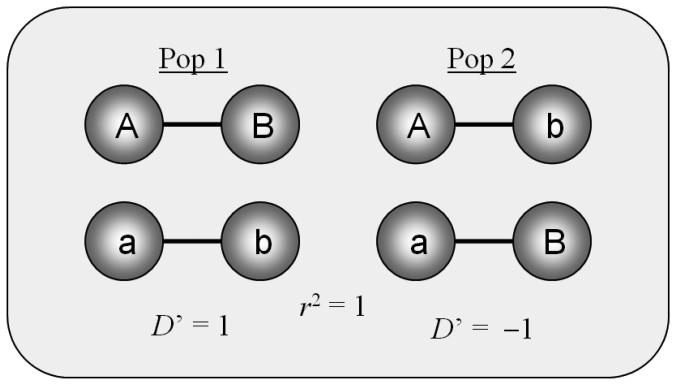
Previous reports have discussed the extent of variation in LD between populations, especially between genetically diverse populations like those represented in the International HapMap Project [International HapMap Consortium, 2005; de Bakker et al., 2006; International HapMap Consortium, 2007]. These reports have often assessed the extent of dissimilarities on the basis of the length of LD [Pe'er et al. 2006a,b; Barrett and Cardon, 2006] and seldom on the direction of the LD [Conrad et al., 2006]. As such it is currently unclear how prevalent the syndrome of opposing LD is between populations (see Fig. 1), with opposing LD defined as the situation where the correlation between two single nucleotide polymorphisms (SNPs) occurs in opposite direction across different populations. The consequence of opposing LD between two SNPs in two populations results in D0 values which is positive in one population and yet negative in another population, and this will not be identifiable when assessed using the conventional r2 metric. One of the implications of opposing LD on genetic association studies was discussed recently, resulting in “flip-flop” associations where disease associations are found on opposite alleles in different populations [Lin et al., 2007, 2008; Zaykin and Shibata, 2008]. In practice, opposing LD often manifests in the form of different common haplotypes between populations, an example of which can be found at the sickle mutation in the beta-globin gene (HBB) where the benin haplotype is common among Jamaicans and the Yoruba while the Senegal haplotype is more common in The Gambia [Hanchard et al., 2007].

Figure 1.

Depicting the LD between two SNPs with alleles (A, a) and (B, b) respectively in two populations. Perfect LD (with r² = 1) exist in both populations, although in population 1, allele A is correlated with allele B, while in population 2, the correlation exists with allele b. This yields a positive D′ in one population, and a negative D′ in the other population. We define this situation as opposing LD.

Reports on population structure often focused primarily on the effects of allele frequency differences and how confounding effects can be managed through the use of sophisticated statistical approaches [Marchini et al., 2004; Devlin and Roeder, 1999; Price et al., 2006; Pritchard and Donnelly, 2001; Prichard et al., 2000a,b; Wellcome Trust Case Control Consortium, 2007; Plenge et al., 2007; Tian et al., 2008]. The use of family-based designs has often been advocated as a counter to the effects of unforeseen population structure [Spielman and Ewens, 1998; Lewis, 2002]. Here we investigated the consequences of population structure represented by variations in patterns of LD between populations on the power of case-control and family trio designs using a series of simulation studies. Data from the HapMap project and from an ongoing genome-wide scan on malaria susceptibility in The Gambia were used to quantify the extent of LD differences, including those in opposing LD differences, and investigate the effect of combining trio data from two African populations. We have chosen the HBB region on chromosome 11, which is known to have unusual patterns of haplotypic variation, thus providing a practical example for the effects of opposing LD. These populations were chosen as they appeared to be genetically similar when assessed in the context of the amount of genetic diversity across the HapMap populations, but can be separated into two distinct clades when assessed without the HapMap CEU and CHB1JPT samples (in review). Our results indicate that the presence of opposing LD between the causal variant and the assayed marker in different populations leads to elevated rates of false associations and decreased power in case-control designs. Although, as expected, association studies using family trios are immune to confounding effects of population structure, we show that the presence of LD differences can dramatically decrease power in an association study combining trios from different populations.

MATERIALS AND METHODS

Defining LD

Consider two biallelic loci on the same chromosome, with alleles A and a at one locus, and alleles B and b at the other locus. Let the associated allele frequencies be written as p_A, p_a, p_B, p_b, and the four haplotype frequencies be written as p_AB, p_Ab, p_aB and p_ab. We measure LD with three metrics:

1. Lewontin's D′³⁹, defined as

   $$D\prime =\{\begin{array}{cc}\frac{p_{\mathit{AB}}-p_A{p}_B}{\min (p_A{p}_b,p_a{p}_B)},\hfill & p_{\mathit{AB}}\ge p_A{p}_B\hfill \\ \frac{p_{\mathit{AB}}-p_A{p}_B}{\min (p_A{p}_B,p_a{p}_b)},\hfill & p_{\mathit{AB}}<p_A{p}_B\hfill \end{array}\phantom{\}};$$
2. the square of the genetic correlation coefficient r^{2 40}, defined as

   $$r^2=\frac{{(p_{\mathit{AB}}-p_A{p}_B)}^2}{p_A{p}_a{p}_B{p}_b};$$

3. signed r², defined as the r² but with the sign from D'.

Quantifying LD differences in different populations

We applied a simple metric based on the signed r² to quantify the extent of LD differences between populations, where the absolute difference in the signed r² for each pair of SNPs across two populations is calculated. To assess the extent of LD differences between different populations, a comparison study of LD was performed using HapMap samples and the 60 Gambian samples. These samples were divided into two population pairings: (i) CEU and CHB+JPT; (ii) YRI and the Gambian samples. Comparisons are made within each population pair across SNPs from the autosomal chromosomes that remained after quality control for the malaria susceptibility study. To avoid double-counting the extent of LD differences, we consider non-overlapping windows of 100kb across each chromosome. A SNP near the middle of each window is chosen as the ‘focal’ SNP, and the LD between this focal SNP and all other SNPs in the window is calculated using the signed r² metric. We have only considered SNPs with less than 5% missing data and have minor allele frequencies ≥ 5% in both populations within each population pair. For each of the focal SNP, we report the maximum absolute difference in the signed r² across all other SNPs in the window. Two measures are used to quantify the extent of opposing LD in each of the population pair considered: (i) the total number of opposing LD relationships observed between the focal SNPs and the surrounding SNPs within 50kb; (ii) the proportion of SNPs in consideration that exhibit at least one opposing LD relationship where the absolute difference of the signed LD is greater than 0.5.

Simulating data in two populations

We directly simulate haplotype data that had different pairwise LD patterns for three scenarios: (i) a matched case-control study with 1000 cases and 1000 controls from each of the two populations; (ii) a case-control study with biased sampling of 1100 cases and 900 controls from population 1, and 900 cases and 1100 controls from population 2; (iii) a family-based design using parents-affected offspring trios, with 1000 trios from population 1 and 1000 trios from population 2. Each of the three scenarios is simulated 1000 times with relative risks (λ) of either 1 or 1.5, to allow the proportion of false positives and power to be evaluated. The details of the simulations can be found in the Supplementary Methods.

Simulating trio data at the HBB region

Haplotypes from 60 Gambian individuals of a single ethnic group and the 60 HapMap YRI parents were used to simulate parents-affected offspring trios at the HBB region on chromosome 11. Subjects from The Gambia were recruited as part of an ongoing genetic study in malaria³⁸, and were genotyped on the Affymetrix GeneChip Human Mapping 500K Array Set. Only SNPs with less than 5% missing data and have minor allele frequencies ≥ 5% in both the Gambian and YRI samples were considered, yielding a total of 254 loci across a 1Mb region beginning at 4.7Mb. Genotype data for the Gambian samples were phased using FASTPHASE⁴¹ while the HapMap phased haplotypes were used for the 60 YRI samples. Switch errors in the haplotype phasing can artificially introduce opposing LD, and the direction of LD for each SNP in the region was verified separately for concordance by a pairwise inference of the D′ value between the SNP and the HbS locus, rs334, with an Expectation-Maximization algorithm using the genotypes. To simulate the parents of each trio, four haplotypes are randomly selected with replacement from the pool of 120 haplotypes in each population. The first pair of haplotypes is assigned to the father, and the remaining pair is assigned to the mother. A haplotype is randomly selected from each of the two parents to be assigned to the offspring and the genotype for each SNP is obtained by combining the alleles observed across the two haplotypes for each individual. The phenotype status of the offspring is assigned as a Bernoulli random variable with parameter conditional on the genotype at the HbS locus, rs334. We assume a dominant disease model at rs334 such that the penetrance of the disease is identical for genotypes AT and TT (denoted as f₁), and the penetrance for the AA genotype is denoted as $\frac{\lambda f_1}{1-f_1+\lambda f_1}$, with λ denoting the relative risk of the AA genotype. In our simulations of 1000 trios for each population, we have assumed identical values for the penetrances and relative risks across the two populations considered, with f₁ to be 0.1 and λ to be 0.1, where the latter is consistent with reported literature^38,42.

Testing for associations

A χ² test of independence was used to test for association between the disease and the marker in the case-control studies, while data for trios are analyzed with the transmission-disequilibrium test (TDT)⁴³. The analyses were performed across a number of configurations. Each of the two populations is first analyzed separately to assess the signals of association from the genetically-homogeneous populations. The genotype data from both populations is subsequently combined to yield a single dataset with twice the sample size, which in theory should yield greater power when analyzed. A standard meta-analytic approach using the Mantel-Haenszel procedure is also implemented to pool the data from both populations⁴⁴. We calibrated the experiment by first defining statistical significance at 0.05 to check that the empirical false positive rates obtained were approximately 5%. Subsequently, we defined genome-wide significance at a P-value threshold of 10⁻⁶. The false positive rate was calculated as the proportion of tests out of 1000 that yielded a P-value more significant than the adopted threshold when the relative risk was set at 1, while similar calculations were performed at the relative risk of 1.5 to yield the empirical power.

RESULTS

In the comparisons of the extent of LD differences between CEU and CHB1JPT, we investigated 398,424 SNPs which were partitioned into 17,779 blocks. By considering the maximum absolute difference of the signed r2 (MADSRsq) across the two populations, we observes a mean MADSRsq of 0.43 with a standard deviation of 0.22 (Table I). In addition, 35.8% of the pairwise LD relationships between the focal SNPs and all other SNPs exhibited opposing LD between CEU and CHB 1JPT. As our interest lies mainly in SNPs that can affect the power and false-positive rates of the experiment when the data from both populations is merged, we narrowed our identification criterion to the number of focal SNPs with opposing LD where the absolute difference between the signed LD in the two populations is greater than 0.5. For CEU and CHB1JPT, 5.0% (889 of 17,779 blocks) of the focal SNPs gave evidence of significant LD differences. For YRI-Gambian, we investigated 392,533 SNPs which were partitioned into 17,997 blocks, where the mean (SD) of the MADSRsq was 0.28 (0.15). Of all the pairwise LD relationships considered, 36.1% exhibited opposing LD and 0.8% (146 of 17,997 blocks) of the focal SNPs displayed opposing LD with absolute difference between the signed r2 to be greater than 0.5.

Table 1.

Summary statistics on the extent of LD differences between two population pairings.

Population pair	# Blocks (# SNPs)	max|diff ($r_{\mathit{signed}}^2$)|		Opposing LD
		Mean (SD)	Median (IQR)	% pairwise SNPs relationships	% blocks with max|diff ($r_{\mathit{signed}}^2$)| > 0.5
CEU − CHB+JPT	17,779 (398,424)	0.43 (0.22)	0.41 (0.33)	35.8	5.0
YRI - Affy	17,997 (392,533)	0.28 (0.15)	0.25 (0.16)	36.1	0.8

In order to assess the effects of population structure resulting from such LD differences in an association study, we performed a series of simulation studies for the casecontrol and family trio experimental designs. While it is common to simulate the presence of population structure through the use of a model-based approach which generates the allele frequencies for SNPs across different populations [Balding and Nichols, 1995; Nicholson et al., 2002; Balding, 2003; Marchini et al., 2004], we chose to vary the LD between the causal variant and the marker variant in population 2 in order to investigate the effect of LD differences. The allele frequencies for population 2 are sampled randomly from the range of possible values that are consistent with the LD between causal variant and the marker variant (see Supplementary Methods).

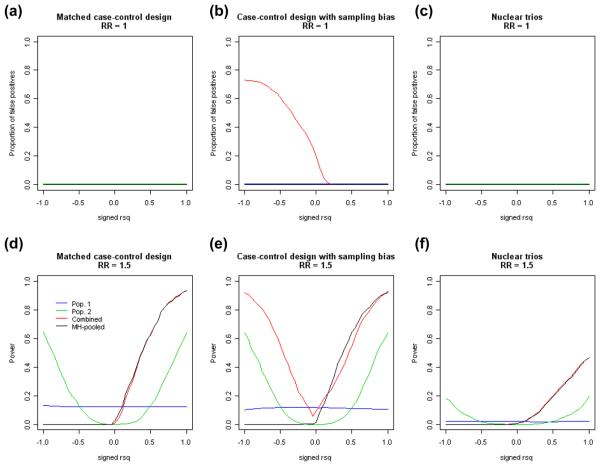
In the absence of any disease effects (RR51), analyzing the data within each of the two populations separately and pooling the data using a Mantel-Haenszel procedure yield the expected rate of false-positive association regardless of the extent of the differences across the two populations (Fig. 2a–c). When the data from both the populations are combined without accounting for inter-population differences, a matched case-control design (Fig. 2a) and the use of family trios (Fig. 2c) are similarly protected against the effects of unaccounted population structure while biased sampling of cases and controls across the two populations can result in elevated rates of false associations (Fig. 2b). This occurred in our simulations when the signed r2 between the untyped causal variant and the assayed marker in population 2 dropped below 0.2 (the signed r2 remains a constant at 0.5 in population 1 throughout the simulation).

Figure 2.

Relationship between the probability of detecting an association and the extent of the LD (signed r²) between a causal variant and the assayed marker SNP when: (a) relative risk (RR) = 1 for a matched case-control design; (b) RR = 1 for a case-control design with sampling bias; (c) RR = 1 using parents-affected offspring trios; (d) RR = 1.5 for a matched case-control design; (e) RR = 1.5 for a case-control design with sampling bias; (f) RR = 1.5 using parents-affected offspring trios. Lines in blue refer to analyses performed with data from population 1 only; green lines for analyses performed with data from population 2 only; red lines refer to analyses performed with data from both populations combined without accounting for inter-population differences; black lines refer to analyses performed with data from both populations pooled using the Mantel-Haenszel procedure.

In the presence of a genuine disease effect at the causal variant (RR51.5), the power of the experiment within each population depended on the LD between the causal variant and the assayed marker (Fig. 2d–f). As the LD was fixed at r250.5 in population 1, the power remained similar throughout the simulations; the power for population 2 had a monotone relationship with absolute r2, with a maximum of 63% at perfect LD and 0% when r2 drops below 0.1. Pooling data from both the populations resulted in higher power when the signed r2 for both the populations are in the same direction and almost no power at all when the LD in the two populations are of opposite directions even when the Mantel-Haenszel procedure is used (Fig. 2d,f). The only exception is when the data are simply combined in the case of a biased casecontrol sampling design, where the power decreases when absolute LD decreases but appears to recover when the signed r2 decreases toward 1 (Fig. 2e). The latter increase in power was primarily driven by differences in allele frequencies between the two populations and does not reflect the genuine association between the marker and the disease status. While we have chosen to simulate a multiplicative model with an allelic relative risk of 1.5 at a baseline penetrance of 0.2, these values and the choice of the disease model do not influence the trend of the changes in power (data not shown). The chosen sample sizes for in our simulations with matched cases-controls, case-controls with biased sampling and family trios yield statistical power of 99%, 99%, and 76%, respectively, when the data at the causal variant is analyzed together using a Mantel-Haenszel procedure.

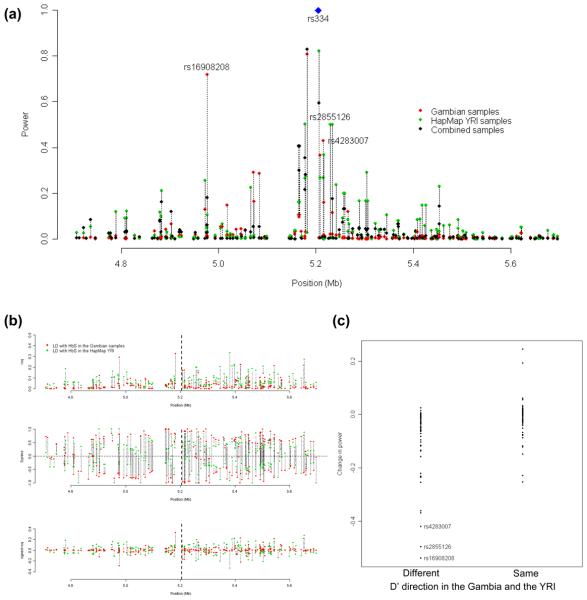
For the simulation experiment at the HBB region using haplotypic data from Gambian and HapMap YRI samples to simulate family trios, complete power was obtained at the HbS locus (rs334), which in the simulations was designated as the causal variant. Due to the different LD patterns between the Gambian and the YRI samples in this region, the power to detect an indirect association was markedly different between the different samples. In particular, an SNP (rs16908208) located 220 kb upstream of the functional variant yielded 73% power in the Gambian samples but had negligible power in the YRI samples, while a SNP located within 1 kb downstream from rs334 yielded the highest power for the YRI samples but had almost no power in the Gambian samples (Fig. 3a). Differences in LD across the HBB region appeared to explain the observed power disparities as different SNPs are in high LD with rs334 in the two populations (Fig. 3b). Overall, SNPs that are in higher LD with rs334 within each population yielded higher power.

Figure 3.

Description of power and the extent of LD in the HBB region in a simulation study using haplotypic data from the Gambia, the HapMap YRI, and the combination of both. (a) Statistical power to detect an association in the region that is driven by the HbS locus (blue diamond) which has been designated in the simulations as the functional polymorphism (represented in the plot with a power of 1). Points in red represent the power to detect an effect with 1000 Gambian parents-affected offspring trios at loci found on the Affymetrix 500K genotyping platform; points in green represent the power at the same loci for 1000 YRI parents-affected offspring trios; points in black represent the power at the same loci for the combined 2000 trios from the Gambia and the Yoruba. Dotted lines join the three points for each SNP. (b) Plot of LD between SNPs in the HBB region with the HbS locus, with points in black and red describing the LD in the Gambia and Yoruba respectively. The top plot shows the r²; the plot in the middle shows the D′; the plot at the bottom shows the r² with the sign from the corresponding D′. The dashed line near the center of each plot represents the position of the HbS locus. Dotted lines join the two points for each SNP. (c) Differences in power for SNPs with LD in the same or in different D′ direction. The vertical axis measures the change in power of the combined 2000 samples when compared to the maximum power obtained from the individual experiments in either the Gambian or the HapMap YRI samples. The rsIDs of three SNPs with the greatest decrease in power upon combining the samples are identified, and are also correspondingly identified in (a).

When the trio data from both the populations are aggregated, we observed that the power provided by the combined samples did not necessarily increase despite having twice the number of trios compared with the marginal analyses (Fig. 3a). Comparing the difference between the power of the combined analyses and the maximum power obtained at each SNP in either the Gambian or the YRI samples, we observed that combining trios from the two different populations can result in a dramatic decrease in power of up to 60% (Fig. 3a,c). Large decreases in power tend to occur in SNPs with opposing LD to the causal variant in the two populations while SNPs with increased power in the combined analysis are found to be in LD with the causal variant in the same direction (third panel in Fig. 3b, and Fig. 3c).

DISCUSSION

Population structure can manifest itself as variations in patterns of LD between populations. We have shown that population differences in LD between a neighboring marker and a functional polymorphism can affect the power for identifying the association when data from these populations are analyzed jointly. Differences in LD between populations, particularly in the presence of opposing LD, can also lead to elevated rates of false associations in the absence of a functional variant for casecontrol designs with biased sampling across populations, although the cause of this is through the well-known mechanism of allele frequency differences. We have also shown that the use of nuclear family trios in association studies can be affected by population structure, and combining trios from different populations can lower the power of the experiment despite the larger sample size. Scanning across the genome at SNPs in non-overlapping windows within two pairs of populations from the HapMap and The Gambia, we have shown that opposing LD with substantial difference in the strength of LD across populations occurs in between 0.8% and 5% of the windows considered and is more often in populations that are more diverse (e.g. CEU versus CHB1JPT, FST57% [Hanchard et al., 2007]) than populations which are considerably more homogeneous (e.g. between samples from two different west African countries, FST51.1%).

Our findings are of importance to large-scale genetic association studies, since these studies typically rely on indirect associations to detect genomic regions which contain the functional polymorphisms. Conventional power calculations [Marchini et al., 2004; Pe'er et al., 2006b; Nannya et al., 2007; Klein, 2007] typically assume homogenous populations which may result in overlyoptimistic calculations as the power may be diluted by population differences. We have shown that in the presence of population structure as defined as LD differences, combining data across populations can reduce power even when meta-analytic procedures (e.g. Mantel-Haenszel) are used. This is problematic in the presence of undetected opposing LD, since the use of meta-analytic approaches to combine data sets from multiple genomewide scans is increasingly common in the discovery phase for prioritizing trait-associated regions for replication studies. Understanding the implications of opposing LD is also relevant when discussing the efficiency of fine mapping versus directed replication in genome-wide association studies [Clarke et al., 2007]. Variations in LD between the population in the initial genome-wide study and the population surveyed in subsequent replication studies may potentially yield conflicting signals when different alleles at the typed markers are correlated with the disease predisposing allele. Fine mapping may yield better results in the presence of significant LD differences, since this at worst allows for the identification of different haplotypic backgrounds across the different populations and at best simplifies the task of identifying the functional variant directly.

The Gambian and HapMap YRI data used in our investigations came from two countries in West Africa. The genetic diversity between these two countries is considerably lower (FST51.1%) when compared against the genetic diversity that exists between the HapMap CEU and YRI populations (FST515.5%) (in review) and is similar to that between the Chinese and Japanese (FST51.3%) [Marchini et al., 2004]. We have chosen the HBB region in our simulation as we know a priori that the HbS allele sits on different haplotypes in the Yoruban region of Nigeria and in The Gambia [Hanchard et al., 2007], and different SNPs have been found to be in strong LD with rs334 in Nigeria and The Gambia. A study on the genetic etiology of malaria in The Gambia found that imputation strategies using the HapMap YRI as a reference panel did not work well across this region (in review).

The complexity of LD across different populations suggests a need for local haplotype maps for imputation strategies to yield maximum benefit in genetic association studies, especially for studies conducted across genetically diverse populations like those found in Africa [International HapMap Consortium, 2005]. This highlights the importance of the next phase of the International HapMap Project, which has been extended to seven additional populations, including two from Kenya in East Africa. Understanding the extent of LD variation across different populations will be crucial in genetic studies of complex diseases and drug responses. Statistical approaches for handling population structure typically focus on minimizing the occurrences of false associations in a genetic study. These approaches either correct for the extent of inflation of the association test statistic at each SNP (e.g. genomic control) [Devlin and Roeder, 1999] or test for association within genetically homogenous clades (e.g. STRAT) [Price et al., 2006]. While these approaches are expected to prevent population structure from introducing false associations in the absence of true functional polymorphisms in the region, they are unlikely to be able to correct for LD differences which lower power, especially in the presence of opposing LD where the direction of the effects across the three genotypes are in fact opposite.

Large-scale genetic association studies that assay hundreds of thousands of SNPs are expected to find a number of the positive associations obtained to be due to chance alone with no biological significance. A common strategy is to replicate the findings across other populations which may be genetically diverse from the original population. Failure to replicate may not necessarily indicate a chance and unsubstantiated finding, but could be caused by differences in LD with the causal variant between the different populations. Statistical procedures to combine data across studies may not be entirely satisfactory in the presence of opposing LD. Family-based designs are not entirely immune to the confounding effects of population structure, and combining trio data across genetically diverse populations may lower the power to detect a true association.