Detection of cancer-specific markers amid massive mass spectral data

Abstract

We propose a comprehensive pattern recognition procedure that will achieve best discrimination between two or more sets of subjects with data in the same coordinate system. Applying the procedure to MS data of proteomic analysis of serum from ovarian cancer patients and serum from cancer-free individuals in the Food and Drug Administration/National Cancer Institute Clinical Proteomics Database, we have achieved perfect discrimination (100% sensitivity, 100% specificity) of patients with ovarian cancer, including early-stage disease, from normal controls for two independent sets of data. Our procedure identifies the best subset of proteomic biomarkers for optimal discrimination between the groups and appears to have higher discriminatory power than other methods reported to date. For large-scale screening for diseases of relatively low prevalence such as ovarian cancer, almost perfect specificity and sensitivity of the detection system is critical to avoid unmanageably high numbers of false-positive cases.

Each year in the United States an estimated 25,000 women are diagnosed with ovarian cancer, and ≈14,500 women die from the disease (1). Ovarian cancer is insidious, producing few symptoms until it has spread regionally beyond complete surgical removal, accounting for an overall cure rate of only 35%. When ovarian cancer is diagnosed at an early stage, however, the cure rate is 90% or better with surgery alone (2–6). An effective screening program for early-stage ovarian cancer has been elusive because of the relatively low disease prevalence and the lack of a highly specific screening test (7, 8).

Petricoin et al. (9, 10) recently reported that mass spectra of serum of ovarian cancer patients when interrogated by a proprietary bioinformatics tool can be shown to contain patterns of molecules diagnostic of even early-stage disease. That group and others have applied this approach to the detection of proteomic profiles in serum that distinguish not only ovarian cancer but also prostate (11) and breast cancer (12) patients from those without cancer. The availability of a relatively inexpensive, accurate blood test for the early diagnosis of most, if not all, cancers has generated great excitement among scientists and the public.

The key to development of such assays is the ability to detect a few marker molecules, assumed to be proteins, that are differentially expressed in the sera of cancer patients. However, the variety and amounts of molecules circulating in the blood at any given moment may differ substantially from one individual to another. The challenge in proteomic diagnosis is to find a method for detecting unique markers amid thousands of elements in the complex milieu of serum or other body fluid.

Most serum protein mass spectrum data have been generated by using the Ciphergen Biosystems (Fremont, CA) ProteinChip array surface-enhanced laser desorption ionization–time-of-flight (SELDI-TOF) MS system (13–16). The underlying principle in SELDI is surface-enhanced affinity capture through the use of specific probe surfaces. Once captured on the SELDI protein chip array, proteins are detected by TOF MS.

The great advantage of MS over other technologies for global detection and monitoring of subtle changes in cell function is the ability to measure rapidly and inexpensively thousands of elements in a few microliters of serum or plasma. Disease processes that result from altered genes, such as cancer, produce altered protein products that circulate in the blood as polypeptides of varying size. Although mass spectrometric patterns of complex fluids such as serum defy visual analysis, computational approaches can distinguish subtle differences in patterns from affected individuals compared with unaffected individuals.

Several statistical analytical tools have been developed to analyze mass spectra. Two routines have been used predominantly to analyze serum proteomic data: proteome quest (Correlogic Systems, Bethesda) and propeak (3Z Informatics, Mount Pleasant, SC). The proteome quest system selects protein biomarkers via a genetic algorithm (17) using a random window approach. The classification is then done by using a self-organizing map (18, 19). The propeak system implements the unified maximum separability analysis procedure that is essentially a variation of the traditional canonical discriminant analysis (12).

We have developed a statistical algorithmic routine that sifts through the entire spectra and selects, using the random field theory, all biomarkers that are significantly different between affected and unaffected subjects in expression levels. The best discriminating pattern is then chosen among all significant biomarkers by using the best-subset discriminant analysis method. Analysis of two independent sets of serum proteomic data from ovarian cancer patients and individuals believed to be free of ovarian cancer, available online (http://clinicalproteomics.steem.com) from the National Institutes of Health and Food and Drug Administration Clinical Proteomics Program Databank, suggests that our statistical routine is highly useful for detection of cancer-specific markers amid massive mass spectral data.

Materials and Methods

Statistical Algorithm. Our statistical algorithmic routine is a combination of the following sequential steps.

Data Preprocessing. This includes standardization for relative spectrum and smoothing via Gaussian filters, performed on each individual spectrum.

Sampling. For discriminant purposes, a training data set is randomly selected from each group (e.g., diseased and control subjects); the remaining data constitute the testing set.

Statgram. Subsequently a pointwise two-sample t/z test between the groups in the training data set is performed. The 2D map of the test statistic values along the spectrum is denoted as the statgram.

Threshold Determination. The random field theory is used to determine the critical region (threshold) of the statgram at each desired experimentwise significance level.

Variance Stability. (Optional) Variance stability is checked on request to select stable markers.

Biomarker Selection. The subset of k biomarkers (k can be any positive integer) from the remaining marker list from threshold determination (or variance stability, if requested) that could best discriminate between the groups in the training set is selected via the best k-subset discriminant method. In practice, the smallest k achieving the best possible classification performance is selected.

Validation. The l-nearest neighbor classification method is used to classify the testing data set. Sensitivity and specificity of the classification are obtained.

Resampling. All steps, except data preprocessing, are iterated. Consistency is checked, and distributions (of specificity, sensitivity, etc.) are obtained.

Mass Spectra of Sera. We analyzed raw mass spectra data provided online at the National Institutes of Health and Food and Drug Administration Clinical Proteomics Program Databank web site (http://clinicalproteomics.steem.com/download-ovar.php) (Ovarian Data Set 4-3-02 and Ovarian Data Set 8-7-02). Data Set 4-3-02 consisted of spectra from 100 patients with ovarian cancer and 116 individuals without cancer, and Data Set 8–7-02, an entirely independent data set, consisted of 162 spectra from ovarian cancer patients and 91 individuals without cancer. The spectra we analyzed were obtained by using a cation exchange protein chip, WCX2, and a Protein Biosystem 2 surface-enhanced laser desorption ionization–time-of-flight mass spectrometer (Ciphergen Biosystems). The samples in the earlier data set were prepared by hand, and the samples in the second set were prepared with a robotic instrument.

We first applied our algorithm to the analysis of the spectra from the 100 ovarian cancer patients and 116 noncancer individuals in Data Set 4-3-02. The serum mass spectrum for each subject consisted of 15,154 mass-to-charge ratios (m/z values) of varying intensities. The average intensity of each m/z value of the spectra from the 116 unaffected women and 100 women with ovarian cancer is shown in Fig. 1. Apparent differences in the intensity of certain biomarkers between the two groups can be appreciated by inspection alone. However, one must ascertain that the differences are statistically significant (systematic and persistent in the population) and not due to random factors such as outliers or other sampling fluctuations.

Fig. 1.

Average serum mass spectra of 116 unaffected women (a) and 100 women with ovarian cancer (b). Certain regions of the spectra (c–h) are enlarged to show apparent differences in expression intensities between unaffected individuals (solid line) and ovarian cancer patients (broken line).

Data Preprocessing: Spectrum Standardization and Smoothing. The relative intensity for each mass spectrum was obtained by dividing the intensity at each m/z value by the average intensity of the entire spectrum. Such standardization ensures comparability across different spectra. Each relative spectrum was then smoothed by a Gaussian kernel with a full width at half maximum (FWHM) of 11 m/z measurement values. The “kernel” for smoothing defines the shape of the function that is used to take the average of the neighboring points. A Gaussian kernel is a kernel with the shape of a Gaussian (normal distribution) probability density curve. In the standard statistical way, we have defined the width of the Gaussian shape in terms of the standard deviation σ. However, when the Gaussian shape is used for smoothing, the convention is to describe its width with another related measure, the FWHM, where 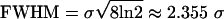(Fig. 2a).

Fig. 2.

(a) Illustration of the Gaussian kernel. The smoothed intensity of the biomarker with m/z value μ is calculated as the weighted average, proportional to the Gaussian density, of the intensities of its neighboring biomarkers. (b) Relationship between the range of the 11 adjacent points within the Gaussian smoothing kernel (y axis) and the median of the range (x axis) when FWHM = 11. (c) Relationship between the ratio of the range over its median (y axis) and the median of the range (x axis) for FWHM = 11.

Smoothing was done to (i) denoise and thus enhance the signal-to-noise ratio and (ii) enable a multiple-test correction via the random field theory in a later step. Determination of the FWHM value depends on the accuracy of the MS and the multiple-test correction considerations. A small kernel would better preserve the original spectra. However, the smoothing kernel should be at least as large as the mass accuracy of the Ciphergen system, which is 0.1% (9, 10). Thus, a particle with a detected mass value of x (m/z) could have the same true mass as particles in its neighborhood within a range of 0.2% x (i.e., x ± 0.1% x).

We found that the smallest FWHM that will achieve a mass accuracy of at least 0.1% for the entire spectrum is FWHM = 11. The relationship between the range of the 11 adjacent points within the Gaussian smoothing kernel (y axis) and the median of the range (x axis) when FWHM = 11 is shown in Fig. 2b. For FWHM = 11, the ratio of the range over its median (y axis) is >0.2% for most of the spectrum and approaches 0.2% only toward the highest m/z values of the spectrum (Fig. 2c). Therefore, we have chosen to use FWHM = 11.

Sampling. After standardization and smoothing, the entire study with 216 subjects was divided into the training set and the testing set. The training set consisted of a random sample of 50 women with ovarian cancer and a random sample of 50 unaffected women. The remaining 50 women with cancer and the 66 unaffected women made up the testing set.

Statgram. An independent samples t/z test was performed at each m/z value to compare the intensities between the two training samples (cancerous and unaffected). The null hypothesis was that the intensities are equal between the groups at each location, and the alternative hypothesis is that they differ. The test was performed at each m/z value, and the test statistic value , where ȳ₁(x), ȳ₂(x), 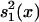, and 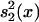are the means and standard deviations of the training samples, was plotted against the m/z value to generate the statgram (Fig. 3). Because both samples are large (n₁ = n₂ =50), the test statistic t(x) followed approximately the standard normal distribution under the null hypothesis.

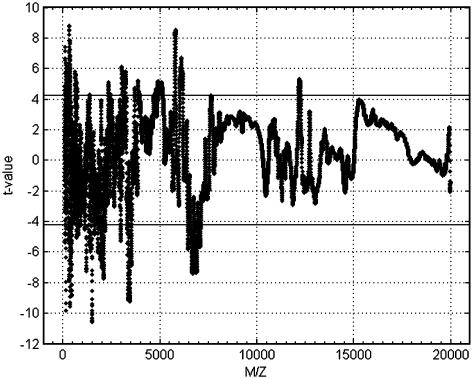
Fig. 3.

Statgram test statistic values and the critical value thresholds at ±4.22 by the random field theory to ensure an experimentwise error rate of 0.05 (two-sided).

At each m/z location, the larger the test statistic in absolute value, the stronger the evidence supporting the alternative hypothesis that the average intensities are different between the two groups. When only one test is performed, one would reject the null hypothesis at the significance level of 0.05 (two-sided) if |t(x)| exceeds the critical value of 1.96. That means we are 95% sure that the difference is real (true for the populations) and not caused by the variability in random sampling.

Threshold Determination/Multiple-Test Correction. Because a total of 15,154 tests were performed to cover the entire m/z range, the confidence level would be much lower than 95% for the entire set of tests if each test were conducted at the significance level of 0.05. That is, one must perform a multiple-test correction to determine a suitable significance level for each test such that we are at least 95% sure that all of the significant differences identified are real. Many traditional methods, for example, the Tukey method or the Bonferroni method, are available for multiple-test correction, but they tend to be more conservative. For example, with the Bonferroni method, to ensure an experimentwise error rate of 0.05 (two-sided), each test must be performed at the significance level of 0.025/15,154 = 1.649729e-006 (one-sided). The corresponding critical value for a normal test is 4.65. That is, one would reject the null hypothesis of equal intensity at the given m/z value if |t(x)| > 4.65. We used a less conservative correction method based on the random field theory (20). The prerequisite for this method is that each spectrum is a 1D Gaussian field that is achieved by presmoothing with a Gaussian kernel.

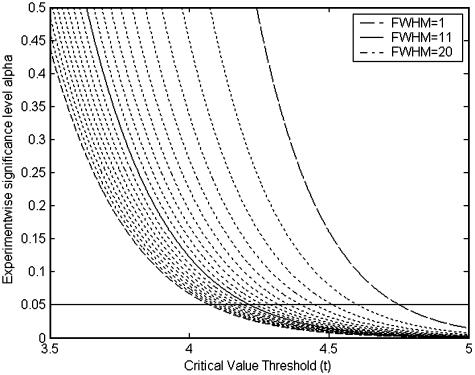
The Gaussian kernel is uniquely determined by its FWHM. The relationship between the experimentwise error rate α and the critical value t is given by

where K is the total number of tests. In this analysis, where K = 15,154, there is little variation in the critical value when the FWHM varies between 10 and 20 points (Fig. 4).

Fig. 4.

Relationship between FWHM, experimentwise error rate, and critical value. FWHM ranges from 20 to 1 from left to right.

For a Gaussian kernel with FWHM = 11 and an experimentwise error rate of α = 0.05 (two-sided), the critical value is 4.22 by the random field theory, less conservative than the Bonferroni threshold of 4.65. Thus, by applying the random field theory, the effective number of tests is reduced from 15,154 to ≈1,025 (the equivalent of a Bonferroni correction). In essence, the reduction is achieved by eliminating redundant tests for m/z values within the same smoothing kernel.

Thresholding at the critical value of 4.22, 563 tests remain significant. The corresponding 563 protein biomarkers were considered significantly different between the two populations (women with ovarian cancer and unaffected women) and were adopted as candidates for the discriminant analysis. These biomarkers are not only critical in deriving the diagnostic/discriminant rule but also invaluable for further biological studies to ascertain and understand their roles in ovarian cancer development and progress, and to develop and evaluate therapeutic drugs and other treatments.

Biomarker Selection/Discriminant Analysis. The subset of k biomarkers from the 563 candidates that best discriminate between the two training samples were selected for any user-defined positive integer k. The procedure starts from k = 1 where k increases by 1 after each iteration until the discriminating performance reaches plateau. In this case, when k = 18, best separation was achieved between the two groups (100% sensitivity and 100% specificity by cross-validation) by using the l-nearest-neighbor classifier with l = 5.

The distance metric for the nearest neighbor classifier is the Mahalanobis distance based on the pooled variance–covariance matrix V. The squared distance between two observation vectors x and y is given by d²(x, y) = (x – y)′V^–1(x – y). Here each vector corresponds to a subject. Its elements are the expression levels (intensities) of the k discriminating markers for the given subject. The nearest-neighbor classifier and the kernel method are two major nonparametric classification methods. The nearest-neighbor classifier is equivalent to the uniform-kernel method with a location-dependent radius.

We chose the nearest-neighbor classifier because of its robustness, flexibility, and intuitive explanations. However, the nearest-neighbor classifier and the kernel methods (normal kernel or uniform kernel) tend to produce similar results. For a nearest-neighbor classifier, the choice of l is usually relatively uncritical (21). A practical approach is to try several different values of l and choose the one that gives the best cross-validated estimate of the classification rate. In our case, we chose l ≥ 5. The smallest l value that achieved perfect discrimination (in this case, it was l = 5) was used for the discriminant analysis of the remaining 116 spectra in the testing data set.

Cross-validation (22) treats n – 1 of n observations as a training set. In our case n = 100. It determines the discrimination functions based on these n – 1 observations and then applies them to classify the one observation left out. This is done for each of the n training observations. The classification rate for each group, that is, sensitivity for the cancer group and specificity for the control group, is the proportion of sample observations in that group that are classified correctly. The selected biomarkers (k = 18) are given in Table 1. The next step was to determine whether the selected 18 biomarkers distinguish the cancer patients from noncancer patients in the testing set of 50 cancer patients and 66 noncancer individuals.

Table 1. Biomarkers selected to the discriminant model.

Marker, m/z (x)	Test statistic value,|t (x)|	Cancerous		Normal
		CV	Percentile	CV	Percentile
167.8031	4.2524	0.50	20.35	0.39	6.44
321.4157	7.1132	0.50	20.41	0.42	8.07
322.4204	5.9783	0.44	11.85	0.38	5.47
359.6322	7.5167	0.22	1.80	0.43	8.49
385.5688	6.0664	0.17	0.71	0.25	1.31
413.1668	5.3706	0.54	27.44	0.38	5.43
433.9079	6.5525	0.67	46.43	0.62	30.76
434.6859	5.8706	0.76	54.88	0.66	34.26
444.4690	7.7466	0.34	5.26	0.42	8.14
445.2563	7.5905	0.30	3.97	0.39	6.06
1222.1849	6.3953	0.63	40.74	0.56	23.04
1528.3431	5.6625	0.77	55.38	0.56	22.91
3345.7995	5.0142	0.89	67.91	0.88	59.65
3449.1503	9.1736	1.00	80.19	0.71	39.20
3473.3084	6.6033	0.84	62.39	0.61	29.68
3528.5266	4.6092	0.74	52.89	0.56	23.68
6101.6299	6.0053	0.60	37.16	0.65	33.69
6123.5190	6.2619	0.52	24.34	0.61	29.55

The coefficient of variation (CV) is the ratio of the sample standard deviation and the sample mean. For each marker, the percentile of its CV across the entire protein spectrum within each group is given.

Validation. Using the l-nearest-neighbor classifier with l = 5 for discrimination and classification, we correctly identified all 50 women with ovarian cancer as positive and all 66 unaffected women as negative. That is, the sensitivity and specificity of the test are both 100%. The 95% confidence intervals for sensitivity and specificity are (93%, 100%) and (95%, 100%), respectively.

Variance Stability Check. This is an optional step that may precede or follow the best discriminating subset selection procedure. The rationale for this step is that the expression level of certain biomarkers may be correlated with disease stages or other individual traits and therefore may have large variability across all subjects in a training set (diseased or unaffected). By examining the coefficient of variation, a standardized measure of variability that is unaffected by the magnitude of the mean (23), one could establish a statistical threshold via the resampling methods (24) to divide the significant markers into two subsets: those with less and those with more variability. To derive a discriminant rule that is more robust to the disease stages and individual traits, one could select only the more stable markers to derive the best k subset of biomarkers. On the other hand, one could correlate more variable markers in the training set of “disease subjects” with disease stages/severity to derive a more stage-sensitive discriminant rule. On the whole, the 18 markers selected are relatively stable. The significance of the coefficient of variation for marker selection and data interpretation should be analyzed further when more subject-specific information is available.

Validation with an Independent Data Set. To test the robustness of our algorithm, we applied the above algorithm to classify subjects from an independent data set of 162 ovarian cancer patients and 91 unaffected individuals (Ovarian Data Set 8-7-02 at http://clinicalproteomics.steem.com/download-ovar.php). The 18 markers identified (Table 1) and the same training set of 50 cancer patients and 50 controls from study 1 (Data Set 4-3-02) also correctly classified, with 100% sensitivity and 100% specificity, all subjects in this second study. If we treat the entire study 2 (162 cancerous and 91 unaffected) plus the testing set from study 1 (50 cancerous and 66 unaffected) as a combined testing set of 212 ovarian cancer patients and 157 unaffected subjects, the 95% confidence intervals for sensitivity and specificity would be (98%, 100%) and (98%, 100%), respectively.

Resampling. To explore whether the perfect specificity and sensitivity may have been caused by a fortuitous choice of the test and training sets, we repeated the entire process by randomly choosing another training set. Fifty iterations later, we obtained 50 perfect classifications. The best subset of biomarkers varied from iteration to iteration. Rounding to the nearest integers, we found 176 distinct markers consistently identified from these 50 resampling iterations. Further studies are necessary to ascertain the roles of these markers and to validate the reliability and accuracy of the serum MS technology.

Conclusions

There are several statistical analytical tools that were developed to analyze mass spectra. The genetic algorithm was first described by John Holland in the mid-1970s (17). It manipulates the complex data sets as the individual elements through a computer-driven analog of natural selection process. Kohonen (18, 19) proposed a cluster analysis method by using a self-organizing map.

The ideas of the genetic algorithm and the self-organizing map were integrated into a software program, proteome quest, Beta version 1.0 and implemented as a pattern discovery algorithm. proteome quest has been used by the National Cancer Institute/Food and Drug Administration proteomics group to analyze the same public ovarian cancer data sets as analyzed in this work (Ovarian Data Set 4-3-02 and Ovarian Data Set 8-7-02). proteome quest yielded 100% sensitivity and 97% specificity for Data Set 4-3-02 and 100% sensitivity and 100% specificity for Data Set 8-7-02. Results are provided online at http://clinicalproteomics.steem.com/download-ovar.php.

proteome quest uses a random window approach to sequentially select the biomarkers and examine their contribution toward the classification of mass spectra as being from one class of individuals (disease-affected) compared with a different class of individuals (disease-unaffected). A limitation of this approach is that only a portion of the spectrum is used for the analysis. The contribution of each biomarker may vary with the window size, and therefore significant protein biomarkers may be excluded from the analysis. Furthermore, the expression intensities of selected biomarkers are not guaranteed to be significantly different between the diseased and the control groups. This would severely reduce the reliability of the resulting discriminating pattern.

In our statistical routine, we examine and quantify the role of each biomarker along the mass spectrum. All biomarkers with significantly different intensities of expression at the given experimentwise error rate between the cancer and noncancer subjects are selected for determination of the optimal set of biomarkers. Application of our method to two independent data sets of mass spectra generated by scientists at the Food and Drug Administration and the National Cancer Institute show that our statistical approach is highly effective in discriminating between diseased and normal subjects. In conclusion, we believe that all biomarkers significantly different between the groups should be examined for their roles in disease etiology. Our method is not only a tool for medical diagnostics but also an instrument for biological discovery.