Abstract
Phylogenetic trees of individual genes of prokaryotes (archaea and bacteria) generally have different topologies, largely owing to extensive horizontal gene transfer (HGT), suggesting that the Tree of Life (TOL) should be replaced by a “net of life” as the paradigm of prokaryote evolution. However, trees remain the natural representation of the histories of individual genes given the fundamentally bifurcating process of gene replication. Therefore, although no single tree can fully represent the evolution of prokaryote genomes, the complete picture of evolution will necessarily combine trees and nets. A quantitative measure of the signals of tree and net evolution is derived from an analysis of all quartets of species in all trees of the “Forest of Life” (FOL), which consists of approximately 7,000 phylogenetic trees for prokaryote genes including approximately 100 nearly universal trees (NUTs). Although diverse routes of net-like evolution collectively dominate the FOL, the pattern of tree-like evolution that reflects the consistent topologies of the NUTs is the most prominent coherent trend. We show that the contributions of tree-like and net-like evolutionary processes substantially differ across bacterial and archaeal lineages and between functional classes of genes. Evolutionary simulations indicate that the central tree-like signal cannot be realistically explained by a self-reinforcing pattern of biased HGT.
Keywords: phylogenetic tree, horizontal gene transfer, species quartets, computer simulation
Introduction
The Tree of Life (TOL) metaphor has dominated evolutionary biology ever since Darwin introduced it in the Origin of species as an adequate depiction of the entire history of life forms on earth (Darwin 1859). The three-domain tree of ribosomal RNA (rRNA) that was subsequently buttressed by trees of other universal genes, such as ribosomal proteins and core RNA polymerase subunits, is perceived as a veritable triumph of tree thinking in biology (Woese 1987; Woese et al. 1990; Pace 1997; Ciccarelli et al. 2006; Pace 2006). However, phylogenomics, that is, genome-wide analysis of gene phylogenies (Delsuc et al. 2005), reveals a more complex picture of evolution. Indeed, at least among prokaryotes (archaea and bacteria), phylogenetic trees of individual genes generally possess different topologies; this diversity of tree topologies cannot be explained away by artifacts of phylogenetic reconstruction and is largely attributed to extensive horizontal gene transfer (HGT) in the prokaryotic world (Doolittle 1999b; Koonin et al. 2001; Koonin and Wolf 2008). These developments suggest that the TOL might need to be replaced by a “net of life” as the paradigm of evolution, at least, for prokaryotes (Hilario and Gogarten 1993; Gogarten et al. 2002; Boucher et al. 2003; Bapteste et al. 2005, 2009; Gogarten and Townsend 2005; Doolittle and Bapteste 2007; Bapteste and Boucher 2008; Dagan et al. 2008; Koonin and Wolf 2008; Doolittle 2009).
Although there is no doubt that HGT often occurs among prokaryotes, the conundrum between the TOL and the net of life is far from being resolved (O'Malley and Boucher 2005; Bapteste et al. 2009). The views of evolutionary biologists differ from the defense of the traditional TOL, when HGT is dismissed as a relatively minor nuisance (Kurland et al. 2003; Ge et al. 2005; Kunin et al. 2005); to proposals that preferential HGT between organisms that are traditionally viewed as related and placed in the same taxon could substantially contribute to the observed topologies of phylogenetic trees in prokaryotes, perhaps, to a greater extent than the tree-like inheritance, and furthermore, the contributions of the two types of evolutionary processes can extremely difficult to disentangle (Gogarten et al. 2002; Andam et al. 2010); and all the way to the iconoclastic idea that any consistent tree-like signal in the evolution of prokaryotes could be an illusion caused by nonrandom patterns of HGT (Olendzenski et al. 2002). The intermediate view, that despite the major role of HGT in the evolution of prokaryotes, TOL might be salvageable as a statistical “central trend,” has been proposed as well (Wolf et al. 2002).
Recently, we reported a comparative analysis of approximately 7,000 phylogenetic trees for prokaryote genes that jointly constitute the “Forest of Life” (FOL) and showed that the FOL does gravitate to a single-tree topology. This statistically significant trend was particularly prominent among nearly universal trees (NUTs), that is, trees for highly conserved genes that are represented in all or almost all prokaryote genomes (Puigbo et al. 2009). Here, we describe a quantitative measure of the tree and net signals in evolution that is derived from an analysis of all quartets of species in all trees of the FOL. We find that, although diverse routes of net-like evolution jointly dominate the FOL, the pattern of tree-like evolution that recapitulates the consensus topology of the NUTs is the single most prominent coherent trend. Evolutionary simulations suggest that the central tree-like signal cannot be realistically explained by a self-reinforcing pattern of biased HGT.
Methods
Phylogenetic Trees
We analyzed the set of 6,901 phylogenetic trees from (Puigbo et al. 2009) that were obtained using the following methodology (supplementary fig. S1, Supplementary Material online). Clusters of orthologous genes were obtained from the COG (Tatusov et al. 1997; Tatusov et al. 2003) and eggNOG (Jensen et al. 2008) databases from 100 prokaryotic species (59 bacteria and 41 archaea). The species were manually selected to represent the diversity of the taxonomy in prokaryotes (the complete list of species is given in supplementary table S1, Supplementary Material online). The BeTs algorithm (Tatusov et al. 2003) was used to identify those orthologs with the highest sequence conservation, so the final clusters have a maximum of 100 species, with no more than one representative of each species. All clusters were aligned using the program Muscle (Edgar 2004) with default parameters. Alignments were refined with the Gblocks program (Talavera and Castresana 2007) with the minimal length of a block set at six amino acid positions, and the maximum number of allowed contiguous nonconserved amino acid positions set at 20. The program Multiphyl (Keane et al. 2007), which selects the best of 88 amino acid substitution models, was used to reconstruct the maximum likelihood (ML) tree of each cluster. The NUTs are defined as trees from COGs that are represented in more than 90% of the species included in the study (supplementary table S2, Supplementary Material online).
Analysis of Quartets of Species
The minimum evolutionary unit in unrooted phylogenetic trees is a group of four species (quartet); each quartet can assume three unrooted tree topologies (Estabrook et al. 1985).
Quartet analysis has been previously used in a different context to detect potential cases of HGT (Zhaxybayeva and Gogarten 2003; Zhaxybayeva et al. 2006). In this work, we analyzed a set of 100 species. Thus, based on combinations of four species from a set of 100 species, the total number of possible quartets is 3,921,225, and the total number of possible topologies is 11,763,675 (supplementary fig. S2a, Supplementary Material online). All possible quartets were constructed using a simple Perl script that also generates the three possible topologies of each cluster.
Mapping Quartets onto Trees
To determine which one of the three possible topologies best represents a quartet, each quartet topology was compared with the whole phylogenetic forest (6,901 trees), resulting in a total number of 8.12 × 1010 tree comparisons (supplementary fig. S2a, Supplementary Material online). A binary version of the split distance (SD) method (Puigbo et al. 2007) was used to compare quartets and trees; when a quartet is represented in the tree, SD = 0, otherwise SD = 1. Using this methodology, the number of trees that support each quartet topology was counted (supplementary fig. S2b, Supplementary Material online): a quartet is supported only by those trees with which it has SD = 0.
Dependence of the Bootstrap Support on the Number of Species in a Tree
The mean bootstrap of each tree was calculated, and the results were plotted against the tree size (supplementary fig. S3, Supplementary Material online). The results show that there are no significant differences in the bootstrap support between trees of different sizes.
The Ultrametric Supertree
The previously published ultrametric version of the supertree of the 102 NUTs (Puigbo, Wolf, and Koonin 2009) was used to perform a series of HGT simulations. The branch lengths in the supertree were obtained from each of the 6,901 trees and rescaled from 0 to 1 (supplementary fig. S4, Supplementary Material online).
Distance Matrices, Heatmaps, and the TNT Score
Using the quartet support values for each quartet, a 100 × 100 between-species distance matrix was calculated as dij = 1 - Sij/Qij, where dij is the distance between two species, Sij is the number of trees containing quartets in which the two species are neighbors, and Qij is the total number of quartets containing the given two species (supplementary fig. S2c, Supplementary Material online). The distance matrices were converted into heatmaps using the matrix2png web-server (Pavlidis et al. 2003). The quartet-based between-species distances were used to calculate the Tree-Net Trend (TNT) score. The TNT score is calculated by rescaling each matrix of quartet distances on a 0–1 scale between the supertree-derived matrix (which is taken to represent solely the tree-like evolution signal, hence the distance of 0) and the matrix obtained from permuted trees, with distance values around the random expectation of 0.67 (supplementary fig. S5, Supplementary Material online). Two situations may occur in the calculation of the TNT score depending on the relationship between the distance in the supertree matrix (Ds) and the distance in the random matrix (Dr = 0.67). When Ds > Dr (e.g., in comparisons of archaea vs. bacteria), STNT = (d − Dr)/(Ds − Dr), where STNT is the TNT score and d is the distance between the two compared species in the matrix. When Ds < Dr (in comparisons between closely related species), STNT = 1 – ((d − Ds)/(Dr − Ds)).
Simulation of Prokaryote Evolution with a Nonuniform HGT Distribution
The first series of simulations used a prototype ultrametric rooted tree of depth 1 with the topology of the supertree of the NUTs (Puigbo et al. 2009) (supplementary fig. S4, Supplementary Material online) to represent the common tree-like component of evolution of prokaryotes. This tree defines a matrix of distances between species and clades (the depth of the last common node); the distance matrix remains fixed during the simulations. To simulate N HGT events, N uniformly distributed random numbers were chosen from the interval [0,1]. These numbers represented the depth levels at which each of the simulated transfer occurred. Proceeding from the deepest (the most ancient) to the most shallow (the most recent) level, all possible pairs of clades represented at the given level were examined as the potential participants in the HGT event. The probability of an exchange for the given pair of clades at the current depth level R was computed using the formula pi = di-α/C with the preset value of α, di = Di − R, where Di is the distance between the compared clades in the fixed distance matrix (supplementary fig. S6, Supplementary Material online) and C = ∑di-α. Then, a specific pair of clades was chosen randomly with these probabilities, and the tree branches were swapped. Starting with the HGTs involving the deepest branches guarantees that the more shallow part of the tree remains unperturbed and thus the original supertree-derived estimates of the distances between branches can be used throughout. After N events were simulated in each of the 100 trees, the number of trees that retained the perfect separation between the bacteria and the archaea (calculated as the separation score, SSB/A) (Puigbo et al. 2009), and the mean SD (Puigbo et al. 2007) between the trees were computed.
The second series of simulations started with 100 star-like trees of 100 species with all internal branches of length zero and random topologies (in other words, although these are star trees and so can be considered to all have the same topology, they technically each have a predefined, randomly chosen topology, with all branch lengths set to zero; this procedure was employed to avoid technical difficulties associated with comparison of truly multifurcating trees). One master matrix of distances between the species and 100 matrices associated with each tree were initialized with unit values. For each preset value of N and α, N uniformly distributed random numbers were chosen from the interval [0,1] to represent the depth levels of HGT events. Proceeding from the deepest (the most ancient) to the most shallow (the most recent) level, at the current depth level R in each tree one random branch (of 100) was selected to be the donor in a HGT event. For all possible 99 HGT acceptors, the probability of the gene exchange between the chosen donor and each acceptor was computed using the same pi = di-α/C formula with the preset value of α and di = Di − R, where Di is the distance between the compared species in the master matrix; as before, C = ∑di-α. The acceptor of a HGT event was chosen randomly with these probabilities, and the acceptor branch was disconnected from its current ancestor and joined to the donor branch at the depth R. Then, the species distance matrices for each tree were updated according to the new tree topologies, and the master species distance matrix was recalculated as the mean between 100 individual species distance matrices. After all N events were simulated in each tree, the mean SD between the trees was computed and a rooted supertree of all 100 trees was calculated. This supertree was used to obtain the root bifurcation and assign “bacteria” and “archaea.” Then, the number of trees retaining the perfect separation between these clades was calculated.
Results and Discussion
Rationale and Approach: the Signals of Tree and Net Evolution in the FOL
We sought to take a quantitative measure of the signals from the tree and net modalities of evolution in the FOL and its different parts. Here, we define the tree signal as the pattern compatible with the consensus topology of the NUTs, which has been shown to represent a central tree-like evolutionary trend in the FOL that was traceable throughout the entire range of phylogenetic depths despite the substantial rate of HGT (Puigbo et al. 2009). By contrast, the net signal is the sum total of all evolutionary patterns that appear incompatible with the consensus NUTs topology, whether caused by HGT or by other processes such as parallel gene loss that are also common among prokaryotes (Koonin and Wolf 2008).
It should be noted that the topology of the supertree (supplementary fig. S4, Supplementary Material online) showed some deviations from the parts of the deep phylogeny of prokaryotes that are considered well established. In particular, the monophyly of the Deinococci (also known as the Deinococcus–Thermus group) that is supported by many phylogenetic trees and gene content analysis (Weisburg et al. 1989; Omelchenko et al. 2005; Griffiths and Gupta 2007). These peculiarities of the supertree topology are likely to reflect “highways” of HGT that significantly affect even the NUTs and appear to differ, specifically, between Deinococcus and Thermus (Omelchenko et al. 2005). Nevertheless, as shown in our previous study, the NUTs do not show significant clustering in the tree topology space, suggestive of a quasi-random overall distribution of the HGT routes (Puigbo, Wolf, and Koonin 2009). Therefore, with the caveat that HGT might have affected some aspects of the supertree topology, we use it a standard of tree-like evolution throughout this work.
Conversely, not all topological conflicts between trees are attributable to HGT or more generally “net-like evolutionary processes” because a fraction of such conflicts that is not easy to estimate is explained by erroneous and poorly resolved trees caused by phylogenetic artifacts such as long branch attraction as well as poor alignment of divergent orthologous sequences (Kolaczkowski and Thornton 2004; Landan and Graur 2009). Nevertheless, the demonstration that even when the comparative analysis of the NUTs is limited to the nodes with high bootstrap support, much of the inconsistency between the topologies persists, suggests that net-like processes substantially contribute to the observed conflicts (Puigbo et al. 2009).
In principle, the FOL encompasses the complete set of phylogenetic trees for all genes from all genomes. However, a comprehensive analysis of the entire FOL is computationally prohibitive, so a representative subset of the trees needs to be selected and analyzed. Previously (Puigbo, Wolf, and Koonin 2009), we defined such a subset by selecting 100 archaeal and bacterial genomes representative of all major prokaryote groups and building 6,901 ML trees for all sufficiently conserved genes in this set of genomes; for brevity, we refer to this set of trees as the FOL (see details in supplementary Materials and Methods and supplementary fig. S1, Supplementary Material online).
Species Quartet Analysis
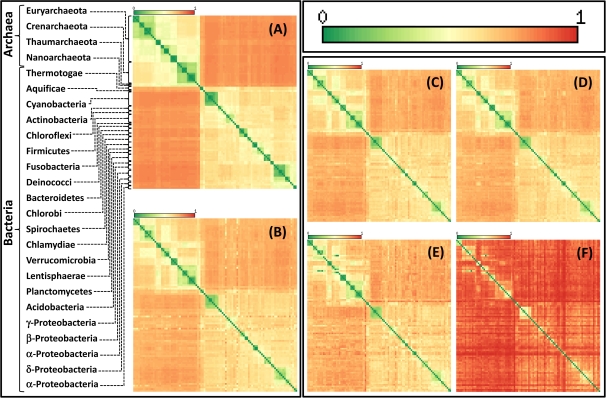
To assess the contributions of the tree-like and the net-like evolution to the observed relationships among prokaryotes across the FOL, we performed an exhaustive analysis of species quartets (Estabrook et al. 1985). Altogether, there are almost four million quartets for 100 species, and given the three possible unrooted topologies for each quartet, the total number of topologies to analyze is close to 12 million. Each quartet topology was mapped onto each tree in the FOL, and the results were used to construct distance matrices and the corresponding “heatmaps” for the analyzed prokaryotes (fig. 1) (see details in supplementary Materials and Methods and supplementary fig. S2, Supplementary Material online). When two species often appear as neighbors in quartets, the distance is small, whereas when the species in question are neighbors only rarely, the distance is large (fig. 1). The order of the species in the matrix was chosen in accordance with the topology of the supertree of the NUTs that was taken to represent the signal of tree-like evolution (Puigbo et al. 2009). The quartet analysis of the NUTs showed a dominant tree-like signal: not only were bacteria and archaea clearly separated but also the major branches within each of these prokaryote domains, such as Crenarchaeota and Euryarchaeota among the archaea and Proteobacteria and Firmicutes among the bacteria, were retrieved (as reflected in the grouping of the green elements along the diagonal of the heatmap in figure 1A). The structure of the matrix closely followed the topology of the supertree of the NUTs, in accord with the concept of the “statistical” TOL as a central trend in the phylogenetic forest (Puigbo et al. 2009). It should be noted that the topology of the supertree (supplementary fig. S4, Supplementary Material online) showed some deviations from the parts of the deep phylogeny of prokaryotes that are considered well established. In particular, the monophyly of the Deinococci (also known as the Deinococcus-Thermus group) that is supported by many phylogenetic trees and gene content analysis (Weisburg et al. 1989; Omelchenko et al. 2005; Griffiths and Gupta 2007). These peculiarities of the supertree topology are likely to reflect “highways” of HGT that significantly affect even the NUTs and appear to differ, specifically, between Deinococcus and Thermus (Omelchenko et al. 2005). Nevertheless, as shown in our previous study, the NUTs do not show significant clustering in the tree topology space, suggestive of a quasi-random overall distribution of the HGT routes (Puigbo et al. 2009). Therefore, with the caveat that HGT might have affected some aspects of the supertree topology (see supernetwork at supplementary fig. S7, Supplementary Material online), we use it a standard of tree-like evolution throughout this work.
FIG. 1.—
Heatmaps derived from quartet distance matrices between 100 archaeal and bacterial species. (A) The 102 NUTs; (B) The FOL without the NUTs (6,799 trees); (C) Trees with 75–90 species (200 trees); (D) Trees with 50–74 species (536 trees); (E) Trees with 26–49 species (947 trees); (F) Trees with 4–25 species (5,218 trees). The quartet distance between species increases from green (small distance, an indication of tree-like evolution) to red (large distance, an indication of net-like evolution). The species in each panel are ordered in accord with the topology of the supertree of the 102 NUTs. In (A), the major groups of archaea and bacteria are denoted. The complete species names are given in supplementary table S1 (Supplementary Material online). For additional heatmaps, see supplementary figs. S8–10 and S18 (Supplementary Material online).
Although substantially weaker than the tree-like signal, additional off-diagonal signals attributable to net-like evolution (conceivably, in large part, highways of HGT; Beiko et al. 2005) were also seen and were substantially stronger within the archaeal and bacterial domains than between the domains (fig. 1A and supplementary fig. S8, Supplementary Material online).
The heatmap for the rest of the FOL (without NUTs) was much different and showed a complex landscape of net-like evolution (fig. 1B and supplementary fig. S9, Supplementary Material online). Strikingly, the subsets of the trees from the FOL with decreasing numbers of species showed a precipitous decline of the tree-like signal, which becomes virtually undetectable for the 4–25 species quartile (fig. 1C–F and supplementary fig. S10, Supplementary Material online). The low correlation observed among quartet distance matrices for small trees suggest largely independent processes of nontree-like evolution; in contrast, the strong correlation among matrices for large trees (over 50 species) emphasizes the coherence of the tree-like signal (supplementary fig. S11, Supplementary Material online). The difference in the relative strengths of the tree and net signals between trees of different size was not due to the low quality of trees with small numbers of species because these trees on average showed even slightly greater bootstrap support than trees with more species (supplementary fig. S3, Supplementary Material online).
The TNT: Quantification of the Tree and Net Components of Prokaryote Evolution
We then directly estimated the tree-like and net-like contributions for each of the between-species quartet distances using the TNT score. The TNT score scales the quartet distance between a pair of species against two reference point: the expectation for net-only evolution (assuming a completely random distribution of quartets, the expectation for the quartet distance is 0.67) and the expectation for tree-like evolution represented by the distance the same two species in the supertree of the NUTs (supplementary fig. S3, Supplementary Material online). These two extremes correspond to the TNT scores of 0 and 1, respectively; the lower the TNT value (i.e., the closer to the random distance), the more the relationship between the given pair of prokaryotes is determined by the net-like processes. At this point, we should reiterate that the topology of the supertree is itself determined not only by the central tree-like trend but also by additional effects of HGT; however, on average, local deformations are not expected to significantly affect the TNT score because this score compares the distances between the given pair of species in a chosen group of trees and in the supertree, and in general, the two distances can be assumed to be similarly affected by HGT biases.
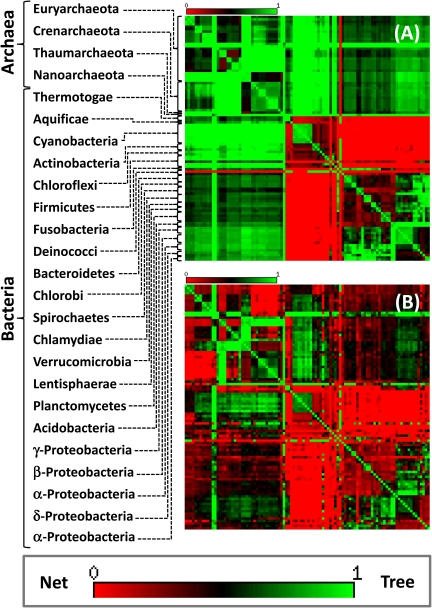
The TNT map of the NUTs was dominated by the tree-like signal (green in fig. 2A): The mean TNT score for the NUTs was 0.63, so the evolution of the nearly universal genes of prokaryotes appears to be almost “two-third tree-like” (i.e., reflects that topology of the supertree). The notable exceptions are the extreme radioresistant bacterium Deinococcus radiodurans that showed, primarily, net-like relationships with most of the archaea and several bacterial taxa (Thermotogae, Aquificales, Cyanobacteria, Actinobacteria, Chloroflexi, Firmicutes, and Fusobacteriae) each of which formed a strongly connected network with other bacteria (fig. 2A and supplementary fig. S12, Supplementary Material online).
FIG. 2.—
The TNT score heatmaps for the 100 analyzed prokaryote species. (A) The 102 NUTs. (B) The FOL without the NUTs (6,799 trees). The TNT increases from red (slow TNT score, close to random, an indication of net-like evolution) to green (high TNT score, close to the supertree topology, an indication of tree-like evolution). The species are ordered in accord with the topology of the supertree of the 102 NUTs. In (A), the major groups of archaea and bacteria are denoted. The complete species names are given in the supplementary table S1 (Supplementary Material online). For additional TNT heatmaps, see supplementary figs. S12, S13, and S24 (Supplementary Material online).
The rest of the FOL stood in a stark contrast to the NUTs, being dominated by the net-like evolution, with the mean TNT value of 0.39 (about “60% net-like”). In a remarkable manner, areas of tree-like evolution were interspersed with areas of net-like evolution across different parts of the FOL (fig. 2B and supplementary fig. S13, Supplementary Material online). The major net-like areas observed among the NUTs were retained but additional ones became apparent including Crenarchaeota that showed a pronounced signal of a nontree-like relationship with diverse bacteria as well as some Euryarchaeota (fig. 2B and supplementary fig. S13, Supplementary Material online).
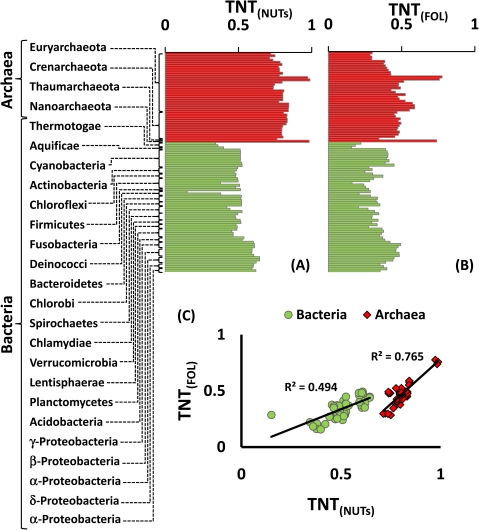
We then applied the TNT score to examine the distribution of the tree and net evolutionary signals among different groups of prokaryotes. The results show a striking split among the NUTs, with the archaea showing a strong dominance of the tree signal (mean TNT = 0.80 ± 0.20) and the bacteria characterized by nearly equal contributions of the tree and net signals (mean TNT = 0.51 ± 0.38) (fig. 3A and supplementary fig. S14a, Supplementary Material online). Among the rest of the trees in the FOL, archaea also showed a stronger tree signal than bacteria, but the difference was much less pronounced than it was among the NUTs (fig. 3B and supplementary fig. S14b, Supplementary Material online). These plots supported the above conclusions based on heatmap examination regarding the dominance of tree-like evolution in some lineages (e.g., Nanoarchaeum equitans and Methanosaeta thermophila among the Archaea, and Proteobacteria), contrasted by the preponderance of the net signal in other lineages (Halobacteria, Cenarchaeum symbiosum among Archaea; D. radiodurans, the hyperthermophilic bacteria Aquifex and Thermotoga), in a general agreement with previous observations on the apparent prevalence of HGT (Aravind et al. 1998; Kennedy et al. 2001; Koonin et al. 2001; Makarova et al. 2001; Lopez-Garcia et al. 2004; Omelchenko et al. 2005; Puigbo et al. 2008; Zhaxybayeva et al. 2009). There was a strong positive correlation between the TNT score values in the NUTs and in the rest of the FOL (fig. 3C and supplementary figs. S15 and S16, Supplementary Material online), a finding that demonstrates the robustness of the observed lineage-specific trends of evolution.
FIG. 3.—
Mean TNT score values for the 100 analyzed prokaryotic species. (A) The NUTs. Archaeal and bacterial species are shown in red and green, respectively. (for the complete version with species names, see supplementary fig. S14, Supplementary Material online). (B) The FOL without the NUTs. Archaeal and bacterial species are shown in red and green, respectively. (for the complete version with species names, see Figure S14). (C) Correlation between TNT values in the NUTs and in the rest of the FOL. Archaeal and bacterial species are shown in red squares and green circles, respectively. (for the complete versions with species names, see Figures S15 and S16).
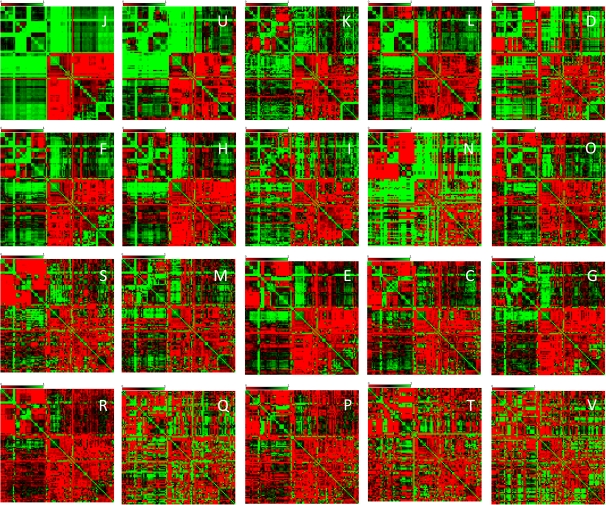
A comparison of the TNT scores revealed dramatic differences between functional classes of genes, with a gradient from a pronounced dominance of the tree signal among genes for translation machinery components and proteins involved in intracellular trafficking to almost fully net-like evolution of genes for ion transport, signal transduction, and defense system components (fig. 4 and supplementary figs. S17–S20, Supplementary Material online). These results are generally compatible with the “complexity hypothesis” according to which genes for components of complex system, such as the ribosome or the replisome, would be subject to limited HGT, whereas genes for proteins that function in relative isolation like metabolic enzymes would be more free to travel horizontally (Jain et al. 1999). However, the present findings revealed a more nuanced picture, with substantial differences, for instance, between enzymes of nucleotide metabolism that evolve mostly in a tree-like fashion and amino acid or carbohydrate metabolism proteins for which the net-like signal was much more prominent (fig. 4 and supplementary fig. S17, Supplementary Material online).
FIG. 4.—
The TNT score heat maps for different functional classes of gene from the 100 analyzed prokaryote species. The order of and numbering of the species are as in Figures 1 and 2. The functional classification of genes was from the COG system (Tatusov et al. 2003). The designations are: J: Translation, ribosomal structure and biogenesis; U: Intracellular trafficking, secretion, and vesicular transport; K: Transcription; L: Replication, recombination and repair; D: Cell cycle control, cell division, chromosome partitioning; F: Nucleotide transport and metabolism; H: Coenzyme transport and metabolism; I: Lipid transport and metabolism; N: Cell motility; O: Posttranslational modification, protein turnover, chaperones; S: Function unknown; M: Cell wall/membrane/envelope biogenesis; E: Amino acid transport and metabolism; C: Energy production and conversion; G: Carbohydrate transport and metabolism; R: General function prediction only; Q: Secondary metabolites biosynthesis, transport and catabolism; P: Inorganic ion transport and metabolism; T: Signal transduction mechanisms; V: Defense mechanisms.
The results of this analysis reveal an apparent paradox of prokaryote evolution: Although the tree-like evolution is the most pronounced single trend in the FOL, quantitatively, evolution of prokaryotes is dominated by the combination of other processes, such as HGT and lineage-specific gene loss, which we collectively denote net-like evolution (figs. 1 and 2). The tree-like pattern accounted for most of the evolution among the NUTs (fig. 2A); however, because the FOL consists mostly of small trees among which the tree signal is barely detectable (fig. 1E and F), the net-like processes that govern the evolution of relatively small gene families are quantitatively dominant (fig. 2B).
Tree-Like Evolution or Biased HGT? A Computer Simulation Analysis
The observed tree-like pattern in the quartet and TNT matrices could, in principle, originate from at least the two, radically different types of processes. First, as it is traditionally assumed in evolutionary biology, this pattern could reflect a history of vertical descent where internal nodes in the tree correspond to ancestral populations prior to speciation events and the branches trace the pattern of descent. Alternatively, according to the radical proposition of Gogarten and coworkers, the appearance of the existence of phylogenetic trees among prokaryotes could be, at least in large part, created by a distinct bias of HGT rates, with a high rate of gene exchange between “closely related” species and progressively decreasing rates between “more distant” species (Gogarten et al. 2002; Olendzenski et al. 2002; Andam et al. 2010). Under this hypothesis, sharing similar genes makes organisms more likely to participate in further horizontal gene exchanges compared with those with less similar genes (both in terms of sequence similarity between orthologs and of gene complement). Thus, initial gene exchanges create a self-reinforcing pattern of preferable exchange between two species or groups of species. The latter form “clades” that, rather than representing the history of speciation, mostly reflect the significantly greater rates of HGT within such clusters of organisms than between clusters.
We designed two series of computer simulations aimed at testing these two alternative hypotheses. For both series of simulations, we assume a particular total rate of HGT (number of events over the course of the simulation) and a particular slope of the HGT rate gradient from the most similar to the least similar species. Specifically, we used a declining power function p ∼ d-α, where d is the distance between the species (clades) and α is the HGT gradient exponent. Both series of simulations were performed with a set of 100 trees containing 100 species each, a data set that mimics the group of NUTs (102 trees with 90–100 species) (Puigbo et al. 2009). To assess the results of the simulated evolution, we used the following two variables to define the targets for the simulation: the fraction of simulated trees that perfectly separate bacteria and archaea (or their operational equivalents in the simulations), with the target value of ∼56% (as observed among the real NUTs) and the mean distance between trees of ∼0.65, again as among the real NUTs (Puigbo et al. 2009) (for details, see Materials and Methods and supplementary Materials and Methods, Supplementary Material online).
The first series of simulations assumed the existence of a tree-like history of vertical descent of prokaryotic species (starting with a single common ancestor) superimposed with nonuniform HGT. The tree-like trend was represented by the rooted ultrametric tree of depth 1 that had the same topology as the supertree of the NUTs (Puigbo et al. 2009) (supplementary fig. S10, Supplementary Material online). This tree defines the distance matrix between species and clades (the depth of the last common node); the distance matrix remained fixed during the simulations. In each simulation, the preset number of HGTs (N) was independently simulated in 100 trees that initially were identical to the prototype ultrametric tree; the probability of each transfer was inversely dependent on the distance between the clades (species) involved in this transfer (for details, see Methods).
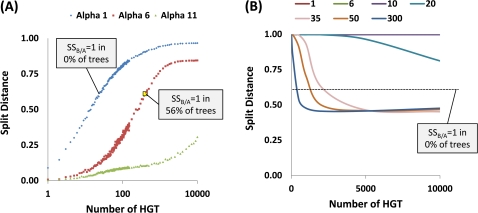
The two target values (56% of trees with perfectly separated superkingdoms and the mean distance of 0.65) were reached after approximately N = 400 simulated HGT events (see the resulting heatmap and supernetwork on supplementary figs. S21 and S22, Supplementary Material online), with a relatively shallow gradient of HGT (α ∼ 6) that allows appreciable gene flow even between the most distant of the analyzed organisms (fig. 5A and supplementary table S3, Supplementary Material online). These appear to be realistic values in the sense that the rate of HGT was at least 25 times lower than the saturating rate given that, even with N = 10,000 HGT events simulated, the mean distance between the trees (0.85) remained far below the random expectation of 1 (fig. 5A).
FIG. 5.—
The dependence of the mean SD among 100 simulated trees on the number of simulated HGT events. The curves obtained with different values of the α coefficient (the exponent that determines the dependence of the rate of HGT on the phylogenetic depth in the simulation—the greater α, the steeper the gradient of the HGT rate from tips to the root of the tree; for details, see supplementary fig. S6a, Supplementary Material online) are color coded. The percentage of the trees with a perfect separation of archaea and bacteria (separation score SSB/A = 1) is indicated where applicable. See text for details. Results of the first series of simulation with three values of the α coefficient (1, 6, 11). The simulation started with the supertree of the NUTs, with the species distance matrix recomputed after each simulated HGT event. Results of the second series of simulations with seven α coefficient values tested (1, 6, 10, 20, 35, 50, 300). The simulations started from 100 random star-like trees of 100 species.
Thus, the results of these simulations show that the observed pattern of similarity between the NUTs is consistent with the vertical descent of prokaryotic clades accompanied by preferential HGT between closely related organisms. This pattern seems biologically plausible because genes from a related donor, in general, are likely to have a better chance to be functionally compatible with their partners in the recipient organism, resulting in a higher rate of HGT fixation.
In the second series of simulations, we attempted to directly test the hypothesis that the coherence between the topologies of the NUTs (which we here equate with the tree-like signal) NUTs could be caused to large extent (Gogarten et al. 2002; Andam et al. 2010) or even exclusively (Olendzenski et al. 2002) by preferential HGT between species that come across as “closely related” in the supertree. In contrast to the simulations described by Andam et al. (2010) that included gene exchange between extant species only, our scheme explicitly incorporated the history of HGT throughout the entire course of evolution. In these simulation runs, the initial topology of the 100 trees was star-like, and the species distance matrix was updated after each simulated transfer (for details, see Methods). At the end of each run, a rooted, ultrametric supertree of the 100 trees was constructed and the two partitions separated by the root bifurcation were denoted “archaea” and “bacteria.” The same target values of the fraction of the trees with perfect separation of archaea and bacteria (56%) and the mean between-tree distance (0.65) were employed.
In this series of simulations, the characteristic distances between trees were reached only at very high values of both N and α (α > 30, N = 300-2000), whereas the perfect archaea–bacteria separation was not observed in any of the simulated trees (fig. 5B and supplementary fig. S23, Supplementary Material online). These results imply that, given a very rate of HGT and extremely strong barriers for gene transfer between distantly related organisms, biased HGT alone can mimic the overall tree-like trend observed in the real FOL. However, this model is incompatible with the existence of well-defined deep clades such as bacteria and archaea. Thus, the results of these simulations suggest that the tree-like signal seen at all phylogenetic depths in the NUTs (Puigbo et al. 2009) is a reflection of a bona fide tree-like history of vertical descent.
Conclusions
Notwithstanding the ubiquity of HGT, trees remain the natural representation of the histories of individual genes given the fundamentally bifurcating character of gene replication and the low frequency of intragenic recombination compared with intergenic recombination at long evolutionary distances (Koonin and Wolf 2009; Koonin, Wolf, and Puigbo 2009). Therefore, although no single tree can fully represent the evolution of prokaryote genomes, the complete picture of evolution will necessarily combine trees and nets (Gogarten et al. 2002; Koonin and Wolf 2008). Taken together, the results of the present analysis reveal a complex landscape of tree-like and net-like evolution of prokaryotes. The signals from these two types of evolution are distributed in a highly nonrandom fashion among lineages of archaea and bacteria and among functional classes of genes. Overall, within the FOL, the net-like signal is quantitatively dominant, vindicating the concepts of “lateral genomics” or net of life (Hilario and Gogarten 1993; Doolittle 1999a, 2009; Gogarten et al. 2002; Gogarten and Townsend 2005; Doolittle and Bapteste 2007; Koonin and Wolf 2008). By no account, are these results compatible with the representation of prokaryote evolution as a TOL adorned with thin, random “cobwebs” of HGT (Kurland et al. 2003; Ge et al. 2005; Kunin et al. 2005). However, the tree-like signal compatible with the consensus topology of the NUTs is also unmistakably detectable and strong as by our measurement up to 40% of the evolution in the prokaryote world conforms with the “statistical TOL.” The reality of prokaryote evolution appears to be that, although net-like processes are quantitatively dominant, the single strongest trend is the tree-like evolution characteristic of the NUTs that also partially recapitulates the rRNA tree (Pace 1997; Puigbo et al. 2009). Of course, the tree-like and net-like processes of evolution are entangled: when we consider a “tree-like” signal, we actually mean the topology of the supertree of the NUTs that is affected not only by the coherent central trend but also biased routes of HGT. However, the strong coherence between the topologies of the NUTs, the quasi-random distribution of HGT events in this set of trees, and the substantial topological similarity between the NUTs and a large fraction of the trees in the FOL, taken together, seem to justify the use of the supertree as the best available standard of tree-like evolution.
Our simulation analysis suggests that, although a bias in HGT rates among prokaryotes could be substantial, and indeed, in favor of gene exchange between closely related microbes, this bias hardly can account for the observed trend of tree-like evolution. Of course, this conclusion is limited to the modeling framework employed in these simulation and requires further analysis. The methodology of species quartet analysis and TNT score comparison implemented in this work could be of general utility to dissect tree-like and net-like trends in evolution.
Supplementary Material
Supplementary figs. S1–S24 and tables S1–S3 are available at Genome Biology and Evolution online (http://www.oxfordjournals.org/our_journals/gbe/).
Acknowledgments
The authors' research is supported by intramural funds of the US Department of Health and Human Services (National Library of Medicine, National Institutes of Health). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Author contributions: P.P., Y.I.W., and E.V.K. designed the study; P.P. performed research; P.P., Y.I.W., and E.V.K. analyzed the data; P.P. and E.V.K. wrote the manuscript.
Competing interests. The authors declare no competing interests
References
- Andam CP, Williams D, Gogarten JP. Biased gene transfer mimics patterns created through shared ancestry. Proc Natl Acad Sci U S A. 2010;107:10679–10684. doi: 10.1073/pnas.1001418107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aravind L, Tatusov RL, Wolf YI, Walker DR, Koonin EV. Evidence for massive gene exchange between archaeal and bacterial hyperthermophiles. Trends Genet. 1998;14:442–444. doi: 10.1016/s0168-9525(98)01553-4. [DOI] [PubMed] [Google Scholar]
- Bapteste E, Boucher Y. Lateral gene transfer challenges principles of microbial systematics. Trends Microbiol. 2008;16:200–207. doi: 10.1016/j.tim.2008.02.005. [DOI] [PubMed] [Google Scholar]
- Bapteste E, et al. Prokaryotic evolution and the tree of life are two different things. Biol Direct. 2009;4:34. doi: 10.1186/1745-6150-4-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bapteste E, et al. Do orthologous gene phylogenies really support tree-thinking? BMC Evol Biol. 2005;5:33. doi: 10.1186/1471-2148-5-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beiko RG, Harlow TJ, Ragan MA. Highways of gene sharing in prokaryotes. Proc Natl Acad Sci U S A. 2005;102:14332–14337. doi: 10.1073/pnas.0504068102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boucher Y, et al. Lateral gene transfer and the origins of prokaryotic groups. Annu Rev Genet. 2003;37:283–328. doi: 10.1146/annurev.genet.37.050503.084247. [DOI] [PubMed] [Google Scholar]
- Ciccarelli FD, et al. Toward automatic reconstruction of a highly resolved tree of life. Science. 2006;311:1283–1287. doi: 10.1126/science.1123061. [DOI] [PubMed] [Google Scholar]
- Dagan T, Artzy-Randrup Y, Martin W. Modular networks and cumulative impact of lateral transfer in prokaryote genome evolution. Proc Natl Acad Sci U S A. 2008;105:10039–10044. doi: 10.1073/pnas.0800679105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darwin C. On the origin of species. London: Murray; 1859. [Google Scholar]
- Delsuc F, Brinkmann H, Philippe H. Phylogenomics and the reconstruction of the tree of life. Nat Rev Genet. 2005;6:361–375. doi: 10.1038/nrg1603. [DOI] [PubMed] [Google Scholar]
- Doolittle WF. Lateral genomics. Trends Cell Biol. 1999a;9:M5–M8. [PubMed] [Google Scholar]
- Doolittle WF. Phylogenetic classification and the universal tree. Science. 1999b;284:2124–2129. doi: 10.1126/science.284.5423.2124. [DOI] [PubMed] [Google Scholar]
- Doolittle WF. The practice of classification and the theory of evolution, and what the demise of Charles Darwin's tree of life hypothesis means for both of them. Philos Trans R Soc Lond B Biol Sci. 2009;364:2221–2228. doi: 10.1098/rstb.2009.0032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doolittle WF, Bapteste E. Pattern pluralism and the Tree of Life hypothesis. Proc Natl Acad Sci U S A. 2007;104:2043–2049. doi: 10.1073/pnas.0610699104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar RC. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004;32:1792–1797. doi: 10.1093/nar/gkh340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estabrook GF, McMorris FR, Meachan A. Comparison of undirected phylogenetic trees based on subtree of four evolutionary units. Syst Zool. 1985;34:193–200. [Google Scholar]
- Ge F, Wang LS, Kim J. The cobweb of life revealed by genome-scale estimates of horizontal gene transfer. PLoS Biol. 2005;3:e316. doi: 10.1371/journal.pbio.0030316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gogarten JP, Doolittle WF, Lawrence JG. Prokaryotic evolution in light of gene transfer. Mol Biol Evol. 2002;19:2226–2238. doi: 10.1093/oxfordjournals.molbev.a004046. [DOI] [PubMed] [Google Scholar]
- Gogarten JP, Townsend JP. Horizontal gene transfer, genome innovation and evolution. Nat Rev Microbiol. 2005;3:679–687. doi: 10.1038/nrmicro1204. [DOI] [PubMed] [Google Scholar]
- Griffiths E, Gupta RS. Identification of signature proteins that are distinctive of the Deinococcus–Thermus phylum. Int Microbiol. 2007;10:201–208. [PubMed] [Google Scholar]
- Hilario E, Gogarten JP. Horizontal transfer of ATPase genes—the tree of life becomes a net of life. Biosystems. 1993;31:111–119. doi: 10.1016/0303-2647(93)90038-e. [DOI] [PubMed] [Google Scholar]
- Jain R, Rivera MC, Lake JA. Horizontal gene transfer among genomes: the complexity hypothesis. Proc Natl Acad Sci U S A. 1999;96:3801–3806. doi: 10.1073/pnas.96.7.3801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen LJ, et al. eggNOG: automated construction and annotation of orthologous groups of genes. Nucleic Acids Res. 2008;36:D250–D254. doi: 10.1093/nar/gkm796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keane TM, Naughton TJ, McInerney JO. MultiPhyl: a high-throughput phylogenomics webserver using distributed computing. Nucleic Acids Res. 2007;35:W33–W37. doi: 10.1093/nar/gkm359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy SP, Ng WV, Salzberg SL, Hood L, DasSarma S. Understanding the adaptation of Halobacterium species NRC-1 to its extreme environment through computational analysis of its genome sequence. Genome Res. 2001;11:1641–1650. doi: 10.1101/gr.190201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolaczkowski B, Thornton JW. Performance of maximum parsimony and likelihood phylogenetics when evolution is heterogeneous. Nature. 2004;431:980–984. doi: 10.1038/nature02917. [DOI] [PubMed] [Google Scholar]
- Koonin EV, Makarova KS, Aravind L. Horizontal gene transfer in prokaryotes: quantification and classification. Annu Rev Microbiol. 2001;55:709–742. doi: 10.1146/annurev.micro.55.1.709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koonin EV, Wolf YI. Genomics of bacteria and archaea: the emerging dynamic view of the prokaryotic world. Nucleic Acids Res. 2008;36:6688–6719. doi: 10.1093/nar/gkn668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koonin EV, Wolf YI. The fundamental units, processes and patterns of evolution, and the Tree of Life conundrum. Biol Direct. 2009;4:33. doi: 10.1186/1745-6150-4-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koonin EV, Wolf YI, Puigbo P. The phylogenetic forest and the quest for the elusive tree of life. Cold Spring Harb Symp Quant Biol. 2009;74:205–213. doi: 10.1101/sqb.2009.74.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunin V, Goldovsky L, Darzentas N, Ouzounis CA. The net of life: reconstructing the microbial phylogenetic network. Genome Res. 2005;15:954–959. doi: 10.1101/gr.3666505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurland CG, Canback B, Berg OG. Horizontal gene transfer: a critical view. Proc Natl Acad Sci U S A. 2003;100:9658–9662. doi: 10.1073/pnas.1632870100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landan G, Graur D. Characterization of pairwise and multiple sequence alignment errors. Gene. 2009;441:141–147. doi: 10.1016/j.gene.2008.05.016. [DOI] [PubMed] [Google Scholar]
- Lopez-Garcia P, Brochier C, Moreira D, Rodriguez-Valera F. Comparative analysis of a genome fragment of an uncultivated mesopelagic crenarchaeote reveals multiple horizontal gene transfers. Environ Microbiol. 2004;6:19–34. doi: 10.1046/j.1462-2920.2003.00533.x. [DOI] [PubMed] [Google Scholar]
- Makarova KS, et al. Genome of the extremely radiation-resistant bacterium Deinococcus radiodurans viewed from the perspective of comparative genomics. Microbiol Mol Biol Rev. 2001;65:44–79. doi: 10.1128/MMBR.65.1.44-79.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Malley MA, Boucher Y. Paradigm change in evolutionary microbiology. Stud Hist Philos Biol Biomed Sci. 2005;36:183–208. doi: 10.1016/j.shpsc.2004.12.002. [DOI] [PubMed] [Google Scholar]
- Olendzenski L, Zhaxybayeva O, Gogarten JP. Horizontal gene transfer: a new taxonomic principle? In: Syvanen M, Kado CI, editors. Horizontal gene transfer. New York: Academic Press; 2002. [Google Scholar]
- Omelchenko MV, et al. Comparative genomics of Thermus thermophilus and Deinococcus radiodurans: divergent routes of adaptation to thermophily and radiation resistance. BMC Evol Biol. 2005;5:57. doi: 10.1186/1471-2148-5-57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pace NR. A molecular view of microbial diversity and the biosphere. Science. 1997;276:734–740. doi: 10.1126/science.276.5313.734. [DOI] [PubMed] [Google Scholar]
- Pace NR. Time for a change. Nature. 2006;441:289. doi: 10.1038/441289a. [DOI] [PubMed] [Google Scholar]
- Pavlidis P, Li Q, Noble WS. The effect of replication on gene expression microarray experiments. Bioinformatics. 2003;19:1620–1627. doi: 10.1093/bioinformatics/btg227. [DOI] [PubMed] [Google Scholar]
- Puigbo P, Garcia-Vallve S, McInerney JO. TOPD/FMTS: a new software to compare phylogenetic trees. Bioinformatics. 2007;23:1556–1558. doi: 10.1093/bioinformatics/btm135. [DOI] [PubMed] [Google Scholar]
- Puigbo P, Pasamontes A, Garcia-Vallve S. Gaining and losing the thermophilic adaptation in prokaryotes. Trends Genet. 2008;24:10–14. doi: 10.1016/j.tig.2007.10.005. [DOI] [PubMed] [Google Scholar]
- Puigbo P, Wolf YI, Koonin EV. Search for a Tree of Life in the thicket of the phylogenetic forest. J Biol. 2009;8:59. doi: 10.1186/jbiol159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talavera G, Castresana J. Improvement of phylogenies after removing divergent and ambiguously aligned blocks from protein sequence alignments. Syst Biol. 2007;56:564–577. doi: 10.1080/10635150701472164. [DOI] [PubMed] [Google Scholar]
- Tatusov RL, et al. The COG database: an updated version includes eukaryotes. BMC Bioinformatics. 2003;4:41. doi: 10.1186/1471-2105-4-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatusov RL, Koonin EV, Lipman DJ. A genomic perspective on protein families. Science. 1997;278:631–637. doi: 10.1126/science.278.5338.631. [DOI] [PubMed] [Google Scholar]
- Weisburg WG, Giovannoni SJ, Woese CR. The Deinococcus–Thermus phylum and the effect of rRNA composition on phylogenetic tree construction. Syst Appl Microbiol. 1989;11:128–134. doi: 10.1016/s0723-2020(89)80051-7. [DOI] [PubMed] [Google Scholar]
- Woese CR. Bacterial evolution. Microbiol Rev. 1987;51:221–271. doi: 10.1128/mr.51.2.221-271.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woese CR, Kandler O, Wheelis ML. Towards a natural system of organisms: proposal for the domains Archaea, Bacteria, and Eucarya. Proc Natl Acad Sci U S A. 1990;87:4576–4579. doi: 10.1073/pnas.87.12.4576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf YI, Rogozin IB, Grishin NV, Koonin EV. Genome trees and the tree of life. Trends Genet. 2002;18:472–479. doi: 10.1016/s0168-9525(02)02744-0. [DOI] [PubMed] [Google Scholar]
- Zhaxybayeva O, Gogarten JP. An improved probability mapping approach to assess genome mosaicism. BMC Genomics. 2003;4:37. doi: 10.1186/1471-2164-4-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhaxybayeva O, Gogarten JP, Charlebois RL, Doolittle WF, Papke RT. Phylogenetic analyses of cyanobacterial genomes: quantification of horizontal gene transfer events. Genome Res. 2006;16:1099–1108. doi: 10.1101/gr.5322306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhaxybayeva O, et al. On the chimeric nature, thermophilic origin, and phylogenetic placement of the Thermotogales. Proc Natl Acad Sci U S A. 2009;106:5865–5870. doi: 10.1073/pnas.0901260106. [DOI] [PMC free article] [PubMed] [Google Scholar]