Development and Initial Evaluation of 7 Tesla Q-Ball Imaging of the Human Brain

Abstract

Diffusion tensor imaging (DTI) noninvasively depicts white matter connectivity in regions where the Gaussian model of diffusion is valid, but yields inaccurate results where diffusion has a more complex distribution, such as fiber crossings. Q-ball imaging (QBI) overcomes this limitation of DTI by more fully characterizing the angular dependence of intravoxel diffusion with larger numbers of diffusion-encoding directional measurements at higher diffusion-weighting factors (b values). However, the former results in longer acquisition times and the latter results in lower signal-to-noise ratio (SNR). In this project, we developed specialized 7 Tesla acquisition methods utilizing novel radiofrequency pulses, 8-channel parallel imaging EPI, and high-order shimming with a phase-sensitive multichannel B₀ field map reconstruction. These methods were applied in initial healthy adult volunteer studies which demonstrated the feasibility of performing 7T QBI. Preliminary comparisons of 3T with 7T within supratentorial crossing white matter tracts document a 79.5% SNR increase for b=3000 s/mm² (p=0.0001), and a 38.6% SNR increase for b=6000 s/mm² (p=0.015). Using spherical harmonic reconstruction of the q-ball orientation distribution function at b=3000 s/mm², 7T QBI allowed accurate visualization of crossing fiber tracts with fewer diffusion-encoding acquisitions than at 3T. The improvement of 7T QBI at b factors as high as 6000 s/mm² resulted in better angular resolution than 3T for depicting fibers crossing at shallow angles. Although the increased susceptibility effects at 7T caused problematic distortions near brain-air interfaces at the skull base and posterior fossa, these initial 7T QBI studies demonstrated excellent quality in much of the supratentorial brain with significant improvements as compared to 3T acquisitions in the same individuals.

INTRODUCTION

There has been continuous progress in magnetic resonance (MR) diffusion imaging technology over the past two decades, revolutionizing scientific studies of the human central nervous system and the clinical practice of neuroradiology. However, despite the development of higher performance gradient systems, multi-element phased array coils and parallel imaging, as well as the latest generation of clinical 3 Tesla (3T) high field scanners, diffusion MR imaging of the human brain in vivo has remained limited by signal-to-noise ratio (SNR) constraints. This is because the progression of new applications for diffusion imaging has created ever increasing demands for spatial resolution and angular resolution. Much recent interest has focused on diffusion tensor imaging [1, 2] and its use in the noninvasive investigation of white matter connectivity with fiber tractography [3–5], which requires high resolution in three spatial dimensions. Moreover, the shortcomings of DTI for accurately characterizing diffusion in complex white matter, where fiber tracts with different orientations intersect or are otherwise partial volume averaged within a voxel, has led to the advent of high angular resolution diffusion imaging (HARDI). HARDI methods attempt to recover more information about the angular structure of intravoxel diffusion by acquiring larger numbers of diffusion-encoding directional measurements at higher diffusion-weighting factors (b values) than is routine for DTI [6–8]. There has been a growing list of proposed techniques for reconstructing fiber orientations from HARDI data, including spherical harmonic modeling of the apparent diffusion coefficient (ADC) profile [7, 8], multitensor modeling [9], generalized tensor representations [10, 11], persistent angular structure [12], circular spectrum mapping [13], q-ball imaging [14, 15], spherical deconvolution [16], fiber orientation estimated on continuous axially symmetric tensors [17] and the diffusion orientation transform [18]. However, all of these HARDI approaches remain SNR-limited even on 3T scanners with parallel imaging capability, because of the need for both high spatial resolution and very strong diffusion-weighting, resulting in long examination times and/or suboptimal discrimination of intravoxel crossing fiber tracts. Indeed, the low SNR of HARDI at 3T has motivated the introduction of different forms of regularization to improve the reliability of fiber orientation determination [19–21]. Proposed methods for more fully sampling q-space often require even higher diffusion-weighting factors than is typical for HARDI [22–24]; hence, these techniques might derive even greater benefits from better SNR.

The most straightforward strategy for improving SNR is to boost the magnetic field strength B₀, thereby increasing proton spin polarization. However, to our knowledge, there have not yet been any reports in the peer-reviewed literature of diffusion imaging of the living human brain at field strengths greater than 3T. Challenges to diffusion-weighted imaging at ultra-high field include T2 and T2* shortening, large chemical shifts, poorer field homogeneity, and increased susceptibility artifacts. The goal of this project was to develop specialized 7 Tesla single-shot spin EPI q-ball acquisition methods and investigate feasibility and performance in initial human studies.

MATERIALS AND METHODS

Image Acquisition

HARDI was performed on three healthy adult male volunteers, ages 26, 36 and 38 years, using a 3T Signa EXCITE scanner (GE Healthcare, Waukesha, WI) equipped with a commercial 8-channel phased array head receive coil (MRI Devices, Waukesha, WI). The volunteers also underwent HARDI on a 7T MR scanner (GE Healthcare, Waukesha, WI) equipped with a 30-cm volume excite coil and 8-channel phased array receiver (Nova Medical, Wilmington, MA). The imaging protocols were approved by the institutional review board at our medical center, and written informed consent was obtained from all participants. At both 3T and 7T, a multislice axial single-shot echoplanar spin-echo pulse sequence was employed for high angular resolution diffusion-weighted imaging. The 7T version of the sequence incorporated a custom-designed high-bandwidth fat saturation pulse for effective lipid suppression. Automated high-order shimming was performed prior to the diffusion-weighted acquisitions using a specialized multichannel B₀ field map reconstruction that preserves phase information when combining signals from the different phased array coil elements [25]. Both the 3T and the 7T scanners were equipped with gradient coil sets that have maximum amplitudes of 40 mT/m and maximum slew rates of 150 T/m/s. At each field strength, conventional Stejskal-Tanner diffusion encoding was applied in each of two HARDI protocols, one with 36 diffusion directional measurements at b=3000 s·mm⁻² (TR=5s; TE=89ms, NEX=1) and the other with 131 diffusion directional measurements at b=6000 s·mm⁻² (TR=6s; TE=108ms, NEX=1). For both protocols, an additional acquisition without diffusion weighting at b=0 s·mm⁻² was also obtained. Total scan time was 6 minutes 30 seconds for the 36-direction experiment and 26 minutes 40 seconds for the 131-direction experiment. For SNR calculation at 3T and at 7T, two identical 6-direction acquisitions were performed at b=3000 s·mm⁻² and also at b=6000 s·mm⁻² using the same sequence parameters as described above for the two HARDI protocols. In all cases, the diffusion-encoding directions were distributed uniformly over the surface of a sphere using electrostatic repulsion [26]. Parallel imaging of the diffusion-weighted data acquired with the 8-channel phased array head coils at 3T and at 7T was accomplished using the Array Spatial Sensitivity Encoding Technique (GE Healthcare, Waukesha, WI) with an acceleration factor of 2. For all acquisitions, spatial resolution was 2 mm in all 3 dimensions (FOV 256×256 mm, 128×128 matrix, 2-mm thick interleaved slices with no gap). For all acquisitions, the supratentorial brain from the vertex to below the level of the corpus callosum was covered with axial slices oriented along the plane passing through the anterior and posterior commissures.

Image Postprocessing

Tensor analysis of the HARDI datasets was performed in DtiStudio v2.4 [27], including generation of color fractional anisotropy (FA) maps using the standard red-blue-green directional encoding convention. The q-ball ODF at each voxel was computed from the HARDI data using spherical harmonic basis functions, using methods we have described in detail previously [19]. Truncating the spherical harmonic series at a low order enables q-ball ODF reconstruction from relatively few diffusion-encoding directional measurements with little noise amplification, but achieving higher angular resolution with larger numbers of directional measurements requires higher harmonic orders in the reconstruction. The penalty of including higher harmonic orders is greater noise amplification. Hence, in the fast acquisition regime at b=3000 s·mm⁻² with only 36 directions, a maximum harmonic order of 4 was used for ODF reconstruction. For the high angular resolution regime at b=6000 s·mm⁻² with 131 directions, a maximum harmonic order of 8 was employed.

Because of the low SNR at b=6000 s·mm⁻² and the greater noise amplification inherent at higher harmonic orders, linear regularization using Damped Singular Value Decomposition – Generalized Cross Validation [21] was applied in the estimation of the q-ball ODFs to improve the reliability of fiber orientation estimation and suppress spurious peaks. As an alternative to harmonic q-ball reconstruction in the high angular resolution regime at b=6000 s·mm⁻², the original linear matrix implementation of QBI using radial basis functions [15] was also used to reconstruct the q-ball ODFs. In selecting the radial basis function (RBF) parameters, we used a spherical Gaussian kernel with width parameter σ_i, calculated to minimize the log condition number of the RBF interpolation matrix. The number of equator points was k = 48. For both harmonic q-ball and RBF q-ball methods, values of the ODF were computed at locations corresponding to the 642 vertices of an 8-fold tessellated icosahedron. A spherical Gaussian smoothing kernel was applied to the RBF reconstructions, where the width of the kernel σ_s was chosen visually to smooth out fluctuations in the ODF [15]. RBF q-ball reconstruction performs less reliably at low spherical sampling densities [19] and therefore was not attempted in the fast acquisition regime at b=3000 s·mm⁻².

To facilitate interpretation of the q-ball ODF results, anisotropy was emphasized by min-max normalization. For display, points corresponding to the desired azimuth and elevation were plotted as a three-dimensional surface. Points on the surface of the ODF were color-coded by direction according to the standard red (left-right), blue (superoinferior) and green (anteroposterior) convention used to represent the direction of the principal eigenvector in DTI. As the normalization step can make relatively isotropic ODFs appear anisotropic, the surfaces are overlaid onto a grayscale background corresponding to the generalized fractional anisotropy (GFA) within each voxel for visualization of the human subject data [15]. The more anisotropic ODFs thus appear superimposed on brighter backgrounds, and the background appears dark in voxels with low GFA. All q-ball analysis was performed using custom software written in MATLAB version 7.0 (MathWorks, Natick, MA).

Since there is a spatially nonuniform distribution of noise in parallel imaging, as applied to our HARDI acquisitions, the effective SNR of the diffusion-weighted images at each field strength and at each b value was calculated using the difference method of Reeder et al. [28] from two separate 6-direction DWI acquisitions using identical experimental parameters.

RESULTS

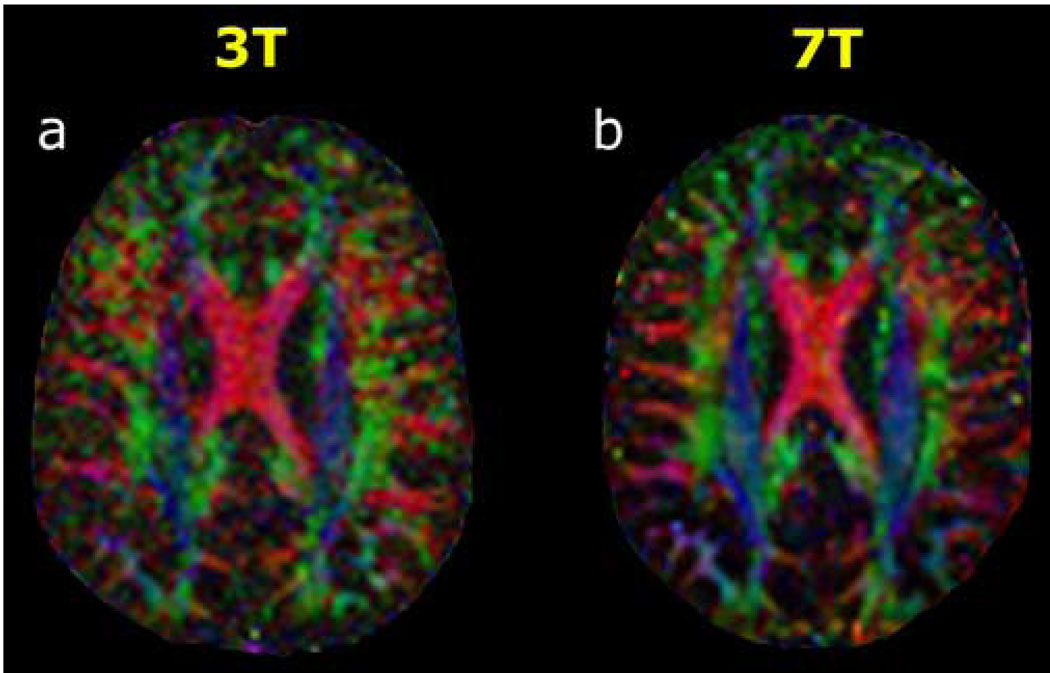
HARDI was successfully performed in all three volunteers at both field strengths and for both diffusion-weighting factors at each field strength. Figure 1 shows examples for 3T and 7T of directionally-encoded color FA maps from tensor analysis of all 36 diffusion-encoding directional measurements at b=3000 s·mm⁻² from one volunteer for a single axial slice location at the level of the body of the corpus callosum. In this fast acquisition regime, visual inspection of the color FA maps clearly manifests the greater SNR of 7T compared to 3T. As demonstrated in Figure 2, the superior SNR at 7T allowed accurate reconstruction of q-ball ODFs from as few as 36 diffusion directional measurements, depicting the known anatomy of crossing fiber tracts in this region of supratentorial white matter. These intersecting axonal pathways consist of the commissural fibers of the corpus callosum (CC), association fibers of the superior longitudinal fasciculus (SLF), and projection fibers of the corticospinal tract (CS). In contradistinction, the lower SNR at 3T yielded poorer visualization of this complex white matter architecture with QBI using such a small number of diffusion-encoding directions.

Figure 1. 3T versus 7T diffusion tensor imaging with 36 diffusion-encoding directions at b=3000 s·mm⁻².

Directionally-encoded color fractional anisotropy (FA) maps at the axial level of the body of the corpus callosum are shown for (a) 3 Tesla and for (b) 7 Tesla in a 38-year-old normal volunteer. The standard DTI color conventions are used, with red representing left-right fiber orientation, green representing anteroposterior, and blue representing craniocaudal. The superior SNR at 7T compared to 3T is evident from these color FA images.

Figure 2. 3T versus 7T q-ball imaging of crossing supratentorial fiber tracts with 36 diffusion-encoding directions at b=3000 s·mm⁻², using spherical harmonic reconstruction.

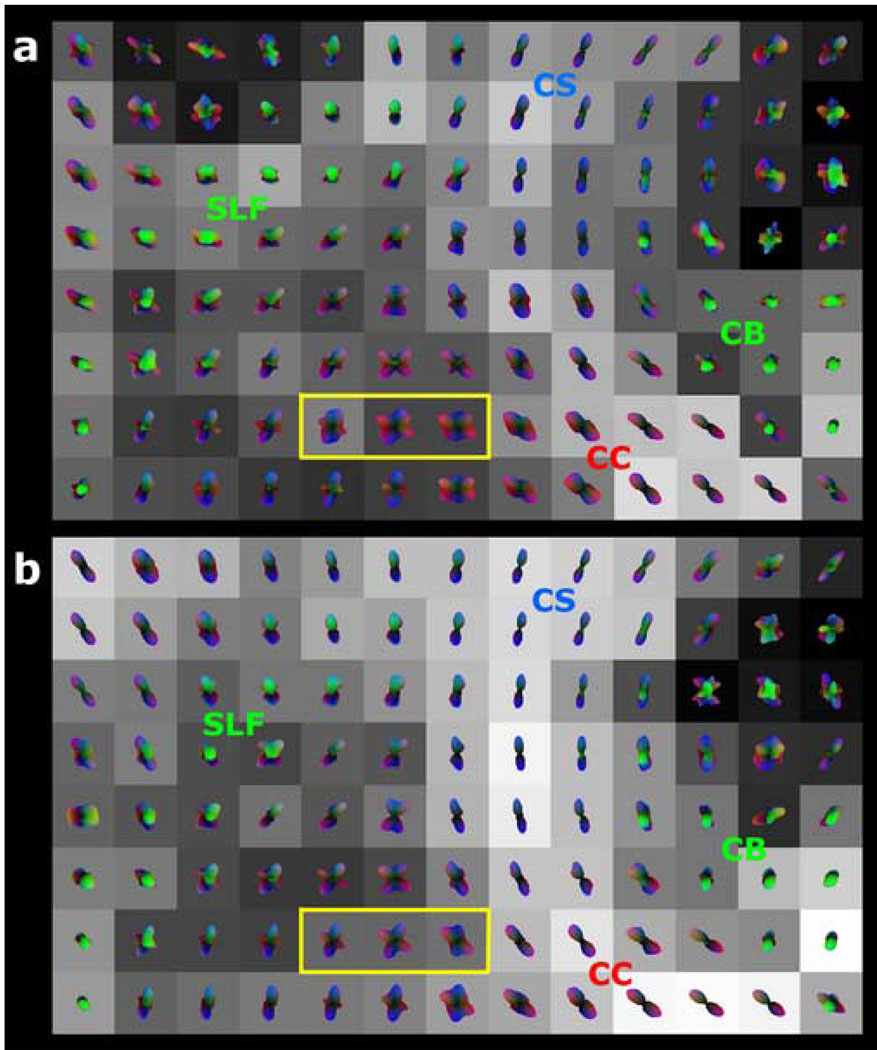
Coronal color FA maps are shown for (a) 3T and for (b) 7T in a 36-year-old normal volunteer, with the region of crossing fibers further analyzed by q-ball imaging indicated by the gray box in each image. The 8 × 13 voxel arrays of q-ball orientation distribution functions (ODFs) are shown for (c) 3T and for (d) 7T, and are derived from spherical harmonic q-ball reconstruction of the HARDI dataset with a maximum model order of 4. Each voxel is cubic and 2 mm on a side. The ODF in each voxel is superimposed on a grayscale background modulated by the generalized fractional anisotropy (GFA) in that voxel (black: GFA=0; white: GFA=1). The color shading of the ODFs indicates orientation using the same 3-color scheme as in the color FA images of Figure 1. The cingulum bundle (CB), corticospinal tract (CS), corpus callosum (CC), and superior longitudinal fasciculus (SLF) are labeled. 7T q-ball imaging results in better visualization of crossing fibers compared to 3T, with more sharply defined peaks. This difference is most readily seen by comparing the 4 voxels enclosed in the yellow box of (c) with the corresponding 4 voxels of (d), both depicting commissural fibers of the corpus callosum intersecting projection fibers of the corticospinal tract.

For each of the three volunteers, the SNR was calculated as described in the Methods from two identical 6-direction DWI acquisitions at b=3000 s·mm⁻² and 2-mm isotropic spatial resolution. The SNR results are presented in Table 1 for the region of crossing fiber tracts depicted by the q-ball ODFs of Figure 2. Averaged across the 3 volunteers, the SNR of DWI at b=3000 s·mm⁻² was found to be 79.5% higher for the 7T data compared to that acquired at 3T. This was a statistically significant difference (p=0.0001).

Table 1.

Signal-to-Noise Ratio of Diffusion-Weighted Imaging at b=3000 s·mm⁻² for 3T vs 7T

Subject	3T	7T	7T vs 3T
vol1	2.9	5.2	+79.3%
vol2	2.8	5.2	+85.7%
vol3	3.1	5.4	+74.2%
Mean	2.93	5.27	+79.5%
SD	0.15	0.12	5.8%

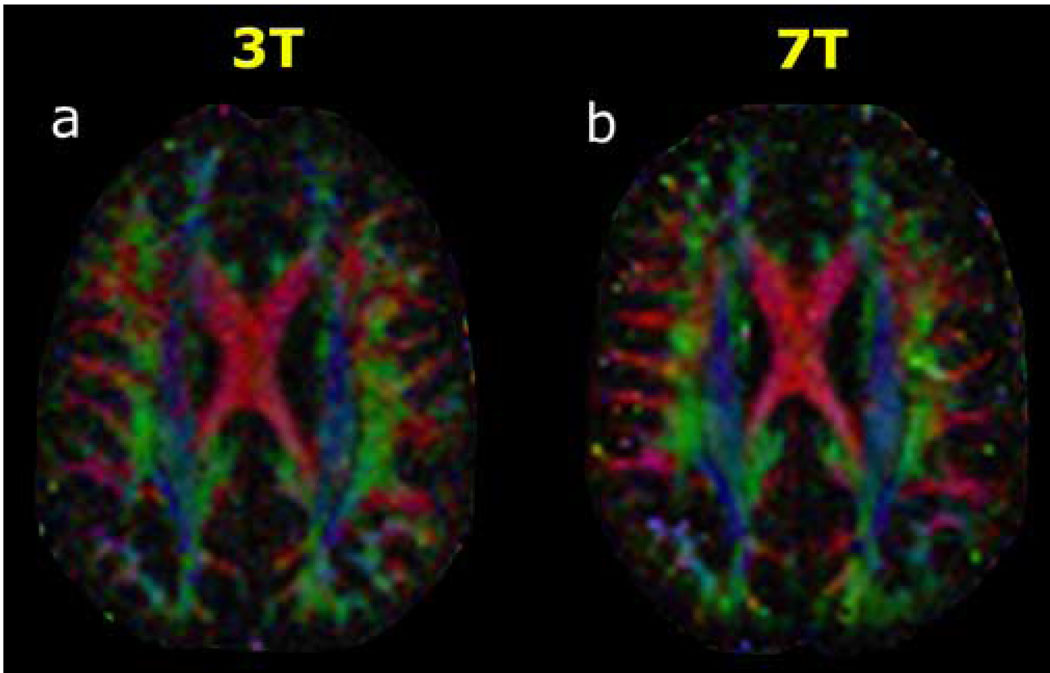
In the high angular resolution regime at b=6000 s·mm⁻² with 131 diffusion-encoding directions, the SNR gain at 7T over 3T was again apparent in the directionally-encoded color FA maps from tensor analysis of the HARDI data (Figure 3) and from the q-ball ODFs in a region of complex white matter architecture (Figure 4). For QBI in particular, intravoxel fiber crossings at shallow angles are better visualized at 7T than at 3T. The higher noise levels at 3T produced many more spurious peaks in the ODFs than at 7T. This was true even with the use of DSVD-GCV regularization to improve the numerical conditioning of the harmonic q-ball ODF reconstruction in the setting of low SNR. Similar to the results with harmonic basis elements, the superiority of 7T over 3T was also apparent when ODFs were reconstructed using radial basis functions (Figure 5).

Figure 3. 3T versus 7T DTI with 131 diffusion-encoding directions at b=6000 s·mm⁻².

Directionally-encoded color FA maps at the axial level of the body of the corpus callosum are shown for (a) 3 Tesla and for (b) 7 Tesla in a 38-year-old normal volunteer. Conventions are as in Figure 1. The superior SNR at 7T compared to 3T is again evident from these color FA images, although the difference is not as great as at b=3000 s·mm⁻² (Figure 1).

Figure 4. 3T versus 7T q-ball imaging of crossing supratentorial fiber tracts with 131 diffusion-encoding directions at b=6000 s·mm⁻², using spherical harmonic reconstruction with regularization.

Coronal color FA maps are shown for (a) 3T and for (b) 7T in a 36-year-old normal volunteer, with the region of crossing fibers further analyzed by q-ball imaging indicated by the gray box in each image. The 8 × 13 voxel arrays of q-ball ODFs are shown for (c) 3T and for (d) 7T, and are derived from spherical harmonic q-ball reconstruction of the HARDI dataset with a maximum model order of 8 and with linear regularization using Damped Singular Value Decomposition – Generalized Cross Validation (DSVD-GCV). All display conventions are as in Figure 2. Again, the 7T results show better visualization of crossing fibers compared to 3T, with more sharply defined peaks and fewer spurious peaks under the low SNR conditions at b=6000 s·mm⁻². This difference is most easily seen by comparing the 3 voxels enclosed in the yellow box of (c) with those of (d), both depicting commissural fibers of the corpus callosum intersecting projection fibers of the corticospinal tract. DSVD-GCV regularization helps reduce noise in the ODF reconstruction at these high harmonic model orders, but the 7T results remain superior to 3T.

Figure 5. 3T versus 7T q-ball imaging of crossing supratentorial fiber tracts with 131 diffusion-encoding directions at b=6000 s·mm⁻², using radial basis function (RBF) reconstruction.

RBF reconstruction of q-ball ODFs was performed for the same HARDI datasets as in Figure 4, using the same conventions for illustration. The 3T results are displayed in (a) and the 7T results are displayed in (b). The interpolation kernel width σ_i=4° optimized the condition number of the RBF reconstruction matrix. The smoothing kernel width σ_s=15° was used for best visual results, as recommended by Tuch (Tuch, 2004). The findings are similar to Figure 4, with superior results found at 7T compared to 3T, again best seen in the voxels enclosed in the yellow boxes of (a) and of (b).

For each of the three volunteers, the SNR was calculated from two identical 6-direction DWI acquisitions at b=6000 s·mm⁻² and 2-mm isotropic spatial resolution, and the results are tabulated in Table 2. In the region of crossing fiber tracts depicted by the q-ball ODFs of Figures 4–5, the SNR of DWI at b=6000 s·mm⁻² was found to be 38.6% higher for 7T compared to 3T. This was a statistically significant difference (p=0.015).

Table 2.

Signal-to-Noise Ratio of Diffusion-Weighted Imaging at b=6000 s·mm⁻² for 3T vs 7T

Subject	3T	7T	7T vs 3T
vol1	1.9	2.5	+31.6%
vol2	1.8	2.8	+55.6%
vol3	2.0	2.6	+30.0%
Mean	1.90	2.63	+38.6%
SD	0.10	0.15	14.3%

DISCUSSION

The burgeoning number of HARDI techniques that have recently been described for reconstructing multiple intravoxel fiber orientations attests to the great interest in overcoming the limitations of DTI in this regard. Of these HARDI methods, q-ball imaging in particular has proven robust in studies by multiple groups [14, 15, 17, 19] and has been validated with both simulations and phantom experiments [29, 30]. For visualizing the complex white matter anatomy of the human brain in vivo, high spatial resolution, high angular resolution, and high SNR of the diffusion-weighted data need to be achieved simultaneously. However, the strong diffusion-weighting required for high angular resolution reduces SNR dramatically. Isotropic voxel dimensions are desirable to avoid biasing anisotropy determinations along a particular axis; however, reducing voxel size along all 3 dimensions to achieve higher spatial resolution also severely reduces SNR. Therefore, 3T MR scanners with high-performance gradient systems have been the platform of choice for performing HARDI, including q-ball imaging. Nevertheless, HARDI on 3T systems remains SNR-limited, which has led to the development of different types of regularization to improve the performance of fiber orientation estimation under low SNR conditions. These include Tikhonov regularization [19], minimization of negative peaks [20], and, most recently, Damped Singular Value Decomposition – Generalized Cross Validation [21]. These regularization methods have previously been applied to q-ball imaging [19] and to spherical deconvolution [20, 21].

Hence, there is clearly a need for the superior SNR of HARDI at ultra-high field. In this study, we have demonstrated the feasibility of performing 7T HARDI using a specialized 7T single-shot spin echo echoplanar pulse sequence with parallel imaging. These initial human results also show a significant boost at 7T in SNR over that of an equivalent acquisition at 3T. To our knowledge, this is the first report of 7T diffusion-weighted imaging of the human brain in vivo. Single-shot spin echo EPI (ssSE-EPI) is by far the most widely used DWI technique because of its efficiency in terms of SNR per unit time and because of its relatively low motion sensitivity. However, there are several technical challenges to performing ssSE-EPI at 7T. A primary concern is the more rapid T2* decay at higher field, which increases T2* blurring, reduces SNR, and increases off-resonance phase errors that contribute to worse EPI image distortion. To a lesser extent, T2 shortening at ultra-high field can also reduce SNR and worsen T2 blurring. These considerations reduce the anticipated SNR gain at 7T, which otherwise would be expected to scale more than linearly with field strength [31]. However, the adverse effects of T2 and T2* shortening can be mitigated by parallel imaging, which shortens the EPI echo train and allows for smaller echo times [32, 33]. We found that using ASSET parallel imaging in conjunction with an 8-channel phased array head coil yielded 7T diffusion-weighted images comparable to 3T in terms of image distortion in the supratentorial brain, while preserving much of the SNR increase that would be expected at 7T compared to 3T. The smaller SNR improvement of 7T over 3T that we documented at b=6000 s·mm⁻² compared to b=3000 s·mm⁻² may at least in part be due to greater T2* decay for 7T compared to 3T at the longer TE needed to achieve stronger diffusion-weighting, and also possibly due to differences in the hardware (coils, gradients, receive-chain, transmit uniformity, etc) between the GE 3T and 7T MR systems. The advent of phased array head coils with 16, 32, or even greater numbers of receiver elements should enable the use of larger parallel imaging reduction factors, which would further reduce the EPI echo train and the TE, thereby increasing the utility of ssSE-EPI for DWI applications. It is noteworthy that 7T has an inherent advantage over lower field strengths in this regime of highly parallel imaging, because the shorter resonance wavelength allows better radiofrequency energy focusing. In this manner, larger reduction factors can theoretically be achieved without as much loss of SNR at 7T as at 3T [34–36].

Another challenge in implementing ssSE-EPI at 7T is the larger chemical shift at ultra-high field, which hinders adequate lipid suppression. We found that incorporating a custom-designed high-bandwidth frequency-selective fat saturation pulse effectively dealt with this issue. The problem of increased sensitivity of ssSE-EPI to B₀ inhomogeneity at 7T was addressed in this study with high-order shimming using a phase-sensitive B₀ field map reconstruction that can be used with multichannel phased array coils [25]. Moreover, the use of parallel imaging reduces ssSE-EPI image distortions related to inhomogeneity effects [32, 33]. These solutions proved adequate in the supratentorial brain, producing image distortions that were no worse than at 3T. However, at the air-tissue interfaces of the skull base and the posterior fossa, image warping at 7T was considerably worse than at 3T, limiting the usefulness of 7T for these more inferior brain regions. As with the problem of shorter T2* relaxation times at ultra-high field, the use of highly parallel imaging with larger reduction factors may mitigate this current drawback of ssSE-EPI DWI at 7T. Another potential solution might be to use the reversed gradient diffusion imaging technique [37]. Other approaches with less sensitivity to B₀ inhomogeneity include multi-shot EPI or single-shot and multi-shot fast spin echo based approaches such as PROPELLER [38]. However, current weaknesses of these pulse sequences at ultra-high field include motion sensitivity, low SNR compared to ssSE-EPI, longer imaging times, and specific absorption rates exceeding FDA guidelines. Recently developed methods that are particularly promising for high field DWI include PROPELLER-EPI [39] and single-shot STEAM [40], the latter of which has recently been applied to 7T DTI of the mouse brain in vivo [41]. As with ssSE-EPI, some of the drawbacks of these alternative sequences at high field might also be solved by highly parallel imaging, as has been shown for PROPELLER-EPI [42].

In this pilot investigation, we present preliminary data showing how the additional SNR of DWI at ultra-high field can be used to benefit HARDI in two different ways: for faster scanning and for higher angular resolution, both without sacrificing spatial resolution. The SNR at the spatial resolution of 2-mm isotropic voxels used in our work compares favorably to that of recent 3T HARDI studies [14, 19, 21]; hence the effect of Rician noise distribution at low SNR on ODF estimation should be comparable in this study to prior q-ball imaging studies of the living human brain. In the fast acquisition regime at b=3000 s·mm⁻², multiple intravoxel fiber orientations in the supratentorial white matter are better visualized from q-ball ODFs at 7T than at 3T when using only 36 diffusion-encoding measurements. We have previously shown that spherical harmonic basis functions are useful for q-ball ODF reconstruction under sparse spherical sampling conditions, allowing accurate visualization of complex white matter architecture from as few as 55 diffusion-encoding directions at 3T with b=3000 s·mm⁻² and 2-mm voxel resolution [19]. The current results illustrate that higher SNR allows accurate fitting of a low-order harmonic model from even fewer measurements at 7T, further reducing whole-brain imaging time to 10 minutes or less. This is important for routine application to clinical patient populations. The sparse spherical sampling necessarily sacrifices angular resolution, and the relatively low b factor and the low harmonic order are tailored for ODF reconstruction in this fast scanning regime. However, as illustrated in Figure 2, important details of the crossing fiber tract anatomy can still be discerned under these experimental conditions.

We focused on the supratentorial crossing tracts that include the corticospinal tract, corpus callosum, and superior longitudinal fasciculus because this is the best studied region in prior HARDI reports [15, 16, 19]. A comprehensive quantitative comparison of 3T and 7T q-ball imaging throughout multiple brain regions is beyond the scope of this pilot study. Such an investigation would need to account for differences in B₁ homogeneity between the two field strengths, as B₁ non-uniformity would be expected to be more pronounced at 7T than 3T; hence, more subjects would be required for a statistically valid comparison. A promising approach in future studies to addressing the greater B1 inhomogeneity at 7T is the use of parallel radiofrequency transmission [43–45].

Although we show results herein only for q-ball imaging, the SNR advantage of 7T should also benefit other HARDI and q-space reconstruction methods. For scientific research requiring higher angular resolution, the superior SNR at 7T enables the use of stronger-diffusion-weighting without the need to reduce spatial resolution by using larger voxels, as exemplified by Figure 4. Although the use of regularization techniques such as DSVD-GCV can improve ODF reconstruction in the setting of low SNR, 7T still retains an advantage over 3T (Figure 4). It is theoretically possible to gain additional SNR at 3T simply by simply scanning longer; however, this entails some practical difficulties in the case of HARDI at very high b values. The most significant is the problem of motion correction for very lengthy acquisitions, even in normal volunteers. The low SNR of each diffusion-weighted measurement, the absence of consistent anatomical landmarks in the DWI images, and the variable signal intensities within white matter across different diffusion-encoding directions all combine to confound current motion correction algorithms. Other strategies to improve the SNR of 3T HARDI include higher performance gradient systems and higher density multi-element phased array receiver coils. With regard to the former, current whole-body gradient systems are already reaching the limits of gradient amplitude and slew rate imposed by the need to avoid peripheral nerve stimulation. Higher density phased array head coils may indeed have an impact on 3T HARDI; however, the electrodynamic advantages of the higher resonance frequency at ultra-high field [34–36] mean that they will likely provide an even greater benefit for 7T HARDI.

In summary, ultra-high field MR imaging shows great promise for in vivo investigation of human white matter architecture and connectivity using HARDI techniques such as q-ball imaging, both in scientific studies of normal volunteers and in clinical research on patient populations. To our knowledge, this is the first demonstration of diffusion imaging of the living human brain at field strengths greater than 3T. Preliminary volunteer studies showed significant SNR improvement over 3T for 7T HARDI of supratentorial crossing fiber tracts using ssSE-EPI with high-order shimming, high-bandwidth fat suppression, and parallel imaging. However, the increased susceptibility induced distortions near brain-air interfaces hindered its application near the skull base and posterior fossa.