Abstract
The neural mechanisms that enable recognition of spiking patterns in the brain are currently unknown. This is especially relevant in sensory systems, in which the brain has to detect such patterns and recognize relevant stimuli by processing peripheral inputs; in particular, it is unclear how sensory systems can recognize time-varying stimuli by processing spiking activity. Because auditory stimuli are represented by time-varying fluctuations in frequency content, it is useful to consider how such stimuli can be recognized by neural processing. Previous models for sound recognition have used preprocessed or low-level auditory signals as input, but complex natural sounds such as speech are thought to be processed in auditory cortex, and brain regions involved in object recognition in general must deal with the natural variability present in spike trains. Thus, we used neural recordings to investigate how a spike pattern recognition system could deal with the intrinsic variability and diverse response properties of cortical spike trains. We propose a biologically plausible computational spike pattern recognition model that uses an excitatory chain of neurons to spatially preserve the temporal representation of the spike pattern. Using a single neural recording as input, the model can be trained using a spike-timing-dependent plasticity-based learning rule to recognize neural responses to 20 different bird songs with >98% accuracy and can be stimulated to evoke reverse spike pattern playback. Although we test spike train recognition performance in an auditory task, this model can be applied to recognize sufficiently reliable spike patterns from any neuronal system.
Introduction
To effectively recognize objects in nature, sensory systems must use neural processing to recognize patterns from the peripheral spike trains evoked in response to those objects. The question of how such object recognition occurs in the brain has been studied using static images in vision (Logothetis and Sheinberg, 1996; Riesenhuber and Poggio, 2000), but how sensory systems recognize objects with time-varying characteristics remains unclear. This type of object recognition requires that sensory processing mechanisms recognize the appropriate time-varying internal representations evoked in response to stimuli, likely in the form of spiking patterns.
The problem of how the brain recognizes time-varying stimuli can be studied effectively in the auditory domain, in which relevant stimuli are defined by time-varying fluctuations in their frequency content. Current auditory stimulus recognition models operate on artificially preprocessed sounds (Tank and Hopfield, 1987; Gütig and Sompolinsky, 2009) or low-level onset–offset auditory inputs (Gollisch, 2008) instead of the input to the auditory recognition system of the brain: namely, neural spike trains, most likely from auditory cortex. This issue is critical for two reasons. First, realistic sensory processing models must deal with the intrinsic variability present in spike trains in vivo, such as spike timing imprecision and unreliability. Second, speech perception and animal vocal communication are disrupted by lesioning auditory cortex (Penfield and Roberts, 1959; Hefner and Heffner, 1986), and the recovery of speech perception in humans requires cortical plasticity (Fitch et al., 1997; Shepherd et al., 1997; Rauschecker, 1999). This suggests that models for auditory object recognition in particular should operate effectively using representations available at the level of cortex, despite the fact that these representations have greater diversity and increased complexity compared with upstream representations (Woolley et al., 2009). To date, no spike pattern recognition model has demonstrated a solution to these problems.
To address this, we designed and tested a novel spike pattern recognition model using a chain of connected neurons. We tested the model in an auditory recognition task using the zebra finch auditory system, a model with striking analogies to humans in the context of speech (Doupe and Kuhl, 1999). We recorded responses in field L, an area analogous to auditory cortex in humans (Wang et al., 2010) evoked in response to zebra finch songs. Field L neurons show a stronger preference for such conspecific vocalizations compared with upstream auditory midbrain areas such as mesencephalicus lateralis, dorsalis (MLd) (Grace et al., 2003; Theunissen and Shaevitz, 2006), which suggests that field L neurons likely play a role in the recognition of such vocalizations in subsequent processing, despite having a higher level of spike train variability compared with MLd neurons (Woolley and Casseday, 2004; Wang et al., 2007; Amin et al., 2010). Using a simple spike-timing-dependent plasticity-based learning rule, we trained the computational model to effectively recognize songs using spike trains recorded from individual field L auditory sites and observed reverse spike pattern playback with a simple alternative activation of the network.
Materials and Methods
Electrophysiological recording.
We performed extracellular neural recordings in field L in adult male zebra finches (Taeniopygia guttata). All procedures were in accordance with the National Institutes of Health guidelines approved by the Boston University Institutional Animal Care and Use Committee. Following previous methods, we conducted acute (Narayan et al., 2006; Billimoria et al., 2008) and awake restrained recordings (Graña et al., 2009) using 3–4 MΩ tungsten microelectrodes. Sounds were presented at 75 dB sound pressure level, and auditory sites were identified using a paired t test for firing rate compared with background firing rate (p ≤ 0.05). For identified sites, we played 100 repetitions of 20 randomly interleaved recordings of conspecific songs truncated to the shortest length (820 ms), and units were isolated using threshold-based spike detection and waveform-based sorting software.
Data analysis.
We used a measure of neural discrimination to quantify the reliability and discriminability of the neural responses (Narayan et al., 2006). First, the van Rossum spike distance metric (van Rossum, 2001) was used to determine the dissimilarity between all pairs of spike trains evoked in response to the 20 stimuli. To determine the dissimilarity between two spike trains, both spike trains (represented as a string of zeros and ones) were convolved with a decaying exponential function with time constant τ, and the van Rossum distance between the spike trains was calculated as the normalized squared Euclidean distance between their convolved responses. Using a template-matching scheme outlined previously (Machens et al., 2003), each spike train evoked in response to the 20 songs was then categorized based on the minimum distance between itself and randomly selected spike trains from each song category; repeating this procedure for all spike trains then yielded a percentage correct discrimination score. To determine the optimal timescale of the neuron, we varied the exponential time constant τ from 1 ms to 1 s and chose the time constant that maximized the percentage correct discrimination score.
We used two previously defined metrics to examine the temporal properties of our recorded spike trains. We measured reliability of the spike trains of a neural recording using a correlation-based measure Rcorr (Schreiber et al., 2003), which assesses both the spike timing precision (timing stability) and reliability (addition/removal of spikes) of a set of responses to a particular stimulus. Rcorr calculates reliability by smoothing spike trains with a normal kernel and computing normalized inner products between smoothed spike trains, yielding reliability values between 0 (unreliable) and 1 (perfectly reliable). We measured spike train sparseness using a previously defined technique (Vinje and Gallant, 2000) that uses a normalized peristimulus time histogram-binning procedure to calculate sparseness values ranging from 0 (not sparse) to 1 (maximally sparse). Both of these metrics have a single parameter that determines the analysis timescale, which was taken to be the same as the optimal neural discrimination timescale. Reliability and sparseness values were calculated for responses to each song, and these were averaged across songs to yield total measures of reliability and sparseness for each recording. Pearson's correlation coefficients were also used to establish significance (p ≤ 0.05) and assess the strengths of relationships between variables.
After testing model performance classifying field L spike trains (see Results), we used a simple spike train modification scheme to help us assess the selectivity and error tolerance of the recognition network. We took each spike train to be classified, selected a time window of varying length (0–800 ms) and varying start time (in increments of 100 ms), and randomized the time of each spike within the window. This scrambled the timing information in part of the spike train. Averaging across the network performance recognizing these modified spike trains across all songs, trials, and start times yielded a percentage correct recognition for a given scrambling window size. These percentage correct values were then normalized by the baseline (unscrambled) performance to yield a percentage error induced by the spike timing randomization procedure. This procedure was then repeated for spike removal within windows of varying duration, yielding percentage error induced by spike deletion. This allowed us to assess how changing varied durations of the spike trains to be recognized affected system performance. One of the 29 recognition networks analyzed was excluded from this analysis because its low baseline performance (<1%) prevented proper induced error normalization.
Computational model and parameter optimization.
Model neurons behaved according to a standard integrate and fire equation (Dayan and Abbott, 2001) for synaptically coupled neurons with an input current, integrated using an exact method (Brette, 2006). For all simulated neurons, we used a leak voltage of 70 mV, threshold voltage of −55 mV, reset voltage of −80 mV, excitatory synapse reversal potential of 0 mV, and inhibitory reversal potential of −90 mV, all chosen to be in the physiologically plausible range. Although all simulations used these particular cell parameters, the model did not require them to take on these specific values to function properly.
Some model parameters (see below, Spike pattern recognition model and Learning rule) were optimized across the recording sites to maximize song recognition performance. Chain-to-detector synapses had a time constant of 1 ms and the detector neuron had membrane time constant of 3 ms, whereas the chain-to-chain synapses had time constants of 0.5 ms and chain neurons had membrane time constant of 1 ms; these short timescales allowed fine timing information to be transmitted. The SD of the Gaussian learning rule was chosen to be σ = 1.5 ms, also to emphasize fine timing features. The depression/potentiation probability ratio was optimized to be 0.6, which is <1 (equal potentiation and depression), likely because the Poisson firing assumption was not well satisfied for our dataset. The learning rate was optimized to be 0.02, and the learning multiplier was optimized to be 1.1, compromising between learning speed (higher rates, larger reinforcement) and more exact final weights (lower rates, smaller reinforcement). The ratio of excitatory weights to inhibitory weights (3.5) was chosen to equal the ratio of the excitatory and inhibitory reversal potentials. The parameters of the intrachain connections were chosen for highly reliable spike transmission. Only the mean chain-to-detector synaptic conductance was optimized for each site individually, and they had a product with the membrane resistance ranging from 0.0031 to 0.0130.
For spike train replay (see below, Spike train replay), three parameters were fixed across all recognition networks to optimize the similarity between the replay-based and data-based discrimination performances: the input current was chosen such that the effective resting potential of the cell was only 0.01mV from threshold; the product of the detector membrane resistance and synaptic conductance of the random Poisson input was 0.09, and the rate was twice that of the original data firing rate to add noise and a baseline firing rate. To trigger playback, 10 successive spikes at 250 Hz were delivered to the detector neuron. This balanced timing precision and replay denoising, but more or fewer spikes at different firing rates could also be used with varying effects on firing rate and reliability of replayed spike trains.
Results
Neural recordings
We recorded extracellular field L neural responses to 100 repetitions of 20 different zebra finch songs (Fig. 1, one example song spectrogram shown in A, four song spectrograms shown in B) from 26 sites in 8 anesthetized birds and 3 sites in 2 awake restrained birds, yielding 29 total recording sites. Previous work has shown no significant difference between awake restrained and anesthetized recordings in zebra finch field L (Graña et al., 2009), and we also found this to be the case, so both types of recording were pooled for subsequent analysis. The rasters from one example site in response to one song are shown in Figure 1A.
Figure 1.
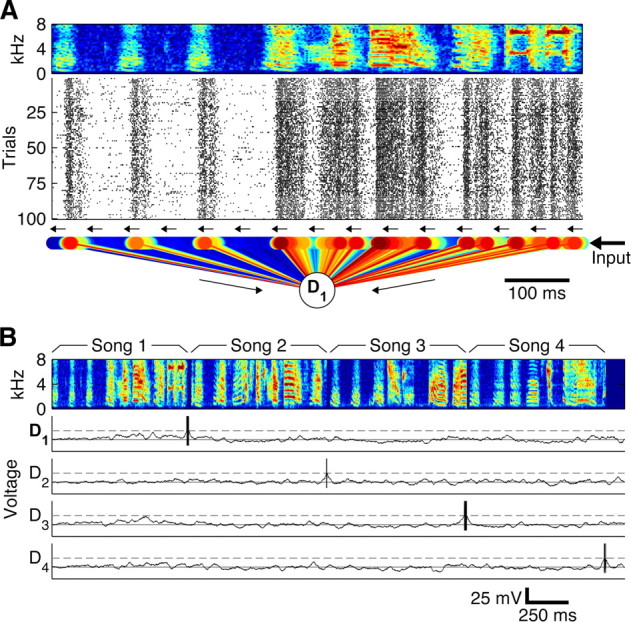
The spike pattern recognition model uses time-varying properties of the neural responses to recognize spiking patterns and consists of a linear chain of neurons. Sensory input (here from field L) feeds into one end of the chain, propagating along the chain using synaptic delays, turning the temporal spiking pattern into a spatial activation of chain neurons. A, Bird song (spectrogram) elicits auditory responses (spike rasters), leading to excitatory (red) and inhibitory (blue) synapses from 298 sequentially connected chained neurons (small circles) that each connect to a detector (D1). The spectrogram shows the power (red, high power; blue, low power) in different frequency bands (y-axis) as a function of time (x-axis), and the rasters show the responses of one field L neuron to 100 repeated presentations (y-axis) of the above stimulus, with each tick mark representing an elicited action potential. B, When the chain recognition circuit (with four detectors D1–D4 shown) is fed input from the field L neuron in response to the concatenation of four different songs (spectrograms), each detector fires only at the end of the correct trained song (D5–D20; data not shown).
Spike pattern recognition model
The recognition model (schematic in Fig. 1A) uses a synaptically coupled chain of integrate-and-fire neurons alongside a set of individual song detector neurons to recognize learned spike sequences. The chain is constructed using sequentially synaptically coupled neurons that preserve previous temporal input states in a distributed spatial activity pattern. Only the first neuron in the chain neuron receives sensory input spikes (here from a field L neuron), and each successive chain neuron only receives input from its neighbor in the form of synaptic excitation with a delay of 2 ms (with neuron and synapse parameters chosen to ensure spikes are transferred with high fidelity; see Materials and Methods). This causes input spikes to traverse successive chain neurons, in which each chain neuron effectively corresponds to a 2 ms time window of activity in the original input; the activity of each chain neuron, then, mirrors the activity of the original sensory input with some fixed delay. To recognize patterns from the original time-varying sensory input, all neurons in the chain of the circuit also either excite or inhibit song detector neurons. The synaptic weights from chain neurons to a given song detector neuron are derived from the time-varying properties of the neural response (Fig. 1A); consistent activity at a particular time in the input causes a particular location in the chain to excite the detector neuron, and consistent temporal inactivity causes a location to inhibit the detector neuron. When a learned spike pattern has been fed into the chain, most active chain neurons activate excitatory synapses on the detector, causing it to fire, signaling detection of that pattern (Fig. 1B). When patterns that do not match the trained spike pattern are fed into the chain, they activate neurons that have inhibitory connections and neurons that have excitatory connections to the detector, but the inhibitory connections prevent the detector from firing (Fig. 1B).
Learning rule
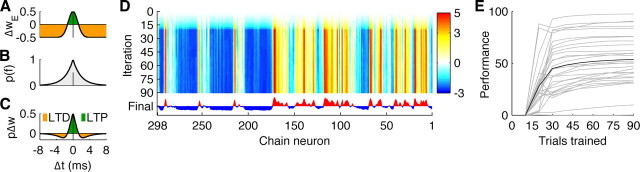
To train the synaptic weights from the chain to the detector of a song, the chain was fed field L responses to 90 repeated presentations of all songs. Every chain neuron began with zero-strength excitatory and inhibitory connections to each of the 20 detection neurons. This is functionally equivalent to having an excitatory and an inhibitory neuron for each member of the chain. During training, a suppressive negative supervisory current was supplied to the 20 detector neurons to prevent them from firing until the spike train to be learned reached the end of the chain (e.g., 820 ms after it started), when a positive current was delivered that caused the appropriate detector neuron to fire. A spike-timing dependent synaptic plasticity (STDP) rule (Abbott and Nelson, 2000) was then applied to modify the chain-to-detector synaptic weights. For the excitatory synapses, a chain neuron (presynaptic) spike that occurred within a small window of time of a detector (postsynaptic) spike caused synaptic strengthening. The change in synaptic conductance was given by the product of an optimized learning rate (0.02) and the value of a vertically offset zero-mean Gaussian (σ = 1.5 ms, unity height) based on the presynaptic-to-postsynaptic timing difference (Fig. 2A). This learning rule was reversed for inhibitory synapses; spikes that occurred within a small time window of the detector spike caused synaptic weakening.
Figure 2.
The network learns synaptic weights through an STDP-based learning rule. A, The learning rule determines how synaptic weights change based on the relative time between presynaptic (chain neuron) and postsynaptic (detector neuron) spikes (x-axis). Closely timed spikes cause excitatory synapse strengthening (green) through long-term potentiation (LTP), whereas less closely timed spikes cause synapse weakening (orange) through long term depression (LTD). The opposite rule occurs for inhibitory synapses. B, The probability of time-to-last spike (scaled to have unity height) given a Poisson input to the chain. C, The vertical offset for the learning rule, which determines the relative levels of potentiation and depression, is set such that the ratio of positive and negative areas under the product of the learning curve (A) and the timing probability (B) is equal to 0.6 to keep learning stable. D, Chain-to-detector synaptic weights (red, excitatory; blue, inhibitory) change as learning progresses for the example site from Figure 1, and the performance of the chain recognition network (E, recording sites in gray lines) plateaus after ∼30 learning iterations.
Because the vertical offset of the Gaussian determined the relative amounts of synaptic strengthening and weakening, a simple rule set the offset value. Assuming chain firing to be Poisson (with firing rate λ given by the chain firing rate during the postsynaptic spike), the probability of time to nearest spike for each chain neuron would be a symmetric exponential distribution with parameter 2λ (Fig. 2B). On each STDP learning iteration, the offset was chosen such that the product between this probability distribution (Fig. 2B) and the offset Gaussian (Fig. 2A) maintained a constant ratio of negative area to positive area (e.g., of depression to potentiation; 0.6 here) (Fig. 2C). Although a static vertical offset would also allow the network to learn, this rate-adapting offset allowed the network to better minimize false alarms while improving correct detections.
During learning, changes in synaptic weights occurred each time the postsynaptic detector neuron fired. To prevent synaptic weights from growing without bound and to stabilize learning, the maximum total (excitatory plus inhibitory) conductance between the chain and each detector was fixed. On each learning iteration, if all conductance had not been used, synaptic conductances were multiplicatively increased (by a factor of 1.1 here). After ∼30 presentations of the spike train to be learned, the synaptic weights stabilized near their 90-presentation final values (Fig. 2D,E). Although this multiplicative increase was not necessary for network functionality, it greatly improved the learning rate.
Auditory recognition using a single trial
For a given recording site, 20 chain detectors (one for each song) were trained using 90 song responses to form chain-to-detector neuron synaptic weights, and the model was tested on recognition of 10 untrained responses to all songs. We used a strict recognition criterion for correct responses: for the duration of a particular song, the correct detector of the song must have fired without any of the incorrect detectors firing. Using this paradigm, three recording sites yielded chain recognition networks that operated with >90% accuracy (average ± SEM, 53.6 ± 4.4%; n = 29). The best recognition network accuracy was 98.3%, achieving 92.4% when trained on only 30 trials (Fig. 2E), because network performance increased the most between 10 and 30 learning iterations. During training, if a static learning vertical offset was used instead of adapting to the chain firing rate, recognition performance decreased on average by 6.8% (σ = 8.3%); if no negative feedback current was used, performance decreased on average by 11.6% (σ = 9.2%). This suggests that the negative current and adaptive threshold assisted learning by preventing mislearning of patterns and by balancing excitation and inhibition.
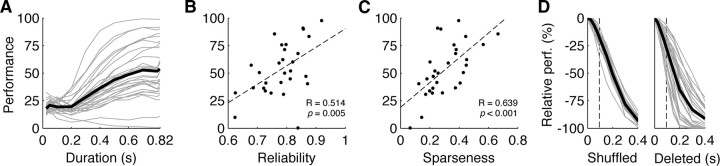
We also examined the relationships between input spike train reliability, sparseness, and performance using the Rcorr and sparseness measures (see Materials and Methods) (Fig. 3B,C). Rcorr gives a quantitative measure of the spike timing precision of the neural input ranging from 0 (unreliable) to 1 (maximally reliable), whereas sparseness gives a measure of how distributed or concentrated in time neural firing is, ranging from 0 (constantly firing, nonsparse) to 1 (rarely firing, very sparse). We found strong correlations between reliability and performance (correlation r = 0.514, p = 0.005) and sparseness and performance (Fig. 2D) (r = 0.639, p < 0.001) but not between performance and firing rate (r = 0.045, p = 0.9) or sparseness and reliability (r = −0.076, p = 0.7). This suggests that the model performs better on more reliable, sparser inputs regardless of firing rate.
Figure 3.
The network performs well for different durations and performs better on more reliable and sparser inputs. A, Model performance (percentage) versus stimulus duration trained (each recording in gray, mean across sites in black). B, C, There was a strong relationship between input spike train reliability and chain recognition model performance (B; r = 0.514, p = 0.005, linear fit in dashed black) and between sparseness and performance (C; r = 0.639, p < 0.001, linear fit in dashed black). D, Normalized model recognition error (y-axis; 0% is baseline performance, −100% is no songs recognized correctly) for each site (in light gray; mean in black) increased with increasing percentage of input spike train corruption, for both shuffling spike times (left) and deleting spikes (right) for different amounts of time (x-axis). The average syllable duration for a zebra finch song (94.5 ms) is shown in dashed black.
We also tested the network by training it on partial spike sequences of shorter duration (25–820 ms). To optimize performance for each duration, we constructed multiple detectors of the appropriate length with different starting times (e.g., for the 400 ms case, constructed detectors trained on input spiking activity from 0–400, 50–450, 100–500 ms, etc. for each song) and selected the detector for each song that had the best detection versus false-alarm performance (e.g., the 50–450 ms detector for song 1, the 200–600 ms detector for song 2, etc.). We then used this optimized network of 20 detectors to recognize songs from the learned partial sequences embedded within the complete 820 ms spike trains, thereby increasing the amount of untrained spiking activity presented and implicitly testing for false-alarm robustness. The best performance recognizing songs based on 400 ms song segments was 88.5% (Fig. 3A), suggesting reliable song recognition for shorter durations despite the presence of additional untrained stimulus.
To quantify the selectivity and error tolerance of the network, we tested performance recognizing spike trains that were systematically corrupted in two ways (see Materials and Methods). For all spike trains in the test set to be recognized, spikes occurring within temporal windows of varying widths were either randomly temporally shuffled (Fig. 3D) or removed entirely (Fig. 3D). The resulting recognition performance was used to calculate the error induced by spike train corruption, which ranged from 0% (same as baseline performance) to −100% (no spike trains recognized correctly). Corruptions by shuffling and deletion of the same duration as the average zebra finch song syllable (94.5 ms or 11.5% of the total duration) (Glaze and Troyer, 2006) caused average errors of 18 and 28%, respectively. This suggests that removing or substituting one song syllable while preserving the absolute timing of other syllables would decrease network recognition performance, with network performance falling off rapidly with increasing spike train corruption.
Spike train replay
This trained network can also be used to play back its learned spike patterns. To trigger replay, the detector neuron received an input current, bringing the cell within 0.01 mV of firing, and an excitatory spiking Poisson input with firing rate equal to twice that of the average firing rate of the sensory input used to train the network. This caused the detector cell to fire with a background rate approximately matched to that of the original sensory input to the circuit. The first chain neuron then received a short burst of spikes (10 spikes at 250 Hz), causing a reliable propagation of activity through the chain that modulated the random firing of the detector neuron. Successive chain neurons modulated this firing according to the synaptic connections formed during learning, which in turn corresponded to temporal activity in the original spike trains, thereby causing the detector neuron to play out the learned spike train in reverse (Fig. 4A).
Figure 4.
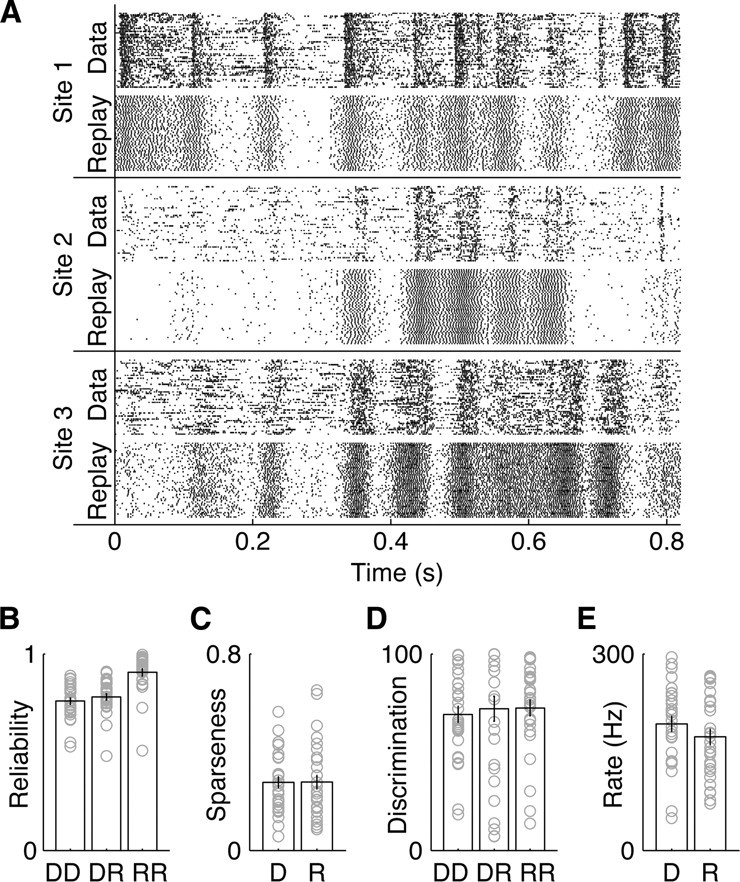
The chain recognition network can faithfully reproduce learned spike trains in reverse. A, Three example sites (at the 75th, 50th, and 25th percentiles of recognition performance of 76, 51, and 36% for sites 1, 2, and 3) with 50 original data rasters (top) and 50 network-based replay rasters (bottom). Replay spike trains come out of the network backward and are have been time reversed here to align with the original data. B–E, The sparseness, reliability, van Rossum-based discrimination performance, and firing rate for DD, DR, and RR comparisons are shown (each unit in light gray, mean plus SE on bars), suggesting that the replay spike trains are similar to the original data.
To quantify how similar these replay spike trains were to the original spike train data, we first used the van Rossum discrimination method. This method uses a spike distance metric (van Rossum, 2001) to determine distances between spike trains, followed by a nearest-neighbor template-matching scheme to classify spike trains (Machens et al., 2003). By varying which spike trains were classified and which templates were used to classify them, for each recording site data (D) and its corresponding reversed replayed spike trains (R), we measured the following: the ability of each sensory neuron to discriminate songs by discriminating data spike trains using data spike train templates (DD); the similarity between the data and replay spike trains by discriminating data using reversed replay templates (DR); and how well the replay spike trains could be used to discriminate songs by discriminating replays using replay templates (RR) (Fig. 4D). We then compared the DD, DR, and RR reliabilities (Fig. 4B). There were no significant differences between the mean DD, DR, and RR discrimination performances or the DD and RR sparseness (Fig. 4C) and firing rates (Fig. 4E), suggesting that the replay spike trains were similar to the original spike trains. However, the RR reliability was significantly greater than DR or DD (p < 0.001). This increase in reliability was likely attributable to the fact that the network learned synaptic weights by effectively averaging noisy spiking responses across trials and uses a highly reliable chain for input activity propagation. Thus, we found that the network would reliably play back the learned spike sequences in reverse using a simple network activation.
Discussion
Model dynamics
The basic architecture of our model builds on a proposal by Tank and Hopfield (1987), using the intuitive idea of “concentrating information” spread over time, effectively transforming temporal information into a distributed spatial representation. However, by avoiding long axonal delay lines that biophysically limit sequence duration, our model can be easily adjusted for duration by varying the number of neurons in the chain. This sequentially activated continuous processing allows the system to compensate for phase alignment by testing all phase relationships between the input and learned patterns. Although the model as proposed here would not correctly recognize inputs that have been stretched or compressed in time, it might be possible to use a hierarchical network to recognize time-warped inputs. Combining a layer of shorter-duration chain detectors to recognize features on short timescales (thereby dealing with local temporal variations) with a more temporally flexible sequence detection circuit (possibly another chain) may enable detection of globally and locally time-warped inputs.
The chain model proposed here shares some similarity to a liquid state machine (LSM) recognition network (Maass et al., 2002) in that it uses a “pool” of neurons to convert temporal spiking patterns into a distributed spatial pattern of neural activity states and performs parallel computations on these states to recognize spiking inputs. However, the LSM and the chain model use different mechanisms for both encoding previous states and reading out patterns from those states (Buonomano and Maass, 2009). In the LSM, a randomly connected pool of neurons implicitly encodes previous states, and readout neurons use linear fitting on those unknown states to achieve desired outputs. In our model, conversely, neural states in the pool (the chain) form a delay line-like structure to explicitly encode previous states, and the readout mechanism (the song detector) training uses a task-specific STDP-based learning paradigm using this organization. This mode of transforming a temporal representation to a spatial one also differentiates our model from a previous model (Jin, 2004), which uses a synaptically coupled chain of neurons to recognize a multiple-input sequence by having the chain gate the propagation of activity based on how multiple sensory input neurons each activate independent chain neurons.
Although previous sound recognition models have used inputs from artificial or natural frontends that signal onsets and offsets (Gollisch, 2008; Gütig and Sompolinsky, 2009) or letter detection events (Tank and Hopfield, 1987), our model operates on real spike trains from an animal model of auditory cortex. This recognition model recognizes learned sounds using representations of those sounds generated by the auditory processing mechanisms of the brain. In addition, this model uses input from only a single sensory neuron to achieve good performance, suggesting that combining across multiple detectors that each used independent sensory neurons as input would yield even higher performance levels. This model also uses a simple spike-timing-dependent plasticity learning rule (Abbott and Nelson, 2000) to teach the chain network the appropriate chain-to-detector weights, suggesting a relatively simple and plausible biological implementation.
Generality and predictions
This model can in principle be trained to recognize any sufficiently reliable sequence of spikes, including those outside the auditory system. In audition or other sensory modalities, the model will better recognize inputs that have higher spike timing precision, reliability, and sparseness. Also, because the model requires a reasonable number of neurons to operate and works with a simple learning scheme, this model could be implemented in hardware for artificial systems use.
In vivo, this model predicts a sequential, temporally sparse activation of a group of neurons in response to sound, reminiscent of the sequential activity observed experimentally in songbird nucleus HVC (formerly known as high vocal center) during singing (Hahnloser et al., 2002) or in rat auditory cortex in vitro (Buonomano, 2003). The recognition mechanism requires that spiking patterns be passed along chain neurons with minimal degradation, which could be achieved in a real system using more robust transmission methods such as bursting propagation (Jin et al., 2007) and might not be required for use in systems with reduced spike timing precision. The particular implementation of the model explored here requires the use of a symmetric learning rule [not unlike that observed in rat barrel cortex (Egger et al., 1999) or hippocampus (Woodin et al., 2003)] and short membrane and synaptic time constants; it is currently unclear whether or not these exist in field L or auditory cortex. Other implementations of this circuit could also make use of longer synaptic and membrane time constants at the cost of timing precision, which might be beneficial for circuit inputs with less precise timing or reliability than field L neurons. In the zebra finch auditory system in particular, this type of network could appear in auditory areas downstream of field L, such as caudal mesopallium. To recognize this type of system, a depolarizing input to the detector unit followed by a set of input spikes to the chain would cause the network to play back the learned sequence in reverse, a phenomenon observed in hippocampus (Foster and Wilson, 2006). This type of spike train playback could be useful in a system, because it could facilitate subsequent learning of subpatterns, memory consolidation during sleep, or recall of spiking activity for other uses.
Footnotes
This work was supported by National Institute on Deafness and Other Communication Disorders Grant 1R01 DC-007610-01A1 and a National Science Foundation Graduate Research Fellowship (awarded to E.L.). Thanks to Larry Abbott and Ralph DiCaprio for helpful suggestions.
References
- Abbott LF, Nelson SB. Synaptic plasticity: taming the beast. Nat Neurosci [Suppl] 2000;3:1178–1183. doi: 10.1038/81453. [DOI] [PubMed] [Google Scholar]
- Amin N, Gill P, Theunissen FE. Role of the zebra finch auditory thalamus in generating complex representations for natural sounds. J Neurophysiol. 2010;104:784–798. doi: 10.1152/jn.00128.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Billimoria CP, Kraus BJ, Narayan R, Maddox RK, Sen K. Invariance and sensitivity to intensity in neural discrimination of natural sounds. J Neurosci. 2008;28:6304–6308. doi: 10.1523/JNEUROSCI.0961-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brette R. Exact simulation of integrate-and-fire models with synaptic conductances. Neural Comput. 2006;18:2004–2027. doi: 10.1162/neco.2006.18.8.2004. [DOI] [PubMed] [Google Scholar]
- Buonomano DV. Timing of neural responses in cortical organotypic slices. Proc Natl Acad Sci U S A. 2003;100:4897–4902. doi: 10.1073/pnas.0736909100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buonomano DV, Maass W. State-dependent computations: spatiotemporal processing in cortical networks. Nat Rev Neurosci. 2009;10:113–125. doi: 10.1038/nrn2558. [DOI] [PubMed] [Google Scholar]
- Dayan P, Abbott LF. Theoretical neuroscience: computational and mathematical modeling of neural systems. Cambridge, MA: Massachusetts Institute of Technology; 2001. [Google Scholar]
- Doupe AJ, Kuhl PK. Birdsong and human speech: common themes and mechanisms. Annu Rev Neurosci. 1999;22:567–631. doi: 10.1146/annurev.neuro.22.1.567. [DOI] [PubMed] [Google Scholar]
- Egger V, Feldmeyer D, Sakmann B. Coincidence detection and changes of synaptic efficacy in spiny stellate neurons in rat barrel cortex. Nat Neurosci. 1999;2:1098–1105. doi: 10.1038/16026. [DOI] [PubMed] [Google Scholar]
- Fitch RH, Miller S, Tallal P. Neurobiology of speech perception. Annu Rev Neurosci. 1997;20:331–353. doi: 10.1146/annurev.neuro.20.1.331. [DOI] [PubMed] [Google Scholar]
- Foster DJ, Wilson MA. Reverse replay of behavioural sequences in hippocampal place cells during the awake state. Nature. 2006;440:680–683. doi: 10.1038/nature04587. [DOI] [PubMed] [Google Scholar]
- Glaze CM, Troyer TW. Temporal structure in zebra finch song: implications for motor coding. J Neurosci. 2006;26:991–1005. doi: 10.1523/JNEUROSCI.3387-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gollisch T. Time-warp invariant pattern detection with bursting neurons. New J Phys. 2008;10 015012. [Google Scholar]
- Grace JA, Amin N, Singh NC, Theunissen FE. Selectivity for conspecific song in the zebra finch auditory forebrain. J Neurophysiol. 2003;89:472–487. doi: 10.1152/jn.00088.2002. [DOI] [PubMed] [Google Scholar]
- Graña GD, Billimoria CP, Sen K. Analyzing variability in neural responses to complex natural sounds in the awake songbird. J Neurophysiol. 2009;101:3147–3157. doi: 10.1152/jn.90917.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gütig R, Sompolinsky H. Time-warp-invariant neuronal processing. PLoS Biol. 2009;7:e1000141. doi: 10.1371/journal.pbio.1000141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahnloser RH, Kozhevnikov AA, Fee MS. An ultra-sparse code underlies the generation of neural sequences in a songbird. Nature. 2002;419:65–70. doi: 10.1038/nature00974. [DOI] [PubMed] [Google Scholar]
- Hefner HE, Heffner RS. Effect of unilateral and bilateral auditory cortex lesions on the discrimination of vocalizations by Japanese macaques. J Neurophysiol. 1986;56:683–701. doi: 10.1152/jn.1986.56.3.683. [DOI] [PubMed] [Google Scholar]
- Jin DZ. Spiking neural network for recognizing spatiotemporal sequences of spikes. Phys Rev E. 2004;69 doi: 10.1103/PhysRevE.69.021905. 021905. [DOI] [PubMed] [Google Scholar]
- Jin DZ, Ramazanoğlu FM, Seung HS. Intrinsic bursting enhances the robustness of a neural network model of sequence generation by avian brain area HVC. J Comput Neurosci. 2007;23:283–299. doi: 10.1007/s10827-007-0032-z. [DOI] [PubMed] [Google Scholar]
- Logothetis NK, Sheinberg DL. Visual object recognition. Annu Rev Neurosci. 1996;19:577–621. doi: 10.1146/annurev.ne.19.030196.003045. [DOI] [PubMed] [Google Scholar]
- Maass W, Natschläger T, Markram H. Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput. 2002;14:2531–2560. doi: 10.1162/089976602760407955. [DOI] [PubMed] [Google Scholar]
- Machens CK, Schütze H, Franz A, Kolesnikova O, Stemmler MB, Ronacher B, Herz AV. Single auditory neurons rapidly discriminate conspecific communication signals. Nat Neurosci. 2003;6:341–342. doi: 10.1038/nn1036. [DOI] [PubMed] [Google Scholar]
- Narayan R, Graña G, Sen K. Distinct time scales in cortical discrimination of natural sounds in songbirds. J Neurophysiol. 2006;96:252–258. doi: 10.1152/jn.01257.2005. [DOI] [PubMed] [Google Scholar]
- Penfield W, Roberts L. Speech and brain mechanisms. Ed 1. Princeton: Princeton UP; 1959. [Google Scholar]
- Rauschecker JP. Auditory cortical plasticity: a comparison with other sensory systems. Trends Neurosci. 1999;22:74–80. doi: 10.1016/s0166-2236(98)01303-4. [DOI] [PubMed] [Google Scholar]
- Riesenhuber M, Poggio T. Models of object recognition. Nat Neurosci [Suppl] 2000;3:1199–1204. doi: 10.1038/81479. [DOI] [PubMed] [Google Scholar]
- Schreiber S, Fellous JM, Whitmer D, Tiesinga P, Sejnowski TJ. A new correlation-based measure of spike timing reliability. Neurocomputing. 2003;52:925–931. doi: 10.1016/S0925-2312(02)00838-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepherd RK, Hartmann R, Heid S, Hardie N, Klinke R. The central auditory system and auditory deprivation: experience with cochlear implants in the congenitally deaf. Acta Otolaryngol Suppl. 1997;532:28–33. doi: 10.3109/00016489709126141. [DOI] [PubMed] [Google Scholar]
- Tank DW, Hopfield JJ. Neural computation by concentrating information in time. Proc Natl Acad Sci U S A. 1987;84:1896–1900. doi: 10.1073/pnas.84.7.1896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theunissen FE, Shaevitz SS. Auditory processing of vocal sounds in birds. Curr Opin Neurobiol. 2006;16:400–407. doi: 10.1016/j.conb.2006.07.003. [DOI] [PubMed] [Google Scholar]
- van Rossum MC. A novel spike distance. Neural Comput. 2001;13:751–763. doi: 10.1162/089976601300014321. [DOI] [PubMed] [Google Scholar]
- Vinje WE, Gallant JL. Sparse coding and decorrelation in primary visual cortex during natural vision. Science. 2000;287:1273–1276. doi: 10.1126/science.287.5456.1273. [DOI] [PubMed] [Google Scholar]
- Wang L, Narayan R, Graña G, Shamir M, Sen K. Cortical discrimination of complex natural stimuli: can single neurons match behavior? J Neurosci. 2007;27:582–589. doi: 10.1523/JNEUROSCI.3699-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Brzozowska-Prechtl A, Karten HJ. Laminar and columnar auditory cortex in avian brain. Proc Natl Acad Sci U S A. 2010;107:12676–12681. doi: 10.1073/pnas.1006645107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodin MA, Ganguly K, Poo MM. Coincident pre- and postsynaptic activity modifies GABAergic synapses by postsynaptic changes in Cl− transporter activity. Neuron. 2003;39:807–820. doi: 10.1016/s0896-6273(03)00507-5. [DOI] [PubMed] [Google Scholar]
- Woolley SM, Casseday JH. Response properties of single neurons in the zebra finch auditory midbrain: response patterns, frequency coding, intensity coding, and spike latencies. J Neurophysiol. 2004;91:136–151. doi: 10.1152/jn.00633.2003. [DOI] [PubMed] [Google Scholar]
- Woolley SM, Gill PR, Fremouw T, Theunissen FE. Functional groups in the avian auditory system. J Neurosci. 2009;29:2780–2793. doi: 10.1523/JNEUROSCI.2042-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]