Abstract
An increasing demand for products such as tissues, proteins, and antibodies from mammalian cell suspension cultures is driving interest in increasing production through high-cell density bioreactors. The centrifugal bioreactor (CCBR) retains cells by balancing settling forces with surface drag forces due to medium throughput and is capable of maintaining cell densities above 108 cells/mL. This article builds on a previous study where the fluid mechanics of an empty CCBR were investigated showing fluid flow is nonuniform and dominated by Coriolis forces, raising concerns about nutrient and cell distribution. In this article, we demonstrate that the previously reported Coriolis forces are still present in the CCBR, but masked by the presence of cells. Experimental dye injection observations during culture of 15 μm hybridoma cells show a continual uniform darkening of the cell bed, indicating the region of the reactor containing cells is well mixed. Simulation results also indicate the cell bed is well mixed during culture of mammalian cells ranging in size from 10 to 20 μm. However, simulations also allow for a slight concentration gradient to be identified and attributed to Coriolis forces. Experimental results show cell density increases from 0.16 to 0.26 when centrifugal force is doubled by increasing RPM from 650 to 920 at a constant inlet velocity of 6.5 cm/s; an effect also observed in the simulation. Results presented in this article indicate cells maintained in the CCBR behave as a high-density fluidized bed of cells providing a homogeneous environment to ensure optimal growth conditions.
Keywords: centrifugal bioreactor, Coriolis force, fluidized bed, high density, mammalian cell
Introduction
The increased demand for complex post-translationally modified proteins for therapeutic and diagnostic purposes has necessitated the use of mammalian hosts.1–4 Industrial methods used for bacterial culture are incapable of meeting production needs exceeding hundreds of kilograms per year when the use of mammalian hosts is necessitated. Slower cellular growth and protein production rates by mammalian cells limits protein production when compared with bacterial cultures. Consequently, two approaches to increase productivity in mammalian cultures are being investigated: increasing specific cellular productivity and increasing volumetric productivity.3,5 The former may be accomplished through modification of the growth environment or cellular genome, whereas volumetric productivity is a direct reflection of maximum bioreactor culture cell density.
The batch culture of hybridoma cells using continuous stirred-tank reactors is limited in density on the order of 106 cells/mL due to cell wash-out at medium flow rates required to sustain optimal growth conditions as cell density increases.6–9 However, density can be increased another order of magnitude to 107 cells/mL if viable cells are separated from spent medium and recycled to the reactor,10 or if a filter device on the reactor effluent is used to prevent cell escape, as is the case with a wave bioreactor-perfusion culture system.5 However, any additional increases in bioreactor cell density require the use of a cell immobilization technique.
Mechanical cell immobilization occurs in packed bed bioreactors (PBRs) and hollow fiber bioreactors (HFBs) with the use of porous packing or membranes, respectively. As a result, cellular densities can reach maximums of 108 cells/mL while cell viability is maintained.11–15 The limitations associated with these bioreactors lie in heterogeneous product formation due to inactive portions of the biomass caused by membrane fouling, mass transport limitations, and non-uniform nutrient and inhibitor gradients.13,16,17
Another bioreactor capable of exceeding cell densities of 108 cells/mL is the continuous centrifugal bioreactor (CCBR). The CCBR used in this manuscript has been described previously18 and is similar to systems studied by Van Wie et al. for yeast and hybridoma culture19 and by Kinetic Biosystems for use in wastewater remediation.20,21 Unique to the CCBR is the method of cell immobilization. In contrast to mechanical immobilization used in PBRs and HFBs, the CCBR immobilizes cells with the use of centrifugal force balanced by opposing buoyant and drag forces during steady-state operation. As medium flows through the reactor chamber at flow rates necessary to sustain high-density cultures, a drag force is imposed on cells which is balanced with centrifugal force resulting from system rotation. Consequently, nutrient and waste transport is by convection, eliminating mass transfer limitations associated with other high-density bioreactors.
Previous work has shown that fluid flows through the CCBR reactor chamber along a circuitous route when cells are not present during reactor operation; a flow profile dominated by Coriolis forces.18 As fluid enters a reactor void of cells, it flows along the leading edge of the rotating reactor as a thin concentrated stream; at the widest cross section, the fluid stream transverses the reactor to the opposite wall in a “Z” shaped pattern before exiting the chamber along the trailing wall of the reactor.18 This flow profile was shown to be unvarying throughout the range of operating conditions used for cell culture raising concerns as to the method of cell retention and nutrient dispersion throughout the reactor chamber.
Obviously, Coriolis forces are present during operation with or without cells, but to what extent is the previously reported flow profile changed by the presence of cells. If the flow profile is unchanged, and the majority of fluid flows up the leading wall of the reactor, it is likely a circulation of cells along previously reported streamlines will result. Alternatively, cells may completely disrupt the nonuniform flow profile creating a uniform flow through the cell bed, emulating particles suspended in a fluidized bed.
This article will examine the fluid flow profile in the CCBR during high-density hybridoma cell culture. Both numerical simulations and experimental observations will be used to determine to what extent the previously reported nonuniform flow profile persists in the presence of cells and if cells and nutrients are sufficiently mixed throughout the reactor chamber to support uniform cell growth. The implications of the resultant flow profile on the culture of various cell types and further uses of the simulation will be discussed.
Theory
The mixture model for laminar flow in COMSOL v3.5 is a macroscopic two-phase flow model which was used to simulate the movement of fluid and cells through the CCBR. The mixture model relies on the following assumptions: the density of each individual phase is constant for both fluid and cells, both phases share the same pressure field, and the relative velocity between the two phases is determined by assuming a balance between pressure, gravity, and viscous drag. The equations defining the system in COMSOL for the momentum of the mixture (Eq. 1), the mixture continuity equation (Eq. 2), and the dispersed phase (cells) transport equation (Eq. 3) are as follows:
| (1) |
| (2) |
| (3) |
where u denotes mixture velocity, ρ is mixture density with subscripts d and c corresponding to the individual phase densities where d denotes the dispersed phase (cells) and c denotes the continuous phase (fluid), Ρ represents pressure, Φd is the volume fraction of the dispersed phase, uslip denotes the relative velocity between the two phases, τ represents the viscous stresses tensor, and F is any additional volume force, i.e., Coriolis forces in the CCBR system. Finally, mdc is the mass transfer rate from the dispersed phase to the continuous phase, which is zero in this instance.
COMSOL’s mixture model calculates mixture properties as weighted averages of the continuous and dispersed phase properties. The mixture velocity is a mass fraction weighted average of the individual velocities, whereas the mixture density is a volume fraction weighted average of the two individual phase densities. Another important parameter to be calculated is the slip velocity which corresponds to the relative velocity between the two phases. The Hadamard-Rybczynski model for solid particles, Eq. 4, is specified in COMSOL and derived from a balance on the viscous drag, pressure, and gravity forces acting on the dispersed phase.
| (4) |
where dd is the particle diameter, Cd is the drag coefficient which for this simulation is taken to be the drag from creeping flow around a sphere, 24/Re. Thus, the slip velocity simplifies to that shown in Eq. 5 in which ηc is the continuous phase viscosity.
| (5) |
Finally, the mixture viscosity must be estimated. The simulation package must account for the increased viscosity and therefore increased viscous drag due to particle–particle interactions at high particle concentrations. The mixture viscosity is estimated using a Krieger type model shown in Eq. 6.
| (6) |
where η mixture viscosity, and Φmax is the maximum packing concentration attainable in the dispersed phase. For randomly packed rigid spheres, the maximum solids concentration is typically about 65%.22 However, because of the deformable nature of a cell membrane, a maximum packing concentration of 0.75 was chosen, as it was found that variations in this parameter from 0.75 to 0.90 did not affect simulation results.
Materials and Methods
Cell line and culture
The cell line used in this research was mouse hybridoma MM1A.23 The MM1A cell line secretes an IgG1 monoclonal antibody specific to the epsilon chain of the CD3 T-cell receptor complex. High-glucose Dulbecco’s Modified Eagle Medium (DMEM) supplemented with 10% Calf Bovine Serum (CBS) (Hyclone, Logan, UT) was used for all cell culture. DMEM was also supplemented with 2 mM l-Glutamine, 100 units/mL penicillin, 100 mg/mL streptomycin, 10 mM HEPES Buffer, and 3 × 10−5 M 2-mercapto-ethanol. All medium ingredients were purchased from Invitrogen (Carlsbad, CA) unless otherwise indicated. Cell counts and viability assays for all cultures were performed using a Trypan Blue Exclusion Assay with a Hemocytometer.
Before inoculating the CCBR, 5 × 108 total cells were cultured using multiple 100- and 150-mm Petri dishes. During this batch culture process, medium and cells from confluent Petri dishes were collected, centrifuged, and counted to determine total cell number and viability. The counted cells were then split into multiple dishes and this process was repeated every 1–2 days until the cell count reached 5 × 108 total cells which were then harvested and suspended in 15 mL of culture medium to be used for CCBR inoculation.
Solution preparation
Phosphate buffered saline (PBS), pH 7.3, was used as the base salt buffer solution in these experiments. The use of PBS allowed cells to remain viable over multiple experiments. A dark blue contrasting solution to the colorless PBS was prepared by the addition of Bromophenol Blue (BPB) to 0.03 mM in PBS, allowing visualization studies of the flow profile to be performed.
Flow profile visualization
The equipment used for this research was a COBE® Spectra™ Apheresis System (Gambro BCT, Lakewood, CO) manufactured for use as a blood separation device. The bioreactor chamber supplied as part of the Cell Purging tubing set (Gambro BCT, Lakewood, CO) was replaced with a similar smooth-walled chamber cut out of a rectangular piece of acrylic. The acrylic block had two threaded bolt holes on either side of the chamber for rotor attachment.
Before reactor inoculation, all fluid lines and the reactor chamber must be filled with fluid. Dyed PBS is supplied from its reservoir to the reactor using pump C in Figure 1, whereas colorless PBS fills all remaining lines and the reactor chamber with the use of pump B. A cell suspension containing 5 × 108 total cells is introduced to the system and evenly dispersed using continuous pumping through the recycle loop without system rotation. Immediately after initiation of system rotation, the three valves shown in Figure 1, E-F-G, are set such that all fluid leaving the reactor is recycled for 10–15 min using colorless liquid pump B. It is necessary to operate at full recycle to give the fluidized cell bed time to establish itself and ensure all cells are retained within the reactor. After the cell bed has been established, fluid exiting the reactor can be sent directly to waste without cell loss, again through manipulation of valves E-F-G.
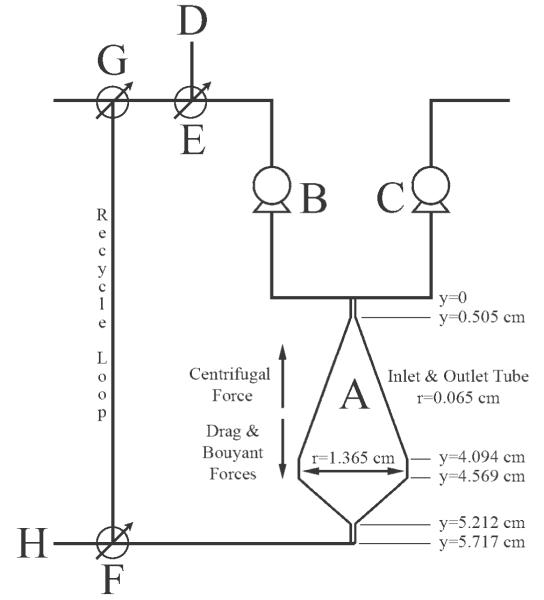
Figure 1. Process flow diagram of the system used to visualize movement of fluid throughout the CCBR (A). Pumps were used to move either undyed PBS (B) or BPB dyed PBS (C) from a reservoir to the reactor. Inoculation line (D) and valve (E) were used to introduce cells into the system, whereas valves (F) and (G) were used to recycle reactor effluent or direct the effluent to waste (H).
During reactor operation, system rotation and fluid movement provided cells with centrifugal force opposed by buoyant and drag forces; when these forces are balanced cells are immobilized in the reactor. Important reactor dimensions needed in numerical simulations are also provided.
To visualize the flow profile pump B, providing colorless PBS, was simultaneously stopped as pump C was started at the same flow rate to provide dyed PBS to the system. Fluid must flow through the reactor chamber at all times to maintain the cell bed in the reactor against the centrifugal force. The flow of dye through the reactor was illuminated using a variable speed strobe light and recorded using a Nikon D-60 Digital SLR camera (Nikon, Melville, NY).
Simulation simplification and setup
The 3D geometry needed for the mathematical simulation was created in COMSOL 3.5 by drawing one half of the 2D projection in the x–y plane and rotating this drawing 360° as has been previously described.18 The dimensions of the reactor chamber used in this work are shown in Figure 1. Only a portion of the inlet and outlet tubes to the reactor are drawn in the simulation as the use of peristaltic pumps supply a constant fluid velocity at the inlet and fluid flow at the outlet is determined by inlet material flux. Therefore, it is unnecessary to simulate all system fluid lines to gain an understanding of the fluid dynamics within the reactor chamber itself.
The COMSOL physics used for this modeling is the Mixture Model for Laminar Flow of multiphase momentum transport which has been outlined in detail in the Theory section. Constants which must be specified in this model include the density and viscosity of the continuous phase which are 992 kg/m3 and 6.123 × 10−4 Pa s, respectively, assuming negligible difference between such values for liquid water and PBS at 37°C. Additionally, hybridoma cell density, diameter, and maximum packing volume fraction were specified for the dispersed phase as 1075 kg/m3,24 15 μm,25 and 0.75, respectively.
Additional volume forces acting on the system must also be specified, these include the Coriolis forces and centrifugal force. Solving the Navier-Stokes Equation in a rotating frame of reference necessitates the inclusion of body forces Fx = −2Ωρuy and Fy = 2Ωρux, where Fx and Fy are the Coriolis forces in the x and y directions, Ω is the angular velocity, ρ is the mixture density and ux and uy are the individual components of velocity in their respective directions. Because of the design of the reactor, the centrifugal force is not constant throughout the reactor chamber and decreases linearly from the inlet to the outlet. Centrifugal force Fc = Ω2(D–y) is incorporated as a gravity term, where Fc is the centrifugal force, D is a constant 13.14 cm representing distance from the center of rotation to the reactor inlet, and y is the positive distance from the reactor inlet to any point in the reactor.
Model set-up is completed by defining boundary conditions throughout the system for both the continuous and dispersed phases. The outlet boundary condition is defined at the end of the simulated exit fluid line. For the continuous phase, a pressure of zero is defined at the outlet boundary such that fluid outflow is determined by the specified influx of material, a condition which is particularly useful when fluid flow leaving the system may not be normal to the boundary. The boundary condition for the dispersed phase at the reactor outlet was defined as the dispersed phase outlet allowing solids to cross the boundary. Therefore, to maintain a steady-state concentration of cells throughout the simulation, the flux across the outlet boundary is defined using an integration coupling boundary variable, which is then specified as the inlet flux boundary condition for the dispersed phase. The continuous phase boundary condition at the inlet consists of a specified fluid velocity.
All other boundaries in the system were defined as no slip wall conditions for the continuous phase and Insulation/Symmetry for the dispersed phase prohibiting cells or fluid from crossing solid boundaries. All simulations were solved with a mesh similar to that described previously in the manuscript discussing flow through the CCBR without cells;18 however, for the current simulation, 100,722 nodes are evenly distributed throughout the system as opposed to 86,037 nodes for the simulation without cells.
Results and Discussion
Formation of the fluidized bed of cells
The development of a fluidized bed of cells can be observed in the experimental CCBR as rotation is increased from 0 to 650 RPM as follows: initially, through continual pumping at an inlet fluid velocity of 6.5 cm/s without system rotation, the 5 × 108 total cells inoculated into the system become evenly dispersed throughout the recycle loop and reactor chamber. Immediately following initiation of rotation, an evenly dispersed low-density cell suspension is observed throughout the reactor chamber, shown in Figure 2A. As rotation reaches steady state, 650 RPM, the settling velocity of the cells is enhanced and the initial formation of a fluidized bed of cells is observed as the opaque white region in the lower portion of the reactor chamber, Figure 2B. The top third of the reactor in Figure 2B still contains some cells which have not yet settled into the fluidized bed as evidenced by the diffuse opaque region. However, operation at a constant rotation rate of 650 RPM for 10 min allows all cells in the recycle loop to circulate into the reactor and form a stable cell bed separated from the rest of the reactor by a sharp interface between the clear fluid and cell bed, Figure 3A.
Figure 2. The progressive development of a fluidized bed of cells beginning with 5 × 3 108 cells/mL evenly distributed throughout the reactor chamber and recycle loop (A).

Cells begin to settle into the opaque cell bed in the lower half of the chamber (B) due to the balanced centrifugal and drag forces from CCBR operation at 650 RPM and an inlet velocity of 6.5 cm/s. At steady state, the region above the cell bed will become clear as all cells will be retained in a well-defined fluidized bed of cells.
Figure 3. Steady-state operation of the CCBR at a constant inlet velocity of 6.5 cm/s at a RPM of 650 (A) and 920 (B).

The centrifugal and drag forces are at a balanced equilibrium (A) resulting in a cell bed volume of 5.5 mL and a cell density of 9.1 × 107 cells/mL. Increasing the RPM to 920 (B) doubles the centrifugal force, requiring a new equilibrium between the centrifugal and drag forces to be reached. As a result the cell bed volume is decreased to 3.4 mL and density is increased to 1.5 × 108 cells/mL.
During steady-state operation, the centrifugal force is balanced against opposing drag and buoyant forces resulting in an equilibrium cell bed volume less than the total volume of the reactor chamber, 11.4 mL. It is important to keep in mind that the centrifugal force is not constant throughout the reactor due to the chamber’s placement in the rotating plane resulting in a linear decrease in centrifugal force from the reactor’s inlet to the outlet. The linear decrease in centrifugal acceleration is compensated by drag force which also decreases linearly from the reactor inlet to the outlet based on the conical design of the chamber. A further in-depth analysis of the design equations governing counterflow centrifugation has been presented by Sanderson and Bird.26 At 650 RPM, the centrifugal acceleration is 613 m/s2 at the inlet and 367 m/s2 at the outlet. It is important to note that the force associated with centrifugal acceleration must be offset by the combination of buoyant and drag forces acting in the opposite direction if a cell bed is to be maintained.
The cell bed is affected by changes in the equilibrium balance of centrifugal force and drag force. This is observed as a decrease in cell bed volume as centrifugal force is doubled, RPM is increased from 650 to 920 RPM, the inlet velocity remains constant at 6.5 cm/s. At 650 RPM, Figure 3A, the top of the cell bed is 3.54 cm above the reactor inlet resulting in a cell bed volume of 5.5 mL; an average value of the cell bed height is estimated from the observation of still images recorded over multiple experiments. Doubling the centrifugal force, Figure 3B, decreases the cell bed height and volume to 2.96 cm and 3.4 mL, respectively. Assuming a cell diameter of 15 μm and all 5 × 108 cells are evenly dispersed throughout the cell bed, at 650 RPM a density of 9.1 × 107 cells/mL and a cell volume fraction of 0.16 results. At 920 RPM, cell density increases to 1.5 × 108 cells/mL and the cell volume fraction increases to 0.26. Similar behavior is observed for variations in inlet fluid velocity at constant RPM, results not shown; however, fluid velocity and the effect on cell density is an inversely proportional relationship.
Experimental visualization results
Previous work has shown that, without cells, fluid moves through the CCBR along streamlines following a circuitous path from the reactor inlet to the outlet during steady-state operation.18 The majority of flow is along the leading wall of the reactor until crossing to the opposite wall along a “Z” shaped path at the reactor widest cross section.18 This flow pattern is dominated by Coriolis forces, and analysis of the Rossby number shows Coriolis forces are no less important when cells are maintained in the CCBR.
An indication the effect Coriolis forces will have on a system can be estimated through evaluation of the Rossby number, defined as U/LΩ; where U is the fluid velocity representative of the system, L is a unit length, and Ω is the angular velocity.27 The Rossby number is a ratio of the inertial forces to Coriolis forces; a value much less than one indicates Coriolis forces contribute significantly to momentum transport, whereas the opposite is true for Rossby numbers much greater than unity. At the widest cross section of the reactor, 2.73 cm, a velocity of 1.4 × 10−2 cm/s results assuming uniform flow at an inlet flow rate of 5.4 mL/min. Using this velocity and diameter, the Rossby number is 7 × 10−5 at 650 RPM, assuming no cells are present. Inclusion of cells in this analysis only minimally increases fluid velocity at a cell volume fraction of 0.16, consequently increasing the Rossby number to 9 × 10−5, clearly indicating the significant role of Coriolis forces in momentum transport during cell culture in the CCBR.
For the previously reported flow profile to remain unchanged during cell culture, the cells would have to circulate along previously reported streamlines. Cells would have to be carried up the leading wall of the reactor along streamlines to the widest cross section where they would begin to move across the reactor to the opposite wall. As cells traverse, the reactor flow is no longer opposite the centrifugal force and cells would begin to settle toward the inlet where they would once again become entrained in the incoming fluid flowing along the leading wall of the reactor, thus creating a constant circulation of cells. However, this scenario seems unlikely as Figure 3 shows the cell bed volume decreases as RPM is increased. Previous work showed no effect on the fluid flow profile when RPM is increased from 650 to 920.18 Therefore, if cells were circulating along streamlines which remain unchanged at normal cell culture operating conditions, the cell bed volume could not be dependent on RPM as is shown in Figure 3; consequently, it is unlikely that cell retention is due to circulation along previously reported streamlines.
It is more likely that cells disrupt the flow profile in the CCBR resulting in a uniform flow of medium which suspends cells against the centrifugal force, much in the same manner as particles are suspended in a traditional fluidized bed. Bed expansion at fluid velocities greater than the minimum fluidization velocity is a distinct characteristic of fluidized beds and is observed in the CCBR. Compression of the cell bed as RPM is increased, as shown in Figure 3, is analogous to what happens as fluid velocity is decreased in a traditional fluidized bed. The dependence of bed volume on reactor settings supports the characterization of cells retained in the CCBR as behaving like a fluidized bed of cells which are suspended against the centrifugal force by a uniform flow through the cell bed.
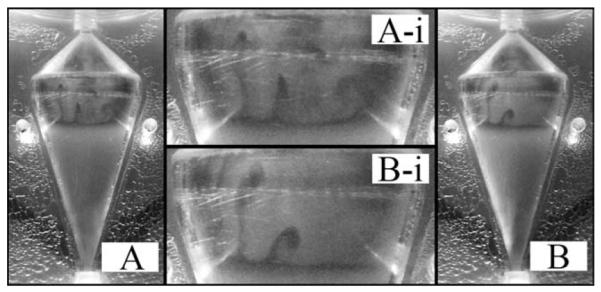
Observations of selected time points during dye injection experiments shown in Figure 4 also suggest a uniform flow of fluid through the cell bed. Before any dye has been injected, Figure 4A, the cell bed again appears as the opaque region in the bottom portion of the reactor. The darker shaded region near the inlet, indicated with an arrow in Figure 4A, is not carryover dye from a previous experiment present at time zero, but instead is a small population of dead cells retained in the cell bed. The cell membranes of dead cells become permeable to the BPB dye and have been permanently dyed during previous experiments which results in this observed shaded region. The dead cells are retained near the inlet as the volume of a cell decreases upon death ultimately resulting in an increase in cell density and thus their retention closer to the inlet. Additionally, it may appear as if the population of dead cells is preferentially retained along the right side of the reactor in Figure 4A, this is not observed during experimentation, but is a result of the strobe light reflecting off the reactor surface giving the impression of a lighter shaded region where dead cells are not retained near the inlet.
Figure 4. Before any dye injection (A) the steady-state result at 650 RPM and an inlet velocity of 6.5 cm/s shows a sharp interface between the opaque cell bed and the cell free clear fluid above.

The darkened region indicated with the arrow (A) is not the presence of a dye gradient, but is a population of dead cells dyed with BPB. The cell bed continually darkens as BPB is supplied to the system, observed at 40 s (B) and 80 s (C) after dye injection begins. Uniform darkening of the cell bed indicates cells are retained in a region which is well mixed.
As dye begins to enter the reactor, the cell bed continuously darkens uniformly as shown at 40 s, Figure 4B, and 80 s, Figure 4C. At 40 s, dye can be seen directly on top of the cell bed and along the left wall, whereas the entire region above the cell bed appears dyed at 80 s. The continual uniform darkening of the entire cell bed and the absence of any observable gradient of dye suggest the cell bed is well mixed which results in even distribution of dye throughout. These observations provide strong evidence and support the premise that a well mixed region of cells disrupts any stable nonuniform flow profile that was observed in the absence of cells, and more importantly flow around each cell provides the necessary drag force resulting in their suspension against the increased settling force.
Macroscopic Rayleigh-Taylor instabilities
An unexpected observation from this work is the putative formation of Rayleigh-Taylor (RT) instabilities at the top interface of the cell bed, as shown in Figure 5. In general, macroscopic RT instabilities result from the perturbation of an unstable system in which surface tension may be neglected, an interface separates two fluids of differing densities, and the more dense fluid is nonuniformly accelerated into a less dense fluid.28–31 This phenomenon has been extensively studied primarily due to its implications in stellar and planetary interiors as well as other applications including geophysical fluid dynamics.
Figure 5. Observed at the interface separating the top of the cell bed from the PBS above is the presence of Rayleigh-Taylor (RT) instabilities.
RT instabilities result from the nonuniform acceleration of a more dense fluid into a less dense fluid, when the two fluids are separated by a sharp interface. Previous results have shown the addition of BPB to a dilute salt solution decreases solution density. Therefore, the observed RT instabilities are an artifact of the dye injection procedure used to visualize the flow profile and would not be present during cell culture with a homogeneous culture medium.
Necessary in the formation of RT instabilities is the presence of a sharp interface separating two fluids of differing densities. In this case, the interface at the top of the cell bed serves this purpose. As previously reported the addition of BPB to a dilute salt solution resulted in a small decrease in fluid density which is exaggerated during high gravity operation of the CCBR.18 Consequently, the BPB colored PBS is less dense than the original colorless PBS. As BPB dyed solution is supplied to the reactor, it becomes evenly dispersed throughout the well-mixed cell bed, and eventually reaches the top of the cell bed forming a thin layer of dye, as can be observed in Figure 5. The enhanced gravity in the CCBR accelerates the more dense colorless PBS into the less dense layer of BPB dyed PBS leading to the formation of RT fingers extending from the upper cell bed interface toward the outlet as shown in Figure 5.
Numerical simulation
It has previously been shown that the fluid flow profile observed experimentally without the presence of cells can be numerically simulated in COMSOL showing a flow pattern dominated by Coriolis forces.18 Experimental results discussed throughout this manuscript have indicated the fluid flow profile dramatically changes in the presence of cells. The results of numerically simulating the experimentally observed fluidized bed of cells will be shown, discussing the similarities and differences when compared with experimentally observed fluid dynamic characteristics.
To complete the fluid dynamic simulation of the CCBR during cell culture, a steady-state simulation was solved using a transient approach in COMSOL; a transient simulation was able to represent steady state when simulation solutions no longer changed with time. First, an initial cell volume fraction of 0.07 was specified throughout the reactor chamber corresponding to 5 × 108 total cells. Then, rotor speed and inlet fluid velocity were ramped up individually from zero to steady state values of 650 and 6.5 cm/s over 10 simulation seconds beginning 5 and 8 s into the simulation, respectively. After 50 simulation seconds, the cell volume fraction no longer changed and a steady-state solution was reached for a specified set of operating conditions.
Numerical and experimental steady-state results show comparable cell volume fractions throughout the reactor in Figure 6 at varying magnitudes of centrifugal force corresponding to 650 and 920 RPM; all results have a constant inlet fluid velocity of 6.5 cm/s. The simulated results indicate cell volume fraction along the reactor midline, and at both RPMs, no cells are retained in the inlet tube of the reactor. At 650 RPM, the maximum simulated cell volume fraction is 0.15 which is maintained for 2.5 cm through the reactor before gradually decreasing back to zero. As cell volume fraction is a function of centrifugal force, which varies with the square of RPM, at constant inlet velocity, the cell volume fraction increases to 0.22 and is maintained for a distance of 2.5 cm as centrifugal force is doubled at 920 RPM. Experimental cell volume fractions are also shown in Figure 6 and calculated from recorded still images, see section “Formation of the fluidized bed of cells,” and correspond to 0.16 and 0.26 at 650 and 920 RPM, respectively.
Figure 6. Cell volume fractions at various RPM and a constant inlet velocity of 6.5 cm/s are shown.
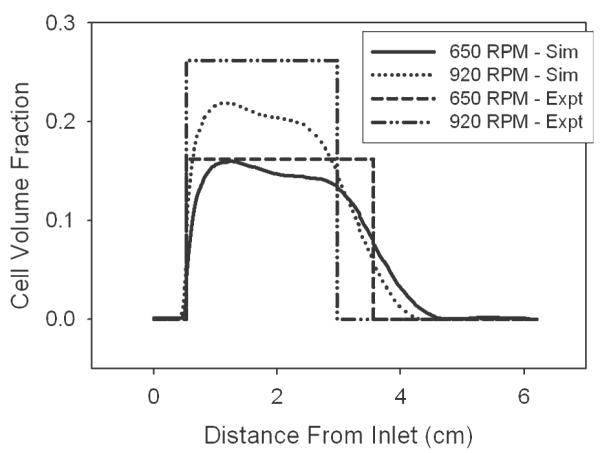
Experimental cell volume fractions of 0.16 and 0.26 at 650 and 920 RPM were determined assuming a cell bed of uniform density and a volume calculated from still photographs. Simulation results along the reactor centerline indicate similar maximum cell volume fractions of 0.15 and 0.22 for RPMs of 650 and 920, respectively. The diffuse interface at the top of the cell bed in numerical results can be attributed to artificial diffusion, while a constant maximum cell volume fraction is not predicted in simulations due to the accumulation of cells along the right wall of the reactor.
There are two apparent differences observed in Figure 6 when comparing experimental and simulation results; particularly the absence of a sharp interface at the top of the cell bed and a slightly lower maximum cell volume fraction observed in the simulation, the former contributing to the latter. The absence of a sharp interface at the top of the cell bed is a notable difference between simulation and experimental results. Contributing to the gradient in cell volume fraction observed at the interface is the necessary inclusion of artificial diffusion for COMSOL to reach a converged solution. The concept of artificial diffusion required for both the momentum and dispersed phase transport equations is the same as that which has been previously described.18 Briefly, artificial diffusion within COMSOL stabilizes an equation set by adding a term to the physical diffusion constant of a particular equation. The addition of artificial diffusion is locally dependant on the mesh size and convective velocity, resulting in the nonuniform incorporation of artificial diffusion only when necessary for solution convergence, typically near steep gradients or sharp interfaces.
Anisotropic streamline diffusion stabilizes the momentum and dispersed phase transport equations through its addition only in the directions of flow (direction of the streamline), whereas isotropic artificial diffusion adds necessary additional stabilization to the dispersed phase transport equation through a general increase of the overall magnitude of diffusion. The term added when using anisotropic diffusion is shown in Eq. 7, whereas the term for isotropic diffusion is shown in Eq. 8.
| (7) |
| (8) |
The tuning parameter, δ, is set at 0.25 in all cases, but isotropic diffusion requires an additional tuning parameter input, the scale factor which is set to 0.01 in this simulation. The mesh element size is defined as h,and β is the convective velocity vector, whereas βi and βj are individual components of the convective velocity tensor ensuring artificial diffusion is only added in the direction of flow. Because of computer memory limitations, further increases in mesh density which would theoretically eliminate artificial diffusion and allow the simulation of a sharp interface are not possible at this time.
The inability of the simulation to produce a sharp interface negates the possibility of simulating the presence of RT instabilities, as a sharp interface is necessary for their formation. However, the inability to simulate RT instabilities is of little significance to the overall validity of the simulation because the instabilities are an artifact of the differing density solutions used to visualize flow through the cell bed. During typical cell culture, DMEM growth medium with a homogeneous density will be supplied to the reactor eliminating the possibility of RT instability formation.
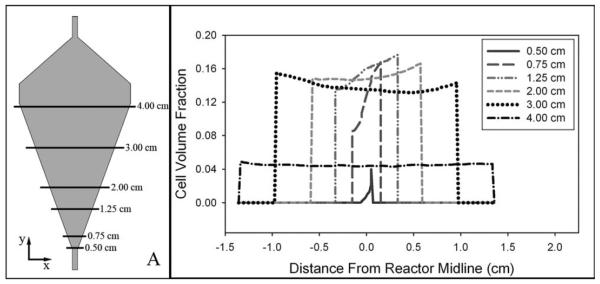
The second obvious difference between simulation and experimental results is that the simulation, Figure 6, does not predict a constant cell volume fraction throughout the cell bed and the maximum value is slightly less than experimental observations. Two peaks in cell volume fraction are observed along the reactor midline for a single RPM, where a region of increased concentration is closest to the reactor inlet. The region of increased cell concentration is in actuality localized to the right wall of the reactor near the inlet which is revealed in Figure 7. The x–y plane at z = 0 corresponds to the gray shaded region in Figure 7A, and the cell volume fraction along each horizontal line at different distances from the inlet is shown in Figure 7B. A region of increased cell concentration along the right wall is shown by cell volume fraction increasing across a reactor cross section and reaching a maximum at the reactor wall, this trend is observed at distance less than 2.00 cm from the inlet. However, at distances greater than 2.00 cm, a constant cell volume fraction across a reactor cross section is predicted, Figure 7B.
Figure 7. An increasing density of cells across a reactor cross section reaching a maximum at the right reactor wall indicates a region of increased cell concentration.
The gray shaded area in panel (A) corresponds to the x–y plane at z = 0 and the volume fraction along each horizontal line is shown in panel (B). Accumulation of cells along the right-side wall of the reactor suggests a preferential flow along the opposite wall. The left wall of the reactor is the same wall along which the majority of fluid flow is observed during CCBR operation in the absence of cells.
It seems likely cells would concentrate in this region along the right wall of the reactor near the inlet based on the fluid flow profile observed in the CCBR without cells, which showed little flow in the same region. Although the results presented in this manuscript have indicated a radically different flow profile in the presence of cells Coriolis forces are no less important and still play a significant role in the fluid mechanics of the system, as evidenced through the previous discussion of the Rossby number. This is shown by a small increase in cell concentration along the right-side wall of the reactor, Figure 7B, due to Coriolis forces causing preferential flow along the opposite wall, similar to that observed without cells.
According to the Taylor-Proudman theorem, the results shown in Figure 7 for a single plane perpendicular to the axis of rotation can be assumed to correspond to all other planes along the axis of rotation. The Taylor-Proudman theorem states that for very small values of the Rossby number, the derivatives of velocity in the axial direction become small, and thus particle velocity becomes 2D in the plane perpendicular to the axis of rotation.18,27,32,33 Thus, the cell volume fractions shown in Figure 7 at various points in a singular plane perpendicular to the axis of rotation depict the concentration profiles in all other planes along the axis of rotation. This is in fact the trend observed in simulation results with the only deviation being small increases at reactor walls, ±0.03 differences in cell volume fraction, due to the no-slip boundary condition for the continuous phase, numerical data not shown.
The concentration of cells along the right wall of the reactor is a trend only observed in simulation results as small differences in cell concentration can not be discerned in experimental results. Observations such as these show the usefulness of the simulation. Not only can the simulation predict the most significant characteristics of the fluidized bed of cells with reasonable accuracy, but smaller less obvious nuances can also be identified with the use of a simulation like that presented in this manuscript.
Implications for CCBR bioprocessing
The most obvious implications this work has for bioprocessing is in understanding how different cell types are retained and distributed throughout the CCBR during long term culture. The numerical simulation has closely approximated cell volume fraction and bed height throughout the CCBR for 15 μm diameter cells, at different operating conditions. CCBR cell culture hinges on balancing the opposing centrifugal and drag forces, both of which are highly dependent on cell size. Therefore, different size cell types will behave differently in the CCBR, and understanding the effect of cell size is critical to successful cultures.
Different applications of the CCBR other than high-density hybridoma culture require various cells types to be retained in the reactor. For instance some cells, white blood cells or bacteria, have much smaller diameters of 10 μm or 2 μm, respectively.21 Larger mammalian cells or particles on the order of 20 μm could also possibly be cultured in the CCBR. Simulation results along the centerline of the CCBR at constant operating conditions of 650 RPM and 6.5 cm/s for various cell sizes are shown in Figure 8. As cell size is decreased from 20 μm, the simulation predicts the maximum cell volume fraction will decrease while dispersion throughout the reactor chamber increases and becomes more uniform, ultimately limiting cell retention.
Figure 8. At constant reactor settings of 650 RPM and an inlet velocity of 6.5 cm/s, the effect of cell size on cell volume fraction distribution throughout the reactor is shown for 5 × 3 108 total cells.
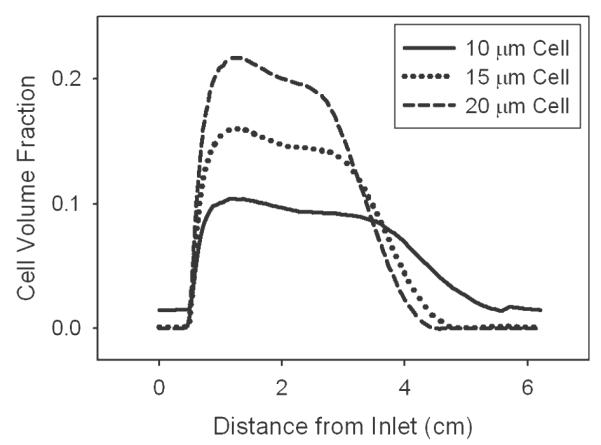
As the diameter of a cell is decreased from 20 μm to 10 μm, the maximum cell volume fraction decreases from 0.22 to 0.10 while cells become more dispersed throughout the entire reactor making cell retention difficult. These effects are due to the fact that as cell size is decreased the magnitude of the settling force decreases faster than the drag force indicating reactor settings must be carefully tuned for each cell type and desired culture density.
An analysis of the effect of cell size on centrifugal, drag and buoyant forces provides insight into the results shown in Figure 8. For example, decreased cell size results in decreased drag, buoyancy, and centrifugal forces; however, from Figure 8, it is clear the reduction in these forces is not at the same rate. If all forces changed at the same rate, the cell volume faction and bed height would remain constant as cell diameter changed. These forces decreasing at different rates are to be expected as drag force depends on cross-sectional area (d2) while the buoyancy and gravitational forces are volume dependent (d3). To illustrate this point, decreasing diameter from 15 μm to 10 μm results in a reduction in the magnitude of the drag force by about 55%, whereas the settling force which accounts for both the centrifugal and buoyant force is reduced by 70%. This analysis clearly shows each individual cell culture will require a unique set of operating conditions which can be estimated using this simulation and then fine tuned experimentally to reach desired densities and cell retention producing efficient long-term cultures.
Although not directly incorporated into the simulation presented in this manuscript, a description of cellular growth rate and its dependence on substrate and inhibitor concentrations would be a valuable addition to the modeling effort. A kinetic model describing the dependence of the MM1A hybridoma cell line growth rate on glucose, ammonium ion, and lactate concentrations has been reported.34 Future incorporation of a similar model into COMSOL Multiphysics would allow for substrate and metabolite concentrations and how they affect cell volume fraction to be investigated and further understood. Future work to understand how inlet fluid velocity affects cell viability would be beneficial as it will provide insight on the impact of drag and associated shear forces on necrosis, apoptosis, and production rates of secreted products.
Concluding Remarks
The inclusion of cells, or other similar particulates, in the fluid dynamic analysis of the CCBR has significant consequences on the observed fluid flow profile. Without cells, flow through the CCBR is dominated by Coriolis forces, where upon entering the reactor chamber fluid is forced to flow along the leading wall of the reactor. This characteristic flow profile remains unchanged at all typical cell culture operating conditions. However, results presented in this manuscript show the flow profile is radically changed in the presence of cells, ultimately allowing for the possibility of cells to be retained in the CCBR during culture.
Both experimental observations and numerical results show cell volume fraction is highly dependent on reactor settings, specifically RPM and inlet velocity. Experimental results have shown that doubling the centrifugal force while inlet velocity remains unchanged can increase the cell volume fraction from 0.16 at 650 RPM to 0.26 at 920 RPM. The simulation predicts similar behavior with small deviations in the maximum cell volume fraction at each RPM, 0.15 and 0.22 for 650 and 920 RPM, respectively.
Furthermore, dye injection experiments show a continually darkening cell bed without the presence of any observable dye gradients, indicating the region of the reactor containing cells is well mixed throughout. Therefore, a uniform flow of fluid through the cell bed results in the suspension of cells against the enhanced settling force of the CCBR. Simulation results also indicate a well-mixed fluidized bed of cells, but allow for further in-depth investigations into less obvious results such as the small increased concentration of cells along the right wall of the reactor due to the persistent effect of Coriolis forces. These results and those showing that the cell bed volume is coupled to operating conditions lead to the conclusion that the cell bed behaves similarly to a well-mixed fluidized bed of cells, ultimately disrupting the previously reported flow profile.
Finally, analyses throughout this manuscript were performed using a general hybridoma cell size of 15 μm. However, the versatility of the CCBR lies in that both the centrifugal and drag force are individually tunable allowing various cells types with different cell sizes to be cultured. An analysis of cell size typical of mammalian cells, and volume fraction distribution for a uniform set of reactor conditions has shown that as cell size decreases the maximum cell volume fraction also decreases. At the same time cell retention is limited due to an increasingly even dispersion of cells throughout the entire reactor chamber at smaller cell diameters.
An understanding that mammalian cells retained in the reactor behave as a well-mixed fluidized bed whose porosity is dependent not only on reactor settings but also cell size greatly increases the understanding of CCBR fluid dynamics. The ability to generally determine necessary reactor settings using numerical simulations is a valuable tool ensuring the successful long-term culture of various cell types, increasing the number of foreseeable applications of CCBR culture.
Acknowledgments
The authors like to acknowledge the Biotechnology Training Grant (NIH 5T32-GM008336-16) and the Gene & Linda Voiland School of Chemical Engineering and Bioengineering for graduate student support and supplies. Equipment in the form of the COBE© Spectra Apheresis System and Cell Purging tubing sets in addition to corporate technical research staff consultation are a result of a donation by Gambro BCT Inc., Lakewood, CO. Mr. R. Hutchinson of the Washington State University College of Engineering and Architecture Machine Shop was instrumental in design and fabrication of the CCBR chambers used in these experiments.
Literature Cited
- 1.Landry Y, Gies JP. Drugs and their molecular targets: an updated overview. Fundam Clin Pharmacol. 2008;22:1–18. doi: 10.1111/j.1472-8206.2007.00548.x. [DOI] [PubMed] [Google Scholar]
- 2.Migliore C, Giordano S. Molecular cancer therapy: can our expectation be MET? Eur J Cancer. 2008;44:641–651. doi: 10.1016/j.ejca.2008.01.022. [DOI] [PubMed] [Google Scholar]
- 3.Kundu PK, Prasad NS, Electricwala SE, Varma R, Datta D. Getting higher yields of monoclonal antibody in culture. Indian J Physiol Pharmacol. 1998;42:155–171. [PubMed] [Google Scholar]
- 4.Werner RG. Economic aspects of commercial manufacture of biopharmaceuticals. J Biotechnol. 2004;113:171–182. doi: 10.1016/j.jbiotec.2004.04.036. [DOI] [PubMed] [Google Scholar]
- 5.Tang YJ, Ohashi R, Hamel JF. Perfusion culture of hybridoma cells for hyperproduction of IgG(2a) monoclonal antibody in a wave bioreactor-perfusion culture system. Biotechnol Prog. 2007;23:255–264. doi: 10.1021/bp060299a. [DOI] [PubMed] [Google Scholar]
- 6.Jan DCH, Petch DA, Huzel N, Butler M. The effect of dissolved oxygen on the metabolic profile of a murine hybridoma grown in serum-free medium in continuous culture. Biotechnol Bioeng. 1997;54:153–164. doi: 10.1002/(SICI)1097-0290(19970420)54:2<153::AID-BIT7>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 7.Kim BJ, Chang HN, Oh DJ. Application of a cell-once-through perfusion strategy for production of recombinant antibody from rCHO cells in a Centritech Lab II centrifuge system. Biotechnol Prog. 2007;23:1186–1197. doi: 10.1021/bp0700861. [DOI] [PubMed] [Google Scholar]
- 8.Miller WM, Blanch HW, Wilke CR. A kinetic analysis of hybridoma growth and metabolism in batch and continuous suspension culture: effect of nutrient concentration, dilution rate, and pH. Reprinted from Biotechnology and Bioengineering, Vol. 32, Pp 947-965 (1988) Biotechnol Bioeng. 2000;67:853–871. [PubMed] [Google Scholar]
- 9.Xie L, Wang DIC. High cell density and high monoclonal antibody production through medium design and rational control in a bioreactor. Biotechnol Bioeng. 1996;51:725–729. doi: 10.1002/(SICI)1097-0290(19960920)51:6<725::AID-BIT12>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- 10.Batt BC, Davis RH, Kompala DS. Inclined sedimentation for selective retention of viable hybridomas in a continuous suspension bioreactor. Biotechnol Prog. 1990;6:458–464. doi: 10.1021/bp00006a600. [DOI] [PubMed] [Google Scholar]
- 11.Golmakany N, Rasaee MJ, Furouzandeh M, Shojaosadati SA, Kashanian S, Omidfar K. Continuous production of monoclonal antibody in a packed-bed bioreactor. Biotechnol Appl Biochem. 2005;41:273–278. doi: 10.1042/BA20040121. [DOI] [PubMed] [Google Scholar]
- 12.Gramer MJ, Poeschl DM. Screening tool for hollow-fiber bioreactor process development. Biotechnol Prog. 1998;14:203–209. doi: 10.1021/bp9800081. [DOI] [PubMed] [Google Scholar]
- 13.Jackson LR, Trudel LJ, Fox JG, Lipman NS. Evaluation of hollow fiber bioreactors as an alternative to murine ascites production for small scale monoclonal antibody production. J Immunol Methods. 1996;189:217–231. doi: 10.1016/0022-1759(95)00251-0. [DOI] [PubMed] [Google Scholar]
- 14.Yang S-T, Luo J, Chen C. A fibrous-bed bioreactor for continuous production of monoclonal antibody by hybridoma. Adv Biochem Eng Biotechnol. 2004;87:61–96. doi: 10.1007/b94364. [DOI] [PubMed] [Google Scholar]
- 15.Nilsang S, Nehru V, Plieva FM, Nandakumar KS, Rakshit SK, Holmdahl R, Mattiasson B, Kumar A. Three-dimensional culture for monoclonal antibody production by hybridoma cells immobilized in macroporous gel particles. Biotechnol Prog. 2008;24:1122–1131. doi: 10.1002/btpr.28. [DOI] [PubMed] [Google Scholar]
- 16.Yang P, Teo W-K, Ting Y-P. Design and performance study of a novel immobilized hollow fiber membrane bioreactor. Bioresour Technol. 2006;97:39–46. doi: 10.1016/j.biortech.2005.02.029. [DOI] [PubMed] [Google Scholar]
- 17.Hay PD, Veitch AR, Gaylor JD. Oxygen transfer in a convection-enhanced hollow fiber bioartificial liver. Artif Organs. 2001;25:119–130. doi: 10.1046/j.1525-1594.2001.025002119.x. [DOI] [PubMed] [Google Scholar]
- 18.Detzel CJ, Thorson MR, Van Wie BJ, Ivory CF. A study of the Coriolis effect on the fluid flow profile in a centrifugal bioreactor. Biotechnol Prog. 2009;25:1025–1034. doi: 10.1002/btpr.183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Van Wie BJ, Brouns TM, Elliott ML, Davis WC. A novel continuous centrifugal bioreactor for high-density cultivation of mammalian and microbial-cells. Biotechnol Bioeng. 1991;38:1190–1202. doi: 10.1002/bit.260381011. [DOI] [PubMed] [Google Scholar]
- 20.Herman HH. Centrifugal fermentation processes. 5,622,819 U.S. Pat. 1997 April 22;
- 21.Herman HH, Lin W, Petrecca PJ, Herman TM, Bates C, Simmons R, Houghton J. Centrifugal bioreactors and their application in remediation. Remediation. 2001;11:15–33. [Google Scholar]
- 22.Jaeger HM, Nagel SR. Physics of the granular state. Science. 1992;255:1523–1531. doi: 10.1126/science.255.5051.1523. [DOI] [PubMed] [Google Scholar]
- 23.Davis WC, MacHugh ND, Park YH, Hamilton MJ, Wyatt CR. Identification of a monoclonal antibody reactive with the bovine orthologue of CD3 (BoCD3) Vet Immunol Immunopathol. 1993;39:85–91. doi: 10.1016/0165-2427(93)90167-3. [DOI] [PubMed] [Google Scholar]
- 24.Graham J. Biological Centrifugation. BIOS Scientific Publishers Ltd; Oxford, UK: 2001. pp. 91–93. [Google Scholar]
- 25.deZengotita VM, Schmelzer AE, Miller WM. Characterization of hybridoma cell responses to elevated pCO(2) and osmolality: intracellular pH, cell size, apoptosis, and metabolism. Biotechnol Bioeng. 2002;77:369–380. doi: 10.1002/bit.10176. [DOI] [PubMed] [Google Scholar]
- 26.Sanderson RJ, Bird KE. Cell separations by counterflow centrifugation. Methods Cell Biol. 1977;15:1–14. doi: 10.1016/s0091-679x(08)60206-x. [DOI] [PubMed] [Google Scholar]
- 27.Batchelor GK. An Introduction to Fluid Dynamics. Cambridge University Press; Cambridge, UK: 1967. [Google Scholar]
- 28.Chen XM, Fried E. Rayleigh-Taylor problem for a liquid-liquid phase interface. J Fluid Mech. 2006;560:395–414. [Google Scholar]
- 29.El-Dib YO. Nonlinear hydromagnetic Rayleigh-Taylor instability for strong viscous fluids in porous media. J Magn Magn Mater. 2003;260:1–18. [Google Scholar]
- 30.Malkin AY. Surface instabilities. Colloid J. 2008;70:673–689. [Google Scholar]
- 31.McFadden GB, Coriell SR, Gurski KF, Cotrell DL. Convective instabilities in two liquid layers. J Res Natl Inst Stand Technol. 2007;112:271–281. doi: 10.6028/jres.112.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Greenspan HP. The Theory of Rotating Fluids. Cambridge University Press; Cambridge, UK: 1968. [Google Scholar]
- 33.Baroud CN, Plapp BB, Swinney HL, She ZS. Scaling in three-dimensional and quasi-two-dimensional rotating turbulent flows. Phys Fluids. 2003;15:2091–2104. [Google Scholar]
- 34.Detzel CJ, Mason DJ, Davis WC, van Wie BJ. Kinetic simulation of a centrifugal bioreactor for high population density hybridoma culture. Biotechnol Prog. 2009;25:1650–1659. doi: 10.1002/btpr.240. [DOI] [PMC free article] [PubMed] [Google Scholar]