Evaluating segmentation algorithms for diffusion-weighted MR images: a task-based approach

Abstract

Apparent Diffusion Coefficient (ADC) of lesions obtained from Diffusion Weighted Magnetic Resonance Imaging is an emerging biomarker for evaluating anti-cancer therapy response. To compute the lesion’s ADC, accurate lesion segmentation must be performed. To quantitatively compare these lesion segmentation algorithms, standard methods are used currently. However, the end task from these images is accurate ADC estimation, and these standard methods don’t evaluate the segmentation algorithms on this task-based measure. Moreover, standard methods rely on the highly unlikely scenario of there being perfectly manually segmented lesions. In this paper, we present two methods for quantitatively comparing segmentation algorithms on the above task-based measure; the first method compares them given good manual segmentations from a radiologist, the second compares them even in absence of good manual segmentations.

1. INTRODUCTION

Diffusion can be described as the thermally induced behavior of molecules moving in a microscopic random pattern in a field. This microscopic motion is also known as Brownian movement. Diffusion-weighted magnetic resonance imaging (DWMRI) is sensitive to this microscopic motion. This motion can be parameterized by means of an apparent diffusion coefficient (ADC).¹ ADC has been shown to be a positive indicator to tumor response to therapy both preclinically and clinically.^{2, 3} However, in order to thoroughly validate DWMRI as an imaging biomarker, it is critical that the ADC be estimated accurately.

To compute the ADC of the lesion, the first step required is accurate segmentation of the lesions. There is ongoing research as well as published literature on methods for performing this segmentation.^4–6 Quantitative evaluation of these segmentation algorithms is done using the same standard approaches as are used for evaluating segmentation results in general images.^4–6 There are two issues with using these quantitative methods for evaluating the segmentation results. The first issue is that lesion segmentation is merely an intermediate step towards the end task of determining the ADC values. Therefore, an objective approach to evaluating the segmentation algorithms should decide which algorithm aids the best in this end task. The standard quantitative measures do not evaluate segmentation algorithms based on this criterion. The second issue is that these standard methods require the user to have very good manual segmentation results for comparison. However, in DWMRI images, due to low signal-to-noise ratio (SNR) and fuzzy lesion boundaries, the manual segmentation is error-prone and therefore cannot be used as the gold standard for comparison with an automated segmentation algorithm. Moreover, manual segmentation is a tedious task, and so is not always available. The purpose of this paper is to propose solutions to these issues in evaluation of segmentation algorithms. The idea is to devise task-based quantitative evaluation techniques that do not require perfect manual segmentations. To our knowledge, this is one of the first papers that explicitly proposes the idea of a task-based evaluation method for an image analysis algorithm and suggests techniques for accomplishing it.

2. MATERIALS AND METHODS

2.1 Image acquisition

In the current study, DWMRI is being used to monitor the therapeutic response in breast cancer patients with metastases to the liver. Conventional T1 and T2-weighted imaging is performed at 1.5T, along with diffusion-weighted single-shot echo-planar imaging (DW-SSEPI) using b values of 0, 150, 300 and 450 s/mm². Image parameters for the DW-SSEPI images are as follows: TE = 91.1 ms, 128 × 128 image matrix, FOV = 38 × 29 cm, TR = 6 s, 250 kHz receiver and 6 mm slice thickness. DWMRI image pairs (b=0 and 150, b=0 and 300, and b=0 and 450 s/mm², respectively) are collected, where each pair is collected within a 24 s single breath-hold. We refer to the procedure to acquire such a pair as an intra-pair scan. In each intra-pair scan, 58 image slices are acquired, 29 at b value 0 s/mm² and the other 29 at the higher b value. The highest gray level seen in the images is around 800. Each patient is imaged at day 0 (baseline), day 4, 11 and 39 following the commencement of cytotoxic therapy.

2.2 ADC computation

Denote the b values by b_i, where i denotes the b value index, so that b₁ = 0 s/mm², b₂ = 150 s/mm², b₃ = 300 s/mm² and b₄ = 450 s/mm². The approach that is common to compute the ADC of the lesion is to compute the ADC of each pixel in the lesion, and therefore obtain an ADC map of the lesion.⁷ However, this approach requires that the lesion remain stationary in an intra-pair scan, which is not true in our case. Due to visceral motion of the liver, movement of the lesion occurs leading to inaccurate ADC maps. This has been studied in further detail in Theilmann et. al.³ Consequently, this method is not reliable when organ movement occurs. Instead, we compute the mean ADC of the whole lesion, a parameter that is mostly invariant to lesion movement.

Assume we have P lesions, each of which are imaged at two b values, b₁ and b₂ to give us P sets of images. In the p^th set of images, the lesion is manually segmented. The pixels within the segmented region define the lesion pixels. Using the segmentation results for the p^th set of images, the mean intensity of all the lesion pixels is calculated at both the b values. Let us denote these mean signal intensities at b values b₁ and b₂ by $s_{p1}^m\text{ and }{s}_{p2}^m,$ respectively. Also, let us denote the mean ADC of the p^th lesion by $a_p^m,$ computed using the results of the manual segmentation. The equation to compute $a_p^m$ is given by

$$a_p^m=\frac{-1}{b_1-b_2}\text{ln}\left(\frac{s_{p1}^m}{s_{p2}^m}\right).$$ (1)

Now, let there be K automated segmentation algorithms that we wish to compare on the task-based measure of performance of ADC estimation. Using the k^th segmentation algorithm, we segment the lesion in the p^th set of images, and using the segmentation result, obtain the mean signal intensity of the lesion at the two b values b₁ and b₂. Let us denote these mean signal intensities at the two b values by $s_{p1}^k\text{ and }{s}_{p2}^k,$ respectively. Using these mean signal intensities, we calculate the mean ADC of the lesion for the p^th set, which we denote by $a_p^k,$ as

$$a_p^k=\frac{-1}{b_1-b_2}\text{ln}\left(\frac{s_{p1}^k}{s_{p2}^k}\right).$$ (2)

Let A, A_m and A_k be the random variables that denote the true ADC value, the ADC value obtained using manual segmentation and the ADC value obtained using the k^th segmentation algorithm, respectively. Also, let a, a_m and a_k denote the instances of these random variables.

2.3 Motivation

In this section, we discuss why the standard measures of evaluating segmentation algorithms do not provide appropriate measure of the accuracy of these algorithms with regards to the task of ADC estimation, even in the presence of perfect manual segmentation results. The fundamental principle that most of the conventional methods use to evaluate segmentation algorithms, given a manual segmentation, is to determine whether the same set of pixels belong to the same region in the manual and automated segmentations. Some of these methods are the region overlap approach,⁵ the boundary matching approach,⁸ and the Normalized Probabilistic Rand Index.⁹ This works well when the user’s requirement is to know whether the set of pixels that represent the object in manual segmentation also describe that object in the automated segmentation. However, the same does not hold true with the segmentation task in diffusion-weighted images. In these images, the purpose of the segmentation algorithm is to aid in accurate estimation of the ADC of the lesion.

From Eqs. [1] and [2], we observe that the parameter of interest while calculating the ADC is the accuracy of the mean signal intensity calculated using the region extracted by the segmentation algorithm. It is not whether the same set of pixels belongs to the same region in manual and automated segmentation. It is true that if the manual and automated segmentations were exactly the same, then the mean signal intensities computed using the manual and the automated segmentation would also be the same. However, the segmentations are almost never exactly the same. And when there is a mismatch, what ought to matter is not the magnitude of mismatch, but how much does it affect the ADC estimate. While missing out on a few pixels may not show up as a significant error using the standard methods for evaluating the segmentation algorithm, it may actually have a crucial effect on the mean signal intensity calculation, and therefore the ADC estimation. The purpose from the diffusion weighted images is to estimate ADC, and therefore, an evaluation technique that ranks the automated segmentation algorithms based on how well they aid in this task, is more useful. This serves as the first reason for the need for an algorithm that evaluates the segmentation algorithm based on the task of ADC estimation, rather than the principle on which standard methods work. This method of evaluating the segmentation algorithms is motivated from the work done in,¹⁰ where the authors stress that an objective approach to assessment of image quality must determine quantitatively how well the task required of the image can be performed from it, after any algorithm has been applied on the image.

The second reason is that the standard methods rely on there being very good manual segmentation results, which are not available in most of these images. We only have approximately good manual segmentation results. At times, we might have poor segmentation results, or even worse, no manual segmentation results at all, given that the segmentation task is so tedious. In fact, in many cases, the radiologists do not perform manual segmentation on the diffusion-weighted images, but rather on a separate set of T1 and T2-weighted images that are acquired along with them. In those cases, we do not have manual segmentation on the diffusion-weighted images, so there is no benchmark to compare the automated segmentation algorithms with. Consequently, there is a need to devise methods to quantitatively evaluate automated segmentation algorithms given either reasonably good manual segmentations or no manual segmentations at all.

2.4 Task-based techniques to evaluate segmentation algorithms

In this section, we present the two methods for comparing the automated segmentation algorithms. The first method can be used when the manual segmentation is reasonably good. The second method can be used when the manual segmentation results are not good or are not available.

2.4.1 Quantifying segmentation algorithms given reasonably good manual segmentations: The EMSE approach

As discussed above, the end task using diffusion weighted images is ADC estimation. Therefore the performance evaluation metric should quantify the difference between the correct ADC value and the ADC estimated using the k^th automated segmentation algorithm. For quantifying this error, we apply a probabilistic analysis and use the ensemble mean squared error (EMSE)^{10, 11} as the figure of merit, which, for the k^th automated segmentation algorithm, is given by

$$\text{EMSE}(A_k)=E({(A_k-A)}^2)$$ (3)

where E( ) denotes the average value of the quantity inside the parentheses.

We do not know A, the true ADC value. Consequently, the EMSE cannot be computed. However, we do have the ADC values of the lesion from the manual segmentations. It would be of interest to see if the EMSE between the ADC values obtained from manual segmentation and the automated segmentation can serve as an indicator of performance. Therefore, let us try to derive an expression for the metric d(A_k,A_m), which we define as

$$d(A_k,A_m)=E({(A_k-A_m)}^2)$$ (4)

The ADC values obtained from manual segmentation, although not perfect, have been estimated after carefully performing manual segmentation. The imperfections in the manual segmentation are due to fuzzy lesion boundaries and low SNR in these images. We therefore make the assumption that the error between the true ADC value and the ADC computed from manual segmentation can be parameterized by a zero-mean noise term. Mathematically,

$$A_m=A+N_m.$$ (5)

Using the assumption that that (A_k − A) and N_m are independent of each other, one being the error in the ADC value estimated using the automated segmentation algorithm, and the other being the noise in the ADC estimate obtained using the manual segmentation, we can derive d(A_k,A_m) to be¹²

$$d(A_k,A_m)=\text{EMSE}(A_k)+{\sigma }_{N_m}^2,$$ (6)

where ${\sigma }_{N_m}^2$ is the variance of N_m. Since ${\sigma }_{N_m}^2$ is just a constant independent of the segmentation algorithm, d(A_k,A_m) can be used to quantify the error between the gold standard ADC estimate and the ADC estimate obtained after using any automated segmentation algorithm. For the k^th segmentation algorithm, d(A_k,A_m) can be computed statistically as

$$d(A_k,A_m)=\frac{{\displaystyle {\sum }_{p=1}^P{(a_p^k-a_p^m)}^2}}{P}.$$ (7)

Among the various automated segmentation algorithms, the best one for the task of ADC estimation is the one that minimizes d(A_k,A_m). We refer to this method in the rest of the paper as the EMSE-based approach. However it is worth noting that for this method to work, the restrictive assumptions mentioned earlier must hold.

2.4.2 Quantifying segmentation algorithms given poor or no manual segmentations: The no-gold-standard approach

If we have only poor manual segmentations, we use the no-gold-standard framework established in^{13, 14} to compare the automated segmentation algorithms. Let there be K segmentation algorithms that we wish to compare, and using each segmentation algorithm, we get P ADC values for P lesions. We denote the ADC value estimated for the p^th lesion using the k^th segmentation algorithm by $a_p^k$ and the true ADC value of the p^th lesion by a_p.

We begin with the assumption that there exists a linear relationship between the true ADC value of the lesion, and the ADC value estimated using the k^th segmentation algorithm. We describe this relationship for the k^th segmentation algorithm and the p^th set using a regression line with slope u_k, intercept v_k and a noise term ${\epsilon }_p^k.$ Therefore

$$a_p^k=u_k{a}_p+v_k+{\epsilon }_p^k.$$ (8)

Let the set of K noise terms $\{{\epsilon }_p^1,{\epsilon }_p^2,\dots {\epsilon }_p^k\}$ be denoted by $\{{\epsilon }_p^k\}.$ The noises due to the segmentation algorithms are independent of each other. Therefore, as in Hoppin et. al.,¹³ we make the assumption that the error terms are statistically independent and normally distributed with zero-mean and standard deviation σ _k. Using this assumption, we can write the joint probability density function of the noise {ε_pk} for the p^th lesion as

$$\mathit{\text{pr}}(\{{\epsilon }_p^k\})={\displaystyle \prod _{k=1}^K\frac{1}{\sqrt{2\pi {{\sigma }_k}^2}}\text{exp}\left(\frac{-{\epsilon }_p^{k^2}}{2{{\sigma }_k}^2}\right)},$$ (9)

where pr() denotes the probability density function of the quantity inside the parenthesis. We also assume, as in,¹³ that the true ADC value a_p is statistically independent from one lesion to another, and that the parameters u_k and v_k are characteristic of the segmentation algorithm and independent of the lesion. Using Eqs. [8] and [9], we get

$$\mathit{\text{pr}}(\{a_p^k\}|\{u_k,v_k,{\sigma }_k\},a_p)={\displaystyle \prod _{k=1}^K\frac{1}{\sqrt{2\pi {{\sigma }_k}^2}}\text{exp}\left(\frac{-{(a_p^k-u_k{a}_p-v_k)}^2}{2\pi {{\sigma }_k}^2}\right)},$$ (10)

where $\{a_p^k\}$ denotes the set of ADC values estimated for the p^th lesion using the K segmentation algorithms. Now if the gold standard ADC value are assumed to have been picked from a probability density function pr(a_p), then we can marginalize Eq. [10] over a_p. We then assume that the ADC values of P lesions are independent of one another, in which case, the log-likelihood that we want to maximize can be derived to be¹²

$$\lambda =P\text{log}\left({\displaystyle \prod _{k=1}^K\frac{1}{\sqrt{2\pi {{\sigma }_k}^2}}}\right)+{\displaystyle \sum _{p=1}^P\text{log}}{\displaystyle \int \mathit{\text{pr}}}(a_p){\displaystyle \sum _{k=1}^K\text{exp}}\left(\frac{-{(a_{\mathit{\text{pk}}}-u_k{a}_p-v_k)}^2}{2\pi {{\sigma }_k}^2}\right){\mathit{\text{da}}}_p.$$ (11)

We pick the beta distribution as the prior probability density function for the true ADC values. The beta distribution is chosen because it can adapt itself to different distributions that the dataset might have. The beta distribution is given by

$$\mathit{\text{pr}}(x)=\frac{x^{\alpha -1}{(1-x)}^{\beta -1}}{B(\alpha ,\beta )},$$ (12)

where B(α, β) is a normalizing constant and x ε (0, 1). We estimate the values {a_k, v_k, σ_k, α, β} that maximize λ in Eq. [11] or, in other words, maximize the probability of the observed data. This method is referred to as maximum likelihood estimation.^{15, 16}

We use a quasi-Newton optimization technique¹⁷ in MATLAB software to determine the values of {u_k, v_k, σ_k, α, β} for which the maximum of the likelihood is obtained. We constrain this optimization to search only between reasonable values of the parameters, that are determined by statistical techniques. By determining the values of {u_k, v_k, σ_k}, we can determine how well the ADC estimate obtained using a certain segmentation algorithm relates to the gold-standard ADC value. The segmentation algorithm for which the value of the noise to slope ratio, σ_k / u_k is the minimum is the best segmentation algorithm¹³ with respect to the task of ADC estimation. Therefore, using this approach, even in the absence of manual segmentations, we can still evaluate the automated segmentation algorithms with respect to the task of accurately estimating ADC values.

2.5 Validation of the methods

In this section, we discuss our approach to validate the EMSE and the no-gold-standard based methods. To validate the EMSE-based method, we have to confirm whether the ranking of certain automated segmentation algorithms obtained using the d(A_k,A_m) metric is the same as the true ranking of the segmentation algorithms. The true ranking is determined by computing the mean squared error between the true ADC of the lesion and the ADC estimated using the segmentation algorithms, and then using this mean squared error to order the algorithms. Therefore, to determine the correct ranking of the segmentation algorithms, we need to know the true ADC of the lesion. We cannot use real lesions because we do not know the true ADC values of the lesion in real data. For this purpose, we use real diffusion-weighted images containing simulated lesions.

To simulate such images, from our dataset, we selected seven sets of real images as templates for the background, where a set comprised of corresponding image slices at b values of 0 and 450 s/mm². Simulation of the lesion was done taking into account the statistics of the lesion, the statistics of the Gaussian noise that corrupted it, and the shape of the various lesions.¹² The lesions simulated at b value 0 s/mm² were added to the background templates at b value 0 s/mm², and similarly the lesions simulated at b value 450 s/mm² were added to the background templates at b value 450 s/mm². The simulated images were then compared with the actual diffusion-weighted images and they were found to be very similar. At the end of this exercise, we had a dataset of seventy simulated diffusion weighted images containing the lesions, on which we could verify the EMSE and the no-gold-standard methods.

We segment the images with simulated lesions manually and using different automated segmentation methods. From the segmentation results, we obtain the mean signal intensity of the lesion and then compute the ADC of the lesion using Eqs. [1] and [2]. This process is repeated for multiple lesions. We then compute d(A_k,A_m) for the different segmentation algorithms using Eq. [7]. Next, the mean squared error is computed between the true ADC value of the lesion and that estimated using the automated segmentation. The segmentation algorithms are ranked based on the mean square error and the d(A_k,A_m) values. If the ranking using both the parameters is the same, that validates our segmentation algorithm. To validate the no-gold-standard approach, we use the ADC estimates computed using three different automated segmentation algorithms. The noise-to-slope ratio for each of the segmentation methods is determined using this method. The algorithms are ranked on the basis of the noise-to-slope ratio, and if the ranking is the same as the ranking based on the root-mean-square-error (RMSE) parameter,¹⁴ then that can validate the no-gold-standard approach.

3. EXPERIMENTS AND RESULTS

3.1 Validating the EMSE method

On a dataset of seventy lesions, one user performed manual segmentation, and then segmentations using three automated algorithms were performed. These three automated algorithms were a clustering-based algorithm inspired by the work of Pappas et. al.,¹⁸ a maximum-likelihood estimation (MLE) based algorithm for segmenting lesions in digital mammograms¹⁹ and a expectation-maximization (EM) based algorithm.²⁰ The ADCs were estimated using each of these methods, and the mean square error and the d(A_k,A_m) values were computed. The results of this experiment are shown in Table 1. We observe that the clustering algorithm gives the least mean square error, as well as the least d(A_k,A_m), while the MLE-based algorithm gives the highest values of both of these parameters. The ranking of the segmentation algorithms determined using the two parameters is the same. Consequently, this verifies that the d(A_k,A_m) parameter is sufficient to quantitatively compare these algorithms for this set of lesions.

Table 1.

Mean Squared Error and d(A_k, A_m) parameters for the three seg. algorithms

Segmentation Method	Clustering	MLE	EM
Mean Squared Error d(Ak,Am)	0.1168 0.1313	0.6548 0.6222	0.4526 0.5088

3.2 Validating the no-gold-standard method

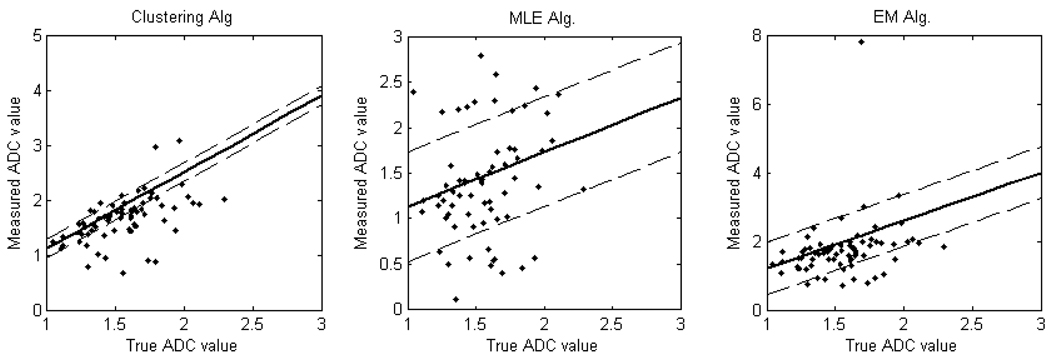
On the dataset of seventy lesions, the above three segmentation methods were compared. The no-gold-standard method was used and the regression line parameters were obtained. Fig. 1 shows the plot of these regression lines. The results are summarized in Table 2. We observe from Table 2 that the ranking determined based on the slope to noise ratio is the same as the ranking of the segmentation algorithms obtained based on the RMSE parameter. This validates the no-gold-standard approach for this set of lesions.

Figure 1.

The plots of regression lines using the no-gold-standard method. The solid line is generated using the estimated linear model parameters for each segmentation algorithm. The dashed lines denote the estimated standard deviations for each algorithm. The scatter plots show the computed ADC values vs. the true ADC value for (a) Clustering-based (b) MLE-based and (c) EM-based segmentation.

Table 2.

RMSE and noise-to-slope ratio parameters for the three seg algorithms

Segmentation Method	Clustering	MLE	EM
Root-Mean-Squared-Error Noise-to-slope ratio	0.1224 0.3193	1.0053 1.000	0.5431 0.6426

4. CONCLUSION

The first main idea proposed in this paper is that of quantifying an image-analysis, in particular a segmentation algorithm, based on how well it can aid in the end task that is required of the images that the algorithm analyzes. In many segmentation tasks, the images that are segmented are acquired for a certain purpose. This is especially true in medical imaging. Therefore, evaluating the automated segmentation algorithms based on this task-based measure is more useful than evaluating them based on certain standard criterion. This idea can be extended to other scenarios where the medical images are acquired for certain tasks and where segmentation, or any image analysis task, is performed as an intermediate step.

The second main idea presented in this paper is to evaluate the segmentation algorithms in the absence of perfect manual segmentation results. In most general images, and especially in medical images, coming up with a perfect manual segmentation is an almost impossible task, because the boundaries of the anatomical structures are not very well defined in the images. This paper recognizes this issue and proposes evaluation methods that take this fact into consideration.

To summarize, we propose two methods to perform quantitative comparison of the automated segmentation algorithms, based on how well they aid in the end task of ADC estimation of a lesion. The first method we propose, the EMSE-based approach, relies on the presence of good manual segmentation results, to quantify the performance of the automated segmentation algorithms, and works under certain restrictive assumptions. We then present a no-gold-standard approach for evaluating the segmentation algorithm when the manual segmentations are not good or not available. As mentioned, the methods we have proposed do not require perfect manual segmentation results to compare them with the automated segmentation results. This makes them particularly significant for our case, since it is very tough to get perfect manual segmentation in the diffusion weighted images, as they are low SNR images and the lesion boundaries are fuzzy. We are currently working on being able to improve the no-gold-standard technique to take into account the effect of prior information regarding ADC distribution if it is available. We are also rigorously analyzing the algorithms for more users performing manual segmentations.