Skip to main content
NCBI home page
The Review of Scientific Instruments logoLink to The Review of Scientific Instruments
. 2010 Nov 11;81(11):113704. doi: 10.1063/1.3495960

A simple backscattering microscope for fast tracking of biological molecules

Yoshiyuki Sowa 1,2, Bradley C Steel 2, Richard M Berry 2,a)
PMCID: PMC2997809  PMID: 21133475

Abstract

Recent developments in techniques for observing single molecules under light microscopes have helped reveal the mechanisms by which molecular machines work. A wide range of markers can be used to detect molecules, from single fluorophores to micron sized markers, depending on the research interest. Here, we present a new and simple objective-type backscattering microscope to track gold nanoparticles with nanometer and microsecond resolution. The total noise of our system in a 55 kHz bandwidth is ∼0.6 nm per axis, sufficient to measure molecular movement. We found our backscattering microscopy to be useful not only for in vitro but also for in vivo experiments because of lower background scattering from cells than in conventional dark-field microscopy. We demonstrate the application of this technique to measuring the motion of a biological rotary molecular motor, the bacterial flagellar motor, in live Escherichia coli cells.

INTRODUCTION

Particle tracking is an essential tool for studying the dynamics of biological processes on a cellular or subcellular level. Measurements with sufficiently high spatial and temporal resolution have helped elucidate information about the kinetics and stepping behavior of molecular motors.1, 2, 3, 4 In an optical microscope, sparse particles can be tracked with arbitrary precision provided that sufficient photons are collected.5 Probes, such as fluorophores, microbeads, or nanoparticles, have been tracked with nanometer accuracy and time resolution of milliseconds or better.

Many biological molecular machines function in complex cell systems. One important approach to understanding the mechanisms by which they function involves extracting and analyzing them in a range of in vitro assays. Probes ranging from single fluorescent dye molecules or fluorescent proteins to polystyrene spheres several microns in diameter have been attached to molecular machines using a range of bioconjugate techniques.6 Localization of single dye molecules is limited to resolutions of ∼1.5 nm at sample rates of ∼2 Hz by their relatively low fluorescent intensity.7 Metallic nanoparticles allow much faster temporal resolution without compromising spatial resolution as they have a very high scattering cross section and do not photobleach or blink. Nanoparticles can be observed with high contrast when viewed in a dark-field microscope, and laser dark-field systems have been developed to increase the illumination level.3, 8, 9, 10, 11

Recent progress in single-molecule research has extended to revealing the molecular mechanics of molecular motors in vivo. For low time-resolution in vivo studies, fluorescent proteins are particularly convenient due to a labeling efficiency of nearly 100% and perfect specificity provided by genetic fusion of the fluorescent protein to the target of interest.12, 13, 14 Gold nanoparticles are also suitable for in vivo tracking because their high scattering cross section makes them very bright compared to the surrounding cell. Gold nanoparticles have recently been used to track vesicle transport by kinesins and dyneins in human cancer cells10 and rotation of the bacterial flagellar motor in E. coli.15 Here, we demonstrate the tracking of gold nanoparticles 50–200 nm in diameter attached to flagellar motors, with subnanometer and ∼10 μs resolution, using a backscattering laser dark-field microscope.

MATERIALS AND METHODS

Optics

Our system of backscattering laser dark-field microscopy is shown in Fig. 1. Light from a He–Ne laser (633 nm, 10 mW, Melles Griot) is split between two beam paths using a polarized beamsplitter (PBS1) and recombined after one mirror and lens element by a second beamsplitter (PBS2). Typically, one of the two paths is blocked and the intensity of the illumination is modulated by rotating a half wave plate positioned before PBS1. In geometric optics, lenses L1 and L2 would be placed a focal length before a point P1 conjugate to the back focal plane of the objective. In practice, their positions are slightly offset such that a focus of the Gaussian beam is achieved at the back focal plane of the objective.

Figure 1.

Figure 1

Open in a new tab

Setup: a schematic diagram of our optical setup for backscattering laser dark-field microscopy. Linearly polarized collimated light from a HeNe laser (633 nm) passes through the half wave plate (HWP) and is divided into two paths at the beam splitter (PBS1). Focal lengths of L1 and L2 are 300 and 100 mm, respectively, to illuminate different sized areas in the sample plane; usually, one path is blocked before PBS2. The laser passing PBS2 is recollimated by L3, modulated to circular polarization by the quarter-wave plate (QWP), and focused onto the back focal plane of the objective lens via the small rod mirror (RM). The sample plane is illuminated with light parallel to the optic axis, and scattered light (dotted lines) from the sample is collected using the same objective lens as for illumination. The ring of scattered light that passes the RM is focused onto the CMOS sensor of the high-speed camera, or the CCD camera or QPD via flipper mirrors (FM1 and FM2), if necessary.

Lens L4 is one focal length distant from both mirror M1 and the back focal plane of the objective such that M1 is conjugate to the image plane. A rod mirror (RM; F47-628, Edmund Optics) couples the laser light into the objective [PlanFluor 100×, numerical aperture (NA) 1.3, Nikon] along its optical axis. Direct reflections from interfaces within the sample emerge along the same axis and are removed by the rod mirror. This mirror is angled at 45° to the rod and optical axis, has a circular cross section with a diameter of 1 mm when viewed along the optical axis, and is held in place by a 0.5 mm wide metal support perpendicular to the optical axis. The mirror is placed as close as possible to the objective back aperture (<5 mm) to allow the laser light to be focused in the objective back aperture. The mirror obscures less than 4% of the scattered light collected by the objective, and the combination of mirror and metal strip allows ∼92% of the scattered light collected by the objective to pass. The system was mounted on an optical bench with passive air damping; no further precautions were taken to isolate the system from mechanical or acoustic noise, unlike some similar setups.16, 17

Microscope slides were mounted in a cantilever-type custom holder on a three-axis dovetail stage (460PD, Newport) for coarse adjustment and a three-axis piezoelectric stage (P-611.3, Physik Instrumente Ltd.), with 100 μm travel in each axis, for fine adjustment. A condenser (not shown in Fig. 1) was mounted above the sample to allow simultaneous bright-field imaging.

Detection

Scattered light collected from the objective was imaged onto a high-speed complementary metal-oxide semiconductor (CMOS) camera (Fastcam 1024 PCI, Photron) and recorded at frame rates of up to 109.5 kHz, depending on the size of the region of interest. Two flip mirrors (FM1 and FM2) alternatively allow position detection using a quadrant photodiode (QPD) (SPOT-4DMI, Silicon Sensor) with custom built circuit or low magnification imaging onto a charge-coupled device (CCD) camera (WAT-902H2, Watec). QPD signals were recorded to computer using a data acquisition board (PCI6034E, National Instruments), while images from the CCD camera were displayed but not recorded. Particle positions were determined from 8 bit images captured with the CMOS camera, using the Gaussian mask algorithm described by Thompson et al.5

Specimen

“Tunnel slides” were formed by using two pieces of double-sided adhesive tape, approximately 3 mm apart, to adhere a glass coverslip to a microscope slide. Solutions were introduced at one end of the tunnel and, if necessary, removed at the other end by capillary action with tissue paper.

Gold nanoparticles (purchased from Corpuscular or BBInternational) with diameters of 50, 60, 80, 100, 150, or 200 nm (CVI=8%) were used as delivered and incubated for 10–30 min in tunnel slides. Tunnel slides were inverted (coverslip downward) during this time to allow the gold particles to settle and adhere spontaneously to the coverslip surface. Particles that were not adhered to the surface were then removed by washing with >10 volumes of de-ionized water.

Bacterial flagellar motor

E. coli strain, YS34 (ΔmotAmotB,fliC::Tn10,ΔcheY) (Ref. 4) carrying pYS13 (chimeric sodium-driven stator proteins pomApotB, cam resistance, IPTG inducible) was grown in T-broth (1% Bacto tryptone and 0.5% NaCl) with 25 μg∕ml chloramphenicol and 20 μM IPTG at 30 °C for 5 h. Cells were washed three times with motility medium (85 mM NaCl, 0.1 mM ethylenediaminetetraacetic acid (EDTA), and 10 mM potassium phosphate, pH 7.0). 100 nm gold particles were attached to the hook of the flagellar motor via antihook antibody following the protocol of Yuan and Berg15 with some minor modifications. Cells were attached to the polylysine coated coverslip of the tunnel slide.

Scattering calculations

Scattering calculations were performed in SCATLAB (http://www.scatlab.org), assuming collimated illumination of either a gold particle with a size of 100 nm, with optical properties as specified by Palik,18 or a “cell,” in a uniform, nonabsorbing medium with a refractive index of 1.33. Scattering by a cell was modeled by taking the average of the scattering profiles of six sizes of nonabsorbing dielectric spheres with a refractive index of 1.38, with diameters equally spaced between 500 and 1000 nm.

The angle between the illumination and the optical axis varied between 0° (forward scatter) and 180° (backscatter). All light scattered within the objective’s numerical aperture (NA, 0.7–1.3) was assumed to be collected. The ratio of the light collected from the gold particle and from the cell was calculated for each combination of illumination angle and objective NA.

RESULTS AND DISCUSSION

The assembly of our backscattering dark-field microscope involves only simple optical components: mirrors, lenses, and polarizing elements. The critical element of the assembly is the positioning of a small 45° mirror just below the objective. This simple configuration allows perfect backscattering optics with homogeneous on-axis illumination at the sample. The mirror also blocks light that is directly reflected at the planar interfaces in the sample, for example, between the coverslip and the sample medium. The mirror and its mountings obscure less than 10% of the area of the back aperture of our high-NA objective, allowing more than 90% of the scattered light collected by the objective to be imaged. This high efficiency of light collection helps assure that we can achieve high spatial and temporal resolution. It also makes the system attractive to combine with light-sensitive techniques such as fluorescence imaging. Because all the optical elements for our backscattering detection system lie on the objective side of the sample, the sample is also accessible from the top, allowing this technique to be combined with other measurements, such as atomic force microscopy or a patch clamp assembly.

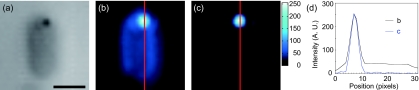
The advantage gained by using backscattering optics instead of side or forward scattering dark-field is demonstrated in Figs. 23. In Fig. 2a, a 100 nm gold particle is visible in a bright-field image of an E. coli cell. Figures 2b, 2c show the same area as in Fig. 2a using conventional condenser-based dark-field and our backscattering system, respectively. Figure 2d shows the intensity profile measured along a vertical line through each image and demonstrates that the backscattering system detects a much reduced (<10%) level of scattering from the cell body compared to conventional dark-field microscopy. In the context of measuring the position of a gold probe, this corresponds to a much lower level of background noise.

Figure 2.

Figure 2

Open in a new tab

Comparison between conventional dark-field and backscattering optics. (a) A bright-field image of a gold nanoparticle attached to a flagellar motor on an E. coli cell. Note that to allow the same field of view to be imaged in (a)–(c), bright-field illumination is through a NA>1.2 “dark-field” condenser, which gives a bright-field image with our NA 1.3 objective, and hence, the image is suboptimal. (b) and (c) show conventional condenser dark-field and backscattering laser dark-field images, respectively, of the same area as in (a). The condenser dark-field image is achieved using an iris within the objective to reduce its effective numerical aperture to approximately 1.0. (d) Intensity profile along the red lines in (b) and (c). Scale bar=1 μm.

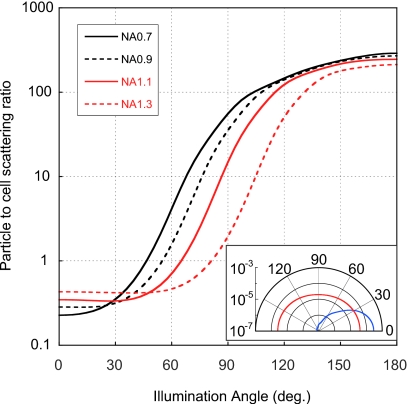
Figure 3.

Figure 3

Open in a new tab

Calculated ratio of scattering from a 100 nm gold particle relative to a larger cell-like body as a function of the illumination angle, for different collecting NAs. Illumination angle is relative to the optical axis of the objective: 180° is direct backscattering as in our setup, 0° is forward-scattering. The visibility of the gold particle is nearly three orders of magnitude greater with illumination close to 180° than with illumination close to 0°. Details of the calculation are described in Sec. 2. (Inset) Polar diagram of the scattering cross section vs scattering angle of a 100 nm gold particle (red) and cell-like body (blue). The gold particle scatters nearly equally in all directions, while the cell scatters mostly forward.

Figure 3 shows the calculated ratios of the total image intensity of 100 nm gold particles to that of cell-like objects, as a function of illumination angle. The gold particles scatter light nearly equally in all directions, while the larger cells scatter mostly forward (Fig. 3, inset). Thus, the relative amount of light detected from the cell increases as the illumination moves away from direct backscattering (180° in Fig. 3).

The intensity distribution of a typical gold particle, with a diameter of 100 nm, obtained by this microscope is shown in Fig. 4a. The intensity distribution is well fit by a two-dimensional (2D) Gaussian curve(R2=0.99), with residuals [Fig. 4b] showing only a slight discrepancy due to the first Airy ring. The full width at half maximum (FWHM) calculated from the fit is 280 nm, indicating that the setup has the full resolution expected from the objective’s high numerical aperture.

Figure 4.

Figure 4

Open in a new tab

Typical image of a gold particle using the backscattering laser dark-field microscope. (a) Intensity distribution of a 100 nm gold nanoparticle on the cover slip with 9 μs shutter frame (surface) and an overlaid 2D Gaussian fit (dashed lines). FWHM of the image is∼3.2 pixels, corresponding to∼280 nm. (b) Residual of the difference between the Gaussian curve fit and the intensity distribution shown in (a).

The size of the field of illumination is dependent on the power of the lenses used to focus the illuminating light; in our setup, we achieve approximately Gaussian-distributed illumination with FWHMs of 3 μm (“small field”) and 15 μm (“large field”) for the two illumination pathways (L2 and L1 in Fig. 1). A 200 nm gold nanoparticle scattered approximately 0.15% of the illumination light under small field illumination, bright enough that the scattered light reaching the detector was easily visible to the naked eye. The brightness of the scattered light depends on the size of nanoparticles used. Figure 5a shows the cross section for light scattered to form the image at the camera, observed for various gold nanoparticle sizes. We also plot the expected cross section calculated for our optical geometry using Mie scattering theory to calculate the intensity and assuming that the optical transfer function of the objective is flat for NA≤1.3.

Figure 5.

Figure 5

Open in a new tab

Performance of the backscattering laser dark-field microscope. (a) Scattering cross section of gold particles from experimental data (circles) and Mie scattering theory (line). Each data point shows mean and standard deviation from 32 independent nanoparticles. The experimental cross sections were calculated as the total laser power in the image of a single particle at the CMOS camera divided by the illumination intensity at the particle. The theoretical line was calculated assuming that particles were illuminated by parallel light along the objective’s optical axis, and that all scattering angles with 0.25<N.A.<1.3 were collected (this criterion is for light to be collected by the objective and also pass the rod mirror). (b) The power spectral density (PSD) of noise in the calculated x position (black, left axis) and y position (gray, right axis) of a 100 nm gold particle stuck on the coverslip, illuminated by 3 μW∕μm2 light intensity, at a sampling rate of 110 kHz, corresponding to a Nyquist frequency of 55 kHz. Power spectra of nine sequential traces, each 0.1 s long, were averaged. (c) The light intensity dependence of the total positional noise for a 100 nm gold particle, over the 1.1–55 kHz bandwidth.

To evaluate the lateral resolution of the microscope, the x and y positions of 100 nm gold nanoparticles firmly stuck to a coverslip (as in Fig. 4) were calculated for each image collected during 0.95 s at 110 kHz. The power spectrum of the calculated x position, shown in Fig. 5b, consists of low frequency drift, two resonance peaks near 250 Hz, and a high frequency shot noise floor. The frequencies of the resonance peaks could be altered by adding or removing weights on the sample or the piezostage (but not in other locations), implying that they result from mechanical vibrations within the piezostage. We expect that the low frequency drift and resonance peaks could be reduced by using a more stable stage or by isolating the setup from external noise sources. The microscope resolution, which we define as the rms variation in measured x position over 0.95 s in the 1 Hz–55 kHz bandwidth, is shown as a function of light intensity for a 100 nm gold particle in Fig. 5c. Collecting images at 110 kHz and 1 μW∕μm2 light intensity, rms displacements in x and y were smaller than 1 nm.

To demonstrate the capabilities of the microscope system in a biological context, especially in vivo, we used it to investigate the rotation of the bacterial flagellar motor. The bacterial flagellar motor is a rotary molecular machine with a size of around 50 nm. It is embedded in the bacterial cell membrane and rotates a flagellar filament extending from the cell envelope at several hundreds of Hertz, to propel the cell body in the medium.19 An ∼55 nm hook that connects the motor and the filament works as a universal joint to transfer smoothly the torque generated in the motor to the filament. The speed of the flagellar motor is dependent on the load that it has to rotate, and previous work20 has suggested that particles smaller than 150 nm are required for the motor to rotate at its maximum “zero-load” speed. We chose to use gold nanoparticles 100 nm in diameter as a compromise between minimizing the load on the motor and photodamage to cells caused by the laser illumination, while maximizing the scattering intensity (to achieve high time resolution) and the ratio of particle to cell scattering. We chose red rather than green laser illumination to further minimize photodamage. These gold nanoparticles were attached to the hook in the absence of filaments and used as a label to study motor rotation at sample rates of up to 110 kHz. Figures 6a, 6b show x and y versus time and x versus y traces of a spinning 100 nm particle on the hook under fully energized conditions. The nanoparticle rotated at∼890 Hz, measured by frequency spectral analysis of a 0.1 s trace, in an approximately circular path with a diameter of∼100 nm. This speed is consistent with an extrapolation to near zero load of the previously measured torque-speed relationship of the sodium-driven chimeric flagellar motor.21

Figure 6.

Figure 6

Open in a new tab

Application to a biological sample, the bacterial flagellar motor. (a) x (black) and y (gray) vs time, and (b) xvs y for a 100 nm gold nanoparticle attached to the hook of the flagellar motor, showing 5 ms of data sampled at 109 500 frames∕s (Ref. 26). (c) Complex power spectral density of the spinning bead over a 0.1 s period showing a clear, dominant motor speed.

CONCLUSION

In standard dark-field microscopy, the objective or the condenser delivers a diagonal illumination beam to the sample and the objective images the light scattered from the sample.10, 22 Our type of setup has the advantage of high alignment stability and does not require the use of a condenser, allowing imaging of thick samples and the use of manipulators or other optics above the sample. Only a small fraction of the back focal plane is used to introduce the illumination and remove interfacial reflections, allowing the collected scattered light to span the full numerical aperture of a high-NA objective and ∼90% of the light entering the objective to be imaged. Our microscope offers two features not shared by any other objective-type laser dark-field microscope. First, the optical illumination is symmetric about the optical axis, minimizing distortion of the illumination with small changes in the focal plane and distortion of the image from off-axis illumination. This would also allow for an extension of the particle tracking along the optical axis (z-direction). Second, unlike any microscope using diagonal illumination, all of the collected light is scattered through an angle greater than 90°. Nanoparticles smaller than the wavelength of light scatter symmetrically in the forward (<90°) and backward (>90°) directions, while objects similar to or greater than the wavelength of illumination light scatter primarily in the forward direction. Thus, this type of illumination results in a lower background signal when imaging nanoparticles against a background of larger objects such as cells (as in Figs. 23). For example, an objective based dark-field that introduces oblique light at NA 1.3 (115°), rather than along the optical axis9, 10 would detect around six times more light from a cell, relative to that collected from the gold particle, while a condenser-based dark-field introducing light at NA 1.2 (65°) would detect more than 100 times more light from the cell.

Our setup offers very sensitive (subnanometer spatial and microsecond temporal) resolution using very simple optics. By using nanoparticles of tens to a hundred nanometers in diameter, fast (∼10 μs) movement of molecular motors can be detected. At incident laser intensities above∼2 μW∕μm2, stage vibration rather than shot noise is limiting even at the maximum frame rate of our camera, 110 kHz, and a resolution of a few angstroms should be obtainable with a more stable stage. Intensities ∼104 times higher are tolerated in a typical optical trap, indicating that a considerably higher time-resolution would be possible with an appropriate detector. The practical limit would probably be set by the tolerance of the biological sample to photodamage or heating due to laser absorption by the gold nanoparticle. To detect motor rotation with nanometer accuracy, micron sized beads are generally attached as a marker, with the large bead size required to achieve a sufficient signal∕noise ratio. Recently, the elementary process in flagellar rotation, i.e., step rotation, was detected at extremely slow speed by lowering the energization of the motor.4 To detect the steps at higher rotation rates of several hundred hertz, we need to use a smaller marker to reduce drag because the rate at which the marker accurately tracks the motor position is determined by the hook stiffness (400 pN nm s) divided by the frictional drag coefficient of the marker.23 Estimating the frictional drag of the system and the hook stiffness gives an expected time constant for the bead motion to track the motor position of around 10 μs for a 100 nm nanoparticle. This would be sufficient to detect steps in rotation at speeds of at least 100 Hz, which could be achieved by control of the extracellular medium.24, 25

ACKNOWLEDGMENTS

This work was supported by BBSRC, under Grant No. BB∕E00458X∕1, and by the European Union FP6 Specific Targeted Research, under Project No. 029084 “NANOMOT.” Y.S. was supported by the Uehara Memorial Foundation, Murata Overseas Scholarship Foundation, and JSPS Postdoctoral Fellowships for Research Abroad. B.C.S. was supported by the EMBO Long Term Fellowship and by NIH, under Grant No. R01GM066223.

References

  1. Svoboda K., Schmidt C. F., Schnapp B. J., and Block S. M., Nature (London) 365, 721 (1993). 10.1038/365721a0 [DOI] [PubMed] [Google Scholar]
  2. Finer J. T., Simmons R. M., and Spudich J. A., Nature (London) 368, 113 (1994). 10.1038/368113a0 [DOI] [PubMed] [Google Scholar]
  3. Yasuda R., Noji H., Yoshida M., K.Kinosita, Jr., and Itoh H., Nature (London) 410, 898 (2001). 10.1038/35073513 [DOI] [PubMed] [Google Scholar]
  4. Sowa Y., Rowe A. D., Leake M. C., Yakushi T., Homma M., Ishijima A., and Berry R. M., Nature (London) 437, 916 (2005). 10.1038/nature04003 [DOI] [PubMed] [Google Scholar]
  5. Thompson R. E., Larson D. R., and Webb W. W., Biophys. J. 82, 2775 (2002). 10.1016/S0006-3495(02)75618-X [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Hinterdorfer P. and Oijen A., Handbook of Single-Molecule Biophysics, 1st ed. (Springer, New York, 2009). 10.1007/978-0-387-76497-9 [DOI] [Google Scholar]
  7. Yildiz A., Forkey J. N., McKinney S. A., Ha T., Goldman Y. E., and Selvin P. R., Science 300, 2061 (2003). 10.1126/science.1084398 [DOI] [PubMed] [Google Scholar]
  8. Masaike T., Koyama-Horibe F., Oiwa K., Yoshida M., and Nishizaka T., Nat. Struct. Mol. Biol. 15, 1326 (2008). 10.1038/nsmb.1510 [DOI] [PubMed] [Google Scholar]
  9. Kim S., Blainey P. C., Schroeder C. M., and Xie X. S., Nat. Methods 4, 963 (2007). 10.1038/nmeth1104 [DOI] [PubMed] [Google Scholar]
  10. Nan X., Sims P. A., and Xie X. S., ChemPhysChem 9, 707 (2008). 10.1002/cphc.200700839 [DOI] [PubMed] [Google Scholar]
  11. Dunn A. R. and Spudich J. A., Nat. Struct. Mol. Biol. 14, 246 (2007). 10.1038/nsmb1206 [DOI] [PubMed] [Google Scholar]
  12. Leake M. C., Chandler J. H., Wadhams G. H., Bai F., Berry R. M., and Armitage J. P., Nature (London) 443, 355 (2006). 10.1038/nature05135 [DOI] [PubMed] [Google Scholar]
  13. Mashanov G. I. and Molloy J. E., Biophys. J. 92, 2199 (2007). 10.1529/biophysj.106.081117 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Iino R., Koyama I., and Kusumi A., Biophys. J. 80, 2667 (2001). 10.1016/S0006-3495(01)76236-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Yuan J. and Berg H. C., Proc. Natl. Acad. Sci. U.S.A. 105, 1182 (2008). 10.1073/pnas.0711539105 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Noda N. and Kamimura S., Rev. Sci. Instrum. 79, 023704 (2008). 10.1063/1.2839914 [DOI] [PubMed] [Google Scholar]
  17. Abbondanzieri E. A., Greenleaf W. J., Shaevitz J. W., Landick R., and Block S. M., Nature (London) 438, 460 (2005). 10.1038/nature04268 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Palik E. D., Handbook of Optical Constants of Solids (Academic, New York, 1997). [Google Scholar]
  19. Sowa Y. and Berry R. M., Q. Rev. Biophys. 41, 103 (2008). 10.1017/S0033583508004691 [DOI] [PubMed] [Google Scholar]
  20. Yuan J., Fahrner K. A., and Berg H. C., J. Mol. Biol. 390, 394 (2009). 10.1016/j.jmb.2009.05.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Inoue Y., Lo C. J., Fukuoka H., Takahashi H., Sowa Y., Pilizota T., Wadhams G. H., Homma M., Berry R. M., and Ishijima A., J. Mol. Biol. 376, 1251 (2008). 10.1016/j.jmb.2007.12.023 [DOI] [PubMed] [Google Scholar]
  22. Braslavsky I., Amit R., Jaffar Ali B. M., Gileadi O., Oppenheim A., and Stavans J., Appl. Opt. 40, 5650 (2001). 10.1364/AO.40.005650 [DOI] [PubMed] [Google Scholar]
  23. Block S. M., Blair D. F., and Berg H. C., Nature (London) 338, 514 (1989). 10.1038/338514a0 [DOI] [PubMed] [Google Scholar]
  24. Lo C. J., Leake M. C., and Berry R. M., Biophys. J. 90, 357 (2006). 10.1529/biophysj.105.071332 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lo C. J., Leake M. C., Pilizota T., and Berry R. M., Biophys. J. 93, 294 (2007). 10.1529/biophysj.106.095265 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. See supplementary material at http://dx.doi.org/10.1063/1.3495960 for the movie of Figs. 5a, 5b slowed by 2000 times relative to real time.

Articles from The Review of Scientific Instruments are provided here courtesy of American Institute of Physics

RESOURCES