Reconstruction of a cone-beam CT image via forward iterative projection matching

Abstract

Purpose: To demonstrate the feasibility of reconstructing a cone-beam CT (CBCT) image by deformably altering a prior fan-beam CT (FBCT) image such that it matches the anatomy portrayed in the CBCT projection data set.

Methods: A prior FBCT image of the patient is assumed to be available as a source image. A CBCT projection data set is obtained and used as a target image set. A parametrized deformation model is applied to the source FBCT image, digitally reconstructed radiographs (DRRs) that emulate the CBCT projection image geometry are calculated and compared to the target CBCT projection data, and the deformation model parameters are adjusted iteratively until the DRRs optimally match the CBCT projection data set. The resulting deformed FBCT image is hypothesized to be an accurate representation of the patient’s anatomy imaged by the CBCT system. The process is demonstrated via numerical simulation. A known deformation is applied to a prior FBCT image and used to create a synthetic set of CBCT target projections. The iterative projection matching process is then applied to reconstruct the deformation represented in the synthetic target projections; the reconstructed deformation is then compared to the known deformation. The sensitivity of the process to the number of projections and the DRR∕CBCT projection mismatch is explored by systematically adding noise to and perturbing the contrast of the target projections relative to the iterated source DRRs and by reducing the number of projections.

Results: When there is no noise or contrast mismatch in the CBCT projection images, a set of 64 projections allows the known deformed CT image to be reconstructed to within a nRMS error of 1% and the known deformation to within a nRMS error of 7%. A CT image nRMS error of less than 4% is maintained at noise levels up to 3% of the mean projection intensity, at which the deformation error is 13%. At 1% noise level, the number of projections can be reduced to 8 while maintaining CT image and deformation errors of less than 4% and 13%, respectively. The method is sensitive to contrast mismatch between the simulated projections and the target projections when the soft-tissue contrast in the projections is low.

Conclusions: By using prior knowledge available in a FBCT image, the authors show that a CBCT image can be iteratively reconstructed from a comparatively small number of projection images, thus saving acquisition time and reducing imaging dose. This will enable more frequent daily imaging during radiation therapy. Because the process preserves the CT numbers of the FBCT image, the resulting 3D image intensities will be more accurate than a CBCT image reconstructed via conventional backprojection methods. Reconstruction errors are insensitive to noise at levels beyond what would typically be found in CBCT projection data, but are sensitive to contrast mismatch errors between the CBCT projection data and the DRRs.

INTRODUCTION

Image-guided adaptive radiation therapy (IGART) uses repetitive imaging to observe and track changes in patient anatomy from the initial treatment planning study to the end of the treatment regimen.¹ The imaging data can be used to compile cumulative dose distributions that show the actual patterns of dose deposition in the changing anatomy.² If necessary, the treatment plan can then be adjusted to compensate for any changes that are observed.³

The present imaging paradigm for IGART is the acquisition of daily (or near-daily) CT images⁴ because CT is the core imaging modality for treatment planning, dose calculation, and adaptation. Presently, these images are used primarily for improved setup of targeted soft-tissue structures via 3D∕3D registration,⁵ but IGART has the greater ambition of using them for daily plan adaptation as well.⁶ Because the daily CT images should be acquired just prior to the beginning of each fraction, they are commonly obtained via cone-beam CT (CBCT) imaging systems attached directly to the linear accelerator gantry.⁶ However, this procedure prolongs treatment and delivers non-negligible imaging dose to the patient. For example, 40 daily pelvic CBCTs using 400 projections acquired at standard technique delivers approximately 100 cGy.⁷ While this dose may seem inconsequential in the context of radiotherapy, it cannot be neglected. The general principle of managing imaging dose is to make it as low as reasonably achievable. If an acceptable image can be obtained with less dose, then one should try to do so. Consequently, dose reduction for daily CBCT has become a topic of growing concern.^{5, 8} Furthermore, in the case of CBCT, conventional backprojection reconstruction methods produce images that have more artifacts, more noise, and less accurate CT numbers than the conventional fan-beam planning CT image.⁹ The IGART process would benefit if these drawbacks to daily CBCT imaging could be rectified.

There are three ways to reduce dose in CBCT: (1) Reduce the technique (mA s) at the cost of higher noise in the projections,^{5, 8} (2) reduce the field of view of the projections,¹⁰ and (3) reduce the total number of projections.¹¹ Current research is examining several methods to reduce dose via these strategies, including tomosynthesis,¹² prior image constrained compressed sensing (PICCS),¹³ and volume-of-interest CBCT (VOICT).¹⁰ Tomosynthesis adapts filtered backprojection to handle projection data acquired over less than a full gantry rotation, which reduces the total number of projections. PICCS builds a sparsified image representation that is consistent with a limited set of projection data and then inverts the sparsified representation to obtain the reconstructed image. The VOICT method uses the conventional number of projections, but substantially reduces dose by filtering the beam so that areas outside the VOI receive less radiation. Tomosynthesis and VOICT attempt to reconstruct the CT image entirely from information in the (limited) projection data set, while PICCS additionally uses a prior source CT image for sparsification.

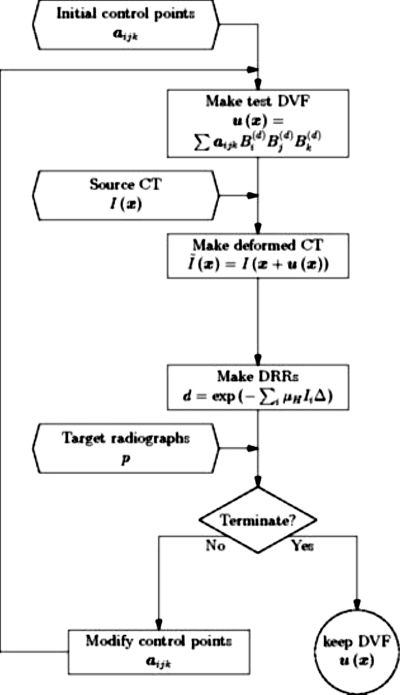
In IGART, each successive CT image adds only incremental information to the original planning CT image. Consequently it should not be necessary, in principle, to obtain a complete new CBCT data set each day. We demonstrate here a novel deformable image registration (DIR) method to reconstruct a CBCT image from a limited number of projections by incorporating prior anatomical imaging knowledge from a planning FBCT into the reconstruction process, thereby reducing acquisition time and imaging dose while maintaining the quality and CT number fidelity of a fan-beam CT (FBCT) image. In our proposed method, we use the planning FBCT image as a source image and then perturb it with a deformation function such that it matches the anatomy recorded in the projection image data set of a subsequent CBCT scan. We reduce the number of CBCT projection images to the minimum number that, in combination with the prior FBCT information, can provide an accurately reconstructed new image. Figure 1 shows a flowchart for the method which proceeds as follows:

• (1)A set of N cone-beam CT projection images are obtained as the target data set;
• (2)A parametrized displacement vector field (DVF) is applied to the prior planning FBCT image;
• (3)A set of N digitally reconstructed radiographs (DRRs) are calculated from the deformed FBCT image using the CBCT imaging geometry;
• (4)The deformation parameters for the DVF are iteratively adjusted until the DRRs optimally match the target CBCT projections;
• (5)The resulting deformed FBCT image portrays the anatomy as it appears during the CBCT scan and can thus be used for IGART in place of the backprojected reconstruction of a complete CBCT scan.

Figure 1.

A flowchart showing how the method takes the initial parameters, the source CT image, and the target radiographs to produce the estimated displacement vector field.

This is essentially a generalization of 2D∕3D rigid registration to incorporate deformation. We will refer to it as CBCT image reconstruction via forward iterative projection matching. It is similar in concept to the projection-to-volume method recently proposed by Long et al.¹⁴

An initial proof of concept for this method, using 2D source images and 1D projections, was reported by Docef and Murphy in 2005.¹¹ To continue developing the method under progressively more realistic conditions, we have carried out two simulation studies using 3D CBCT imaging scenarios. The first study used a synthetic source image to which a known deformation was applied. Synthetic target radiographs representing the CBCT projection data were then generated. The reconstruction method was then applied to the source image and target radiographs and the resulting DVF and deformed source CT image were compared to the known deformation and the known deformed target CT image. The second study was simulated in the same way using an actual pelvic CT image as the source image.

To emulate a realistic data and reconstruction scenario, we added varying levels of noise to the synthetic target projections and altered their contrast relative to the iterated source DRR projections. This way we simulated the kind of DRR∕CBCT projection discrepancies that will exist in the real world and explored the DRR fidelity needed to achieve accurate CBCT reconstruction.

To find the minimum necessary number of CBCT projection images, we systematically reduced the number of projections used in the iterative matching process until a substantial loss of reconstruction accuracy was observed.

Our numerical tests provide a ground truth for the accuracy of the CBCT reconstructed via our method. Under these idealized circumstances, we show here that an accurate reconstruction of the anatomy recorded by the CBCT projections can be obtained with only a small fraction of the total number of projections needed to reconstruct a CBCT image from scratch via backprojection. This shows that successive daily CBCT images can be acquired in considerably less time and with much less imaging dose than a conventional CBCT reconstruction while preserving the CT number fidelity and image quality of the planning FBCT image.

METHOD AND MATERIALS

We begin by defining some terms. We will refer to the initial FBCT image as the source image and the patient’s anatomy at that moment as the source anatomy. This is the “prior knowledge” that will be used by the iterative reconstruction process. We will refer to the patient’s anatomy at some later time as the target anatomy. The CBCT projections of the target anatomy will be called the target projection data set. The anatomy that results from applying the DVF to the source anatomy during the iterative process will be called the deformed source anatomy.

For the present feasibility study we have applied a known deformation to the source CT images to create a simulated target anatomy, from which we have created a synthetic set of target CBCT projection images. We have then used our method to determine the accuracy with which we can recover the known deformation.

We hypothesize that the accuracy with which the actual target anatomy deformation can be reproduced in the deformed source CT image will depend on three factors: (a) The number of target projections and their angular sampling range, (b) the noise in the target images, (c) and imperfections in the DRRs relative to the actual target radiographs, exemplified by contrast differences. We have therefore organized our simulations to test the effect of these three variables.

Source and target CT image data

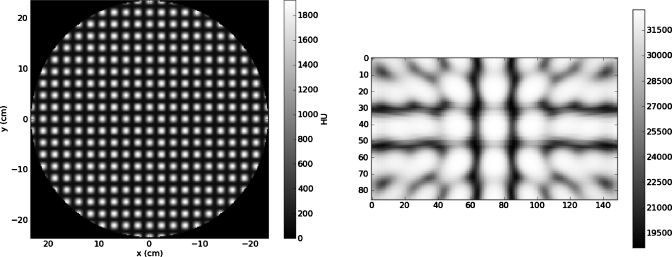
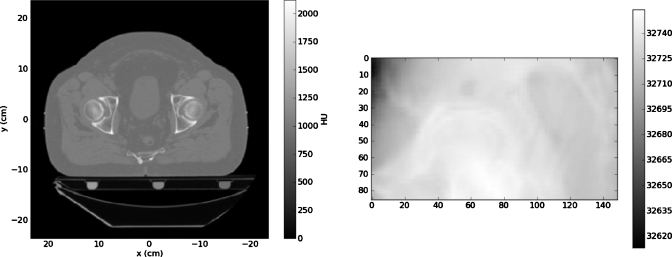
Our simulations used two different 3D image data sets as source CT images: (1) A simple numerical phantom object consisting of a sphere with spatially variable internal texture and (2) a 3D fan-beam CT image of a male prostate cancer patient. The synthetic sphere CT had 256×256×74 voxels of dimension1.844×1.844×3.000 mm³. A slice through the numerical phantom is shown in Fig. 2. A representative projection through this object is also shown in Fig. 2. The pelvic CT image had 512×512×74 voxels of dimension0.9219×0.9219×3.00 mm³, which was downsampled to 256×256×74 voxels. Figure 3 shows a representative pelvic CT slice and a representative projection through this anatomy.

Figure 2.

A slice through the spherical CT image (left) and a projection through the CT image (right).

Figure 3.

A slice through the pelvic CT image (left) and a projection through the CT image (right).

To create a deformed version of the source CT image to represent the target anatomy at a later time, we deformed a region of interest (ROI) having 86×86×30 voxels (154.9×154.9×90 mm³) and centered at the source image center. The deformation was a free-form DVF u(x) that transformed the 3D source image I_S to the target image I_T according toI_S(x+u(x))=I_T(x). The DVF repositions each anatomical point in the source image to its new position in the target image. This DVF and the associated deformed image became the known DVF and target CT image that we attempted to recover via the forward iterative projection matching procedure.

The known DVF had a three-dimensional Gaussian shape as follows:

$$\mathit{u}\left(\mathit{x}\right)=\left(A_x,A_y,A_z\right)\text{exp}\left(-\frac{{\left(x-{\mu }_x\right)}^2+{\left(y-{\mu }_y\right)}^2}{{\sigma }_{xy}}-\frac{{\left(z-{\mu }_z\right)}^2}{{\sigma }_z}\right),$$ (1)

where(A_x,A_y,A_z)=(0,0,−14.75 mm), μ_x=0, μ_y=0, μ_z=0, σ_xy=208.9 mm, andσ_z=70.5 mm. This was applied to each of the two source CT images to create the synthesized target CT images, which were then used to create synthetic sets of target CBCT projection images via DRR ray-tracing.

Digitally reconstructed radiograph projections

DRRs can be made from a CT image by ray-tracing a line integral of x-ray attenuation coefficients from the center of each pixel in the projected image plane back through the CT image to the x-ray source position, taking incremental steps of length Δ along the ray and interpolating the nearby CT numbers at each step to get the local x-ray attenuation coefficient. A pixel value p is calculated according to Eq. 2,

$$p=\text{exp}\left(-\sum _i\mu I\left({\mathit{x}}_i\right)\Delta \right),$$ (2)

where I(x_i) is the CT number at the position of the ith step along the ray, μis the conversion factor from CT number to attenuation coefficient, and Δ is the step length.

From each of the target deformed CT images, we made 64 target projections at equally spaced angular intervals about the superior-inferior axis to simulate the CBCT target projection data. This is the typical cone-beam axial projection geometry. Each projection had dimensions of 232.8×135.2 mm² and had149×87 pixels. We then added noise to the target radiographs and altered their contrast relative to the iterated DRRs to emulate conditions that will be encountered when applying this method to real CBCT data.

Parameterized displacement (i.e., deformation) vector field

To iteratively deform our source FBCT image for the projection matching process, we applied a parametrized model of u(x) that transformed the 3D source image I_S into a deformed source image $I_S^{\prime }$ according to$I_S\left(\mathit{x}+\mathit{u}\left(\mathit{x}\right)\right)=I_S^{\prime }\left(\mathit{x}\right)$. The 3D deformed source image $I_S^{\prime }$ was then used to generate the DRRs for matching against the target CBCT projection images. We used parametric B-splines to modelu(x), thus greatly reducing the dimensionality of the problem.¹⁵ In this representation, the vector field u(x) is expanded on a basis of nth order B-spline functions B⁽ⁿ⁾(x) as follows:

$$\mathit{u}\left(\mathit{x}\right)=\sum _{ijk}{\mathit{a}}_{ijk}B_i{}^{\left(n\right)}\left(x\right)B_j{}^{\left(n\right)}\left(y\right)B_k{}^{\left(n\right)}\left(z\right),$$ (3)

where (x,y,z) are coordinates in the CT image coordinate frame, the subscripts (i,j,k) designate the (x,y,z) B-spline functions, and the B-spline basis functions are defined by the following recursion relations:

$$B_i{}^{\left(n\right)}\left(x\right)=\left[\left(x-x_i\right)∕\left(x_{i+n}-x_i\right)\right]B_i{}^{\left(n-1\right)}\left(x\right)+\left[\left(x_{i+n+1}-x\right)∕\left(x_{i+n+1}-x_{i+1}\right)\right]B_{i+1}{}^{\left(n-1\right)}\left(x\right),$$$$B_i{}^{\left(0\right)}\left(x\right)=1;x_i<x<x_{i+1},$$$$B_i{}^{\left(0\right)}\left(x\right)=0;\text{otherwise}.$$ 4

The control points a_ijk are adjustable parameters in the iteration process. In our tests, we used second order B-splines with up to seven control points uniformly distributed along each axis. The DVF is constructed by evaluating Eq. 3 at points x that correspond to the voxel centers in the deformed CT. The control points a_ijk are free parameters that alter the deformation of the CT.

Iterative matching procedure and similarity metric

The model DVF was iterated via the nonlinear conjugate gradient method (NCGM).¹⁶ The NCGM uses the gradient of the similarity function to update the model parameters. For the proposed method, the similarity function S is the sum of the squared differences of the pixel intensities in all of the DRRs d_i and the target radiographs p_i

$$S=\sum _i{\left(d_i-p_i\right)}^2.$$ (5)

To determine the gradient of the similarity function, the derivative of each test DRR with respect to the DVF model parameters (i.e., the B-spline control points) is needed. Following from Eqs. 2, 3, the derivative of the DRR pixel value (p) with respect to some control point component (a_ijk) is given in Eq. 6

$$\frac{\partial }{\partial a_{ijk}}p={\mu }_{H}p\sum _n\nabla I\cdot \frac{\partial }{\partial a_{ijk}}\mathit{u}\Delta .$$ (6)

The iterative process was terminated when the rate of change of the similarity function dropped below a threshold value. To be explicit, the termination condition is2(S_i−S_i−1)≤ε(S_i+S_i−1).

This iterative matching procedure was carried out in stages beginning with two control points and continuing with three, five, and seven control points. This multiscale technique is a common and effective strategy for avoiding traps in local minima. At each stage, a multiresolution method was employed whereby the number of pixels used in the similarity function was 1∕64, 1∕16, 1∕4, and 1 times the total number of pixels. This also helps defend against trapping in local minima.

Testing matrix and evaluation

We made a set of tests in which we varied three parameters: Projection noise, projection contrast mismatch, and number of projections. Noise levels were 1%, 3%, or 5% of the mean pixel value. Figure 4 shows one of the projections for the 1% noise case for the pelvic CT image. Contrast mismatch was introduced by altering the target projection pixel intensities by the nonlinear gamma function of Eq. 7

$$p=p-\epsilon p_{\text{max}}\text{\hspace{0.17em}sin}\left(2\pi p∕p_{\text{max}}\right),$$ (7)

with ε values of 0.0025 and 0.005, which is also shown in Fig. 4. The numbers of radiographs used were 64, 32, 16, 8, and 4. For each test, the projection matching process was run to convergence, after which the estimated DVF was compared to the known Gaussian DVF using the normalized root mean squared error (nRMSE) between the two as the similarity metric. The similarity of the final deformed source CT image to the known target CT image was also measured via the nRMSE. The nRMSE of an iterated test data set A_i compared to the target data set B_i is defined as

$$\text{nRMSE}={\left[\frac{\sum _i{\left(B_i-A_i\right)}^2}{\sum _i{\left(B_i-\mu \right)}^2}\right]}^{1∕2},$$ (8)

where μ is the average of all the B_i in the target data. For the CT image nRMSE, Aand B represent CT numbers within the ROI, while for the DVF nRMSE, Aand B represent the (x,y,z) components of the DVF within the ROI. Note that the DVF nRMSE calculation was carried out using thex, y, and z components of the all of the vectors of the DVF and not on the magnitudes of these vectors. To obtain a more clinically useful error measure, the difference between the known DVF and estimated DVF was taken to obtain a set of error vectors. Then, the mean and maximum of the magnitude of the error vectors was calculated.

Figure 4.

A projection through the pelvic CT image with a 1% noise level added (left); ε=0.0025contrast mismatch (right).

To establish a gold standard for the accuracy with which the known Gaussian DVF can be estimated, we fitted it directly with a 3D B-spline model with seven control points and calculated the nRMSE. This is the best result one can obtain. We then registered the original source CT images to their known target counterparts using a 3D∕3D B-spline DIR algorithm¹⁷ and calculated the nRMSE for that. This gave us a second gold standard defined by a conventional 3D∕3D registration process. The quality of our DVF estimated via the 2D projection matching process can be compared to these two standards.

RESULTS

Figure 5 depicts the center y-z planes of the ROIs of the source CT image, the known deformed CT image, and the reconstructed CT images for both the numerical phantom and the pelvic CT image. (Note: The reconstructed CT images are for the cases with no noise or contrast mismatch.) A comparison of the resultant images with the source images shows that the method is able to reconstruct the CT image with a visual quality comparable to that of the source CT image. Also, it is difficult to (visually) distinguish the differences between the known deformed CT image and the deformed image resulting from the reconstruction. However, the quantitative assessment which follows reveals some differences.

Figure 5.

The region of interest for the source CT images for the numerical phantom (upper left) and the pelvic CT image (upper right), the known deformed CT images for the numerical phantom (middle left) and the pelvic CT image (middle right), and the resultant CT images reconstructed via projection matching for the numerical phantom (lower left) and the pelvic CT image (lower right) show that the source (FBCT) image quality is preserved.

The 3D Gaussian DVF applied to the two source CT images can be fit by a 3D B-spline model with seven control points per axis with a nRMSE of 0.0227. When the deformed target CT images were registered directly to the source CT images using the parametric B-spline DVF model with seven control points, the Gaussian DVF was recovered with a nRMSE of 0.0271 for the numerical phantom and nRMSE of 0.0299 for the pelvic CT image. These results represent gold standards against which the accuracy of the iterative projection matching process can be compared.

The results using 64 target projections are summarized in Tables 1, 2 for the numerical phantom and pelvic CT image, respectively. (We note that the maximum errors invariably occur around the perimeter of the reconstructed im-age volume, due to edge effects.) Table 3 shows the results for 1% noise with the 64, 32, 16, 8, and 4 target projections for the pelvic CT image. When there is no noise or contrast mismatch in the CBCT projection images, a set of 64 projections allows the known deformed CT image to be reconstructed to within a nRMS error of 1% for both the numerical phantom and pelvic CT image. Under the same conditions, the known deformation is reconstructed to within a nRMS error of 3% for the numerical phantom and 7% for the pelvic CT image. A CT image nRMS error of less than 4% is maintained at noise levels up to 3% of the mean projection intensity for both CT images and under these conditions, the deformation error is 5% for the numerical phantom and 12% for the pelvic CT image. At a 1% noise level, the number of projections can be reduced to 8 while maintaining CT image and deformation errors of less than 5% and 13%, respectively, for the pelvic CT image.

Table 1.

Summary of the DVF and CT image errors for the spherical CT image with 64 target radiographs and varying levels of noise and contrast mismatch.

	DVF nRMSE	CT nRMSE	Mean∕max. DVF error magnitude (mm)
Direct fit	0.0227	0.0116	0.045∕0.396
3D3D registration	0.0271	0.0125	0.063∕0.334
2D3D No noise, ε=0	0.0300	0.0137	0.071∕0.603
2D3D 1% noise	0.0338	0.0170	0.083∕1.31
2D3D 3% noise	0.0499	0.0300	0.128∕1.14
2D3D 5% noise	0.0873	0.0552	0.220∕1.56
2D3D ε=0.0025	0.0560	0.0331	0.146∕0.755
2D3D ε=0.005	0.0924	0.0574	0.241∕0.940

Table 2.

Summary of the DVF and CT image errors for the pelvic CT image with 64 target radiographs and varying levels of noise and contrast mismatch.

	DVF nRMSE	CT nRMSE	Mean∕Max. DVF error magnitude (mm)
Direct fit	0.0227	0.0116	0.045∕0.396
3D3D registration	0.0299	0.0072	0.060∕0.693
2D3D No noise, ε=0	0.0706	0.0108	0.123∕3.35
2D3D 1% noise	0.1071	0.0182	0.185∕4.36
2D3D 3% noise	0.1208	0.0356	0.295∕3.33
2D3D 5% noise	0.1682	0.0630	0.447∕1.96
2D3D ε=0.0025	0.3700	0.1222	0.990∕4.85
2D3D ε=0.005	0.8905	0.2388	2.279∕10.4

Table 3.

Summary of the DVF and CT image errors for the pelvic CT image with 1% noise level added to a varying number of target radiographs.

	DVF nRMSE	CT nRMSE	Mean∕Max. DVF error magnitude (mm)
Direct fit	0.0227	0.0116	0.045∕0.396
3D3D registration	0.0299	0.0072	0.060∕0.693
2D3D 64 projections	0.1071	0.0182	0.185∕4.36
2D3D 32 projections	0.0921	0.0203	0.189∕3.73
2D3D 16 projections	0.1126	0.0272	0.247∕4.62
2D3D 8 projections	0.1316	0.0370	0.309∕4.53
2D3D 4 projections	0.2043	0.0846	0.532∕4.50

For the contrast mismatch, the reconstruction errors for the numerical phantom and pelvic CT image differ greatly. With contrast mismatch, the pelvic CT image was reconstructed with a nRMS error approximately four times greater than that of the numerical phantom for both cases.

DISCUSSION

The method described here, which supplements a limited set of CBCT projection data with prior knowledge from a FBCT image, differs fundamentally from tomosynthesis and other limited projection methods that reconstruct a CBCT image entirely from the projection data set. These other limited projection methods will have more artifacts and image irregularities than a CBCT image reconstructed from a full projection set, which itself is inferior to a FBCT image. Our method preserves the quality and integrity of a FBCT image.

A method similar to ours has recently been described by Hurvitz and Joskowicz¹⁸ but in their approach, the prior information is supplied by an atlas model rather than a patient-specific CT image and they are primarily concerned with bone surface reconstruction for intraoperative purposes. We require accurate reconstruction of all soft-tissue image content, which is inherently a more difficult problem.

With contrast mismatch, the reconstruction accuracy for the deformed pelvic CT image differed greatly from that of the numerical phantom. We hypothesize that this is due to the inherent differences in the CT image contrast. The numerical phantom has a pronounced variation from high CT number to low CT number, resulting in projections with high-contrast deformed structures, while the pelvic CT image has low-contrast deformed structures interspersed with high-contrast structures. In the projections, the apparent deformation of the low-contrast structures can be substantially affected by a slight DRR∕projection contrast mismatch. From the results for the pelvic CT image, we conclude that when the deformed anatomical structures appear with low contrast in the CBCT projections, the method requires accurate projection simulation.

The results for both the numerical phantom and the pelvic CT image show that the method is tolerant of noise levels that exceed what is found in actual CBCT projections. This is consistent with the earlier findings of Murphy et al.¹⁷ for 3D∕3D CT deformable registration and may allow for an increase in noise during image acquisition in order to lower imaging dose to the patient.

Using as few as eight images (with a 1% noise level), the pelvic CT image could be reconstructed with reasonable accuracy (nRMS error of 0.0370). The typical CBCT scan consists of 600–700 images. Our results show that if a prior FBCT image is available, then this number can be reduced by an order of magnitude or more. This shortens the scan time and allows a significant reduction of imaging dose to the patient.

All optimizations were carried out using an Intel Core i7 2.8 GHz processor. A complete calculation required from 47 to 194 iterations, each iteration requiring the calculation of anywhere from 136 to 238 DRRs. For the numerical phantom, the time to run 194 iterations of 238 DRRs was 19.61 min and for the pelvic CT image the corresponding time was 20.75 min. These times are not practical for clinical use in online IGART therapy. Profiling the code has shown that 90% of this time is spent doing DRR calculations. We are consequently porting the DRR calculations to a graphics processing unit that is capable of computing 160 DRRs per second. This will bring running times below 6 min for the most computationally intensive cases.

Our feasibility study has so far relied on numerical simulations to maintain a ground truth for accuracy assessments. A real clinical reconstruction case will present additional complications. For example, CBCT projection images receive considerable scatter on top of the directly attenuated x-ray flux. This scatter is responsible for the degradation of CT number in CBCT images reconstructed via backprojection. For our application, it reduces the contrast in the projections. However, unlike scatter correction methods for backprojection, in our method we do not need to remove the scatter, we only need to match it approximately by adding a scatter contribution to the DRRs. To determine the scatter contribution exactly would require a Monte Carlo calculation for each patient, which would be prohibitively time-consuming. We anticipate, though, that for our purposes we can use a generic first-order scatter approximation made a priori using a representative patient’s anatomy and the known imaging geometry. Contrast in the projections will also be affected by beam hardening, which will not be so readily mimicked in the DRRs. The present study of contrast mismatch effects gives us some guidance on how accurately we must compensate these effects.

We presently use parametric uniform B-splines to reduce the dimensionality of the DVF. This can have the unwanted side effect of smoothing out the fine structure in the DVF. To reproduce locally complex or discontinuous DVF features can require an impractically large number of uniformly spaced control points. We will address this limitation through the use of nonuniform rational B-splines to enhance the DVF resolution where it is most needed.

Reconstruction methods that incorporate prior information tacitly assume that the basic anatomical structures remain more or less unchanged from one day to the next, aside from shape differences. In particular, they assume that there are no image features that are present one day but not the next. This will not be the case if, for example, there are significant differences in bowel gas from one day to the next. This problem confounds all deformable registration processes for pelvic CT images. Methods to deal with it are being researched, but it remains a challenge for image registration.

Even in clinical cases involving mismatched image contents (such as bowel gas) that will complicate the complete reconstruction of a CBCT via projection matching, the method will still have utility in soft-tissue image-guided target setup of, e.g., the prostate. In this case we are simply performing a 2D∕3D (semi)rigid registration of a low-contrast soft-tissue structure to find its translational shifts.

SUMMARY

We conclude that CBCT reconstruction via forward iterative projection matching, using prior FBCT data, has the potential to maintain FBCT image quality in a CBCT image while reducing the number of projection images and allowing for increased noise in them. One can then reduce total acquisition time and imaging dose to the patient with no adverse impact. This can be particularly important when imaging is done on a (near) daily basis.