Ossicular motion related to middle ear transmission delay in gerbil

Abstract

The middle ear transmits sound efficiently from the air in the ear canal (EC) to the fluid filled cochlea. In gerbil, middle ear transmission produces a constant pressure gain between the EC and the cochlea of ~ 25 dB from 2 to 40 kHz, and a delay-like phase corresponding to a ~25 – 30 μs delay. The mechanisms by which the air-born signal is collected and delivered to the cochlea are not thoroughly understood, and the source of the delay is controversial. We investigated these issues by observing ossicular motion along a single line of sight, roughly parallel to the EC and perpendicular to the stapes footplate. Measurements were made at the umbo, the lateral process of the manubrium, across the malleus-incus joint, at the long process of the incus, and the stapes head. While the overall delay between EC pressure and stapes velocity was fairly constant with frequency, subcomponents of the delay were frequency dependent. Up to ~ 17 kHz, most of the overall delay was between the EC and umbo with a much smaller contribution along the ossicles, whereas in the range from ~17 to 30 kHz, more of the overall delay was along the ossicles.

1. Introduction

The middle ear efficiently transmits sound energy to the inner ear, and the simplest explanation of its operation is as a lever whose action results in an increase in pressure (from ear canal to cochlea) and a decrease in volume velocity (velocity × area) from umbo to stapes (Rosowski, 2003). This leveraging allows for impedance matching between the relatively small acoustic impedance of air in the ear canal and the relatively large cochlear input impedance. In gerbil, the pressure gain has been observed to be quite flat with frequency from 1–2 kHz to at least 40 kHz (Olson, 1998; Dong and Olson, 2006). However, a fundamental observation that was at odds with the simplest lever model was that the sound stimulus traveled through the middle ear with substantial phase accumulation. The phase varied approximately linearly with frequency, a relationship that corresponds to a frequency-independent delay. In gerbil, it takes ~ 25 μs for the sound to travel from the ear canal close to the umbo to the scala vestibuli (SV) behind the stapes (Olson, 1998). These observations, and related observations in the cat (Puria and Allen, 1998) seemed to point to the tympanic membrane (TM) for producing the delay (Parent and Allen, 2007) because of its known wave-like motion, which would result in traveling-wave delays (Tonndorf and Khanna, 1972; Decraemer et al., 1989; Decraemer, 1999). However, a series of experiments aimed at altering the delay through stiffening the TM (Kachroo et al., 2004; Aarnisalo et al., 2010) did not produce the expected changes; moreover, the speed of the waves observed on the TM seemed too slow to be responsible for the middle ear transmission delay (Rosowski et al., 2009; de La Rochefoucauld and Olson, 2010). Thus, the source of the middle ear delay remained uncertain.

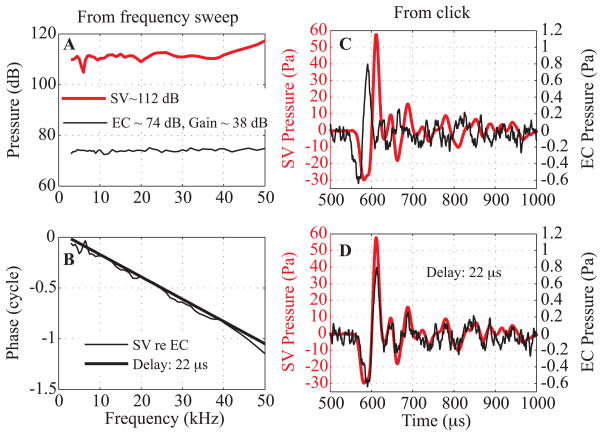
Fig. 1 illustrates the basic observations that motivated this study: SV pressure measured close to the stapes compared to the ear canal (EC) pressure measured close to the umbo in response to tones (A, B) and a click (C, D). The pressures were measured using micro pressure sensors developed in the laboratory (Olson, 1998). The stimulus for Fig. 1 was delivered with a sound source sealed to the ear canal (termed closed-field configuration), with pars flaccida (PF) closed and the bulla open. In response to tones (Fig. 1A), the SV pressure variation was less than 2 dB from 2 to 40 kHz, except for a sharp 5 dB notch at 6–7 kHz. The ~ 38 dB gain (SV relative to EC pressure) is higher than the ~ 25 dB average but is consistent given the +/− 10 dB uncertainty known to exist in the micro pressure sensor calibration (Olson, 1998; Dong and Olson, 2006). The phase-vs-frequency response (Fig. 1B) was close to a straight line from 8 to 50 kHz, with a slope corresponding to a 22 μs delay. At ~ 6–7 kHz there was a ripple in phase, corresponding to the amplitude notch. This feature might be a result of a resonance involving the volume of air within the middle ear cavity and the hole in the bulla. Ravicz et al (Ravicz et al., 1992) have described how variations in the size of the bulla opening can lead to variations in the resonance. EC and SV pressures in response to a click are in Fig. 1C (same ear as A, B). In Fig. 1D, the EC pressure has been shifted 22 μs, resulting in the two pressure waveforms overlapping nearly perfectly. The preservation of the time waveform is indicative of a linear system whose frequency response has broad bandwidth and delay-like phase, and is as expected given the frequency responses in A and B. The flat amplitude, delay-like phase and click responses indicate that over a wide range of frequencies, the middle ear and its cochlear termination have the properties of a frequency-independent transmission line. The primary goal of the present project was to investigate the source of the delay by measuring velocity along the middle ear path, from the umbo to the stapes head.

Fig. 1. EC and SV pressure responses to tone and click stimuli (color online).

Responses to tones: A: EC (thin line) and SV (thick red line) pressures. B: SV re EC pressure phase (thin line) compared to a theoretical delay of 22 μs (thick line). C: Responses to a click stimulus measured in the EC (thin line) and in the SV (thick red line), same animal as A&B. D: EC click response was shifted 22 μs to overlap the SV click response. Sound stimulation was closed-field with bulla open. EC pressure measured close to the eardrum with a micro pressure sensor, SV pressure measured adjacent to the stapes with a micro pressure sensor.

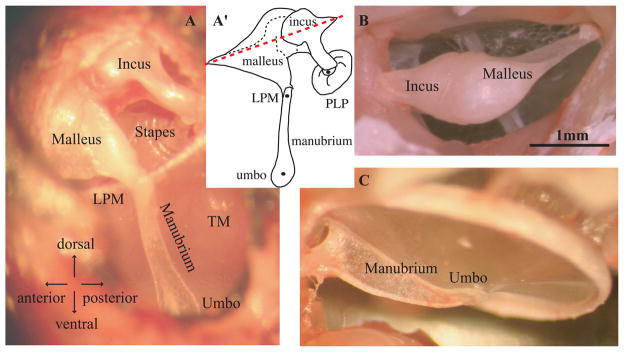
We recorded ossicular motion along what can be thought of as the transmission direction through the middle ear, parallel to the ear canal, and nearly perpendicular to the TM and the stapes footplate. Fig. 2A and its cartoon outline in A′ show the approximate direction of observation. In the classic view of ossicular motion, the malleus and incus are thought to rotate around an axis through their heads as illustrated by the dashed line in Fig. 2A′. Seen from the front as in panel A, the axis is not obvious, but from the back view in Fig. 2B, the narrow attachment points of the malleus and incus to the wall of the bulla suggest a structure that would rotate about the long axis through these points. These properties of the gerbil anatomy have been discussed before (Rosowski et al., 1999). Panel C is included to show that the manubrium has a reinforced blade-like structure, becoming flattened at the umbo. The anatomy and the classic view of middle ear transmission guided our experimental approach. On the other hand, the anatomy and classic view do not predict delay and one of our major goals was to better understand the source of this delay.

Fig. 2. Anatomy of the ossicular chain in gerbil (color online).

A, A′: View and corresponding sketch through widened ear canal shows transmission path of sound stimulus through the middle ear. B: View from the opposite side in an excised temporal bone shows how incus and malleus are attached to the bulla. On the malleus (right side) a blade-like structure (gonial) terminates in a thin bony attachment. The narrow attachment points and long geometry suggest a rotating motion would occur, as in the classic view of ossicular motion (axis indicated in A′). C: View of the tympanic membrane (TM) from the open bulla, where the manubrium has a reinforced blade-like shape except at the umbo where it is flattened at the “spoon.” PLP: plate of the lenticular process of the incus, LPM: lateral process of the malleus.

A recent study showed that the SV pressure was proportional to the piston component of the stapes velocity (Fig. 9 in (de La Rochefoucauld et al., 2008)): the SV pressure to stapes velocity amplitude ratio was flat from 3 to 30 kHz and their relative phase was ~ 0 over the same frequency range. With this understanding, we used stapes velocity, rather than SV pressure, as our final point of measurement. To observe the ossicles, we widened the EC and opened the TM’s pars flaccida as shown in Fig. 2A and described below. In order to view through the ear canal, the sound system couldn’t be sealed to the EC entrance (as for a closed-field configuration), and was placed close to the entrance (open-field configuration). These variations on the closed-field conditions of the measurements highlighted in Fig. 1 diminished the crisp delay-like relationship and nearly constant gain between EC pressure and stapes velocity, particularly at frequencies below ~ 7 kHz. Nevertheless, a fairly constant delay of ~ 25 μs was still apparent between EC (close to umbo) and stapes.

From this starting point, motion measurements were made at intermediate points in order to trace the delay along the ossicles. Measurements at the umbo, lateral process of the malleus (LPM) and long process of the incus (LPI) showed that up to a frequency of ~ 17 kHz most of the delay accumulated between the EC (close to umbo) and umbo, with little delay from umbo to incus. In contrast, above ~17 kHz, substantial delay accumulated along the ossicles. A significant delay occurred between the umbo and the LPM, seemingly related to the bending motion of the manubrium (de La Rochefoucauld and Olson, 2010). There was also a significant delay across the malleus-incus joint (MIJ), with additional small delays along both the malleus and incus, indicating that they do not move strictly as rigid bodies. The umbo moved with an amplitude almost twice as large as the LPM, and the LPM moved with a slightly larger amplitude than the LPI; these amplitude relations are as expected if motion of the ossicles is a rotation about the axis noted above.

As we have shown previously, there was a small amplitude increase and almost no phase change across the pedicle that bridges the LPI and the plate of the lenticular process (PLP) (de La Rochefoucauld et al., 2008). The PLP is part of the incus and forms a tight cap onto the stapes head. A very narrow layer between the PLP and stapes is the actual incus-stapes (IS) joint; see figures in (de La Rochefoucauld et al., 2008) and (Funnell et al., 2005). Because of this tight coupling between the PLP and the stapes head, we have assumed that the PLP and stapes move together (de La Rochefoucauld et al., 2008). Previous work showed a close correspondence between PLP velocity and intracochlear pressure close to the stapes, supporting the view that the stapes and PLP move together (de La Rochefoucauld et al., 2008). Measurements in chinchilla and cat also support this view (Guinan and Peake, 1967; Ruggero et al., 2007). Thus relative motion between the stapes and incus-body is more likely to occur across the pedicle between the LPI and PLP than across the actual IS joint. In fact, the relative motion across the pedicle seems to have species dependence, with more motion in chinchilla (Ruggero et al., 2007) than in gerbil (de La Rochefoucauld et al., 2008). In the present work we do not present true stapes motion data, all the “stapes” measurements are actually PLP measurements. In light of the background above, we refer to this position as stapes(PLP).

Above 30 kHz, motion of the ossicles often showed phase reversals (phase-frequency slope positive rather than negative) and substantial inter-animal variability. It has been proposed that at high frequencies the basic mode of ossicular motion changes in some species (Puria et al., 2007) and complexity of ossicular motion is well documented (Gyo et al., 1987; Decraemer et al., 1991). Thus, the observations made with a one-dimensional view appear to be useful in describing the path for sound transmission through a wide frequency range, up to ~ 30 kHz.

2. Materials and methods

2.1. Stimulus and data acquisition

The Tucker Davis Technologies data acquisition system used in these experiments was described recently (de La Rochefoucauld et al., 2008). Measurements were performed under open-field stimulation using a Sony earphone (~ 1cm diameter) oriented towards the EC, about 1.5 cm away. Either a ¼″ Brüel & Kjær (BK) microphone or a ½″ BK microphone with probe tube was used to calibrate the sound field ~1 cm from the EC entrance, and 0.5 cm from the speaker. (As noted above, the Fig. 1 experiment used closed-field stimulation. Methods for this experiment were as in (Olson, 1998).) Two stimuli were used: i) frequency sweeps, which have the benefit of showing the response at all the frequencies and ii) clicks, which make the delay very apparent. Tones were set at levels between 80 and 100 dB SPL. A series of clicks was produced by repeatedly delivering a 10 μs voltage pulse to the speaker. The resulting signals (EC stimulus and motion responses) were acquired and averaged (~ 430 averages was typical) using a 1 GHz oscilloscope (LeCroy, LC 534, Chestnut Ridge, New York). A perfect click of duration T has a nearly flat spectrum up to a frequency of ~1/(4T) and then drops off slowly, crossing zero at a frequency of 1/(2T). Due to the frequency response of the speaker and EC, our voltage click did not produce a perfect acoustic click in the EC but nevertheless was fairly broadband from ~ 5 to 28 kHz.

2.2. Technical aspects of velocity and pressure measurements

Velocity was measured using two different interferometers. Both systems were described previously (de La Rochefoucauld et al., 2008). For Exp # 41, 43, 44, 45, 47, 48, 49 and 59 the confocal microscope/heterodyne laser interferometer developed in the laboratory (Khanna et al., 1996) was used. The sound system was mounted on the same post as the animal. Accurate coordinates of the measurement positions were saved. The animal and sound system could be rotated. With this configuration, we measured the velocity at many points from the umbo to the PLP. Reflecting beads were not needed, allowing for more freedom in choosing measurement locations. For Exp# 48, a miniature pressure sensor was glued to the EC entrance, allowing simultaneous measurements of velocity and EC pressure. For Exp# 50, 51, 53, 55, 57 and 58 a Polytec interferometer (Polytec, sensor head OFV-534 with controller OFV-5000-VD06) was used. The ossicular velocity was measured at landmark locations such as the umbo, the LPM and the PLP. In this configuration pressure in the EC was measured simultaneously with the velocity, using miniature fiber-optic based pressure sensors developed in the laboratory (Olson, 1998). The pressure sensors are ~ 145 μm in diameter, allowing their insertion inside the ear canal close to the umbo. The sensitivity of the sensors is known to be stable throughout the course of experiments, based on repeatability of measurements over many hours. However, their absolute calibration (pressure/voltage output) is at an uncertainty level of +/− 10 dB. A delicate (micrometer in thickness) plastic membrane is at the very tip of the sensor. The uncertainty is caused by a combination of temperature variations and susceptibility of the membrane to small perturbations. Calibrations done before and after experiments often differ by 10 dB and sometimes more, if a sensor is damaged. Calibration changes occur across frequency and do not influence the phase, although in rare instances a half-cycle jump occurs (at all frequencies – this corresponds to a sign change). This did not occur in the present experiments. With room-temperature preparations and several repeats of calibration better calibration control is possible (Nakajima et al., 2008) but has not been attempted in in-vivo experiments.

In the present experiments the sensor was inserted parallel to the manubrium, and positioned above the umbo at a distance of ~ 0.5 mm. Variations in ear canal pressure along the ear canal and radially across it were described in (Ravicz et al., 2007), and showed that the radial variations were very small below 60 kHz, and the longitudinal variations small below 30 kHz. In Figs. 1, 3(D,F), 4, 5, 9 and 10 pressure was measured within the EC close to the umbo with a pressure sensor (Pec) and Pec is the reference for delay and transfer functions in these figures. In contrast, the reference pressure used in Fig. 3H was measured outside the EC with a BK microphone (Pstim) (because Pec was not measured in this experiment). As noted above, the sound stimulus was calibrated ~ 1cm outside the EC entrance by a BK microphone (except in the experiment of Fig. 1) and this is how Pstim was measured in Fig. 3H.

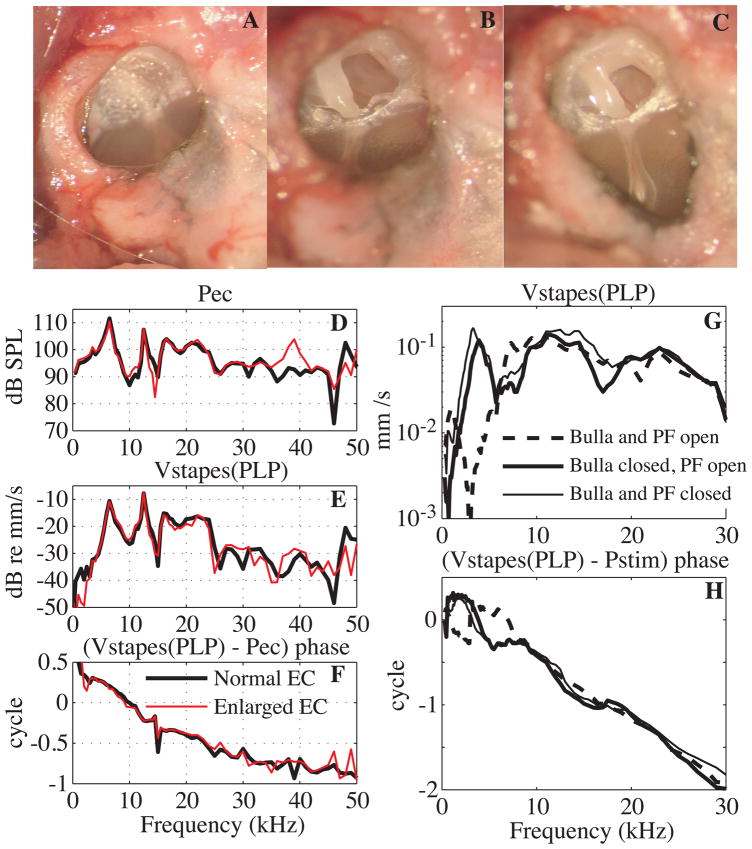
Fig. 3. Surgical approach and its effects (color online).

A: View of the EC entrance with intact PF. B: PF opened widely; the malleus and incus were then visible. C: the EC entrance was enlarged to visualize the manubrium and umbo. D, E, F: Effect of enlarging the EC opening. D: EC pressure close to the umbo. E: stapes velocity, measured at the PLP and denoted stapes(PLP). Conditions as follows: bulla and PF open with a normal (thick black line) and an enlarged (red thin line) EC entrance. F: Stapes(PLP) velocity relative to EC pressure phase (Exp#53, R# 38 and 51). G, H: Effect of the PF opening. G: Stapes(PLP) velocity amplitude. H: Phase relative to the stimulus pressure (Pstim). Conditions as follows: bulla and PF open (dashed line), bulla closed and PF open (thick solid line), bulla and PF closed (thin solid line). (Same experimental data as Fig. 8 in (de La Rochefoucauld et al., 2008): Exp#3 R#18, 26, 28.)

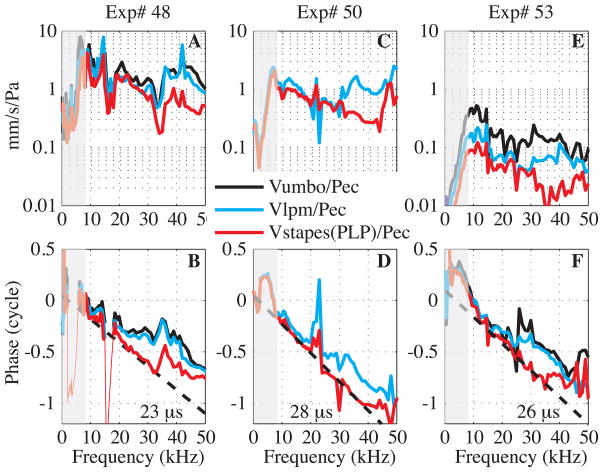
Fig. 4. Transmission through the middle ear from EC pressure to stapes (color online).

Experimental results from three experiments. A, B: Exp# 48 R#13, 25, 28, C, D: Exp#50 R#20, 21, E, F: Exp#53 R#39, 44, 51. A, C, E: Velocity amplitude measured at the umbo (black), at the LPM (cyan) and at the stapes(PLP) (red) relative to EC pressure measured close to the umbo. (Umbo velocity was not measured in Exp#50.) B, D, F: Umbo (black), LPM (cyan) and stapes(PLP) (red) velocity relative to EC pressure phase compared to the theoretical delay curve (dashed line). When relative phase responses presented large notches (red thin line in B), points were removed. Experimental conditions: alive, EC enlarged, PF and bulla open for all. Sound level was set outside the EC to ~ 90–100 dB SPL, see appendix for details on experimental conditions.

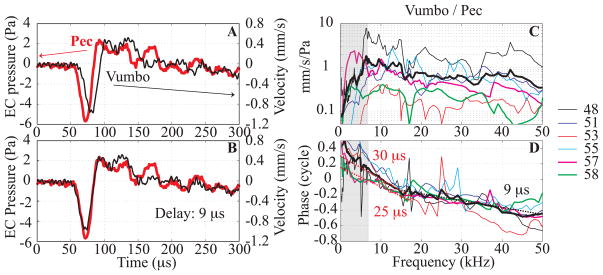
Fig. 5. Umbo velocity relative to EC pressure (color online).

Responses to a click stimulus (A, B) and to tones (C, D). A: Umbo velocity (black thin line), EC pressure measured close to the umbo (red thick line). B: The umbo velocity response has been shifted 9 μs to line up with the EC pressure. (Exp# 58, R#25). C: Umbo velocity amplitude relative to EC pressure (mm/s/Pa) for six experiments. The thick black line is the averaged amplitude response. D: Umbo velocity phase relative to the EC pressure phase. The dashed thick lines correspond to 9 μs, 25 μs and 30 μs delay. Except for Exp# 57 and 58 (for which both the bulla and the PF were closed or vented), data below ~ 7 kHz were affected by the open bulla. Color code for C, D: Exp# 48 R#28 (black), Exp#51 R#20 (blue), Exp# 53 R#40 (red), Exp#55 R#11 (cyan), Exp#57 R#34 (magenta), Exp#58 R#37 (green). Similar results were obtained with the animal alive or a few hours post mortem. See appendix for details on experimental conditions.

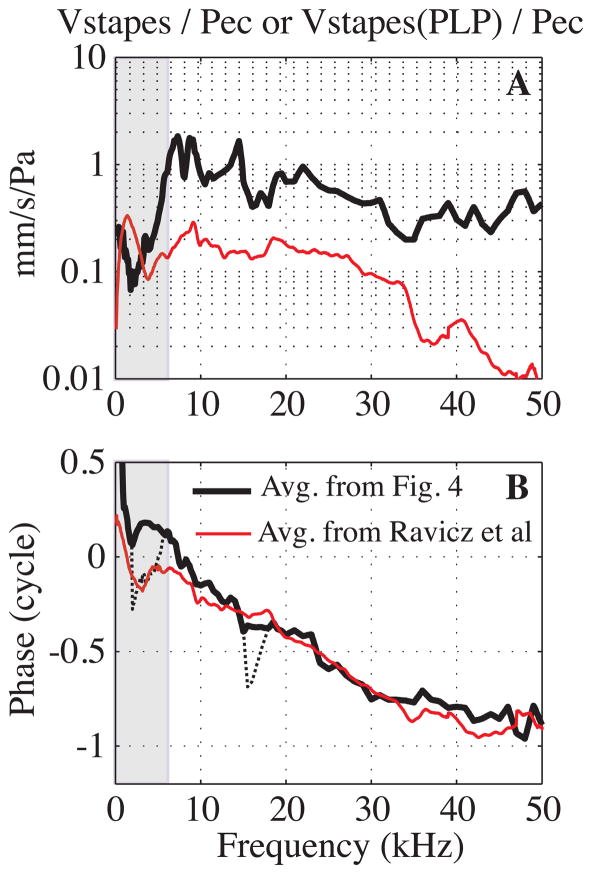
Fig. 9. Grouped results from the literature: stapes velocity relative to EC pressure (color online).

A: Amplitude. The thick black line is the average of our data from Fig. 4 (Exp#48, 50 and 53). The thin red line is from (Ravicz et al., 2008), as presented in their Fig. 12. B: Phase. The black thick line corresponds to the average phase from our Fig. 4 data with Exp#48 phase jump excluded and the thin black dotted line includes the phase jump in the average. The thin red line is from Ravicz et al.

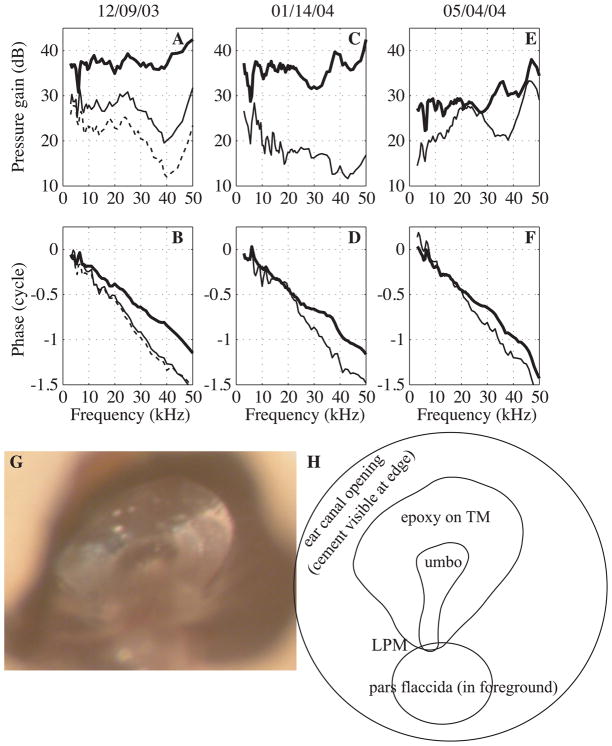
Fig. 10. Middle ear transmission with altered TM.

SV pressure relative to EC pressure, before and after epoxy was applied liberally to the manubrium and surrounding area. A, C, E: Pressure gain, SV re EC. B, D, F: Phase, SV re EC. G: picture taken through the EC following the experiment illustrating the epoxy on the TM. H: corresponding sketch. Conditions as follows: normal (thick line), after the first application of epoxy (thin line) and after the 2^nd application of epoxy (thin dashed line). Results are from three experiments.

To compare pressure and velocity measurements, we needed to account for filtering and delays in the opto-electronic processing of the interferometers. A similar experiment to one done previously was performed to determine the needed correction for each interferometer (de La Rochefoucauld et al., 2008). In brief, a pressure sensor was stimulated with sound in air and the motion of the membrane was measured on one side with the interferometer and on the other with the sensor’s fiber optic system. The delay of the Polytec system was 8 μs, with no correction needed for the frequency response of the amplitude. Polytec provided an approximate delay (11 μs) as part of the factory specifications, and the user is directed to return the unit to the factory for testing if an exact delay number is needed. With the interferometer developed by S. Khanna, a small amplitude correction and a delay of 14 μs had to be taken into account.

2.3. Animal preparation

Experimental results presented here are from 11 live gerbils (Exp# 41, 43, 45, 47, 48, 49, 50, 51, 53, 57 and 59) and three a few hours post-mortem (Exp#44, 55, 58). The care and use of animals were approved by the Institutional Animal Care and Use Committee of Columbia University.

The animal (50–70g in mass) was first sedated with ketamine (40 mg/kg) and then deeply anesthetized with sodium pentobarbital (initial dose 60 mg/kg; supplemental dose 10 mg/kg). Buprenex was used as an analgesic; the initial dose (0.2 mg/kg) was renewed every 6 h. The animal was lying on a heated blanket to keep its body temperature at 37°C. A head holder was cemented to the top surface of the skull to secure the animal’s position during surgery and measurement. A tracheotomy was performed to maintain a clear airway. The external ear canal was cut short to its bony end. To measure the velocity responses along the middle ear path, the ossicles were viewed through the EC entrance. PF was not transparent enough to view the ossicles through it (Fig. 3A) and so was opened widely using a small hook in most experiments (Fig. 3B). For Exp# 43, the PF was sealed using saran wrap while for Exp# 57 and 58, PF was not opened. The open PF allowed measurements from the LPM to the PLP of the incus. As described above, this location is referred to as stapes(PLP).

The view through the open PF permitted direct measurements of the plunging motion of the stapes(PLP) under open-field stimulation. However, this view was not wide enough to measure motion along the manubrium and at the umbo. Therefore the EC entrance was enlarged using a scalpel and the resulting view is illustrated in Fig. 3C. For most of the experiments, the bulla was open (Exp# 41, 45, 47, 48, 49, 50, 51, 53 and 55) but for Exp# 43 and 44, the bulla opening was sealed with clay and for Exp# 57, 58 and 59, the bulla was not opened at all. For Exp# 58 the middle ear was vented by drilling a small hole in the bulla wall. We tabulate the experimental conditions in Appendix A.

Appendix A.

Experimental conditions of data used in the paper1

Exp #	R #	SPL	Conditions: BK, set-up, alive vs post mortem
41	3, 15, 39	80	MC, ½″ BK with probe tube, alive EC enlarged, PF open, Bulla open
43	17, 22, 23	80	MC, ½″ BK with probe tube, alive EC enlarged, PF re-closed, Bulla sealed
44	14, 23	80	MC, ½″ BK with probe tube, 3–4hrs post mortem EC enlarged, PF sealed, Bulla closed
45	12, 17, 21, 22, 23, 26, 27	80	MC, ½″ BK with probe tube, alive EC enlarged, PF open, Bulla open
47	17, 24, 25, 29, 30	80	MC, ½″ BK with probe tube, alive EC enlarged, PF open, Bulla open
48	13, 16, 22, 23, 25, 28	100	MC, ¼″ BK, Pec, alive EC enlarged, PF open, Bulla open
49	4, 10, 12, 15, 22, 23, 26, 28, 30, 32, 35	80	MC, ¼″ BK, alive EC enlarged, PF open, Bulla open
50	20, 21	100	PC, ¼″ BK, Pec, alive EC enlarged, PF open, Bulla open
51	20	95	PC, ¼″ BK, Pec, alive EC enlarged, PF open, Bulla open Bulla wall broken
53	38	90	PC, ¼″ BK, Pec, alive Normal EC opening, PF open, Bulla open
	39, 40, 44, 51	90	PC, ¼″ BK, Pec, alive EC enlarged, PF open, Bulla open
55	11	90	PC, ¼″ BK, Pec, 2hrs post mortem EC enlarged, PF open, Bulla open
57	34	90	PC, ¼″ BK, Pec, alive EC enlarged, PF closed, Bulla closed
58	25	Click 3V, 10μs duration	PC, ¼″ BK, Pec, 3hrs 30 min post mortem EC enlarged, Bulla vented, PF closed
	37	90	PC, ¼″ BK, Pec, 4hrs 30 min post mortem EC enlarged, Bulla vented, PF closed
59	7–10, 12, 14–16, 27–30	80	MC, ¼″ BK, alive EC enlarged, PF open, Bulla closed

PC – Velocity measurement using the Polytec interferometer

MC – Velocity measurement using the confocal heterodyne interferometer developed in the laboratory by Shyam Khanna.

SPL = Sound pressure level set at ~ 1cm from the EC entrance

Velocity was measured along the path with two viewing angles to maintain the best direct view, perpendicular to the flat part of the umbo and also to the stapes footplate (see Fig. 2A). With the first view measurements at the umbo, along the manubrium and the malleus were performed. Then usually the animal was rotated ~ 20 degrees to have the stapes footplate perpendicular to the viewing axis (= laser axis), and measurements at the PLP and along the incus were made. The stability of the preparations was checked by repeat measurements during the course of the experiment.

2.4. Changes in responses due to surgical openings

After opening the bulla and placing a silver electrode on the bone of the round window, the compound action potential (CAP) response to tone pips (0.5 to 40 kHz) was measured to gauge the consequences that opening the PF and enlarging the EC had on the hearing. After opening PF, CAP changes were less than +/− 5 dB, as illustrated in Fig. 2 of (de La Rochefoucauld et al., 2008). The effect of enlarging the EC on stapes(PLP) velocity and EC pressure was studied in Exp # 53. The EC pressure close to the umbo, and stapes(PLP) velocity were measured before and after enlarging the EC entrance, with both bulla and PF open. Results are presented in Figs. 3D–F: the EC pressure measured close to the umbo (Fig. 3D), the stapes(PLP) velocity amplitude (Fig. 3E) and their relative phase (Fig. 3F). After enlarging the EC entrance, amplitudes and relative phase stayed nearly the same. Thus, valid measurements could be made with an enlarged EC entrance since CAP thresholds, stapes(PLP) velocity, EC pressure and middle ear delay were almost unaffected.

Figs. 3G and H show the effect of the bulla and PF openings on stapes(PLP) velocity, amplitude (3G) and phase (3H). The amplitude results were shown previously (de La Rochefoucauld et al., 2008). In Fig. 3H the stimulus pressure that was the reference for the velocity results was measured ~ 1 cm from the EC entrance, which explains the long delay seen in the curves. After opening the bulla, the velocity amplitude presented a deep notch at 3 kHz accompanied by a shift of + 0.5 cycle in the phase response. The amplitude response did not change much for frequencies above 7 kHz, and was relatively flat. Closing the bulla while keeping PF open eliminated the notch and phase shift at 3 kHz, thus extending the frequency region of relatively flat stapes(PLP) response to lower frequencies. The umbo velocity had similar opening-dependent changes as the stapes(PLP); when the openings were closed, the umbo velocity amplitude was relatively constant over a wide frequency range (above 3 kHz) compared to when the openings were open (~ flat response above 7 kHz). Evidence for this will be seen in Fig. 5, which shows results for which the bulla and PF were both closed and open. The frequency dependence of the observed effects of openings can be understood as follows: The stimulus to the TM is the pressure difference across it. With an open-field sound stimulation and an open bulla, the TM is driven from both sides: sound travels through the EC and reaches the “front” of the TM and the sound travels into the open bulla, reaching the “back” of the TM. In contrast, with a closed-field stimulation, the back of the TM is not driven. The effect of the open-field stimulation with an open bulla is more substantial at low frequencies since the “back” pressure will be more attenuated at high frequencies (due to the shadowing of structures) than at low frequencies (for which shadowing is diminished due to diffraction). At low frequencies, the effect of the PF being open with bulla closed can be explained as a change in driving pressure across the TM as discussed in (Voss et al., 2001b; a). Thus, the open-field stimulus pressure was roughly equivalent to a closed-field stimulus pressure at frequencies above ~ 7 kHz (wavelength of ~ 5 cm). In summary, when using an open-field stimulation with the bulla open, with or without PF open, the ossicular velocity was affected at frequencies below ~7 kHz. Thus, when velocity is related to the EC pressure, frequencies above ~ 7 kHz can be considered as normal. However, because the velocities along the ossicular path are downstream of the affects of the open condition, we will compare these velocities to each other without limiting the frequency range.

3. Experimental results

3.1. Overview of sound transmission along the middle ear path

Fig. 1 motivated this study by showing the relationship between EC pressure (input to the middle ear) and pressure in SV near the stapes (output of the middle ear). As illustrated in (de La Rochefoucauld et al., 2008) the SV pressure follows the piston component of the stapes(PLP) velocity closely over a wide frequency range (3 to 30 kHz). Based on that understanding, we used stapes(PLP) velocity to represent the output of the middle ear in the present study.

Fig. 4 assembles frequency responses from three experiments where the EC pressure and the velocity were measured simultaneously. For these measurements, the EC was widely enlarged, the PF and the bulla were open and the EC pressure was measured close to the umbo with a pressure sensor (~ 0.5 mm from the umbo). As noted above, only frequencies above ~ 7 kHz should be considered representative of the intact case and frequencies below 7 kHz are shaded in Fig. 4.

Figs. 4A, C, E show the amplitude responses of the velocities at the stapes(PLP), the LPM and the umbo normalized by the EC pressure. Umbo velocity was not measured in Exp# 50 (Fig. 4C). The umbo and LPM velocities had similar shapes and at frequencies above 7 kHz had transfer functions that were flat to within ~10 dB with additional fine structure. The frequency response of the stapes(PLP) velocity was similar to that of the umbo up to ~30 kHz, beyond which it was reduced by ~10 dB. The LPM moved less than the umbo (factor of 0.8 for Exp#48 and 0.5 for Exp#53) and the stapes(PLP) moved even less compared to the umbo (up to 30 kHz, a factor of 0.6 for Exp#48 and 0.3 for Exp#53). The difference in overall velocity values between experiments is likely due at least in part to uncertainty in the EC pressure, due to the uncertainty in the pressure sensor calibration noted above.

Figs. 4B, D, F show the velocity phases referenced to the EC pressure. For all the experiments, there was accumulating delay from the EC, to the umbo, the LPM and then the stapes(PLP). For the three experiments, the phases of stapes(PLP) relative to EC pressure were approximately straight lines from 7 to 35 kHz, characteristic of the middle ear transmission delay illustrated in Fig. 1. Over this frequency range they compared well to constant delays of 23–28 μs, shown in the straight dashed lines. There was some steepening of the phase in the 7–10 kHz range in Fig. 4F. In Exp#53, a phase jump at ~ 23 kHz that was obvious at the umbo was less pronounced as the measurement location moved along to the LPM and the stapes(PLP). In Exp#50 an umbo measurement was not made, but for the other two, the LPM and umbo phases were quite similar, with LPM motion delayed just slightly relative to the umbo. There was a frequency dependence in the delay: up to ~17 kHz the majority of the delay accumulated between the EC and LPM (with ~2–3 μs between the umbo and the LPM (de La Rochefoucauld and Olson, 2010)), whereas above ~17 kHz, there was a substantial contribution to the phase delay between LPM and stapes(PLP). All delays were determined by straight-line fits by eye.

3.2. From Pec close to umbo to Vumbo

In several experiments we explored the relationship between the EC pressure and the umbo velocity, as shown in Fig. 5. In these experiments the distance between the pressure sensor in the EC and the umbo was less than 0.5 mm.

Figs. 5A, B show the EC pressure and the umbo velocity in response to a click stimulus (Exp#58). In Exp#58 the bulla was vented but not open and the PF was closed. The umbo velocity was delayed relative to the EC pressure and the click response waveforms were similar enough that a delay of ~ 9 μs was easy to demonstrate by shifting the velocity curve so the curves overlap as in Fig. 5B. With the speed of sound in air (~340 m/s), the time required for sound to travel the ~0.5 mm between the pressure sensor and the umbo is less than 2 μs, so the observed delay is not acoustic.

Figs. 5C, D show frequency responses. Fig. 5C shows the umbo velocity amplitude relative to the EC pressure close to umbo, and the relative phase is in Fig. 5D. Results from six experiments are shown. The region below 7 kHz is shaded because the bulla and PF were open for most of the experiments. For Exp#57 and 58 (bolder magenta and green curves) the bulla and PF were closed. The straight dashed lines correspond to delays of 9 μs (black), 25 and 30 μs (red). Beginning at ~17 kHz and going through 50 kHz, the average slope of the data runs approximately parallel to the straight line with slope 9 μs. From 7 to 15–20 kHz the slope of the data tends steeper, and shows substantial inter-animal variability. The average corresponds to a 30 μs delay, and for Exp#57 and #58 the delay in this region was ~25 μs. The straight line fits were determined by eye.

3.3. Grouped velocity data at key points from umbo to stapes(PLP)

In Fig. 4 we showed an accumulating delay from the EC to the stapes(PLP). Within each frequency range we have identified, the delay from EC to stapes(PLP) must be equal to the sum of the delays along the path. The overall delay between the EC and stapes(PLP) was ~ 25 μs over the frequency range from ~ 7 – 30 kHz. Fig. 5 showed that between the EC close to the umbo and the umbo, there was a delay of ~ 25 μs at frequencies from ~7 to 17 kHz. Thus at frequencies from 7 to 17 kHz the entire transmission delay seems to occur between the EC and the umbo and we expect little or no additional delay between the umbo and the stapes(PLP). In contrast, at frequencies above ~ 17 kHz, the EC to umbo delay was relatively short, ~ 9 μs. Thus from 17 to 30 kHz a substantial part of the 25 μs total delay must occur along the ossicular chain. In the next sections we report on measurements at different points on the ossicles to observe how the delay accumulates along the chain.

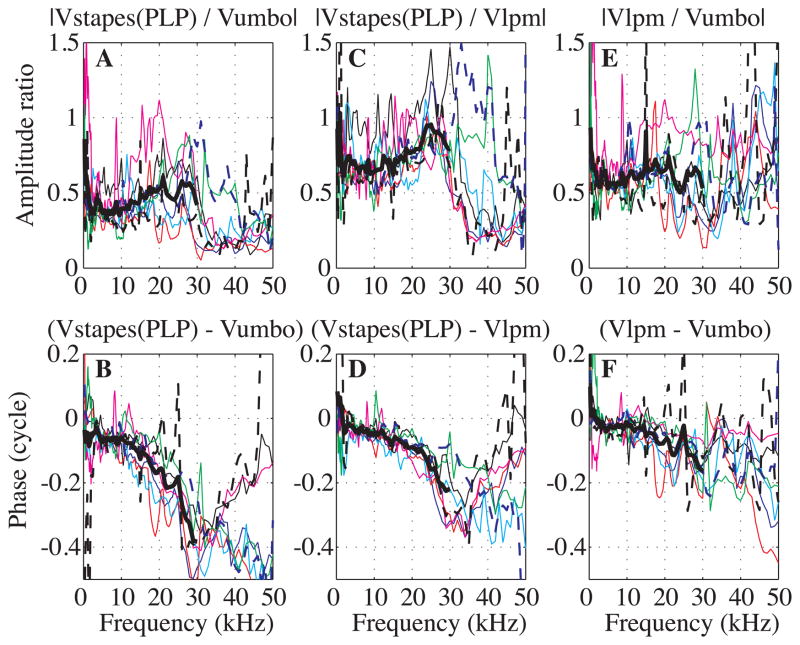
In Fig. 6 we compare velocity data measured at the umbo, at the LPM and at the stapes(PLP). The upper curves (Figs 6A, C, E) show amplitude ratios while the lower curves (Figs 6B, D, F) show the corresponding phase differences. Stapes(PLP) velocity is compared to umbo velocity in Figs. 6A, B: these results show the full extent of ossicular transmission, with umbo considered the beginning point and stapes(PLP) considered the end point. Fig. 6 panels C and D relate stapes(PLP) to LPM velocity and panels E and F relate LPM to umbo. The idea that the stimulus travels from the umbo to the LPM is only approximate; the entire manubrium has attachments to the TM (Fig. 2B) and the LPM does not need to wait for the umbo to be stimulated by TM vibration. Nevertheless, it is possible to observe the amplitude and phase relationships between the ossicular points, and the conceptualization of stimulus flow is useful to the extent that the data bear the concept out. Results from eight experiments are shown. Thick black lines are the averaged curves plotted up to 30 kHz; above 30 kHz there was so much variability that the average was not very meaningful. Because Fig. 6 compares velocity measurements to each other, the full frequency range can be considered, rather than just those above 7 kHz.

Fig. 6. Velocity amplitude ratios and relative phases of umbo, LPM and stapes (color online).

A, B: Stapes(PLP) relative to umbo, C, D: Stapes(PLP) relative to LPM. E–F: LPM relative to umbo. Results are from eight experiments and the thick black lines are the averaged data, plotted up to 30 kHz. Exp#41 R#3, 15, 39 (black), Exp#43 R#17, 22, 23 (blue), Exp#45 R#12, 17, 23 (red), Exp#47 R#17, 25, 30 (cyan), Exp#48 R#13, 25, 28 (magenta), Exp#49 R#4, 12, 35 (green), Exp#53 R#39, 44, 51 (dashed black), Exp#59 R#7, 15, 16 (dashed blue). Experimental conditions are in the appendix and did not affect the relative ossicular motion in a systematic way.

To discuss these data it is useful to consider three frequency regions, 1 to ~17 kHz, ~17 to 30 kHz, and > 30 kHz. (1) From 1 to ~17 kHz, the amplitude ratios were relatively flat, with the following average values: |V_stapes(PLP)/V_umbo| ~0.4, |V_LPM/V_umbo| ~0.6 and |V_stapes(PLP)/V_LPM|~0.7. In this frequency region the phase-frequency slope from LPM to stapes(PLP) (Fig. 6D) corresponded to a delay of ~ 3 μs. From umbo to LPM the phase was nearly flat up to 10 kHz and then steepened (Fig. 6F), to give an average slope of ~ 2 μs. Thus, the slope of the umbo to stapes(PLP) phase-vs-frequency curve (Fig. 6B) also steepened above 10 kHz and the average slope was ~ 5 μs. (2) From ~17 to 30 kHz, the LPM to umbo amplitude ratio (Fig. 6E) maintained its average value of ~ 0.6, but showed more variability. On the other hand, the stapes(PLP) to LPM amplitude ratio (Fig. 6C) grew from ~0.7 to ~0.9 and then flattened. Thus, the stapes(PLP) to umbo amplitude ratio (Fig. 6A) also exhibited a gradual increase, with a maximum of ~ 0.6. In this higher frequency region the LPM re umbo phase (Fig. 6F) did show some delay, with slope corresponding to ~ 3 μs. The phase-vs-frequency relationship between the LPM and stapes(PLP) (Fig. 6D) steepened to a slope corresponding to ~ 9 μs delay. Thus, the net umbo to stapes(PLP) delay (Fig. 6B) in this region was ~ 12 μs. As expected, the ossicular delay was much longer at frequencies from ~17 to 30 kHz than from ~7 to ~ 17 kHz. The ossicular delays from Fig. 6 were not exactly as we predicted from Fig. 5, which must be due to the approximate way that delays were determined and inter-experiment variability. (3) Above 30 kHz, the amplitude ratio of stapes(PLP) to LPM (Fig. 6C) dropped from 0.9 to ~ 0.25 in most cases. At the same time the phase either flattened or reversed direction, with a positive slope. Thus, up to 30 kHz, the concept of stimulus flow from umbo to LPM to stapes(PLP) is validated in the data, but above that the simple view is at odds with the observations. This might be due to a breakdown in the simple transmission-line concept at those frequencies. However, it is possible that the transmission-line concept can be retained even at high frequencies; we will show in the discussion that impedance mismatching in a transmission line can produce pronounced amplitude variations and phase reversals.

3.4. Detailed velocity along the middle ear

Velocity was measured at many locations along the manubrium and the ossicles for 11 experiments (Exp#41 - 50 and 59).

Results along the manubrium were presented in (de La Rochefoucauld and Olson, 2010) and are summarized here: The manubrium moved as a rigid body below 13.5 kHz, and exhibited flexing at higher frequencies. Frequency responses along the manubrium presented some regular fine structure in addition to a delay of 2–3 μs between the umbo and the LPM (see Fig. 6 F in this paper). We have also previously made measurements across the incudo-stapedial pedicle and those results showed that up to 35 kHz the LPI and the PLP moved with a constant amplitude ratio of ~ 1.35 (PLP more than LPI) and a phase of ~ 0 (de La Rochefoucauld et al., 2008). Above 35 kHz there were small departures, but these two structures moved very similarly (+/− 0.1 cycles and amplitude ratio decreasing to 1) up to 50 kHz.

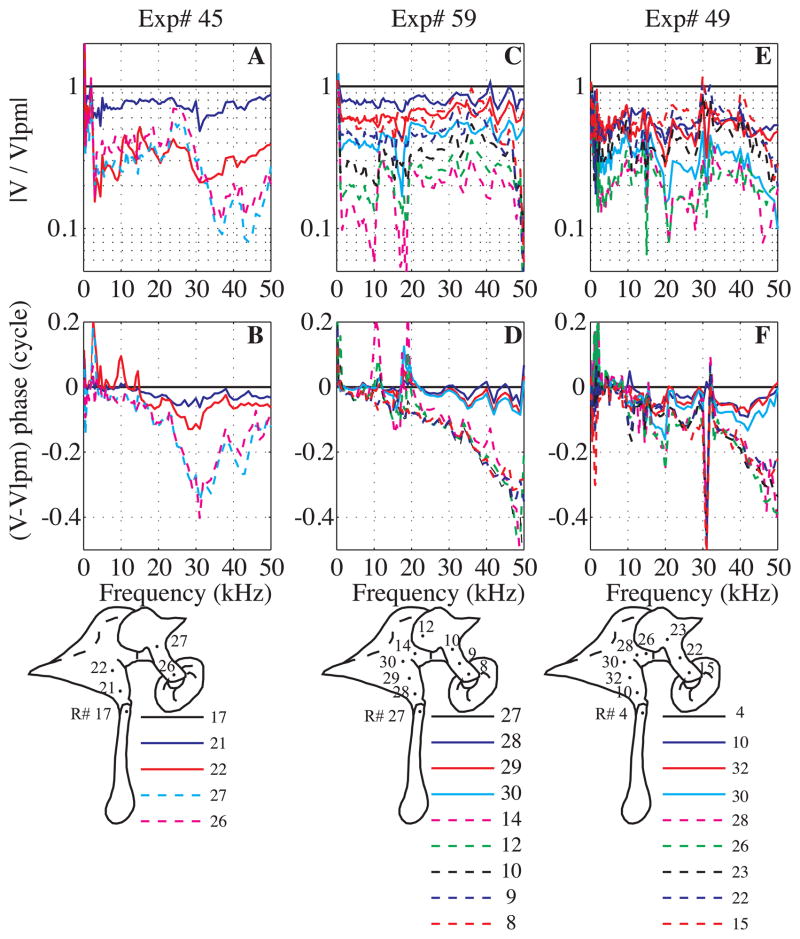
In the present paper, we explored the relationship between incus and malleus motion, measuring the motion with views as in Fig. 2A. The velocities measured at many positions along the malleus and incus (from LPM to LPI) are illustrated for three experiments (Exp#45, 49 and 59) in Fig. 7. The dots with run numbers in the diagrams illustrate the recording positions. The measurement on the LPM served as the reference for velocities at other locations along the path. Upper curves correspond to the relative amplitudes and lower curves to the relative phases. Locations on the malleus and incus are represented by solid and dashed lines respectively. (The true malleus-incus boundary is not clearly delineated visually and it was not always clear which side of the joint the laser was on. In those cases the phase data were used to determine the ossicle of measurement, since we assumed that the phase jump occurred across the joint.)

Fig. 7. Velocity amplitude ratios and relative phases along the malleus and the incus (color online).

A, B: Exp# 45 R#17, 21, 22, 26, 27, C,D: Exp#59 R#8, 9, 10, 12, 14, 27, 28, 29, 30, E, F: Exp#49 R#4, 10, 15, 22, 23, 26, 28, 30, 32. A, C, E: Velocity amplitude ratios relative to LPM. B, D, F: Velocity phase relative to the LPM velocity phase. The dots and numbers in the diagrams illustrate the positions where the measurements were taken along the path from the LPM to the lateral process of the incus (LPI). Solid lines are along the malleus and dashed along the incus.

Results for Exp#45 are in Figs. 7A, B. From 3 to 22 kHz, the amplitude ratio was relatively flat with frequency. At higher frequencies, the amplitude and phase responses presented some fine structure, with dips and valleys at frequency-fixed positions, with the frequencies of valleys in the amplitude corresponded to the steepest phase slopes. Locations on the malleus (solid lines) moved ~ in phase, as did points on the incus (dashed lines). There was a substantial delay between the malleus and the incus motion. Two different viewing angles were used to collect this set of data: the animal was rotated 22 deg on the horizontal plane and 8 deg in the vertical plane between malleus and incus measurements.

Results from Exp# 59 are presented Figs. 7C, D. Two viewing angles were also used to collect this set of data. After recording the velocity at positions 8 to 14 the animal was rotated 23 deg in the horizontal plane, and velocity was recorded at positions 27 to 30. Velocities are referenced to the LPM (R#27). The relative amplitude responses were ~flat with frequency through the entire 50 kHz range. They showed a regular decrease of the amplitude from the LPM to its minimum on the malleus-incus joint (R#14) and then the relative amplitude increased as the measurement position was moved along the incus with a local maximum at the LPI (R#8). The LPI moved less than the LPM. All points on the malleus (from R#28 to 30) were nearly in phase but not exactly. There was a small and gradual change of the phase along the malleus compared to the LPM velocity phase (difference between R#27 and 28 for example). All points on the incus (R#12 to 8) moved ~ in phase. There was a phase jump representing a delay (between R#30 and 14) at the malleus-incus joint. As in Exp #45, the viewing angle was changed to better view the incus. Experimental results of Exp#49 (Figs. 7E, F) were similar to Exp#59. The phase jump appeared between R#28 and 30. In this experiment a single viewing angle was used to collect all the data. Thus the phase change that was observed in all three experiments was due to whether malleus or incus was being viewed and not due to the change in viewing angle.

In the anatomical diagrams it is clear that some regions are not well represented by the measurements, for example between R# 22 and 27 in Exp#45, and between R# 23 and 26 in Exp#49. In fact, measurements were made at locations between these points but the responses were beneath the noise level. The small motions at these points, and the increasing motion at points closer to the LPM and LPI support the classic model, with rotation around an axis as described in Fig. 2A′.

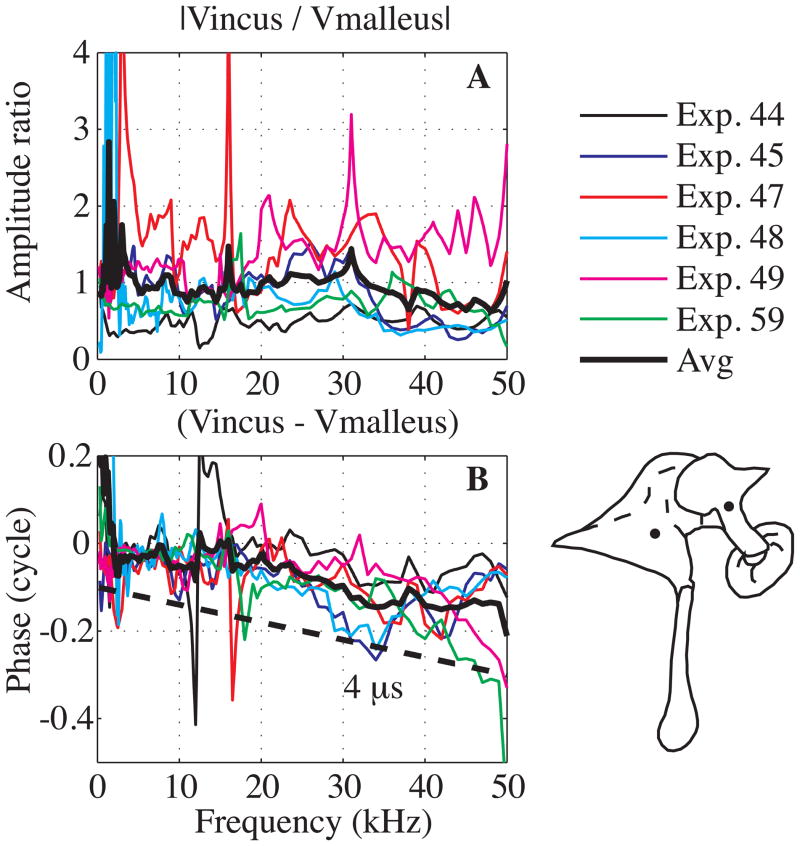
Fig. 8 assembles data from six experiments to compare the velocity measured close to and on both sides of the MIJ. The approximate recording positions are illustrated by the dots in the diagram. The average amplitude ratio was almost flat at ~ 1 through the entire frequency range with a reduction to ~ 0.7 above 40 kHz. The motion was delayed across the joint by ~ 4 μs.

Fig. 8. Velocity amplitude and relative motion across the malleus-incus joint (color online).

A: amplitude ratio, B: relative phase compared to a theoretical delay of 4 μs (dashed thick line). The dots in the diagram illustrate the approximate recording positions on the malleus and incus. Results are from six experiments as indicated in key. Black thick line is the average. (Exp#44 R#14, 23, Exp#45 R#22, 27; Exp#47 R#24, 29; Exp#48 R#22, 23; Exp#49 R#23, 30; Exp#59 R#10, 30).

Table I summarizes the delays measured along the middle ear path.

Table I.

Table of delays

Positions	7– ~17 kHz	~17–30 kHz
EC to Stapes(PLP) (Fig. 4)	~30 μs	23–28 μs
EC to umbo (Fig. 5D)	25–30 μs	9 μs
Umbo to Stapes(PLP) (Fig. 6B)	5 μs	12 μs
Umbo to LPM (Fig. 6F)	2 μs	3 μs
LPM to Stapes(PLP) (Fig. 6D)	3 μs	9 μs

Summary of all the delays presented in the paper: delays measured along the middle ear path are detailed in two frequency ranges. References of the figures in the paper are given in bracket.

4. Discussion

The present study was motivated by the simplicity of the relationship between middle ear input (EC pressure) and output (SV pressure near the stapes) that had been observed in the gerbil: Through a wide frequency range the relationship between the two can be expressed in two numbers, gain and delay. The objective of this study was to probe this relationship with detailed measurements along the transmission path. Up to 30 kHz the stapes(PLP) velocity was delayed by ~25–30 μs compared to the EC pressure measured close to the umbo, similar to the documented delay between EC pressure and SV pressure. There were major contributions to this delay both between EC pressure and umbo and along the ossicular chain. In addition to delay, amplitude leveraging was observed. In our discussion we first compare some basic aspects of our results – delay, leveraging and slippage at the MIJ – with results in the literature. We discuss the observed TM delay with respect to previous data and models. Finally, we apply a lumped element model to our ossicular motion data, and discuss the utility of this picture of ossicular mechanics.

4.1. EC pressure to stapes velocity, comparison to the literature

Measurements of stapes velocity in gerbil from two labs were recently reported in (Ravicz et al., 2008). These were closed-field measurements with PF closed and bulla open, but the open bulla will be less influential in the closed-field case than it was in our open-field case. With the view through the bulla, stapes motion was measured at an angle of ~ 27° – 47° from the piston direction. The results from the two labs were very similar and the paper’s Fig. 12 showed a grouped average of 19 animals. In Fig. 9 we compare the average curve from that study with the three stapes(PLP) response curves in Fig. 4 (these data are shown because they have partner EC pressure data). In all cases the responses were normalized to the EC pressure measured close to the umbo. Our amplitude curves are ~ 12 dB above those of Ravicz et al. There are two likely sources for this disparity. The first is the +/− 10 dB uncertainty in our EC pressure sensor calibration, which might have shifted our result up in level. The second is that the stapes motion of Fig. 12 in (Ravicz et al., 2008) was not measured along the piston axis. The authors noted that, based on their results and analysis, the off-piston measurement would lead to an underestimate of stapes piston velocity by no more than a factor of two below 10 kHz, and less at higher frequencies. This corresponds to up to 6dB of downward shift in the Ravicz et al result below 10 kHz, with less of a shift expected above 10 kHz. The sum of these two sources can account for the 12 dB offset between results. Except for the 12 dB offset, the data sets, both amplitude and phase, are very similar between 8 and 32 kHz. There were substantial departures below 7 kHz as expected due to the open condition of our measurements. Departures in amplitude occurred above 35 kHz although the phase agreement extends to 50 kHz. At frequencies above ~ 30 kHz the sound pressure varies substantially within the EC (Ravicz et al., 2007) and systematic differences in the EC pressure measurement between the labs likely contributes to the disparity in results above 35 kHz. The overall agreement between data sets reassures us that above ~ 7 kHz the middle ear is operating normally in the open condition of our experiments. And because the abnormal behavior in our results below 7 kHz can be attributed to coupling between the sound pressure and the TM, measurements along the ossicular chain were considered to be normal throughout the entire frequency range of measurement.

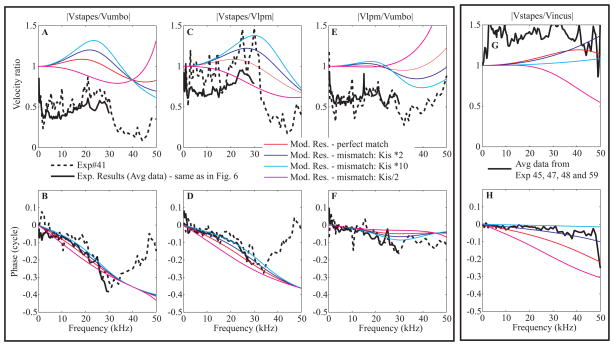
Fig. 12. Modeling results are compared to experimental results (color online).

A, B: Stapes relative to umbo, C, D: Stapes relative to LPM. E, F: LPM relative to umbo. G, H: Stapes relative to incus.

From A to F, dashed lines correspond to Exp#41 R#3, 15, 39 and thick solid lines are the averaged data from Fig. 6. In G and H, the thick lines correspond to the average curve from four experiments (Exp# 45 R#26, 23, Exp#47 R#29, 25, Exp#48 R# 16, 13 and Exp# 59 R# 8, 7). Experimental curves are compared to numerical results, first considering a perfect match of the impedances along the path (red thin line) and then after applying a mismatch by changing the incus-stapes junction stiffness (× 2 in blue, × 10 in cyan and /2 in magenta).

4.2. Lever ratio

Lever ratio is based on the concept that the ossicular chain’s response to sound stimulation is a rotation around the axis shown in Fig. 2A′. If the ossicles move with an axial rotation, the motion at the stapes is reduced from that at the umbo by the ratio of the lengths, axis-stapes:axis-umbo. Rosowski et al. (Rosowski et al., 1999) estimated the anatomical lever ratio in gerbil as 0.32, and found that from 100 Hz (the minimum frequency probed) to 2 kHz, the stapes/umbo velocity ratio was very close to the anatomical value. Above 2 kHz, the velocity ratio fluctuated, and decreased to a value of 0.13 at 6 kHz. Their highest frequency of measurement was ~ 10 kHz. Our studies extend from 1 kHz to 50 kHz, and for comparative measurements along the ossicular chain the open pars flaccida and bulla was not limiting, so we considered the entire range when plotting the velocity ratio in Fig. 6. From 2 to 10 kHz, we find a stapes(PLP)/umbo lever ratio that is very close to the anatomical value – about 0.35. In this frequency range, there is a small amount of delay at the stapes(PLP) relative to umbo – amounting to about 15 degrees at 10 kHz. Above 10 kHz, there is a gentle change in lever ratio, up to 0.5 at ~ 30 kHz. Through this region there is a considerable accumulation of delay. The presence of delay is not counter to the lever concept, but requires flexibility along the lever system. We know there is slippage at the MIJ and a bit of flexing along the malleus and incus (Figs. 7, 8). There is also considerable flexing of the umbo above 20 kHz (de La Rochefoucauld and Olson, 2010). Our results argue that the leveraging/rotating concept is valid up to at least 10 kHz, and is still very useful up to ~ 30 kHz. It has been pointed out (Decraemer and Khanna, 1994) that one can only speak about a lever ratio when the rotation axis remains fixed. Our experimental results point to an approximately fixed axis of rotation, for example in the smoothly increasing velocity amplitude as the observation point moves away from the putative rotation axis in Exp#59. A detailed look (not shown) indicates that the rotation axis does move to some degree. However, the simple picture is a useful approximation, reasonably close to the anatomical prediction (velocity ratio of 0.35 – 0.5 compared to anatomical ratio of 0.32) up to 30 kHz.

4.3. The role of the tympanic membrane in middle ear delay

EC pressure is coupled to the TM, which is coupled to the ossicles along the manubrium, from the umbo to the LPM. The attachment point at the umbo is relatively flexible and continuous with the TM, and therefore might be where sound coupling between the TM and ossicles is most substantial. Our results supported this view, in that the signal progressed in delay from the EC to the umbo to the LPM. Below ~17 kHz the EC to umbo delay accounted for most of the ~ 25 μs delay through the middle ear. The delay must arise in the coupling between acoustics and mechanics. Relatively realistic acoustic-mechanical coupling has been the subject of several modeling studies, for example (Funnell, 1983; Rabbitt and Holmes, 1986; Puria and Allen, 1998; Gan et al., 2002; Fay et al., 2006; Parent and Allen, 2007; Tuck-Lee et al., 2008). A wave-like motion has been observed on the TM (Tonndorf and Khanna, 1972; Decraemer et al., 1989; Decraemer, 1999; Cheng et al., 2010; de La Rochefoucauld and Olson, 2010), and it is reasonable to think the observed delay is a traveling wave delay. However, the delays of the wave-like motion were too long to be responsible for the middle ear delay, at least in a simple way. Some other experimental observations are relevant to the question of whether the EC-umbo delay resides in the TM wave. The experiments of Kachroo et al. (Kachroo et al., 2004), attempted to modify the middle ear delay by stiffening the TM by applying substances to it including Formalin (a fixative that would cross link TM), Formvar (a solution that dries to a plastic film), and quickly curing epoxy. However, the middle ear delay (measured with pressure sensors inside the EC close to the umbo and in SV behind the stapes) appeared very robust to TM modification. Results from three experiments in which epoxy was applied are in Fig. 10. After applying epoxy generously along the manubrium and surrounding TM as illustrated Figs. 10G-H, a change in the pressure gain (decrease of 10–15 dB) and overall delay (increased delay of ~ 14 μs when calculated from the phase responses between 10 and 40 kHz) was observed. Due to the stiffening effect of the epoxy, an increase in TM wave speed and decrease in the delay was expected, but the opposite was observed. The relatively thick layer of epoxy introduced substantial inhomogeneity within the TM and a straightforward interpretation of this result with respect to the TM traveling wave is not possible. In a similar vein, measurements of Aarnisalo et al. (Aarnisalo et al., 2010) showed little change in stapes velocity when large parts of the TM were covered by relatively thick fascia in human temporal bone.

We showed in a previous study (de La Rochefoucauld and Olson, 2010) that the TM motion could be approximated as the superposition of an in-and-out approximately piston-like motion and a wave-like motion, and suggested that the piston motion was the mode that was responsible for sound transmission. At this point, a simple intuitive way to think about TM transmission is lacking. A piston view is inconsistent with the wave-like TM motion, and a traveling wave view is not in keeping with the observations outlined above. It is notable that the hybrid shell-based TM model of (Fay et al., 2006) produces both transmission delay and complex TM motion that are roughly in line with observations in cat.

4.4. Slippage and delay at the malleus-incus joint

Our Fig. 8 showed substantial slippage at the MIJ. Sunil Puria looked at the anatomy of the gerbil middle ear using CT scans (personal communication). He saw that the malleus and incus were tightly coupled but not fused. The gap between the ossicles was significantly smaller than in cat or human, but larger than in chinchilla and guinea pig (Puria et al., 2007). A better understanding of what is happening at the joint will require a 3D reconstruction of the velocity, and such a study is underway in our lab.

In human temporal bone ossicular delay is well known and was altered in studies by Hato and colleagues (Hato et al., 2003). They measured the velocity delay between the umbo and stapes before and after fixation of the incus at both the MIJ and incus-stapes joint. The delay decreased from 89 μs to 35 μs, indicating that slippage at the joints was responsible for most of the ossicular delay. Nakajima et al. documented ossicular flexibility with a progression of ossicular fixations (Nakajima et al., 2005) and a description of the relationship and slippage between the malleus and incus is in Willi et al. (Willi et al., 2002).

4.5. Lumped element model of ossicular motion

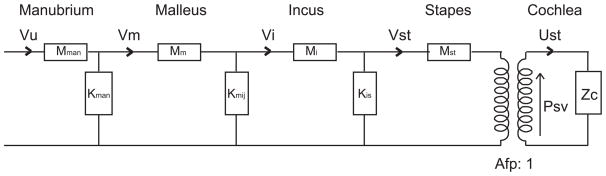
The ossicles have been modeled in the past using lumped elements (Møller, 1961; Zwislocki, 1962; Shaw and Stinson, 1983; Kringlebotn, 1988, Puria and Allen, 1998; Feng and Gan, 2004; Parent and Allen, 2007) and finite element models (Funnell and Laszlo, 1978; Gan et al., 2002; Fay et al., 2006). Some authors used lumped elements to describe the ossicles, combined with a distributed model for the TM (Puria and Allen, 1998; Parent and Allen, 2007). At the outset of this study a lumped element model appeared inappropriate. The observation that launched this study was of a frequency-independent middle ear delay and in order to produce the observed delay many elements would have been needed in a lumped element model, arguing that a distributed model would be more meaningful. However, the observations in the current study showed that the overall ~ frequency independent delay was due to the sum of delays that were frequency dependent. In particular, the ossicular delay was relatively short up to ~ 17 kHz and longer at higher frequencies, with the TM delay showing the opposite behavior. The frequency dependent ossicular delay we observed could be modeled reasonably well with a lumped element model. The malleus and incus appeared to move as almost rigid bodies, except for significant flexing along the malleus’s manubrium. Therefore, our ossicular model has four masses: manubrium, malleus, incus and stapes. The model is illustrated in Fig. 11.

Figure 11. Circuit diagram.

Middle ear modeled as a succession of mass/stiffness elements in a transmission line. Masses (M) are in g and stiffness (K) in dyn/cm. The first sub-circuit corresponds to the manubrium, which because of its flexibility has properties of both mass (M_man) and stiffness (K_man). The second sub-circuit corresponds to the malleus (M_m) and malleus-incus joint (K_mij). The third sub-circuit corresponds to the incus (M_i) and incus-stapes junction (K_is). The stapes mass is terminated by the cochlear input impedance, Z_C. The values for Z_C and the masses were informed by values in the literature, see text for details. The stapes footplate area, A_fp is also in the literature. We used an impedance matching assumption to find the K values, as follows (see text): $Z_c{A}_{fp}^2=\sqrt{K_{\mathit{man}}{M}_{\mathit{man}}}=\sqrt{K_{\mathit{mij}}{M}_m}=\sqrt{K_{is}{M}_i}$. The parameter values used in the model are:

$$\begin{array}{l}{M}_{st}=1.16\times {10}^{-4}g,M_i=1.055\times {10}^{-4}g,M_m=1.27\times {10}^{-4}g,M_{\mathit{man}}=6.36\times {10}^{-5}g\\ K_{is}=1.4\times {10}^7\mathit{dyne}/cm,K_{\mathit{mij}}=1.16\times {10}^7\mathit{dyne}/cm,K_{\mathit{man}}=2.32\times {10}^7\mathit{dyne}/cm\\ A_{fp}=6.2\times {10}^{-3}{cm}^2,Z_c=1\times {10}^6\mathit{dyne}·s/c{m}^5\end{array}$$

The ossicles were modeled as a succession of masses (M) followed by shunt stiffness (K). In order to reduce the number of free parameters, and because quantitative information on joint stiffness is lacking, the shunt stiffnesses were chosen based on a matched impedance assumption (Puria and Allen, 1998), $\sqrt{KM}=Z_{C-\mathit{mech}}$ where Z_C-mech is the terminating mechanical impedance at the cochlea, expressed as force/velocity. Using the impedance matching condition the manubrium mass was used to find manubrium stiffness, the malleus mass to find the stiffness of the MIJ, and the incus mass to find the stiffness of the IS-junction. (As noted above, the pedicle of the incus appears to be most flexible part of the junction between the incus and stapes.) The stapes was terminated at the cochlea. The cochlea’s input impedance is primarily resistive, with a value when expressed as acoustic impedance (pressure/volume velocity) of Z_C = 10¹¹ N.s/m⁵ = 10⁶ dyn.s/cm⁵ (de La Rochefoucauld et al., 2008). To convert from acoustic to mechanical impedance requires multiplying Z_C by footplate area squared, and with stapes footplate area, A_fp = 6.2·10⁻³ cm² (Lay, 1972; Hemila et al., 1995), Z_C-mech ~ 38.4 10⁻³ N.s/m = 38.4 dyn.s/cm. With the masses of the ossicles and the terminal impedance known, and the impedance-matching condition assumed, the model is quite constrained. The masses of the ossicles were given in (Nummela, 1995). They are: stapes, 0.116 mg, malleus, 1.145 mg and incus, 0.633 mg. One third of the malleus mass was attributed to the manubrium, using a visual approximation. The mass values for malleus and incus have to be adjusted because these ossicles do not translate but rotate; this reduces their effective masses. The effective mass will be small when most of the mass is concentrated close to the axis of rotation, and large (similar to the actual mass) when the mass is concentrated far from the axis (see “moment of inertia” in a physics textbook). For a simple geometry like a rod rotating about one end like a spoke, the effective mass is 1/4M, but we had better results in our model when the effective masses were taken as 1/6M and that was used. For the stapes, whose motion is translational, the actual mass was used. By using the reduced “effective masses,” rotational motion is recast as translational motion and therefore leveraging, which is based on rotational lever arms, is not produced by the model. (The data show overall amplitude shifts due to leveraging – here we only consider the frequency dependence, not the level shifts in comparing model to data.) The model is useful for understanding the frequency dependence of the motion, the accumulating delay along the ossicular path, and for illustrating the effects of an impedance mismatch.

Fig. 12A–F compares the modeling results (thin lines) to experimental results: The thick line is the averaged data from Fig. 6 and the thick dashed line shows results from Exp#41, to include an individual case. The red lines show the model output with stiffnesses chosen using the impedance matching as described above and we begin by considering these curves. The model reproduces several characteristics of the umbo-LPM-stapes(PLP) ratios. Both the amplitude and phase of the model LPM/umbo ratio are quite flat up to ~ 30 kHz, where the phase shows a small dip. Above 30 kHz, following a very gentle dip the amplitude ratio climbs, which is similar to what was observed (although is more pronounced) in Exp#41. The model stapes/LPM ratio shows a steadily advancing phase delay, whereas the data showed a more structured delay with a less-steep region, followed by a more steep-region above and below ~ 20 kHz. Similarly, the stapes(PLP)/LPM amplitude ratio of the data show more structure than the model output, climbing to a peak at ~20–25 kHz and then dropping abruptly, whereas the model shows similar but less structured trends.

Understanding the relationship between the model and data was aided by including another set of results. In panels G and H, the average stapes(PLP)/incus amplitude and phase responses from four experiments (Exp#45, 47, 48 and 59) are shown. Similar experimental results were presented in Fig. 4 of (de La Rochefoucauld et al., 2008), with the main conclusion from that study being that the stapes(PLP) and LPI moved very similarly. Model results are plotted along with the data in these panels, and it can be seen in the red lines of the impedance matched model that there is significant delay between the incus and stapes, which is not present in the experimental data. In order to bring the model and experimental results into closer agreement, the stiffness of the IS-junction was increased by a factor of 10. These model results are shown in the cyan curves. We also looked at the results with IS-junction stiffness increased by a factor of two (dark blue curves) and for completeness, reduced by a factor of two (magenta curves). With the IS-junction stiffness increased by a factor of 10, the delay between incus and stapes is nearly eliminated, and both amplitude and phase of the model reproduce the data quite well. The ×10 increase also leads to a better fit between model and results in panels A – F. In particular, the results show more pronounced structure, which is more in keeping with the experimental data, with gradual-then-steepening delays between LPM and stapes(PLP) (panel D), and a more pronounced phase dip between umbo and LPM (panel F). The pronounced peak in the stapes(PLP)/LPM amplitude is better predicted, and the dip and then climb in amplitude in LPM/umbo ratio is also predicted.

Thus, the four mass lumped element model of the ossicular chain can do a reasonable job of fitting the experimental data. In the model, the manubrium was considered as a spring and mass, so some “bending” was allowed. Other than that, the ossicles were considered as rigid bodies. Our experimental data showed some bending along the malleus and incus body (via phase delays) but the bulk of the delay was across the malleus-incus joint, supporting the rigid body approximation. The model did not show as pronounced frequency structure as the actual experimental data and we did not attempt to modify the parameters very much to get a better fit. Our objective with the model was to see if we could get reasonable agreement, starting with an impedance matched model. We found a reasonable agreement was possible when the final spring (IS-junction) was stiffened.

The major result of this study was that the ossicular chain contributes substantially to the middle ear transmission delay at frequencies above ~ 17 kHz, but that at frequencies below that the delay is primarily in the coupling between sound in the EC and the ossicles, with little additional delay along the ossicular chain. Thus the question that motivated this study – what gives rise to the nearly frequency-independent middle ear transmission delay has been answered in part: the frequency-independent delay arises from the sum of two frequency-dependent delays. The frequency dependence of the delay along the ossicular chain can be understood with a simple lumped element model. The basis for the frequency dependence of the delay between EC and ossicles – with a longer delay at low frequencies and a shorter delay at high frequencies – is still an open question, which can be explored by some of the middle ear models referenced above.

Abbreviations

SV

scala vestibuli

TM

tympanic membrane

EC

ear canal

PF

pars flaccida

LPM

lateral process of the malleus

LPI

long process of the incus

MIJ

malleus-incus joint

PLP

plate of the lenticular process of the incus

IS

incus-stapes

BK

Brüel & Kjær

SPL

sound pressure level

CAP

compound action potential