Everything you always wanted to know about evaluating prediction models (but were too afraid to ask)

Many urology papers describe the development of statistical prediction models, what are often described as “nomograms”. Indeed, a simple search of Medline for urology prediction models retrieves close to 1000 papers. These studies come from investigators across the globe, including those researching both malignant and benign disease in organs from the kidney on down. In short, everyone is doing it.

This can make asking questions about prediction modeling a bit embarrassing (if everyone is doing it, shouldn’t I know all about it?). As such, we present a short list of “Everything you always wanted to know about evaluating prediction models (but were too afraid to ask)”. This is a personal take on some well-known statistical principles; we have not added citations to the text, but a list of further reading is given at the end.

1. A “nomogram” is not the same thing as a prediction model

Urology researchers commonly use the terms “nomogram” and “prediction model” interchangeably. For example, authors of papers about prediction models often describe their aims as “to develop a nomogram”. But a nomogram is simply a graphical calculating device. For example, the first nomogram one of us ever saw was to calculate sample sizes for a clinical trial; other well-known nomograms include those for weather forecasting and electrical engineering. Urology researchers typically analyze data sets using logistic or Cox regression. The resulting statistical model can be described by citing odds or hazard ratios, or in graphical form as a nomogram. But a nomogram is not the model any more than a map is the territory.

2. Predictive accuracy is not the same as discrimination

It is routine to see investigators makes claims such as “our model has a predictive accuracy of 70.2%”. The 70.2% figure is typically either an area-under-the-curve (AUC) or a concordance index (C-index). Both the AUC and the C-index provide an estimate of the probability that the model will correctly identify which of two individuals with different outcomes actually has the disease (e.g. AUC of a model to predict prostate cancer on biopsy) or had the event sooner (e.g. C-index of a model to predict life expectancy). Statisticians describe AUC and C-index in terms of “discrimination”, that is, the measures tell you how well the model discriminates between different patients. The other key statistic that describes prediction models is “calibration”. A model is well calibrated if, for every 100 men given a prediction of x%, the actual number of events is close to x. Now imagine that we took the well-known Kattan model (which has a C-index around 0.80), and divided all predictions by 10, so that, for example, someone with a 50% risk of recurrence is given a risk of 5%. The new model would have exactly the same discrimination as the Kattan score, after all, patients with higher predicted probabilities are more likely to have recurrences. However, we would give patients with even very aggressive disease a low risk of recurrence, and so we would not want to say that our new model was “80% accurate”.

3. Discrimination depends on how much the predictors vary

The C-index or AUC depends critically on the variation of the predictors in the study cohort. As a simple illustration, imagine that two models for life expectancy were published, both of which only included age as a predictor. In addition, both models reported exactly the same odds ratio of 1.10 for a 1 year increase in age. However, one model was tested on a group of men aged 50 – 60 and the other on a group aged 40 – 70. The C- index would be less than 0.60 for the first model but above 0.70 for the second. As a second illustration, take a binary risk factor associated with an odds ratio of 5. If 5% of the population had the risk factor, a typical value for AUC would be around 0.55. In comparison, discrimination would be 0.70 if the prevalence of the risk factor was 50%.

4. Internal validation often doesn’t help much

The discrimination and calibration of a model are assessed by applying it to a data set and comparing predictions with outcome. Very commonly, the data set to which the model is applied is the same as the one used to create the model in the first place. This is known as “internal validation”, and is somewhat problematic for two reasons. First, models tend to have above average fit to the data on which they were created simply due to the play of chance. As a trivial example, if the recurrence rate in a data set of 100 patients is 53%, then applying a risk of 53% back to that data set will result in perfect calibration (indeed, calibration is almost always perfect on internal validation). But 53 recurrences out of 100 is consistent with a true risk anywhere from 43% to 63%, and so applying an estimated risk of 53% to a different set of 100 patients might well lead to an inaccurate prediction. The second problem with internal validation concerns true differences between cohorts. For example, Gleason grading has changed over time and so a model created on patients treated in the early 1990’s may give inaccurate predictions when applied to contemporary patients. Statisticians have proposed some sophisticated methods to improving internal validation, including “leave one out” cross-validation, k-fold cross-validation and bootstrap resampling. The problem is that these methods only deal with the first of the two problems, statistical overfit, they do not address true differences between patient cohorts such as those concerning changes in pathology analysis.

5. The concordance index is heavily influenced by length of follow-up

It is easier to predict what is going to happen tomorrow than in five years time. This means that a C-index must be interpreted in the context of follow-up time. As a simple example, imagine that Brown and Smith had each published separate nomograms predicting life expectancy, with the C-index index for Brown being somewhat higher. The typical interpretation would be that Brown’s model is superior. But it might also be that Smith’s follow-up was longer. To illustrate this point, we looked at the univariate C-index for extraprostatic extension (EPE) in a data set of US patients treated 2000 – 2003 and followed to 2005. There is no reason to believe that there were important changes in patients or pathologic staging during this short period of time. Nonetheless, applying the model to patients treated in 2000 (median follow-up 37 months) resulted in a C-index of 0.66. The C-index for EPE in patients treated in 2001, who had a median follow-up of only 5 months less, was 0.73. This rises all the way to 0.79 for patients treated in 2003, with a median follow-up of 14 months. Now it is not unusual to see in the literature comparisons of models with C-indices of, say, 0.69 and 0.71. So a model reporting a C-index of 0.79 would be seen as in a different league to one with a C-index of 0.66. Yet the only difference between the 0.79 and 0.66 is the length of follow-up.

6. Calibration is not an inherent property of a prediction tool

Investigators commonly describe the results of their study as showing that their model was “well calibrated”. But it is perfectly possible for a model to be well-calibrated on one data set and poorly calibrated on another. As a simple example, an investigator might develop a predictive tool for life expectancy and demonstrate that predicted risks are close to observed proportions in a variety of European and US data sets. However, the model might well have poor calibration when applied to a population from a developing country. Accordingly, calibration is best seen not as a property of a prediction model, but of a joint property of a model and the particular cohort to which it is applied.

7. A good model can be clinically useless, a poor model very valuable

Take the case of a model to predict the outcome of prostate cancer biopsy. The model might have good discrimination (say, 0.85) and perfect calibration, yet might have no clinical role. This could be because, for example, the predicted risks from the model ranged from 50 – 95%. Patients with prostate cancer tended to have higher predicted risks – leading to good discrimination – but no patient was given a probability low enough that a urologist would forgo biopsy. To put it another way, specifying that a patient with cancer is at very high risk, rather than just high risk, reflects that the model is a good one, but makes no clinical difference as the patient would be biopsied in both cases. On the other hand, a model with only moderate discrimination might be useful if the clinical decision is a “toss-up”, providing just enough information to push a clinical decision one way or the other. As such, predictive models need to be evaluated by decision analytic techniques that determine whether the model would change medical decisions and, if so, whether outcome would improve as a result. For an example of a simple decision analytic technique that can be readily applied to any predictive modeling data set, see www.decisioncurveanalysis.org.

8. A predictor that adds accuracy to a prediction model may not be worth measuring

Just as it is possible for a model to be accurate, but useless, it is possible to add to accuracy, but for this to make no difference to clinical decision making. Again, decision analytic techniques are required to investigate the clinical implications of using the marker.

9. Just because you can create a predictive model, it doesn’t mean that you should

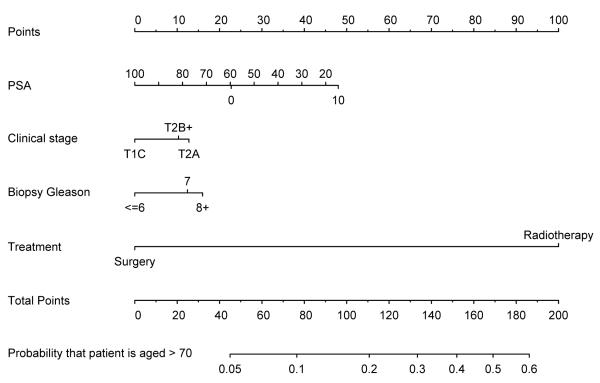
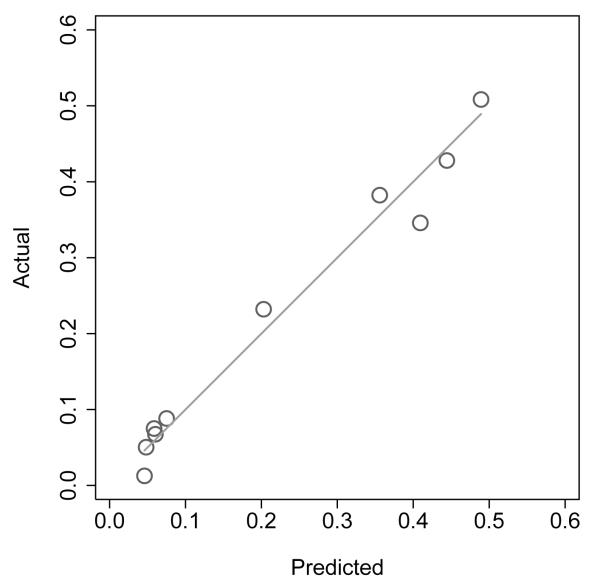
Figure 1 shows a nomogram to predict the probability that a patient is aged over 70 on the basis of stage, grade, PSA and treatment chosen (surgery vs. radiotherapy). The model is very accurate (AUC of 0.78) and has good calibration (see figure 2). In other words, the model is terrific in all ways other than the fact that it is totally useless. So why did we create it? In short, because we could: we have a data set, and a statistical package, and add the former to the latter, hit a few buttons and viola, we have another paper. It is tempting to speculate that the ubiquity of nomograms in the urologic literature is simply because it is particularly easy research to do: you don’t need to go and collect any data, or even think up an interesting scientific question. We would argue that a predictive model should only be published if it is has a compelling clinical use, and that is only rarely the case.

Figure 1.

Nomogram to predict the probability that a prostate cancer patient is aged over 70

Figure 2.

Calibration plot of nomogram to predict whether patient is aged over 70

In conclusion, papers on nomograms often involve esoteric statistics - restricted cubic splines, for example, or bootstrap resampling – in an effort to fine tune models. But small differences in follow-up, or in the heterogeneity of a predictor, can result in very large differences in C-index or AUC. Moreover, minor differences between cohorts can similarly lead to substantial differences in predictive accuracy between internal and external validation.

Researchers are often told to KISS: “keep it simple, stupid”. With respect to prediction models, then, here is how to keep it simple: develop models that will be of clinical value; evaluate your model on several different independent data sets that have mature follow-up; focus on the clinical implications of your model.