Conformational profile of a proline-arginine hybrid

Abstract

The intrinsic conformational preferences of a new non-proteinogenic amino acid have been explored by computational methods. This tailored molecule, named (^βPro)Arg, is conceived as a replacement for arginine in bioactive peptides when the stabilization of folded turn-like conformations is required. The new residue features a proline skeleton that bears the guanidilated side chain of arginine at the C^β position of the five-membered pyrrolidine ring, either in a cis or a trans orientation with respect to the carboxylic acid. The conformational profile of the N-acetyl-N'-methylamide derivatives of the cis and trans isomers of (^βPro)Arg has been examined in the gas phase and in solution by B3LYP/6–31+G(d,p) calculations and molecular dynamics simulations. The main conformational features of both isomers represent a balance between geometric restrictions imposed by the five-membered pyrrolidine ring and the ability of the guanidilated side chain to interact with the backbone through hydrogen-bonds. Thus, both cis and trans (^βPro)Arg exhibit a preference for the α_L conformation as a consequence of the interactions established between the guanidinium moiety and the main-chain amide groups.

Introduction

Design of specific chemical modifications in natural amino acids is a powerful strategy to control the conformational properties of short peptides.^1–2 Moreover, non-coded residues in a peptide chain may result in increased resistance to proteolytic degradation.^3–7 Non-proteinogenic amino acids are useful in engineering peptide analogues with improved pharmacokinetics and medicinal applications.^3–9

A non-coded amino acid can replace residues in natural peptide sequences if it does not disrupt the bioactive conformation of the preplaced segment. The resulting peptide must preserve the native shape that interacts with the receptor. When dealing with small flexible peptides, a non-coded residue can improve the targeted peptide by biasing its conformational equilibrium to a conformational set that guarantees function. Thus, the non-proteinogenic amino acid should exhibit a high preference for the conformation adopted by the natural residue that is to be replaced.

Theoretical methods can assist so that only those candidates yielding satisfactory results in silico are selected for experimental studies. This evaluation requires (i) theoretical study of the wild-type bioactive conformation (if not available experimentally); (ii) assessing which amino acid should be replaced; and (iii) design of a new non-coded amino acid adequate to replace the targeted position of the peptide. The conformational preferences of the new non-coded amino acid need to be determined before the replacement is performed. If such conformational preferences do not match those of the targeted position, the replacement will not be successful.

We are involved in a project aimed at improving the bioactivity of the pentapeptide Cys-Arg-Glu-Lys-Ala (CREKA). This peptide has biotechnological interests because it recognizes molecular markers that are present in tumor blood vessels but not in the vasculature of normal tissues,¹⁰ thus showing promising applications in cancer diagnosis and therapy. Medicinal use is however hampered by the poor stability against proteases and short half-life time typically exhibited by small and medium-size natural peptides. The conformational landscape of CREKA was explored by computational methods under different environmental conditions.¹¹ This analysis led to a bioactive conformation exhibiting a turn motif, with the charged side chains of Arg, Glu, and Lys oriented toward the same side of the molecule.¹¹ The peptide backbone is folded in β-turn centered at the Arg and Glu residues. Arginine occupies the first corner position of the β-turn (i+1) and adopts dihedral angles corresponding to the α-helical (α_L) region of the Ramachandran map.

The first attempt to decrease the peptide sensitivity to proteases was made though by introducing unspecific chemical modifications that did not affect its overall conformational properties.¹² Hence, a methyl group replaced the hydrogen atom at either N position or C^α position. This simple approach increased in vivo the half-life time of the CREKA coated nanoparticles in the tumor vessels.¹² However, no effort had been made to enhance the stability of the bioactive conformation.¹¹ Then in a second stage, we undertook the design of new non-coded amino acids that could bias the folding of CREKA towards its bioactive organization, focusing our efforts on arginine surrogates. The main goal was to incorporate the side-chain functionality of arginine, which is essential for CREKA's activity, in residue that presented clear conformational preferences for the α_L region of the Ramachandran map.

A first amino acid was designed by combining a non-coded amino acid of the family 1-aminocycloalkane-1-carboxylic acids (Ac_nc, where n refers to the size of the cycle) and the side chain functionality of arginine (Figure 1).¹³ These amino acid series had been previously investigated and shown to exhibit a restricted conformational space characterized by a high propensity to adopt φ,ψ backbone angles typical of the 3₁₀-/α-helix (with some distortion in the case of Ac₃c).^14–18 The new amino acid (denoted as c₅Arg) was built by incorporating the side chain of arginine at the β-carbon atom of Ac₅c.¹³ The intrinsic conformational preferences of the new amino acid were studied using theoretical methods, showing that α-helical conformation was favored both in the gas phase and in solution. It was remarkable that the ability of the guanidinium moiety to form hydrogen bonds with the peptide backbone conditioned the conformational features of the parent Ac₅c,¹⁷ which tends to favor the formation γ-turn based conformations before α-helix like arrangements.

Figure 1.

Structure of arginine (Arg) and some studied analog s. The first presented analog was designed upon 1-aminocyclopentane-1-carboxylic acid (Ac₅c), which led to the amino acid c₅Arg (ref. 7) and those based on proline structure (Pro): cis-(^γPro)Arg (ref. 9), trans-(^βPro)Arg and cis-(^βPro)Arg, being the latter one the object of this study. The arginine surrogates are named according to the γ/β position of the proline skeleton bearing the guanidilated side chain and to the trans/cis relative orientation between this side chain and the carboxylic acid.

The latter challenge was though to achieve similar results with a backbone constitution closer to that of coded amino acids. Among proteinogenic amino acids, proline is known to impart protection against proteolytic cleavage^19–22 as well as to nucleate peptide turns,^23–25 with a marked propensity to occupy the i+1 position of β-turns. Accordingly, following the previous strategy we generated a new residue by attaching the arginine side chain to the proline skeleton (see the Supporting Information for details). It should be noted that the cyclic nature of proline, that includes the amine nitrogen atom in the ring constitution, facilitates a cis arrangement of the peptide bond involving the pyrrolidine nitrogen, as compared to other peptide bonds, for which the cis form is almost nonexistent.^26–27 Here, however, this issue has not been addressed since the targeted arginine in wild-type CREKA presents both peptide bonds in trans⁵ and the new residue is therefore useful only for the latter geometry.

In a previous work,²⁸ the guanidilated side chain was attached to the γ-carbon of the pyrrolidine ring in a cis configuration with the carboxylic acid moiety, thus giving rise to the residue denoted cis-(^γPro)Arg in Figure 1. The chain length of this arginine analogue proved insufficient to reproduce the interactions observed for the guanidinium group in the bioactive conformation of CREKA.^11,28 Although the addition of another methylene unit to the exocyclic guanidilated substituent was favorable, incorporation of the resulting residue into CREKA led to the disruption of the β-turn conformation of the natural peptide.²⁸

These results led us to design a new arginine surrogate built on a proline skeleton. Here, it is the β pyrrolidine carbon that bears the guanidilated arginine side chain and the resulting residue is termed cis-(^βPro)Arg, where cis refers to the position of the guanidilated substituent relative to the carboxylic acid and β denotes the carbon atom of the five-membered ring where this substituent is placed (Figure 1). Prior to testing the modified pentapeptide Cys-cis(^βPro)Arg-Glu-Lys-Ala, the conformational propensities of the single amino acid have been investigated in depth by theoretical methods. As noted above, cis-(^βPro)Arg presents a cis orientation between the guanidinium and carbonyl moieties –as the previously studied²⁸ cis-(^γPro)Arg– in agreement with the spatial relationship characterized for the guanilidated segment of natural arginine in CREKA.¹¹ However, beyond the CREKA project, other peptides incorporating key arginine residues may present the guanidilated side chain oriented away form the carbonyl group in the bioactive form. This consideration prompted us to also evaluate in this work the conformational propensities of trans-(^βPro)Arg (Figure 1).

We have therefore performed quantum mechanics calculations on the N-acetyl-N'-methylamide derivatives of both cis-(^βPro)Arg and trans-(^βPro)Arg, hereafter denoted Ac-c-(^βPro)Arg-NHMe and Ac-t-(^βPro)Arg-NHMe, respectively. The results are compared with those reported previously²⁸ for the analogous cis γ-substituted derivative, Ac-c-(^γPro)Arg-NHMe. Additionally, parameterization of the two non-proteinogenic amino acids under study has been carried out before analyzing the conformational impact derived from their incorporation into biologically active peptides. The dynamical conformational features of the two residues have been explored in aqueous solution at room temperature using classical Molecular Dynamics (MD) simulations with explicit water molecules.

Computational Methods

Quantum mechanical calculations

Density Functional Theory (DFT) methods were applied for quantum mechanical calculations, which were performed using the Gaussian 03 computer program.²⁹ Specifically, calculations were carried out by combining the unrestricted formalism of the B3LYP functional^30,31 with the 6–31+G(d,p) basis set.³² Frequency analyses were carried out to verify the nature of the minimum state of all the stationary points obtained and to calculate the zero-point vibrational energies (ZPVE) and both thermal and entropic corrections. These statistical terms were then used to compute the conformational Gibbs free energies in the gas phase (ΔG^gp) at 298K.

Figure 2 shows the backbone (ω₀,φ,ψ,ω) and side chain (χⁱ,ξⁱ) dihedral angles that define the conformations adopted by Ac-t-(^βPro)Arg-NHMe and Ac-c-(^βPro)Arg-NHMe. The minimum energy structures characterized for these compounds have been denoted using a three-label code that specifies the arrangement of the peptide backbone, the puckering of the five-membered cycle and the conformation adopted by the exocyclic substituent. The first label identifies the backbone conformation type according to Perczel's nomenclature,³³ which categorizes the potential energy surface E = E(φ,ψ) of α-amino acids in nine different regions: γ_D, δ_D, α_D, ε_D, β_DL, ε_L, α_L, δ_L, and γ_L. The presence of the pyrrolidine ring in proline fixes the φ angle near −60° and, accordingly, only three of such regions can be accessed,^23,24 namely, γ_L (γ-turn), α_L (α-helix), and ε_L (polyproline II). Identical geometric restrictions should apply to the arginine surrogates under study since they have a proline skeleton. A trans configuration was considered for the amide bonds (ω₀, ω ≈ 180°). The second label describes the down [d] or up [u] puckering of the five-membered pyrrolidine ring.^23,34,35 Such conformational states are also called C^γ_endo and C^γ_exo, respectively, and correspond to those in which the C^γ atom and the carbonyl group of proline (or the proline-like residue) lie on the same and opposite sides of the plane defined by C^δ, N, and C^α. Specifically, a down puckering was assigned when χ¹ and χ³ were positive while χ² and χ⁴ were negative. Conversely, negative values of χ¹ and χ³ and positive values of χ² and χ⁴ correspond to an up-puckered pyrrolidine ring. Finally, the orientation of the polar exocyclic substituent is described by the third label, which indicates the gauche⁺ (g⁺), skew⁺ (s⁺), trans (t), skew⁻ (s⁻), gauche⁻ (g⁻), or cis (c) state of each ξⁱ dihedral angle.

Figure 2.

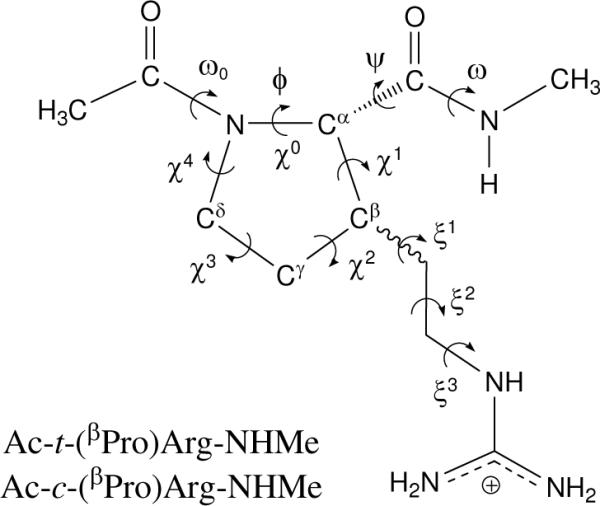
Dihedral angles used to identify the conformations of the N-acetyl-N'-methylamide derivatives of trans-(^βPro)Arg and cis-(^βPro)Arg studied in this work. The (φ,ψ) dihedral angles are defined by the atoms in the backbone, whereas the side-chain dihedral angles χⁱ and ξⁱ are given by the pyrrolidine atoms and the exocyclic side-chain atoms, respectively. In particular, φ and χ⁰ are defined as C(O)–N–C^α–C(O) and C^δ–N–C^α–C^β, respectively. The dihedral angle ξ¹ is given by C^α–C^β–C(H₂)–C(H₂).

The conformational search was performed following the strategy used in our previous work on cis-(^γPro)Arg.²⁸ It was assumed that the two (^βPro)Arg derivatives under study maintain the geometric restrictions derived from the cyclic nature of proline. Thus, the three minimum energy conformations characterized³⁶ for Ac-Pro-NHMe with trans amide bonds, i.e. γ_L[d], γ_L[u], and α_L[u], were considered as starting geometries for Ac-t-(^βPro)Arg-NHMe and Ac-c-(^βPro)Arg-NHMe in the present work. Regarding the substituent attached to the β-carbon of the pyrrolidine moiety, each ξⁱ dihedral was expected to exhibit minima of the gauche⁺, trans and gauche⁻ type. Accordingly, 3 (minima of Ac-Pro-NHMe¹⁶) × 3 (minima of ξ¹) × 3 (minima of ξ²) × 3 (minima of ξ³) = 81 minima were anticipated for the potential energy hypersurface E = E(φ,ψ,χⁱ,ξⁱ) of each (^βPro)Arg derivative. All these structures were used as starting points for subsequent full geometry optimizations.

The influence of the solvent on the conformational preferences of the compounds under study was quantified by performing Self-Consistent Reaction Field (SCRF) calculations on the optimized geometries. Under this formalism, the solute is treated at the quantum mechanical level, while the solvent is represented as a dielectric continuum. In particular, we used the Polarizable Continuum Model (PCM) developed by Tomasi and co-workers to describe the bulk solvent.^37–40 PCM calculations were performed following the standard protocol and considering the dielectric constants of carbon tetrachloride (ε = 2.228), chloroform (ε = 4.9), and water (ε = 78.4). The conformational free energies in solution (ΔG^sol, where sol refers to the solvent) were computed using the classical thermodynamics scheme, i.e. for each minimum, the free energy of solvation provided by the PCM model was added to the ΔG^gp value.

Force-field parameterization

The stretching, bending, torsion and van der Waals interactions of trans-(^βPro)Arg and cis-(^βPro)Arg were described classically by extrapolating the force-field parameters contained in the AMBER libraries⁴¹ for proline and arginine. For selected minimum energy conformations, electrostatic atomic centered charges were calculated by fitting the UHF/6–31G(d) quantum mechanical and the Coulombic Molecular Electrostatic Potentials (MEPs) to a large set of points placed outside the nuclear region. The electrostatic parameters derived at this level of theory are fully compatible with the current parameters of the AMBER force-field.⁴¹ Electrostatic force-field parameters for the two (^βPro)Arg isomers were obtained by applying to such atomic charges a strategy based on a Boltzmann distribution of multiple conformations, which was originally proposed by different authors^42–44 and has been shown to be specially suitable for non-proteinogenic residues.^{13,16,17,43,45} Moreover, this strategy provides conformationally independent electrostatic parameters.

Force-field calculations

MD simulations in water solution were performed using the NAMD program.⁴⁶ The Ac-t-(^βPro)Arg-NHMe or Ac-c-(^βPro)Arg-NHMe molecules were placed in the center of a cubic simulation box (a = 30.6 Å) filled with 955 explicit water molecules, which were represented using the TIP3 model.⁴⁷ Negatively charged chloride atoms were added to reach electron neutrality. Before the production runs, the simulation box was equilibrated for each compound. Thus, 0.5 ns of NVT-MD at 500K were used to homogeneously distribute the solvent and ions in the box. Next, 0.5 ns of NVT-MD at 298K (thermal equilibration) and 0.5 ns of NPT-MD at 298K (density relaxation) were carried out. The last snapshot of the NPT-MD was used as the starting point for production NVT-MD runs at standard conditions.

The energy was calculated using the AMBER potential.⁴¹ Atom pair distance cutoffs were applied at 12.0 Å to compute the van der Waals and electrostatic interactions. In order to avoid discontinuities in the potential energy function, non-bonding energy terms were slowly converged to 0 by applying a smoothing factor from a distance of 10.0 Å. Both temperature and pressure were controlled using the weak coupling method⁴⁸ applying a time constant for heat bath coupling and a pressure relaxation time of 1 ps. Bond lengths were constrained using the SHAKE algorithm⁴⁹ with a numerical integration step of 2 fs.

Results and Discussion

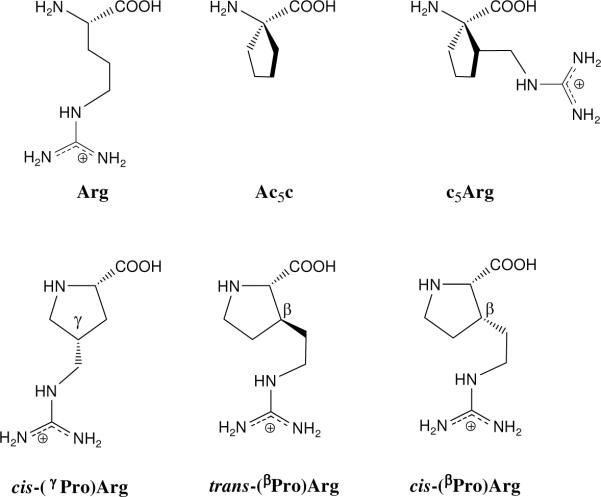
A total of 21 minimum energy conformations were found and characterized for Ac-t-(^βPro)Arg-NHMe in the gas phase. The conformational parameters of those with relative energies (ΔE^gp) below 5.0 kcal/mol are listed in Table 1 (the complete list is provided as Supporting Information). In the global minimum (γ_L[u]s⁻g⁺t, Figure 3a), the terminal acetyl CO and methylamide NH groups are linked by a hydrogen bond [d_H…O= 1.793 Å, <N−H…O= 151.3°] closing a seven-membered cycle (γ-turn or C₇ conformation), and the pyrrolidine ring adopts an up puckering. The orientation of the exocyclic guanidilated side chain, which is defined by the skew⁻, gauche⁺ and trans arrangement of ξ¹, ξ² and ξ³, respectively, enables the formation of a strong hydrogen bond between the carbonyl oxygen of the trans-(^βPro)Arg residue and the guanidinium NH site [d_H…O= 1.628 Å, <N−H…O= 176.2°]. The second (γ_L[u]g⁻g⁻s⁺, Figure 3b) and third (γ_L[u]g⁻g⁻s⁻, Figure 3c) minima also exhibit the seven-membered hydrogen-bonded ring typical of a C₇ conformation and an up-puckered pyrrolidine moiety, while they differ from the global minimum in the orientation of the guanidilated side chain. In the (γ_L[u]g⁻g⁻s⁺ conformer, the side chain…backbone interaction involves an NH₂ group in the guanidinium substituent instead of the NH site. The less favorable arrangement of the exocyclic side chain in these two conformers produces a destabilization of 1.1–1.5 kcal/mol with respect to the global minimum. A similar but more pronounced effect is observed for the last minimum listed in Table 1 (γ_L[u]s⁻tg⁻, Figure 3g). This conformer presents identical shapes for both the peptide backbone and the pyrrolidine moiety to those described above for the first, second and third minima, but a much higher energy (ΔE^gp = 3.7 kcal/mol). This destabilization should be attributed to the unfavorable steric interactions produced within the methylene groups in the side chain to allow the formation of a hydrogen bond between the trans-(^βPro)Arg CO and the guanidinium NH₂.

Table 1.

Dihedral angles (see Figure 2; in degrees), pseudorotational parameters of the pyrrolidine ring (A, P; in degrees), and relative energy (ΔE^gp; in kcal/mol) of the minimum energy conformations with ΔE^gp < 5.0 kcal/mol characterized for Ac-t-(^βPro)Arg-NHMe at the B3LYP/6–31+G(d,p) level.

Conformer	ω 0	φ	ψ	ω	A, Pa	ξ 1	ξ 2	ξ 3	Δ Egp
γL[u]s−g+t	−169.6	−77.8	54.8	178.2	40.1, 92.5b	−127.0	61.1	162.8	0.0c
γL[u]g−g−s+	−170.3	−79.9	59.5	179.1	39.0, 98.3d	−84.2	−77.5	117.9	1.1
γL[u]−g−s−	−170.3	−80.5	56.1	179.3	38.0, 103.3e	−59.8	−49.6	−115.6	1.5
αL[u]s−g+t	−169.7	−89.7	−3.5	176.5	36.0, 112.0f	−92.4	61.2	156.5	2.1
αL[u]g+g−t	−170.2	−73.1	−20.2	179.0	40.5, 76.2g	39.5	−77.7	−173.7	3.0
αL[u]g−tg−	−169.9	−76.5	−16.0	177.2	38.0, 85.5h	−88.4	155.2	−86.1	3.5
γL[u]s−tg−	−169.4	−73.5	44.0	177.3	40.8, 85.5i	−126.2	157.4	−87.1	3.7

^aSee ref. 16 for definition.

^bχ⁰ = −1.7°, χ¹ = −22.3°, χ² = 37.5°, χ³ = −38.2°, χ⁴ = 25.2°.

^cE = −856.5567162 a.u.

^dχ⁰ = −5.7°, χ¹ = −18.4°, χ² = 34.9°, χ³ = −38.0°, χ⁴ = 27.5°.

^eχ⁰ = −8.7°, χ¹ = −15.1°, χ² = 32.5°, χ³ = −37.3°, χ⁴ = 29.1°.

^fχ⁰ = −13.5°, χ¹ = −9.2°, χ² = 27.4°, χ³ = −35.4°, χ⁴ = 30.7°.

^gχ⁰ = 9.7°, χ¹ = −30.7°, χ² = 40.2°, χ³ = −34.5°, χ⁴ = 15.5°.

^hχ⁰ = 3.0°, χ¹ = −24.6°, χ² = 36.8°, χ³ = −35.1°, χ⁴ = 20.0°.

ⁱχ⁰ = 3.2°, χ¹ = −26.6°, χ² = 39.6°, χ³ = −37.4°, χ⁴=21.5°.

Figure 3.

Selected minimum energy conformations of Ac-t-(^βPro)Arg-NHMe obtained from B3LYP/6–31+G(d,p) calculations (ΔE^gp < 5.0 kcal/mol, see Table 1): (a) γ_L[u]s⁻g⁺t; (b) γ_L[u]g⁻g⁻s⁺; (c) γ_L[u]g⁻g⁻s⁻; (d) α_L[u]s⁻g⁺t; (e) α_L[u]g⁺g⁻t; (f) α_L[u]g⁻tg⁻; and (g) γ_L[u]s⁻tg⁻. Intramolecular hydrogen bonds are indicated by dashed lines (H…O distances and N–H…O angles are given).

The most stable structure in Table 1 exhibiting a backbone conformation other than a γ-turn is α_L[u]s⁻g⁺t, which is unfavored by 2.1 kcal/mol with respect to the global minimum. This is noteworthy, since the most stable α_L conformation with trans amide bonds characterized for Ac-Pro-NHMe exhibits a ΔE^gp value of 4.9 kcal/mol.³⁶ The α_L[u]s⁻g⁺ t minimum of Ac-t-(^βPro)Arg-NHMe (Figure 3d) presents no hydrogen-bonding interaction within the backbone amide groups, but is stabilized by a strong backbone…side chain hydrogen bond. The two additional α_L conformers in Table 1, α_L[u]g⁺g⁻t (Figure 3e) and α_L[u]g⁻tg⁻ (Figure 3f), exhibit similar arrangements for the peptide backbone and the pyrrolidine ring, while differing in the orientation of the guanidilated substituent and the topology of the associated backbone…side chain interaction. Local repulsions within the aliphatic segment in this exocyclic side chain produce a destabilization of 0.9 and 1.4 kcal/mol, respectively, relative to the most stable α_L conformer.

Comparison with the results previously reported²⁸ for Ac-c-(^γPro)Arg-NHMe provides evidence for the higher flexibility of the β-substituted derivative Ac-t-(^βPro)Arg-NHMe studied in the present work. This is due to the presence of an additional exocyclic methylene unit in the latter case (Figure 1), which broadens the conformational space that may be explored by the guanidilated side chain. Yet, the number of energetically accessible conformers is small in both cases, as expected from the restrictions imposed by the proline skeleton. The two compounds share the main structural features of the global minimum, which belongs to the γ_L[u] category and exhibits identical patterns for both the backbone···backbone and side chain···backbone hydrogen-bonding interactions. However, a highly stable γ_L[d] conformer was located²⁸ for Ac-c-(^γPro)Arg-NHMe at only 0.4 kcal/mol, whereas no γ_L[d] structure appears in Table 1 for Ac-t-(^βPro)Arg-NHMe. Indeed, the only γ_L[d] minimum located for the latter compound presents ΔE^gp = 19.0 kcal/mol (see Supporting Information). Another important difference is the presence of α_L conformers in Table 1, whereas no Ac-c-(^γPro)Arg-NHMe minima²⁸ presented this backbone conformation.

Table 2 gives the conformational parameters of the five minima characterized for Ac-c-(^βPro)Arg-NHMe with ΔE^gp values below 5.0 kcal/mol (see the Supporting Information for a complete list of minima). Interestingly, the backbone shape preferred by this compound corresponds to the α-helix, whereas the γ-turn is unfavored by at least 2.0 kcal/mol. This is in sharp contrast with that described above for the trans-(^βPro)Arg derivative, as well as with the behavior observed before for the analogous γ-substituted compound²⁸ [Ac-c-(^γPro)Arg-NHMe] and for proline itself³⁶ (Ac-Pro-NHMe). Indeed, the most stable α-helical minimum characterized for Ac-Pro-NHMe with trans amide bonds lies 4.9 kcal/mol above the preferred γ-turn conformer,³⁶ and no minimum energy structure was characterized in the α-helix region for Ac-c-(^γPro)Arg-NHMe.²⁸ This comparative analysis provides evidence for the enormous impact that the incorporation of a functionalized side chain able to establish hydrogen-bonding interactions with the main-chain amide groups may have on the conformational preferences of the peptide backbone. It also illustrates the fact that the conformational profile of arginine analogues bearing a proline skeleton depends dramatically on the specific position of the guanidilated side chain, that is, the pyrrolidine carbon bearing it and its relative orientation with respect to the carboxyl terminus.

Table 2.

Dihedral angles (see Figure 2; in degrees), pseudorotational parameters of the pyrrolidine ring (A, P; in degrees), and relative energy (ΔE^gp; in kcal/mol) of the minimum energy conformations with ΔE^gp < 5.0 kcal/mol characterized for Ac-c-(^βPro)Arg-NHMe at the B3LYP/6–31+G(d,p) level.

Conformer	ω 0	φ	ψ	ω	A,Pa	ξ 1	ξ 2	ξ 3	Δ Egp
αL[d]g+g−t	−169.7	−86.3	−11.6	175.3	39.6, −108.3b	75.3	−71.4	178.9	0.0c
αL[d]g+ts+	−169.2	−90.1	−4.3	174.5	40.1, −111.7d	69.2	−172.0	95.2	1.3
γL[d]s−g+t	−171.1	−84.1	75.5	−176.7	39.8, −117.0e	−116.3	70.4	164.2	2.0
γL[d]s−ts−	−170.3	−83.1	66.4	−178.5	40.0, −113.6f	−104.8	168.1	−93.4	3.1
γL[u]s+g−t	−168.7	−66.8	31.8	174.5	43.7, 78.2g	127.7	−65.4	178.3	3.9

^aSee ref. 16 for definition.

^bχ⁰ = −12.4°, χ¹ = 31.7°, χ² = −39.6°, χ³ = 32.0°, χ⁴ = −12.2°.

^cE = −856,554209 a.u.

^dχ⁰ = −14.8°, χ¹ = 33.5°, χ² = −40.1°, χ³ = 31.0°, χ⁴ = −10.0°.

^eχ⁰ = −18.1°, χ¹ = 35.0°, χ² = −39.5°, χ³ = 28.3°, χ⁴ = −6.3°.

^fχ⁰ = −16.0°, χ¹ = 34.1°, χ² = −40.0°, χ³ = 30.0°, χ⁴ = −8.8°.

^gχ⁰= 8.9°, χ¹ = −32.1°, χ² = 43.4°, χ³ = −38.2°, χ⁴= 18.1°.

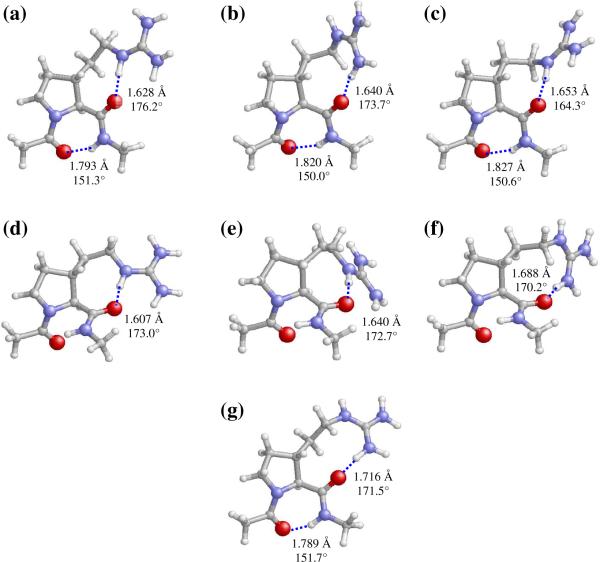
As expected for an α-helical conformer, the lowest energy minimum of Ac-c-(^βPro)Arg-NHMe (α_L[d]g⁺g⁻t, Figure 4a) exhibits no hydrogen-bonding interaction involving the backbone amide groups. However, a very strong hydrogen bond is established between the cis-(^βPro)Arg CO and the guanidinium NH sites [d_H···O= 1.595 Å, <N−H···O= 173.4°]. The α_L backbone conformation and the down pyrrolidine puckering are also present in the second minimum (α_L[d]g⁺ts⁺, Figure 4b). However, the less favorable backbone···side chain interaction in this case, which involves a guanidinium NH₂ moiety, produces a destabilization of 1.3 kcal/mol.

Figure 4.

Selected minimum energy conformations of Ac-c-(^βPro)Arg-NHMe obtained from B3LYP/6–31+G(d,p) calculations (ΔE^gp < 5.0 kcal/mol, see Table 2): (a) α_L[d]g⁺g⁻t; (b) α_L[d]g⁺ts⁺; (c) γ_L[d]s⁻g⁺t; (d) γ_L[d]s⁻ts⁻; and (e) γ_L[u]s⁺g⁻t. Intramolecular hydrogen bonds are indicated by dashed lines (H…O distances and N–H…O angles are given).

The remaining Ac-c-(^βPro)Arg-NHMe minima in Table 2 exhibit a γ-turn conformation stabilized by the corresponding hydrogen bond connecting the acetyl CO and methylamide NH groups. The two most stable conformers of this type, γ_L[d]s⁻g⁺t (Figure 4c) and γ_L[d]s⁻ts⁻ (Figure 4d), retain the down pyrrolidine puckering observed in the helical minima and differ from each other in the guanidinium site (NH/NH₂) that is hydrogen-bonded to the carbonyl group of cis-(^βPro)Arg. Comparison of their relative energies (2.0 and 3.1 kcal/mol, respectively) suggests that the guanidinium NH provides a better geometry for hydrogen bonding to the main chain and therefore produces a higher stabilizing effect, as observed before for the helical conformers (Figures 4a and 4b). It should be noted that the most stable α_L and γ_L conformers characterized for the trans-(^βPro)Arg derivative (Table 1) also present backbone···side chain interactions involving the NH guanidinium site. Therefore, this seems to be a general trend of (^βPro)Arg, independently of the cis/trans relative orientation of the guanidilated side chain.

The trans-(^βPro)Arg and cis-(^βPro)Arg derivatives investigated in this work not only differ in their respective preferences to accommodate γ-turn or α-helical backbone arrangements. These compounds also exhibit different conformational propensities in their five-membered ring. Thus, all minima in Table 1 exhibit an up-puckered pyrrolidine unit, whereas the most stable Ac-c-(^βPro)Arg-NHMe minima (Table 2) present a down puckering. Moreover, the preference for a particular arrangement of the five-membered ring is much more pronounced in the former case as evidenced by the fact that the first up-puckered minimum of cis-(^βPro)Arg lies 3.9 kcal/mol above the global minimum (Table 2) whereas no minima exhibiting a conformation other than up was identified below 7.0 kcal/mol for the trans isomer (see Supporting Information). Indeed, arrangements of the pyrrolidine ring rarely observed in proline and proline-like residues were found to be preferred over the down conformation for this compound (see Supporting Information). The contrast between the puckering tendencies of the five-membered ring in trans-(^βPro)Arg and cis-(^βPro)Arg becomes most evident when minima in the γ_L region are compared. Thus, for the cis isomer (Table 2), the most stable γ_L[d] and γ_L[u] minima are separated by an energy gap of 1.9 kcal/mol only, whereas the corresponding energy difference for the trans derivative amounts to 19.0 kcal/mol (Table 1 and Supporting Information). This distinct behavior should be ascribed to the different spatial relative disposition between the (^βPro)Arg carbonyl and guanidinium groups in the compounds under study. In both cases, the pyrrolidine puckering providing optimal geometry for the establishment of hydrogen-bonding interactions between the two groups mentioned is preferred. For cis-(^βPro)Arg, both substituents lie on the same face of the five-membered cycle and are therefore close enough to interact for any puckering state. In contrast, the two interacting groups exhibit a trans relative orientation in trans-(^βPro)Arg, and it is the up (but not the down) arrangement of the pyrrolidine ring that brings them in close proximity, thus allowing for strong hydrogen bonding. For the trans isomer, the up puckering is particularly favorable in the case of γ_L conformers, because positive ψ values make the carbonyl oxygen of trans-(^βPro)Arg point in the opposite direction to where the guanidilated side chain is located. It should be noted that no hydrogen bond between the guanidinium group and the backbone exists in the only γ_L[d] minimum characterized for this compound.

Table 3 displays the free energies in the gas phase (ΔG^gp) at 298K for the Ac-t-(^βPro)Arg-NHMe and Ac-c-(^βPro)Arg-NHMe minima described above. Consideration of the ZPVE, thermal, and entropic corrections to transform ΔE^gp into ΔG^gp affects substantially the relative energy order of the minimum energy conformations characterized for the trans-(^βPro)Arg derivative. Specifically, α_L[u]s⁻g⁺t becomes the most stable conformer, with γ_L[u]s⁻g⁺t being destabilized by 0.9 kcal/mol. Regarding the cis isomer, the relative stability of the α_L[d]g⁺g⁻t minimum is enhanced upon addition of these statistical contributions. The ΔG^gp values in Table 3 therefore indicate that α_L is the preferred backbone arrangement for both compounds in the gas phase. Assuming a Boltzmann distribution, the population of α_L conformers at room temperature is about 80% and 100% for the trans and cis compound, respectively. In contrast, minima of the γ_L type showed the lowest ΔG^gp value for both Ac-c-(^γPro)Arg-NHMe,²⁸ and Ac-Pro-NHMe,³⁶ thus indicating a substantially higher tendency to adopt conformations in the α_L region for the arginine surrogates investigated in the present work, especially, the cis isomer.

Table 3.

Relative free energy^a in the gas phase (ΔG^gp) and in carbon tetrachloride, chloroform and aqueous solutions (ΔG^CCl4, ΔG^CHCl3, and ΔG^H2O, respectively) at 298K for selected^b minimum energy conformations of Ac-t-(^βPro)Arg-NHMe and Ac-c-(^βPro)Arg-NHMe at the B3LYP/6–31+G(d,p) level.

Conformer	Δ Ggp	Δ GCCl4	Δ GCHCl3	Δ GH2O
Ac-t-(βPro)Arg-NHMe
γL[u]s−g+t	0.9	1.2	2.5	6.5
γL[u]g−g−s+	2.6	0.6	0.3	2.6
γL[u]g−g−s−	2.0	1.5	1.9	4.9
αL[u]s−g+t	0.0c	0.0	0.5	2.7
αL[u]g+g−t	3.1	3.2	3.6	4.9
αL[u]g−tg−	4.1	1.2	0.0	0.0
γL[u]s−tg−	5.1	2.4	1.9	4.2
Ac-c-(βPro)Arg-NHMe
αL[d]g+g−t	0.0d	0.0	1.1	2.1
αL[d]g+ts+	3.0	0.2	0.0	0.0
γL[d]s−g+t	3.9	4.4	6.5	9.4
γL[d]s−ts−	5.9	3.6	4.1	5.7
γL[u]s+g−t	5.8	6.0	7.9	10.2

^aIn kcal/mol.

^bThose given in Tables 1 and 2 (ΔE^gp < 5.0 kcal/mol).

^cG = −856.257478 a.u.

^dG = −856.256685 a.u.

The effect of solvation was next evaluated by performing single point calculations on the optimized structures through the PCM method. The presence of chlorinated solvents results in the stabilization of several Ac-t-(^βPro)Arg-NHMe minima (Table 3), in particular, γ_L[u]g⁻g⁻s⁺ and α_L[u]g⁻tg⁻. The relative stability of the latter notably increases with the polarity of the solvent. Indeed, it becomes the preferred structure in chloroform, even if two other minima exhibit relative free energies within a 0.5 kcal/mol interval, and is the only accessible conformation at room temperature in aqueous solution. Regarding Ac-c-(^βPro)Arg-NHMe, only α_L structures are predicted to be populated either in the gas phase or in the different solvents considered (Table 3). For this compound, solvation seems to affect mainly the arrangement of the exocyclic substituent, with the g⁺ts⁺ disposition being favored with increasing polarity. Accordingly, α_L[d]g⁺ts⁺ becomes the preferred conformation in chloroform and, to a larger extent, in aqueous solution.

Comparison of the solvation effects described above with those observed before¹² for the γ-substituted compound Ac-c-(^γPro)Arg-NHMe provides further evidence for the higher stability of the α_L conformation in the arginine surrogates investigated in the present work. Indeed, minima of the γ_L type showed the lowest ΔG value for the cis-(^γPro)Arg derivative not only in the gas phase but also in carbon tetrachloride and chloroform solutions.²⁸ In water, conformations devoid of intramolecular hydrogen bonds between the backbone amide groups are usually favored for small peptides like the ones considered and, accordingly, an ε_L conformer became the most populated structure for Ac-c-(^γPro)Arg-NHMe in this solvent.²⁸ Interestingly, Ac-Pro-NHMe was predicted³⁶ to prefer the α-helical structure in water. The latter point shows that the conformational preferences of proline in aqueous solution are retained to a larger extent when the arginine side-chain is attached to the β position of the pyrrolidine moiety.

As stated in the Introduction, trans-(^βPro)Arg and cis-(^βPro)Arg are conceived as arginine substitutes in biologically active peptides. The conformational consequences arising from the incorporation of these arginine surrogates into such peptides may be performed by methods like molecular dynamics (MD) simulations. For this purpose, previous parameterization of the non-proteinogenic residues is necessary. A specific set of force-field parameters was developed for trans-(^βPro)Arg and cis-(^βPro)Arg to describe the inter- and intramolecular interactions within the classical formalism. Our previous work showed that there is no special electronic effect that might condition the conformational preferences of proline upon addition of the arginine side chain²⁸ and, therefore, the stretching, bending, torsional, and van der Waals parameters for trans-(^βPro)Arg and cis-(^βPro)Arg were transferred directly from the AMBER force-field.⁴¹ Accordingly, electrostatic charges were the only force-field parameters specifically developed for these non-proteinogenic residues.

Atomic charges were calculated by fitting the HF/6–31G(d) quantum mechanical and the Coulombic MEPs to a large set of points placed outside the nuclear region. The electrostatic parameters were obtained by weighting the charges calculated for the low-energy conformers of each compound according to a Boltzmann distribution.^42–45 The latter was estimated with the ΔG^gp values listed in Table 3. The α_L[u]s⁻g⁺t, γ_L[u]s⁻g⁺t and γ_L[u]g⁻g⁻s⁻ structures were considered for the trans isomer, whereas α_L[d]g⁺g⁻t was the only conformer used for the cis derivative since all the local minima are destabilized by at least 3.0 kcal/mol. The electrostatic parameters obtained for trans-(^βPro)Arg and cis-(^βPro)Arg are given in Figure 5.

Figure 5.

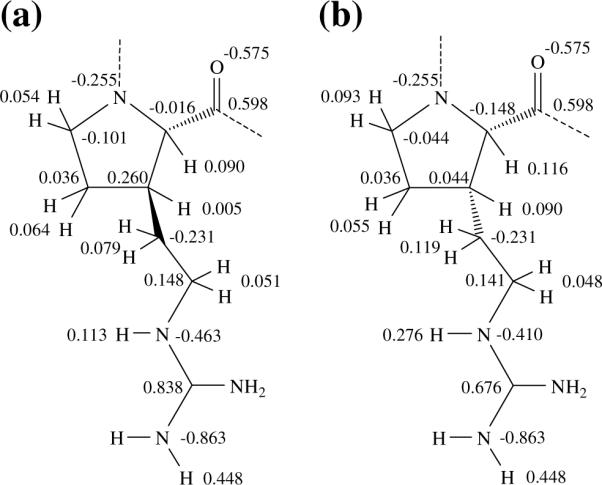
Electrostatic parameters determined for the (a) trans-(^βPro)Arg and (b) cis-(^βPro)Arg residues.

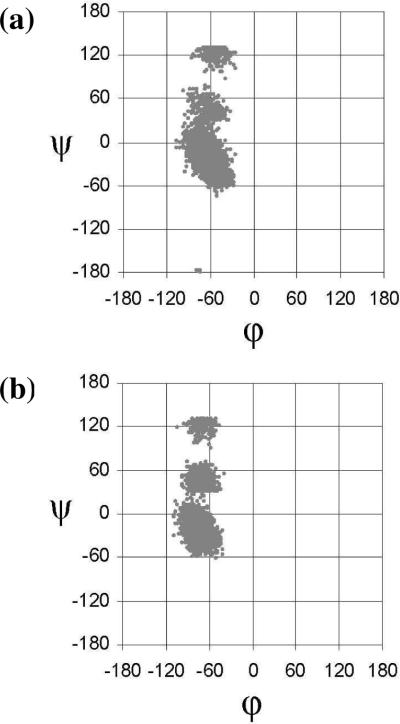
To check the validity of classical MD simulations in describing the conformational properties of the arginine analogues under study, MD with explicit solvent molecules were performed on Ac-t-(^βPro)Arg-NHMe and Ac-c-(^βPro)Arg-NHMe in aqueous solution at 298K. For each compound, the lowest-energy conformation was used as the starting point of a 10 ns trajectory. Figure 6 represents the accumulated Ramachandran plot obtained for each derivative. In both cases, the most populated backbone structure corresponds to α_L, which is visited much more frequently than the γ_L region during the trajectory. This finding is in excellent agreement with the results displayed in Table 3, which indicate that α_L is the most favored conformation in aqueous solution for both compounds.

Figure 6.

Accumulated Ramachandran plots for (a) Ac-t-(^βPro)Arg-NHMe and (b) Ac-c-(^βPro)Arg-NHMe derived from MD simulations in aqueous solution.

Conclusions

Two isomers of an arginine surrogate have been built by attaching the arginine side chain to the proline β-carbon in either a trans or a cis disposition relative to the carboxylic acid. The resulting amino acids, respectively denoted trans-(^βPro)Arg and cis-(^βPro)Arg, combine the conformational restrictions associated with the cyclic nature of proline with the side-chain functionality of arginine. Quantum mechanics calculations on the N-acetyl-N'-methylamide derivatives of these arginine surrogates show that the conformational space available is highly restricted, as expected from their proline-like character. Their conformational preferences are essentially determined by their cyclic structure and the capacity of the guanidilated side chain to establish hydrogen-bonding interactions with the peptide backbone. The latter factor is especially significant for the α_L conformation, which is stabilized with respect to natural proline³⁶ and is predicted to be the most populated structure for both (^βPro)Arg isomers not only in the gas phase but also in aqueous solution. MD simulations show that the restricted flexibility and the preference for α-helical conformations are kept when thermal agitation is included.

The two non-coded amino acids studied in the present work are suitable candidates to replace arginine in bioactive peptides when the natural residue is found in the α_L region, and more specifically, occupying the i+1 position of a β-turn of type I. In particular, cis-(^βPro)Arg may be an excellent replacement for arginine in CREKA, and more appropriate than the arginine surrogate considered in a previous work.²⁸ Thus, cis-(^βPro)Arg is expected not only to increase resistance to proteases but also to greatly stabilize the type I β-turn found for CREKA. For other biologically relevant peptides, either the cis or the trans isomer of (^βPro)Arg may be adequate to replace arginine depending on the orientation attained by the guanidilated side chain in the bioactive conformation.