Adhesive–cohesive model for protein compressibility: An alternative perspective on stability

Abstract

As a dynamic property of folded proteins, protein compressibility provides important information about the forces that govern structural stability. We relate intrinsic compressibility to stability by using molecular dynamics to identify a molecular basis for the variation in compressibility among globular proteins. We find that excess surface charge accounts for this variation not only for the proteins simulated by molecular dynamics but also for a larger set of globular proteins. This dependence on charge distribution forms the basis for an adhesive–cohesive model of protein compressibility in which attractive forces from solvent compete with tertiary interactions that favor folding. Further, a newly recognized correlation between compressibility and the heat capacity of unfolding infers a link between compressibility and the enthalpy of unfolding. This linkage, together with the adhesive–cohesive model for compressibility, leads to the conclusion that folded proteins can gain enthalpic stability from a uniform distribution of charged atoms, as opposed to partitioning charge to the protein surface. Whether buried charged groups can be energetically stabilizing is a fundamental, yet controversial, question regarding protein structure. The analysis reported here implies that one mechanism to gain enthalpic stability involves positioning charge inside the protein in an optimal structural arrangement.

Structural stability of a folded protein is a delicate balance between specific protein–protein interactions and transient protein–solvent interactions. Atoms buried in the core of the folded protein are in direct contact with only protein atoms, and protein atoms on the surface are highly solvated. Nevertheless, the folding of protein molecules results in only a weak partitioning of amino acids between the interior and surface; the probability for an amino acid type to occur preferentially in the interior or on the surface exceeds a factor of ten for only two residues: Lys and Arg (1). Other residues, including the charged residues Glu and Asp, show smaller preference for the interior or surface. The weak partitioning of protein residues indicates a small free energy difference for positioning at the surface and interior for a particular amino acid type and may be contrasted to a strong bias in the distribution of chemical groups for other systems such as membrane bilayers. Overall, folded protein molecules endure a continual competition between dissolution by attractive solvation forces and folding to a compact structure with well ordered intramolecular interactions.

Dynamic properties of proteins and the influence of solvent on protein dynamics are probes of the potential energy surface that provide information central to understanding structural stability and protein function (2). Moreover, there is accumulating evidence that protein dynamics and conformational relaxation is strongly influenced by solvent viscosity and other solvent properties (3–5). A particularly noteworthy finding is that solvent mobility, rather than the protein potential surface, determines the magnitude of the protein fluctuations (5). By using independent temperature coupling to protein and solvent in molecular dynamics simulations, the protein atomic fluctuations were observed to follow the solvent temperature, independent of the protein kinetic energy. The strong interaction between protein and water originates from electrostatics (5, 6).

Compressibility and heat capacity, as functions of the fluctuations in molecular volume and internal energy, respectively, also reveal characteristics of the free energy surface governing protein structural stability. The intrinsic compressibility of a folded protein is largely determined by fluctuations in the interstitial spaces of the folded protein (7). The heat capacity of unfolding reflects differences in nonbonding energies of intraprotein and protein–solvent interactions on exposure of buried groups to solvent (8). As such, both compressibility and the change in heat capacity on unfolding are a consequence of the folded protein conformation and the presence of a protein interior that excludes water.

We exploit the detailed information of molecular dynamics simulations to identify a molecular basis underlying the variation in compressibility among different proteins. Our intention is to explain the observed trends in compressibility for different proteins, not to predict compressibility in an absolute sense. The present analysis finds that differences in compressibility are explained by a competition of the attractive forces between solvent and protein (adhesive forces) and the favorable intramolecular interactions in the protein interior (cohesive forces), as expressed by the excess in surface charge fraction relative to the overall charge fraction. We propose an adhesive–cohesive model whereby the intrinsic compressibility of a protein molecule derives in part from the difference in the adhesive and cohesive forces that originate from charged atoms, and thus reflects a thermodynamic “tug-of-war” between solvation and intraprotein folding interactions.

This article also reports a previously unrecognized correlation between the compressibility of a protein solution and the heat capacity change on unfolding, ΔC_P; experimental values of these quantities show a strong positive correlation. We suggest that this correlation exists because both of these properties reflect the same underlying physical features of the folded state of the protein and propose the origin of this correspondence to be the distribution of charged atoms with respect to the protein interior and surface, as put forward in the adhesive–cohesive model. Moreover, the linear relationship between ΔC_P and the enthalpy and entropy of unfolding (9) has long been a topic of considerable interest in efforts to understand the free energy balance of protein folding (10–12). Together, this relationship, the similarity reported here between compressibility and heat capacity, and the adhesive–cohesive model lead to the conclusion that folded proteins gain enthalpic stability from buried charged atoms. The energetic balance associated with buried charged groups is a controversial topic (ref. 13 and references therein). Although the transfer of charge from water to a low dielectric environment is energetically quite costly, it is reasonable that charge networks can be arranged within a protein to overcome the desolvation energy and contribute favorably to the folded state (12, 14, 15). Thus, the present deduction that buried charge provides enthalpic stability is testimony to the capacity of proteins to evolve a structural organization whereby charge can be stabilized in the protein interior.

In what follows, we first provide the motivation for focusing on charged atoms to explain the variations in protein compressibility. The dependence of compressibility on excess surface charge is then described, followed by a discussion of the correlation between compressibility and the heat capacity of unfolding. How these results lead to the conclusion regarding the effect of buried charge on enthalpic stability is presented in the final section.

Methods

Molecular Volume Calculation. The total molecular volume of the protein, V, comprising the van der Waals (vdW) volume and the interstitial volume, was estimated from a grid-based, extended-vdW-radius approach (7) by using a grid spacing of 0.2 Å and a vdW extension parameter of 1.3. Time-averaged values for the fluctuations, ΔV² and 〈\V〉, were calculated from 800-ps trajectories by using coordinate sets every 0.1 ps and were well converged. Molecular dynamics trajectories were calculated with the all-hydrogen CHARMM22 topology and parameter set (16) as described (7) for α-lactalbumin (Protein Data Bank ID code 1HFZ), hen egg-white lysozyme (ID code 1LZT), RNase A (ID code 5RSA), and trypsin (ID code 2PTN).

Atom Types. Protein atoms were placed in three categories: charged (crg), polar (pol), or apolar (apl). Charged atoms include the side-chain carboxyl groups of Asp and Glu, the guanidinium group of Arg, the side-chain amino group of Lys, the amino and carboxylate termini of the polypeptide chain, and the charged Ca²⁺ ions in α-lactalbumin and trypsin. The polar category comprises atoms with an absolute partial charge >0.30 e, excluding those atoms defined as charged. All other atoms are apolar atoms. The numbers of charged, polar, and apolar atoms are N^crg, N^pol, and N^apl, respectively. The fraction of atom type i is fⁱ = Nⁱ/total number of atoms in the protein (i = crg, pol, apl).

Atomic Type Distribution Between Surface and Interior. The solventaccessible surface area (17) was used to identify surface and interior atoms. The accessible surface was calculated from the protein coordinates by using a 1.4-Å probe radius. The radii for protein atoms were from the CHARMM22 parameter set except for hydrogen atoms. All hydrogen-atom radii were set to 0.85 Å in place of the CHARMM22 values. The CHARMM22 values range from 0.2 to 1.3 Å as a result of force-field parameterization, whereas a single hydrogen radius to model steric features is used in this analysis. The value 0.85 Å was determined by fitting results so that atom-number fractions approximated surface-area fractions (unpublished data). Values from 0.85 to 1.25 Å do not alter the trends based on the atom distributions reported here, although the absolute values for the atom-number fractions vary. Surface atoms are those atoms with a nonzero solvent-accessible surface area. All other atoms are interior protein atoms. The number of surface atoms is N_S and the number of interior atoms is N_I. The atom-type composition was assessed from the number of charged, polar, and apolar atoms overall on the surface and in the interior: Nⁱ_j where j is the overall (= 0), surface (= S), or interior (= I) number and i is the atom type, crg, pol, or apl. The corresponding fractional atom numbers are fⁱ_j = Nⁱ_j/N_j. On average, ≈6% of all protein atoms are charged, 32% are polar, and 62% are apolar. On the protein surface, 12% of the atoms are charged, 37% are polar, and 51% are apolar (Table 1). This leads to an overall excess of charged atoms on the surface of ≈6%, an excess of polar atoms of 5%, and a depletion of apolar atoms of 11%.

Table 1. Fraction of atoms that are charged (crg), polar (pol), and apolar (apl) based on the total atom number (f₀), surface atom number (f_S), excess fraction of charged atoms on the surface, and depletion of charged atoms in the interior.

Protein	*	†	†	†	‡	‡	‡	§	¶
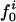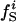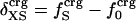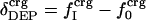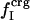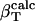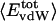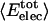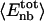Trypsin	5.16	3.5	34.9	61.7	8.6	43.8	47.7	5.1	-1.8
α-Lactalbumin	12.4	6.4	31.1	62.5	15.0	33.3	51.7	8.5	-3.2
Hen egg-white lysozyme	7.73	8.0	32.5	59.5	14.7	39.2	46.1	6.7	-2.5
RNase A Sixteen-protein set∥	5.48	6.1	34.6	59.3	11.0	41.4	47.5	4.9	-2.0
Mean		5.6	31.9	62.4	12.2	37.4	50.4
SD		1.8	2.2	1.5	4.0	5.0	2.7
SD/mean, %		32.0	6.8	2.4	33.0	13.3	5.3

^*β_T^exp from ref. 19.

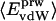^† is the ratio between the overall number of atoms of type i, where i = (crg, pol, apl), and the total number of atoms in the protein (details in Methods).

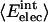^‡ is the ratio between the number of atoms of type i on the protein surface and the total number of atoms on the surface.

^§.

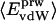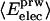^¶ where 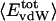is the fractional number of charged atoms buried inside the protein.

^∥Proteins used in this study were (with Protein Data Bank ID codes) ovalbumin (1OVA), pepsin (1AM5), chymotrypsinogen A (1EX3), α-chymotrypsin (4CHA), trypsinogen (1TGN), myoglobin (1MDN), subtilisin BPN (1UBN), ovomucoid (1TUS), carbonic anhydrase (1AVN), β-lactoglobulin (1B8E), peroxydase (1A20), cytochrome c (1A7V), trypsin inhibitor (1BP1), hemoglobin (1A9W), and anionic trypsin (1ANE).

Time-Averaged Nonbonded Energy. The dynamics trajectories were postprocessed to estimate nonbonded interactions by using the Lennard–Jones 6–12 function for van der Waals energy, E_vdW, and the coulomb potential for electrostatic energy, E_elec, with the CHARMM22 all-hydrogen parameter set and a dielectric of 1 (16). The nonbonding energy was switched to zero value over the distance 8–12 Å.

Information for the full set of proteins used in this study, including the type and surface distribution of atoms, the atomic fractional numbers, the individual values for 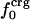, , 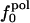and 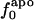and atom fractions 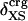and 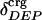can be obtained on request.

Results and Discussion

Intrinsic Protein Compressibility. Molecular dynamics is used here to study the intrinsic isothermal compressibility, β_T, of globular proteins. In an ensemble with constant number of particles, N, at constant pressure, P, and temperature, T, compressibility is directly related to the volume fluctuation (18). The statistical definition of isothermal compressibility is as follows:

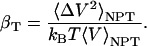[1]

In the case of globular proteins, the solution compressibility measured experimentally comprises effects from the protein intrinsic compressibility and hydration (19–23). Intrinsic compressibility of the protein is a result of protein molecular volume fluctuations due largely to changes in the interstitial volume present in the folded state, with the result that structural features of the native protein are primary determinants of compressibility. Values for β_T of several solvated globular proteins calculated from protein molecular volume fluctuations by using Eq. 1 vary in agreement with the observed experimental measurements of protein solution compressibility (7). Values are listed in Table 2 for the four proteins lysozyme, α-lactalbumin, trypsin, and RNase A. Because the complete description afforded by molecular dynamics allows independent evaluation of the protein intrinsic compressibility and effects on compressibility from hydration waters, it is possible to distinguish the two contributions. Importantly, the net contribution from hydration water molecules is small and the experimental trends in the solution compressibility are largely accounted for by the protein intrinsic compressibility. As such, it is reasonable to explore the protein structural and dynamical properties for an understanding of the observed differences in protein solution compressibility. Hereafter, β_T refers to the protein intrinsic compressibility calculated from the protein molecular volume properties by using Eq. 1. Protein compressibility values (Table 2) vary from ≈6 to 12 × 10^–6 atm^–1.

Table 2. Calculated isothermal compressibility and time-averaged nonbonding energy from molecular dynamics.

Protein	*	†	†	†	†	†	†	†
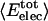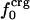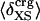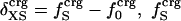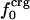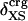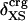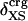Trypsin	6.4	-5.0	-27.5	-32.5	-3.4	-7.6	-1.6	-20.0
RNase A	7.5	-5.7	-43.5	-47.5	-3.7	-15.0	-1.9	-28.5
Hen egg-white lysozyme	9.9	-5.6	-53.4	-59.0	-3.8	-25.6	-1.8	-27.8
α-Lactalbumin	11.5	-4.4	-51.7	-56.2	-2.8	-16.4	-1.7	-35.3

^*β_T^calc (in 10^-6 atm^-1) is the calculated isothermal compressibility from molecular dynamics simulations (7).

^†Angle brackets represent time averages of the per-residue energy components (in kcal mol^-1): van der Waals (vdW), electrostatic (elec), and the nonbonding (nb) energy, which is the sum of van der Waals and electrostatic components. The contributions to the total (tot) energy are decomposed into the intraprotein (int) and protein—water (prw) interactions.

Nonbonding Energy: Proteins Are Distinguished by Electrostatic Interactions but Not van der Waals Interactions. Starting with the premise that molecular volume fluctuations and β_T reflect the nature of interatomic interactions, the nonbonding energies were examined for a set of globular proteins with varying compressibility. Time-averaged electrostatic and vdW components of the nonbonding energy are shown in Table 2 for lysozyme, α-lactalbumin, trypsin and RNase A. The per-residue vdW energy, 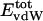, is remarkably constant and small in magnitude for the five proteins; 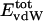is equal to approximately –5 kcal·mol^–1·residue^–1. In marked contrast, the residue-specific electrostatic energy, 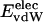, varies considerably among the different proteins and is larger in magnitude; 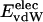ranges from –27 to –53 kcal·mol^–1·residue^–1, fivetoten times more favorable than 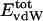. This difference is consistent with a previously reported assessment of enthalpic stability (24) that also finds a larger per-residue electrostatic energy than van der Waals energy even though charged residues were made to be electrically neutral in that study. When the nonbonding energy is decomposed into intraprotein (E^int) and protein–water (E^prw) interactions, the pattern of relatively constant van der Waals and variable electrostatic energies remains (last four columns of Table 2).

Variations in residue-specific nonbonding energy are explained by the different composition of atom types in proteins. The overall atom-number percentages were determined for charged (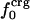), polar (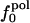), and apolar (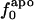) atom types (atom types are defined in Methods) for the four proteins. We find (Table 1) that the relative differences in 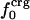are considerably larger than those in 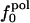or 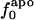. Comparison of the atom-type percentages was also made from a larger set of proteins and by using the ratio of the standard deviation to the average value as a measure of relative differences (Table 1, bottom). The larger set of proteins confirms the point that relative variations in 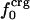are large; SD/mean is 32 for 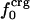and only 6.8 and 2.4 for 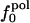and 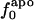, respectively. That proteins differ in relative amount of charged atoms is also born out by an assessment of surface area (1). 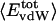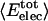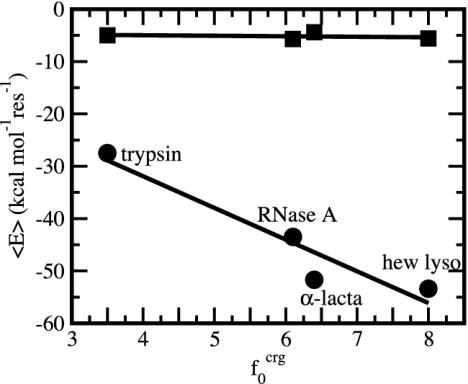Accordingly, we consider the dependence of and as a function of the overall fraction of charged atoms, 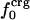, in each protein. A clear trend is observed in Fig. 1. Proteins are distinguished by the residue-specific electrostatic energy, and the van der Waals interactions are similar in magnitude. An increasingly negative 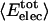with 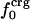is intuitive. The residue-specific 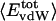is surprisingly constant despite heterogeneous local densities associated with apolar groups compared with polar and charged groups (7, 25–27). Even though local densities can vary between 0.5 and 0.9 (27), the overall packing density of proteins is constant to the extent of yielding nearly equal per-residue values for .

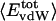Fig. 1.

Time-averaged van der Waals (, ▪) and electrostatic (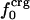, •) per-residue energies as a function of the overall percentage of charged atoms in the proteins, 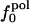. Molecular dynamics coordinates saved every 0.1 ps were averaged over a 0.8-ns period.

Protein Isothermal Compressibility: Competition of Adhesive and Cohesive Forces. Because β_T is governed by interatomic interactions, and given the trend shown in Fig. 1, it is reasonable that a feature of the number of charged atoms underlies the variations in β_T. We propose a model whereby the compressibility of globular proteins arises in part from the excess charge on the surface of the native protein defined by the difference between the fraction of charged atoms on the surface and the overall fraction of charged atoms: 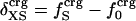. β_T values for four proteins calculated from molecular dynamics trajectories (Eq. 1) are well correlated with the time-averaged excess surface charge, 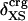(Fig. 2).

Fig. 2.

Isothermal compressibility, β_T^calc, calculated for four globular proteins from molecular dynamics trajectories shown as a function of the time average excess charge on the protein surface, 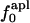, where 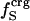is the fraction of charged atoms on the surface, and 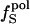is the overall fraction of charged atoms.

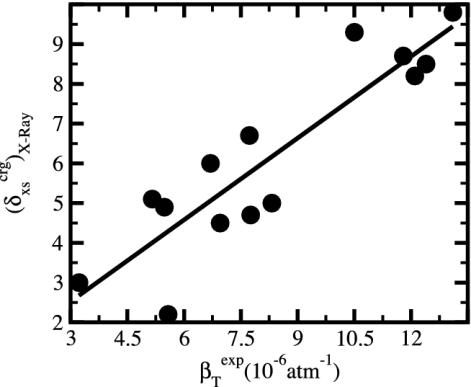
The generality of the adhesive–cohesive model was tested with a larger set of globular protein structures from the Protein Data Bank for which experimental compressibility values are available. The simplicity of the model lends itself to direct evaluation from static structures because the excess surface charge, 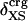, is readily determined from the crystallographic coordinates. Values of 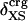were calculated for a set of 14 globular proteins and are shown as a function of experimental isothermal compressibility in Fig. 3. The strong correlation between excess surface charge and β_T (correlation coefficient equal to 0.86) establishes a firm basis for the adhesive–cohesive model of protein compressibility.

Fig. 3.

The excess charge, 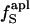, versus protein experimental isothermal compressibility, β_T^exp, for a set of 14 globular proteins. Values for 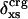were calculated from coordinates taken from the Protein Data Bank. Compressibility data are from Gekko and Hasegawa (19).

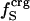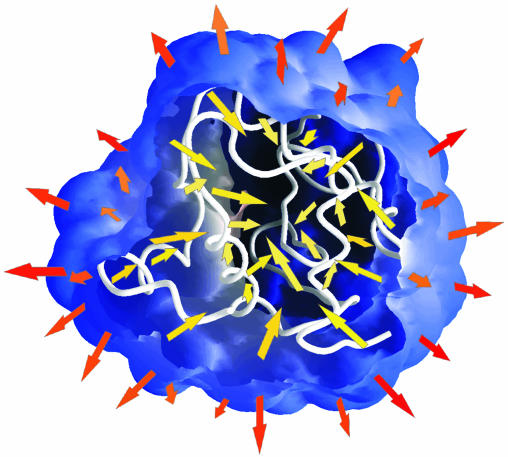
We interpret the increase in β_T with excess surface charge to be the result of competition between attractive solvation forces, reflected by the value of , and the intraprotein attractive forces, reflected by 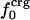. Solvation, an adhesive-like force between protein surface atoms and water molecules, works to expand the protein molecular volume. It is opposed by intraprotein, cohesive-like forces that work to maintain a compact form. We propose that the molecular volume fluctuations defining protein compressibility result from the competition in the adhesive versus cohesive interactions of the folded protein as illustrated by the cartoon in Scheme 1. If the adhesive–cohesive interactions are well balanced at all times, the volume fluctuations are small and compressibility is low. On the other hand, strong adhesive forces due to a high percentage of charged surface atoms, combined with little buried charge, lead to large fluctuations in volume and high compressibility. The dynamic equilibrium between the two opposing forces partly determines the magnitude of the isothermal compressibility and is a basis for variation in β_T among proteins. This adhesive–cohesive model of compressibility takes into account the folded state and the dominant electrostatic component of the nonbonding energy while forming an intuitive picture of protein compressibility. Consider two proteins with similar percentages of charged atoms but which differ in the percentage of surface area contributed by charged atoms. The higher percentage of charged surface atoms implies a lower effective surface tension at the protein–water interface that would allow larger fluctuations in molecular volume and thus higher compressibility. In contrast, the lower percentage of charged surface atoms results in less favorable solvation and a higher surface tension that serves to reduce any tendency toward expansion in volume. This description for compressibility underlines the importance of solvent interactions on protein dynamics.

Scheme 1.

The adhesive–cohesive model for protein compressibility. A slice through the protein solvent-accessible surface reveals the main chain in the interior of a globular protein (white). The model proposes that protein compressibility is a competition between adhesive forces from protein–water interactions (orange arrows) and cohesive forces from protein–protein (yellow arrows) interactions.

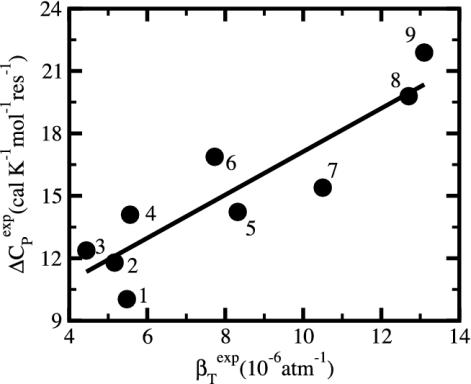
Protein Compressibility and Unfolding Heat Capacity Reflect Common Structural Features. Numerous studies have investigated the heat capacity of protein unfolding, ΔC_P, and its implications on the entropic and enthalpic contributions to protein structural stability. In addition, the relationship between protein compressibility and thermodynamic stability of the folded state has been described (28). The integration of information from these investigations leads to the realization that there is a strong correspondence between β_T and ΔC_P, and that β_T and ΔC_P appear to be reporting on similar properties (29). Indeed, plotting compressibility against ΔC_P for several proteins (Fig. 4) finds that proteins with high compressibility also have a large change in heat capacity on unfolding. That is, there is a strong correspondence between protein compressibility and the heat capacity of unfolding that, to the our knowledge, has not been previously recognized.

Fig. 4.

The change on unfolding in protein heat capacity per residue, ΔC_P, versus the native-state isothermal compressibility, β_T^exp. Values are for measurements at 25°C and near pH 7. Data are computed from tables in refs. 36 and 41. The proteins are as follows: 1, ribonuclease A; 2, trypsin; 3, BPTI; 4, trypsinogen; 5, chymotrypsin; 6, lysozyme; 7, carbonic anhydrase; 8, pepsin; 9, myoglobin.

The adhesive–cohesive model for protein compressibility provides a rationale for the correlation between protein compressibility, a native-state property, and the difference in heat capacity between the unfolded protein and the native state (Fig. 4). In the adhesive–cohesive model, protein compressibility increases with δ_XS and is related to the distribution of charged atoms between surface and interior of the protein. ΔC_P also depends on this distribution. The change in heat capacity on denaturation has long been credited to the exposure of buried groups to water when a protein unfolds (8, 30, 31), although other factors are also likely to contribute (32). ΔC_P is therefore a function of the interior composition of atoms in the folded state of proteins, and neither β_T nor ΔC_P are predictable from linear sequence alone. Further, the positive correlation between β_T and ΔC_P can be rationalized from a related dependence on the distribution of atom types. Hydration of both buried apolar and polar/charged atoms contribute to ΔC_P but with opposite sign (33, 34); apolar groups make a positive contribution to ΔC_P, while exposure of polar and charged groups reduces heat capacity, with the net positive value of ΔC_P evidence that the effect due to apolar atoms dominates. A decrease in the number of buried charged atoms therefore would tend to increase the value of ΔC_P. Proteins with little buried charge and a highly apolar interior are expected to have large ΔC_P values. Correspondingly, an interior depleted of charge is consistent with a large excess of charge on the surface and higher values for β_T as put forward by the adhesive–cohesive model. Thus, proteins with large β_T and ΔC_P have a core depleted of charged atoms and an excess of surface charge, whereas proteins with small β_T and ΔC_P have charged atoms distributed more uniformly between the surface and interior, including charged atoms present in the protein core.

Globular Protein Stability and Protein Compressibility. Murphy, Privalov, and Gill (9) recognized a relationship in globular proteins between ΔC_P and not only the entropy but also the enthalpy of unfolding; both the enthalpy and entropy of unfolding have an inverse linear dependence on ΔC_P. The implications of these relationships have been discussed in detail (10, 29). The correlation reported in the present paper between experimental compressibility and the heat capacity of unfolding further supports the premise that compressibility reflects stability (28). We consider in this section the connection between compressibility and observed trends in the energetics of protein stability and what this connection implies regarding the role of charge distribution on stability.

For temperatures near room temperature, protein unfolding occurs with an increase in entropy and enthalpy: ΔS^unf and ΔH^unf are positive. Thus, the folded protein state is disfavored entropically but stabilized by enthalpic interactions. The change in heat capacity on protein unfolding is inversely related to both the enthalpy and entropy of unfolding such that a plot of per-residue values for ΔS^unf or ΔH^unf against ΔC_P (also specific values) is linear and has negative slope (9, 10, 35). These plots demonstrate that proteins for which unfolding is accompanied by a large heat capacity change have small values of ΔS^unf and ΔH^unf. Consistent with the correlation between ΔC_P and β_T (Fig. 4), a negative slope is also observed when ΔS^unf (28) and ΔH^unf are plotted against compressibility (D. K. Phelps and C.B.P., unpublished results). Therefore, proteins with greater compressibility also have small ΔS^unf and ΔH^unf. The dependence of ΔS^unf on heat capacity or compressibility has been rationalized (9, 28). In contrast, the enthalpic destabilization of the native protein relative to the folded state at large values of ΔC_P and β_T is less well understood (29, 35). Important contributions from theory and experimental results have elucidated some of the issues for understanding the enthalpic stability (24, 35, 36). In the rest of this section we consider what insight is gained from the adhesive–cohesive model to explain the range of residue-specific ΔH^unf values observed among proteins.

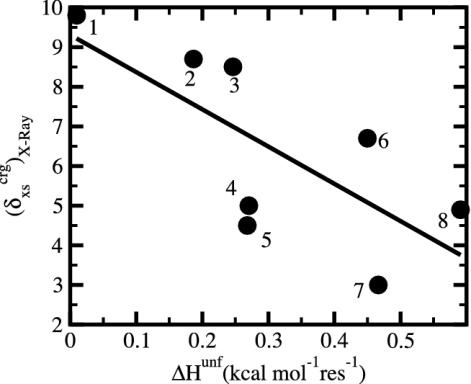
The previous section describes the tendency for proteins with large ΔC_P and β_T to have a protein core depleted of charged atoms, and as shown by Murphy, Privalov, and Gill (9), these proteins are also enthalpically less stable (small ΔH^unf). Correspondingly, proteins with small ΔC_P and β_T have charged atoms more uniformly distributed between the surface and interior, and a relatively high, specific enthalpic stability. Taken together, these trends infer that enthalpic stability is gained in the native state when the charged atoms are more evenly distributed between the surface and the interior, in contrast to expectation. As such, we consider the relationship between ΔH^unf and 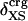for a set of globular proteins (Fig. 5). Overall, larger values of ΔH^unf, corresponding to greater enthalpic stability of the folded state, are indeed found to occur for proteins with smaller excess surface charge, and without a strong preference for positioning charge on the protein surface. It is concluded that proteins gain enthalpic stability from charge groups positioned in the protein interior and that the desolvation of charge is more than compensated by intraprotein, cohesive interactions.

Fig. 5.

Excess surface charge fraction, , versus the unfolding enthalpy per residue, ΔH^unf, near 25°C and pH 7. Data are computed from tables in refs. 36 and 41. The proteins are as follows: 1, myoglobin; 2, β-lactoglobulin; 3, α-lactalbumin; 4, chymotrypsinogen A; 5, α-chymotrypsin; 6, hen egg-white lysozyme; 7, subtilisin BPN; 8, RNase A.

The question of whether protein structure can be stabilized by buried charged atoms has been addressed by a number of experimental and theoretical studies (ref. 13 and references therein), although these studies do not always include a separation of effects into enthalpic and entropic terms. Most often, investigations focus on a single charged group or a pair of charged groups. Although results for some cases show that a buried charged group appears to be destabilizing (15, 37), other cases find that in the context of certain structures, electrostatic interactions of buried charged groups are overall favorable and provide thermal stability (12, 38, 39). Conclusions regarding the stabilization effect of buried charge on protein structure depend strongly on the specific system under investigation, as well as the particular approach taken by the researchers to address the question of stability.

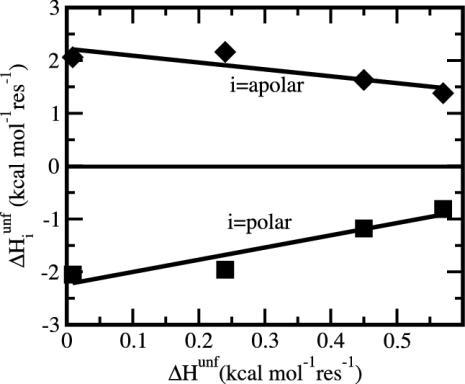
Here our conclusion about buried charge is drawn from a comparison of the overall behavior of various globular proteins, in contrast to studies focused on individual charged groups but similar in spirit to other experimental (36) and theoretical work (24). Interestingly, we note the presence of a trend in the results for the enthalpy of denaturation in solution reported by Karplus and coworkers (24) that is consistent with the present conclusions. In their analysis of enthalpic stability of proteins by molecular mechanics and continuum solvation, these workers decompose the enthalpy of denaturation into contributions from polar and apolar atoms. (Charged groups are neutralized in this study and included as polar atoms.) Although the net contribution from polar atoms is reported to oppose folding, an assessment of their results finds that higher enthalpic stability of a protein arises from polar atom contributions, not apolar ones. This assessment is shown in Fig. 6, where values from table E-V of Lazaridis et al. (24) for the polar and apolar enthalpy contributions are plotted as a function of the total enthalpy of unfolding (all values are per residue). An increase in the total ΔH^unf, corresponding to a more stable folded state, is the result of increasingly favorable polar interactions, whereas the energies contributed by apolar atoms oppose this tendency. The positive slope in Fig. 6 for the polar component is consistent with the premise that polar atoms are responsible for the higher per-residue enthalpic stabilization among proteins.

Fig. 6.

Contributions to the total enthalpy of unfolding (abscissa) decomposed into the polar atom contributions (▪) and apolar atom contributions (⋄). All enthalpies are per-residue values. The increase in folded-protein stability, shown by an overall increase in total ΔH^unf, derives from the increase in polar atom enthalpy (positive slope) and is opposed by the decrease in apolar atom enthalpy (negative slope). Values are from table E-V of ref. 24.

The conclusion that proteins with charge more uniformly distributed between the surface and interior exhibit greater perresidue enthalpic stability (Fig. 5) follows directly from the adhesive–cohesive model of compressibility, combined with the linear relationships of ΔC_P with β_T and with ΔH^unf. Whether buried charge and intraprotein ionic interactions (salt bridges, hydrogen bonds, and networks of polar atoms) generally enhance or hinder the thermodynamic stability of a folded protein is a controversial question. A difficulty in addressing this question is that net stabilization from electrostatic interactions of folded proteins is the coordinated effect among numerous sites so that mutation of a single charged group or ion pair cannot adequately address the structural context as a whole. One point is certain: enthalpic stabilization of buried charged atoms requires a well arranged structure with optimal geometry for electrostatic interactions that overcomes the strong attraction of solvation. General principles regarding the electrostatic and hydration effects on stability will require a description of the whole protein structure including concerted networks of electrostatic interactions and topological effects (40). Mutagenesis studies have established that some buried charge interactions are stabilizing and others are not, which raises the challenge of identifying the underlying structural features responsible for the different behavior. Our results suggest that a more uniform charge distribution between surface and interior has evolved in proteins with enhanced enthalpic stability and reduces an overall destabilizing polar contribution to folding.