A detailed predictive model of the mammalian circadian clock

Abstract

Experimental data on the circadian (≈24-h) clock in mammalian cells are vast, diverse, and detailed. Mathematical models are therefore needed to piece these data together and to study overall clock behavior. Previous models have focused on Neurospora or Drosophila or can be converted to a Drosophila model simply by renaming variables. Those models used Hill-type terms for transcription regulation and Michaelis–Menten type or delay terms for posttranslation regulation. Recent mammalian experimental data call into question some of the assumptions in these approaches. Moreover, gene duplication has led to more proteins in the mammalian system than in lower organisms. Here we develop a detailed distinctly mammalian model by using mass action kinetics. Parameters for our model are found from experimental data by using a coordinate search method. The model accurately predicts the phase of entrainment, amplitude of oscillation, and shape of time profiles of clock mRNAs and proteins and is also robust to parameter changes and mutations.

Men and women lead scheduled lives in which the time of day dictates when to eat, sleep, work, or relax. To live this way, our bodies must have internal clocks to know when to be prepared for eating, sleeping, working, or relaxing. Amazingly, many cells in our bodies have such a clock that is coordinated by the cellular clocks within the suprachiasmatic nucleus (SCN) cells of the brain. Each cell's clock is much more complex than some might naively imagine, because it involves many interacting genes and proteins. For this reason, mathematical models are needed for any hope of understanding cellular clocks in a detailed way.

At its core, the circadian clock within a cell is a series of biochemical reactions that produce ≈24-h oscillations. As long as the details of these reactions were largely unknown, early modeling attempts made simplifying assumptions about the reactions within the clock to keep the number of equations at a minimum. For instance, some authors represented many biochemical processes as simply a delay (1). Most models also assumed low enzyme concentrations (summarized in ref. 2). Both of these simplifying assumptions made it easier for a model to oscillate.

Recent advances provide a more detailed picture of mammalian cellular circadian clocks than these earlier models represent and even challenge some assumptions made in previous models. There is no pure delay in the clock. Likewise, the key enzyme in the mammalian circadian clock, casein kinase Iε (CKIε), is expressed at a higher concentration than its substrates, the PERIOD proteins, PER1 and PER2 (3). Moreover, with the recent advances in computational speed and software designed to simulate biochemical processes (e.g., biospice, www.biospice.org), the number of equations in a model does not need to be limited by computational resources. In short, we are now able to identify many of the specific reactions involved in the clock and directly simulate them on computers. Here, we do this for the circadian clocks found in mouse cells.

Model Description and Rationale

A very good overview of the circadian system in mice can be found in Reppert and Weaver (4). Oversimply stated, the PER1 and PER2 proteins transport the CRYPTOCHROME proteins CRY1 and CRY2 into the nucleus, where CRY1 and CRY2 inhibit the production of the PERs and CRYs. This gives the basic structure of a negative feedback loop, which could oscillate. However, such an oversimplified view omits most of the details of the clock (e.g., how phosphorylation affects the location and stability of the PER proteins). We therefore formulate a much more detailed model of the mammalian circadian clock. This model can be completely described by the set of biochemical reactions outlined in Table 1, which we describe below in detail. Our model system is the clock within the cells of the SCN, the main circadian pacemaker in mouse, which is located in the hypothalamus. We also need to use data from liver cells, as well as educated guesses when data directly from the SCN cells are not available.

Table 1. Reactions and rates of the model.

Description of reaction class	Name	Value	Sensitivity	Minimum	Maximum
Translation of PER1 and PER2	tlp	10.00	0.00	0.003	Big
Translation of CRY1 and CRY2	tlr	1.031	0.14	0.2	Big
Translation of REV-ERBα	tlrv	2.53	0.00	0	Big
Degradation of phosphorylated PER unbound to CRY	up	3.39	0.16	0.7	2,000
Degradation of unphosphorylated PER	upu	0.08	0.17	0	3
Initial phosphorylation of PER2	hot	0.09	0.00	0	Big
Degradation of CRY1 unbound to PER	uro	0.44	0.12	0.2	Big
Degradation of CRY2 unbound to PER	urt	0.59	0.24	0.2	Big
Binding of PER1 and PER2 to kinases	ac	0.47	1.87	0.007	Big
Unbinding of PER1 and PER2 to kinases	dc	5.09	0.70	2	600
Binding of PER1 and PER2 to CRY1 and CRY2	ar	0.27	0.07	0.06	1
Unbinding of PER1 and PER2 to CRY1 and CRY2	dr	0.35	0.04	0.14	1.6
Nuclear localization of initially phosphorylated PER and bound proteins	nl	2.31	0.02	0.005	7
Nuclear export of PER bound Proteins	ne	0.71	0.41	0.2	100
Initial phosphorylation of PER1	hoo	0.29	0.00	0	Big
Phosphorylation that stops nuclear localization of PER1 and bound proteins	hto	1.45	0.04	0.08	Big
Total kinase concentration	Ct	7.71	1.95	0.6	Big
Binding of CRY to CLK:BMAL1 in nucleus	bin	1,476.52	0.01	200	Big
Unbinding of CRY to CLK:BMAL1 in nucleus	unbin	23.78	0.00	0.002	300
Transcription of PER1	trPo	807.4	0.03	0	100,000
Transcription of PER2	trPt	308.8	0.10	0	Big
Transcription of CRY1	trRo	9.03	0.07	0	Big
Transcription of CRY2	trRt	7.66	0.13	0	Big
Transcription of Rev-erbα	trRv	0.05	0.00	0	Big
Preparation and nuclear export of all mRNA	tmc	0.42	7.15	0.08	3
Dimerization of Rev-erbα	arv	0.21	0.00	0	Big
Undimerization of Rev-erbα	drv	3.62	0.00	0	Big
Normalized binding of nuclear REV-ERBα to RORE element	binRv	0.13	0.00	0	Big
Normalized unbinding of nuclear REV-ERBα to RORE element	unbinRv	21.76	0.00	0	Big
Degradation of REV-ERBα	uRv	16.25	0.00	0	Big
Degradation of PER1 mRNA	umPo	6.21	0.00	0.1	Big
Degradation of PER2 mRNA	umPt	0.38	8.55	0.08	Big
Degradation of CRY1,2 mRNA	umR	0.30	0.30	0	3
Degradation of REV-ERBα mRNA	umRv	15.11	0.00	0	Big
Strength of light stimulus	Lon	3.39E-4	0.02	n/a	n/a
Ratio of nuclear to cytoplasmic compartment volume	Nf	115.76	0.01	4	1600

See text for a detailed description of individual reactions. Protein binding or unbinding, as well as degradation, could occur in either the cytoplasm or the nucleus. If binding occurs in the nucleus, the rate constant is multiplied by Nf to account for the smaller nuclear volume. The units of time are hours, and concentrations are expressed in nanomole. See Appendix 1, which is published as supporting information on the PNAS web site, for all reaction rates. Sensitivity (rounded to the nearest 0.01) was calculated by dlog(Y)/dlog(X), where dY was the change in the badness of fit for a 10% decrease in the parameter value X. The minimum and maximum values of the parameters that gave oscillations in darkness are shown (big = >1,000,000). Each reaction class could represent many (>20) individual reactions. n/a, not applicable.

We begin with the control of the transcription of genes that encode for clock proteins. The sequence CACGTG (called an E box) can be found in the control region (promoter) of the PER1 and CRY1 genes. PER1 has five E boxes (5), whereas CRY1 has one (6). Because transcription control of the PER2 promoter is not fully understood, we treat its promoter as we do the PER1 promoter, because some choice must be made, and because the PER2 gene appears to be controlled in a similar way as the PER1 gene (7). Because very little information is available about the CRY2 promoter, we treat it as we treat the CRY1 promoter. When the CLOCK (CLK) and BMAL1 proteins bind together (dimerize), the CLK:BMAL1 heterodimer can bind to an E box and increase the rate of transcription of the corresponding gene (8). Although CLK and BMAL1 levels vary throughout the circadian day and night in liver cells, CLK and BMAL1 are constitutively bound to E boxes (3), perhaps because of saturation. CLK and BMAL1 do not vary throughout the circadian day in SCN cells and are expressed at high levels (9).

Although we do not consider varying levels of CLK:BMAL1 in this study, they might be considered in future work. CLK:BMAL1 bound to just one E box can enhance transcription (6, 8), and when bound to more than one E box, they enhance transcription in an additive way (8). This suggests that there are no allosteric interactions between E boxes. Moreover, if the binding of CLK:BMAL1 to one E box were to facilitate the binding of CLK:BMAL1 to other E boxes, transcription enhancement in a multiple E box promoter should be greater than the sum of the transcription enhancement by each E box alone (i.e., nonadditive). For these reasons, we cannot justify cooperativity between E boxes in the transcription activation by CLK:BMAL1 [note that similar cooperativity is assumed in virtually all other molecular models of circadian clocks (10)]. We instead propose that binding of CLK:BMAL1 to individual E boxes and the resulting transcription enhancement in one E box occur independently of the state of the other E boxes, and that the effects of the different E boxes on transcription are additive.

CRY1 and CRY2 have not been shown to bind directly to DNA. Instead, they bind to CLK:BMAL1 and inhibit the ability of CLK:BMAL1 to enhance transcription (11). When CRY1 and CRY2 are bound to CLK:BMAL1 on promoters, transcription is stopped (6, 7). It appears that oscillations in the CRY proteins, rather than in CLK:BMAL1, control the rhythmic E box-mediated activation of promoters (3, 7). Because CLK:BMAL1 does not bind cooperatively to E boxes, CRY most likely does not bind cooperatively to the different CLK:BMAL1 dimers on a given promoter. CRY could, however, act allosterically to control transcription. Indeed, this happens in our model, because we assume that if CRY is bound to just one CLK:BMAL1 at an E box of a given gene, all transcription of that gene stops. In line with this, we know that CRY can stop transcription of a gene with just one E box (6). Based on these data, our model assumes that CLK:BMAL1 is found at constitutive high levels in the nucleus of the cell (i.e., that its concentration is constant throughout the circadian day), and that the nuclear concentration of CLK:BMAL1 is high enough that there is always one heterodimer bound to an E box in each promoter. We are concerned only with CLK:BMAL1 in the nucleus [also BMAL1 appears to be almost exclusively found in the nucleus (3)]. We also assume that the fraction of CLK:BMAL1 bound to CRY1 and CRY2 is the same regardless of whether the CLK:BMAL1 is bound to an E box. Also, our model would not change if CLK:BMAL1 bound instead to sites that were not CACGTG E boxes [such as what is seen in the Drosophila tim promoter (12)], or if CRY bound to something else on the promoter besides CLK:BMAL1.

In addition to transcription regulation through E boxes, the REV-ERBα protein can inhibit transcription through a sequence on the promoter known as a RORE element (13). There are three E boxes of the type described above in the Rev-erbα's promoter. Rev-erbα homodimerizes, and the dimer binds and unbinds with the RORE element (13). There are two RORE-binding elements on the BMAL1 promoter (13) and three on the CRY1 promoter (7). Because we assume that CLK:BMAL1 is constitutively expressed, we do not consider the effect of REV-ERBα on BMAL1 gene expression. Instead, we model the effect of REV-ERBα on CRY1 transcription (13) (this interaction has never been modeled previously). Because little is known about the specifics of REV-ERBα's control of CRY1, we used the model of transcription inhibition described earlier, where just one REV-ERBα molecule bound to any RORE element can stop transcription.

The mRNAs considered in the model are those that encode PER1, PER2, CRY1, CRY2, and REV-ERBα. All of these species of mRNA are produced in the nucleus of the cell, transported to the cytoplasm, and degraded. In the cytoplasm, mRNA is translated into protein. Four key proteins then interact to complete one arm of the feedback loop (the other arm being provided by REV-ERBα): PER1, PER2, CRY1, and CRY2. PER1 and PER2 can each bind with kinases and can be phosphorylated (14). The kinases CKIε and CKIδ are constitutively expressed (3) and can bind and phosphorylate PER1 and PER2 (3, 15). To model this, we assume a general kinase concentration, which represents CKIε, CKIδ, and perhaps other unidentified kinases. These kinases bind to PER1 and PER2 and can be transported into and out of the nucleus when bound to PER1 or PER2 (3). Phosphatases are probably important as well, but the specific phosphatases, as well as their effects, have not yet been characterized. For this reason, we consider only kinases.

PER1 and PER2 are phosphorylated at many sites, and detailed knowledge about individual sites is not available. We instead model overall states of phosphorylation, each of which can represent the combined phosphorylation of many individual sites. The implications of these phosphorylations are somewhat complex. In the unphosphorylated state, we assume PER1 and PER2 are confined to the cytoplasm, are incapable of binding with CRY1 and CRY1, and are degraded at a slow rate. Once a primary state of phosphorylation has been reached, we assume PER1 and PER2 become unstable in agreement with experiments on PER1 (16). CRY1 and CRY2 bind to PER1 and PER2 at different sites from the binding sites for the kinases (16, 17). PER1 and PER2 bind to CRY1 or CRY2 only when they are phosphorylated (3). We thus treat the binding of the PER proteins to the CRY proteins and the binding of the PER proteins to the kinases as occurring independently, except that the primary phosphorylation of the PERs must have occurred before they can bind to the CRYs. When PER1 or PER2 is bound to CRY1 or CRY2, both proteins of the dimer are protected from degradation (18). In our model, we assume the dimer does not degrade at all. It also appears that CRY1 and CRY2's effects on the nuclear or cytoplasmic localization of PER1 and PER2 are indirect and occur because of this dimer stabilization (19). We shall discuss this later.

PER1 and PER2 each contain an active nuclear localization signal (NLS) [PER1 (14), PER2 (20)] and nuclear export sequences (14, 18). Phosphorylation appears to be needed for PER1 or PER2 to enter the nucleus (3). Somewhat paradoxically, phosphorylation of PER1 can also block PER1's NLS (14), thereby preventing PER1 from entering the nucleus of the cell. To model this, we assume a secondary phosphorylation of PER1 can occur whose sole effect is to stop the nuclear entry of PER1. We allow for this secondary phosphorylation also in PER2 in our model. Because this has little effect on the behavior of our model (unpublished observations), we report simulations where the rate of PER2 secondary phosphorylation was set to zero.

Moreover, it is important to make some distinctions between PER1 and PER2, and between CRY1 and CRY2. PER1 requires more phosphorylation to bind with CRY1 or CRY2 or to enter the nucleus than PER2 (3). To model this, we assume the primary phosphorylation of PER1 (which represents several phosphorylation steps) proceeds at a slower rate than that of PER2. Once this phosphorylation has occurred, PER2 can undergo more phosphorylation than PER1 (3), and accordingly we assume that PER2's secondary phosphorylation proceeds at a slower rate than that of PER1. CRY2 is ubiquitinated more quickly than CRY1 (18), which suggests that it is degraded faster.

Certain proteins related to the circadian clock will not be considered in our model. We do not consider PER3, because targeted disruption of PER3 does not significantly disrupt clock function (21, 22). Although Dec1,2 may be important for the clock (23), we do not consider them, because very little is known about how they function.

Finally, it is important to model the effects of light on the circadian clock. Light has been shown to induce PER1 and PER2 transcription regardless of the state of their E boxes (24, 25). Accordingly, we assume that light causes the production of PER1 and PER2 mRNA in an E box-independent manner.

Model Structure

Our model is completely described by the reactions in Table 1. We now list the variables of the model, whose differential equations can be derived directly from Table 1. The actual equations are included in Appendix 1. The variable names used in the different equations and in Table 1 are in parentheses here. The proteins considered in our model are PER1 (Po), PER2 (Pt), CRY1 (Ro), CRY2 (Rt), REV-ERBα (Rv), and the kinases (C), each of which can bind with other proteins. PER1 and PER2 can bind with the kinase and be phosphorylated (we use p for phosphorylated; PoC, PopC, PoppC, PtC, PtpC, PtppC, Pop, Popp, Ptp, and Ptpp). PER1 and PER2 can also bind with CRY1 and CRY2 when phosphorylated (PopRo, PoppRo, PopRt, PoppRt, PopCRo, PoppCRo, PopCRt, PoppCRt, PtpRo, PtppRo, PtpRt, PtppRt, PtpCRo, PtppCRo, PtpCRt, and PtppCRt). PER1 and PER2 when phosphorylated can bring CRY1 and CRY2 as well as kinases into the nucleus of the cell (we use n for a protein in the nucleus; PopRon, PoppRon, PopRtn, PoppRtn, PopCRon, PoppCRon, PopCRtn, PoppCRtn, PtpRon, PtppRon, PtpRtn, PtppRtn, PtpCRon, PtppCRon, PtpCRtn, PtppCRtn, PopCn, PoppCn, PtpCn, PtppCn, Popn, Poppn, Ptpn, Ptppn, Ron, Rtn, and Cn). REV-ERBα can dimerize (RvRv) and can enter (and exit) the nucleus of the cell (Rvn, RvRvn). The mRNAs of these proteins can be in the nucleus of the cell (MnPo, MnPt, MnRo, MnRt, and MnRv) or the cytoplasm (McPo, McPt, McRo, McRt, and McRv). Finally, let G be the probability that CRY is bound to a given binding site on a promoter, and let GRv be the probability that REV-ERBα is bound to a binding site on a promoter. Overall, we have 74 variables but 73 differential equations, because the total kinase concentration does not vary. The differential equations are available in Appendix 1. All reactions are governed directly by mass action except transcription, whose rate is the activated transcription rate multiplied by the probability that the gene is activated. For instance, transcription on the PER1 promoter is trPo(1-G)⁵, because there are five sites where CRY could bind with probability G, and because all sites must be unoccupied for transcription to occur.

Time is in units of hours. All “concentrations” are defined with respect to the volume of cytoplasm where cytoplasmic reactions occur. That is, the “concentration” of any molecular species is the number of mols of that species divided by the cytoplasmic volume. To get the true concentration of a species confined to the nucleus, one must multiply by the ratio of the cytoplasmic volume to the nuclear volume. We assume a typical volume of 5,000 μm³ (26) and that there are ≈5,000 molecules at the maximum of the CRY1 concentration in the cell; then we have ≈1 molecule/μm³, which gives concentrations in the nanomolar range.

All simulations were done by using mathematica (Wolfram Research, Champaign, IL) and were verified by jigcell/xpp (www.biospice.org). Copies of our model in mathematica are available as Mathematica, which is published as supporting information on the PNAS web site. The model can also be accessed through biospice.

Fitting the Model and Comparison with Experimental Data

The parameter search was done as follows. First, an initial set of parameters was chosen by trial and error that gave ≈24-h oscillations. Mimicking experiments, we then entrained this model to 40 days and 40 nights, each 24-h period comprised of 12 h of constant light and 12 h of constant darkness. The model entrained to this light–dark cycle, so the particular initial conditions are not important. We then recorded the total concentrations of several of the model's mRNAs and proteins during the next 24 h in darkness and compared these with the SCN data presented in Reppert and Weaver (4). We also used liver data for the relative concentrations of the different clock proteins (3), because no SCN data were available. The following formula was used to measure badness of fit of the model to the data:

where j runs through the mRNA, and proteins; n_j is the number of data points for the jth mRNA or protein; s_i,j and e_i,j are the model predictions (scaled so their peak was 100 and trough 0, which is how experimental SCN data are presented) and experimental data points from Reppert and Weaver (4), respectively; k runs through the proteins; pm_k and tm_k are the predicted peak and trough for the kth protein (scaled so that the maximum of the CRY1 rhythm was 1, which is how the experimental data are presented); and p_k, t_k are the measured peak and trough for the kth protein (scaled in the same manner). In this way, each mRNA or protein contributed equally to the fit of model to data. Our procedure for minimizing the badness of fit was to cycle through the parameters one at a time: keeping it the same, increasing it, and decreasing it by 20%. Of the three tested values of each parameter, we retained the value that gave the best fit. If increasing or decreasing a given parameter did not improve the fit, on the next cycle for that parameter, we would try a 10%, 5%, change, etc. This kind of optimization procedure is often called a coordinate search method.

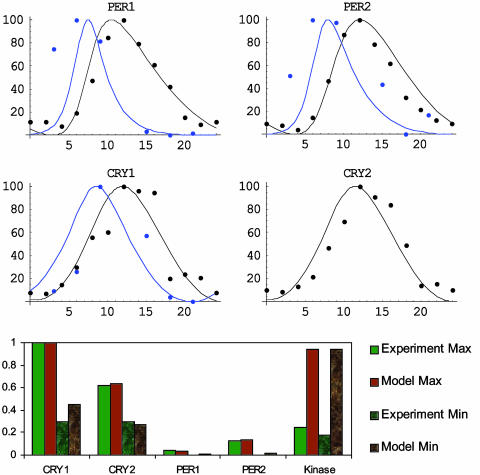
The fitting procedure found a set of parameters for which our model is in very good agreement with experimental data (Fig. 1). When not entrained to 24 h, the autonomous period of our model is 24.299 h, which is well within the range of autonomous periods found for mammals from hamsters to humans (27). The total amount of kinase predicted by our model (including CKIε and CKIδ) is more than the total amount of CKIε experimentally observed (Fig. 1). Our model predicted a slightly higher CRY1 minimum than predicted by the experimental data from liver. However, our intent is to model cells within the SCN where the CRY1 rhythm appears to have a smaller amplitude than those in liver (ref. 28, supporting information). Most important, our model's predictions of the time profiles of the total PER1, PER2, CRY1, CRY2, mRNA, and protein levels after entrainment to 24-h light–dark cycle (12 h of light followed by 12 h of darkness) fit experimental data remarkably well, especially with respect to their phase of entrainment (Fig. 1), general shape (Fig. 1), and relative amplitude (Fig. 1).

Fig. 1.

Model comparison with experimental data. Our model was first entrained to a 24-h day consisting of 12 h of light and 12 h of darkness at time 0, the expected onset of light; darkness for 24 h followed as we recorded the rhythms and compared their time profiles, peak, and trough with experimental data (4). Blue represents mRNA rhythms, whereas black represents protein rhythms. Curves are from the model, and filled circles are experimental data. See text for more details.

Essentially every parameter in our model (shown in Table 1) is a prediction of an experimentally testable biochemical rate constant or protein concentration. Indeed, many of these rates agree with the limited available experimental data. For instance, CRY1 degrades more quickly than CRY2 (18), and PER1 takes longer to be initially phosphorylated than PER2 (3). The PER proteins also degrade more quickly when phosphorylated than when not phosphorylated.

Two questions can now be asked. First, “How precisely does our fitting procedure determine the rates in Table 1?” To assess this, we tested the sensitivity of the badness of fit in our model to a 10% reduction in each parameter (see Table 1). Indeed, some parameters seem to be rather precisely determined (e.g., the degradation rate of PER2 mRNA) and others not, as precisely determined (e.g., the rates associated with REV-ERBα). Nevertheless, because of the limited data on the circadian clock, it is hard to consider any of these parameters as anything more than ballpark estimates. We also note that in real life, many of these parameters may be tissue- or cell-specific.

The second question (actually the same question but from a different point of view) is, “How robust is our model to parameter changes?” Or, stated another way, “Does the qualitative behavior of our model change when the parameters are varied?” Indeed, the model will oscillate even if each parameter is individually varied over many orders of magnitude, with the exception of the binding and unbinding of CRY to PER, which can be varied over one order of magnitude (see Table 1). In short, this model appears to be rather robust to parameter changes.

Testing Model Assumptions

Phosphorylation. Experimental studies of the phosphorylation of PER1 by CKIε have produced some perplexing results. In Cos7 cells, CKIε moves PER1 into the nucleus of the cell (16). A similar mechanism is seen in our model where an initial phosphorylation of the PER proteins is required for nuclear entry. In HEK293 cells, overexpressed PER1 enters the nucleus without overexpressed CKIε. Overexpressing CKIε has the opposite effect in HEK293 cells as it does in COS7 cells: it moves PER1 to the cytoplasm of the cell (14). Our model provides a possible explanation by suggesting that in HEK293 cells, CKIε overexpression mainly changes the secondary phosphorylation of PER1, which blocks nuclear entry.

Several studies also suggest that phosphorylation affects transcription rates. In our model, phosphorylation can promote both the nuclear and/or cytoplasmic accumulation of PER1 and PER2, which can bring with them the transcription factors CRY1 and CRY2. For instance, in HEK293 cells, expression of dominant negative kinase (a kinase that is ineffective at phosphorylation) reduces transcription (17). Because phosphorylation blocks the entry of PER1 into the nucleus of these cells (14), using an ineffective kinase would allow more PER1 to enter the nucleus, bringing with it CRY1 and CRY2, which would reduce transcription.

Nuclear Localization. In line with studies by the Okamura group (especially ref. 18), we assume that CRY1 and CRY2 affect the stability of PER1 and PER2 but do not directly affect PER1 and PER2's ability to enter and exit the nucleus of the cell. How then can CRY promote PER entry into the nucleus of the cell (as was shown in ref. 3)? The fit of our model to data predicts that the volume in the nucleus of the cell where PER and CRY interact is much smaller than the corresponding volume in the cytoplasm of the cell. Thus, when PER and CRY are in the nucleus of the cell, they are more prone to be bound together because of the smaller volume. When PER and CRY are bound, they are protected from degradation, thus PER is more stable, especially in the nucleus, when CRY is present. PER2 achieved its primary phosphorylation quicker than PER1, and more PER2 is in this phosphorylated state than PER1 (Fig. 2). Indeed, once the PER proteins are phosphorylated, they are found at much higher concentrations in the nucleus of the cell (Fig. 4, which is published as supporting information on the PNAS web site). More PER2 is found in the nucleus than PER1, because PER2 is expressed at higher concentrations and requires less phosphorylation to enter the nucleus (Fig. 4). Both of these predictions match experimental data (3). Finally, we predict that there is more CRY in the nucleus than PER, even though CRY can enter or exit the nucleus only through PER association (3) (Fig. 4).

Fig. 2.

Fractions of PER1 and PER2 that are phosphorylated. Shown are the same simulations as in Fig. 1.

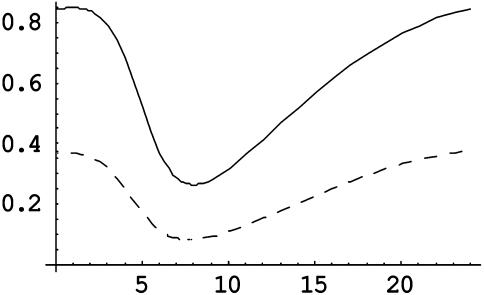
PER and CRY Mutants. We next explored the behavior of our model when some of the PERs or CRYs were removed. These null mutations can be included in our model by setting the corresponding rates of transcription (including that mediated by light) to zero. Removing either PER1, CRY1, or CRY2 individually did not abolish rhythmicity, but removing PER2 did (Fig. 3; Fig. 5, which is published as supporting information on the PNAS web site). This is in agreement with experimental data (21, 29–31). Indeed, of all four simulated null mutations, PER2 had the strongest phenotype: it greatly shortened the period of the clock [as is seen in experimental data (21)] and significantly decreased the clock's amplitude to undetectable levels (Fig. 3). Perhaps individual cells in the PER2 mutant are rhythmic, but because of the decreased rhythm amplitude predicted by our model, cells are unable to couple together, which leads to desynchrony. Somewhat amazingly, our model also agrees with experimental data in that removing CRY1 or CRY2 in PER2 mutants restores rhythmicity (32).

Fig. 3.

PER null mutants. Simulated time profile of promoter binding in the PER1 null mutant (solid) and the PER2 null mutant (dashed). See Fig. 5 for more detail. Note that the PER1 mutant is rhythmic and the PER2 mutant is not (the small-amplitude oscillation disappears with time).

The CRY1 null mutant had a shorter period than the CRY2 null mutant, also in agreement with experimental data (31). This occurs in our model, because CRY2 degrades more quickly than CRY1. PER1-PER2 double mutants and CRY1-CRY2 double mutants were not rhythmic in our model, in agreement with data [PER1-PER2 (21), CRY1-CRY2 (31)]. Finally, as experimentally (31), rhythmicity can be seen in our model, even if only one of the four CRY alleles is present. This circumstance is simulated by reducing the transcription rate of the one active CRY by a factor of two.

Conclusion

Our model is unique in the detail with which we model the mammalian intracellular circadian clock. By (i) not making certain conventional simplifying assumptions; (ii) accounting for the specific interactions of proteins; (iii) accounting for differences between PER1 and PER2, as well as between CRY1 and CRY2; and (iv) directly fitting parameters by using a direct search method, we are able to explain many circadian clock properties, including entrainment and the effects of single and double null mutants, as well as the role of the feedback loop in which REV-ERBα regulates CRY1 transcription.