Structures and relative free energies of partially folded states of proteins

Abstract

The ability of proteins to fold to well defined compact structures is one of the most remarkable examples of the effect of natural selection on biological molecules. To understand their properties, including the stability, the mechanism of folding, and the possibilities of misfolding and association, it is necessary to know the protein free energy landscape. We use NMR data as restraints in a Monte Carlo sampling procedure to determine the ensemble of structures populated by human α-lactalbumin in the presence of increasing concentrations of urea. The ensembles of structures that represent the partially folded states of the protein show that two structural cores, corresponding to portions of the α and β domains of the native protein, are preserved even when the native-like interactions that define their existence are substantially weakened. Analysis of the network of residual contacts reveals the presence of a complex interface region between the two structural cores and indicates that the development of specific interactions within this interface is the key step in achieving the native structure. The relative probabilities of the conformations determined from the NMR data are used to construct a coarse-grained free energy landscape for α-lactalbumin in the absence of urea. The form of the landscape, together with the existence of distinct cores, supports the concept that robustness and modularity are the properties that make possible the folding of complex proteins.

The folding of small single-domain proteins is now relatively well understood as a result of recent progress in describing the structural properties of the transition state ensembles of a range of representative proteins that fold with two-state kinetics (1–3). A particularly important conclusion of these studies is that the protein fold is encoded by the sequence through key nucleation sites (1, 4, 5). By contrast, the folding mechanism of larger proteins, in which the population of one or more partially folded states can be significant, still remains to be resolved. We show here that it is possible to use experimental data to determine the structures and relative free energies of partially folded states for such more complex systems, which include the vast majority of proteins. These results provide the information necessary for the construction of the accessible portions of the free energy surface (3, 6) or “landscape” (7) from which the thermodynamic description of the folding process can be determined. The present approach incorporates experimental restraints into the energy function used in Monte Carlo simulations to bias the conformations that are sampled to the portions of space compatible with the measurements (5). In this way the conformation space accessible to rather complex proteins can be fully characterized. The work described here thus extends the theoretical analyses of energy landscapes for smaller proteins (see, for example, ref. 8).

To illustrate the approach we apply it to the extensively studied protein human α-lactalbumin (HLA), which populates a partially folded “molten globule” state at low pH. NMR measurements have shown that placing the protein under increasingly denaturing conditions results in the gradual and progressive loss of the native-like fold (9). In the absence of denaturants at pH 2, the cross-peaks in ¹⁵N-¹H heteronuclear sequential quantum correlation (HSQC) NMR spectra of the protein are dramatically broadened by motional averaging. These cross-peaks become narrower and readily detectable as the denaturant concentration increases and regions of the protein become gradually unfolded (9). In the present study, the NMR data were converted into a set of restraints describing the involvement of individual residues in nonrandom conformations for each denaturant concentration. The restraints were used in Monte Carlo simulations to determine the ensembles of possible unfolded structures and free energy landscape as a function of the radius of gyration and the rms deviation (rmsd) from the native structure. The resulting landscape is used to obtain information concerning the thermodynamics of the folding process.

Methods

Interpretation of NMR Data. It has been shown (9–11) that it is possible to determine experimentally the concentration U_k of urea at which the main-chain resonance of residue k becomes visible in the ¹⁵N-¹H HSQC spectrum of a protein. The experimental results on HLA (9, 10) show that the unfolding of the low pH molten globule state does not occur in an all-or-none fashion, but rather that certain regions unfold at lower urea concentrations than do others. To interpret the above observation in a model that can be used for determining the structures at different urea concentrations, in analogy with the interpretation of φ values (1, 5), we assume that if U_k is the measured concentration where residue k becomes visible in the HSQC spectrum, the fraction 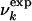of native contacts at urea concentration U can be expressed as a sigmoidal function by

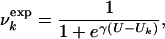[1]

where γ is a parameter that determines the rate of disruption of the native-like environment with increasing U (see below). In this phenomenological interpretation, for U ≪ U_k, the native environment of residue k is preserved (i.e., most native contacts are present) and for U ≫ U_k it is completely disrupted (most native contacts are absent). The decrease of 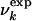for increasing U is consistent with the gradual increase in the intensity of the random coil peaks observed in the case of β₂-microglobulin (12). The influence of tertiary interactions on chemical shifts has been recently reviewed by Xu and Case (12).

Monte Carlo Simulations. To determine the ensembles of conformations consistent with the experimental data (i.e., the values of the urea concentration at which residues become visible in the HSQC spectrum) we use a Monte Carlo method in which two replicas of the protein are simulated in parallel. Given the conformations C₁ and C₂ of the two replicas, we introduce an experimentally based pseudo-energy function (at urea concentration U)

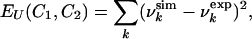[2]

where for each residue k,

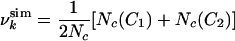[3]

is the sum of the ratios of the number N_c(C_i) of native contacts in conformation C_i (i = 1, 2) to the number of native contacts N_c. The use of replicas allows for a possible multimodal distribution of contacts while keeping constant the average value of 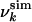. In HLA a very small fraction (3 of 123 at pH 2 in the absence of urea) of residues shows a bimodal distribution; a similar result was found by a reanalysis of molecular dynamics simulations of the molten globule state (14). The Monte Carlo sampling was carried out by performing simulated annealing cycles, so that the pseudo-energy E_U is close to zero. The only parameter that needs to be fitted in the present scheme is γ (see Eq. 1). To determine γ we used the experimental result for the radius of gyration, R_g = 14.8 Å, for the molten globule state (10). We carried out Monte Carlo simulations for vales of γ increasing from 0.01 to 1, resulting in R_g values decreasing from 15.6 to 13.9 Å. The closest agreement with the experimental value of R_g was obtained for γ = 0.1; this value was used in the present study, although the results are not very sensitive to the value used.

The structure of the protein is represented by its C^α backbone, so that the only variables are the C^α pseudodihedral angles; steric constraints between nonneighboring residues along the chain were imposed by requiring that C^α atoms do not get closer than 5 Å, and pseudo bond lengths were fixed at 3.8 Å. Two residues are assumed to be in contact if their C^α atoms are closer than a threshold distance R_c, set here to 8.5 Å. All-atom models were generated from the C^α structures by using the maxsprout program (14), and the energy was minimized by using the charmm program (15) with the EEF1 force field (16).

Free Energy Calculations. Within our structural interpretation of the HSQC spectra, the experimentally based energy E_U (see Eq. 2) represents the approximate energy of the system at urea concentration U. Hence, it is possible to estimate the free energy F_U(A) for the system at urea concentration U as a function of any given set of parameters A by an appropriate sampling procedure; R_g and the rmsd from the native state are used as the parameters to describe the system in the present study. F_U(A) is constructed as a histogram by counting the number, M_U(A), of conformations within a given range of values for the parameters A; i.e., F_U(A) = –k_BT ln M_U(A) + κ_U, where κ_U is an additive constant, determined as described below (17). In this way, we constructed a series of free energy landscapes of HLA at pH 2, corresponding to the states populated at urea concentrations increasing from 0 to 10 M. It is expected that each F_U is most accurate near the minimum because the sampling is most complete. Consequently, we constructed the entire free energy landscape at zero urea, F₀, by using the values of F_U in the neighborhood of the minimum for each U. To evaluate the relative free energies of these states with respect to the state at pH 2 and 0 M urea (i.e., to determine κ_U), we used the experimental relationship F_U = F₀ –mU (1) and m = 0.8 kcal·mol^–1·M^–1, as obtained from experiment (18). The different F_U were concatenated smoothly into a complete landscape by choosing for each bin in the histogram the free energy of the lowest value among those at different U. To obtain the native ensemble, sampling was performed with 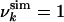for all residues, i.e., with all of the native contacts present. Its relative free energy with respect to the molten globule state at pH 2 was determined by using the result that at pH 2 the native state has a population of ≈10% (19).

Results

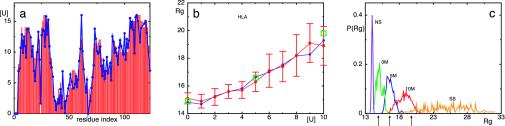
Ensembles of structures (see Fig. 2) were determined by a Monte Carlo sampling method that incorporates restraints derived from ¹⁵N-¹H HSQC spectra into the energy function used in the simulations (see Methods). The average fraction of native contacts formed by each residue in the ensemble was then calculated and related to the denaturation conditions at which the cross-peak corresponding to that residue becomes resolvable in the HSQC spectrum. The consistency of the assumptions made in this fitting procedure is supported by a correlation coefficient 0.94 between the experimental and calculated values (Fig. 1a).

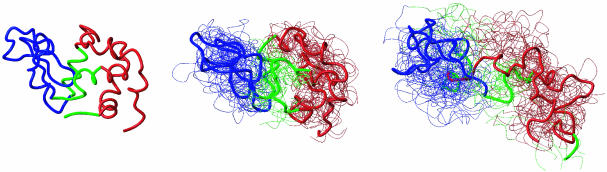
Fig. 2.

Ensembles of structures determined from NMR data at 0 (Center) and 10 (Right) M urea. The native structure is shown for comparison (Left). The thick line corresponds to the average structure, the two stable cores are shown in red (α core) and blue (β core), and the less stable interface is shown in green (see text).

Fig. 1.

(a) Comparison between and 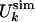for the molten globule state of HLA. 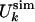was computed by inverting Eq. 1 with 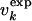replaced by 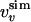for 0 M urea (for U > 10 M, see figure 4 of ref. 10). The coefficient of correlation is ρ = 0.94. (b) Comparison between the experimental R_g (blue line) (ref. 10 and T. Pertinhez and C. Redfield, personal communication) and the calculated R_g (red line) obtained by using the model of Eq. 2. The coefficient of correlation is ρ = 0.95. For comparison, we also show the R_g corresponding to groups 1, 2, and 3 of the molecular dynamics simulations of Paci et al. (13) (squares). (c) Probability distribution function P(R_g) in the native state (NS) and at 0, 5, and 10 M urea for the molten globule state of HLA calculated by using the model of Eq. 2. The corresponding values by Paci et al. (13) are indicated by arrows. The distribution of R_g for a random chain constrained only by the four disulfide bonds is also shown (SS). Values of R_g are in Å and U in M.

Knowledge of these structural ensembles, ranging from nearly native to nearly unfolded, provides the information necessary to determine properties of the partially folded states that are not accessible by direct examination of the experimental NMR data (9, 10). As a global measure of structural change, the distribution function of the radius of gyration, P(R_g), as a function of denaturant concentration was first calculated (see Fig. 1c). In the native state P(R_g) is sharply peaked at R_g = 13.9 Å, and essentially no structures are found with R_g >14.5 Å. The ensembles of structures that were determined for the protein at pH 2 in the presence of 0, 5, and 10 M urea correspond to increases in R_g of 7%, 19%, and 33%, respectively; in the random coil state (estimated from a simulation of a freely jointed chain with excluded volume that is constrained only by the four native disulfide bonds), we found R_g = 24 ± 6 Å, corresponding to an expansion of 73%. The distributions calculated at different urea concentrations are intermediate between those of the native and the random coil states. The average values of R_g agree closely with experimental NMR diffusion measurements (Fig. 1b) (ref. 10 and T. Pertinhez and C. Redfield, personal communication); only the value at zero urea was fitted. While the experimental data give the average value of R_g in the ensemble of molecules in solution, the distributions that we determined show the entire range of accessible values for R_g (and rmsd). Of particular interest is the fact that the most compact conformations within the ensemble at high urea concentrations are found to be similar to the most expanded ones in the absence of denaturant.

At high denaturant concentrations, when native-like contacts are greatly weakened, the overall structure of the protein is substantially expanded and disordered relative to the native state. The structures, however, reveal that within localized regions of the protein the basic architecture of the fold is preserved to a remarkable extent. One such region, designated as the α core, is a portion of the native-state α domain and consists of residues 5–29 and 95–123 (in red in Fig. 2). Within this region at 10 M urea the rmsd of the structures from the average is 5.0 ± 0.6 Å, and from the native structure is 5.7 ± 0.9 Å. Moreover, average contact maps reveal that the structures in the ensemble fluctuate around a native-like topology (see Fig. 3). Similarly, another region designated as the β core is formed by residues 40–49, 56–71, and 75–83 (in blue in Fig. 2). It is also rather well defined and its overall fold is broadly preserved; at 10 M urea the rmsd of the structures from the average is 4.9 ± 0.7 Å, and from the native structure is 4.2 ± 0.6 Å. Although the overall topology of the polypeptide chain in the α and the β cores is preserved within each substructure, the relative positions of the two cores become increasingly ill-defined as the concentration of denaturant is increased (see Fig. 5, which is published as supporting information on the PNAS web site).

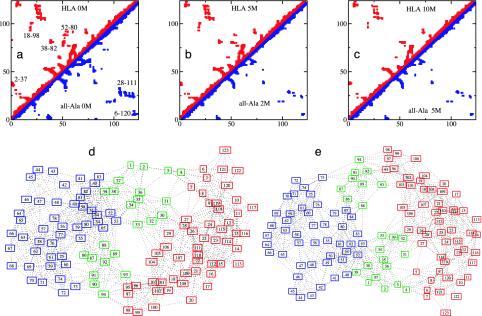
Fig. 3.

(a–c) Comparison between the average contact maps of HLA and all-Ala. (a) HLA and all-Ala at 0 M urea. (b) HLA at 5 M urea and all-Ala at 2 M urea. (c) HLA at 10 M urea and all-Ala at 5 M urea. Contacts with occupation probability >0.3 are shown. Clusters of contacts (labeled in a) in the regions of the WT long-range disulfide bonds 6–120 and 28–111 are visible also in the all-Ala protein. Other long-range clusters, including 2–37, 18–98, 38–82, and 52–80, are indicated. (d and e) Comparison of the graphs for HLA and all-Ala at 0 M urea, showing the modular assembly of the fold of both proteins. Each node of the graph represents an amino acid residue and each link represents a contact present with probability >0.3 in the ensemble of structures. The α core (residues 5–29 and 95–123) is in red, the β core (residues 40–85) is in blue, and the interface (residues 1–4, 30–39, and 86–94) is in green.

The reason for the preservation of the local folds of the two cores was examined by constructing graphs in which the nodes represent an amino acid and each link represents a contact present with probability >0.3 in the ensembles of structures (see Fig. 3). The α core is characterized by a set of residues that occupy central positions in the network of interactions. These residues have high betweenness (20, 21), i.e., they are highly connected within the structures (see Fig. 6, which is published as supporting information on the PNAS web site), and they are mainly hydrophobic in character (in particular Leu-26, Ile-27, Ile-95, Ile-98, Trp-104, and Leu-105). This result is consistent with mutagenesis experiments that show that nonspecific hydrophobic packing is important for stabilizing this region in the native state (22). The sequence of the β core is characterized by a high β-sheet propensity (23) and is again stabilized by residues whose hydrophobic character is highly conserved (24) (in particular residues Leu-59, Trp-60, Ile-75, Phe-80, and Leu-81). A significant number of important interresidue contacts is persistent in the β core even at high denaturant concentrations (see clusters labeled 38–82 and 52–80 in Fig. 3). The structure of the β core is characterized by the partial preservation of β strands, although the hydrogen-bonding patterns, as determined from the all-atom model generated from the C^α results (see Methods), is not always fully in-register relative to the native structure (see also ref. 13), in agreement with Fourier transform infrared results (25). The nature of these structures provide an explanation for the appearance of the resonances of the β-core residues at relatively low urea concentrations in the HSQC spectrum (Fig. 1a); many contacts in this core are lost, and the resulting structures have large fluctuations in the partially unfolded ensemble, allowing rapid motional averaging even though the overall β fold is maintained.

Corresponding Monte Carlo calculations were carried out by using NMR results from the progressive unfolding of a variant of HLA (denoted all-Ala), in which the four native disulfide bridges are eliminated by cysteine to alanine mutations (10). The results of these calculations are shown in Figs. 3 and 5 b, d, and f). In the absence of the disulfide cross-links, the behavior of all-Ala, as deduced from the HSQC spectra, is remarkably similar to that of the WT protein except that in all-Ala the appearance of the random coil peaks is shifted substantially to lower urea concentrations relative to the WT protein (10). The structures that we determined are consistent with this interpretation. We compared the contact maps and the graphs of the proteins with and without disulfide bonds (see Fig. 3) at concentrations of urea such that the two proteins are unfolded to a similar extent, as measured by R_g. We found that essentially the same subsets of interactions are present (see contacts labeled 2–37, 18–98, 38–82, and 52–80 in Fig. 3), thus showing that the structures of these regions of the protein are encoded by interactions other than those arising from the presence of the disulfide bonds; the latter serve to stabilize the more compact structures within a denatured ensemble, especially the more long-range ones in the α domain (10, 26).

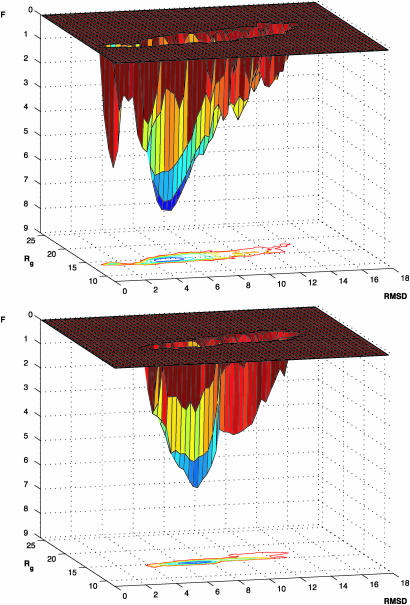
Knowledge of the structural ensembles and their variation with urea concentration can be used to determine a coarse-grained free energy landscape of the molten globule state of HLA (see Methods). Free energy landscapes of proteins provide information about their properties, including the stability, the mechanism of folding, and the possibilities of misfolding and association (3, 6–8). The landscape of HLA, shown in Fig. 4, can be extended to include the native state by incorporation of the ensemble of structures associated with this state (see Methods). The extended landscape reveals that a large barrier exists between the molten globule state and the native state, a finding consistent with experimental studies of the kinetics and the thermodynamics of HLA folding (27, 28). The rmsd between the native state and the molten globule state is only ≈5 Å, and such a barrier is likely to originate at least in part from the fact that the entropic gain of the molten globule state due to the greater freedom of the side chains is lost in the transition to the native state (13), which is stabilized by strong interactions in a tightly packed low-energy structure.

Fig. 4.

Free energy landscapes. (Upper) Molten globule state of HLA reconstructed from the 11 landscapes determined from the NMR data corresponding to progressive denaturation in urea. (Lower) Free energy landscape for all-Ala, the protein without the four disulfide bonds; for this system the fully native state is not accessible under known experimental conditions. The stability of the all-Ala molten globule relative to that of the WT molten globule was estimated from the midpoint of the urea denaturation curve (F in kcal/mol and rmsd in Å).

Conclusions

The HSQC NMR data for the noncooperative unfolding of HLA in its low pH molten globule state at increasing urea concentrations have been used for an exploration of the conformational space accessible to the protein. The results revealed that the free energy landscape is characterized by a deep valley, whose existence demonstrates that significantly misfolded states of the protein have highly unfavorable free energies (6). The landscape is “robust” in the sense that it preserves its overall shape and is only minimally deformed at high concentrations of urea, as well as in the absence of stabilizing disulfide bonds. This robustness arises from the fact that certain contacts in key regions are present under denaturing conditions and that the overall organization of the network of interactions defining the protein is not destroyed. The robustness of protein free energy landscapes is evidenced also by mutation studies (1) and high temperature simulations (29). Interestingly, a similar landscape has been suggested recently for an RNA molecule (30).

In small single-domain proteins, the presence of key residues in the interaction network leads to the formation of transition states with the architecture of the native state (5). We have shown that folding to the native state of a larger protein is based on its modularity: specific cores are formed first, and their folds (like those of single-domain proteins) are defined by a network of native-like interactions. These cores are then positioned through key interfacial interactions that ensure that the preformed local elements are assembled correctly. The present analysis is consistent with the original interpretation of experimental data (9, 10), but provides more detailed structural and energetic information. Moreover it supports the suggestion that the complex structures typical of large proteins are assembled in a stepwise manner (1, 3, 31, 32).

Robustness and modularity minimize misfolding events over the wide range of environments that proteins experience under normal physiological conditions. These features of the landscapes are likely to have arisen as a consequence of evolutionary pressure to fold to a specific native state without sampling misfolded structures that are aggregation prone, as well as nonfunctional (33).