Converting conformational changes to electrostatic energy in molecular motors: The energetics of ATP synthase

Abstract

F₁-ATPase is the catalytic component of the ATP synthase molecular machine responsible for most of the uphill synthesis of ATP in living systems. The enormous advances in biochemical and structural studies of this machine provide an opportunity for detailed understanding of the nature of its rotary mechanism. However, further quantitative progress in this direction requires development of reliable ways of translating the observed structural changes to the corresponding energies. This requirement is particularly challenging because we are dealing with a large system that couples major structural changes with a chemical process. The present work provides such a structure–function correlation by using the linear response approximation to describe the rotary mechanism. This approach allows one to evaluate the energy of transitions between different conformational states by considering only the changes in the corresponding electrostatic energies of the ligands. The relevant energetics are also obtained by calculating the linear response approximation-based free energies of transferring the ligands from water to the different sites of F₁-ATPase in their different conformational states. We also use the empirical valence bond approach to evaluate the actual free-energy profile for the ATP synthesis in the different conformational states of the system. Integrating the information from the different approaches provides a semiquantitative structure–function correlation for F₁-ATPase. It is found that the conformational changes are converted to changes in the electrostatic interaction between the protein and its ligands, which drives the ATP synthesis.

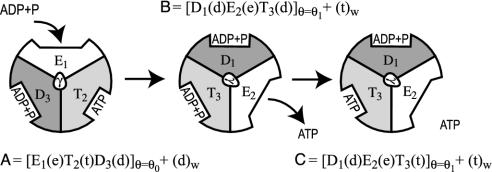
Understanding the nature of energy transduction in biology in general and molecular machines (1–8) in particular is one of the central problems in bioenergetics. The pioneering work of Boyer (1, 3) and subsequent structural work of Walker and coworkers (2) have established that the action of molecular machines involves conversion of external energy to conformational changes. However, the nature of the coupling of these changes to the chemical process (e.g., ATP synthesis) is not completely clear. More specifically, the elucidation of the structure of F₁-ATPase (2) has confirmed early hypotheses (1, 3) and provided a molecular picture of a remarkable molecular machine. Yet the understanding of the detailed operation of this system is far from being clear. Basically, we have a very complex system that involves conformational changes leading to changes in binding strength and catalytic activity for different possible ligands (ATP, ADP, P_i, and Mg²⁺). Although a generic mechanism (2–4) (see Fig. 1) and reasonable variations (e.g., ref. 8) are available, it is extremely hard to determine experimentally a one-to-one correspondence between the x-ray structure and the different states of the operating subunits (see below).

Fig. 1.

Schematic description of a generic mechanism for the action of F₁-ATPase.

Considering the current difficulties of a unique experimental analysis, it is important to try to advance computer-aided structure–function correlations for F₁-ATPase and related systems. One of the major difficulties in developing such an analysis is the evaluation of the free energy of large conformational changes in proteins as a response to changes in the charges of bound ligands. In previous studies (9, 10), we demonstrated that the best way to correlate such structural changes with the corresponding energetics is to use Marcus-type parabolas (11). The same idea was used in our empirical valence bond (EVB) analysis of enzymatic reactions (12), in conceptual studies of linear free-energy relationships (e.g., refs. 13 and 14), and in our studies of binding free energies (15, 16). Here we use this idea in the framework of the linear response approximation (LRA) to correlate the structural changes in F₁-ATPase with the corresponding energetics. We also augment our analysis by direct EVB studies of the chemical conversion of ADP to ATP. The picture that emerges from our combined approaches helps in providing a molecular insight on the energetics of F₁-ATPase.

Defining the Problem

Although different mechanisms are feasible for F₁-ATPase, we will consider the mechanism of Fig. 1 as a starting canonical model. In Fig. 1, we consider the conventional notation of the three subunits (each composed of α and β chains), i.e., the structures E, T, and D, which correspond to the structures of a relaxed empty subunit in an “open” state, ATP-bound configuration, and an ADP-bound configuration, respectively. These three configurations are related to the “open,” “tight,” and “loose” states in the classical picture (e.g., ref. 4). We do not, however, associate at this stage (see Formulating the Problem in a Computationally Tractable Way) D and T with a specific x-ray structure. We also use the notations t, d, and e for ATP + H₂O, ADP+P_i, and empty, respectively. The steps described in Fig. 1 start with a 120° rotation of the γ-subunit, which forces the subunits to change their structure and the binding energies of the ligands, leading to binding of ADP and release of ATP (step A→B). Next, the “strained” ADP, formed as the result of step A→B, is converted to ATP (step B→C).

Significant progress has been achieved in recent years in providing a mechanical picture of the action of ATP synthase (5, 6). However, the current description is based on a macroscopic description, and the actual molecular details are not fully understood. Instructive simulations (17) have shown that the system could be driven from one state to another by exerting a large force. However, a study of a process that occurs on a millisecond time scale [the time of the first step is 0.2 ms (18)] by a nanosecond molecular dynamics simulation might miss key relaxation events. An alternative attempt (7) to explore the energetics of the second step in Fig. 1 involved free-energy perturbation calculation of the change in energy in the B→C step. This study did not, however, simulate the actual reaction. Furthermore, it is not clear from the calculations of ref. 7 how the conformational energy of the protein is converted to the energy of the ATP synthesis.

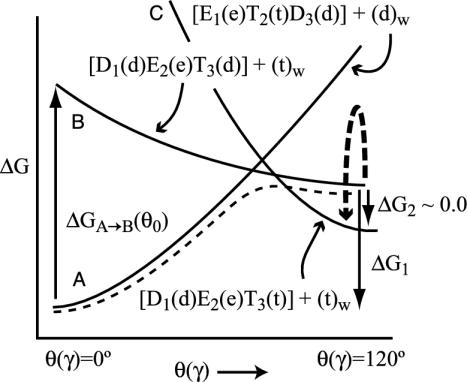
Here we would like to convert the structural information about F₁-ATPase to a clear structure–energy correlation. As a starting point, we convert Fig. 1 to a schematic energy diagram (Fig. 2). In this diagram, we consider the three states A, B, and C in Fig. 1 as a function of a rotation of the γ stalk. In the zero-order picture, the structure and ligation states of the subunits are kept fixed (or allowed a limited relaxation), whereas the γ subunit performs 120° rotation. The actual A→B process also involves a relaxation of the subunits, and the corresponding energy is designated in Fig. 2 by a plain dashed line.

Fig. 2.

Schematic description of the dependence of the energy of the three states in Fig. 1 on the rotation of the γ stalk and the resulting energetics of the system. The energy of each state is considered in the hypothetical situation where the ligands and the subunits are kept at their designated configuration, and only the γ stalk is rotated. In the actual process, the system starts in state A and crosses to state B, where the subunits are allowed to relax. The corresponding energy is represented by the plain dashed line. The transition from state B to state C involves the chemical d→t step, which is described by the curved arrow with thick broken lines.

Consideration of Fig. 2 can be useful as a conceptual framework, and some of the points in Fig. 2 can be elucidated by using experimental information. However, the construction of the actual free-energy curves cannot be accomplished without some form of free-energy calculation. Unfortunately, brute force approaches, such as calculations of potential of mean force, are not likely to give quantitative results in the near future, due to convergence problems (see, e.g., ref. 19). Macroscopic calculations of the direct interaction between the γ stalk and its surrounding subunits might also be problematic, because the reorganization of the system should have a large effect that is hard to model by a uniform dielectric constant (20). Thus, we will try to put special emphasis on the selection of an effective simulation approach.

Methods

Our main strategy for modeling the energetics of protein conformational changes is based on the LRA treatment of the ligands (substrates) (15). This approximation evaluates the overall free-energy change by considering only the interactions between the substrate and its surroundings while evaluating implicitly the interaction between the protein and itself (see Formulating the Problem in a Computationally Tractable Way). The LRA appears to provide a good estimate for the free energy associated with change between two potential surfaces (U₁ and U₂) by ref. 10 (see also ref. 21 for a related approach).

[1]

where 〈 〉_i designates an average over trajectories propagated on U_i.

Another element of our simulation strategy is the use of the semimacroscopic version of the protein dipole Langerin dipole model (the PDLD/S-LRA approach) in calculations of binding free energies. The corresponding binding cycle involves electrostatic steps of uncharging and charging the ligand in the protein and in water, respectively, as well as a step of binding of the uncharged ligand. The calculated free energy of the binding of the uncharged ligand includes hydrophobic, van der Waals, water penetration, and entropic contributions. This approach, which has been described in detail in several works (e.g., ref. 16), provides a stable estimate of binding free energies for highly charged systems. Specific aspects of the binding calculations performed in this work will be considered in Formulating the Problem in a Computationally Tractable Way.

Our approach for the study of the “chemical” part of the problem involves the use of the EVB method (12), which has been used extensively by us and others (for a review, see ref. 22). Here we describe the ATP hydrolysis and synthesis reactions by considering the three VB structures described in the Fig. 7, which is published as supporting information on the PNAS web site. The parameters for the potential surfaces of these states and the off-diagonal terms were obtained in studies of the hydrolytic reaction of GTP in water and in the RasGAP complex (23, 24). These studies started by using ab initio calculations and experimental information to construct a generic potential surface for the hydrolysis of the γ—β bond in GTP (and, thus, the γ—β bond in ATP). Our EVB parameters were obtained by forcing the EVB surface for GTP (ATP) hydrolysis in solution to reproduce the above surfaces. The corresponding parameters are given in Table 3, which is published as supporting information on the PNAS web site. The free energy of the EVB surface was evaluated by the umbrella-sampling/free-energy perturbation method (12). The simulations were subjected to the surface constraint all-atom solvent model and its special polarization constraints (25), and long-range effects were treated by the local reaction field long-range treatment (26).

Our study was conducted by using Protein Data Bank structures of bovine mitochondrial F₁-ATPase [PDB ID codes 1E1R (27) and 1H8E (28)] as starting points for the free-energy simulations. Only the relevant pair of α and β units was considered explicitly in the simulations of the E, D, and T chains. Both the EVB and LRA simulations were done by using the enzymix module of the program molaris (29). The radius of region II of the surface constraint all-atom solvent model (see ref. 29 for the definition) was taken as 20 and 18 Å in the initial calculations. Because the results for the two sets were similar, we used a radius of 18 Å for the rest of the study. The free-energy perturbation mapping of the chemical step in both the solution reference system and the protein was typically evaluated after 220-ps equilibration time, followed by 31 windows of 5 ps each moving along the reaction coordinate. The microscopic LRA calculations involved 70 ps on each state. The PDLD/S-LRA calculations involved molecular dynamics generation of 20 configurations for the charged and uncharged forms by using 20-ps simulation for each configuration. All of the simulations were done at 300 K with a 1-fs time step. Several initial conditions were used in each case to ensure the stability of the results and to obtain a proper average over the protein configurations.

The simulations considered the following residues to be explicitly ionized: Lys-162, Glu-188, Arg-189, Glu-192, and Arg-260 of the β-chain; and Arg-373 of the α-chain. The effect of other ionized residues was considered macroscopically after the microscopic calculations were carried out. This was done by our standard approach, which scales the corresponding electrostatic interactions by an effective dielectric constant (20). The justification of this approach is given elsewhere (30).

Formulating the Problem in a Computationally Tractable Way

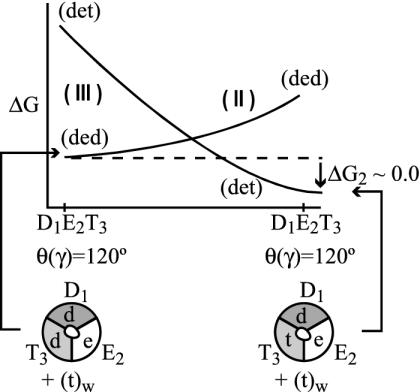
Analyzing the energetics of Fig. 2 by reliable calculations may look hopelessly complicated. Not only do we have to deal with a complex system, but we also have to consider the interactions among different subunits in different conformational states. In addition, we must consider the interactions between the subunits and their ligands. Fortunately, it is possible to simplify the problem enormously by using the LRA. That is, within the LRA, it is enough to look on the change in ligand–protein interaction on a conformational change (without evaluating the interaction between the protein and itself) to obtain a reasonable approximation for the corresponding change in the interaction between the subunits. This treatment is based on the fact that, according to the LRA, the change in the electrostatic interaction between the environment and itself, on ligand binding, is the negative half of the interaction between the environment and the ligand. Thus, the change in the interaction between and within the subunits is about the negative half of the change in the interaction between the subunits and the ligands, and there is no need to evaluate the change in the energy of the environment (note that Eq. 1 does not include the interaction between the environment and itself). The LRA approach can be used for transformations between different states in the system and for the binding process. To illustrate our LRA approach, we will start with the “simplest” case of moving from state B to state C at θ = 120°. Here we will try to follow the reaction not along the θ coordinate of Fig. 2 but along the coordinate that defines the response of the protein to the chemical process of the ligands (or the change of ligands) as well as structural changes of the ligands. In other words, we try to use the LRA to evaluate ΔG(B→C)_θ=θ1 (ΔG₂ in Fig. 2) by considering the free-energy surfaces (the Δg_κs) for the states that are defined by the bound ligands (K = I, II, or III). These free-energy functions reflect the configurational changes of the β units, rather than the energetics of the states with fixed configurations of the β units (the above A, B, and C states). However, the minima of the free-energy surfaces of states I, II, or III correspond to the minima of A, B, and C. Now, using the Marcus-type parabola of Fig. 3 and the LRA, we obtain

[2]

where the U_K are the potential surfaces of the indicated states and 〈 〉_K designates an average over structures generated with the potential surface U_K (K = I, II, or III). It is also understood that the average is performed near the equilibrium configuration of each designated subunit. Thus, 〈U(d₁, e₂, d₃)〉_II indicates that U(d₁, e₂, d₃) is averaged over configurations where the β subunits are constrained by weak constraints to be near observed structure at D₁(d)E₂(e)T₃(d). The above average is also designated by 〈β₁(d)β₂(e)β₃(d)〉_II. We can further simplify our treatment by using the explicit nature of the subsystems. For example, we can write

[3]

where β_i(x) designates that the ligand x is bound to the ith subunit in the configuration β = (T, D, E). Thus, for example, 〈β₁(d)β₂(e)β₃(t)〉_{D1(d)E2(e)T3(t)} designates an average over the interaction of d and t with their surroundings when β₁, β₂, and β₃ are held (by the fixed γ) near the D, E, and T configurations, respectively. Next, we can write

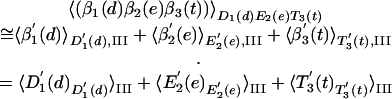[4]

Here we designate by the fact that the ligand x (at site β_i) interacts with both β_i and the rest of the system (the interaction with other subunits is evaluated by a macroscopic treatment). The only approximation here is the neglect of the direct long-range interaction between the ligands, which is justified because we do not neglect the structural changes of the protein due to each ligand, and because in each term of Eq. 3, we consider the difference between the interaction of system of an equal total charge (e.g., ATP and ADP + P_i) and a very far ligand.

Fig. 3.

Schematic description of the free energies of configurations II and III as a function of the reaction coordinate that connects conformational states B and C. The notation K (K = II or III) designates the corresponding Δg_κ.

With the help of Eq. 4, we obtain

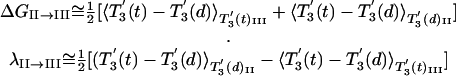[5]

Here the simplified notation 〈 〉_βi(x)K means that the average is over the configuration generated with ligand x, where the system is kept near the specified structure of β_i, and the rest of the subunits are kept at their structure at the minimum of the Δg_K of the indicated state.

Although ΔG_I–II can be evaluated by applying the LRA to Fig. 8, which is published as supporting information on the PNAS web site, we exploit here the fact that the energetics of this process can be modeled by considering it as a two-step binding process, using the thermodynamic cycle of Fig. 4. It is possible to represent the electrostatic contribution to the binding process by the LRA (15). Thus, we can write

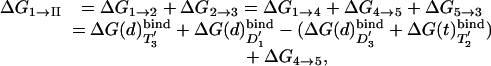[6]

where, for simplicity, we omitted the index of the specific state. Now, because ΔG_4→5 = 0, we obtain

[7]

The binding energies can be evaluated conveniently (see refs. 15 and 16) by using an electrostatic cycle where the ligand is transformed from its actual charged form to a fully nonpolar form (n in the present notation) and then by being moved to water and transformed back to its actual charged form. The free energy of this cycle can be expressed as

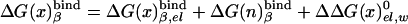[8a]

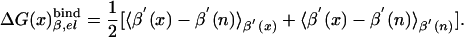[8b]

The first term in Eq. 8b represents the electrostatic contribution of charging x from a fully nonpolar form (n) to its actual charge distribution in the protein. The second term is the solvation energy of x in water. This term can be evaluated conveniently by the PDLD/S-LRA method. ΔG(n)^bind represents the contribution to the cycle from the binding of the nonpolar form of the ligand. 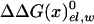is the free energy of taking the substrate fragments from the entire volume available for them at standard conditions and bringing them to the same solvent cage (see Supporting Text, which is published as supporting information on the PNAS web site). The term ΔG(n)^bind involves contributions from water penetration, van der Waals interactions, hydrophobic effects, and entropic effects. These contributions are evaluated by the approach of ref. 16, by using the semimacroscopic cycle and evaluating the entropy by a restraint release approach.

Fig. 4.

An alternative description of the transition between A and B in terms of a binding cycle.

The binding cycle of Fig. 4 can also be used to provide an alternative estimate of ΔG_II→III in the same way used to obtain Eq. 7, which gives

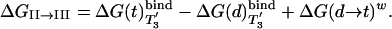[9]

The last term is known from solution experiments (≈7.3 kcal/mol in standard conditions (31).

The binding cycle of Fig. 4 can also be used to evaluate the free energy ΔG_1→2 of the first step in the I→II process. That is, we can use

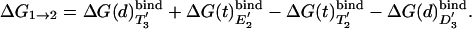[10]

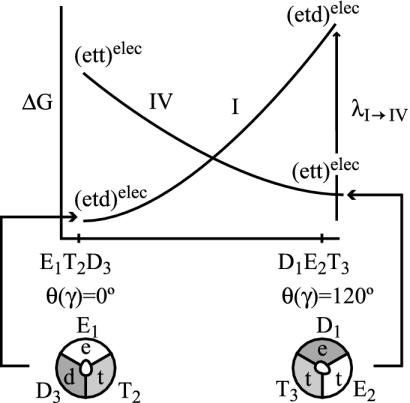
Finally, we can even estimate a lower limit for the activation barrier for the step 1→2 (the rotation of the γ stalk by 120°) by using the LRA approach. Here, we use a nonstandard trick, because step 1→2 does not involve any change of the ligand charges. However, we can generate a hypothetical process whose reorganization energy corresponds to the desired free energy of rotation. That is, we can consider the fictitious process I→IV of Fig. 5 and obtain

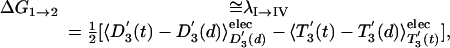[11]

where the 〈 〉^elec designates the electrostatic contribution to the given term.

Fig. 5.

A hypothetical process used to evaluate the energetics for rotation of the γ stalk. The energetics is approximated by the reorganization free energy for the transfer from state I to state IV. Note that this hypothetical process considers only the electrostatic energy contribution (designated by “elec”).

Evaluating the Energetics of the Chemical Step

To study the chemical step, we use the EVB approach that has been used repeatedly for the closely related case of GTP hydrolysis in Ras (23, 24).

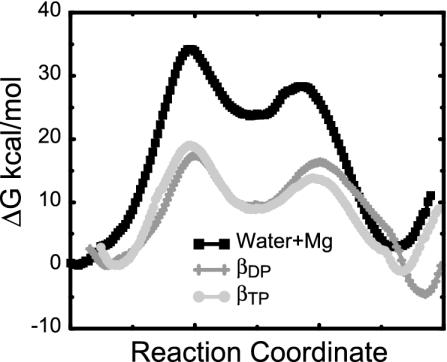
With the EVB and the same parameters used in our latest study of the GTPase reaction in the RasGap complex (24), we obtained the results summarized in Table 4 and Movie 1, which are published as supporting information on the PNAS web site, and Fig. 6.

Fig. 6.

The free-energy profiles for the ATP synthesis reaction in water (black squares), in subunit β_DP (dark gray plus signs), and β_TP (light gray circles) obtained from an average over four different profiles, calculated by using the EVB free-energy perturbation/umbrella sampling procedure (see Table 4 for more details).

As seen from Fig. 6 and Table 4, we reproduced the catalytic effect of the enzyme with 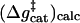19 ± 3 and (32).

Although the EVB calculations are extremely effective in reproducing the enormous catalytic effect, they do not yet provide conclusive results about the identity of β chains. That is, the calculations in both β_TP and β_DP provide a major part of the observed catalytic effect, and both reproduce ΔG₀ ≅ ±5 kcal/mol, whereas the requirement for an effective T state is ΔG₀ ≅ ±0 kcal/mol. This means that, at present, our microscopic estimates of ΔG₀ are not accurate enough to provide a conclusive assignment of the subunit that corresponds to T in Fig. 1. The establishment of a reliable conclusion must involve a demonstration of stability with regard to different initial conditions for the simulations, the sensitivity to different assumed ionization states of the protein groups, and the representation of their electrostatic screening. At any rate, we provide in the next section a semimacroscopic analysis of this issue.

The Reorganization (Conformational) Effect

The calculation presented in the previous section cannot tell us the origin of the effect of the protein or how the protein structural change is coupled to ΔG₀. To explore this question, we need to evaluate the ligand–protein binding energy and not just evaluate the change in binding energy during the reaction. Here we follow our experience in studies of the binding of GDP and GTP to p21^ras (33). We consider several alternative binding modes: (i) binding the ligand to a site that already contains the Mg²⁺ ion, (ii) a simultaneous binding of the ligand and the accompanying Mg²⁺, and (iii) binding of the ligand first and then the Mg²⁺ ion. As in the p21^ras case (33), we found binding of the ligand with the Mg²⁺ ion to represent the most reasonable binding mode.

The results of the binding calculations are summarized in Table 1 for ε_p = 4 and ε_p = 8 [using larger ε_p reflects the possibility that some reorganization processes are not fully captured in the simulations (20)]. The results with ε_p = 4 seem somewhat more consistent with the observed binding energies (note, however, that our calculations correspond to the multisite situation). The largest contributions come from 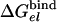, which by itself reflects a balance between very large contributions. The difference between the binding of t and d reflects in part the corresponding difference in 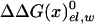, due to the repulsion between ADP and P_i (see also Conclusion). The PDLD/S-LRA results reported in Table 1 are used in Table 2 to provide the energetics of the F₁-ATPase system. As can be seen from Table 2, we reproduce the observed trends of ΔG_II→III and ΔG_I→II with T identified as β_TP. In addition to the PDLD/S-LRA studies, we examined the performance of the microscopic LRA results of Eqs. 5 and 11. It appears that these calculations do not yet provide quantitative results. That is, we obtained from Eq. 5 ΔG_II→III = 8 and –10 kcal/mol for T = β_TP and T = β_DP, respectively. We also obtained from Eq. 11 ΔG_1→2 = 28 kcal/mol for T = β_TP (which is probably an overestimate). The current difficulties of obtaining full quantitative results with the microscopic LRA are not surprising, because we have a balance of enormous electrostatic contributions [for example, a typical value of the microscopic estimate of 〈T(t)–T(n)〉 is ≈800 kcal/mol, but the compensation of these gas-phase energies leads to a net electrostatic effect of <20 kcal/mol]. Future studies may attempt to obtain better convergence for the microscopic calculations. At any rate, the present study indicates that the energetics associated with the conformational changes reflect mainly electrostatic effects. That is, all of the reported energies can be expressed in terms of the corresponding binding free energies, which are obtained here by an LRA charging process (electrostatic free energy in the protein and in water) and the ΔΔG^bind term. Even the ΔΔG^bind term includes major electrostatic contributions from water penetration and from 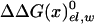With the help of Tables 1 and 2, we can see (by using ε_p = 4, which provides more reasonable results) that the main effect of the conformational change from D(d) to T(d) on the d → t step is due to the electrostatic contribution to ΔG^bind. When the structure of β is changed from β_DP to β_TP, the energy of β(d)→β(t) becomes close to zero (note that the binding energy in Table 1 includes the 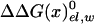contribution). This is due in part to the increase in the electrostatic stabilization of t as a result of the conformational change of the β-subunit. Thus, the ATP synthesis by F₁-ATPase can be described, to a significant extent, as an electrostatic process.

Table 1. PDLD/S-LRA free energies of binding of (t) and (d) to different subunits of F₁-ATPase.

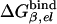
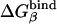
Term	Identity	εp = 4	εp = 8	-ΔΔGbind	εp = 4	εp = 8	Observed
	β = βTP	-20	-5	1	-19	-4	-13*
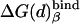	β = βTP	-21	-5	10	-11	5
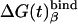	β = βDP	-13	-3	-2	-11	-5	-9*
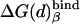	β = βDP	-20	-6	7	-13	-1

(t) and (d) designate, respectively, ATP^-4 plus Mg²⁺ and ADP^-3 plus P_i^-1 plus Mg²⁺. β designates either T or D, energies in kcal/mol. 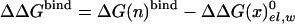. The values of 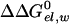are 0 and 6 kcal/mol for t and d, respectively. The entropic contribution (-TΔS^bind(n)) to ΔG(n) was evaluated by the restraint release approach of ref. 40 and found to be 8 and 10 kcal/mol, respectively, for t and d in β_TP and assumed to be similar in β_DP.

^*The reported values are taken from unisite experiments (41), which might not correspond exactly to our multisite system. Note that if the identity of T changes, this assignment will be reversed.

Table 2. Energetics of the key steps in the action of F₁-ATPase.

		ΔGcalc
Energy term	Identity	εp = 4	εp = 8	ΔGobs
ΔGII→III*	T = βTP	-1	-2	∼0
ΔGII→III*	T = βDP	9	2	∼0
ΔGI→II†	T = βTP	8	9	≥10
ΔGI→II†	T = βDP	-2	5	≥10

^*Evaluated by using Eq. 9.

^†Evaluated by using Eq. 7.

Conclusion

This work provides a general way of correlating the structure of F₁-ATPase with its function. This correlation converts x-ray structures to energies by using the LRA approach and the resulting reorganization free energies and binding free energies. In addition, we use the EVB method to evaluate the detailed reaction profiles for ATP synthesis in the different conformational states of the system. The integration of our different simulation strategies provides a promising way of analyzing the energetics of the rotary mechanism.

It is interesting to note the analogy between the electrostatic effects in F₁-ATPase and the action of the RasGAP system. That is, the hydrolysis of GTP by p21^ras is greatly accelerated by the binding of GAP (e.g., ref. 23). This step can be described as a shift of positive charges from the γ-phosphate to the β-phosphate (13, 23, 33). This process leads to stabilization of the GDP+P_i state relative to the GTP state. The synthesis reaction of F₁-ATPase can be described as the opposite process. Here, the D→T conformation change stabilizes the ATP state relative to its energy in D probably by a shift of the electrostatic potential from the β-phosphate to halfway between the β- and γ-phosphates. This effect may be quantified in future studies. It is also interesting to comment on the finding that a significant part of the difference between the energy of ATP and ADP+P_i is the electrostatic repulsion between the ADP and P_i fragments. With this in mind, we can view the B→C process as a step where the electrostatic energy of assembling the fragments of the ADP+P_i system is already paid for by the binding process. Now it is rather simple for the protein to tune up or down the energies of the ATP state, which is done in F₁-ATPase by increasing the electrostatic stabilization of the ATP state (t) during the D→T transition.

Our approach has been used for the mechanism of Fig. 1. The same approach can be used for any alternative mechanisms including stepwise release of P_i (e.g., ref. 5). However, examination of alternative mechanisms and determination of the overall free-energy profile (or profiles) for the rotary mechanism is left to subsequent work.

Most studies in this field have been based on mechanical elastic concepts, which are what an outside observer may see when examining the F₁-ATPase system. We prefer to consider a more microscopic picture, where the origin and nature of the phenomenological elastic force constants become more apparent. In fact, the force constant can be obtained from our calculated reorganization energies and related calculations. As much as we can see from the present study, most of the energetics of the system can be described as electrostatic free energy rather than steric energies. The response to the change in ligand charges can be described as a restoring force constant (34) that is associated mainly with the protein reorganization (this is formally equivalent to the electrostatic reorganization of polar solvents).† It is also likely that the effect of the rotation of the γ stalk is mainly electrostatic.

Because electrostatic effects play such an important role in the action of ATP synthase, it is important to clarify what is meant by the term “electrostatic effects.” Such effects are represented by the energy contributions associated with the interaction between the environment (protein + water) and the charges of the substrate and can be classified as the “solvation” of the substrate charges (e.g., refs. 34 and 35). The main electrostatic contributions are due to the interaction between the substrate and the nearest shell of polar groups (dipoles) and ionized groups (charges). The effect of distance charges is usually quite small. The conformational changes of F₁-ATPase may result in both steric and electrostatic effects, but because proteins are flexible, the steric effects are not effective in energy transduction processes (e.g., refs. 12 and 34).

Finally, we would like to comment here on the overall issue of the mechanical efficiency of the F₁-ATPase system. Some studies have focused on mechanical concepts such as elastic strain and optimal friction (e.g., refs. 5, 17, and 36). However, our experience with closely related problems, such as the efficiency of light-induced charge separation in photosynthesis, led to a more microscopic time-dependent concept (37, 38). It appears that, at least in the system studied by us, the efficiency is defined by the forward and backward rate constants, and concepts such as friction and heat transfer play a rather small role. The energy dissipation in proteins is almost instant [relaxation times of ≈100 fs (39)], and the key issue is the storage of electrostatic free energy. In other words, we would obtain an efficient system if we converted electrostatic forces to electrostatic free energy with the minimal downhill gradient to prevent significant back reaction. It remains to be seen whether this concept applies to ATP synthase.