Thermodynamic treatment of oligonucleotide duplex–simplex equilibria

Abstract

Thermodynamic formulations have been devised to obtain ΔG° values directly from spectroscopic data at a fixed common temperature in nucleic acid duplex–simplex melting curves. In addition, the dependence of melting on salt concentration has been expressed in terms of a stepwise stoichiometric representation, which leads to a specific equation for the partition of the added sodium ions between the different oligonucleotide forms.

Generally the free energy of melting of an oligonucleotide duplex, D, into its constituent complementary single strands, S₁ and S₂, is obtained from the temperature at the midpoint of the melting curve, T_m. To compare the ΔG°s of a series of duplexes of varying composition, one obtains the respective T_m values and adjusts them to a common temperature using data for the ΔH° of the transition.

It is also possible to obtain ΔG° for a series of duplexes from absorbance data at only one fixed common temperature in the melting curves. We have explored this alternative mode of treatment with a set of duplexes having oligonucleotide lengths of 10 bp.

Melting curves of duplex DNA are very sensitive to salt concentration. The dependence of T_m and of ΔG° on Na⁺ molarity has been generally formulated on the basis of the following chemical equation for the oligonucleotide equilibrium,

[1]

where ν is the net number of sodium ions preferentially taken up by the duplex D. Eq. 1 is a very abridged formulation. For thermodynamic analysis, a fuller description is essential, which explicitly maintains conservation of mass of each species and takes into account binding of Na⁺ to the single-stranded oligonucleotides S₁ and S₂,

[2]

where ν = C – (A + B). One can then write an equation for the concentration's quotient at equilibrium,

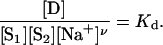[3]

From Eq. 3, the following equation can be derived (1),

[4]

where R is the ideal gas constant and ΔH° is the standard enthalpy for the formation of the duplex. Eq. 4 has been widely used in the analysis of the effect of Na⁺ concentration on T_m. In practice, the value of ν is obtained by fitting a plot of 1/T_m vs. ln[Na⁺] to a straight line, and it is implicitly assumed that ΔH° does not vary with temperature or sodium ion concentration.

This situation is analogous to that encountered in very early studies of the uptake of O₂ by Hb (2),

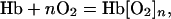[5]

where a relation analogous to Eq. 3 was proposed by A. V. Hill (3),

[6]

The Hill equation,

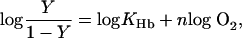[7]

where Y is the percent saturation of Hb with oxygen, follows directly from Eq. 6. However, a Hill-type equation is essentially an empirical statement truly representative of the equilibrium only when the coupling of successive steps in binding is infinitely cooperative, and hence concentrations of the intermediate species, which are partially saturated with ligand, are negligible throughout the binding curve. In such a case, the value of n, the Hill coefficient, equals the number of binding sites. For Hb, this would be 4. However, this is not observed experimentally. With the acquisition of more extensive oxygen-binding data for Hb, it has become clear that n is not a constant but varies continuously from a value of 1.0, at both very low and very high concentrations of oxygen, to a maximum near the midpoint of the oxygen-binding curve (4). Typically, oxygen-binding data for Hb plotted according to Eq. 7 can be reasonably well fit to a straight line with a slope (n) between 2.5 and 3.0 from ≈10% to 90% saturation with oxygen.

Similarly, a plot of 1/T_m vs. ln[Na⁺] for DNA duplex formation can be fit approximately to a straight line over a limited range of Na⁺ concentrations. However, an extensive set of experiments has shown that the dependence is not linear.† In a study of >90 duplexes ranging in length from 10 to 60 bp, we found for each DNA duplex that the magnitude of the derivative ∂(1/T_m)/∂ ln[Na⁺] decreased continuously with increasing Na⁺ concentration from 69 mM to 1 M. Because ΔH° is nearly independent of Na⁺ concentration, these results suggest that the value of ν is not constant (see Eq. 4) but rather must decrease with increasing Na⁺ concentration.

For Na⁺ binding to DNA, as for oxygen binding to Hb, species partially saturated with ligand cannot be ignored. The values of A, B, and C in Eq. 2 are in fact the mean values of the amount of Na⁺ bound to each species. A formalism that allows these values, and hence ν, to vary with Na⁺ concentration must be used (5).

We have formulated a detailed stoichiometric description of the uptake of Na⁺ by oligonucleotides. This leads to a specific equation for the partition of sodium ions between the duplex (double-stranded) and simplex (single-stranded) forms, which displays the dependence of partitioning on the Na⁺ concentration.

Materials and Methods

DNA Synthesis. Oligonucleotides were synthesized by using solid-phase phosphoramidite chemistry, and each had an OH group on the 5′ end as well as on the 3′ end. Oligomers were purified by using denaturing polyacrylamide gel electrophoresis. Capillary electrophoresis on Beckman PACE 5000 (Beckman Coulter) demonstrated that all oligomers were at least 93% pure. Delayed extraction matrix-assisted laser desorption ionization/time-of-flight mass spectrometry on a Voyager DE Biospectrometry workstation (Applied Biosystems) showed that relative molecular masses of all oligomers were within 0.22% of expected molecular masses.

Melting Studies. DNA duplex oligomers were melted in buffers containing 3.87 mM NaH₂PO₄; 6.13 mM Na₂HPO₄; 1 mM Na₂EDTA; and 50, 100, 200, 600, or 1,000 mM NaCl, adjusted to pH 7.0 ± 0.03 with NaOH. DNA samples were dialyzed against melting buffers in a 28-Well Microdialysis System (Invitrogen) and filtered through a 0.45-μm nylon filter. Concentrations of single-stranded oligomers were determined from absorbance at 260 nm and estimated extinction coefficients (6). All DNA duplex oligomers were melted at the same concentration (C_t = 2 μM), where C_t is the total strand concentration, [S₁(total)] + [S₂(total)]. Melting experiments were carried out in a Beckman DU 650 spectrophotometer with a Micro Tm Analysis accessory, a Beckman High Performance Peltier Controller, and 1-cm path-length cuvettes (Beckman Coulter). Absorbance values at 268 nm, A₂₆₈, were measured every 0.1°C in the temperature range of 10–95°C. Both heating (denaturation) and cooling (renaturation) transition curves were recorded at a constant rate of temperature change of 24.9 ± 0.3°C/hr. Temperatures were collected from the internal probe located inside of the Peltier holder. From three to eight melting curves were collected for each DNA duplex oligomer in different cuvettes and different positions inside of the Peltier holder to minimize systematic errors. Melting profiles of buffers alone were subtracted from the raw absorbance vs. temperature curves of DNA samples.^† The upper- and lower-sloping baselines were determined from the graph of absorbance vs. temperature and subtracted to calculate the fraction of broken base pairs, θ. Melting profiles were smoothed by a digital filter, and transition (melting) temperatures were determined as temperatures at midpoints of the transitions where θ = 0.5. Melting temperatures were reproducible within 0.3°C.

Calculation of the Equilibrium Constant. The equilibrium constant for the simplex–duplex equilibrium,

[8]

was calculated from values of θ observed experimentally with the relationship,

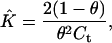[9]

which applies when S₁ and S₂ are at the same concentration.

Results

Direct Evaluation of Free Energy Changes at Fixed Temperature. Duplex (D) complementary–simplex (S₁, S₂) equilibria of oligonucleotides were followed by measurements of A₂₆₈ vs. temperature as described above. ΔG°s are generally calculated from T_m and the temperature variation of absorbance. It is also possible to obtain ΔG° values directly from the absorbance data at a fixed common temperature in the melting curves. We have explored this alternative mode of treatment with a set of duplexes having oligonucleotide lengths of 10 bp.

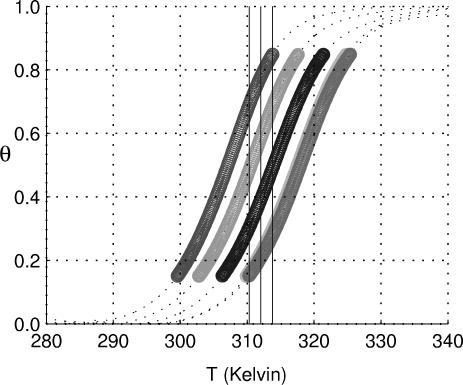
Fig. 1 displays melting curves for the 10-bp DNA duplex,

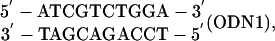(ODN, oligodeoxynucleotide duplex) in a series of solutions containing 0.069, 0.12, 0.22, 0.62, and 1.0 M Na⁺, respectively (from left to right). For each curve, the range of 0.15–0.85 for θ is graphically displayed as a thick line to emphasize the region of greatest accuracy. Outside this range, the experimental results are less precise and are displayed as thin broken lines; data from these regions were not used in calculations.

Fig. 1.

Melting curves for the 10-bp DNA duplex oligomer (ODN1, f_GC = 0.50) (f_GC, fraction of G·C base pairs in the duplex) 5′-ATCGTCTGGA-3′ (at a C_t of 2 × 10^–6 M) in solutions of sodium concentrations (left to right curves) 0.069, 0.12, 0.22, 0.62, and 1.0 M. The thick black curves span a range of θ from 0.15 to 0.85, where the data are the most accurate. The central vertical line through the curves shows the temperature chosen.

In the neighborhood of 312 K, three vertical lines have been drawn. Each line intersects each of the melting curves at a value of θ between 0.15 and 0.85 and hence provides a common temperature for the calculation of equilibrium constants for formation of the duplex. The left- and rightmost lines mark the lowest and highest common temperature that can provide reliable values of θ. The inner straight line intersects the full cassette of curves at points most removed from the dotted regions. This line corresponds to the temperature 312.0 K (38.8°C), which we designate the reference temperature (T_R).

Equilibrium constants for the formation of the duplex from its oligonucleotides at a series of Na⁺ concentrations have been calculated from θ values at the common temperature of 38.8°C by using Eq. 9 and are listed in Table 1. The corresponding ΔG° values obtained from the general thermodynamic equation

[10]

are assembled in the column adjacent to the K̂s.

Table 1. Standard thermodynamic parameters at T = 312.0 K (38.8°C) for duplex—simplex equilibria of the 10-bp DNA duplex sequence 5′-ATCGTCTGGA-3′ (ODN1, f_GC = 0.50).

Total [Na+], mol/liter	θ	K̂, M-1	ΔG°, kJ/mol	ΔH°, kJ/mol	ΔS°, J/(mol·K)
0.069	0.78	3.7 × 105	-33.3	-284	-805
0.119	0.58	1.22 × 106	-36.4	-281	-784
0.220	0.39	4.03 × 106	-39.5	-282	-776
0.621	0.22	1.58 × 107	-43.0	-291	-796
1.020	0.21	1.85 × 107	-43.4	-290	-790

Changes of Enthalpy and Entropy at Fixed Temperature. From the data in Fig. 1, the most convenient way to compute ΔH° is to plot lnK̂ vs. 1/T, as suggested by the thermodynamic relation

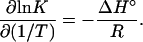[11]

For each of the curves in Fig. 1, a plot of ln K̂ vs. 1/T (Fig. 2) shows almost no curvature in the neighborhood of 312 K and hence was fitted to a straight line whose slope gave ΔH°. Once values of ΔH° (as a function of temperature) have been established, one calculates the entropy change ΔS° from

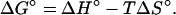[12]

For ODN1, ΔH°, ΔS°, and ΔG° were computed from each melting curve in Fig. 1. These quantities are listed in Table 1.

Fig. 2.

Plots of ln K̂ vs. 1/T for the five Na⁺ concentrations (mol/liter) for ODN1.

The values of ΔH°, ΔS°, and ΔG° for ODN1 at 1 M Na⁺ and 38.8°C, estimated from nearest-neighbor thermodynamic parameters (7), are –295 kJ/mol, –804 J/(mol·K), and –44.4 kJ/mol, respectively, and agree well with those observed experimentally under the same conditions.

Dependence of Duplex–Simplex Stability on Sodium Ion Concentration. The variation of the equilibrium of oligonucleotide helix, D, with single-strand species, S₁ and S₂, can be presented in various formats. A condensed description widely used is that of Eq. 1, which, as noted above, is analogous to the classical Hill equation for the uptake of O₂ by Hb (3). Eqs. 3 and 6 are valid only if the successive ligand-binding constants are accentuated enormously (2), that is, if the binding of Na⁺ or O₂, respectively, is infinitely cooperative and the intermediate partially liganded species can be ignored. In both cases, a more generalized description of the binding states is needed.

A proper description of the binding of Na⁺ by oligonucleotides should be a set of successive stepwise equilibria (see, for example, ref. 8). To take into account variation in the number of Na⁺ ions bound to the duplex, the following series of equations is appropriate:

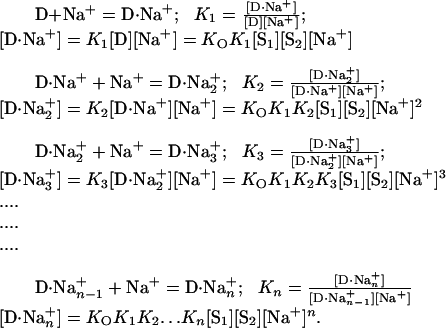[13]

The subscript n represents the number of Na⁺ bound by D at saturation with this ion.

The experimentally accessible equilibrium constant, K̂, is extracted from the absorbance measurements in the ultraviolet region. K̂ can be expressed as

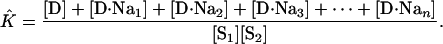[14]

Using the relationships assembled in Eq. 13, we can transform Eq. 14 into

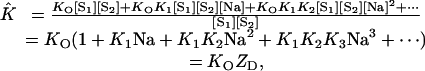[15]

where Z_D is the partition function for the Na⁺ ions bound to the duplex D.

After converting Eq. 15 to logarithmic form

[16]

we can differentiate with respect to log [Na⁺] and obtain

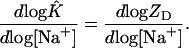[17]

The right-hand side of this equation is the mean number of Na⁺ bound by the duplex D (9–11), the value of C in Eq. 2. So, we can write

[18]

Strictly speaking, Eqs. 13 are incomplete. A full description of the sodium interactions with the duplex–simplex equilibrium should also include explicit equations for the uptake of Na⁺ by each of the single-stranded oligonucleotides S₁ and S₂, equations analogous to those for D.

Thus for S₁, we write

[19]

Correspondingly for S₂, the relevant equations are

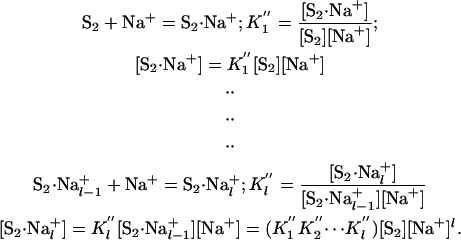[20]

The subscripts m and l represent the number of Na⁺ bound by S₁ and S₂, respectively, at saturation. In place of Eq. 14 for K̂, we now write

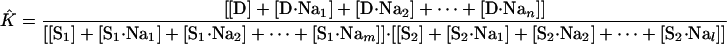[21]

Using the relationship assembled in Eqs. 13, 19, and 20, we transform Eq. 21 into

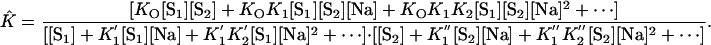[22]

With straightforward algebraic steps, Eq. 22 can be reduced to

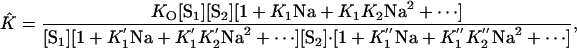[23]

from which it follows that

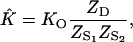[24]

each Z representing the partition function of the oligonucleotide indicated. Following the steps shown in Eqs. 14–18, one can show that

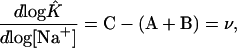[25]

where A, B, and C are the mean number of ligand Na⁺ bound by the respective oligonucleotide (see Eq. 2). Experimental melting curves reveal only ν, the net result of the partitioning of Na⁺ between the duplex and separated simplex oligonucleotides, not the individual values of A, B, and C. It should be noted that K̂ of Eqs. 21–25 is the equilibrium constant obtained experimentally from values of θ by using Eq. 9.

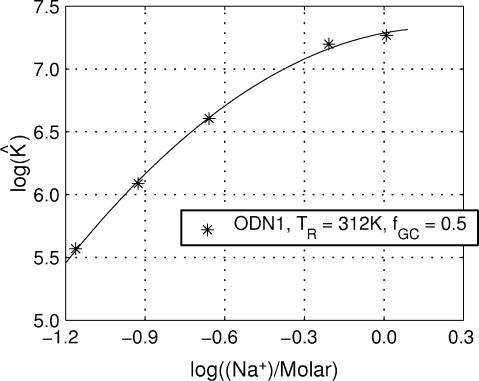
Fig. 3 presents the values of log K̂, calculated from the experimental θs in Table 1 as a function of log[Na⁺] at a common temperature. It is obvious that the relationship between log K̂ and log[Na⁺] is not linear. The slope clearly decreases with increasing concentration of salt, and hence the preferential uptake of Na⁺ by the duplex must decrease. The same behavior is observed when log K̂ is plotted against the log of the activity of Na⁺ rather than the log of Na⁺ concentration.

Fig. 3.

Dependence of duplex–simplex equilibrium constant for duplex ODN1 on concentration of sodium ions at 312 K. The curve is a least-squares fit to a quadratic function of log[Na⁺].

The data in Fig. 3 were fit to a second-order polynomial by using a nonlinear least-squares algorithm. The resulting equation,

[26]

is graphically displayed in Fig. 3. From this function, one can compute explicit values of ν by finding the slope defined by Eq. 25. With increasing concentration of salt, the preferential uptake of Na⁺ by the duplex decreases (Fig. 4), tending toward zero. This behavior contrasts sharply with that obtained by using Eq. 2, where ν is assumed to be a constant.

Fig. 4.

Variation of ν, the net result in partitioning of Na⁺ between D and S₁ and S₂, for four 10-bp duplex DNA oligomers at specific common temperatures. Base sequences are ODN1, 5′-ATCGTCTGGA-3′; ODN3, 5′-CCAACTTCTT-3′; ODN4, 5′-AGCGTAAGTC-3′; and ODN5, 5′-CGATCTGCGA-3′. T_R is the reference temperature chosen for each duplex.

This result is not unique to duplex ODN1. Values of ν determined for three other duplexes as a function of Na⁺ concentration are also plotted in Fig. 4. In each case, the preferential uptake of Na⁺ by the duplex decreases with increasing salt concentration. It is apparent that the value of ν depends not only on salt concentration but also on the oligonucleotide sequence.

Discussion

The selection of a common temperature in a cassette of melting curves to compute ΔG° values obviates inclusion of temperature dependencies in these calculations. Because derivatives of a function have greater uncertainties than do the original data in the function, a procedure for comparison at a common temperature within a cassette of melting curves provides an attractive alternative for evaluating ΔG°s.

In the studies reported here, the concentration of DNA was held constant (C_t = 2 μM). If we relax this constraint, the scope of the method can be very much expanded. Measurement of θ as a function of C_t, at fixed salt concentration and temperature, will not only yield a more precise determination of K̂ but will also allow different oligonucleotide sequences with varying T_m to be compared at exactly the same temperature. It should be noted, with the data available, the four sequences in Fig. 4 had to be compared at slightly different temperatures. If C_t is varied from 0.5/K̂ to 100/K̂, values of θ range from 0.83 to 0.13. In practice, if UV absorbance is used to follow melting of the duplex, C_t can be varied at least 50-fold. With other methods such as NMR spectroscopy or calorimetry, even higher DNA concentrations can be explored. Such studies will be particularly useful to probe duplex melting behavior at very low salt concentrations.

The use of Eq. 4 to analyze the effects of salt on T_m has generally led to the conclusion that the number of additional Na⁺ ions bound on forming the duplex, ν, is independent of Na⁺ concentration. Indeed, most algorithms to predict T_m incorporate the assumption (or make it implicitly) that 1/T_m varies linearly with ln[Na⁺]. However, a graph of 1/T_m vs. ln[Na⁺], like the Hill plot, is a very compressed presentation of the data. With a limited set of experimental observations, it may appear that the results fit a straight line. Studies we have performed on a large number of DNA duplexes have shown, however, that the relationship is not linear and suggest that the value of ν decreases with increasing Na⁺ concentration.^† Variation of ν with Na⁺ concentration in turn indicates that multiple states of Na⁺ binding to DNA must be considered.

The approach formulated here to describe the linkage between Na⁺ binding to DNA and the duplex–simplex equilibrium has been used extensively in the analysis of coupled receptor systems such as Hb (12). It is independent of any model for the binding of Na⁺ by DNA. At constant temperature, ν is related directly to K̂ by Eq. 25. No assumptions regarding ΔH° for formation of the duplex are needed.

The results in Fig. 4 show that ν does indeed decrease with increasing Na⁺ concentration. This conclusion appears to be quite general, independent of oligonucleotide sequence.^† Because it is likely that the DNA duplex is already saturated with Na⁺ ions at concentrations below the lowest concentration included in this study (69 mM), it would seem necessary to postulate that the binding of Na⁺ to the single-stranded species, S₁ and S₂, increases with increasing Na⁺ concentration.

It will be very interesting to examine the behavior of ν at Na⁺ concentrations below 69 mM. At some point, Eq. 26 must break down, otherwise ν would increase without limit. In principle, if we assume no binding of Na⁺ ions to the single strands and that the duplex is fully saturated, the greatest value of ν for a 10-mer duplex would be ≈18. On the basis of counterion concentration theory, if we assume the single strands adopt a fully extended conformation at very low salt, the largest value one would predict for ν is 6. As alluded to above, studies of duplex–simplex melting at higher DNA concentrations should make it possible to explore these conditions.

The thermodynamic analysis of the dependence of melting curves on Na⁺ concentration provides a format that can be applied also to a wide range of other solutes that perturb duplex–simplex equilibria. Of particular interest would be tetramethylammonium ion and betaine.

The former and some related tetraalkylammonium ions raise the T_m values of nucleic acid melting curves (13–18). The reason for this behavior is not obvious. The charge on the naked

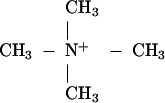is dispersed over a larger volume than is that on a naked Na⁺. However, spectroscopic studies show that at least four water molecules constitute the first solvent shell (19, 20) around cations associated with DNA, so the charge on the alkali ion is also widely dispersed. There is some evidence that tetramethylammonium ions are bound more strongly to DNAs than are sodium ions (13). In regard to melting of helical oligonucleotides, the more germane question is whether [CH₃]₄N⁺ is bound preferentially by the duplex rather than by the simplexes. That can be established by appropriate observations with oligonucleotides and the algebraic treatment presented herein.

In strong contrast to (CH₃)₄N⁺, betaine, (CH₃)₃N⁺CH₂COO^–, lowers markedly the T_m values of nucleic acids (21, 22). The cationic end, (CH₃)₃N⁺ —CH₂—, of this molecule would be expected to mimic tetramethylammonium ion and raise the melting temperature. Clearly, the anionic —COO^– substituent introduces a marked perturbation. A unit + charge and a unit–charge separated (by a CH₂ bridge) by 3 Å should have a dipole moment of ≈15 debye units (23) (that of H₂O is 1.8 debye units). This large electrostatic feature of a betaine molecule is manifested macroscopically in water, where a 1 M solution has a relative dielectric constant (23) near 105 (compared to 80 for pure solvent). This striking increase in the dielectric constant must be an expression of the strong effect of betaine on the structure of liquid water. Another surprising capability of an ionic dipole is its influence on ligand binding by proteins (24), where several-fold increases in affinity are observed. At the cellular level, betaine is a well known osmoprotective agent protecting bacteria, algae, plants, and marine invertebrates from a variety of environmental stresses, particularly high salinity (22, 25, 26). Clearly betaine interacts strongly with water molecules that form the environment of dissolved biomacromolecules. Another important feature of (CH₃)₃N⁺CH₂COO^– becomes evident if one places its cationic end in the condensation sleeve around the anionic core of the oligonucleotide. In contrast to (CH₃)₄N⁺, whose charge balances that of the oligonucleotide, betaine with its anionic —COO^– group in effect moves the negative charge of the polymer outward from the core. Thus, the salt condensation layer is displaced outward from the axis of the DNA.

It would be desirable to have studies of melting curves of small oligonucleotides of defined structure in the presence of tetraalkylammonium compounds and of betaine. With the algebraic treatment described in this paper, one could establish, for each of these charged molecules, whether they are bound preferentially to the duplex or single-stranded oligonucleotides. This information would provide some guidance for interpretation of the molecular basis for the differences in their effects.