Abstract
Myosin crossbridges in muscle convert chemical energy into mechanical energy. Reported values for crossbridge efficiency in human muscles are high compared to values measured in vitro using muscles of other mammalian species. Most in vitro muscle experiments have been performed at temperatures lower than mammalian physiological temperature, raising the possibility that human efficiency values are higher than those of isolated preparations because efficiency is temperature dependent. The aim of this study was to determine the effect of temperature on the efficiency of isolated mammalian (mouse) muscle. Measurements were made of the power output and heat production of bundles of muscle fibres from the fast-twitch extensor digitorum longus (EDL) and slow-twitch soleus muscles during isovelocity shortening. Mechanical efficiency was defined as the ratio of power output to rate of enthalpy output, where rate of enthalpy output was the sum of the power output and rate of heat output. Experiments were performed at 20, 25 and 30°C. Maximum efficiency of EDL muscles was independent of temperature; the highest value was 0.31 ± 0.01 (n= 5) at 30°C. Maximum efficiency of soleus preparations was slightly but significantly higher at 25 and 30°C than at 20°C; the maximum mean value was 0.48 ± 0.02 (n= 7) at 25°C. It was concluded that maximum mechanical efficiency of isolated mouse muscle was little affected by temperature between 20 and 30°C and that it is unlikely that differences in temperature account for the relatively high efficiency of human muscle in vivo compared to isolated mammalian muscles.
Introduction
The fundamental energy transduction process in muscle is the conversion of chemical free energy (from ATP splitting) into mechanical energy by myosin crossbridges. The fraction of the available free energy converted into mechanical work is called the thermodynamic efficiency (η). The reported maximum efficiency values for human muscle are high compared to the value expected on the basis of efficiency values obtained in experiments using isolated muscles from other species. For example, Whipp & Wasserman (1969) measured O2 consumption during cycling exercise and used these values to estimate that η was ∼50%. More recently, Jubrias et al. (2008) used NMR to measure the ATP breakdown in a muscle in the human hand, the first dorsal interosseous, during voluntary contractions and concluded that 68% of the free energy of ATP hydrolysis was converted into work. Relatively high values have also been reported for isolated preparations of human muscle. The maximum η for permeabilised, single fibres from human vastus lateralis and tibialis anterior muscles at 20°C was 34% for slow fibres and 41% for fast fibres (He et al. 2000). Reported values of η for non-mammalian muscle are generally lower than those described above for human muscle. In studies using isolated, non-human mammalian muscles, the fraction of free energy converted into work by crossbridges, under conditions designed to maximise efficiency, is typically between 20 and 30% (Smith et al. 2005; Barclay et al. 2010).
One factor that may account for at least part of the difference in efficiency between in vivo studies with human muscle and in vitro studies with non-human muscles is the temperature at which the measurements are made. Most isolated muscle studies have been performed at relatively low temperatures (e.g. 20–25°C), which improves muscle viability in vitro (Segal & Faulkner, 1985). The possibility that temperature is an important factor is suggested by measurements of the efficiency of permeabilised human muscle fibres (He et al. 2000). In those experiments, maximum thermodynamic efficiency increased from 20% at 12°C to ∼40% at 20°C. If efficiency increases further between 20 and 37°C then an efficiency of 68% at 37°C could be possible. However, the idea that efficiency data from mammalian muscle at low temperatures can be simply extrapolated to higher temperatures should be treated with caution. Many mechanical aspects of contraction of mammalian muscle (e.g. maximum isometric force, rate of force development, maximum shortening velocity (Vmax) and maximum power output) are more sensitive to temperature below 20°C than above (Renaud & Stevens, 1981; Ranatunga, 1982, 1984; Bennett, 1984).
In contrast to the data from permeabilised human muscle fibres, data from experiments with intact isolated muscles do not support the idea that maximum efficiency is temperature dependent. For instance, Fenn (1923) and Hartree & Hill (1928a,b); showed that maximum efficiency of frog sartorius muscle did not alter between 0 and 18°C and Gibbs & Chapman (1974) showed that maximum efficiencies of frog and toad sartorius muscles were independent of temperature between 10 and 20°C. Those experiments used muscles from amphibians rather than a mammal and the temperature ranges used spanned the physiological range for those ectothermic animals. So it is not clear whether efficiency of muscles from amphibians but not mammals is insensitive to temperature or whether temperature-dependent maximum efficiency is a characteristic of permeabilised, but not intact, muscle fibres.
The first purpose of the current study was to determine the temperature dependence of maximum efficiency of intact mammalian (mouse) skeletal muscles at temperatures approaching the physiological temperature. These experiments will show whether temperature-dependent maximum efficiency is a characteristic of mammalian muscle and whether efficiency of mammalian muscle increases as temperature approaches physiological temperature. The second purpose was to gain insight into the mechanism underlying the high efficiency of slow-twitch muscles relative to fast-twitch muscles (Buschman et al. 1995; Barclay, 1996; Reggiani et al. 1997). Data obtained in the current study combined with those from previous studies in which crossbridge-dependent energy turnover was quantified using the same preparation (Barclay, 1996; Barclay et al. 2008) provide the basis for determining whether the high efficiency of slow muscles is most likely to reflect greater crossbridge force generation or greater filament displacement generated by each crossbridge while attached to the thin filament.
To determine the effects of temperature and fibre type on power output and efficiency of mammalian muscle, we measured the work and heat produced by bundles of intact fibres from fast- and slow-twitch muscles of the mouse during isovelocity shortening at temperatures of 20, 25 and 30°C. Temperatures below 20°C were not used to avoid the progressive decrease in fibre excitation that can occur during tetanic contractions of mammalian muscles at low temperatures (Stein et al. 1982). Over the range of temperatures used, both Vmax and maximum power output doubled. The rate of enthalpy output during shortening at low to moderate velocities increased in proportion to power output so that there was little change in maximum efficiency.
Methods
Muscle preparations
Experiments were performed using bundles of fibres dissected from slow-twitch soleus and fast-twitch extensor digitorum longus (EDL) muscles of adult, male mice (Swiss strain). The mice were rendered unconscious by inhalation of a mixture of 20% O2 and 80% CO2 (Kohler et al. 1999) and then killed by cervical dislocation. All animal handling procedures were in accord with the requirements of the Griffith University Animal Ethics Committee. During dissection and experiments, preparations were bathed in oxygenated (95% O2–5% CO2) Krebs–Henseleit solution (composition (mm): NaCl 118; KCl 4.75; MgSO4 1.18; NaHCO3 24.8; KH2PO4 1.18; CaCl2 2.54; glucose 10).
The mean masses (±s.e.m.) of the EDL (n= 15) and soleus fibre bundles (n= 17) were 3.9 ± 0.3 and 3.4 ± 0.1 mg, respectively. The number of fibres in the bundles can be estimated using data for muscle mass and fibre number reported by Luff & Goldspink (1970). Averaged across the four strains of mice those authors studied, mean fibre mass was 8.0 ± 0.5 μg for EDL and 6.9 ± 0.3 μg for soleus. Therefore, the EDL fibre bundles in this study would have contained ∼1000 × 3.9/8.0 = 490 fibres and, calculated in the same way, the soleus bundles would also have had about 500 fibres.
Recordings and analysis
Fibre bundles were mounted between a fixed clamp and the lever of a servo-controlled ergometer (300B, Aurora Scientific Instruments, Ontario, Canada) and lay along the active junctions of a thermopile. Muscle force output and change in muscle length were measured using the ergometer, and changes in muscle temperature were measured using the thermopile. All signals were sampled at 1 kHz, digitized and stored on disk. Experimental protocols were controlled and data acquired using software developed using Test Point (Capital Equipment Corporation, MA, USA) and a multifunction board (1802AO, Keithley Instruments, Cleveland, OH, USA).
Electrical stimuli were delivered to fibre bundles via fine platinum wires, lightly touching either side of the preparation (amplitude, 4–6 V; duration, 1 ms). Stimulation frequency was set to that sufficient to produce a fully fused tetanus for each muscle type and at each temperature used. For EDL, stimulation frequencies were 120, 140 and 160 Hz at 20°C, 25°C and 30°C and for soleus the corresponding values were 80, 100 and 120 Hz. Higher stimulus frequencies could produce maximum forces 5 to 10% greater than achieved with the frequencies used (Brooks et al. 1990) but would have also increased heat produced in the muscle by passage of the stimulus current to an unreasonably large fraction of the measured heat.
The recording region of the thermopile was 5 mm in length, contained 20 antimony–bismuth thermocouples (Mulieri et al. 1977; Barclay et al. 1995) and produced 1.4 μV °C−1. To calculate the heat produced, the measured temperature change was corrected for heat lost from the thermopile during recording and multiplied by the heat capacity of the muscle (and any adhering saline) over the recording section of the thermopile. The rate of heat loss and muscle heat capacity were calculated from the time course of heat loss following a period of heating the unstimulated muscle using the Peltier effect (Kretzschmar & Wilkie, 1972). Heat produced by the stimulus current passing through the preparation was determined by measuring the heat produced during stimulation of preparations made inexcitable by exposure to procaine (20 mm in Krebs solution). Stimulus heat accounted for 10–15% of measured heat at all temperatures and was subtracted from the measured heat output.
An isovelocity shortening protocol was used to study energy turnover during shortening (Fig. 1). Rate of enthalpy output (i.e. heat + work output) was used as the index of energy turnover. The rate of enthalpy output during the force plateau of an isometric contraction 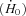 is equal to the rate of heat output because no external work is performed and was calculated by fitting a straight line through the heat record between 0.2 s and 0.5 s after the start of stimulation. The heat recorded while force was increasing was excluded because during this time the contractile component is not isometric but shortens and performs work against series elastic elements (SEE). Once force output was steady, the rate of heat output was constant during isometric contraction (dotted record, Fig. 1). The rate of enthalpy output from shortening muscle is the sum of the rates of work and heat output. The rate of work output (i.e. the power output) during isovelocity shortening was taken as the average power output when shortening force output was steady; power produced during the first ∼20 ms of shortening was excluded because during that time, force output was decreasing and the SEE contributed to the power output. The average rate of heat output was calculated as described previously (Barclay, 1996; Lichtwark & Barclay, 2010). This method minimises contributions to the measured heat production from thermal changes associated with changes in SEE length (i.e. heat was measured between times at which force output, and hence SEE length, was the same), changes in the distribution of crossbridge states, thermoelastic effects and any heat unrelated to PCr splitting (produced early in a contraction) (Homsher, 1987). Mechanical efficiency was defined as the ratio of the average power output to the average rate of enthalpy output during shortening.
is equal to the rate of heat output because no external work is performed and was calculated by fitting a straight line through the heat record between 0.2 s and 0.5 s after the start of stimulation. The heat recorded while force was increasing was excluded because during this time the contractile component is not isometric but shortens and performs work against series elastic elements (SEE). Once force output was steady, the rate of heat output was constant during isometric contraction (dotted record, Fig. 1). The rate of enthalpy output from shortening muscle is the sum of the rates of work and heat output. The rate of work output (i.e. the power output) during isovelocity shortening was taken as the average power output when shortening force output was steady; power produced during the first ∼20 ms of shortening was excluded because during that time, force output was decreasing and the SEE contributed to the power output. The average rate of heat output was calculated as described previously (Barclay, 1996; Lichtwark & Barclay, 2010). This method minimises contributions to the measured heat production from thermal changes associated with changes in SEE length (i.e. heat was measured between times at which force output, and hence SEE length, was the same), changes in the distribution of crossbridge states, thermoelastic effects and any heat unrelated to PCr splitting (produced early in a contraction) (Homsher, 1987). Mechanical efficiency was defined as the ratio of the average power output to the average rate of enthalpy output during shortening.
Figure 1. Isovelocity protocol used to measure energy output during steady shortening.
The upper trace shows the change in muscle length, the middle panel the force output and the lower panel the heat produced. Time is relative to the delivery of the first stimulus pulse. Isovelocity shortening started after 0.5 s of isometric contraction. The duration of shortening is indicated by the vertical dashed lines; the amplitude of shortening was 10%L0. Stimulation continued for at least 0.5 s after shortening ended to allow force to redevelop. The heat record shown by the continuous line is from the recording containing shortening; the dotted heat record was made during a preceding isometric contraction. Record from a soleus fibre bundle: mass, 3.6 mg; preparation length, 10.7 mm; fibre length, 8.9 mm; temperature, 25°C.
The maximum efficiency for each muscle was determined by fitting a third-order polynomial through four to six measured efficiency values spaced across the velocity range that encompassed the maximum value. The maximum value of the fitted curve and the velocity at which the maximum occurred were taken to be the maximum efficiency and the velocity at which efficiency was maximal for that muscle. The same method was used to determine the maximum power output and velocity at which power output was maximal.
Vmax was determined for each muscle by fitting a hyperbola (Hill, 1938) through measured force–velocity data using non-linear regression. Vmax was determined by solving the force–velocity equation for the case of force equal 0.
Experimental protocol
At the start of experiments, stimulus strength was set to 10% above that eliciting maximum twitch force and muscle length was set to 10% above L0, the length at which tetanic force was maximal.
Each muscle performed isovelocity shortenings at 10 shortening velocities at one temperature. The order of application of velocities was varied amongst preparations. Muscles rested for 5 min between measurements. At the end of experiments muscle length was measured using callipers, muscles were removed from the apparatus, the tendons were removed, adhering saline was blotted from the muscle and preparation mass was measured using an electronic balance. Fibre length (FL) was calculated for each preparation assuming fibre length to muscle length ratios of 0.89 and 0.79 for soleus and EDL, respectively (Barclay et al. 1993). Average fibre cross-sectional area was calculated as blotted mass/(FL × muscle density), with density taken to be 1.06 kg l−1. Shortening velocity was normalised by fibre length, force output by fibre cross-sectional area and rates of energy output by blotted wet mass.
Data presentation and statistics
For presentation of average values, data from all preparations at one temperature were binned according to shortening velocity (FL s−1). Bin width was determined using Sturges’ rule (Sturges, 1926) and was typically ∼0.1 Vmax. In all cases there were at least six observations in a bin. Thus, average values are the means of between 6 and 15 observations. The number of preparations used at each temperature is given in Table 1. Data are presented as means ± 1 standard error. The effects of temperature are quantified using the Q10 value which is the factor by which a variable changes for a 10°C increase in temperature.
Table 1.
Effects of temperature on mechanical and energetic properties of mouse soleus and EDL muscle
| 20°C | 25°C | 30°C | |
|---|---|---|---|
| Soleus | |||
| n | 5 | 7 | 5 |
| F0 (kPa) | 220 ± 12 | 232 ± 11 | 226 ± 12 |
| Vmax (FL s−1) | 2.9 ± 0.2 | 4.1 ± 0.2* | 5.2 ± 0.2† |
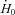 (mW g−1) (mW g−1) |
23 ± 1 | 32 ± 2* | 49 ± 5† |
| Max. power (mW g−1) | 25 ± 3 | 47 ± 2* | 60 ± 6† |
| VMax power/Vmax | 0.28 ± 0.02 | 0.31 ± 0.01 | 0.30 ± 0.02 |
| Emax | 0.39 ± 0.02 | 0.48 ± 0.02* | 0.46 ± 0.01* |
| VEmax/Vmax | 0.20 ± 0.03 | 0.20 ± 0.01 | 0.19 ± 0.01 |
| EDL | |||
| n | 5 | 5 | 5 |
| F0 (kPa) | 215 ± 14 | 210 ± 12 | 193 ± 13 |
| Vmax (FL s−1) | 5.4 ± 0.2 | 7.3 ± 0.5* | 8.9 ± 0.7† |
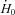 (mW g−1) (mW g−1) |
118 ± 10 | 144 ± 12* | 195 ± 8† |
| Max. power (mW g−1) | 57 ± 5 | 70 ± 7* | 100 ± 4† |
| VMax power/Vmax | 0.34 ± 0.01 | 0.34 ± 0.02 | 0.34 ± 0.02 |
| Emax | 0.28 ± 0.02 | 0.26 ± 0.01 | 0.30 ± 0.01 |
| VEmax/Vmax | 0.28 ± 0.03 | 0.30 ± 0.02 | 0.31 ± 0.02 |
Significant difference from value at 20°C.
Significant difference from values at both 20°C and 25°C. F0 corrected for the ratio of fibre length to muscle length using values reported by Barclay et al. (1993). Emax, maximum mechanical efficiency. VMax power/Vmax, velocity at which power output was maximum, expressed relative to Vmax; VEmax/Vmax, velocity at which mechanical efficiency was maximal, expressed relative to Vmax.
The influences of muscle type (soleus and EDL) and temperature (20, 25 and 30°C) on Vmax, maximum power output and maximum efficiency were assessed using 2-way analysis of variance. Post hoc analyses were made using Dunnett's multiple comparison test. Decisions regarding statistical significance were made with respect to the 95% level of confidence.
Results
Effects of temperature on mechanical performance
Peak isometric force (F0) was independent of muscle type and temperature (Table 1). The pooled mean F0 was 220 ± 6 kPa (n= 30). Note, however, that the protocol used was not designed to determine the absolute maximum isometric force (see Methods).
The effects of temperature on the velocity dependencies of power output, rate of enthalpy output and mechanical efficiency are summarised in Fig. 2 and Table 1. In general, for both muscle types, rates of energy output and the range of shortening velocities increased with temperature (Fig. 2A and B). That is, Vmax increased significantly with temperature in both muscles, with Q10 values of 1.7 and 1.8 between 20 and 30°C for EDL and soleus, respectively (Fig. 3A). Maximum power output also increased with temperature. This effect was greater for soleus (Q10, 2.4 between 20 and 30°C) than EDL (Q10, 1.8). Although the absolute velocity at which maximum power output occurred increased with temperature (Fig. 2A and B), the relative velocity at which power output was maximum was independent of temperature in both muscle types and was approximately one-third of Vmax (Table 1, Fig. 2C and D).
Figure 2. The effects of shortening velocity and temperature on rates of energy output and mechanical efficiency of muscles from mouse soleus (left) and EDL (right).
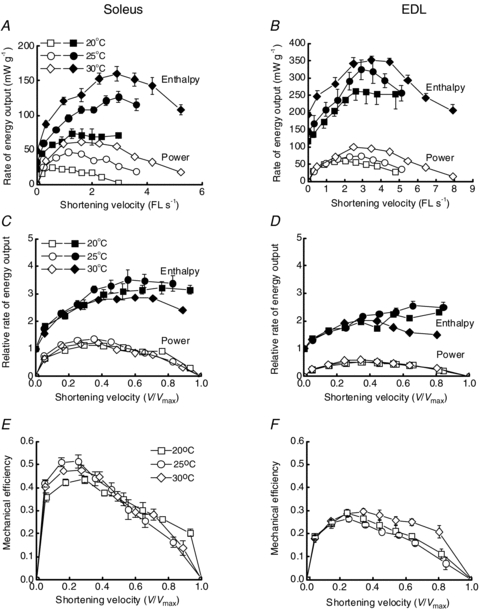
A and B, effects of temperature on absolute power output (open symbols) and rate of enthalpy output (filled symbols). Data are expressed as a function of absolute shortening velocity (fibre length (FL) s−1). Note the different ordinate scales on the two graphs. The key in A also applies to B. Symbols, mean; error bars, ±1 s.e.m.; error bars omitted where smaller than symbol. Details of number of preparations and mean rates of energy output are given in Table 1. C and D, power output and rate of enthalpy output expressed relative to the rate of enthalpy output in isometric contraction at the relevant temperature. Energy output data for each preparation were normalised by the rate of isometric enthalpy output for that preparation and shortening velocity for each preparation was normalised by its Vmax. Key in C also applies to D. E and F, effects of temperature and normalised shortening velocity on mechanical efficiency. Mechanical efficiency is the ratio of power output to rate of enthalpy output.
Figure 3. Effects of temperature on maximum values of shortening velocity (A), power output (B) and mechanical efficiency (C) for soleus (open bars) and EDL (shaded bars).
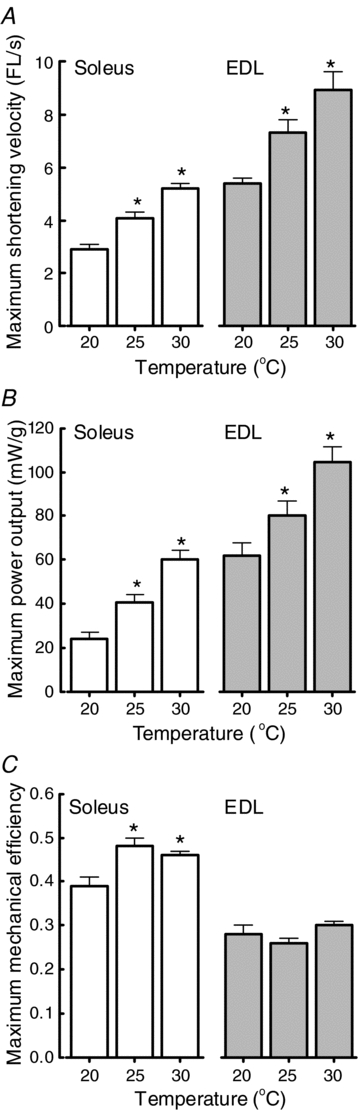
*Significantly different (P < 0.05) to value at 20°C.
Effects of temperature on energy turnover
The rate of enthalpy output during isometric contraction 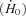 increased with temperature for both muscles (Table 1). As with the mechanical variables, the relative magnitude of the increase with temperature was greater for soleus than EDL (Table 1). Between 20 and 30°C,
increased with temperature for both muscles (Table 1). As with the mechanical variables, the relative magnitude of the increase with temperature was greater for soleus than EDL (Table 1). Between 20 and 30°C, 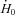 increased 2.3-fold for soleus and 1.7-fold for EDL. The effects of temperature on the rate of enthalpy output during shortening are illustrated in Fig. 2. The absolute rate of enthalpy output during shortening at a given absolute velocity also increased with temperature (Fig. 2A and B). The size of the temperature effects were similar to those for isometric energy turnover. For example, Q10 values between 20 and 30°C for the mean rate of enthalpy output when shortening with maximum efficiency were 2.1 for soleus and 1.7 for EDL.
increased 2.3-fold for soleus and 1.7-fold for EDL. The effects of temperature on the rate of enthalpy output during shortening are illustrated in Fig. 2. The absolute rate of enthalpy output during shortening at a given absolute velocity also increased with temperature (Fig. 2A and B). The size of the temperature effects were similar to those for isometric energy turnover. For example, Q10 values between 20 and 30°C for the mean rate of enthalpy output when shortening with maximum efficiency were 2.1 for soleus and 1.7 for EDL.
In Fig. 2C and D, rate of enthalpy output is expressed relative to the isometric rate at each temperature and velocity expressed relative to Vmax. For both soleus and EDL preparations at velocities <0.5 Vmax, the relative rate of enthalpy output increased with velocity. The superposition of the relationships for all three temperatures at velocities <0.5 Vmax indicates that the magnitude of the temperature effect was independent of relative shortening velocity below 0.5 Vmax. At 20 and 25°C, increasing shortening velocity above 0.5 Vmax resulted in little further increase in the rate of enthalpy output. However, at 30°C the rate of enthalpy output from both EDL and soleus decreased at high shortening velocities.
Effects of temperature on mechanical efficiency
The maximum mechanical efficiency of EDL preparations was unaffected by temperature (Fig. 2F, Fig. 3C) and the highest mean value was 0.31 ± 0.01 at 30°C. At all three temperatures, the relative shortening velocity at which efficiency was maximal for EDL preparations was ∼0.3 Vmax (Table 1). Although the maximum value was independent of temperature, the velocity dependence of mechanical efficiency was affected by temperature: at velocities >0.5 Vmax, efficiency was higher at 30°C than at either 20 or 25°C (Fig. 3C). This reflects the relatively low rate of enthalpy output (i.e. the denominator in the mechanical efficiency calculation) over that velocity range at 30°C (Fig. 2D).
For soleus muscle, the maximum efficiencies at 25 and 30°C were significantly greater than that at 20°C (Fig. 3C). The highest maximum efficiency was 0.48 ± 0.02 (at 25°C) and occurred at a velocity of 0.2 Vmax. As for EDL, the relative velocity at which efficiency was maximal was independent of temperature (Table 1). Efficiency of soleus preparations at 20°C was lower only at shortening velocities close to 0.2 Vmax; at both lower and higher shortening velocities efficiency was similar at all three temperatures.
Discussion
The main result of this study is that maximum mechanical efficiency of isolated, intact mouse muscle fibres was little affected by temperature between 20 and 30°C. This result is consistent with those from amphibian muscle (Fenn, 1923; Hartree & Hill, 1928a,b; Gibbs & Chapman, 1974). Taken together, those results and the current results indicate that lack of effect of temperature on efficiency is a characteristic of not only amphibian muscle but also mammalian muscle. The large effect of temperature on the efficiency of permeabilised fibres from human muscle reported by He et al. (2000) must, therefore, reflect either a difference between human and non-human (e.g. mouse) mammalian muscle or an effect peculiar to the experimental protocol used in that study.
The basis of the large temperature dependence of efficiency in the human fibre study was that power output was much more sensitive to temperature than ATP turnover. For example, comparing the power outputs and rates of ATP turnover for fast fibres at the velocities at which efficiency was maximal gives Q10 values of 5.6 for power output and 1.2 for rate of ATP breakdown between 12 and 20°C (from Figs 6 and 7, He et al. 2000). The Q10 for rate of ATP breakdown during low velocity shortening in that study is low compared to both the current study (Q10 values, 1.6–2.0) and the studies using amphibian muscle (Q10 values slightly over 2) (Hartree & Hill, 1928a; Gibbs & Chapman, 1974). High Q10 values for maximum power output at low temperatures have been reported previously. For instance, values close to 4 were found for amphibian muscles between 5 and 15°C but at higher temperatures (15 to 35°C), power output is less sensitive to temperature with Q10 values of 1.8 to 2 (Renaud & Stevens, 1981; Bennett, 1984), similar to that reported here. From the available information, it is unclear why the rate of ATP breakdown, which was determined from the time course of release of inorganic phosphate (Pi) from cycling crossbridges, was less temperature sensitive in the human muscle study than in studies with other isolated preparations.
Comparison with permeabilised mammalian muscle fibres
A number of measurements of efficiency have been made using permeabilised mammalian muscle fibres. Comparison amongst these studies provides further information about the effects of species and temperature on the energetics of mammalian muscle. Two methods have been used to measure the rate of ATP hydrolysis in permeabilised fibres: coupling ATP hydrolysis to NADH oxidation (Potma & Stienen, 1996; Reggiani et al. 1997; Sun et al. 2001) and measurement of Pi release using a fluorescent Pi-binding protein (He et al. 1997, 2000). In all cases, rate of ATP hydrolysis increases with shortening velocity. However, in most reports rate of ATP splitting does not plateau or decline at high shortening velocities (Reggiani et al. 1997; He et al. 1999, 2000; Sun et al. 2001).
The difference between permeable and intact fibres in velocity dependence of energy turnover at velocities >0.5 Vmax may reflect the different range of temperatures used with the two types of preparation. To preserve fibre function, most permeabilised fibre experiments have been performed at 10–15°C. In the current study, the tendency for rate of enthalpy output to decline at high shortening velocities became more prominent as temperature increased (Fig. 2C and D). Similarly, in the one permeabilised fibre study of shortening energetics that has used a relatively high temperature (He et al. 2000), the rate of ATP hydrolysis in permeabilised fast fibres from human muscle increased for all velocities up to Vmax at 12°C but at 20°C increased only at velocities below ∼0.5 Vmax. The decline in energy turnover at high shortening velocities apparent in the data from mouse EDL muscle at 30°C (Fig. 2D) has an important functional consequence: at near-physiological temperature: efficiency is near its maximum across a broad range of velocities. This effect is less prominent in slow-twitch fibres (He et al. 2000) and muscles (Fig. 2E).
To compare efficiency values from experiments with intact and permeabilised fibres, it is necessary to ensure that the efficiency is calculated in a comparable manner. In permeabilised fibre studies, efficiency is calculated using rates of ATP breakdown converted into energy units using the free energy for ATP hydrolysis (ΔGATP). In most skinned fibre studies, it is assumed that ΔGATP is 50 kJ mol−1, as measured in frog muscle (Kushmerick & Davies, 1969). This is most probably an underestimate: ΔGATP is ∼60 kJ mol−1 in intact mammalian muscle (Kushmerick et al. 1992) and this is also the value calculated from composition of the solutions used in the permeabilised fibre experiments (Barclay et al. 2010). In Table 2, crossbridge thermodynamic efficiency values (η; ratio of power output to rate of free energy produced from ATP splitting by crossbridges) from several studies using permeabilised mammalian muscle fibres are compared using a common ΔGATP value of 60 kJ mol−1.
Table 2.
Maximum crossbridge thermodynamic efficiency of mammalian muscle
| Fibre type | Species/muscle | Temp (°C) | η1 (max, %) | Reference |
|---|---|---|---|---|
| Fast | Mouse EDL2 | 20 | 20 | Current study |
| Mouse EDL | 30 | 23 | Current study | |
| Rat EDL | 12 | 24 | Reggiani et al. (1997) | |
| Rabbit psoas | 10 | 34 | Sun et al. (2001) | |
| Rabbit psoas | 12 | 30 | He et al. (1999) | |
| Rabbit psoas | 15 | 23 | Potma & Steinen (1996) | |
| Human | 12 | 23 | He et al. (2000) | |
| Human | 20 | 34 | He et al. (2000) | |
| Slow | Mouse soleus | 20 | 30 | Current study |
| Mouse soleus | 30 | 35 | Current study | |
| Rat soleus | 12 | 35 | Reggiani et al. (1997) | |
| Human | 12 | 18 | He et al. (2000) | |
| Human | 20 | 28 | He et al. (2000) |
Efficiency re-calculated from reported values so that all are consistent with ΔGATP of 60 kJ mol−1.
Mouse data from Fig. 3, adjusted to exclude non-crossbridge energy turnover.
For comparison, the data from the current study are also shown in Table 2. For mouse muscles η was calculated from mechanical efficiency values (Fig. 2E and F) by subtracting from the measured enthalpy rate the rate of enthalpy output due to processes other than crossbridge cycling (Barclay et al. 2007), the relative magnitude of which is independent of temperature between 20 and 30°C (Barclay et al. 2008), and adjusting for the difference between ΔHPCr and ΔGATP (see eqn (8) of Barclay et al. 2010). It was assumed that ΔGATP was 60 kJ mol−1 in both soleus and EDL. In resting mouse soleus and EDL muscle, ΔGATP is 61 and 65 kJ mol−1, respectively (Kushmerick et al. 1992). At the time that efficiency of EDL was measured in the current study, ΔGATP would probably have been reduced to ∼60 kJ mol−1 due to the increase in Pi concentration during the period of contraction before shortening began. This effect is greater in EDL than soleus because (i) the rate of ATP breakdown is higher in EDL and (ii) ΔGATP is more sensitive to changes in Pi in EDL than soleus because the resting Pi concentration is very low in that muscle (Kushmerick et al. 1992).
The data in Table 2 show that when the same value for ΔGATP is used to determine efficiency, maximum efficiency is quite consistent among permeabilised fibre and intact muscle studies across a range of species and temperatures (Table 2). The one unusual value is the human slow fibre data at 12°C (18%, just over half the value for slow fibres from other species). Why this value differs from the others is unclear but it should be noted that there was considerable scatter in the data for power output and rate of ATP splitting, which limits the precision with which maximum efficiency can be specified. Excluding the data for human slow fibres, the average maximum η for the other slow fibres and muscles listed in Table 2 is 32% and that for fast muscle is 26%.
There is an inconsistency in previous reports concerning the maximum efficiency of mouse soleus muscles. The values in this study are similar to those reported by Barclay (1996) but are higher than in Barclay et al. (1993). In the latter study, maximum efficiencies of both soleus and EDL muscles were ∼0.3. In both the earlier studies, the isometric energy turnover rates and maximum power outputs are consistent with those in the current study. However, the cause of the relatively low maximum efficiency for soleus muscle in the 1993 study was that the rate of enthalpy output increased more with shortening velocity than in either the current study or that of Barclay (1996). The reason for this difference is unclear but the consistency of the two more recent studies suggests that it is most likely that maximal mechanical efficiency for mouse soleus is between 0.4 and 0.5, and is higher than that for EDL.
Overall, the figures in Table 2 indicate that it is unlikely that either species (amongst mammals) or temperature greatly affect maximum η. How do the isolated muscle values compare to data for exercising humans?Whipp & Wasserman (1969), who calculated that η was ∼50%, used a different convention, compared to the isolated muscle experiments, concerning the ‘baseline’ against which energy turnover during exercise should be measured. They calculated efficiency using the O2 consumed in excess of that during unloaded cycling. In contrast, all the isolated muscle data shown in Table 2 were calculated using energy turnover in excess of that of the resting muscle. O2 consumption during unloaded cycling is higher than that at rest (Whipp & Wasserman, 1969; Gaesser & Brooks, 1975). To make a direct comparison with the isolated muscle data, we recalculated Whipp & Wasserman's value using the resting O2 consumption that they reported as the baseline; this gave an efficiency of 33%. Those authors also used a lower estimate of ΔGATP (46 kJ mol−1) than now regarded as appropriate (∼60 kJ mol−1; Kushmerick et al. 1992; Jubrias et al. 2008). Using the higher ΔGATP would reduce efficiency to 28%. Although this is similar to the isolated muscle values (Table 2), some caution should be exercised when comparing efficiency measured during exercise with that of isolated muscle. The exercise efficiency value must be reduced below the maximum efficiency of the power-generating muscles alone by additional energetic costs not directly associated with generating mechanical power and because it is unlikely that during exercise muscles shorten with maximum efficiency throughout their active cycle. For example, when a contraction protocol designed to simulate realistic patterns of length change and stimulation was used to measure the efficiency of isolated mouse muscles at 35°C (Barclay & Weber, 2004), the maximum mechanical efficiencies measured (soleus, 30%; EDL, 23%) correspond to η values of ∼20% and 16% in soleus and EDL, respectively. These values are lower than the corresponding values measured during steady shortening (Table 2) because shortening commenced only after a brief period of isometric contraction during which energy was expended but no work performed. That result also indicates that it is unlikely that efficiency increases between 30°C, the highest temperature used in the current study, and 35°C.
Overall, it seems likely that the thermodynamic efficiency of crossbridges in human muscle estimated from exercising people remains slightly higher than expected from isolated muscle data. It is unlikely that this can be accounted for by temperature or species effects (Table 2). The η value of 68% reported for human hand muscles (Jubrias et al. 2008) is clearly much greater than values determined from isolated fibres and greater than the revised estimate from the Whipp & Wasserman data and remains an anomaly.
What is the crossbridge basis of the difference in efficiency of fast- and slow-twitch muscle?
The data for maximum crossbridge efficiency of mouse muscles (Table 2 and Fig. 4) can be combined with information about mechanical properties of crossbridges and the contractile filaments to provide insights into the cause of the different maximum efficiencies of fast- and slow-twitch mouse muscles. The data for this analysis come from experiments with a variety of mammalian muscle preparations. Ideally, all the information required (e.g. fibre stiffness, filament compliance, T2 curves) could be obtained for mouse muscle but a comprehensive set of information is not yet available for any mammalian preparation.
Figure 4. Work produced per ATP split.
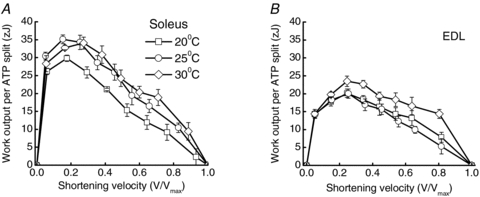
Calculated by dividing power output by rate of ATP splitting. Rate of ATP splitting was calculated from rate of crossbridge-dependent enthalpy output, assuming that (i) ATP hydrolysis was fully buffered by the creatine kinase reaction, (ii) non-crossbridge processes accounted for 35% of isometric enthalpy output (Barclay, 1996; Barclay et al. 2008) and was independent of temperature (Barclay et al. 2008) and (iii) that ΔHPCr is 34 kJ mol−1 (Woledge & Reilly, 1988) and ΔGATP is 60 kJ mol−1 (Kushmerick et al. 1992). Data shown for soleus (A) and EDL (B). Different temperatures are indicated by the symbols as described in A. Symbols, mean; error bars, ±s.e.m.; number of muscles in each group as specified in Table 1.
The first step in the analysis is to determine the work performed by crossbridges (WCB) in mouse muscles during one attachment cycle. The maximum value of η is the fraction of ΔGATP that is converted into work, and applies at both the muscle and individual crossbridge level; that is, if it is assumed that one ATP is used in each crossbridge cycle (Linari et al. 2007), then WCB can be calculated from η. The effects of muscle type, shortening velocity and temperature on WCB are shown in Fig. 4. In that figure, WCB is given in units of zJ per ATP (where z is the SI prefix for 10−21). For mouse soleus, the average maximum work performed in each ATP-splitting crossbridge cycle at 30°C is 35 zJ and for EDL the corresponding value is 23 zJ (Fig. 4). For comparison, ΔGATP of 60 kJ mol−1 is equivalent to 100 zJ molecule−1. WCB calculated for shortening muscle can be compared with the theoretical maximum work that a crossbridge could do in one cycle (Wmax), which can be determined from the results of rapid transient experiments. A detailed description of the calculation of Wmax is provided in the Appendix and the comparison between WCB and Wmax is summarised in Table 3.
Table 3.
Fraction of maximum work per crossbridge cycle achieved in shortening muscle
| F0 (N cm−2) | c (cm−3) | TCB (pN) | Wmax (zJ) | WCB/Wmaxv | |
|---|---|---|---|---|---|
| Soleus | 22 | 1.11 × 1017 | 5.0 | 45.0 | 0.73 |
| EDL | 20 | 1.04 × 1017 | 5.1 | 46.1 | 0.50 |
TCB calculated using eqn (A2) (see Appendix), Wmax using eqn (A1) with integral of T2 curve = 9 TCB zJ (where z is 10−21). c is crossbridge concentration per unit volume of muscle. Fraction of fibre volume occupied by myofibrils: EDL, 0.75; soleus, 0.8 (Luff & Atwood, 1971). Half-sarcomere length, 1.2 × 10−4 cm; fraction of crossbridges attached (natt), 0.33 (Higuchi et al. 1995; Linari et al. 2007).
Wmax is the product of crossbridge isometric force (TCB) and the area under the normalised force–extension curve for a crossbridge (eqn (A1), Appendix). Neither of these factors appears likely to differ substantially between muscle types. The only factors that both determine TCB (eqn (A2)) and differ between EDL and soleus are F0 (Table 1) and crossbridge concentration (Table 3). Crossbridge concentration differs because myofibrils account for 75% of cell volume in mouse EDL and 80% in soleus (Luff & Atwood, 1971). However, the difference in crossbridge concentration between the two muscles is small and similar in magnitude to the difference in mean F0 values so the two differences cancel and TCB is calculated to be ∼5 pN for both muscles (Table 3). The crossbridge force–extension relationship or T2 curve (Fig. A1) (with force expressed relative to isometric force) is also likely to be the same in fast- and slow-twitch muscle (see Appendix). Consequently, the estimates of Wmax for the two muscle types were comparable (∼46 zJ; Table 3). It can be concluded that the difference in efficiency between soleus and EDL is not due a difference in TCB or Wmax but rather must be due to a difference in the fraction of Wmax achieved by crossbridges in fast and slow muscle. Crossbridges in EDL generated less than half Wmax in each cycle whereas those in soleus generated three-quarters of the maximum work possible (Table 3).
Figure A1. T2 curves from fibres of rat and frog muscle.
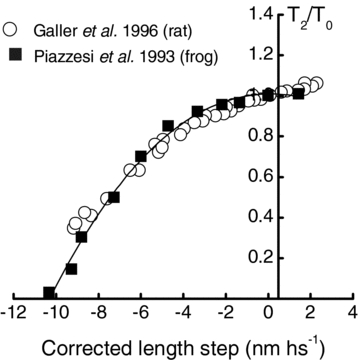
T2 curves from fibres of rat muscle of various types (I, 2A, 2B and 2D; all indicated by open symbols) (data from Galler et al. 1996) and frog sartorius muscle (filled symbols) (data from Piazzesi & Lombardi, 1995). Length step amplitudes have been corrected for filament compliance assuming a combined actin and myosin compliance of 0.012 μm hs−1 kPa−1 for frog data (Barclay et al. 2010) and 0.015 μm hs−1 kPa−1 for rat fibres (measured using rabbit psoas fibres; Linari et al. 2007). T2 forces are expressed relative to isometric force (F0).
A scheme that can account for crossbridges producing less work than Wmax in each cycle at the moderate velocities at which efficiency is maximum is that crossbridges traverse only part of their force–extension relation in each cycle. Crossbridges in the slow-twitch soleus traverse a greater part of the force–extension curve than those in fast-twitch EDL, accounting for the higher efficiency of the slow muscle. The characteristic low efficiency and high power output of EDL (Fig. 3) would occur if crossbridges in that muscle detach before traversing the descending, low-force limb of the force–extension curve, reducing WCB and hence efficiency. Since crossbridges that detach will reattach further up the curve, fibre force output will be relatively high, in accord with the flat force–velocity curve of fast muscle (Barclay et al. 1993; Barclay, 1996), and power output will be high, albeit achieved at the expense of efficiency. The results of the current study show that increasing temperature has little influence on how much of the force–extension curve is traversed; as temperature increases, each crossbridge covers the same region of the curve, so efficiency is constant, but does so more rapidly, increasing power output and rate of ATP splitting.
Conclusion
In conclusion, the relatively low temperatures (20–25°C) at which isolated muscle experiments are performed appear unlikely to provide a basis for reconciling the efficiency of human muscle with that for isolated preparations. The consistency in maximum efficiency values for isolated preparations across studies, animal species, experimental techniques and temperatures gives confidence that these experiments are providing an accurate measure of the efficiency with which crossbridges generate mechanical work in maximally activated muscle. It seems likely, therefore, that the difference between efficiency of human muscle in vivo and isolated muscle, and which is probably smaller than suggested previously, lies in factors other than inherent crossbridge properties. For example, muscles can be more efficient when sub-maximally activated (Steiger & Ruegg, 1969; Buschman et al. 1996) and subtle elastic mechanisms may enhance power output without a direct energetic cost (Lichtwark & Barclay, 2010). Factors such as these warrant further investigation.
Glossary
Abbreviations
- EDL
extensor digitorum longus
- Pi
inorganic phosphate
- SEE
series elastic element
Appendix
Calculation of the potential maximum crossbridge work generation
This analysis is based on the Huxley–Simmons model of the behaviour of attached crossbridges. Huxley & Simmons (1971) described the relationship between the force developed during the quick recovery after an abrupt change in the length of a contracting fibre – the T2 force – and the amplitude of the applied length change. This rapid force recovery is likely to be due to re-equilibration among attached states of crossbridges that were attached when the length step was applied (Ford et al. 1977). In that case, the relationship between T2 force and length step amplitude is the average force–extension relationship of attached crossbridges, and the integral of the curve, between the limits of attachment, is the maximum work that could be achieved in one crossbridge cycle (Wmax) (Huxley & Simmons, 1971). It is envisaged that during a single attachment a crossbridge traverses at least part of the length–tension curve shown in Fig. A1, moving from right to left along the relationship.
The compliance of a contracting fibre arises from both crossbridges and the contractile filaments so only part of the length change applied to a fibre when measuring T2 forces is transmitted to the crossbridges; the remainder is taken up by changes in the length of the contractile filaments. To determine Wmax from the T2 curve, the abscissa values must adjusted to reflect only the length changes experienced by the crossbridges (for a detailed description, see Barclay et al. 2010). The compliance of the actin and myosin filaments in mammalian muscle is between 0.015 and 0.02 μm kPa−1 (half-sarcomere)−1 (Higuchi et al. 1995; Linari et al. 2007); the lower of these values was used to correct the length changes applied to permeabilised rat muscle fibres by Galler et al. (1996). In Fig. A1, T2 data, with corrected step amplitudes, are shown for muscle fibres from both rat and frog. For rat, data from three different fibre types have been pooled because T2 data for rat muscle are independent of fibre type (Galler et al. 1996). The data for rat muscle (open symbols, Fig. A1) are similar to those from the more thoroughly characterised frog muscle (filled symbols, Fig. A1). The independence of the T2 curve from species (Fig. A1), fibre type (Galler et al. 1996) and temperature (Galler & Hilber, 1998) provide support for the idea that the T2 curve reflects a fundamental aspect of crossbridge mechanics.
The maximum work a crossbridge can perform is the area under the T2 curve between the limits of attachment. We previously presented an argument that the maximum attachment range is between +2.75 nm and −10 nm (Barclay et al. 2010) so the absolute value of Wmax would be:
| (A1) |
Here T2 refers to the normalised T2 curve (i.e. with force normalised by the isometric force) as shown in Fig. A1 and TCB is the isometric force per attached crossbridge. The area under the normalised T2 curve is ∼9 TCB zJ (with TCB in pN; zJ = 10−21 J) and is the same for fast- and slow-twitch rat muscle fibres (Fig. A1). TCB depends on muscle isometric force (F0), the crossbridge concentration (c), fraction of crossbridges attached (natt) and length of a half-sarcomere (Lhs):
| (A2) |
Values for F0 are given in Table 1, Lhs was taken to be 1.2 μm (Higuchi et al. 1995) and muscle crossbridge concentration was calculated on the basis of the dimensions of a sarcomere, the arrangement of crossbridges along myosin filaments, the arrangement of myosin filaments in a half-sarcomere and the density of myofibrils (for a detailed description, see Barclay et al. 2010). Fibre crossbridge concentration is 1.35 × 1017 crossbridges cm−3 for mouse soleus and 1.26 × 1017 crossbridge cm−3 for EDL; if extracellular space accounts for 17.5% of the volume of a multi-fibred preparation (Goldspink, 1966; Cieslar et al. 1998), then the muscle crossbridge concentrations for mouse soleus and EDL are 1.11 × 10−17 and 1.04 × 10−17 crossbridge cm−3, respectively. The concentrations differ because myofibrils account for 80% of mouse soleus fibre volume and 75% of EDL fibre volume (Luff & Atwood, 1971).
There is no direct information about natt for mouse muscle but its value is reflected in the stiffness of a contracting fibre, and fibre stiffness for rat muscle fibres is independent of fibre type (Galler et al. 1996) and temperature (Galler & Hilber, 1998). By comparison with rat muscle, it seems likely that natt is the same in mouse soleus and EDL muscles. natt has been quantified in permeabilised fibres from rabbit psoas muscle by comparing the stiffness of fibres in rigor, when all crossbridges are attached, with that during isometric contraction (Linari et al. 2007). In that study, isometric force (190 kPa) was similar to that in the current study (200–220 kPa Table 1), which is important because natt is proportional to isometric force (Barclay et al. 2010). Linari et al. (2007) determined natt to be 0.33 for rabbit fibres and we used this value for estimating TCB for mouse soleus and EDL (Table 3).
Author contributions
The experiments were performed in the Muscle Energetics laboratory in the School of Physiotherapy & Exercise Science, Griffith University, Queensland, Australia. C.J.B. designed and performed the experiments. All the authors contributed to the conception of the project, interpretation of the data and development of the manuscript. All authors approved the final version.
References
- Barclay CJ. Mechanical efficiency and fatigue of fast and slow muscles of the mouse. J Physiol. 1996;497:781–794. doi: 10.1113/jphysiol.1996.sp021809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barclay CJ, Arnold PD, Gibbs CL. Fatigue and heat production in repeated contractions of mouse skeletal muscle. J Physiol (Lond) 1995;488:741–752. doi: 10.1113/jphysiol.1995.sp021005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barclay CJ, Constable JK, Gibbs CL. Energetics of fast- and slow-twitch muscles of the mouse. J Physiol. 1993;472:61–80. doi: 10.1113/jphysiol.1993.sp019937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barclay CJ, Lichtwark GA, Curtin NA. The energetic cost of activation in mouse fast-twitch muscle is the same whether measured using reduced filament overlap or N-benzyl-p-toluenesulphonamide. Acta Physiologica. 2008;193:381–391. doi: 10.1111/j.1748-1716.2008.01855.x. [DOI] [PubMed] [Google Scholar]
- Barclay CJ, Weber CL. Slow skeletal muscles of the mouse have greater initial efficiency than fast muscles but the same net efficiency. J Physiol. 2004;559:519–533. doi: 10.1113/jphysiol.2004.069096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barclay CJ, Woledge RC, Curtin NA. Energy turnover for Ca2+ cycling in skeletal muscle. J Muscle Res Cell Motil. 2007;28:259–274. doi: 10.1007/s10974-007-9116-7. [DOI] [PubMed] [Google Scholar]
- Barclay CJ, Woledge RC, Curtin NA. Inferring crossbridge properties from skeletal muscle energetics. Prog Biophys Mol Biol. 2010;102:53–71. doi: 10.1016/j.pbiomolbio.2009.10.003. [DOI] [PubMed] [Google Scholar]
- Bennett AF. Thermal dependence of muscle function. Am J Physiol Regul Integr Comp Physiol. 1984;247:R217–R229. doi: 10.1152/ajpregu.1984.247.2.R217. [DOI] [PubMed] [Google Scholar]
- Brooks SV, Faulkner JA, McCubbrey DA. Power outputs of slow and fast skeletal muscles of mice. J Appl Physiol. 1990;68:1282–1285. doi: 10.1152/jappl.1990.68.3.1282. [DOI] [PubMed] [Google Scholar]
- Buschman HPJ, Elzinga G, Woledge RC. Energetics of shortening depend on stimulation frequency in single muscle fibers from Xenopus laevis at 20°C. Pflugers Archiv. 1995;430:160–167. doi: 10.1007/BF00374646. [DOI] [PubMed] [Google Scholar]
- Buschman HPJ, Elzinga G, Woledge RC. The effects of the level of activation and shortening velocity on energy output in type 3 muscle fibres from Xenopus laevis. Pflugers Archiv. 1996;433:153–159. doi: 10.1007/s004240050261. [DOI] [PubMed] [Google Scholar]
- Cieslar J, Huang MT, Dobson GP. Tissue spaces in rat heart, liver, and skeletal muscle in vivo. Am J Physiol Regul Integr Comp Physiol. 1998;275:R1530–R1536. doi: 10.1152/ajpregu.1998.275.5.R1530. [DOI] [PubMed] [Google Scholar]
- Fenn WO. A quantitative comparison between the energy liberated and the work performed by isolated sartorius muscle of the frog. J Physiol. 1923;58:175–203. doi: 10.1113/jphysiol.1923.sp002115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ford LE, Huxley AF, Simmons RM. Tension responses to sudden length change in stimulated frog muscle fibres near slack length. J Physiol. 1977;269:441–515. doi: 10.1113/jphysiol.1977.sp011911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaesser GA, Brooks GA. Muscular efficiency during steady-rate exercise: effects of speed and work rate. J Appl Physiol. 1975;38:1132–1139. doi: 10.1152/jappl.1975.38.6.1132. [DOI] [PubMed] [Google Scholar]
- Galler S, Hilber K. Tension/stiffness ratio of skinned rat skeletal muscle fibre types at various temperatures. Acta Physiol Scand. 1998;162:119–126. doi: 10.1046/j.1365-201X.1998.0272f.x. [DOI] [PubMed] [Google Scholar]
- Galler S, Hilber K, Pette D. Force responses following stepwise length changes of rat skeletal muscle fibre types. J Physiol. 1996;493:219–227. doi: 10.1113/jphysiol.1996.sp021377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibbs CL, Chapman JB. Effects of stimulus conditions, temperature, and length on energy output of frog and toad sartorius. Am J Physiol. 1974;227:964–971. doi: 10.1152/ajplegacy.1974.227.4.964. [DOI] [PubMed] [Google Scholar]
- Goldspink G. An attempt at estimating extrafiber fluid in small skeletal muscles by a simple physical method. Can J Physiol Pharmacol. 1966;44:765–775. doi: 10.1139/y66-095. [DOI] [PubMed] [Google Scholar]
- Hartree W, Hill AV. The energy liberated by an isolated muscle during the performance of work. Proc R Soc Lond B Biol Sci. 1928a;104:1–27. [Google Scholar]
- Hartree W, Hill AV. The factors determining the maximum work and the mechanical efficiency in muscle. Proc R Soc Lond B Biol Sci. 1928b;103:234–251. [Google Scholar]
- He H, Giordano FJ, Hilal-Dandan R, Choi DJ, Rockman HA, McDonough PM, Bluhm WF, Meyer M, Sayen MR, Swanson E, Dillmann WH. Overexpression of the rat sarcoplasmic reticulum Ca2+ ATPase gene in the heart of transgenic mice accelerates calcium transients and cardiac relaxation. J Clin Invest. 1997;100:380–389. doi: 10.1172/JCI119544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He ZH, Bottinelli R, Pellegrino MA, Ferenczi MA, Reggiani C. ATP consumption and efficiency of human single muscle fibers with different myosin isoform composition. Biophys J. 2000;79:945–961. doi: 10.1016/S0006-3495(00)76349-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He ZH, Chillingworth RK, Brune M, Corrie JE, Webb MR, Ferenczi MA. The efficiency of contraction in rabbit skeletal muscle fibres, determined from the rate of release of inorganic phosphate. J Physiol. 1999;517:839–854. doi: 10.1111/j.1469-7793.1999.0839s.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Higuchi H, Yanagida T, Goldman YE. Compliance of thin filaments in skinned fibers of rabbit skeletal muscle. Biophys J. 1995;69:1000–1010. doi: 10.1016/S0006-3495(95)79975-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill AV. Heat of shortening and the dynamic constants of muscle. Proc R Soc Lond B Biol Sci. 1938;126:136–195. doi: 10.1098/rspb.1949.0019. [DOI] [PubMed] [Google Scholar]
- Homsher E. Muscle enthalpy production and its relationship to actomyosin ATPase. Annu Rev Physiol. 1987;49:673–690. doi: 10.1146/annurev.ph.49.030187.003325. [DOI] [PubMed] [Google Scholar]
- Huxley AF, Simmons RM. Proposed mechanism of force generation in striated muscle. Nature. 1971;233:533–538. doi: 10.1038/233533a0. [DOI] [PubMed] [Google Scholar]
- Jubrias SA, Vollestad NK, Gronka RK, Kushmerick MJ. Contraction coupling efficiency of human first dorsal interosseous muscle. J Physiol. 2008;586:1993–2002. doi: 10.1113/jphysiol.2007.146829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohler I, Meier R, Busato A, Neiger-Aeschbacher G, Schatzmann U. Is carbon dioxide (CO2) a useful short acting anaesthetic for small laboratory animals? Lab Anim. 1999;33:155–161. doi: 10.1258/002367799780578390. [DOI] [PubMed] [Google Scholar]
- Kretzschmar KM, Wilkie DR. A new method for absolute heat measurement, utilizing the Peltier effect. J Physiol. 1972;224:18P–21P. [PubMed] [Google Scholar]
- Kushmerick MJ, Davies RE. The chemical energetics of muscle contraction. II. The chemistry, efficiency and power of maximally working sartorius muscles. Appendix. Free energy and enthalpy of ATP hydrolysis in the sarcoplasm. Proc R Soc Lond B Biol Sci. 1969;174:315–353. doi: 10.1098/rspb.1969.0096. [DOI] [PubMed] [Google Scholar]
- Kushmerick MJ, Moerland TS, Wiseman RW. Mammalian skeletal muscle fibers distinguished by contents of phosphocreatine, ATP, and Pi. Proc Natl Acad Sci U S A. 1992;89:7521–7525. doi: 10.1073/pnas.89.16.7521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lichtwark GA, Barclay CJ. The influence of tendon compliance on muscle power output and efficiency during cyclic contractions. J Exp Biol. 2010;213:707–714. doi: 10.1242/jeb.038026. [DOI] [PubMed] [Google Scholar]
- Linari M, Caremani M, Piperio C, Brandt P, Lombardi V. Stiffness and fraction of myosin motors responsible for active force in permeabilized muscle fibers from rabbit psoas. Biophys J. 2007;92:2476–2490. doi: 10.1529/biophysj.106.099549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luff AR, Atwood HL. Changes in the sarcoplasmic reticulum and transverse tubular system of fast and slow skeletal muscles of the mouse during postnatal development. J Cell Biol. 1971;51:369–383. doi: 10.1083/jcb.51.2.369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luff AR, Goldspink G. Total number of fibers in muscles of several strains of mice. J Anim Sci. 1970;30:891–893. doi: 10.2527/jas1970.306891x. [DOI] [PubMed] [Google Scholar]
- Mulieri LA, Luhr G, Trefry J, Alpert NR. Metal-film thermopiles for use with rabbit right ventricular papillary muscles. Am J Physiol. 1977;233:C146–156. doi: 10.1152/ajpcell.1977.233.5.C146. [DOI] [PubMed] [Google Scholar]
- Piazzesi G, Lombardi V. A cross-bridge model that is able to explain mechanical and energetic properties of shortening muscle. Biophys J. 1995;68:1966–1979. doi: 10.1016/S0006-3495(95)80374-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Potma E, Stienen G. Increase in ATP consumption during shortening in skinned fibres from rabbit psoas muscle: effects of inorganic phosphate. J Physiol. 1996;496:1–12. doi: 10.1113/jphysiol.1996.sp021660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. Temperature-dependence of shortening velocity and rate of isometric tension development in rat skeletal muscle. J Physiol. 1982;329:465–483. doi: 10.1113/jphysiol.1982.sp014314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. The force–velocity relation of rat fast- and slow-twitch muscles examined at different temperatures. J Physiol. 1984;351:517–529. doi: 10.1113/jphysiol.1984.sp015260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reggiani C, Potma EJ, Bottinelli R, Canepari M, Pellegrino MA, Stienen GJM. Chemo-mechanical energy transduction in relation to myosin isoform composition in skeletal muscle fibres of the rat. J Physiol. 1997;502:449–460. doi: 10.1111/j.1469-7793.1997.449bk.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renaud JM, Stevens ED. Effect of acclimation temperature and pH on contraction of frog sartorius muscle. Am J Physiol Regul Integr Comp Physiol. 1981;240:R301–R309. doi: 10.1152/ajpregu.1981.240.5.R301. [DOI] [PubMed] [Google Scholar]
- Segal SS, Faulkner JA. Temperature-dependent physiological stability of rat skeletal muscle in vitro. Am J Physiol Cell Physiol. 1985;248:C265–C270. doi: 10.1152/ajpcell.1985.248.3.C265. [DOI] [PubMed] [Google Scholar]
- Smith NP, Barclay CJ, Loiselle DS. The efficiency of muscle contraction. Prog Biophys Mol Biol. 2005;88:1–58. doi: 10.1016/j.pbiomolbio.2003.11.014. [DOI] [PubMed] [Google Scholar]
- Steiger GJ, Ruegg JC. Energetics and “efficiency” in the isolated contractile machinery of an insect fibrillar muscle at various frequencies of oscillation. Pflugers Archiv. 1969;307:1–21. doi: 10.1007/BF00589455. [DOI] [PubMed] [Google Scholar]
- Stein RB, Gordon T, Shriver J. Temperature dependence of mammalian muscle contractions and ATPase activities. Biophys J. 1982;40:97–107. doi: 10.1016/S0006-3495(82)84464-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sturges HA. The choice of a class-interval. J Am Stat Assoc. 1926;21:65–66. [Google Scholar]
- Sun YB, Hilber K, Irving M. Effect of active shortening on the rate of ATP utilisation by rabbit psoas muscle fibres. J Physiol. 2001;531:781–791. doi: 10.1111/j.1469-7793.2001.0781h.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whipp BJ, Wasserman K. Efficiency of muscular work. J Appl Physiol. 1969;26:644–648. doi: 10.1152/jappl.1969.26.5.644. [DOI] [PubMed] [Google Scholar]
- Woledge RC, Reilly PJ. Molar enthalpy change for hydrolysis of phosphorylcreatine under conditions in muscle cells. Biophys J. 1988;54:97–104. doi: 10.1016/S0006-3495(88)82934-5. [DOI] [PMC free article] [PubMed] [Google Scholar]


