USING STIMULUS EQUIVALENCE TECHNOLOGY TO TEACH STATISTICAL INFERENCE IN A GROUP SETTING

Abstract

Computerized lessons employing stimulus equivalence technology, used previously under laboratory conditions to teach inferential statistics concepts to college students, were employed in a group setting for the first time. Students showed the same directly taught and emergent learning gains as in laboratory studies. A brief paper-and-pencil examination, suitable for classroom use, captured effects demonstrated previously through laboratory tests. The results support the extension of the lessons to more naturalistic settings.

In three recent studies (Critchfield & Fienup, in press; Fienup & Critchfeld, 2010; Fienup, Critchfield, & Covey, 2009), we addressed teaching psychology undergraduates about inferential statistics (e.g., see Kranzler, 2007). Students mastered a few foundational skills (conditional discriminations) that were directly taught and, consistent with the generativity that is inherent in stimulus equivalence (e.g., Stromer, Mackay, & Stoddard, 1992), also mastered many others. In other words, students reliably learned more than they were taught. This outcome occurred under laboratory conditions in which students could work without the distraction of others in close proximity and learning could be evaluated via detailed and time-consuming test batteries that are incompatible with classroom routines.

It is important to note that not all interventions that work under controlled conditions perform well in the field (Schoenwald & Hoagwood, 2001). The present study, therefore, was designed as a first step toward evaluating our statistics lessons under classroom conditions by addressing two goals: (a) to determine whether a group setting adversely affected learning outcomes by using our lessons simultaneously with a group of students approximately equal in size to the roster of a statistics class at our university; and (b) to determine whether learning gains like those seen in the lab in match-to-sample procedures would register on a paper-and-pencil multiple-choice examination like those commonly employed in college classes.

METHOD

Participants were 27 undergraduates (18 women and 9 men) with means (and standard deviations) of 19.4 years (1.2) for age, 3.0 (0.6) for grade point average, and 23.5 (3.7) for SAT college entrance exam score. All scored below 75% correct on a paper-and-pencil pretest and earned course bonus credit for participating. Four participants were self-identified as racial minorities (two African-American, one Latino, and one Asian). Students worked simultaneously, in a room that contained 30 computer workstations, on computerized lessons identical to those of our previous studies plus a brief review lesson (Lesson 4, see below). The entire investigation (including administrative tasks such as instructions and informed consent, training phases, and assessments) was completed in one sitting that required up to 2 hr.

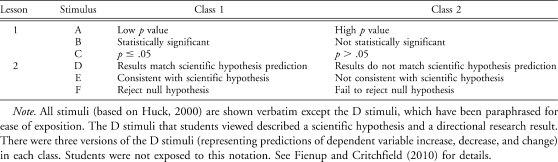
The lessons, described briefly here due to space limitations (for details, see Fienup & Critchfield, 2010), used match-to-sample procedures to teach conditional relations that contributed to the formation of equivalence classes involving the stimuli shown in Table 1. Figure 1 summarizes the relations involving these stimuli that were taught (black arrows) or were subsequently expected to emerge (gray arrows). On each trial, students viewed stimuli (one sample, two comparisons) on the computer screen and made responses by pointing and clicking a mouse. Each lesson contained one or more learning units in which students practiced one type of directly taught relation with feedback on every trial until making 12 consecutive correct responses. Mastering a lesson's learning units led to a computerized skill check (the mode of assessment in our laboratory studies) that consisted of relations (trained and emergent for Lessons 1 and 2, trained only for Lessons 3 and 4) that the lesson was expected to establish. No feedback was provided. Scoring at or above 89% advanced a student to the next scheduled task. A lower score required a student to repeat the lesson's learning units and skill check.

Table 1.

Stimuli in Lessons 1 and 2 and the Notation Used in the Text

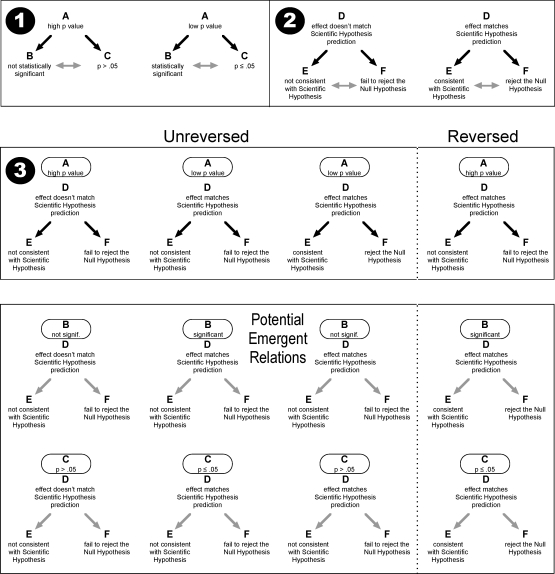
Figure 1.

Summary of relations that were taught (black arrows) and expected to emerge (gray arrows). Lessons are indicated by white numbers in black circles. See text for definition of reversed and unreversed relations. Stimuli are shown verbatim except the D stimuli, which have been paraphrased for ease of exposition. The D stimuli that students viewed described a scientific hypothesis and a directional research result. There were three versions of the D stimuli (representing predictions of dependent variable increase, decrease, and change) in each class. See Fienup and Critchfield (2010) for details.

Lesson 1 (three units) taught concepts related to statistical significance. In our notation (Table 1), teaching A→B and C→A relations was expected to promote emergent B→A, A→C, B→C, and C→B relations. Lesson 1 also included a preliminary unit (not shown in Table 1 or Figure 1) in which students matched inequality expressions (e.g., p ≤ .05) to specific numerical values (e.g., .001). Lesson 2 (six units) taught concepts related to hypothesis decisions. In our notation, teaching D→E and D→F relations was expected to promote emergent E→D, F→D, E→F, and F→E relations.

Lesson 3 (12 units) taught students to select hypothesis decisions (E and F stimuli) when shown combinations of hypotheses and results (D stimuli) plus statistical information (A stimuli). Figure 1 shows that for unreversed relations, the correct hypothesis decision was identical to what students had learned in conjunction with D stimuli alone in Lesson 2. For reversed relations, statistical information demanded a different decision than was taught in Lesson 2. Thus, because the Class 1 E and F stimuli (Table 1) became associated with different D samples depending on the presence of statistical information (A stimuli), Lesson 3 established contextual control (Bush, Sidman, & de Rose, 1989) over equivalence class membership. The skill check of Lesson 3 included only directly taught (D+A)→E and (D+A)→F relations; however, because the A stimuli were part of an equivalence class (Lesson 1), without additional training students should have been able to use Lesson 1 stimuli other than A to guide hypothesis decisions (for rationale, see Gatch & Osborne, 1989), yielding emergent contextual relations [(D+B)→E, (D+B)→F, (D+C)→E, and (D+C)→F] that were probed in the paper-and-pencil test (see below). Finally, Lesson 4 (one unit) reviewed Lesson 1 relations in which sample stimuli were D+A combinations of Lesson 3 and the comparison stimuli were B stimuli of Lesson 1.

Before and after the lessons, students completed a paper-and-pencil test (available from the first author) that contained 40 multiple-choice items, many of which were based on questions that had been used in past exams in a research methods course. Each item included two possible answers, one representing each of the two stimulus classes that the lessons were designed to create, plus a third option stating, “Not enough information to decide.” The questions evaluated (a) relations that were explicitly taught during Lessons 1 and 2 (15 items); (b) relations that were expected to emerge, untaught, based on Lessons 1 and 2 (nine items); (c) unreversed and reversed contextual relations that were explicitly taught during Lesson 3 (four items each); and (d) unreversed and reversed contextual relations that were expected to emerge, untaught, based on Lesson 3 training (four items each). To be clear, the relations that training could have established were too numerous to evaluate thoroughly in this test format; the paper-and-pencil assessment merely sampled from among the many dozens of relations that Fienup and Critchfield (2010) described and tested in detail.

RESULTS AND DISCUSSION

Figure 2 (top left panel, white bar) shows that scores on the pencil-and-paper pretest tended to be low (range, 33% to 73% correct). The bottom panel (white bars) shows that scores tended to be low for each of several clusters of items that represented the various thematic emphases of the lessons. Results of subsequent training may be described at two levels of analysis. First, training proceeded quickly and with few errors, so that students achieved mastery (12 consecutive correct responses) in fewer than 20 trials on 527 of 594 initial attempts at learning units (27 students times 22 learning units). Second, training mastery usually was confirmed by computerized skill checks. In 94 of 108 total skill checks (27 students times four lessons), students achieved mastery (≥89% correct) on the first attempt. Because 8 of the 14 first-try failures occurred during Lesson 1, these may partly represent the process of students adapting to an unfamiliar learning environment.

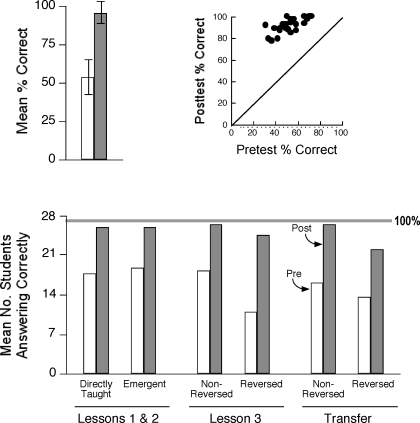
Figure 2.

Top left: mean percentage correct on the paper-and-pencil pretest (white bars) and posttest (gray bars) for 27 students. Range bars show ± 1 standard deviation. Top right: relation between pretest and posttest scores for individual students. Cases above the diagonal represent improvements from pretest to posttest. Bottom: mean number of students who answered pretest and posttest questions correctly for the different types of directly taught and emergent relations.

We observed no relation between pretest score and skill check failure, but students who failed the initial attempt at a unit's skill check also tended to require more trials to meet the mastery criterion on that lesson's learning units, compared to students who passed on the first try. This was true (a) during Lesson 1 for the preliminary unit on inequalities and for the first unit in which conditional discriminations were taught, and (b) during Lesson 3 for several units involving reversed relations, particularly the first one in which reversed relations were introduced. These outcomes suggest individual differences in which the need for remediation may be anticipated based on student performance during training, thus providing targets for future efforts to improve instruction.

Although skill check failures sometimes occurred, postfailure remediation always produced mastery. Students performed nearly without error on their final skill check attempt for Lesson 1 (M  =  98% correct, range, 92% to 100%), Lesson 2 (M  =  99%, range, 93% to 100%), Lesson 3 (M  =  99%, range, 92% to 100%), and Lesson 4 (M  =  99%, range, 92% to 100%). Thus, students ultimately learned everything that was directly taught, and in the cases of Lesson 1 and 2 skill checks, also reliably demonstrated expected untaught abilities.

Figure 2 (top left panel, gray bar) shows that students also tended to score well on the paper-and-pencil posttest (range, 78% to 100% correct). The top right panel shows that, although there was a significant correlation between pretest and posttest scores (r  =  .70, p < .0001), all students improved compared to the pretest. Because on posttests every student scored higher than the best pretest score, the pretest–posttest difference was statistically significant, t test for paired scores, t(26)  =  23.92, p < .0001. If a standard academic grading scale is considered as a frame of reference, 20 of 27 students achieved a posttest score equivalent to an A (≥90% correct), six scored equivalent to a B (≥80% correct, with four scoring ≥85%), and the remaining student scored equivalent to a high C (78%). Overall, the lessons succeeded in building statistical inference skills, as measured on the paper-and-pencil tests.

Figure 2 (bottom) indicates that at the group-aggregate level, posttest gains occurred for all types of relations, although the paper-and-pencil test included too few items to gauge these effects for individual students. Posttest accuracy was similar for Lesson 1 and 2 relations that were directly taught versus those that emerged without direct instruction. Lesson 3 successfully taught contextually controlled hypothesis decision making, in that students usually responded accurately to questions about both unreversed relations (as expected based on Lesson 2 training) and reversed relations (in which joint consideration of Lesson 1 statistical information and Lesson 2 hypothesis-plus-results information required different hypothesis decisions than based on Lesson 2 information alone). The rightmost bars show similar results for contextual relations that were expected to emerge untaught based on Lesson 3 training. That is, when the statistical information (A stimuli) that Lesson 3 employed was replaced with other stimuli from Lesson 1, students usually responded accurately to questions about both reversed and unreversed relations.

The present results broadly replicate our previous laboratory findings and bolster expectations that the statistics lessons can be productively employed with students in an academic course. The training portions of the lessons (minus administrative activities and assessments), which took students a mean of 15 min (range, 9 to 38) to complete, easily could fit into a 50-min instructional period. Assessments probably would have to take place on other days, which could hinder learning in two ways. First, delayed assessment introduces a risk of forgetting (although some stimulus equivalence studies suggest that both directly taught and emergent relations are quite resistant to forgetting; e.g., Fienup & Dixon, 2006; Rehfeldt & Root, 2004). Second, testing in the same format used in training may help to promote emergent relations (Sidman, 1992); therefore, dropping the Lesson 1 and 2 skill checks to save classroom time potentially could impair learning outcomes. Classroom applications will have to confront these issues.

Another pivotal point is that the current participants probably differed in important ways from students who are enrolled in an academic course. To cite just one example, course grading contingencies might be expected to improve student motivation, although we have sometimes seen students work energetically as research volunteers to gain bonus credit even while neglecting course assignments that could make bonus credit unnecessary. Only field studies can show whether such factors will systematically affect learning outcomes.

With an eye toward extensions to the classroom, we concede that before–after experimental designs like the present one provide only weak demonstrations of student learning. What before–after designs lack—clear documentation that students progress only with instruction—can be provided through repeated baseline assessments (for an example involving equivalence-based instruction, see Fienup, Covey, & Critchfield, 2010) or group comparison designs that involve a no-treatment group, as is common in randomized controlled trials. To be clear, however, no-treatment controls verify only that an intervention works better than doing nothing. A long-term goal of any applied research is to determine whether an intervention works better than alternative means of changing behavior (e.g., Drake, Latimer, Leff, McHugo, & Burns, 2004). Future studies on equivalence-based instruction must address not only the setting of application but also the relative efficacy of instruction.