Diminishing Returns From Beneficial Mutations and Pervasive Epistasis Shape the Fitness Landscape for Rifampicin Resistance in Pseudomonas aeruginosa

Abstract

Because adaptation depends upon the fixation of novel beneficial mutations, the fitness effects of beneficial mutations that are substituted by selection are key to our understanding of the process of adaptation. In this study, we experimentally investigated the fitness effects of beneficial mutations that are substituted when populations of the pathogenic bacterium Pseudomonas aeruginosa adapt to the antibiotic rifampicin. Specifically, we isolated the first beneficial mutation to be fixed by selection when 96 populations of three different genotypes of P. aeruginosa that vary considerably in fitness in the presence of rifampicin were challenged with adapting to a high dose of this antibiotic. The simple genetics of rifampicin resistance allowed us to determine the genetic basis of adaptation in the majority of our populations. We show that the average fitness effects of fixed beneficial mutations show a simple and clear pattern of diminishing returns, such that selection tends to fix mutations with progressively smaller effects as populations approach a peak on the adaptive landscape. The fitness effects of individual mutations, on the other hand, are highly idiosyncratic across genetic backgrounds, revealing pervasive epistasis. In spite of this complexity of genetic interactions in this system, there is an overall tendency toward diminishing-returns epistasis. We argue that a simple overall pattern of diminishing-returns adaptation emerges, despite pervasive epistasis between beneficial mutations, because many beneficial mutations are available, and while the fitness landscape is rugged at the fine scale, it is smooth and regular when we consider the average over possible routes to adaptation. In the context of antibiotic resistance, these results show that acquiring mutations that confer low levels of antibiotic resistance does not impose any constraint on the ability to evolve high levels of resistance.

POPULATIONS adapt to novel environments by the successive fixation of beneficial mutations, so the fitness effect of a fixed beneficial mutation is a quantity of key interest in evolutionary genetics (Fisher 1930; Orr 2005; Bell 2008). Unfortunately, the fitness effects of novel beneficial mutations are difficult to study empirically because these mutations are very rare and often lead to small changes in fitness (Eyre-Walker and Keightley 2007). Microbial experimental evolution provides a solution to this problem because the short generation time and large population size of lab cultures of microbes allow for beneficial mutations to appear rapidly, and the fitness effects of these mutations can be determined with a high degree of precision using replicated fitness assays (Elena and Lenski 2003; Buckling et al. 2009). Experimental evolution studies have used two basic approaches to study the fitness effects of beneficial mutations. In long-term selection experiments, replicate populations are selected in a novel environment over long periods of time (hundreds to thousands of generations). Fitness assays are then used to reconstruct the dynamics of adaptation, and the contribution that individual mutations make to increased fitness is determined by identifying selective sweeps using sequencing or statistical methods (Lenski and Travisano 1994; Novella et al. 1995; Bull et al. 1997; Elena et al. 1998; Elena and Lenski 2003; Barrick et al. 2009; Schoustra et al. 2009; Hall et al. 2010). The great advantage of this method is that it provides information on the fitness effects of beneficial mutations that are substituted over entire adaptive walks as populations ascend to peaks on the adaptive landscape. However, most long-term selection experiments follow only a small number of populations, and this lack of replication can make it difficult to make powerful statistical inferences regarding the distribution of fitness effects of beneficial mutations that are substituted at any one point in an adaptive walk. In “mutation trap” experiments, a much larger number of replicate populations are selected over a shorter period of time, and the first beneficial mutation to be fixed by selection is isolated, usually by using neutral genetic markers that are linked to beneficial mutations (Bull et al. 2000; Rozen et al. 2002; Barrett et al. 2006; Hegreness et al. 2006; Perfeito et al. 2007). The great advantage of this method is that high levels of replication allow for an accurate measurement of the distribution of the fitness effects of fixed beneficial mutations; the drawback is that it provides information on only a single step in an adaptive walk.

This article addresses two questions: (1) How does the distribution of the fitness effects of fixed beneficial mutations change as a population approaches a peak on the adaptive landscape? And, (2) to what extent are changes in this distribution attributable to epistasis? To address these questions, we used a novel experimental approach that involves carrying out mutation trap experiments using a range of ancestral genotypes that are at different distances from a known adaptive peak. This approach combines the high levels of replication permitted by mutation trap experiments with information on how mutational distributions shift as populations approach a peak on the adaptive landscape. Specifically, we challenged three different genotypes of the bacterium Pseudomonas aeruginosa that vary substantially in fitness in the presence of the antibiotic rifampicin with adapting to a common environment containing a high dose of rifampicin. We then isolated a single clone carrying the first beneficial mutation to be fixed by natural selection in a large number of populations (96) derived from each of our ancestral genotypes and measured the fitness of each clone carrying a beneficial mutation, giving a total of 288 putative beneficial mutations.

Our choice of adaptation to rifampicin as a model system was largely dictated by the genetic and biochemical tractability of this selective pressure. Rifampicin binds to a highly conserved pocket on the β-subunit of RNA polymerase (rpoB), and it inhibits bacterial growth by preventing transcript elongation. Resistance to rifampicin usually occurs by mutations in this domain of RNA polymerase that either fully or partially block the binding of rifampicin to RNA polymerase (Campbell et al. 2001, 2005; Trinh et al. 2006; MacLean and Buckling 2009). By sequencing the region of rpoB that is usually implicated in rifampicin resistance, we were able to determine the genetic basis of adaptation in >50% of our selection lines. This genetic tractability allowed us to test for epistasis between beneficial mutations and to make some inferences regarding the structure of the adaptive landscape linking genotype to fitness in this system.

We show that the average fitness benefit provided by fixed beneficial mutations follows a clear pattern of diminishing returns; as populations near an adaptive peak, they fix mutations with progressively smaller selection coefficients. The genetic architecture underlying this simple pattern is complex. Selection lines founded by different genotypes show a strong tendency to fix the same beneficial mutations, implying that sign epistasis is either uncommon or absent in this environment. We find evidence of a tendency toward diminishing-returns epistasis between beneficial mutations, but in general the fitness effects of beneficial mutations are highly idiosyncratic across genetic backgrounds. Finally, we argue that adaptation shows predictable geometric patterns of diminishing returns, despite pervasive epistasis between beneficial mutations, because many beneficial mutations are available, and while the fitness landscape is rugged at the fine scale, it is smooth and regular when we consider the average over possible routes to adaptation.

MATERIALS AND METHODS

Strains and culture conditions:

We used three isogenic mutants of P. aeruginosa strain PAO1 containing a single missense mutation in rpoB (A455T, A455G, or C1550T) that confers low-to-medium levels of resistance to rifampicin as ancestral strains for this experiment (MacLean and Buckling 2009). Culture medium consisted of M9KB (12.8 g/liter Na₂HPO₄.7H₂O, 3 g/liter KH₂PO₄, 0.5 g/liter NaCl, 1 g/liter NH₄Cl, 2 mm MgSO₄, 10 g/liter glycerol, 20 g/liter proteose peptone #3) supplemented with rifampicin and agar (16 g/liter) where necessary. All cultures were incubated at 37° in microtiter plates.

Selection experiment:

Overnight cultures of each ancestral strain were diluted into fresh M9KB to set up 96 replicate cultures, each founded with a small number of cells (10³–10⁴). These cultures were incubated overnight. To initiate the selection experiment, 2 μl of each overnight culture was transferred into 200 μL of fresh M9KB supplemented with 120 mg/liter of rifampicin. After 24 hr of incubation, selection lines were diluted 100-fold into fresh medium supplemented with 120 mg/liter rifampicin for a further three rounds of selection.

Identifying selective sweeps:

None of the ancestral strains that we used in this experiment are capable of forming visible colonies when grown on M9KB agar plates containing a very high dose of rifampicin (240 mg/liter). However, preliminary studies determined that selection lines derived from these ancestral lines rapidly and repeatedly evolve high levels of rifampicin resistance, allowing them to form colonies on M9KB plates supplemented with this high dose of rifampicin. To identify selective sweeps, we plated out 1-μl aliquots of a 10-fold dilution series from 32 replicate selection lines derived from each ancestral strain on M9KB agar plates containing 240 mg/liter of rifampicin at the end of each growth cycle, allowing us to crudely score the frequency of highly resistant genotypes in each line.

Fitness assay:

Following the fourth cycle of selection, we streaked out all 288 selection lines and the three ancestral strains on M9KB agar plates supplemented with 120 mg/liter of rifampicin. After overnight growth, we transferred a single randomly chosen colony from each selection line and 32 randomly chosen colonies of each ancestral strain into M9KB medium. After overnight growth, we diluted down each culture 100-fold into fresh M9KB supplemented with 120 mg/liter rifampicin, and we measured the optical density of each culture (OD₆₀₀) at hourly intervals over a 16-hr period using an automated microplate reader. In total, we assayed the fitness of 64 replicate cultures of each ancestral strain and 4 replicate cultures of each colony isolated from the 288 selection lines. We estimated the log-phase growth rate of each culture, r, such that fitness can be estimated as w_x,y = exp(r_x − r_y), where r_x is the growth rate of an evolved strain and r_y is the growth rate of the ancestral rpoB mutant from which it is derived (Hartl and Clark 1997). All growth rates were standardized by dividing by the growth rate of an isogenic wild-type strain (PAO1) lacking rpoB mutations in rifampicin-free M9KB. To determine the fitness effect of a given mutation, we averaged across all cultures of mutants carrying the mutation in each genetic background. Preliminary work demonstrated that the estimates of fitness obtained using growth rate assays (w_growth) are equal to measures of competitive fitness (w_competitive) against an isogenic marked tester strain (rpoB A1592G) in M9KB supplemented with 120 mg/liter of rifampicin (w_competitive = w_growth × 1.01; F_1,7 = 22, P = 0.0023, r² = 0.76). To estimate the fitness of the ancestral strains, we compared the growth rate of the ancestral strains in medium containing rifampicin (120 mg/liter) with the fitness of the wild-type strain in medium lacking rifampicin. The ancestral strain is at an adaptive peak in rifampicin-free culture medium, as demonstrated by the fact that no further increases in growth rate occur after hundreds of generations of selection at a large population size (Hall et al. 2010).

Sequencing:

We sequenced approximately the first 2 kb of rpoB, which spans the region of this protein that is usually implicated in rifampicin resistance using previously described methods (MacLean and Buckling 2009). We sequenced the first 1 kb of rpoB, which is rarely implicated in rifampicin resistance, in 51 clones, and we sequenced between 1 and 2 kb that is often involved in rifampicin resistance in 226 clones. We estimated the frequency of the fixation of beneficial mutations by dividing the number of clones carrying a particular beneficial mutation by the number of times the site at which the mutation occurred was sequenced. This estimation was carried out independently in each genetic background.

RESULTS AND DISCUSSION

Selection experiment:

We selected 288 populations initiated by three different isogenic clones of P. aeruginosa PAO1 carrying missense mutations in rpoB (A455T, A455G, or C1550T) that confer low levels of resistance to rifampicin in culture medium supplemented with a high dose of rifampicin. The response to selection in this experiment was very rapid and uniform: After 1 round of selection, genotypes with beneficial mutations conferring high levels of rifampicin resistance were present at a frequency >1% in only 5% of selection lines, but after two rounds of selection, genotypes carrying beneficial mutations were present at a frequency of >1% in 98% of selection lines. After four rounds of selection, we isolated a single randomly chosen clone from each selection line. Several lines of evidence confirm that this method allowed us to isolate a large collection of genotypes carrying a single beneficial mutation. First, we sequenced the region of rpoB that is usually involved in rifampicin resistance in a sample of our clones to directly test for the acquisition of beneficial mutations. We identified second-site mutations in rpoB in 111 clones; in no case did we identify more than one second-site mutation in the same clone, and the original rpoB mutation was present in each clone that we sequenced. Although we cannot exclude the possibility that some of the clones that we sampled carried more than one beneficial mutation, our sequencing results suggest that these genotypes were isolated from <1% of our lines. A rigorous test for second-site mutations and comprehensive mutation identification would have required sequencing the entire genome of each of the 288 clones that we identified, which is not practical, given current sequencing technology. Second, four of four replicate cultures gave fitness estimates of w > 1 for 284 of the 288 clones carrying putative beneficial mutations that we isolated. Sequencing revealed that these four false positives lacked mutations in the region of rpoB that we sequenced, and these clones were excluded from further analysis.

Fitness effects of fixed mutations:

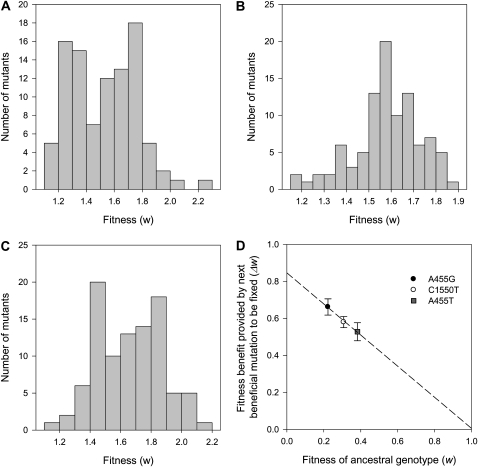
In agreement with theory (Kimura 1983; Rozen et al. 2002; Hegreness et al. 2006) and previous experimental results (Imhof and Schlotterer 2001; Rozen et al. 2002; Barrett et al. 2006; Hegreness et al. 2006; Perfeito et al. 2007; Schoustra et al. 2009), adaptation tends to occur as a result of the fixation of mutations of intermediate effect, giving rise to hump-shaped distributions of fitness effects of fixed beneficial mutations in each genetic background (Figure 1, A–C). Interestingly, the form of this distribution varies between genetic backgrounds; the distribution is bimodal in the A455T and A455G backgrounds and unimodal in the C1550T background. To the best of our knowledge, this is the first study to report a bimodal distribution of fitness effects of fixed beneficial mutations. Unfortunately, it is very difficult to make precise inferences regarding the shape of the underlying distribution of fitness effects of all beneficial mutations on the basis of the distribution of fitness effects of fixed beneficial mutations, essentially because many different underlying distributions can give rise to the same distribution of fixed mutations (Rozen et al. 2002). We speculate, however, that bimodal distributions of fixed mutations arise in the A455T and A455G backgrounds because the underlying distribution of fitness effects of beneficial mutations is also bimodal in these backgrounds.

Figure 1.—

Diminishing returns from beneficial mutations. (A–C) The distribution of fitness effects of beneficial mutations that were fixed by natural selection when three different strains of P. aeruginosa PAO1, each carrying a different missense mutation in RNA polymerase (A455T, A455G, or C1550T), were challenged with adapting to culture medium containing a high dose (120 mg/liter) of rifampicin. (D) A linear regression of the average (±95% C.I.; n = 93, 95, or 96) fitness effect of beneficial mutations that were fixed by selection as a function of the fitness of the genetic background in which the mutations were fixed.

In long-term selection experiments, it is commonly observed that populations fix beneficial mutations with progressively smaller benefits as they approach a peak on the adaptive landscape (Lenski and Travisano 1994; Novella et al. 1995; Bull et al. 1997; Elena et al. 1998; Elena and Lenski 2003; Schoustra et al. 2009; Hall et al. 2010). To test for diminishing returns from beneficial mutations, we first had to estimate the relative fitness of the three ancestral strains used to initiate the experiment. We assumed that the maximal possible growth rate (i.e., fitness) that could be obtained in the presence of rifampicin was equivalent to the growth rate of the rifampicin-sensitive ancestral strain (P. aeruginosa PAO1) in the absence of rifampicin. Evidence that this growth rate presents an adaptive peak comes from the observation that the growth rate of the ancestral strain in rifampicin-free culture medium does not increase, even after hundreds of generations of selection at large population size (Hall et al. 2010). Preliminary experiments also indicated that rifampicin-resistant strains can evolve to match this growth rate in the presence of rifampicin (R. C. MacLean, unpublished results). The ancestral genotypes used to initiate the selection experiment vary considerably in fitness (F_2,188 = 16.27, P < 0.0001) with fitness varying between ∼0.2 (A455G) and 0.4 (A455T).

The average fitness effect of fixed beneficial mutations varies among genetic backgrounds (F_2,281 = 11, P < 0.0001), and linear regression reveals that the average fitness effect of fixed beneficial mutations declines as fitness increases (F_1,2 = 128, r² = 0.995, P = 0.028; Figure 1D), providing direct evidence for diminishing returns adaptation as populations approach a peak on the adaptive landscape.

Identification and characterization of beneficial mutations:

We identified a total of 36 unique beneficial mutations across the three genetic backgrounds, all of which are nonsynonymous, and we estimated the frequency of fixation of each of these mutations across all three genetic backgrounds (Table 1). It is important to point out that our method for mutation detection could identify only mutations in the proximity of the rifampicin-binding pocket; we could not detect mutations elsewhere in the genome or gene amplifications, which can be an important mechanism for adaptation when bacterial populations are challenged with a novel selective pressure (Andersson and Hughes 2009; Sandegren and Andersson 2009; Sun et al. 2009). Despite these limitations, we were able to identify the mutations that were fixed in 50–80% of our selection lines, depending on genetic background (Table 1). Given the large number of replicate populations used in this experiment, it was not feasible to use whole-genome sequencing to identify mutations outside of our target region in any systematic manner.

TABLE 1.

Frequency of fixation and fitness of beneficial mutations

	Frequency of fixation (%)			Relative fitness
Beneficial mutation	A455G	A455T	C1550T	A455G	A455T	C1550T
1630+CCCGTG	0	0	1.28			1.43
A1540C	0	0	1.28			1.40
A1553G	0	1.28	3.85		1.68	1.69
A1553T	0	0	3.85			1.64
A1562G	20	19.23	7.69	1.75	1.65	1.51
A1562T	1.43	0	0	1.92
A1567G	0	2.56	0		1.94
A1592T	0	1.28	0		1.78
A1718G	0	1.28	0		1.24
A1729C	1.43	0	0	1.89
A455G	NP	NP	5.26	NP	NP	1.63
A455T	NP	NP	47.37	NP	NP	1.63
C1341A	0	0	1.28			1.74
C1375T	0	0	1.28			1.63
C1547T	1.43	0	0	1.45
C1550G	0	1.28	0		1.70
C1550T	7.14	11.54	NP	1.86	1.52	NP
C1563A	1.43	0	0	1.67
C1563G	0	1.28	1.28		1.49	1.56
C1591G	2.86	0	1.28	1.91		1.67
C1591T	0	5.13	1.28		1.48	1.66
C1593A	1.43	0	0	1.82
C1607T	0	1.28	1.28		1.39	1.25
C1610T	0	0	1.28			1.40
C1619T	0	0	1.28			1.18
C1736T	2.86	1.28	1.28	1.76	1.84	1.39
G1561A	0	0	1.28			1.51
G1622A	0	0	1.28			1.65
G1624T	0	0	1.28			1.54
G1716T	0	0	1.28			1.58
G1724C	1.43	0	0	1.45
T1529C	1.43	0	0	1.44
T1549G	2.86	1.28	0	1.96	1.20
T1655G	0	0	1.28			1.39
T1731C	0	1.28	0		1.12
T449C	7.69	5.26	0	1.73	1.31
Sum	53.42	55.24	88.5

This table shows the frequency of fixation and the relative fitness of beneficial mutations identified in this study across all three genetic backgrounds used to initiate selection lines. NP indicates mutations that were not physically possible.

The frequency of fixation varies widely between beneficial mutations: a small number of mutations, such as A1562G, were fixed at a high frequency in all three genetic backgrounds, while most beneficial mutations were fixed very rarely. It is also noteworthy that the A455T and A455G mutations were fixed at a high frequency in the C1550T background and, conversely, that the C1550T mutation was fixed at a high frequency in the A455T and A455G backgrounds. This strong bias is at least partially explainable by among-site variation in the mutation rate (Table 2): sequencing of 80 spontaneous rifampicin-resistant mutants isolated from a P. aeruginosa PAO1 rifampicin-sensitive strain reveals that mutation A1562G occurs at a very high rate (2.49 × 10⁻⁸) and that the frequencies of the A455G mutation (5.8 × 10⁻⁹) and the A455T mutation (1.57 × 10⁻⁸) are also very high in comparison with the typical mutation rate found for most beneficial mutations that we identified (modal mutation rate = 8.29 × 10⁻¹⁰). Mutation landscape models predict that the probability of fixation of beneficial mutations correlates linearly to the selection coefficient associated with the beneficial mutations or, in the case where the mutation rate is variable, to the product of the mutation rate and the selection coefficient (Orr 2002; Rokyta et al. 2005). In this experiment, we do not observe a correlation between expected and observed fixation frequencies for all three genetic backgrounds (P > 0.05). This lack of correlation may be driven by the fact that mutation landscape models make two assumptions that are unlikely to have been upheld in this experiment (Orr 2002). First, these models assume that mutation supply rate is low, so that competition between independently derived beneficial mutations is negligible. Given the rapid rate of fixation of beneficial mutations, clonal interference is likely to have been common in our experiment. Second, mutation landscape models assume that selection acts on an underlying exponential distribution of fitness effects of beneficial mutations, which is unlikely to have been the case, given the relatively low fitness of the ancestral genotypes that were used to initiate the selection experiment (MacLean and Buckling 2009).

TABLE 2.

Among-site variation in the mutation rate

Beneficial mutation	No.of isolates	Mutation rate
A1553G	4	3.32E-09
A1553T	2	1.66E-09
A1562G	30	2.49E-08
A1562T	1	8.29E-10
A1592T	4	3.32E-09
A455G	7	5.80E-09
A455T	19	1.57E-08
C1550T	2	1.66E-09
C1563G	1	8.29E-10
C1591T	3	2.49E-09
C1607T	1	8.29E-10

The number of spontaneous rifampicin-resistant mutants carrying beneficial mutations identified in this study in a collection of 80 spontaneous rifampicin-resistant mutants that were isolated from a rifampicin-sensitive clone of P. aeruginosa PAO1 using a fluctuation test (MacLean and Buckling 2009) are shown. Any beneficial mutations not shown in this table were not found in this collection of mutants. Mutation rates at each site were calculated using an overall estimate of the mutation rate to rifampicin resistance of 6.64 × 10⁻⁸.

Testing for diminishing-returns epistasis:

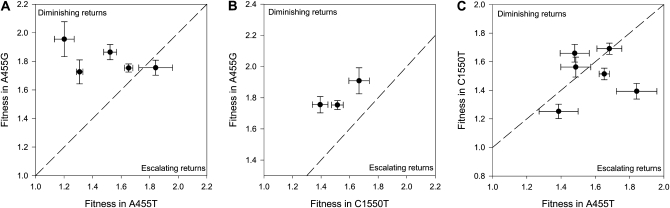
One very simple explanation for why we observe diminishing returns from beneficial mutations is that individual beneficial mutations exhibit diminishing-returns epistasis; that is, the benefit provided by individual mutations decreases as fitness increases (Lenski 1988; Bull et al. 2000). To test for diminishing-returns epistasis, we compared the fitness effects of mutations that were fixed in more than one genetic background across backgrounds (Table 1). There is a significant trend toward diminishing returns when comparing the fitness effects of mutations fixed in the low-fitness background (A455G) and in the high-fitness background (A455T) (mean difference in w = −0.30, SE = 0.14, N = 5, t = 2.13, P(one-tailed) = 0.025; Figure 2A) and the low-fitness background and the intermediate-fitness (C1550T) background (mean difference in w = −0.28, SE = 0.04, N = 3, t = 6.95, P(one-tailed) = 0.01; Figure 2B). However, there is no evidence of a trend toward diminishing returns when comparing the fitness effects of beneficial mutations between the medium-fitness background and the high-fitness background (mean difference in w = 0.07, SE = 0.089; Figure 3C). Comparing the fitness effects of beneficial mutations across genetic backgrounds reveals that the correlation of fitness effects of beneficial mutations in different genetic backgrounds is low and does not differ significantly from zero between the low-fitness background and the high-fitness background (r = 0.53, t = 1.1, P = 0.35; Figure 3A) or between the intermediate-fitness background and the high-fitness background (r = 0.13, t = 0.26, P = 0.80; Figure 3C).

Figure 2.—

Idiosyncratic fitness effects of individual fixed beneficial mutations in different genetic backgrounds. This figure shows the mean (±SEM; n ≥ 4) fitness effect of beneficial mutations across genetic backgrounds. (A) Mutations that were fixed in both A455T (high initial fitness) and A455G (low initial fitness). (B) Mutations that were fixed in both C1550T (intermediate initial fitness) and A455G (low initial fitness). (C) The fitness effects of mutations that were fixed in the A455T and C1550T backgrounds. The dashed line is a plot of y = x; mutations that fall along this line have additive effects across backgrounds, mutations that fall above the line show diminishing returns, and mutations that fall below this line show escalating returns.

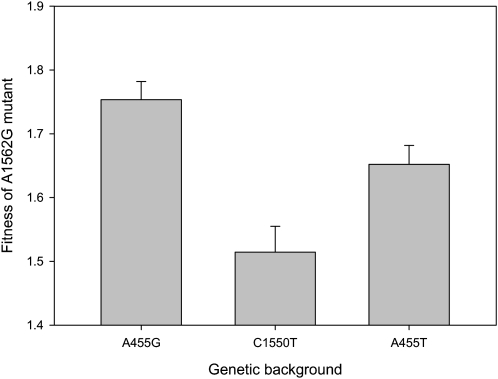
Figure 3.—

Complex epistatic effects of mutation A1562G. This figure shows the mean (±SEM) fitness effect of the A1562G mutation across genetic backgrounds. The A1562G mutation has a different effect on fitness in each genetic background, as determined by a one-way ANOVA (F_2,136 = 10.5, P < 0.0001) followed by a Tukey test (P < 0.05).

The complexity of interactions between mutations in this system is highlighted by the common beneficial mutation A1562G. The fitness effects of A1562G are highly epistatic (Figure 3; F_2,136 = 10.5, P < 0.0001); A1562G provides the greatest fitness benefit in the lowest-fitness background (A455G), but the benefit provided by A1562G is greater in the highest-fitness genetic background (A455T) than in the intermediate-ranked genetic background (C1550T). The evidence for diminishing returns from this important beneficial mutation therefore depends entirely on the comparison being made: A1562G shows diminishing returns if its effects in A455G are compared with those in either A455T or C1550T, but comparing its effects in A455T and in C1550T does not provide any evidence for diminishing returns.

A model of diminishing-returns adaptation on a geometric fitness landscape:

To address the problem of diminishing returns from a more general perspective, we used a one-dimensional version of Fisher's (1930) geometric model of adaptation to derive exact predictions for how the average fitness effect of beneficial mutations declines upon approach to an evolutionary optimum. Previously, approximate results were given by Orr (1998) and Martin and Lenormand (2008). We consider that the set of phenotypes is represented by the real number line, with the current phenotype at the origin and the optimum phenotype at 1. Fitness w is assumed to be a monotonically decreasing function of a phenotype's Euclidean distance z from the optimum (Fisher 1930): following Orr (1998), we assume a Gaussian form w(z) = exp(−γz²), where the dimensionless quantity γ simultaneously scales phenotype and fitness space and provides the sole parameter of the model. Mutation is implemented as a random leap in phenotype space from the origin, and we will restrict attention to those that bring the phenotype closer to the origin (i.e., those falling in the interval [0,2]). We assume that all directions are equally likely (Fisher 1930) and that distance from the origin is uniformally distributed [at least within the interval under consideration (Orr 1998)].

The selection coefficient associated with a beneficial mutation is s = w*/w⁺ − 1 = exp(γx(2 − x)) − 1, where w* is the fitness of the mutant phenotype, w⁺ is current fitness, and x is the phenotypic value of the mutant. Assuming that the probability of fixation for a beneficial mutation is proportional to its selection coefficient (Haldane 1927; Kimura 1983), the probability density of fixed mutations over the interval [0,2] is φ(x) = c(exp(γx(2 − x)) −1), where c is chosen so that the total density over the interval is unity. Thus, the expected selection coefficient is 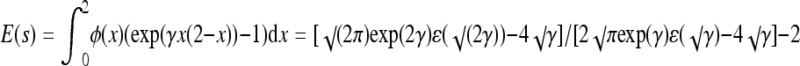, where ɛ is the error function 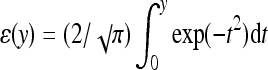. Of interest is the expected fitness increment owing to the next beneficial allele to fix: E(Δw) = E(w*) − w⁺ = w⁺E(s). Since w⁺ = exp(−γ), and hence γ = −lnw⁺, we have E(Δw) = w⁺[√π(w⁺)⁻²ɛ(i√(2lnw⁺)) − 2i√(2lnw⁺)]/[√(2π)(w⁺)⁻¹ɛ(i√(lnw⁺)) −2i√(2lnw⁺)] −2w⁺. This relation is plotted in Figure 4.

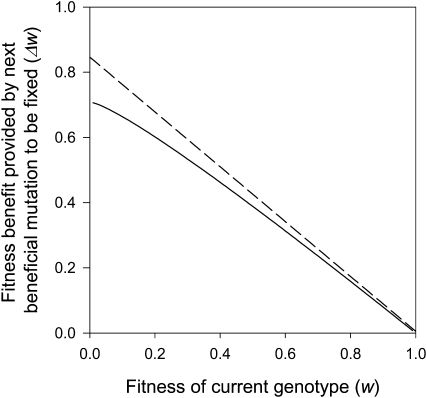
Figure 4.—

Diminishing returns from beneficial mutations in Fisher's geometric model. This figure shows how the fitness effects of beneficial mutations that are substituted by natural selection change as a population approaches an adaptive peak in Fisher's geometric model (solid line). The dashed line shows the linear regression of ΔW against W inferred from our experimental data (Figure 1D).

Conclusion:

Following the pioneering experiment of Rozen et al. (2002), a number of studies have measured the distribution of the fitness effects of beneficial mutations that are substituted by selection when a single genotype is challenged with adapting to a novel environment. These studies have shown that beneficial mutations of relatively large effect are substituted by selection when populations are challenged with a stressful environment (Bull et al. 2000; Barrett et al. 2006), whereas beneficial mutations with small effects are substituted by selection when populations are challenged with relatively benign environments (Rozen et al. 2002; Hegreness et al. 2006; Perfeito et al. 2007). In agreement with these experiments, and with studies that have measured the fitness effects of beneficial mutations that are substituted over entire adaptive walks (Lenski and Travisano 1994; Novella et al. 1995; Bull et al. 1997; Elena et al. 1998; Elena and Lenski 2003; Schoustra et al. 2009; Hall et al. 2010), we find that adaptation is a process of diminishing returns: As populations of P. aeruginosa approach an adaptive peak for high levels of rifampicin resistance, they fix beneficial mutations with progressively smaller average fitness benefits (Figure 1).

Although diminishing-returns adaptation has been observed in a wide range of previous experiments, the genetic mechanisms underlying diminishing returns remain poorly understood. We have exploited the simple and well-characterized genetics of rifampicin resistance (Campbell et al. 2001; Garibyan et al. 2003; Trinh et al. 2006) to determine the genetic basis of adaptation in a large number (>100) of replicate populations (Table 1), and this provides insight into the genetic causes of diminishing-returns adaptation. In contrast to the simple pattern of diminishing returns that is observed when comparing the average fitness effects of beneficial mutations that are substituted during adaptation, individual beneficial mutations often show highly idiosyncratic effects on fitness in different genetic backgrounds (Figures 2 and 3), implying the existence of pervasive epistasis between beneficial mutations and a complex fitness landscape linking genotype to fitness.

The most obvious feature of the topology of the fitness landscape is that there is an overall tendency for diminishing-returns epistasis between beneficial mutations, which is in agreement with previous microbial experiments (Lenski 1988; Bull et al. 2000). In the case of antibiotic resistance, this overall tendency toward diminishing-returns epistasis can be explained simply. The maximum possible level of resistance to a given dose of antibiotic that can be obtained is 100%, and this upper limit on resistance must generate a tendency toward diminishing returns. For example, if mutations have additive effects on resistance, a mutation that confers complete resistance to an antibiotic will provide a small benefit in a genotype that already has a high level of antibiotic resistance and a large benefit in a genotype that has a low level of antibiotic resistance. The complexity of genetic interactions that we observed shows that this simple argument does not provide a universal explanation for the structure of the fitness landscape, and we suggest that the complexity of the landscape may be attributable to two factors. First, mutations may have non-additive effects on antibiotic resistance, as has been observed by Weinreich et al. (2006). Second, resistance mutations have variable costs. We have previously shown that many rifampicin-resistant mutations are associated with a fitness cost in P. aeruginosa (MacLean and Buckling 2009), and this cost of resistance will partially offset the increase in fitness provided by resistance mutations due to decreased antibiotic sensitivity, complicating the structure of the fitness landscape. Preliminary work shows that the costs of acquiring secondary resistance mutations differ between the three different genetic backgrounds that we employed as a result of epistatic interactions between resistance mutations (A. R. Hall and R. C. MacLean, unpublished results), and this form of epistasis is expected to further increase the complexity of the fitness landscape underlying rifampicin resistance. The available evidence shows that fitness costs associated with resistance (Andersson and Hughes 2010) and epistatic interactions between the costs of alternative resistance mutations (Trindade et al. 2009; Ward et al. 2009) are universal features of the evolution of antibiotic resistance (MacLean et al. 2010), suggesting that the complexity of the fitness landscape that we have described here may be quite typical for antibiotic resistance.

Does the fitness landscape for rifampicin resistance contain multiple peaks? Recent studies in a range of model systems, including antibiotic resistance (Weinreich et al. 2006), have shown that sign epistasis between beneficial mutations generates a rugged adaptive landscape containing numerous isolated peaks (Weinreich et al. 2005; Pepin and Wichman 2007; Poelwijk et al. 2007; de Visser et al. 2009). Rigorously testing for sign epistasis requires constructing all possible pairwise combinations of beneficial mutations that can contribute to adaptation to a given environment (Weinreich et al. 2005, 2006; Poelwijk et al. 2007), which is not possible in this case, given the large number (>36) of beneficial mutations that can contribute to increased rifampicin resistance. If sign epistasis commonly occurs between rifampicin-resistant mutations, we would expect that many beneficial mutations would have been fixed in only only one or two genetic backgrounds. Although most mutations that we identified were found in only one genetic background (24 mutations) or two genetic backgrounds (7 mutations), the total frequency of clones carrying these beneficial mutations is low, amounting to 24% (Table 1). For this calculation, we excluded mutations present in the ancestral clones used to initiate the selection experiment (A455G, A455T, or C1550T), as these could be fixed in only one or two backgrounds. In contrast, mutations that were beneficial in every possible genetic background that we tested occurred at a small number of sites (5 mutations: A1562G, A455G, A455T, C1550T, C1736T), but the total frequency of clones carrying these beneficial mutations was high (41.2%). These simple calculations show that sign epistasis does not make a large contribution to adaptation in this experiment, as most populations fix mutations that have unconditionally beneficial effects.

To complement our experimental work, we have also extended previous theoretical models of adaptation (Orr 1998; Martin and Lenormand 2008) based on Fisher's geometric model to predict how the fitness effects of mutations that are fixed by selection change as a population approaches a peak on the adaptive landscape. The pattern of diminishing returns revealed by this simple model (Figure 4) is in striking agreement with our experimental data (Figure 1D). Although this agreement is compelling, this convergence of theoretical and experimental results must be treated with caution because our model makes two simplifying assumptions that may not be true under the conditions of the experiment. First, we have assumed that the distribution of phenotypic effects of mutations is uniform although this might not be the case. Second, we have assumed that the relationship between phenotype and fitness is described by a simple Gaussian function that may, of course, not correspond to the biological reality of selection for elevated antibiotic resistance.

The view of adaptation that emerges from this study is that the average fitness effects of beneficial mutations that are fixed by selection show a simple and predictable pattern of diminishing returns, while individual beneficial mutations have highly idiosyncratic effects on fitness in different genetic backgrounds that cannot be predicted without a detailed understanding of the molecular basis of fitness. We suggest that a simple overall pattern of diminishing-returns adaptation emerges, despite pervasive epistasis between beneficial mutations, because many beneficial mutations are available, and while the fitness landscape is rugged at the fine scale, it is smooth and regular when we consider the average over possible routes to adaptation. This result provides strong justification for the “phenotypic gambit” (Grafen 1984), which applies adaptationist thinking at the level of phenotypes, for which the underlying genetic bases are unknown, and which has formed the theoretical bedrock for disciplines such as behavioral ecology.

Our results also have important implications for understanding the evolutionary dynamics of antibiotic resistance. Many antibiotic resistance mutations confer only partial resistance, and these mutations could theoretically represent isolated low-fitness peaks on the adaptive landscape under selection for high levels of antibiotic resistance. In the case of rifampicin resistance, our study shows that the acquisition of a low-level resistance mutation does not hinder the evolution of resistance; instead, genotypes with low levels of resistance rapidly acquired secondary resistance mutations that conferred very high levels of antibiotic resistance.