Abstract
Genetic correlations are expected to be high among functionally related traits and lower between groups of traits with distinct functions (e.g., reproductive vs. resource-acquisition traits). Here, we explore the quantitative-genetic and QTL architecture of floral organ sizes, vegetative traits, and life history in a set of Brassica rapa recombinant inbred lines within and across field and greenhouse environments. Floral organ lengths were strongly positively correlated within both environments, and analysis of standardized G-matrices indicates that the structure of genetic correlations is ∼80% conserved across environments. Consistent with these correlations, we detected a total of 19 and 21 additive-effect floral QTL in the field and the greenhouse, respectively, and individual QTL typically affected multiple organ types. Interestingly, QTL × QTL epistasis also appeared to contribute to observed genetic correlations; i.e., interactions between two QTL had similar effects on filament length and two estimates of petal size. Although floral and nonfloral traits are hypothesized to be genetically decoupled, correlations between floral organ size and both vegetative and life-history traits were highly significant in the greenhouse; G-matrices of floral and vegetative traits as well as floral and life-history traits differed across environments. Correspondingly, many QTL (45% of those mapped in the greenhouse) showed environmental interactions, including approximately even numbers of floral and nonfloral QTL. Most instances of QTL × QTL epistasis for floral traits were environment dependent.
EVOLUTIONARY responses to selection are dependent on genetic architecture. The proportion of phenotypic variation with a heritable genetic basis affects the response to selection, as does the structure of genetic correlations among selected traits. For example, an evolutionary response will be constrained if selection favors an increase in the value of two traits that are negatively correlated; i.e., a negative correlation is antagonistic to the joint vector of selection. Alternatively, if the vector of selection is parallel to the genetic correlation, then trait covariation is reinforcing and the population mean may more rapidly approach favored trait values (Etterson and Shaw 2001; Merilä and Björklund 2004). One measure of genetic architecture is the G-matrix (Lynch and Walsh 1998), which is composed of genetic variances (diagonal matrix elements) and genetic covariances among traits (off-diagonal matrix elements). G-matrices have been shown to vary across environments (Donohue et al. 2000; Conner et al. 2003; Brock and Weinig 2007), indicating that the molecular-genetic underpinnings of matrix elements (e.g., identity and/or relative effect of additive and epistatic loci, degree of pleiotropy, etc.) and the traits' evolutionary potential vary across environments. Few studies, however, have related matrix and QTL architectures; and, therefore, the molecular-genetic underpinnings of quantitative-genetic estimates remain unclear (but see Gardner and Latta 2007; Kelly 2009).
In angiosperms, covariances between floral whorls (e.g., petal and stamen length) are frequently positive among functionally related traits. These positive correlations can arise from pollinator-mediated (or pollination-mediated) selection for specific allometric relationships among floral traits and ensuing linkage disequilibrium (LD) among causal loci (Berg 1959, 1960; also referred to as phenotypic integration, see Pigliucci 2003; Klingenberg 2008). For example, in outcrossing species, male fitness may be more dependent on the frequency and efficiency of pollinator visitation than female fitness (Bell 1985; but see Hodgins and Barrett 2008). Anther placement relative to the corolla opening can affect the efficiency of pollen dissemination (Conner and Via 1993; Morgan and Conner 2001); in addition, comparative work indicates that petal–stamen length correlations are stronger than stamen–pistil length correlations in outcrossers, whereas species that reproduce via autogamous selfing show the opposite pattern (Ushimaru and Nakata 2002). Alternatively, strong floral integration could be attributed to the developmental hypothesis that genetic correlations arise due to pleiotropic genes coregulating floral whorls (Herrera 2001; Herrera et al. 2002). Strong correlations resulting from linkage disequilibrium or from developmentally based pleiotropy may constrain the evolution of novel reproductive morphologies when biotic or abiotic factors (and selection) change (Cheverud 1984; Clark 1987; Smith and Rausher 2008; Agrawal and Stinchcombe 2009).
Similar to genetic covariances among floral traits, covariances between floral and nonfloral traits could also alter the evolutionary response of reproductive traits. In contrast to hypotheses regarding the adaptive significance of floral-trait integration, genetic correlations between floral and nonfloral traits (e.g., vegetative or phenological traits) are hypothesized to be disadvantageous (Berg 1960). More specifically, floral allometry may be shaped by selection for reproductive success, as described above, whereas vegetative morphology is shaped primarily by selection to optimize other functions, such as light capture. If floral and nonfloral traits have a common genetic basis, then selection on phenological or morphological traits may result in maladaptive expression of floral organ size. As a result, functionally integrated floral traits are predicted to be genetically decoupled from vegetative and phenological traits (Berg 1960).
QTL mapping provides a powerful tool to explore the genetic architecture of evolutionarily important traits. The QTL architecture of interspecific floral traits has been explored in diverse systems (Bradshaw et al. 1995; Fishman et al. 2002; Goodwillie et al. 2006; Bouck et al. 2007; Moyle 2007); however, insight into the molecular genetic basis of intraspecific floral variation comes almost exclusively from Arabidopsis thaliana (Juenger et al. 2000, 2005) and Mimulus guttatus (Hall et al. 2006). Floral traits in these intraspecific crosses are polygenic with a majority of detected QTL being of small to moderate effect size. Consistent with other quantitative-genetic studies (reviewed in Ashman and Majetic 2006), floral traits in A. thaliana and M. guttatus mapping populations exhibited moderate to high genetic correlations. In both systems, mapped QTL often affected multiple floral traits. In the few cases where QTL underlying intraspecific floral morphology have been evaluated, only a single growth environment was used; estimation of floral quantitative genetics across environments and subsequent comparison with the QTL architecture underlying observed across-environment patterns are lacking.
Using a segregating progeny of Brassica rapa (recombinant inbred lines, RILs) and a small sample of crop and wild accessions, we examine the quantitative-genetic and QTL architecture of floral traits under field and greenhouse environments. Specifically, we address the following questions: (1) Does this RIL population express significant genetic (co)variation for floral traits when growing in the field or greenhouse? (2) Is there significant genetic variation for vegetative traits and days to flowering in field and greenhouse environments, and is there evidence for genetic correlations between floral and nonfloral traits? (3) Does the genetic architecture of floral and nonfloral traits, as measured by the G-matrix, differ across environments? (4) What is the number and effect size of additive and epistatic QTL in field and greenhouse environments? (5) What is the relationship between mapped QTL and quantitative genetic estimates of trait (co)variation within and between floral and nonfloral traits? And (6) what is the relationship between the quantitative-genetic architecture of floral traits in the RILs vs. in the accessions?
MATERIALS AND METHODS
B. rapa L. (syn: B. campestris) is an annual (occasionally biennial) crop plant native to Eurasia that has been introduced in the Americas (Holm et al. 1997); naturalized populations typically develop where it is cultivated. Plants produce an erect stem with alternating cauline leaves and secondary branches. Flowers of B. rapa are yellow, perfect, and borne on indeterminate racemes, and individual flowers are composed of four sepals, four petals, six stamens (four long plus two short), and a compound pistil of two carpels. Although B. rapa plants are commonly obligate outcrossers due to a well-characterized sporophytic self-incompatibility system (Bateman 1955), some genotypes are capable of self-fertilization.
A segregating progeny of RILs was created utilizing two self-compatible genotypes of B. rapa (yellow sarson, R500, and the rapid cycling IMB211) (Iniguez-Luy et al. 2009, genotypic data of RILs available as supplementary material therein; RIL seeds publically available, http://www.brassica.info/resource/plants/mapping-populations.php). IMB211 was derived from the Wisconsin Fast Plant (WFP) population, a rapid-cycling population produced from 10 generations of selection for early flowering and rapid generation time (Williams and Hill 1986). The IMB211 genotype was produced by intermating WFPs and selecting for self-compatibility and high fecundity. This selection regime was followed by seven generations of selfing and single-seed descent. The artificial selection for rapid generation time and high fecundity in IMB211 is similar to that experienced by naturalized populations and agricultural weeds of this species (Dorn and Mitchell-Olds 1991; Mitchell-Olds 1996). Moreover, self-compatibility arises frequently in the subspecific clade to which R500 belongs (Zhao et al. 2005), a pattern also observed in ruderal/weed species (Baker 1965). The yellow sarson (R500) genotype is a cultivar planted in India for at least 3000 years (Hinata and Prakash 1984). In comparison with IMB211, R500 delays flowering and attains substantially greater biomass. Although they are often self-compatible (Zhao et al. 2005), yellow sarson plants produce flowers similar in size to self-incompatible varieties (Hinata et al. 1994). Sarson varieties significantly increase fruit and seed production in the presence of visiting insects (Mishra et al. 1988; Mishra and Kaushik 1992), suggesting moderate to high levels of outcrossing. In many regards, the IMB211 and R500 parental genotypes have experienced selection similar to other weed and crop B. rapa populations, and genetic variation segregating in the RILs used here may resemble that segregating in crop × wild hybrids found in nature (Adler et al. 1993).
The two parental genotypes were crossed to produce an F1 individual that was subsequently selfed. An F2 generation of 160 plants was established and advanced to the S5 generation via self-fertilization and single-seed decent with an expectation of at least 93.75% homozygosity on average genome-wide. Seeds of this S5 generation (used in two QTL mapping experiments described below) were bulked by selfing replicate plants of each RIL during January 2004 and 2007, depending on the experiment. In each bulking generation, plants were raised in 13-cm-diameter clay pots containing MetroMix 200 (Scotts, Marysville, OH) and ∼0.68 g of fertilizer (14-14-14 Osmocote; Scotts) in the University of Minnesota (St. Paul) greenhouses under supplemental lighting [12 hr light (L):12 hr dark (D)]. Flowers were self-pollinated by hand, and fruits were allowed to ripen for 2 weeks following plant senescence.
Field environment:
As part of a larger QTL mapping project exploring plant responses to variation in local density, seeds of 150 RILs were planted into density treatments in the agricultural fields at the University of Minnesota (April 19–21, 2004; St. Paul). Here, we report data from the competitive treatment (see below); for discussion of additional treatments see Dechaine et al. (2007). Each RIL was randomly assigned to 1 of 150 planting locations that were divided evenly among three subplots in each of three spatial blocks (i.e., 50 RILs per subplot × three subplots per block). We planted seeds of each RIL in a three-column by six-row configuration with 5 cm separating each of the 18 plants and 20 cm separating the next adjacent planting. All data were collected on the four central plants of the middle column (i.e., rows 2–5 for column 2). This design was chosen so that competing neighbors were of the same genotype, a situation common in natural populations due to passive seed dispersal as well as in crop settings. However, because replicates within the same subplot were grouped spatially, observed phenotypes are not statistically independent, and the group is referred to as replicate cluster in Statistical analyses. In sum, there are 12 replicate plants per RIL (three blocks × 4 replicates per block).
Over the growing season, we censused the four central plants for a variety of vegetative and reproductive traits, including hypocotyl length at bolting (stem length from the ground to cotyledons), longest leaf length at bolting, and flowering date. During flowering, we collected up to two newly opened flowers per focal plant; we predominantly sampled floral nodes four and five to limit developmental variation. Flowers were sampled between 1000 and 1300 hr, during which petals reflexed and anthers dehisced. Flowers were preserved in 70% ethanol and later processed in the lab (see below). Once plants had finished flowering and were ripening fruits (>50% of fruits were yellow), we measured primary inflorescence height and longest secondary branch length (hereafter, branch length). (For phenotypic data, see supporting information, File S1.)
Flowers were dissected under a stereomicroscope [Nikon (Tokyo) SMZ-800], and petals, stamens, and pistils were arranged flat on the stage. A digital image was recorded via a sideport-attached camera, and from these images, we measured petal length and width, midpoint length (base of the petal to the point at which the petal blade reflexes, i.e., the transition point between petal claw and petal limb), filament length (base of the filament to the anther), anther length, ovary length (from receptacle to the top of the ovary), and combined style–stigma length (from the top of the ovary to the top of the stigma). All floral-image measurements were processed with ImageJ (ver 1.31; Wayne Rasband, National Institutes of Health, Bethesda, MD).
Floral morphology in cultivated and wild B. rapa accessions:
To explore the level of genetic (co)variation in floral traits within cultivated and wild B. rapa populations during the common-garden field experiment, we obtained 20 accessions from the National Genetic Resources Program (for the 13 accessions that flowered, see Table S1). These accessions originate from the native range of B. rapa, including India and neighboring Eurasian countries (Table S1). Each accession was integrated into the common-garden field experimental design, and seeds were randomly planted with identical replication as described above. Flowers were collected and measured with the same methodology as for RILs (see above).
Greenhouse environment:
To examine the expression of floral and vegetative traits (and the covariation among traits) in a second, more benign environment, we raised RILs in the greenhouses at the University of Minnesota. On March 14, 2007, we planted seeds of each RIL into eight 7.6-cm square pots that were randomized across six blocks, such that each block had at least one replicate (but no more than two) of each RIL. Each block consisted of plants surrounded by a 314 × 72 × 70-cm rectangular polyvinylchloride frame on which laminated filters (Full Tough Spun filter, no. 214; LEE Filters, Burbank, CA) were suspended. These filters reduced photosynthetically active radiation by ∼40%, simulating the light available to plants during early development when grown under field conditions. Following 1 month of growth, plants were censused for a variety of early vegetative and phenological traits; here, we present hypocotyl length and the length and width of the second true leaf.
On April 17, 2007, we planted a second cohort of RILs in the greenhouse with the same design as above; however, each RIL was replicated in only six pots, one pot per block. In this second cohort, plants were raised under ambient light for 2 weeks prior to being placed under light filters. Plants were censused for flowering date, and newly opened flowers from nodes four and five were removed, preserved in 70% ethanol, and measured as described previously. Primary inflorescence height was measured when at least 50% of fruits were yellowing, indicating that plants were close to senescence.
Statistical analyses:
Quantitative genetic analysis of B. rapa traits:
Variation in the expression of floral vegetative and phenological traits in the field environment was analyzed using ANOVA (PROC MIXED, SAS v. 8.02). We included the following random factors in each model: line, subplot (as a spatial blocking term), and replicate cluster nested in the line × subplot term. The replicate cluster term was a unique identifier assigned to each planting location for each RIL and was included to account for lack of independence among the four replicate plants in one column. Some traits failed to meet assumptions of ANOVA, and prior to analysis, we utilized the Box–Cox transformation to identify transformations that improved normality. Using this ANOVA model, we calculated RIL best linear unbiased predictors (BLUPs) for each trait with significant genetic variation. These BLUPs were subsequently used to estimate bivariate genetic correlations between all traits measured in the field experiment (PROC CORR, SAS v. 8.02). Floral traits measured from wild and cultivated B. rapa accessions were analyzed with ANOVA models identical to those presented for RILs above. In our initial analyses, replicate cluster and subplot were nonsignificant for all floral traits and were subsequently pooled with the error term. Genotypic BLUPs were estimated for all floral traits and used to estimate bivariate genetic correlations between all floral traits (PROC CORR).
We applied the same statistical approach to data from B. rapa plants raised in the greenhouse environment. Using ANOVA, variation in measured traits was partitioned among the random factors block and line (PROC MIXED). Traits were again transformed on the basis of the Box–Cox procedure and, for each trait, BLUPs were estimated for the line term as RIL genotypic values. We calculated correlation matrices for all greenhouse traits as described above.
To determine if RILs differed in floral and nonfloral trait expression across field and greenhouse environments, we used a mixed-model ANOVA (PROC MIXED) to partition variation between the fixed effect, growth environment, and the following random factors: line and the line × environment interaction. Due to the different experimental designs used in the field and greenhouse environments, analyses were performed on plant residuals after accounting for spatial blocking factors within each environment.
To examine variation in the genetic architecture of B. rapa traits across environments, we tested for significant differences in standardized G-matrix structure across the field and greenhouse environments. We tested three separate hypotheses. First, we tested for differences in “floral” correlation matrices across environments; matrices were estimated using the following traits: petal width and the length of petal, filament, anther, ovary, and style–stigma. Second, we tested for differences between “floral–vegetative” correlation matrices estimated from floral traits (listed above), leaf length, and primary inflorescence height. Finally, we tested for differences between “floral–flowering phenology” correlation matrices, using floral traits (listed above) and days to flower. We include these specific nonfloral traits because they were measured in both environments and at comparable developmental stages; however, we test them in separate analyses because of the distinct functions of vegetative vs. phenological traits and because we were interested in identifying the traits underlying any matrix differences.
We employed Flury's hierarchical common principal components (CPC) analysis to test for differences between matrices (Flury 1988; Phillips and Arnold 1999). This procedure transforms G-matrices into eigenvectors and eigenvalues and then compares hierarchically related matrices. From the lowest hierarchical level, the procedure explores the following: unrelated structure, matrices do not share any eigenstructure; CPC(1), matrices share the first principal component; CPC(2), matrices share first and second principal components; …; CPC(p-2), where p is the number of traits per p × p matrix; full CPC, where matrices share all principal components but not eigenvalues (the variance explained by each principal component axis); proportional, where matrices share principal components but all eigenvalues differ by a single constant; and equality, where matrices share all elements of eigenstructure. We use the “jump-up” method for interpreting results (Phillips and Arnold 1999). This approach compares each level in the hierarchy of relatedness against a matrix of unrelated structure, and because each level in the hierarchy includes lower levels, testing stops when a significant difference is detected.
CPC matrix comparisons can be performed on either nonstandardized (covariance) or standardized (correlation) G-matrices. However, utilizing correlation matrices may be preferable when measurement scales differ among traits or across environments (Phillips and Arnold 1999). Here, variation in measured traits differed dramatically across environments, and because our interest was in exploring trait covariances, we standardized our data to genetic correlations. For example, flowering phenology variation in the greenhouse was 17.7 times greater than that expressed in the field, which could potentially overshadow differences across environments in floral–flowering phenology covariation. Finally, results utilizing the correlation matrix were more conservative (i.e., detected more matrix similarity) than when using variance–covariance matrices, which were all significantly different at the first principal component. For these reasons, we present analyses of standardized G-matrices. Because CPC analysis can be sensitive to normality, we confirmed initial findings with CPCrand (Phillips and Arnold 1999), which determines test significance via a randomization procedure. CPCrand and CPC findings were always identical; we present the CPC results. To corroborate our CPC results, we estimated multivariate G-matrices (PROC MIXED) from phenotypic data and tested whether a common G-matrix provided a better fit to the data than separate G-matrices for the field and greenhouse environments (e.g., Stinchcombe et al. 2009). Results of the mixed-model analyses were consistent with those from the CPC analyses, and therefore only the latter analyses are presented.
The CPC and mixed-model analyses examine differences in the multivariate relationship among traits. We used Fisher's Z-tests to identify bivariate correlations that differed significantly across field and greenhouse environments and, therefore, contributed to matrix differences.
Linkage map construction and QTL mapping:
We used JoinMap 3.0 (Van Ooijen and Voorrips 2001) to estimate the initial linkage map (N = 215 markers) in all 160 RILs of B. rapa (for genotypic data of RILs, see Iniguez-Luy et al. 2009). Linkage groups were determined using a LOD score between 5 and 8 and a recombination fraction of 0.4. We used the Kosambi mapping function when estimating mapping distances. Due to the loss of RILs in both the field and the greenhouse environments, we reestimated the marker locations (in centimorgans) for RILs that were present in either of the two environments (N = 153) using R/qtl (Broman et al. 2003), which maintains the original marker order as estimated for the whole population in JoinMap.
We identified QTL affecting floral, vegetative, and phenological traits using composite interval mapping (Zeng 1994) as estimated in QTL cartographer (QTLcart v. 2.5; Wang et al. 2007). The CIM procedure tests the hypothesis that a QTL resides in the interval defined by two adjacent markers, while statistically controlling for additional QTL segregating elsewhere in the genome. All QTL mapping analyses (here and below) were performed on genotypic BLUP values (or back-transformed BLUPs when appropriate). We used a CIM testing interval (walking speed) of 2 cM and a window size for excluding background QTL (i.e., nearest markers) of 5 cM. Background QTL were determined using the forward–backward stepwise regression method (P-values set to 0.05) under the standard model (model 6). A genome-wide significance threshold (type I error rate, ∝ = 0.05) was estimated for each trait with 2000 random permutations of the data set (Doerge and Churchill 1996). We calculated 2-LOD support limit intervals for the location of each significant QTL (i.e., the peak likelihood ratio) as the flanking markers where the LR dropped by ∼9.22 (Van Ooijen 1992). To formally test for possible QTL × environment interaction effects (i.e., a shift in the detection of, or magnitude of effect of, QTL across environments), we selected the closest markers to significant QTL in each environment and included all markers as well as two-way marker × environment interactions as main effects in an ANOVA model for each trait (PROC GLM, SAS v. 8.02). Specifically, a QTL may have a significant phenotypic effect in a genome-wide scan in one environment, but have only a minor and statistically undetectable effect in a second environment due to low power. The ANOVA described above distinguishes true QTL × environment interactions from statistical artifacts.
We also tested for the influence of epistatic interactions (i.e., QTL × QTL interaction effects) on each trait using the scantwo procedure in R/qtl (Broman et al. 2003). We used the Haley–Knott regression method (Haley and Knott 1992) to test all possible marker × marker interactions on all traits using a 2-cM testing interval. To determine a genome-wide significance threshold, we permuted the data 1000 times per trait. We also used Epistacy (Holland 1998) to test for QTL × QTL epistasis and confirm results of the scantwo procedure; this program tests the influence of all possible pairwise combinations of markers on each trait in SAS (PROC GLM). To control for multiple comparisons, the authors of Epistacy recommend adjusting the P-value threshold to ∝ = 0.05/[g(g − 1)/2] (Holland 1998), where g is the number of linkage groups (for B. rapa N = 10 and ∝ = 0.001). A slightly more conservative threshold (∝ = 0.0001) resulted in comparable results between these two methods; we report the scantwo results.
For significant epistatic interactions, we formally tested the hypothesis that QTL × QTL interactions differ across environments. We used ANOVA (PROC GLM), and for each significant epistatic interaction, we included markers closest to epistatic QTL positions, the two-way marker × marker interaction, and the three-way marker × marker × environment interaction (i.e., the QTL × QTL × E interaction).
Contribution of main-effect QTL to genetic correlations:
To compare the genetic architecture estimated by the G-matrix to architecture estimated from QTL mapping, we calculated the bivariate genetic correlation (rQ) attributable to QTL affecting trait pairs (Falconer and Mackay 1996). We follow the calculation of rQ described in Gardner and Latta (2007) (see also Kelly 2009) as
 |
where p and q are the frequencies of alleles at a QTL locus (i), ai(Z1) and ai(Z2) are the additive effects of QTL locus i on the two traits (Z1 and Z2), and these estimates of covariance (numerator) and trait variances (denominator) are summed across all QTL that affect one (or both) of the traits in the bivariate pair. Our inclusion of QTL detected for only one of the two traits allows for incorporation of possible “minor” QTL that were not formally significant at the genome-wide threshold. This estimate of genetic correlation assumes no dominance (an assumption met in RILs where heterozygotes are not present), no linkage disequilibrium between QTL, and no epistasis. We estimated rQ for all trait pairs with significant genetic correlations. We calculated the correlation between rG and rQ in each environment (PROC CORR) to evaluate the extent to which mapped QTL account for genotypic correlations.
RESULTS
Quantitative genetics:
We detected significant genetic variation in this population of RILs for all measured traits under both field and greenhouse conditions (Table 1; for full ANOVA results see Table S2 and Table S3). Similarly, we detected significant line × environment interactions for all measured traits (Table 1; for full ANOVA results, see Table S4), indicating genetic variation for plasticity of floral and nonfloral traits. In general, RILs growing in the field produced smaller floral and vegetative organs and flowered later in comparison to those raised in the greenhouse (Figure 1). For all traits, we detected evidence of transgressive segregation; that is, the range of trait expression among RILs exceeded that of the parental lines (e.g., hypocotyl length, Figure 1). Broad-sense heritability was lower when estimated from RILs growing in the field (floral mean 0.30, range 0.23–0.41; nonfloral mean 0.20, range 0.07–0.35; Table 1) than from RILs growing under greenhouse conditions (floral mean 0.43, range 0.36–0.55; nonfloral mean 0.49, range 0.36–0.62; Table 1).
TABLE 1.
ANOVA results partitioning variation in Box–Cox-transformed phenotypic traits among lines (i.e., RILs; for full ANOVA see Table S2 and Table S3) and associated quantitative genetic parameters of variance components (VG and VP) and broad sense heritability (H2) for B. rapa RILs growing in field and greenhouse environments
| Field environment |
Greenhouse environment |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Trait | Line significance | VG | VP | H2 | Line significance | VG | VP | H2 | Line × environment | Across-environment correlation |
| Hypocotyl Ln | *** | 0.06 | 0.71 | 0.09 | ***** | 27.88 | 59.95 | 0.47 | ***** | 0.42***** |
| Leaf Ln | ***** | 0.53 | 2.16 | 0.25 | ***** | 0.0045 | 0.012 | 0.39 | *** | 0.62***** |
| Leaf Wd | NA | NA | NA | NA | ***** | 0.0049 | 0.014 | 0.36 | NA | NA |
| Branch Ln | ***** | 4.31 | 18.27 | 0.24 | NA | NA | NA | NA | NA | NA |
| Primary inflorescence height | ***** | 5.49 | 15.79 | 0.35 | ***** | 271.68 | 462.79 | 0.59 | **** | 0.59***** |
| Days to flower | ** | 2.37 | 31.80 | 0.07 | ***** | 13.04 | 21.01 | 0.62 | ***** | 0.17* |
| Petal Ln | ***** | 0.29 | 0.91 | 0.32 | ***** | 0.0092 | 0.025 | 0.38 | **** | 0.48***** |
| Midpoint Ln | ***** | 0.040 | 0.16 | 0.25 | ***** | 0.022 | 0.061 | 0.36 | **** | 0.42***** |
| Petal Wd | ***** | 0.0024 | 0.0073 | 0.33 | ***** | 0.016 | 0.029 | 0.55 | *** | 0.65***** |
| Filament Ln | ***** | 0.68 | 2.34 | 0.29 | ***** | 0.37 | 1.0 | 0.37 | ***** | 0.39***** |
| Anther Ln | ***** | 0.039 | 0.096 | 0.41 | ***** | 0.48 | 0.90 | 0.53 | ***** | 0.56***** |
| Ovary Ln | ***** | 0.0083 | 0.029 | 0.29 | ***** | 0.59 | 1.38 | 0.43 | ***** | 0.38***** |
| Style–stigma Ln | ***** | 0.030 | 0.13 | 0.23 | ***** | 0.0033 | 0.0079 | 0.42 | **** | 0.43***** |
From an additional ANOVA, the line × environment interaction (for full ANOVA see Table S4) tests for evidence of genetic variation in trait plasticity across environments (minimum number of RILs common to both environments; N = 112). *P = 0.0779; **P = 0.0548; ***P < 0.01; ****P < 0.001; *****P < 0.0001. Ln, length; Wd, width (throughout tables).
Figure 1.—
Back-to-back histograms of genotypic trait values of B. rapa RILs when grown in the field (left side, open bars) and greenhouse (right side, shaded bars) environments. Parental trait means are designated by arrows (I, IMB211; R, R500). A few plots have data for only one side, because some trait distributions could not be illustrated on the same axis or because a few traits were measured in only one environment.
CPC comparisons of correlation matrices composed of floral traits were marginally significant for the fourth principal component [CPC4, χ2 = 22.8, d.f. = 14, P ≤ 0.0638; i.e., matrices share the first three principal components (PCs) but differ at the fourth of six PCs]. The first three PCs that are shared between field and greenhouse environments explain 80% of the variation among the traits. Thus, the correlation matrices differ across field and greenhouse environments, but only once significant variation is explained. Genetic correlation matrices of floral–vegetative traits differed across environments (CPC5, χ2 = 44.4, d.f. = 27, P = 0.0188; i.e., matrices share four of eight PCs), and a large number of bivariate correlations differed across environments (see Fisher's Z-tests below). Finally, the floral–flowering time correlation matrices differed significantly at the second principal component across environments (CPC2, χ2 = 19.6, d.f. = 11, P ≤ 0.0506; i.e., matrices share only one of seven PCs), and nearly half of the bivariate correlations differed across environments.
We detected strong positive genetic correlations among floral traits within the field and greenhouse environments (Table 2). Floral–floral genetic correlations were largely similar across environments with only 3 significant differences (of 21 possible) in the floral correlation matrix (Table 2). Similarly, the vegetative traits, leaf length and primary inflorescence height, were positively correlated in this RIL population and did not significantly differ across environments. Interestingly, anther length was positively correlated with two vegetative traits (leaf length and primary inflorescence height) when grown in the field, as were, to a lesser degree, midpoint and style–stigma length (Table 2, top right, italics). Contributing to matrix differences detected in CPC analyses, significant floral–vegetative correlations were more numerous and stronger for plants growing in the greenhouse (Table 2, bottom left, italics), including all floral traits except petal width. Fisher's Z-tests indicate that 9 of 14 possible pairwise correlations between floral traits and either leaf length or inflorescence height differed significantly across environments. Also consistent with CPC results, correlations between floral traits and flowering phenology were nonsignificant in the field, but with the exception of petal width, all floral traits were significantly positively correlated with phenology in the greenhouse. Fisher's Z-tests indicate that 3 of 7 possible bivariate correlations between floral traits and phenology were significant (including midpoint and anther length as well as petal width due to the reversal in sign across environments).
TABLE 2.
Genotypic correlations of floral, vegetative, and phenological traits for B. rapa RILs raised in the field (above diagonal) and greenhouse (below diagonal) environments
| rG | Hy L | Lf L | Br L | PI H | DTF | Pet L | Mid L | Pet W | Fil L | An L | Ov L | Sty L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hypocotyl Ln (Hy L) | −0.08 | 0.02 | 0.04 | −0.14 | 0.02 | 0.02 | 0.00 | −0.08 | 0.01 | −0.01 | −0.20* | |
| Leaf Ln (Lf L) | 0.17 | 0.54** | 0.64** | −0.23* | 0.14 | 0.26* | −0.06 | 0.05 | 0.29** | 0.04 | 0.11 | |
| Branch Ln (Br L) | NA | NA | 0.77** | −0.41** | 0.20* | 0.21* | 0.18* | 0.07 | 0.40** | 0.14 | 0.28* | |
| Primary inflorescence height (PI H) | 0.15 | 0.61** | NA | −0.38** | 0.11 | 0.21* | −0.01 | 0.04 | 0.41** | 0.07 | 0.18* | |
| Days to flower (DTF) | −0.33** | 0.35** | NA | 0.52** | 0.13 | 0.08 | 0.11 | 0.14 | −0.16 | 0.04 | 0.16 | |
| Petal Ln (Pet L) | 0.08 | 0.40** | NA | 0.46** | 0.35** | 0.75** | 0.67** | 0.75** | 0.55** | 0.62** | 0.38** | |
| Midpoint Ln (Mid L) | 0.09 | 0.47** | NA | 0.46** | 0.39** | 0.79** | 0.34** | 0.64** | 0.51** | 0.54** | 0.31* | |
| Petal Wd (Pet W) | 0.02 | 0.14 | NA | 0.09 | −0.15 | 0.41** | 0.05 | 0.41** | 0.31** | 0.37** | 0.22* | |
| Filament Ln (Fil L) | 0.03 | 0.21* | NA | 0.29** | 0.26* | 0.75** | 0.74** | 0.20* | 0.55** | 0.49** | 0.23* | |
| Anther Ln (An L) | 0.27* | 0.5** | NA | 0.57** | 0.23* | 0.67** | 0.50** | 0.33** | 0.39** | 0.39** | 0.35** | |
| Ovary Ln (Ov L) | 0.17 | 0.47** | NA | 0.48** | 0.22* | 0.73** | 0.60** | 0.24* | 0.60** | 0.58** | 0.26* | |
| Style–stigma Ln (Sty L) | 0.03 | 0.36** | NA | 0.34** | 0.38** | 0.53** | 0.46** | 0.20* | 0.42** | 0.41** | 0.35** |
Bivariate correlation significance is indicated with superscripts and significant differences in bivariate correlations across environments (Fisher's Z-tests) are indicated in boldface type. Italics designate floral–nonfloral correlations; *P < 0.05; **P < 0.001. Boldface type indicates Fisher's Z-test significant at P < 0.05.
QTL mapping:
We list all QTL identified for floral, vegetative, and phenology traits in Tables 3 and 4 for field and greenhouse environments, respectively (Figure 2; see Table S5 for markers closest to QTL in Tables 3 and 4). We detected a total of 27 main-effect QTL in the field environment; 8 QTL influenced multiple traits, of which 3 QTL influenced floral and vegetative traits (FQTL 3-2, which affected inflorescence and anther lengths; FQTL 6-1, which affected branch length, filament length, petal width, and petal length; and FQTL 6-2, which affected inflorescence and anther lengths). In the greenhouse, we detected 29 total main-effect QTL; 8 QTL affected multiple phenotypic traits, of which 1 QTL (GQTL 6-3) coregulated floral and nonfloral traits (inflorescence length, leaf width and length, and anther length).
TABLE 3.
QTL identified for floral, vegetative, and phenological traits for B. rapa RILs grown under field conditions
| QTL | Trait | Chr | cM | LOD | 2-LOD range (cM) | PVE | a0 | QTL × E |
|---|---|---|---|---|---|---|---|---|
| FQTL1-1 | Anther Ln | 1 | 20.2 | 4 | (15.2, 28.3) | 8.4 | −0.049 | NS |
| Petal Wd | 1 | 21.7 | 2.9 | (16.5, 26.3) | 6.3 | −0.091 | NS | |
| FQTL1-2 | Days To flower | 1 | 32.8 | 3.2 | (26.3, 46.3) | 8.8 | 0.24 | NS |
| FQTL2-1 | Leaf Ln | 2 | 2.0* | 2.7 | (0.0, 4.0) | 6.2 | −1.87 | NS |
| FQTL2-2 | Leaf Ln | 2 | 52.9 | 2.9 | (47.4, 66.4) | 7 | −2.04 | NS |
| FQTL3-1 | Ovary Ln | 3 | 19.2 | 3.5 | (0, 25.5) | 6.9 | 0.08 | 0.0039 |
| FQTL3-2 | Primary inflorescence height | 3 | 33.3 | 4.4 | (25.5, 37.8) | 13.1 | −21.26 | 0.0398 |
| Anther Ln | 3 | 33.3 | 6.9 | (27.1, 39.8) | 9 | −0.052 | NS | |
| FQTL3-3 | Anther Ln | 3 | 77.1 | 4.8 | (72.6, 79.4) | 9.7 | −0.056 | NS |
| Petal Ln | 3 | 77.1 | 3.7 | (72.6, 85.0) | 7.6 | −0.13 | NS | |
| Filament Ln | 3 | 79.1 | 2.8 | (66.9, 85.0) | 5.5 | −0.088 | NS | |
| FQTL3-4a | Midpoint Ln | 3 | 86.5 | 2.9 | (79.1, 93.7) | 5.5 | −0.038 | NS |
| FQTL3-5a | Petal Wd | 3 | 91 | 3.1 | (86.5, 101.7) | 6.7 | 0.074 | 0.0083 |
| FQTL5-1 | Style–stigma Ln | 5 | 0 | 4.0 | (0.0, 12.0) | 7.5 | −0.04 | NS |
| FQTL5-2 | Petal Wd | 5 | 21.4 | 3.4 | (14.0, 28.4) | 7.4 | −0.076 | NS |
| FQTL6-1 | Filament Ln | 6 | 22.8 | 6.0 | (17.1, 31.6) | 5.7 | −0.087 | 0.0571 |
| Branch Ln | 6 | 22.8 | 2.9 | (17.1, 27.6) | 13.1 | −14.78 | — | |
| Petal Wd | 6 | 24.3 | 3.3 | (15.4, 32.1) | 7.4 | −0.077 | 0.0196 | |
| Petal Ln | 6 | 24.3 | 3.3 | (15.4, 32.1) | 7 | −0.12 | NS | |
| FQTL6-2 | Primary inflorescence height | 6 | 44.8 | 3.9 | (39.5, 61.0) | 6.7 | −15.06 | NS |
| Anther Ln | 6 | 46.8 | 5.1 | (40.6, 69.0) | 10.4 | −0.058 | NS | |
| FQTL7-1 | Branch Ln | 7 | 0 | 4.3 | (0.0, 10.0) | 8.7 | −13.62 | — |
| FQTL7-2a | Ovary Ln | 7 | 23.5 | 3.8 | (15.4, 29.2) | 7.5 | 0.085 | NS |
| FQTL7-3a | Filament Ln | 7 | 29.2 | 3.0 | (23.5, 37.8) | 6 | 0.087 | 0.0624 |
| Midpoint Ln | 7 | 29.2 | 4.3 | (17.7, 37.8) | 8.5 | 0.047 | NS | |
| FQTL7-4a | Petal Ln | 7 | 39.8 | 3.9 | (37.2, 43.5) | 9.1 | 0.17 | NS |
| FQTL7-5 | Hypocotyl Ln | 7 | 58.5† | 2.6 | (51.8, 59.3) | 7.3 | −0.25 | NS |
| FQTL8-1 | Ovary Ln | 8 | 10.4 | 4.6 | (0.4, 26.8) | 11.9 | 0.11 | 0.0248 |
| FQTL8-2 | Style–stigma Ln | 8 | 34.5 | 2.8 | (28.0, 34.5) | 5.6 | −0.033 | 0.0495 |
| FQTL9-1a | Petal Ln | 9 | 7.6 | 4.2 | (0.0, 12.5) | 9.7 | −0.14 | NS |
| FQTL9-2a | Midpoint Ln | 9 | 18.5 | 3.1 | (11.6, 23.1) | 6 | −0.039 | NS |
| FQTL9-3a | Primary inflorescence heightt | 9 | 22.7 | 3.7 | (14.5, 28.6) | 6.7 | −15.72 | NS |
| FQTL9-4 | Hypocotyl Ln | 9 | 37.3 | 3.8 | (31.5, 44.8) | 10.1 | 0.26 | NS |
| Leaf Ln | 9 | 38.7 | 3.8 | (35.3, 44.8) | 8.5 | −3.03 | NS | |
| FQTL9-5 | Ovary Ln | 9 | 61.8 | 3.1 | (52.3, 66.4) | 5.9 | −0.083 | NS |
| Midpoint Ln | 9 | 61.8 | 2.8 | (52.3, 66.4) | 6.1 | −0.039 | NS | |
| Filament Ln | 9 | 63.3 | 4.1 | (52.3, 66.4) | 8.5 | −0.1 | NS | |
| FQTL10-1 | Hypocotyl Ln | 10 | 0 | 3.6 | (0.0, 11.2) | 9.6 | 0.25 | NS |
| FQTL10-2 | Style–stigma Ln | 10 | 29.4 | 3.2 | (21.9, 34.7) | 7 | −0.039 | NS |
Traits influenced by each QTL are listed along with chromosome, position, LOD score, 2-LOD support limits, percentage of variance explained by each QTL, additive effect (positive values indicate that IMB211 alleles increase trait means), and P-values from ANOVA that tested if QTL differ in their effect on a trait across environments. *Genome-wide significance threshold P < 0.075.
QTL assignment based on 1-LOD confidence intervals.
TABLE 4.
QTL identified for floral, vegetative, and phenological traits for B. rapa RILs grown in the greenhouse
| QTL | Trait | Chr | cM | LOD | 2-LOD range (cM) | PVE | a0 | QTL × E |
|---|---|---|---|---|---|---|---|---|
| GQTL1-1a | Petal Wd | 1 | 13.2 | 4.1 | (8.3, 18.4) | 7.2 | −0.13 | NS |
| GQTL1-2a | Anther Ln | 1 | 18.4 | 4.0 | (13.2, 26.3) | 8.5 | −0.056 | NS |
| GQTL1-3 | Primary inflorescence height | 1 | 30.3 | 6.1 | (24.9, 36.3) | 10.7 | −33.7 | 0.0484 |
| Leaf Wd | 1 | 32.1* | 2.8 | (24.9, 48.7) | 5.4 | −0.97 | — | |
| GQTL2-1 | Anther Ln | 2 | 26.4 | 3.6 | (19.2, 35.6) | 8.3 | −0.056 | NS |
| Midpoint Ln | 2 | 27.5 | 3.3 | (20.0, 35.6) | 6.1 | −0.058 | 0.021 | |
| GQTL2-2a | Style–stigma Ln | 2 | 43.8 | 3.6 | (36.9, 55.1) | 6.9 | −0.066 | 0.0128 |
| GQTL2-3a | Leaf Wd | 2 | 55.4 | 4.1 | (42.0, 65.1) | 7 | −1.1 | — |
| GQTL2-4 | Hypocotyl Ln | 2 | 76.7* | 2.7 | (63.1, 87.3) | 6.7 | 1.3 | 0.0164 |
| GQTL3-1 | Petal Ln | 3 | 19.2 | 2.9 | (6.0, 25.5) | 7.3 | −0.13 | 0.0398 |
| Anther Ln | 3 | 23.2 | 4.8 | (8.0, 35.8) | 10.2 | −0.063 | NS | |
| GQTL3-2 | Primary inflorescence height | 3 | 40 | 4.0 | (33.8, 47.6) | 6.5 | −28.11 | 0.0398 |
| GQTL3-3 | Anther Ln | 3 | 66.1 | 3.2 | (55.2, 72.6) | 8.3 | −0.057 | NS |
| GQTL3-4a | Petal Ln | 3 | 79.4 | 2.8 | (74.0, 105.7) | 6.3 | −0.13 | NS |
| GQTL3-5a | Petal Wd | 3 | 91 | 3.9 | (86.5, 103.7) | 14 | 0.18 | 0.0083 |
| Midpoint Ln | 3 | 91 | 7.4 | (83.4, 97.7) | 7.3 | −0.065 | NS | |
| GQTL4-1 | Midpoint Ln | 4 | 31.7 | 3.4 | (24.3, 36.5) | 6.7 | −0.061 | NS |
| GQTL4-2 | Hypocotyl Ln | 4 | 57.4 | 2.8 | (47.3, 65.7) | 7.9 | −1.4 | 0.0222 |
| GQTL6-1a | Petal Wd | 6 | 22.4 | 3.1 | (15.4, 32.1) | 5.3 | −0.11 | 0.0196 |
| GQTL6-2a | Anther Ln | 6 | 36.1 | 3.2 | (31.6, 43.0) | 8.2 | −0.056 | NS |
| Ovary Ln | 6 | 37 | 3.4 | (31.6, 42.3) | 7.2 | −0.1 | NS | |
| GQTL6-3a | Anther Ln | 6 | 40.3 | 4.1 | (39.6, 43.0) | 10 | −0.063 | NS |
| Leaf Wd | 6 | 42.3 | 7.1 | (37.5, 47.0) | 15.1 | −1.6 | — | |
| Primary inflorescence height | 6 | 42.3 | 6.2 | (39.5, 57.0) | 10.3 | −33.87 | NS | |
| Leaf Ln | 6 | 46.8 | 11.5 | (40.3, 55.0) | 25.4 | −5.4 | 0.0088 | |
| GQTL7-1 | Petal Wd | 7 | 15.4 | 3.2 | (6.0, 23.0) | 5.6 | −0.11 | 0.0125 |
| GQTL7-2 | Midpoint Ln | 7 | 41.5 | 5.3 | (29.2, 44.9) | 9.9 | 0.081 | NS |
| GQTL7-3 | Midpoint Ln | 7 | 58.5 | 4.8 | (51.8, 59.3) | 9.7 | −0.08 | NS |
| GQTL8-1 | Petal Wd | 8 | 10.4* | 2.8 | (0, 18.8) | 5.5 | 0.11 | NS |
| GQTL8-2 | Style–stigma Ln | 8 | 30.5 | 2.9 | (18.8, 34.5) | 5.5 | −0.056 | 0.0495 |
| GQTL9-1 | Days to flower | 9 | 2.0* | 2.6 | (0, 5.6) | 5 | −0.77 | 0.0034 |
| GQTL9-2a | Primary inflorescence height | 9 | 22 | 6.2 | (12.5, 27.1) | 10.4 | −34.42 | NS |
| GQTL9-3a | Petal Wd | 9 | 33.3 | 3.1 | (23.1, 38.0) | 5.5 | −0.11 | NS |
| GQTL9-4a | Midpoint Ln | 9 | 37.3 | 3.8 | (35.3, 44.7) | 7.2 | −0.094 | NS |
| GQTL9-5a | Ovary Ln | 9 | 46 | 4.2 | (38.7, 53.8) | 9 | −0.12 | NS |
| Filament Ln | 9 | 52.3 | 5.5 | (38.7, 66.4) | 13.2 | −0.11 | NS | |
| GQTL10-1 | Midpoint Ln | 10 | 2.0* | 2.7 | (0.0, 11.2) | 5.2 | −0.055 | 0.0282 |
| GQTL10-2 | Days to flower | 10 | 25.4 | 11.7 | (17.9, 29.4) | 26.1 | −1.77 | <0.0001 |
| Primary inflorescence height | 10 | 29.4 | 2.9 | (27.1, 35.8) | 8.07 | −29.83 | 0.0003 | |
| Leaf Ln | 10 | 29.4 | 4.8 | (13.9, 29.7) | 8.1 | −4.3 | NS | |
| Hypocotyl Ln | 10 | 30.4 | 8.9 | (17.9, 34.7) | 19.8 | 2.3 | 0.0003 |
Traits influenced by each QTL are listed along with chromosome, position, LOD score, 2-LOD support limits, percentage of variance explained by each QTL, additive effect (positive values indicate that IMB211 alleles increase trait means), and P-values from ANOVA that tested if QTL differ in their effect on a trait across environments. *Genome-wide significance threshold P < 0.075.
QTL assignment based on 1-LOD confidence intervals.
Figure 2.—
Genomic locations of QTL identified for floral, vegetative, and phenological traits of B. rapa RILs raised in (A) field and (B) greenhouse environments. Chromosome number (A1–A10, international nomenclature) is listed at the top of each linkage group and position (in centimorgans) is detailed on the left. Phenotypic traits are listed next to estimated QTL position and 2-LOD support limits. Floral traits are in uppercase and nonfloral traits are in lowercase.
In total for each trait, QTL in the field account for between 20.1 and 37.5% (style–stigma length and anther length, respectively; floral mean 29.0%) of the total genetic variation in floral traits and between 8.8 and 27.0% (days to flower and hypocotyl length, respectively; nonfloral mean 21.2%) of the variation in nonfloral traits. For RILs growing in the greenhouse, QTL together account for between 12.4 and 52.2% (style–stigma length and midpoint length, respectively; floral mean 29.2%) of the total genetic variation in floral traits and between 27.6 and 45.9% (leaf width and primary inflorescence height, respectively; nonfloral mean 34.5%) of the variation in nonfloral traits.
The effect of 21 QTL regulating floral and nonfloral traits varied across the field and greenhouse environments (QTL × E interaction; Tables 3 and 4). In 17 instances, QTL affected traits in only one environment (4 and 13 environment-specific QTL from the field and the greenhouse, respectively). For example, FQTL 3-1 and FQTL 8-1 regulated ovary length only in the field. In four cases, a QTL regulating the same trait [e.g., petal width QTL (FQTL 3-5 and GQTL 3-5)] was detected in both the field and the greenhouse environments; however, the degree of influence of the QTL differed across environments. Interestingly, slightly different loci contribute to positive floral–vegetative genotypic correlations observed in both environments. For instance, GQTL 6-3 shows a significant QTL × E interaction for leaf length, indicating that this QTL contributes to the observed correlation with anther length only in the greenhouse environment.
In genome-wide scans, we detected significant QTL × QTL epistasis in the field and the greenhouse (Table 5; see Table S6 for markers closest to QTL). In the field, six epistatic interactions influenced four traits (one floral and three vegetative), individually accounting for between 9.5 and 12.5% of the variation for these traits. For RILs grown in the greenhouse, we detected eight epistatic interactions for seven measured traits (five floral and two vegetative); QTL × QTL interactions individually account for between 10.5 and 13.9% of the trait variation. Interestingly, the epistatic interactions between markers on chromosome 2 and chromosome 10 influenced four floral traits (petal, midpoint, filament, and ovary lengths), suggesting that in the greenhouse these traits are partially regulated by pleiotropic epistatic interactions (Figure S1). Three of these pleiotropic epistatic interactions differed significantly across environments (QTL × QTL × E interaction; Table 5). We also detected significant QTL × QTL × E interactions for primary inflorescence height and anther length, indicating that epistatic interactions influenced these traits in only the field and the greenhouse, respectively.
TABLE 5.
Epistatic interactions influencing floral and vegetative traits detected in A) a common garden field experiment and B) a greenhouse experiment using B. rapa RILs
| Marker A |
Marker B |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Trait | Chr | Position (cM) | Chr | Position (cM) | PVE (%) | 4i |
 00 00
|
 02 02
|
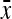 20 20
|
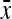 22 22
|
QTL × QTL × E |
| Field | |||||||||||
| Leaf Ln | 5 | 34 | 7 | 8 | 12.5 | 10.8 | 53.6 (±1.4) | 49.4 (±1.8) | 47.7 (±1.4) | 54.2 (±1.5) | NS |
| Branch Ln | 2 | 20 | 5 | 8 | 9.5 | −14.5 | 213.0 (±8.1) | 166.6 (±8.1) | 167.8 (±6.4) | 173.1 (±5.3) | — |
| Branch Ln | 2 | 36 | 8 | 28 | 11.1 | −54.2 | 163.8 (±8.7) | 198.6 (±6.7) | 185.1 (±6.4) | 165.7 (±5.7) | — |
| Branch Ln | 3 | 8* | 6 | 72* | 10.5 | 11.8 | 187.0 (±6.5) | 166.9 (±6.2) | 167.4 (±7.5) | 201.3 (±9.0) | — |
| Primary inflorescence height | 3 | 4 | 6 | 72 | 12.4 | 83.5 | 237.1 (±9.1) | 204.6 (±8.8) | 201.7 (±10.6) | 252.6 (±12.7) | 0.0009 |
| Style–stigma Ln | 4 | 48* | 9 | 66* | 12.1 | −0.2 | 1.8 (±0.03) | 1.9 (±0.02) | 1.9 (±0.02) | 1.8 (±0.02) | NS |
| Greenhouse | |||||||||||
| Leaf Ln | 4 | 4 | 8 | 34 | 10.9 | 13.7 | 74.8 (±1.5) | 70.1 (±1.8) | 68.0 (±2.0) | 77.1 (±2.0) | NS |
| Leaf Wd | 3 | 34 | 9 | 56 | 12.6 | 5.9 | 29.4 (±0.7) | 25.6 (±0.7) | 24.8 (±0.8) | 26.9 (±0.6) | — |
| Petal Ln | 2 | 78 | 10 | 46 | 13.7 | −0.7 | 7.6 (±0.08) | 7.9 (±0.08) | 8.1 (±0.10) | 7.7 (±0.09) | 0.0508 |
| Petal Ln | 4 | 56 | 5 | 50 | 11.4 | 0.6 | 8.0 (±0.08) | 7.8 (±0.08) | 7.6 (±0.10) | 8.0 (±0.07) | NS |
| Midpoint Ln | 2 | 76 | 10 | 42 | 13.6 | −0.4 | 3.1 (±0.04) | 3.2 (±0.04) | 3.3 (±0.05) | 3.1 (±0.04) | 0.0108 |
| Filament Ln | 2 | 78 | 10 | 48 | 10.5 | −0.4 | 4.0 (±0.05) | 4.0 (±0.05) | 4.3 (±0.06) | 3.9 (±0.05) | NS |
| Anther Ln | 3 | 86 | 4 | 64 | 15.0 | −0.3 | 2.4 (±0.03) | 2.6 (±0.04) | 2.4 (±0.03) | 2.3 (±0.03) | 0.0437 |
| Ovary Ln | 2 | 78 | 10 | 42 | 13.9 | −0.6 | 4.3 (±0.06) | 4.6 (±0.06) | 4.7 (±0.08) | 4.4 (±0.07) | 0.0014 |
Chromosome and positions of interacting QTL are listed along with the percentage of variance explained by the interaction, the epistatic effect (4i), and traits means (±SE) of each combination of IMB211 alleles (designated as 2) and R500 alleles (designated as 0). The final column tests the hypothesis that epistatic interactions differ in their effect on traits across environments (i.e., QTL × QTL × E). *P-value <0.07.
Contribution of main-effect QTL to genetic correlations:
Genetic correlations based on identified QTL (rQ; Table 6) were strongly positively correlated with those estimated from trait genotypic means (Table 2; field, r = 0.81, P < 0.0001; greenhouse, r = 0.78, P < 0.0001); that is, mapped QTL largely account for bivariate genotypic correlations. Despite the strong association between rQ and rG for many trait pairs, some rQ under- or overestimate rG, presumably because some QTL of small effect were not identified or because epistasis and LD are not accounted for in the calculation of rQ.
TABLE 6.
Genetic correlations based on the additive effect of QTL (rQ) identified for vegetative, phenological, and floral traits of B. rapa RILs raised in the field (above diagonal) and in the greenhouse (below diagonal)
| rQ | Hy L | Lf L | Br L | PI H | DTF | Pet L | Mid L | Pet W | Fil L | An L | Ov L | Sty L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hypocotyl Ln (Hy L) | — | — | — | — | — | — | — | — | — | — | −0.15 | |
| Leaf Ln (Lf L) | — | 0.51 | 0.75 | −0.41 | — | −0.07 | — | — | 0.33 | — | — | |
| Branch Ln (Br L) | NA | NA | 0.51 | −0.38 | 0.34 | 0.21 | 0.70 | — | 0.27 | — | 0.03 | |
| Primary inflorescence height (PI H) | — | 0.78 | NA | −0.55 | — | 0.13 | — | — | 0.81 | — | −0.17 | |
| Days to flower (DTF) | −0.63 | 0.68 | NA | 0.62 | — | — | — | — | — | — | — | |
| Petal Ln (Pet L) | — | 0.18 | NA | 0.61 | 0.62 | 0.78 | 0.71 | 0.80 | 0.61 | 0.61 | 0.33 | |
| Midpoint Ln (Mid L) | — | 0.26 | NA | 0.25 | 0.24 | 0.58 | 0.23 | 0.82 | 0.19 | 0.46 | 0.31 | |
| Petal Wd (Pet W) | — | — | NA | — | — | 0.11 | — | 0.47 | 0.61 | 0.24 | 0.25 | |
| Filament Ln (Fil L) | — | 0.53 | NA | 0.22 | 0.33 | 0.44 | 0.70 | −0.10 | 0.35 | 0.53 | 0.58 | |
| Anther Ln (An L) | 0.26 | 0.38 | NA | 0.46 | 0.28 | 0.91 | 0.36 | 0.49 | 0.17 | −0.07 | −0.08 | |
| Ovary Ln (Ov L) | — | 0.46 | NA | 0.64 | 0.08 | 0.88 | 0.50 | −0.13 | 0.81 | 0.75 | 0.11 | |
| Style–stigma Ln (Sty L) | — | 0.30 | NA | 0.13 | 0.39 | 0.57 | 0.43 | 0.05 | 0.03 | 0.38 | 0.09 |
Dashes indicate that rQ was not estimated because the correlation estimated with genotypic trait means was not significant (Table 2). Italics designate floral–nonfloral correlations.
Floral morphology in cultivated and wild B. rapa accessions:
We detected significant genetic variation for all floral traits measured in 13 accessions of B. rapa (all P-values ≤ 0.05; see Table S7 for ANOVA). Floral trait means estimated among the accessions [petal length, 8.8 ± 0.3 mm (BLUP ± SE); midpoint length, 3.1 ± 0.1 mm; petal width, 4.5 ± 0.2 mm; filament length, 5.3 ± 0.1 mm; anther length, 2.6 ± 0.1 mm; ovary length, 5.0 ± 0.1 mm; and style–stigma length, 2.3 ± 0.1 mm] were 37% (range 16–50%) larger on average than those of RILs. Despite the small sample size (N = 13), we detected significant positive genetic correlations among all petal traits (range 0.68–0.89), between filament length and both petal and midpoint length (0.80 and 0.83, respectively), and between style–stigma length and each of petal, midpoint, and filament lengths (range 0.64–0.85; see Table S8 for all correlation coefficients), and many correlations were of similar or greater magnitude relative to the RILs.
DISCUSSION
Plant reproductive success is contingent upon floral morphology. Floral organ size and allometry are targeted by selection due effects on, for instance, pollinator attraction (Conner and Rush 1996), physiological function (Galen 2000; Herrera 2005), and response to herbivore damage (Strauss 1997). For example, in this B. rapa RIL population, stigma–anther separation (herkogamy) explained significant variation in outcrossing rate (M. T. Brock and C. Weinig, unpublished results), which can in turn affect the quantity or quality of offspring (Charlesworth and Charlesworth 1987). Yet, despite the selective importance of intraspecific floral variation, the genetic dissection of floral traits has been largely explored through interspecific comparisons (Bradshaw et al. 1995; Fishman et al. 2002; Goodwillie et al. 2006; Bouck et al. 2007; Moyle 2007; but see Juenger et al. 2000, 2005; Hall et al. 2006). Using B. rapa RILs, we detect significant genetic variation and additive and/or epistatic QTL for floral and nonfloral traits of RILs raised under field and greenhouse conditions. Within environments, floral traits exhibited strong genotypic correlations indicative of phenotypic integration, and mapped QTL correspondingly regulated multiple floral traits. Floral genetic architecture, as estimated by genetic correlations, showed only modest differences across these distinct environments. Surprisingly and in contrast to prior studies (Conner and Via 1993; Conner and Sterling 1996; Juenger et al. 2005), floral traits showed a moderate to high level of phenotypic integration with vegetative and phenological traits in the more favorable greenhouse environment; genotypic correlations between these functional trait groups were less frequent and of lesser magnitude in the field.
Quantitative genetics of floral morphology:
Genetic variances can fluctuate across environments (Hoffmann and Merila 1999; Charmantier and Garant 2005), with a common expectation that estimates of genetic parameters are greater in benign environments (Conner et al. 2003). We detected substantial genetic variation for all measured floral traits in both the greenhouse and the field environments (Table 1), but average estimates of genetic variances and broad-sense heritabilities were in fact greater in the greenhouse. Our estimates of floral broad-sense heritabilities in the RILs are commensurate with reported values in other mapping studies (e.g., Hall et al. 2006) as well as average heritabilities of floral traits from natural populations (reviewed in Ashman and Majetic 2006). Genetic variances in mapping populations may be lower than those in natural populations (in part, due to the fact that only two alternative alleles segregate in such experimental populations) or greater than those in natural populations (due to independent assortment and the potential that some RILs harbor alleles of predominantly positive/negative effect at contributing QTL). Nevertheless, our survey of floral morphology in publicly available B. rapa accessions (Table S7) supports the hypothesis of standing genetic variation for floral traits in cultivated and wild populations. Taken together, these results suggest that floral morphology can respond to natural (or artificial) selection across a broad range of environmental conditions.
Genetic correlations among all measured floral traits were strongly positive in both greenhouse and field environments (Table 2), consistent with prior studies in both natural and controlled environments (reviewed in Ashman and Majetic 2006). This strong floral phenotypic integration is the result of either pleiotropic loci that regulate the development of multiple floral whorls [e.g., the ABC model of floral development (Coen and Meyerowitz 1991)] or linkage disequilibrium between multiple causal loci. In both environments, the strongest interwhorl correlations were observed between petal length (or midpoint length) and filament length in the RILs. Despite the small sample, we also detect genotypic correlations of similar or greater magnitude between petal and filament lengths in wild and cultivated B. rapa accessions relative to the RILs (Table S8). This correlation influences the degree to which anthers protrude from the corolla opening (i.e., anther exsertion), a trait that contributes to efficient pollen dispersal (Morgan and Conner 2001). Conner et al. (2009) argue that correlational selection for the joint expression of petal and filament length in Raphanus raphanistrum (and other related Brassicaceous species) produces significantly stronger correlations between petal and filament lengths than between other pairs of floral traits. While the occurrence of this petal–filament correlation in the accessions is consistent with the hypothesis of past selection and enhanced LD, the similar patterning of floral trait correlations in our B. rapa RIL population, in which LD arising from selection is at least somewhat disrupted, suggests that significant petal–filament correlations may also arise from floral developmental genetics in this species (i.e., from pleiotropic effects of floral regulatory loci). The strong phenotypic integration of floral organ dimensions should result in consistent expression of floral allometry across environments, but these genetic correlations could also constrain the evolution of novel floral shapes and sizes if trait correlations are not parallel to the joint vector of selection (Smith and Rausher 2008).
The genetic architecture of floral traits, as measured by the correlation matrix, was subtly but significantly different across environments. Multivariate CPC analysis detected differences between correlation matrices, but at least 80% of the variance in floral correlations did not differ across environments. The similarity of individual G-matrix elements (i.e., only 2 of 15 correlations in the floral–matrix CPC comparison differed significantly across environments) is consistent with the multivariate view of environmentally invariant floral correlations. A growing number of studies have explored G-matrix constancy across a variety of environmental and taxonomic categories; however, G-matrix behavior, including that of across-environment floral morphological matrices (Conner et al. 2003; Brock and Weinig 2007; Brock et al. 2009), can be variable (Steppan et al. 2002; Björklund 2004). Similar to the findings presented here, Conner et al. (2003) detected differences in higher-level principal component axes of unstandardized floral G-matrices of R. raphanistrum raised in field and greenhouse environments. We should note that our initial CPC analyses of unstandardized G-matrices revealed fundamental differences across field and greenhouse environments for this population of B. rapa RILs (i.e., differences in the first principal component axis). However, we chose to standardize these matrices due to the dramatic difference in trait variances across environments (see Figure 1). As a result, our matrix comparisons suggest that the structures of genetic correlations are relatively similar across environments, but that differences in trait variances across environments could alter the magnitude of floral morphological responses to selection.
QTL architecture of floral morphology:
We detected numerous main-effect floral QTL in both field and greenhouse environments (Tables 3 and 4). On average, floral QTL segregating in this population are of moderate to small effect size [average percent variance explained (PVE) in the field and the greenhouse, 7.5 and 7.9, respectively]. Further, additive-effect QTL detected for individual floral traits explain on average only 29% of the genetic variation in each environment (although significant epistatic-effect QTL in these selfed RILs also explain on average 15% of floral trait variation). Our results suggest that floral morphological variation is controlled by many genes of small to moderate additive effect, a pattern observed in both environments. Many of the mapped QTL are likely floral-specific regulators of organ size, as opposed to QTL that simply influence overall plant size: we observed similar QTL for floral traits when we mapped residuals that accounted for plant size (i.e., plant size-corrected floral traits, data not shown). The exception, of course, is that pleiotropic QTL that influenced both floral traits and the size of vegetative organs differed between the original and the residuals-based analysis of QTL.
In total, we detected 19 main-effect floral QTL in the field and 21 QTL in the greenhouse, of which 5 QTL in each environment influenced multiple floral traits. Instances of such “pleiotropic” QTL and/or QTL in close proximity contribute to the strong genetic correlations observed among floral whorls (Table 2). In both environments, estimates of genetic correlations based on QTL additive effects (rQ) (Table 6) strongly correlate with those based on RIL trait means (rG). For example, petal and filament length have two pleiotropic QTL (FQTL 3-3 and FQTL 6-1) and one instance of physically proximate QTL (FQTL 7-3 and FQTL 7-4) under field conditions (Figure 2), at which alleles affect petal and filament morphology in the same direction (Table 3). Correspondingly, petal–filament length rQ closely approximates rG (0.8 and 0.75, respectively), suggesting that mapped QTL largely account for the genetic correlation. (It is, however, worth noting that rQ for many other trait pairs underestimates rG, a pattern potentially attributable to undetectable QTL of small effect). Intriguingly, other features of the QTL architecture may explain the absence of significant floral–floral correlations. Greenhouse QTL 3–5 influenced petal width and midpoint length in opposing directions (Table 4). This case of antagonistic pleiotropy may counter other QTL that have parallel additive effects on petal width and midpoint length (e.g., GQTL 9-3 and 9-4), resulting in the nonsignificant genetic correlation observed under greenhouse conditions (Table 2).
A majority of the main-effect QTL had significant effects on floral traits in both environments; however, we did detect significant QTL × E interactions that arose either because QTL had statistically significant effects in only one environment or because QTL had statistically significant phenotypic effects in both environments, but the magnitude of effect differed across environments (Tables 3 and 4). Although the overall similarity in floral G-matrices across environments may seem at odds with the extent of QTL × E, those QTL whose phenotypic effects differed across environments typically regulated floral organs for which bivariate correlations likewise differed across environments. For example, QTL regulating petal traits (petal width as well as petal and midpoint lengths) and ovary length accounted for a majority of the detected QTL × E interactions, and it is genetic correlations involving these traits that differed across environments (Table 2).
In spite of the statistical hurdles, an increasing number of studies illustrate the important role of epistasis in regulating trait expression and potentially maintaining genetic variation (Kroymann and Mitchell-Olds 2005; Malmberg et al. 2005). In genome-wide scans, we detected epistatic interactions in both the field (one interaction) and the greenhouse (six interactions) that regulated floral phenotypes (see PVE in Table 5). The small number of two-way epistatic interactions we detected across both environments should be viewed as a minimum estimate, a measure constrained by the stringent significance levels needed to properly account for multiple comparisons and by the limited ability to detect epistatic interactions of small effect. As with pleiotropic main-effect QTL, epistatic interactions contributed to the observed integration among floral whorls. Illustrating this last point, the interaction between QTL on chromosome 2 (∼78 cM) and chromosome 10 (∼46 cM) detected in the greenhouse affected multiple floral traits (Table 5, Figure S1). Finally, we note that most floral epistatic interactions differed significantly across environments; however, the small number of detected epistatic interactions limits our ability to determine the generality of this pattern.
Floral–vegetative correlations within multiple environments:
Floral and vegetative traits in natural populations are hypothesized to be genetically decoupled (Berg 1960; reviewed in Murren 2002), a genetic independence that has arisen despite the developmental homology between shoots and flowers and between leaves and floral organs (Goethe 1790; Frohlich and Chase 2007). This decoupling should facilitate independent evolutionary responses to environmental heterogeneity of functionally divergent trait groups. In the field, floral traits were indeed less integrated with nonfloral traits than with other floral traits; instances of significant correlations between floral and nonfloral traits were less frequent and weaker than those between floral traits.
We did, however, find evidence of significant floral–vegetative genetic correlations in both environments. For example, anther length was positively correlated with primary inflorescence height in the field, which in turn was supported by the detection of pleiotropic QTL on chromosomes 3 and 6 (FQTL 3-2 and FQTL 6-2, respectively) that influenced these traits in a coordinated manner (Table 6). When RILs were raised in the greenhouse, apparent integration estimated from G-matrices increased significantly between floral and vegetative traits and, to a greater extent, between floral and phenological traits. All greenhouse floral traits, except petal width, were significantly positively correlated with later-staged vegetative traits and days to flower (Tables 2 and 6). Of the floral–vegetative correlations, anther length again exhibited the strongest genetic correlations with nonfloral traits, and QTL regulating anther length overlapped or neighbored those influencing primary inflorescence height (e.g., chromosomes 1, 3, and 6). However, much of the increased integration between floral and nonfloral traits in the greenhouse was not reflected in the underlying QTL architecture, suggesting that undetected small-effect QTL and/or higher-order epistatic interactions coregulate floral and nonfloral traits under these more benign environmental conditions.
The detection of floral–vegetative and floral–phenological genetic correlations in our B. rapa population (especially those in the greenhouse) stands in contrast to studies of the close relatives A. thaliana (Juenger et al. 2005) and R. raphanistrum (Conner and Via 1993; Conner and Sterling 1996). In the Brassicaceous systems, strong genetic correlations were detected within floral and vegetative modules, but correlations between floral and vegetative traits were much weaker and rarely significant (Conner and Via 1993; Juenger et al. 2005). Furthermore in A. thaliana, pleiotropic QTL were most commonly observed to influence either vegetative or floral trait groups, but not both (Juenger et al. 2005). Other studies examining the independence of floral–vegetative correlations are more equivocal (Armbruster et al. 1999; Hall et al. 2006). In M. guttatus, Hall et al. (2006) detected QTL that jointly affected floral, vegetative, and phenological traits. It is possible that genetic correlations between floral and nonfloral traits in this last QTL study (and our own) are more a consequence of the very divergent populations used in the experimental cross [e.g., annual vs. perennial (Hall and Willis 2006; Hall et al. 2006)] than a reflection of floral–vegetative correlations within populations experiencing more natural levels of migration and gene flow. Nevertheless, utilizing segregating progeny from divergent populations is fundamental for understanding genetic mechanisms underlying complex traits. Moreover, gene flow between weedy and cultivated genotypes of B. rapa (Heenan and Dawson 2005; Warwick et al. 2008) and of other species of agricultural importance (Ellstrand et al. 1999; Pilson and Prendeville 2004), as well as between native and exotic populations (e.g., Culley and Hardiman 2009), argues that similar crosses between distinct populations are frequent in nature.
Acknowledgments
We thank numerous individuals who helped maintain and measure plants and flowers. These individuals include E. Boehlke, L. Demink, K. Dorn, A. Hanson, Z. German, K. Krueger, P. Lien, B. Meyer, N. Paulson, and C. Willis. We are especially grateful to J. Johnston for her efforts in the design and collection of data during the field experiment. The insightful and constructive comments of Z. Gompert, C. Jones, and two anonymous reviewers were extremely valuable in revising the manuscript. This work was supported by National Science Foundation grants DBI-0227103 to C.W. and J.N.M. and DBI-0605736 to C.W.
Supporting information is available online at http://www.genetics.org/cgi/content/full/genetics.110.119982/DC1.
References
- Adler, L. S., K. Wikler, F. S. Wyndham, C. R. Linder and J. Schmitt, 1993. Potential for persistence of genes escaped from canola: germination cues in crop, wild, and crop-wild hybrid Brassica rapa. Funct. Ecol. 7 736–745. [Google Scholar]
- Agrawal, A. F., and J. R. Stinchcombe, 2009. How much do genetic covariances alter the rate of adaptation? Proc. R. Soc. B Biol. Sci. 276 1183–1191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armbruster, W. S., V. S. Di Stilio, J. D. Tuxill, T. C. Flores and J. L. Velasquez Runk, 1999. Covariance and decoupling of floral and vegetative traits in nine neotropical plants: a re-evaluation of Berg's correlation-pleiades concept. Am. J. Bot. 86 39–55. [PubMed] [Google Scholar]
- Ashman, T. L., and C. J. Majetic, 2006. Genetic constraints on floral evolution: a review and evaluation of patterns. Heredity 96 343–352. [DOI] [PubMed] [Google Scholar]
- Baker, H. G., 1965. Characteristics and modes of origin of weeds, pp. 147–168 in The Genetics of Colonizing Species, edited by H. G. Baker and G. L. Stebbins. Academic Press, New York.
- Bateman, A. J., 1955. Self-incompatibility systems in angiosperms. III. Cruciferae. Heredity 9 52–68. [Google Scholar]
- Bell, G., 1985. On the function of flowers. Proc. R. Soc. Lond. Ser. B Biol. Sci. 224 223–265. [Google Scholar]
- Berg, R. L., 1959. A general evolutionary principle underlying the origin of developmental homeostasis. Am. Nat. 93 103–105. [Google Scholar]
- Berg, R. L., 1960. The ecological significance of correlation pleiades. Evolution 14 171–180. [Google Scholar]
- Björklund, M., 2004. Constancy of the G matrix in ecological time. Evolution 58 1157–1164. [DOI] [PubMed] [Google Scholar]
- Bouck, A., S. R. Wessler and M. L. Arnold, 2007. Qtl analysis of floral traits in Louisiana Iris hybrids. Evolution 61 2308–2319. [DOI] [PubMed] [Google Scholar]
- Bradshaw, H. D., S. M. Wilbert, K. G. Otto and D. W. Schemske, 1995. Genetic mapping of floral traits associated with reproductive isolation in monkeyflowers (Mimulus). Nature 376 762–765. [Google Scholar]
- Brock, M. T., and C. Weinig, 2007. Plasticity and environment-specific covariances: an investigation of floral-vegetative and within flower correlations. Evolution 61 2913–2924. [DOI] [PubMed] [Google Scholar]
- Brock, M. T., J. R. Stinchcombe and C. Weinig, 2009. Indirect effects of FRIGIDA: floral trait (co)variances are altered by seasonally variable abiotic factors associated with flowering time. J. Evol. Biol. 22 1826–1838. [DOI] [PubMed] [Google Scholar]
- Broman, K. W., H. Wu, Ś. Sen and G. A. Churchill, 2003. R/qtl: QTL mapping in experimental crosses. Bioinformatics 19 889–890. [DOI] [PubMed] [Google Scholar]
- Charlesworth, D., and B. Charlesworth, 1987. Inbreeding depression and its evolutionary consequences. Annu. Rev. Ecol. Syst. 18 237–268. [Google Scholar]
- Charmantier, A., and D. Garant, 2005. Environmental quality and evolutionary potential: lessons from wild populations. Proc. R. Soc. B Biol. Sci. 272 1415–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheverud, J. M., 1984. Quantitative genetics and developmental constraints on evolution by selection. J. Theor. Biol. 110 155–171. [DOI] [PubMed] [Google Scholar]
- Clark, A. G., 1987. Genetic correlations: the quantitative genetics of evolutionary constraints, pp. 25–45 in Genetic Constraints on Adaptive Evolution, edited by V. Loeschcke. Springer, New York.
- Coen, E. S., and E. M. Meyerowitz, 1991. The war of the whorls: genetic interactions controlling flower development. Nature 353 31–37. [DOI] [PubMed] [Google Scholar]
- Conner, J., and S. Via, 1993. Patterns of phenotypic and genetic correlations among morphological and life-history traits in wild radish, Raphanus raphanistrum. Evolution 47 704–711. [DOI] [PubMed] [Google Scholar]
- Conner, J. K., and S. Rush, 1996. Effects of flower size and number on pollinator visitation to wild radish, Raphanus raphanistrum. Oecologia 105 509–516. [DOI] [PubMed] [Google Scholar]
- Conner, J. K., and A. Sterling, 1996. Selection for independence of floral and vegetative traits: evidence from correlation patterns in five species. Can. J. Bot. 74 642–644. [Google Scholar]
- Conner, J. K., R. Franks and C. Stewart, 2003. Expression of additive genetic variances and covariances for wild radish floral traits: comparison between field and greenhouse environments. Evolution 57 487–495. [DOI] [PubMed] [Google Scholar]
- Conner, J. K., H. F. Sahli and K. Karoly, 2009. Tests of adaptation: functional studies of pollen removal and estimates of natural selection on anther position in wild radish. Ann. Bot. 103 1547–1556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Culley, T. M., and N. A. Hardiman, 2009. The role of intraspecific hybridization in the evolution of invasiveness: a case study of the ornamental pear tree Pyrus calleryana. Biol. Invasions 11 1107–1119.
- Dechaine, J. M., J. A. Johnston, M. T. Brock and C. Weinig, 2007. Constraints on the evolution of adaptive plasticity: costs of plasticity to density are expressed in segregating progenies. New Phytol. 176 874–882. [DOI] [PubMed] [Google Scholar]
- Doerge, R. W., and G. A. Churchill, 1996. Permutation tests for multiple loci affecting a quantitative character. Genetics 142 285–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donohue, K., E. H. Pyle, D. Messiqua, M. S. Heschel and J. Schmitt, 2000. Density dependence and population differentiation of genetic architecture in Impatiens capensis in natural environments. Evolution 54 1969–1981. [DOI] [PubMed] [Google Scholar]
- Dorn, L. A., and T. Mitchell-olds, 1991. Genetics of Brassica campestris. I. Genetic constraints on evolution of life-history characters. Evolution 45 371–379. [DOI] [PubMed] [Google Scholar]
- Ellstrand, N. C., H. C. Prentice and J. F. Hancock, 1999. Gene flow and introgression from domesticated plants into their wild relatives. Annu. Rev. Ecol. Syst. 30 539–563. [Google Scholar]
- Etterson, J. R., and R. G. Shaw, 2001. Constraint to adaptive evolution in response to global warming. Science 294 151–154. [DOI] [PubMed] [Google Scholar]
- Falconer, D. S., and T. F. C. Mackay, 1996. Introduction to Quantitative Genetics. Longman, Harlow, UK.
- Fishman, L., A. J. Kelly and J. H. Willis, 2002. Minor quantitative trait loci underlie floral traits associated with mating system divergence in Mimulus. Evolution 56 2138–2155. [DOI] [PubMed] [Google Scholar]
- Flury, B., 1988. Common principal components and related multivariate models. John Wiley & Sons, New York.
- Frohlich, M. W., and M. W. Chase, 2007. After a dozen years of progress the origin of angiosperms is still a great mystery. Nature 450 1184–1189. [DOI] [PubMed] [Google Scholar]
- Galen, C., 2000. High and dry: drought stress, sex-allocation trade-offs, and selection on flower size in the alpine wildflower Polemonium viscosum (Polemoniaceae). Am. Nat. 156 72–83. [DOI] [PubMed] [Google Scholar]
- Gardner, K. M., and R. G. Latta, 2007. Shared quantitative trait loci underlying the genetic correlation between continuous traits. Mol. Ecol. 16 4195–4209. [DOI] [PubMed] [Google Scholar]
- Goethe, J. W., 1790. An attempt to explain the metamorphosis of plants. Ettinger, Gotha, Germany (in German).
- Goodwillie, C., C. Ritland and K. Ritland, 2006. The genetic basis of floral traits associated with mating system evolution in Leptosiphon (Polemoniaceae): an analysis of quantitative trait loci. Evolution 60 491–504. [PubMed] [Google Scholar]
- Haley, C. S., and S. A. Knott, 1992. A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity 69 315–324. [DOI] [PubMed] [Google Scholar]
- Hall, M. C., and J. H. Willis, 2006. Divergent selection on flowering time contributes to local adaptation in Mimulus guttatus populations. Evolution 60 2466–2477. [PubMed] [Google Scholar]
- Hall, M. C., C. J. Basten and J. H. Willis, 2006. Pleiotropic quantitative trait loci contribute to population divergence in traits associated with life-history variation in Mimulus guttatus. Genetics 172 1829–1844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heenan, P. B., and M. I. Dawson, 2005. Spontaneous hybrids between naturalised populations of pak choi (Brassica rapa var. chinensis) and wild turnip (B. rapa var. oleifera) from near Ashburton, Canterbury, New Zealand. N. Z. J. Bot. 43 817–824. [Google Scholar]
- Herrera, C. M., 2001. Deconstructing a floral phenotype: Do pollinators select for corolla integration in Lavandula latifolia? J. Evol. Biol. 14 574–584. [Google Scholar]
- Herrera, C. M., 2005. Post-floral perianth functionality: contribution of persistent sepals to seed development in Helleborus foetidus (Ranunculaceae). Am. J. Bot. 92 1486–1491. [DOI] [PubMed] [Google Scholar]
- Herrera, C. M., X. Cerda, M. B. Garcia, J. Guitian, M. Medrano et al., 2002. Floral integration, phenotypic covariance structure and pollinator variation in bumblebee-pollinated Helleborus foetidus. J. Evol. Biol. 15 108–121. [Google Scholar]
- Hinata, K., and S. Prakash, 1984. Ethnobotany and evolutionary origin of Indian oleiferous Brassicae. Indian J. Genet. Plant Breed. 44 102–112. [Google Scholar]
- Hinata, K., A. Isogai and K. Isuzugawa, 1994. Manipulation of sporophytic self-incompatibility in plant breeding, pp. 102–115 in Self-Incompatibility and Reproductive Development in Flowering Plants, edited by E. G. Williams, A. E. Clarke and R. B. Knox. Kluwer Academic, Dordrecht, The Netherlands.
- Hodgins, K. A., and S. C. H. Barrett, 2008. Natural selection on floral traits through male and female function in wild populations of the heterostylous daffodil Narcissus triandrus. Evolution 62 1751–1763. [DOI] [PubMed] [Google Scholar]
- Hoffmann, A. A., and J. Merila, 1999. Heritable variation and evolution under favourable and unfavourable conditions. Trends Ecol. Evol. 14 96–101. [DOI] [PubMed] [Google Scholar]
- Holland, J. B., 1998. EPISTACY: a SAS program for detecting two-locus epistatic interactions using genetic marker information. J. Hered. 89 374–375. [Google Scholar]
- Holm, L., J. Doll, E. Holm, J. Pancho and J. Herberger, 1997. World Weeds: Natural Histories and Distribution. John Wiley & Sons, New York.
- Iniguez-Luy, F. L., L. Lukens, M. W. Farnham, R. M. Amasino and T. C. Osborn, 2009. Development of public immortal mapping populations, molecular markers and linkage maps for rapid cycling Brassica rapa and B. oleracea. Theor. Appl. Genet. 120 31–43. [DOI] [PubMed] [Google Scholar]
- Juenger, T., M. Purugganan and T. F. C. Mackay, 2000. Quantitative trait loci for floral morphology in Arabidopsis thaliana. Genetics 156 1379–1392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juenger, T., J. M. Perez-Perez, S. Bernal and J. L. Micol, 2005. Quantitative trait loci mapping of floral and leaf morphology traits in Arabidopsis thaliana: evidence for modular genetic architecture. Evol. Dev. 7 259–271. [DOI] [PubMed] [Google Scholar]
- Kelly, J. K., 2009. Connecting QTLs to the G-matrix of evolutionary quantitative genetics. Evolution 63 813–825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klingenberg, C. P., 2008. Morphological integration and developmental modularity. Annu. Rev. Ecol. Evol. Syst. 39 115–132. [Google Scholar]
- Kroymann, J., and T. Mitchell-Olds, 2005. Epistasis and balanced polymorphism influencing complex trait variation. Nature 435 95–98. [DOI] [PubMed] [Google Scholar]
- Lynch, M., and B. Walsh, 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates, Sunderland, MA.
- Malmberg, R. L., S. Held, A. Waits and R. Mauricio, 2005. Epistasis for fitness-related quantitative traits in Arabidopsis thaliana grown in the field and in the greenhouse. Genetics 171 2013–2027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merilä, J., and M. Björklund, 2004. Phenotypic integration as a constraint and adaptation, pp. 107–129 in Phenotypic Integration: Studying the Ecology and Evolution of Complex Phenotypes, edited by M. Pigliucci and K. Preston. Oxford University Press, New York.
- Mishra, R. C., and H. D. Kaushik, 1992. Effect of cross pollination on yield and oil content of Brassica spp. and Eruca sativa with pollination efficiency of honeybees, Apis spp. Ann. Entomol. 10 33–37. [Google Scholar]
- Mishra, R. C., J. Kumar and J. K. Gupta, 1988. The effect of mode of pollination on yield and oil potential of Brassica campestris L. var. sarson with observation on insect pollinators. J. Apicult. Res. 27 186–189. [Google Scholar]
- Mitchell-Olds, T., 1996. Pleiotropy causes long-term genetic constraints on life-history evolution in Brassica rapa. Evolution 50 1849–1858. [DOI] [PubMed] [Google Scholar]
- Morgan, M. T., and J. K. Conner, 2001. Using genetic markers to directly estimate male selection gradients. Evolution 55 272–281. [DOI] [PubMed] [Google Scholar]
- Moyle, L. C., 2007. Comparative genetics of potential prezygotic and postzygotic isolating barriers in a lycopersicon species cross. J. Hered. 98 123–135. [DOI] [PubMed] [Google Scholar]
- Murren, C. J., 2002. Phenotypic integration in plants. Plant Species Biol. 17 89–99. [Google Scholar]
- Phillips, P. C., and S. J. Arnold, 1999. Hierarchical comparison of genetic variance-covariance matrices. I. Using the flury hierarchy. Evolution 53 1506–1515. [DOI] [PubMed] [Google Scholar]
- Pigliucci, M., 2003. Phenotypic integration: studying the ecology and evolution of complex phenotypes. Ecol. Lett. 6 265–272. [Google Scholar]
- Pilson, D., and H. R. Prendeville, 2004. Ecological effects of transgenic crops and the escape of transgenes into wild populations. Annu. Rev. Ecol. Evol. Syst. 35 149–174. [Google Scholar]
- Smith, R. A., and M. D. Rausher, 2008. Selection for character displacement is constrained by the genetic architecture of floral traits in the ivyleaf morning glory. Evolution 62 2829–2841. [DOI] [PubMed] [Google Scholar]
- Steppan, S. J., P. C. Phillips and D. Houle, 2002. Comparative quantitative genetics: evolution of the G matrix. Trends Ecol. Evol. 17 320–327. [Google Scholar]
- Stinchcombe, J. R., C. Weinig, K. D. Heath, M. T. Brock and J. Schmitt, 2009. Polymorphic genes of major effect: consequences for variation, selection and evolution in Arabidopsis thaliana. Genetics 182 911–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strauss, S. Y., 1997. Floral characters link herbivores, pollinators, and plant fitness. Ecology 78 1640–1645. [Google Scholar]
- Ushimaru, A., and K. Nakata, 2002. The evolution of flower allometry in selfing species. Evol. Ecol. Res. 4 1217–1227. [Google Scholar]
- Van Ooijen, J. W., 1992. Accuracy of mapping quantitative trait loci in autogamous species. Theor. Appl. Genet. 84 803–811. [DOI] [PubMed] [Google Scholar]
- Van Ooijen, J. W., and R. E. Voorrips, 2001. JoinMap Version 3.0, Software for the Calculation of Genetic Linkage Maps. Plant Research International, Wageningen, The Netherlands.
- Wang, S., C. J. Basten and Z.-B. Zeng, 2007. Windows QTL Cartographer 2.5. Department of Statistics, North Carolina State University, Raleigh, NC. (http://statgen.ncsu.edu/qtlcart/WQTLCart.htm).
- Warwick, S. I., A. Legere, M. J. Simard and T. James, 2008. Do escaped transgenes persist in nature? The case of an herbicide resistance transgene in a weedy Brassica rapa population. Mol. Ecol. 17 1387–1395. [DOI] [PubMed] [Google Scholar]
- Williams, P. H., and C. B. Hill, 1986. Rapid-cycling populations of Brassica. Science 232 1385–1389. [DOI] [PubMed] [Google Scholar]
- Zeng, Z. B., 1994. Precision mapping of quantitative trait loci. Genetics 136 1457–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao, J. J., X. W. Wang, B. Deng, P. Lou, J. Wu et al., 2005. Genetic relationships within Brassica rapa as inferred from AFLP fingerprints. Theor. Appl. Genet. 110 1301–1314. [DOI] [PubMed] [Google Scholar]




