Improved Hidden Markov Models for Molecular Motors, Part 1: Basic Theory

Abstract

Hidden Markov models (HMMs) provide an excellent analysis of recordings with very poor signal/noise ratio made from systems such as ion channels which switch among a few states. This method has also recently been used for modeling the kinetic rate constants of molecular motors, where the observable variable—the position—steadily accumulates as a result of the motor's reaction cycle. We present a new HMM implementation for obtaining the chemical-kinetic model of a molecular motor's reaction cycle called the variable-stepsize HMM in which the quantized position variable is represented by a large number of states of the Markov model. Unlike previous methods, the model allows for arbitrary distributions of step sizes, and allows these distributions to be estimated. The result is a robust algorithm that requires little or no user input for characterizing the stepping kinetics of molecular motors as recorded by optical techniques.

Introduction

Single-molecule studies have contributed tremendously to the understanding of molecular motors. High-resolution fluorescence-based tracking has revealed step sizes and detailed mechanisms of myosin V, VI, and kinesin processivity (1,2). Recent optical trap studies have measured the individual step size of RNA polymerase to be ∼3.4 nm as it translocates along a double-stranded DNA (3). Motor activity in these experiments is detected by nanometer-scale position changes of a reporter tag that is rigidly attached to the molecular motor and recorded with a charge-coupled device camera or a quadrant photodetector. The interpretation of the recordings is complicated by the presence of substantial measurement noise, by the nonuniform step size seen in some motor types, and the mismatch in time between the detector's integration and the transitions in a motor's mechano-chemical cycle.

The standard approach to the analysis of motor recordings is to employ a step-detector algorithm to identify the times and sizes of motor position changes (4). From this idealization of the recording, histograms of step sizes and dwell times are constructed as a first step in building a chemical-kinetic model of the motor's reaction cycle (5). As an alternative, signal processing techniques based on hidden Markov models (HMMs) allow a more powerful analysis strategy to be used.

First, the entire digitized recording is used in estimating the model parameters. These parameters are the transition probabilities (the discrete-time analogs of kinetic rate constants) and the distributions of step sizes. The estimates are generally better than those obtained in the conventional analysis because the HMM strategy does not rely on a local assignment of step times and sizes.

Second, once the HMM model parameters are known, they can be used in obtaining an idealized time course of the motor activity. In simulations described here and in the following article (6), we find that this idealized time course agrees better with the true, noiseless motor position than what is obtained with conventional step detectors.

HMMs have been widely used for computer voice recognition (7) and for DNA sequence analysis (8). HMM signal-processing techniques are also routinely used in the analysis of single ion channel recordings, providing useful information even when the recordings have a signal/noise ratio too low to allow conventional interpretation of the data (9–12). Similarly, HMMs have been applied to single-molecule fluorescence fluctuations, in which the molecular system switches among several states (13). HMMs are naturally suited as descriptions of single-molecule activity because each state in the reaction sequence can be identified as a state of a Markov model, where the transition to a new state depends only on the current state of the system. Identifying the states and transition probabilities of models for molecular motors is of particular interest because these models reflect the details of reaction cycles. From the point of view of an experimenter, such Markov models are said to be hidden because the measurements are corrupted by noise, and also because, in many cases, some of the state transitions produce no observable effect.

Molecular motors present a special challenge to the application of HMMs. Like other single-molecule systems, motors undergo transitions among a small number of what we will call molecular states. However, the observable quantity is the molecule's position, a variable that reflects the ongoing accumulation of elementary steps of random size. This sort of variable is not represented in classical HMMs. Milescu et al. (14) first showed that a periodic Markov model can describe the position variable, with the accumulation of random deviations modeled as a sum of Gaussian random variables. With the resulting HMM these authors were able to provide maximum-likelihood (ML) estimates of motor parameters and also obtain the restored time course. They also noted that, in principle, an HMM could be constructed in which each possible value of the position variable corresponds to a state of the model.

A model of this sort has been constructed by Beausang and co-workers (15,16) for studying DNA looping kinetics as reported by a DNA-tethered bead. These authors extend the HMM framework to a diffusive HMM with many states, with each state corresponding to a particular combination of the molecular state and the distance of the bead from its central position. This model is able to describe the Brownian motion of the bead as the DNA tether changes its effective length because loops are formed by the binding of protein complexes to the DNA. The result is a method for determining the microscopic kinetics of the loop-forming reactions.

We report here the implementation of another HMM, one which describes both the molecular state and the position of a processive molecular motor. This variable stepsize HMM (VS-HMM) allows the characterization of motor stepping behavior. In comparison to the algorithm of Milescu et al. (14), it is more computationally intensive, but functionally more versatile. The algorithm allows the characterization of motor activity with arbitrary distributions of step sizes, and for its operation little prior knowledge about the stepping characteristics is required.

Theory

Markov model

Although the behavior of a molecular motor is a continuous-time process, we employ a discrete-time Markov model because the observations occur at discrete times. We denote these times by t = 1, 2,…T, reflecting the sequence of frames of data acquisition by an electronic camera. The position of the motor is also represented as a discrete quantity, which is chosen to be sufficiently fine-grained (with the quantum being smaller than the noise standard deviation) so that the discrepancy from the true, continuous value is negligible.

The position at time t is taken to be x_t ∈ {1, 2,…M}, an integer representing the position in quanta of, for example, 1 nm. Adopting the framework of a discrete stochastic model (17), the motor can also be found in any of several molecular states, which describe the particular conformation of the molecule and its occupancy by ligands such as ATP. The molecular state at time t is s_t ∈ {1, 2,…n}. The special feature of the VS-HMM described here is that the position and the molecular state together form a composite state (s_t, x_t) and provide a complete description of the system at a given time. According to the Markov assumption, the probability of making a change in the state in the system depends only on the current composite state.

A typical model may have only n = 2 molecular states, but could have the position represented by M = 1000 or more values (Fig. 1, A and B). The result is a Markov model with a very large total number nM of composite states. In practice, however, changes in the position variable from one time point to the next are bounded and relatively small; we call these position-change steps. A simple way to exploit the local nature of steps is to replace the position variable x with a variable u ∈ {1, 2,…m} having reduced range, but which is periodic (Fig. 1 C), such that x_t = u_t +l_tm, where l_t is an integer and a typical value of m might be 100. We use this periodic coordinate throughout the signal processing algorithms, but at the end are able to restore the original x coordinate by unwrapping the periodic variable using the l values.

Figure 1.

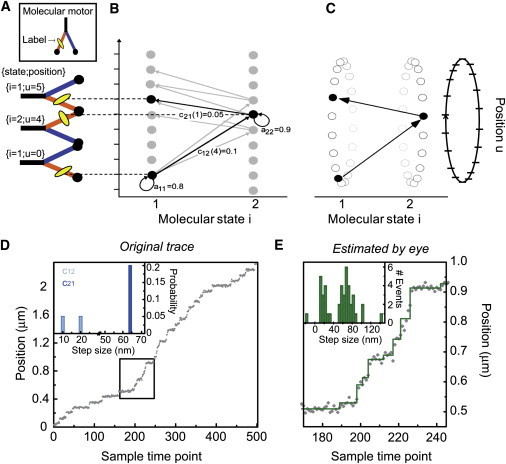
Models of molecular motor activity. (A) A two-state model for a linear molecular motor. The system starts in molecular state i = 1 with its fluorescent label (oval) at position u = 0. After a certain dwell time, the molecule undergoes a conformational change swinging its trailing leg forward, displacing the label by w = 4 units and settling into state 2. Subsequently, the molecule makes a transition back to state 1 with the label making a displacement of w = 1. (B) Two transitions of a Markov model describing the molecule in panel A. Initially, the molecule has a probability of a₁₁ = 0.8 of staying in state 1 with a mean dwell time of 1/(1–0.8) = 5 time units in this state. When the molecule makes a transition to state 2, it can change position with a step of size w = 3, 4, or 5 units; exemplary step of four units in bold (with transition probability c₁₂(4) = 0.1). After a dwell in state 2 (mean dwell of 10 time units), a transition can be taken back to state 1 with size w = 1, 2, or 3 units (step of one unit in bold). (C) The position values are wrapped around into a periodic coordinate system, exploiting the local nature of changes in the motor's position. (D) An example simulation of a molecular motor that moves with alternating short (10 or 20 nm) and long (64 nm) steps. Average dwells after short and long steps are 10 and 5 time points, respectively. Gaussian noise with σ = 7 nm was added to simulate the noisy trace (gray dots). (Inset) Simulated step probabilities c₁₂ and c_21. (E) An enlarged section (box in D) showing details of the time course. A fit by eye (solid line) yields the apparent step size distribution shown in the inset.

Using the standard HMM notation (18), we let the molecular state transition probabilities be given by the matrix A having elements

$$a_{ij}=P\left(s_{t+1}=j|s_t=i\right)$$

giving the probability of a molecular transition from i to j during the interval (t, t +1). The matrix A is related to the matrix of rate constants Q for the underlying chemical kinetics according to

$$A=e^{Q\delta t}$$

where δt is the sample interval. A useful approximation is to assume that, at most, one step is occurring per sample interval, in which case

$$A\approx I+Q\delta t.$$ (1)

This approximation allows a simple interpretation of the elements of A obtained from the HMM analysis, but is valid only when δt is sufficiently small. From an experimental standpoint, the interpretation of recordings is always difficult when they are sampled so slowly that multiple transitions occur within one sample interval.

The problem of missed events, well known in the analysis of single-ion-channel kinetics, also arises in this context. A more rigorous way to obtain the Q matrix from the hidden Markov model is described in the Supporting Material. However, as long as shot noise predominates over instrumentation noise (e.g., camera readout noise), there is no penalty—apart from computation time—in choosing δt to be small and presenting the HMM analysis with unfiltered data sampled at a high rate. A reasonable choice of δt would be one that makes the dwell time in each molecular state at least 5–10 sample intervals. In this case, the diagonal element of A corresponding to the probabilities of remaining in the i^th molecular state would lie between 0.8 and 0.9. The mean dwell time in state i can be estimated as

$${\tau }_i=\frac{1}{1-a_{ii}}.$$ (2)

We assume that a molecule's position changes only when there is a molecular state change. Let the random variable w be the size of a position step. For a transition from molecular state i to state j, the step size has the probability density f_ij(w). We can write the overall probability of a transition from the composite state (i,u) to (j,u + w) in this model as

$$c_{ij}\left(w\right)=P\left(s_{t+1}=j,x_{t+1}=u+w|s_t=i,x_t=u\right),$$

given by

$$c_{ij}\left(w\right)=\{\begin{array}{c}{a}_{ii}\delta \left(w\right),i=j\\ a_{ij}{f}_{ij}\left(w\right),i\ne j\end{array},$$ (3)

where δ is the discrete delta function. An example trajectory of a model with n = 2 states is shown in Fig. 1 B.

In general, the composite transition probability c_ij(w) can take any form as long as it is nonnegative and satisfies the stochastic condition

$$\sum _{j,w}{c}_{ij}\left(w\right)=1.$$

This general Markov model can be used in cases where only some molecular transitions are accompanied by a step, as seen in the case of a kinesin labeled on one head (1) or in a number of other complex kinetic schemes (5). It is also possible to create a so-called one-state model in which there is only n = 1 molecular state. In this case, Poisson random stepping is modeled by having c₁₁(0) be nonzero (reflecting the probability of no step) and also c₁₁(w) > 0 for some nonzero step sizes w. Such a one-state model is useful for describing observations when the underlying molecular reaction scheme is unknown.

Hidden Markov model

In the hidden Markov model, the state of the system is not known exactly, because of silent kinetic transitions and also because of measurement noise. In the simple description of the measurement process used in this article, the observed position variable is represented (in periodic coordinates, as in the previous section) as y_t = u_t + g_t, where u_t is the true position at the instant t and g_t is a random variable, having a normal distribution with zero mean and standard deviation σ_t, representing additive noise. The measurement we have in mind is the determination of the center of a Gaussian spot representing the fluorescence of a single molecule, as analyzed by Thompson et al. (19). In practice, the variance in this measurement comes from shot noise, and therefore we set

$${\sigma }_t^2={\sigma }_0^2{I}_0/I_t,$$ (4)

where σ₀ is a parameter to be determined, the nominal standard deviation; I₀ is the maximum reporter fluorescence intensity in the entire recording; and I_t is the intensity at time point t. This noise model allows for recordings in which blinking or other variations in fluorescence intensity produce changes in the reliability of the reporter's position measurement.

The noise model is formally described by a so-called emission probability function that gives the probability of the observation y, given a particular state of the underlying Markov model. The Gaussian noise results in a Gaussian probability density that depends on the position variable u,

$$b_t\left(y_t,u_t\right)={\left(2\pi {\sigma }_t^2\right)}^{-1/2}\exp \left[-{\left(y_t-u_t\right)}^2/2{\sigma }_t^2\right].$$ (5)

Goals of the hidden Markov analysis

There are two goals of the analysis.

The first is to estimate the parameters of the model, including the step-size distribution and the dwell times in molecular states. This is done by ML estimation, yielding asymptotically unbiased estimates. That is, these estimates, even from data with very low signal/noise ratios, are guaranteed to approach the correct values if the statistical model of signal and noise is correct, and if sufficiently long recordings are available.

Further, the quality of estimates can be judged from likelihood intervals and likelihood ratio tests. Let λ = (π, C, σ₀) be the parameters of the VS-HMM which are to be optimized: π is a vector of the initial probabilities, C is the matrix of transition probabilities (Eq. 3), and σ₀ is the noise parameter. The likelihood is defined to be the probability P(Y|λ) of the observed data sequence Y = y₁, y₂, …, y_T given the model l. For numerical convenience, it is the log likelihood L = ln P(Y|λ) that is maximized.

The second goal of the analysis is to construct an idealized time course of the molecular behavior from the observations. This process, called restoration, aims at restoring the noiseless position and the hidden molecular-state information. The resulting dwell-time sequence can then be analyzed through the construction of dwell-time histograms (5) or by direct fitting of models (20). Unfortunately the restoration is not guaranteed to be unbiased, but if it is based on correct model parameters it will tend to enforce the correct step sizes and dwell times. To perform restoration we use the Viterbi algorithm (21), which finds the most likely sequence of composite states.

Forward-backward algorithm

In principle, the likelihood can be computed by constructing all possible sequences of composite states of length T, and summing for each sequence S the probability that the sequence would occur, times the probability that the sequence underlies the observations,

$$P\left(Y|\lambda \right)=\sum _{S}P\left(S|\lambda \right)P\left(Y|S,\lambda \right).$$ (6)

Here the probability-of-state sequence

$$S=\left(i_i,u_1,i_2,u_2,\dots i_T,u_T\right),$$

given the model parameters

$$\lambda =\left(\pi ,C,\sigma \right),$$

is

$$P\left(S|\lambda \right)={\pi }_{i_1{u}_1}{c}_{i_1{i}_2}\left(u_2-u_1\right)c_{i_2{i}_3}\left(u_3-u_2\right)\dots \cdot c_{i_{T-1}{i}_T}\left(u_T-u_{T-1}\right),$$ (7)

and the probability of the data sequence given S, because the noise is independent from one observation to the next, is the product of probabilities

$$P\left(Y|S,\lambda \right)=\prod _{t=1}^T{b}_t\left(y_t,u_t\right).$$ (8)

Evaluation of Eq. 6 appears unwieldy, as the total number of possible state sequences is on the order of T^mn. However, the forward-backward algorithm forms this sum in an efficient way, requiring only the order of m²n²T operations (18); acceleration with the fast Fourier transform (FFT) reduces this further to m n²T log₂ m.

We follow the standard HMM formalism (18), defining the forward variable as the probability of the observations up to time t and the molecule being in a particular composite state (i,u), given the model λ,

$${\alpha }_t\left(i,u\right)=P\left(y_1,y_2,\dots y_t\text{and}{s}_t=i,x_t=u|\lambda \right),$$ (9)

with its initial value given by

$${\alpha }_1\left(i,u\right)={\pi }_{iu}{b}_1\left(y_1,u\right)$$ (10)

and subsequent variables obtained by recursion,

$$\begin{array}{c}{\alpha }_{t+1}\left(j,v\right)=b_{t+1}\left(y_{t+1},v\right)\sum _{i=1}^n\sum _{u=1}^m{\alpha }_t\left(i,u\right)c_{ij}\left(v-u\right),\\ t=1,2,\dots T\end{array}.$$ (11)

The sum over u is seen to be a discrete convolution of α_t with c_ij. Further, because the convolution is taken over variables u and v which have periodic boundary conditions, the Fourier convolution theorem allows the sum over u to be replaced by the product of discrete Fourier transforms,

$${\alpha }_{t+1}\left(j,v\right)=b_{t+1}\left(y_{t+1},v\right)\sum _{i=1}^n{\mathcal{F}}_v^{-1}\left\{{\mathcal{F}}_z\left[{\alpha }_t\left(i,z\right)\right]{\mathcal{F}}_z\left[c_{ij}\left(z\right)\right]\right\},$$ (12)

where F_z is the discrete Fourier transform over a position variable z and F_v⁻¹ is the inverse transform into the variable v. Because the FFT has computational complexity m log₂ m, the forward algorithm has the reduced complexity m n²Tlog₂ m; in our implementation the advantage of using FFTs becomes apparent for m > 32.

At the end of the forward recursion, the likelihood is computed according to

$$P\left(Y|\lambda \right)=\sum _{i,u}{\alpha }_T\left(i,u\right).$$ (13)

The backward variable is defined to be the probability of the observations from times t +1 to T, given the composite state (i,u) at time t and the model λ:

$${\beta }_t\left(i,u\right)=P\left(y_{t+1},y_{t+2},\dots y_T|s_t=i,x_t=u;\lambda \right).$$ (14)

The variable at the final time point is defined as

$${\beta }_T\left(i,u\right)=1,i=1\dots n,u=1\dots m$$ (15)

and for all other previous times t = T − 1, T − 2,…1, the β_t are obtained by recursion

$${\beta }_t\left(i,u\right)=\sum _{j=1}^n\sum _{v=1}^m{c}_{ij}\left(v-u\right)b_{t+1}\left(y_{t+1},v\right){\beta }_{t+1}\left(j,v\right)$$ (16)

or, using FFTs,

$${\beta }_t\left(i,u\right)=\sum _{j=1}^n{\mathcal{F}}_u^{-1}\left\{{\mathcal{F}}_z\left[c_{ij}\left(z\right)\right]{\mathcal{F}}_z\left[b_{t+1}\left(y_{t+1},z\right){\beta }_{t+1}\left(j,z\right)\right]\right\}.$$ (17)

The repeated products that arise in the computation of α and β would cause underflow except that rescaling is performed. We follow the rescaling strategy given by Levinson et al. (18).

The product of the forward and backward variables yields the joint probability of the observations and being in a specific composite state at a given time, P(Y and s_t = i, x_t = u|λ). Dividing this quantity by the likelihood yields the probability γ_t(i,u) of the motor protein occupying a certain composite state at a particular time, given by

$$\begin{array}{c}{\gamma }_t\left(i,u\right)=P\left(s_t=i,x_t=u|Y,\lambda \right)\\ =\frac{P\left(Y\text{and}{s}_t=i,x_t=u|\lambda \right)}{P\left(Y|\lambda \right)}\\ =\frac{{\alpha }_t\left(i,u\right){\beta }_t\left(i,u\right)}{P\left(Y|\lambda \right)}\end{array}.$$ (18)

Another useful quantity is the probability of making a transition at time t from molecular state i to j with a position change of w,

$$\begin{array}{l}{\xi }_t\left(i,j,w\right)=\sum _{u}P\left(s_t=i,x_t=u,s_{t+1}=j,x_{t+1}=u+w|Y,\lambda \right),\\ t=1,\dots ,T-1\text{.}\end{array}$$

In terms of previously defined quantities, it is obtained as

$${\xi }_t\left(i,j,w\right)=\frac{\sum _u{\alpha }_t\left(i,u\right)c_{ij}\left(w\right)b\left(y_{t+1},u+w\right){\beta }_{t+1}\left(j,u+w\right)}{P\left(Y|\lambda \right)},$$ (19)

a computation that, like the forward and backward algorithms, can be accelerated by FFTs.

Reestimation of model parameters

The model parameters π_iu, c_ij, and σ₀ are reestimated by the Baum-Welch formulas (22), a special case of the expectation-maximization (E-M) algorithm for ML estimation. Because we are making a straightforward application of the standard theory (18), we provide only the results here.

The initial probability is that of being in the composite state (i,u) at t = 1. At the k+1^st iteration, it is given simply by γ_t(i,u) computed from the k^th model parameters at the first time point

$${\pi }_{i,u}^{\left(k+1\right)}={\gamma }_1^{\left(k\right)}\left(i,u\right).$$ (20)

The reestimated value of σ₀ is obtained by

$${\sigma }_0^{k+1}={\left[\frac{1}{T}\sum _t\sum _{u,i}{\left(y_t-u\right)}^2\left(I_t/I_0\right){\gamma }_t^{\left(k\right)}\left(i,u\right)\right]}^{1/2}.$$ (21)

The reestimation formula for the transition probabilities (18) can be understood as the sum of ξ_t(i,j,w) over all t, divided by the total number of transitions leaving from the molecular state i:

$$c_{ij}^{\left(k+1\right)}\left(w\right)=\frac{\sum _t{\xi }_t^{\left(k\right)}\left(i,j,w\right)}{\sum _{t,l,v}{\xi }_t^{\left(k\right)}\left(i,l,v\right)}.$$ (22)

Alternatively, to allow comparison with the results of Milescu et al. (14) we can model the distribution of step sizes as a Gaussian. The k + 1^st estimates of the transition probability a_ij, the mean step-size μ_ij, and its standard deviation s_ij are obtained from the sum and the first and second moments of c_ij(w) taken as a function of w. Then, to iteratively provide an E-M update, c_ij^(k+1)(w) is replaced with a normal distribution computed from these parameters,

$$c_{ij}\left(w\right)=\frac{a_{ij}}{\sqrt{2\pi }{s}_{ij}}\exp \frac{{\left(w-{\mu }_{ij}\right)}^2}{2s_{ij}^2},$$ (23)

where, to preserve precision in the discrete distribution, the quantization of w is best chosen such that s_ij remains larger than unity.

Each of these reestimation formulas results in a new value of a model parameter that increases the likelihood. The forward-backward and reestimation process is iterated until the likelihood approaches a stationary value. Fewer than 100 iterations are typically required to provide convergence.

Initial parameter values

Because there is no prior information about the initial state of the system, we set the initial probability vectors to a uniform distribution,

$${\pi }_{iu}^{\left(0\right)}=\frac{1}{nm}.$$

The transition probabilities c_ij(w) are initialized according to initial values of the molecular transition probabilities a_ij (Eq. 3). The reestimation of c_ij(w) is such that if, for a given combination of i, j, and w its value is zero, the value of c_ij(w) remains zero throughout all iterations. Thus, the initialization of c is sufficient to constrain molecular transitions that do not produce steps, or to constrain step sizes to certain bounds.

For transitions that are accompanied by position steps, we find that c_ij(w) can be initialized to very broad distributions in the step size w, for example Gaussian distributions with standard deviations of m or more. For one-state models, it is sufficient to make it a uniform distribution; for multistate models, it usually suffices to make the distributions of step sizes very broad, but slightly different for different i and j.

We find that a reasonable initial estimate for the root-mean-square (RMS) noise σ₀ can be obtained by first computing the scaled differences

$$\begin{array}{c}{d}_t=\left|y_{t+1}-y_t\right|\sqrt{\left(I_{t+1}+I_t\right)/2I_0},\\ t=1\dots T-1\end{array}$$ (24)

where I_t+1 and I_t are the intensities at the recording times and I₀ is the maximum intensity in the data set. The initial value σ₀⁽⁰⁾ is then obtained as the median of these differences {d_t}. Assuming that steps occur between a minority of sample pairs, the median difference provides a good initial estimate of the noise standard deviation.

Viterbi algorithm

After maximizing L to obtain model parameters, the final task is to restore the position variable. This can be done with the Viterbi algorithm, which requires only the order of m²n²T operations. It finds the sequence of composite states

$${\overline{s}}_1,{\overline{x}}_1,{\overline{s}}_2,{\overline{x}}_2,\dots ,{\overline{s}}_T,{\overline{q}}_T$$

that yields the maximum joint probability P^∗ of that sequence and the observed data, given the particular model parameters found earlier,

$$P^{\ast }=P\left({\overline{s}}_1,{\overline{x}}_1,{\overline{s}}_2,{\overline{x}}_2,\dots ,{\overline{s}}_T,{\overline{x}}_T,Y|\lambda \right).$$ (25)

To do this we calculate the quantity ϕ_t(j,v), which is the probability of the best sequence of states that ends at time t with the composite state (j,v); and we calculate ψ_t(j,v), which identifies which composite state (i,u) at time t−1 is in the best sequence that leads to (j,v) at time t.

Computation of the sequence probability and the best path variable is started with

$${\varphi }_1\left(i,u\right)={\pi }_{iu}{b}_1\left(y_1,u\right).$$ (26)

The calculation is continued iteratively with

$$\begin{array}{l}{\varphi }_t\left(j,v\right)=\underset{i,u}{\max }\left[{\varphi }_{t-1}\left(i,u\right)c_{ij}\left(v-u\right)b_t\left(y_t,v\right)\right]\\ \text{and}\\ {\psi }_t\left(j,v\right)=\underset{i,u}{\arg \max }\left[{\varphi }_{t-1}\left(i,u\right)c_{ij}\left(v-u\right)b_t\left(y_t,v\right)\right],\\ t=2,\dots T.\end{array}$$ (27)

Underflow is prevented in the Viterbi algorithm by calculating the logarithms of the ϕ-variables, instead of the variables themselves.

The best path probability is then obtained as

$$P^{\ast }=\underset{i,u}{\max }\left[{\varphi }_T\left(i,u\right)\right],$$ (28)

and the sequence of states yielding this probability is traced in reverse order, starting with

$$\left({\overline{s}}_T,{\overline{x}}_T\right)=\underset{i,u}{\arg \max }\left[{\varphi }_T\left(i,u\right)\right]$$ (29)

and proceeding recursively as

$$\begin{array}{c}\left({\overline{s}}_t,{\overline{x}}_t\right)={\psi }_{t+1}\left({\overline{s}}_{t+1},{\overline{x}}_{t+1}\right),\\ t=T-1,T-2,\dots 1.\end{array}$$ (30)

Software implementation

To provide artificial data for testing the algorithms, we used a discrete-time simulator that follows a Markov chain defined by the transition probabilities c_ij(w). In this simulator, at most, one state transition occurs per time step. To each position value provided by the simulator, a Gaussian random number is added to emulate the measurement noise. Because in all cases shown here the added noise was at least 2 nm in standard deviation, we rounded the position to the nearest 1 or 2 nm to yield the quantized position values.

The simulator and the VS-HMM algorithms were all implemented using MATLAB, in functions named StepSimulator.m, ForBackF.m, and ViterbiRestoration.m. This code, including auxiliary functions and example programs that reproduce the analyses in Figs. 2–4 of this article, are available at The MathWorks File Exchange site at www.mathworks.com/matlabcentral/fileexchange/24697.

Figure 2.

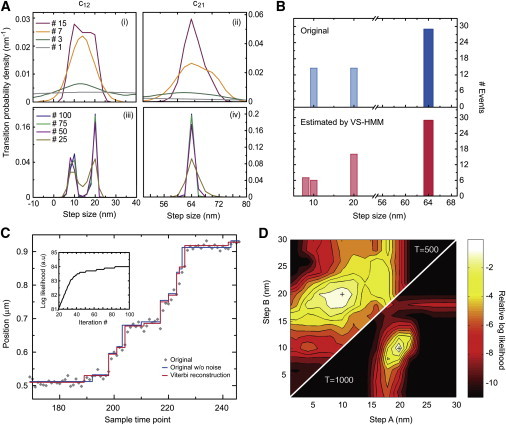
VS-HMM analysis of the simulation in Fig. 1D. (A) The transition probability distributions converge with iterations of the E-M algorithm. The initial transition probability distributions of the HMM (gray sloping lines) were chosen to be nearly uniform but differing slightly. (i and ii) Distributions at iterations 1–15. (iii and iv) Distributions at iterations from 25 to 100. The value c₁₂ converges to 10- and 20-nm steps, c₂₁ converges to 64-nm steps. (B) The estimated step size distribution (red bars) are compared to the actual step sizes used in the simulation (blue bars). (C) The Viterbi restoration (red line) plotted with the noisy data (gray dots) and the underlying noiseless trace (blue line). (Inset) Convergence of the log likelihood L with iterations of the E-M algorithm. Positions were quantized in units of 2 nm and the position range m was equal to 84. Each iteration of the HMM parameter reestimation for this problem (n = 2, T = 500) required ∼1.5 s of computation time on a 2 GHz processor. (D) Confidence intervals in the estimation of the 10- and 20-nm short steps. Each point in the plane represents a pair of the two short step sizes A and B. With the short steps constrained to these two values, the likelihood was maximized by varying all other HMM parameters, and the log likelihood value is represented in the contour plot, with a contour interval of one unit and with zero corresponding to the global maximum values (crosses). The two-unit drop in the log likelihood corresponds roughly to a 95% confidence interval. (Left upper part) Computed from a 500-point simulation, the existence of two distinct small step sizes is seen to be just significant, with the likelihood values along the diagonal being >2 units below the maximum. (Right lower part) Corresponding result for a 1000-point dataset. Note the much sharper peaks and narrower confidence intervals for the step-size values.

Figure 3.

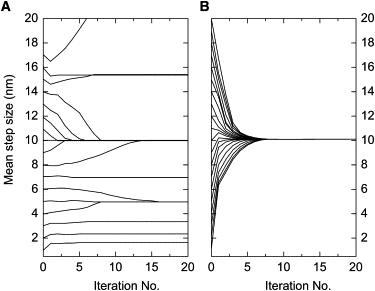
Sensitivity to initial guesses of step size. Analysis of a 200-point time course with HMM algorithms. The simulation had Gaussian-distributed step sizes of 10 ± 1 nm, mean dwell time of 8 and noise σ = 2 nm, chosen to match the simulations in Milescu et al. (14). Initial guesses of step size were Gaussian distributions with mean values of 1 to 20 nm, with standard deviations of 2 nm. The estimated mean step size is plotted as a function of iteration number. (A) Results of the HMM algorithm of Milescu et al. (14), reproduced from their Fig. 7B. Only starting distributions with means between 8 and 14 nm result in convergence to the correct step size. (B) Convergence of step-size estimates from the one-state VS-HMM algorithm described in this article, employing Gaussian-constrained reestimation (Eq. 23) to allow a direct comparison. Convergence is reliable with initial guesses throughout the range of 1–20 nm.

Figure 4.

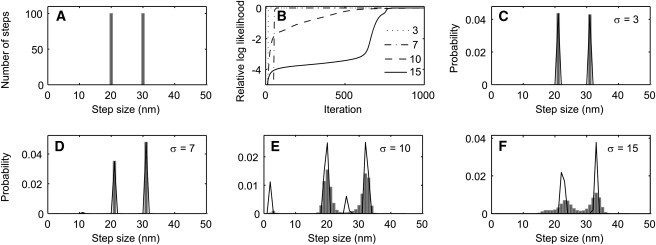
Estimation of a discrete step-size distribution in the presence of various levels of measurement noise; results from one representative simulation. A 2000-point time course was simulated consisting of 200 steps of either 20 or 30 nm and geometrically distributed dwell times with a mean of 10 sample points. (A) Step-size histogram of the 200 generated steps. (B) Convergence of L with a one-state HMM when the simulated time-course had 3, 7, 10, or 15 nm RMS of added Gaussian noise. The value of L after 1000 iterations was taken to be the maximum value. (C–F) Estimated step-size distributions from data having the indicated noise standard deviations σ. The final estimated step-size distributions c(w) (solid lines) and the distributions obtained after partial convergence, when L was 1 log-unit below its final value (solid bars), are plotted . The mean step sizes are recovered with high accuracy up to σ = 15 nm, although at a noise level of 10- or 15-nm spurious peaks in the distribution also appear. In this problem (n = 1, m = 160, T = 2000), each iteration required 1 s of CPU time using a 2 GHz processor.

Results

We first tested the fidelity of the VS-HMM method with a broad range of simulated problems. The computer-generated scenarios involved models with 1–4 molecular states, dwell periods having exponential distributions with average values from 2 to 20 time points, and noise standard deviation ranging up to twice the smallest step size of the simulated motor.

Fig. 1 D shows a 500-datapoint simulation of a motor like the one diagrammed in Fig. 1 A that walks with alternating long and short steps. The simulation does not reflect the behavior of any actual motor, but is designed to test various capabilities of the analysis. The large steps are 64 nm, but the small steps are randomly chosen with equal probability to be either 10 or 20 nm in size; at the level of noise, the difference between these small steps is very difficult to distinguish by conventional step detectors.

The mean dwell times after the short and long steps were given different values of 10 and 5 time points, respectively (a₁₁ = 0.9, a₂₂ = 0.8 in Eq. 1); the choice of a brief five-point dwell will serve, in the following article, as a test of the missed-event issues surrounding Eq. 1. Gaussian noise with standard deviation σ = 7 nm was added to the original signal to generate the trace shown in the Fig. 1 D. In Fig. 1 E the solid staircase represents a subjective fit to the noisy trace by eye; the steps found this way range between 20 and 140 nm (Fig. 1 E, inset), in contrast to the actual 10, 20, and 64 nm.

Fig. 2 shows an HMM analysis of the same artificial recording. The gray curves in the top panels in Fig. 2 A show the initial c₁₂ and c₂₁ step-probability distributions, chosen to be nearly uniform but differing slightly. The E-M algorithm was started with these distributions, an incorrect value of σ₀, and a uniform distribution for π. By 15 iterations, the c₁₂ and c₂₁ distributions showed peaks at step sizes near 15 and 64 nm (Fig. 2 A, i and ii), and after 50 iterations converged to very narrow distributions centered on 9.5 and 20 nm for c₁₂ and 64 nm for c₂₁ (panels iii and iv, Fig. 2 A). The approach of L to its final value is seen to be nearly complete (within one natural-log unit) after 38 iterations (Fig. 2 C, inset), while subsequent computations further sharpened the functions while producing an insignificant increase in L. The other reestimated model parameters after 100 iterations of E-M, a₁₁ = 0.75, a₂₂ = 0.94, and σ = 8.6 nm, were also in excellent agreement with their input values (0.8, 0.9 and 9 nm, respectively).

Based on the estimated parameters, the Viterbi algorithm provided a restored position trace, shown as the red staircase in Fig. 2 C. Note the close similarity of the Viterbi output with the original noiseless trajectory (blue staircase), and the reconstructed step histogram with the actual step distribution (Fig. 2 B). The concurrence between the final estimated parameters and molecular trajectory with those of the original model demonstrates the high fidelity of this approach. The total computation time for the analysis (100 iterations) in Fig. 2, A–C, was 70 s using a single 2 GHz processor; here T = 500 points were analyzed, the quantum of position was 1 nm, and the numbers of states were n = 2 and m = 160.

The log-likelihood value can be used to determine the significance of changes in the model parameters. Profile likelihood confidence intervals can be placed on the parameters by maximizing the likelihood while some parameters are constrained to fixed values (Fig. 2 D). Here changes in L are shown, because the two short-step sizes in the HMM are constrained to values deviating from the optimum (and true) values of 10 and 20 nm. In the case of the 500-point simulation, it is seen that the 2-log likelihood confidence intervals extend from 18 to 21 nm for the larger step, and 6–12 nm for the smaller step. In the case of a 1000-point simulation, the confidence intervals are much tighter. In general, having a larger data set makes the peaks in the likelihood function sharper.

The VS-HMM algorithm, like the HMM algorithm of Milescu et al. (14), maximizes the likelihood, and therefore is expected to converge to the correct model parameters when presented with a sufficiently large dataset. However, one of the major advantages of the VS-HMM algorithm is that it is much less sensitive to initial estimates of step size. Fig. 3 compares the convergence of the two algorithms when used to estimate Gaussian-distributed step sizes. When the algorithm of Milescu et al. (14) is started with an estimate that differs by >25% from the true value of 10 nm, its estimate of the mean step size does not converge to the correct value (Fig. 3 A). The limited range of convergence is intrinsic to this HMM in which the quantum of position is the size of an individual step, even though the size of this quantum is varied in the E-M reestimation.

On the other hand, the VS-HMM algorithm is computationally more intense, but because it models an entire distribution of step sizes, it reliably converges to the true step size from a wide range of starting values (Fig. 3 B). In this example, the initial step-size distributions were Gaussian with standard deviations of 2 nm. VS-HMM converges even faster when the starting step-size distribution is very broad, or even uniform, in which cases almost no prior assumption is being made about step sizes. For example, using an initial distribution that was uniform from −64 to 64 nm, the step size converges to within 2% of the true value after only five iterations (data not shown). Because both algorithms maximize essentially the same likelihood function, they should, in the end, yield the same results within their ranges of convergence.

Because the VS-HMM algorithm models arbitrary step-size distributions, it is of interest to examine its behavior when the step size is highly variable, as is seen in some molecular motors (23). Milescu et al. (14) found that of the various model parameters estimated by the HMM analysis, the standard deviation of step sizes had the greatest uncertainty. This parameter shows a strong anticorrelation with the noise standard-deviation σ. That is, essentially the same likelihood value is obtained when a slight overestimation of σ is coupled with an underestimation of the step-size standard deviation. We find a similar limitation with the VS-HMM method, where step-size distributions tend to be sharpened in the analysis.

We simulated time courses in which the steps have a discrete distribution or a broad distribution of step sizes. The results from the discrete distribution are shown in Fig. 4, and are similar to the results of the simulation of Figs. 1 and 2. Given steps of either 20 or 30 nm, the estimated step-size distribution is essentially correct until the noise standard deviation reaches the large value of 10 nm, equal to the difference in step size, where spurious peaks in the distribution appear. Note that even under these low signal/noise conditions, the major peaks still recover the original step sizes with <5 nm error.

Fig. 5 shows the results from a simulation of a broad, double-Gaussian distribution of step sizes with peaks at 20 and 30 nm. In the VS-HMM analysis, the distribution is sharpened into a series of narrow peaks. Comparing the two Figs. 4 and 5, it is seen that a broad distribution of step sizes can under some conditions be indistinguishable from a discrete distribution with multiple closely-spaced peaks.

Figure 5.

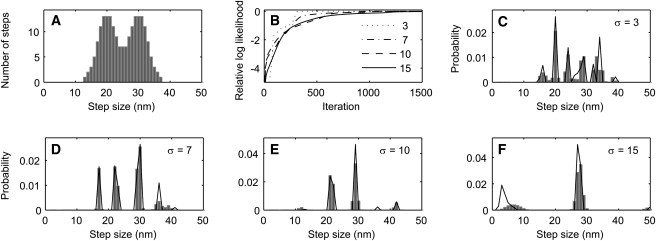
Estimation of a broad step-size distribution in the presence of measurement noise; results from one representative simulation. As in Fig. 4, a 2000-point time course was simulated, but in this case it consisted of variable-sized steps. (A) Step-size histogram of the 200 generated steps; the distribution approximates a mixture of Gaussians with means of 20 and 30 nm having standard deviations of 3 nm. (B) Convergence of L with a one-state HMM when the simulated time-course had 3, 7, 10, or 15 nm RMS of added Gaussian noise. The value of L after 1500 iterations was taken to be the maximum value. (C–F) Estimated step-size distributions from data having the indicated noise standard deviations σ. The final estimated step-size distributions c(w) (solid lines) and the distributions obtained after partial convergence, when L was 1 log-unit below its final value (solid bars), are plotted. Note that the continuous distribution in panel A is recovered as spikes in the analyses of panels C–F.

However, ML estimation is asymptotically unbiased: that is, in the limit of infinite data, the correct model parameters should be obtained. In Fig. 6, we show the results from a simulation with a 20-fold longer time course, with 4000 instead of 200 steps. There are more and broader peaks in the estimated step-size distributions, and at all levels of noise the estimated step-size distributions are distinguishable from the discrete-distribution case in Fig. 4. Therefore, sharpening of distributions appears to be a problem of insufficient sampling from the step-size distribution, which can be circumvented by supplying recordings of sufficient length to the analysis. In all cases, the VS-HMM analysis recovered the step sizes with a remarkably low false positive rate, even at very low signal/noise ratios.

Figure 6.

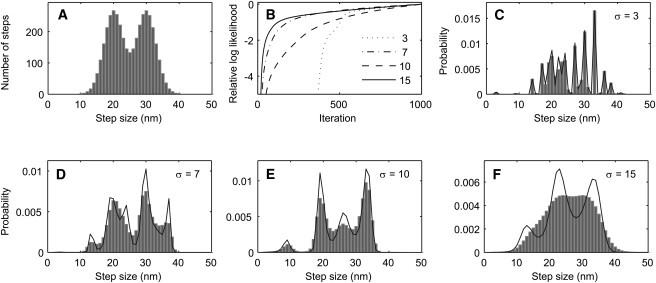
Estimation of a broad step-size distribution as in Fig. 5, but from a 40,000-point time course containing 4000 steps. (A) Simulated step-size distribution. (B) Convergence of L with a 1-state HMM when the simulated time-course had 3, 7, 10, or 15 nm RMS of added Gaussian noise. (C–F) Estimated step-size distributions from data having the indicated noise standard deviations σ. The final estimated step-size distributions c(w) (solid lines) and the distributions obtained after partial convergence, when L was 1 log-unit below its final value (solid bars), are plotted. Note that the continuous distribution in panel A is better recovered with this larger dataset as compared with Fig. 5.

Fig. 7 demonstrates how likelihood values can be used to select the correct kinetic scheme from among several possible candidates. The analysis of the two-state, 64-10/20-nm simulation of Fig. 1 D was analyzed with six different Markov models. Models were constructed with n=1–4 states (n = 2, correct model) and with differing fractions of molecular transitions that result in steps. Models are ranked according to the Bayesian information criterion (see (24)), which compensates for the addition of parameters to the model.

Figure 7.

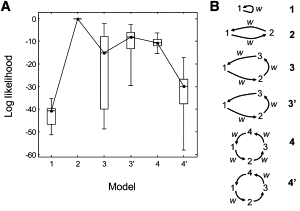
Using likelihood ratios to find the best model for a molecular motor trajectory. (A) Employing 20 different simulations having the same parameters as in Fig. 1D, the maximum log-likelihood is compared for six test models shown in panel B. The Bayes information criterion (24) penalty s = (k/2)ln T has been subtracted from each L value. Here k is the number of parameters (k = 2, 4, 6, 5, 8, and 6 is assumed for models 1–4′, respectively) and T = 500 is the number of data points. Values of L have been shifted so that the value for model 2 is zero. In this box plot the median is plotted, with boxes representing the 25 and 75 percentiles of the distribution of values, and whiskers the extreme values. (B) Models 1–4 involve n = 1–4 molecular states. In these models, each molecular transition is allowed to be accompanied by a position step. In contrast, the 3′ model includes three states but one transition is constrained not to produce a step. Similarly, the 4′ model is composed of four states with every alternate transition not producing a step. In the diagram, w indicates a nonzero step.

Here we use the Bayesian information criterion with the assumption that the inclusion of a nonzero position step represents the introduction of a single new parameter. In Models 1–4, steps were allowed for all molecular transitions, while Models 3′ and 4′ incorporated silent molecular transitions (Fig. 7 B) in which no step is allowed. After subtraction of the penalty, all of the models were consistently inferior to the correct Model 2. Thus the VS-HMM can be used to identify the best among specific models, but it should be kept in mind that the user ultimately has to choose which models to test.

Discussion

Milescu et al. (14) first showed that hidden Markov models can be used for the modeling and restoration of the stepping time courses of molecular motors. We present a related algorithm, called VS-HMM, which in some ways is more useful for answering basic questions about the behavior of molecular motors. The main impetus was to develop an algorithm that models the dynamics of molecular motors from recordings suffering from poor signal/noise ratio, and that is insensitive to initial parameter choices. The activity of a motor protein is modeled as a Markov process, and the problem of representing the motor's position is solved by using a very large number of states in the hidden Markov model. ML estimation is used to obtain kinetic parameters for the motor's reaction cycle, and the Viterbi algorithm is applied to provide an estimate of the noiseless motor position as a function of time.

The VS-HMM method described here fills a critical gap in the currently available techniques to analyze and restore noisy molecular motor traces when the step sizes and distributions are unknown. In the past, the most robust methods for step-size determination have quantified fluctuations in velocity or position to yield an average value for the step size (25). These methods rely on the constraints of uniform step sizes and particular distributions of the dwell times, but have the advantage of yielding useful results even when the individual steps cannot be resolved. On the other hand, when recordings have better signal/noise, the individual steps can be determined by step-detecting methods such as t-test, χ², and wavelet approaches (4). Milescu et al. (14,20) have applied HMM theory to provide ML estimates of kinetic parameters and the mean and variance of step sizes by assuming a Gaussian distribution of step sizes. Although computationally efficient, their HMM formulation allows convergence only when the initial user-defined step sizes are close to the true value.

Our algorithm also provides ML estimates, but is quite insensitive to initial parameter values (Fig. 3); this insensitivity is the central improvement of our method, because it frees the user from specifying the size or distribution of the molecular steps. Starting from flat initial distributions, or very broad Gaussian distributions centered at some arbitrary values, the step-size probabilities c₁₂ and c₂₁ of a two-state model rapidly converge to show the variety of step sizes in the simulated data, even when the RMS noise is comparable to the size of the smallest steps (Fig. 2). Indeed, our algorithm correctly identifies the size and kinetics of 10-nm steps in the presence of noise up to σ = 14 nm (see Fig. S1 in the Supporting Material). These features make the program very powerful and essentially automatic.

Owing to the inherent confusion in interpreting noisy recordings by eye, conclusions from single-molecule experiments are often limited by data quality. In the case of the simulated stepping data used here, the HMM clearly distinguishes correct small and large step sizes in cases like Fig. 1 D where a human observer easily misses the small steps. Yildiz and Selvin (1) cite examples where only 74-nm steps were originally identified, while subsequent analysis of the same data with the VS-HMM described here showed alternating 10- and 64-nm steps (6). Although previous HMM analyses find small steps if the hypothesis of small steps is tested explicitly (14), the improved method presented here can automatically uncover their presence. In the following article (6) we describe the application of the HMM method to such data, along with enhancements to the hidden Markov model to better describe experimental recordings.