Abstract
Cancer is the consequence of an unwanted evolutionary process. Cells receive mutations that alter their phenotype. Especially dangerous are those mutations that increase the net reproductive rate of cells, thereby leading to neoplasia and later to cancer. The standard models of evolutionary dynamics consider well mixed populations of individuals in symmetric positions. Here we introduce a spatially explicit, asymmetric stochastic process that captures the essential architecture of evolutionary dynamics operating within tissues of multicellular organisms. The “linear process” has the property of canceling out selective differences among cells yet retaining the protective function of apoptosis. This design can slow down the rate of somatic evolution dramatically and therefore delay the onset of cancer.
Mutations in oncogenes and tumor suppressor genes can increase the net reproductive rate of cells (1–5) and therefore provide a selective advantage for mutated cells. Mutations in genes that maintain the integrity of the genome can trigger genetic instability (6–10), which may come at a selective cost but increases the chance of acquiring further mutations that are advantageous for the cell (11–13). Hence, both advantageous and deleterious mutations can represent steps toward cancer (14). Most human cancers arise in epithelial tissues, which are organized into small compartments of cells (15–21). In this article, we study how the architecture of cells within a compartment determines the evolutionary process of cancer initiation (14).
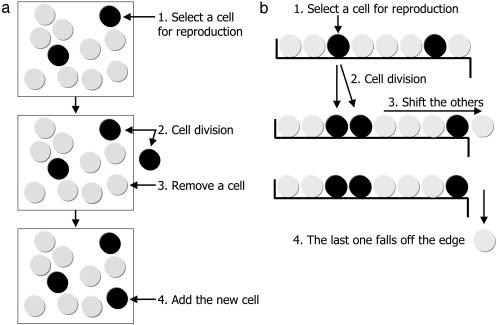
Consider a compartment of N cells within a tissue of a multicellular organism. Suppose a mutation in a particular gene alters the reproductive rate of a cell. Wild-type and mutant cells have reproductive rates r1 and r2, respectively. The relative fitness of mutant compared with wild type is s = r2/r1; it can be greater than, equal to, or less than one. The probability that the gene is mutated during cell division is given by u. To calculate the rate at which mutated cells accumulate, we have to define a specific stochastic process. Fig. 1a illustrates the Moran process (22). Any single time step consists of two elementary events: (i) a random cell is chosen for division proportional to its reproductive rate, and (ii) a random cell is chosen for elimination. Hence, the total number of cells is always constant. Division of a wild-type cell gives rise to a mutant cell with probability u. We ignore back mutation.
Fig. 1.
Two stochastic processes of evolutionary dynamics. (a) In the Moran process, cells are in identical positions. For reproduction, a cell is chosen proportional to its reproductive rate. The offspring of this cell replaces a randomly chosen cell. The total number of cells is always constant. (b) In the linear process, cells are arranged in a row and labeled i = 1,..., N. For reproduction, cells are again chosen proportional to their reproductive rate. The reproducing cell is replaced by two daughter cells. All cells to the right are shifted by one position. The rightmost cell undergoes apoptosis (falls off the edge of the one-dimensional table). The linear process captures fundamental properties of the architecture of cell division in multicellular organisms. We propose that this architecture evolved to delay the onset of cancer. In the linear process, mutations in oncogenes or tumor suppressor genes that increase the reproductive rate of cells accumulate as slowly as neutral mutations.
Mutant cells are produced at rate Nu. The probability of fixation (taking over the whole population) of a single mutant cell with relative fitness s is given by ρ = (1 – 1/s)/(1 – 1/sN). The probability that a compartment of N cells has been taken over by mutant cells at time t is given by P(t) = 1 – exp(–Nuρt). Time is measured in units of cellular generations. If t ≪ 1/(Nuρ), then the approximation P(t) ≈ Nuρt holds. This means that we are interested in time scales for which most cells of an organism are not yet mutated with respect to a particular gene.
If the mutation confers a strong selective advantage, s ≫ 1, then ρ ≈ 1 and P(t) = Nut. If the mutation is neutral, s = 1, then ρ = 1/N and P(t) = ut. This is Kimura's well known result, that the rate of fixation of neutral mutants is independent of the population size (23). If the mutant has a strong selective disadvantage, s ≪ 1, then the probability of fixation is much smaller than 1/N. Hence, cellular dynamics that follow the Moran process allow rapid accumulation of advantageous mutations and slow accumulation of deleterious mutations.
The Moran process describes evolutionary dynamics in a well mixed population of cells. All cells are in equivalent positions and are in direct reproductive competition with each other. There are no spatial effects. There is no cellular differentiation. Tissues of multicellular organisms, however, are not organized in this way. Instead, geometric arrangements and cellular differentiation induce asymmetries. Stem cells produce differentiated cells, thereby generating a flow that can “wash out” harmful mutations (24). Epithelial compartments such as the colonic crypt, for example, are replenished by a small number of tissue-specific stem cells. The adult colon contains ≈107 crypts. Each crypt consists of 1,000–4,000 cells. A small number of intestinal stem cells reside at the base of each crypt. They divide to maintain their own number and to generate differentiated daughter cells. These daughter cells migrate up the crypt, continuing to divide until they reach its midportion. Then they stop dividing and differentiate to mature cells. When the cells reach the top of the crypt, they undergo apoptosis and are engulfed by stromal cells or shed into the gut lumen.
Let us define the most elementary stochastic process that captures such an architecture of cell division. Suppose cells are organized into a linear array, labeled i = 1,..., N (Fig. 1b). At each time step, a cell is chosen for reproduction. Wild-type and mutant cells are chosen proportional to their reproductive rates, r1 and r2. The chosen cell divides into two daughter cells. One daughter cell takes the position of the parent cell, and the other daughter cell takes the position to the right of it. All cells to the right of the two new cells are shifted by one position. The cell in position i = N is eliminated. If a wild-type cell divides, then each daughter cell is mutated with probability u/2. Hence, the probability that the gene is mutated during cell division is given by u, as before. We call this stochastic process the “linear array process,” or “linear process” for short.
Surprisingly, the fixation rate of the linear process is given by P(t) = ut/2, independent of the relative fitness, s = r2/r1, of the mutant cells and independent of the population size, N. All mutations behave like neutral mutations. For a mutation to be fixed in the linear process, it must occur in the cell at position i = 1. The rate at which this cell becomes mutated is u/2. Once this cell is mutated, the mutation will become fixed with a probability of 1 irrespective of differences in reproductive rates.
Table 1 provides numerical examples for the rate of evolution in the Moran and linear processes. The rate of evolution of any mutant in the linear process is half as fast as the rate of neutral evolution in the Moran process. The factor 1/2 comes from the fact that the left daughter cell generated by a division of the cell in position i = 1 needs to be mutated for fixation to occur. Consider the possibility that the cell in position i = 1 is a stem cell and divides asymmetrically into a stem cell that stays in position i = 1 and a differentiated cell that goes into position i = 2. There is evidence that stem cell division has asymmetric mutation rates (25) with a lower probability of mutating the DNA that remains in the stem cell. This effect can further reduce the rate of evolution in the linear process. Note that these asymmetric mutation rates have no consequence for the rate of evolution in the Moran process.
Table 1. Numerical examples for the rate of evolution in the Moran and linear processes.
| Moran
|
Linear, independent of N
|
|||
|---|---|---|---|---|
| τ = 1
|
||||
| r | N = 10 | N = 20 | τ0 = 1 | τ0 = 10 |
| 2 | 5.0 | 10.0 | 0.5 | 0.05 |
| 1.2 | 1.99 | 3.42 | 0.5 | 0.05 |
| 1 | 1 | 1 | 0.5 | 0.05 |
| 0.8 | 0.30 | 0.06 | 0.5 | 0.05 |
| 0.5 | 0.01 | 10 | 0.5 | 0.05 |
In the Moran process with random cell death, the probability that mutant cells have become fixed is P(t) = N ρut/τ. In the linear process, we have P(t) = ut/(2τ0). We list the factor that multiplies ut. In the Moran process, advantageous mutants, r > 1, accumulate faster than neutral mutants, r = 1, which accumulate faster than deleterious mutants, r < 1. In the linear process, mutants accumulate independent of their selective value at a rate that is τ/(2τ0) times the rate of neutral evolution in the Moran process.
There is also evidence that stem cells divide at a slower rate than differentiated cells (18). In this case, the fixation rate is reduced to P(t) = ρut/(2τ0), where τ0 is the average duration of a stem cell generation. Therefore, the architecture of the linear process facilitates further mechanisms to reduce the rate of somatic evolution.
Thus far we have assumed that wild-type and mutant cells are equivalent with respect to cell death. In the Moran process cell death is random, whereas in the linear process only the cell in position N dies. Let us now introduce different rates of apoptosis for wild-type and mutant cells. In the linear process, the cell in position N dies with probability p. With probability 1 – p, a random cell is chosen proportional to its rate of undergoing apoptosis. A natural choice is p = 1/(1 + a1N1 + a2N2), where a1 and a2 denote the rates of premature apoptosis of wild-type and mutant cells, respectively, whereas N1 and N2 denote their respective numbers. Similarly, in the Moran process a random cell is eliminated with probability p, whereas a cell is chosen proportional to its apoptosis rate with probability 1 – p.
For the Moran process the same calculation holds as before, but the relative fitness of the mutant is now given by s = [r2/(1 + a2N)]/[r1/(1 + a1N)]. Thus, the Moran process is symmetric with respect to selection affecting cell birth or death.
For the linear process, we obtain analytic solutions in two limiting cases. First, suppose that premature apoptosis of wild-type cells is negligible, a1 = 0. In this case, the probability that a single mutant cell starting in position one takes over the whole compartment is given by
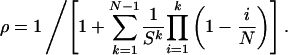 |
[1] |
Here s = r2/(r1a2N). The probability that a compartment is mutated by time t is given by P(t) = ρut/2. Numerical simulations show that this solution is also an excellent approximation for small rates of apoptosis of wild-type cells, a1 > 0. For s ≫ 1, Eq. 1 can be approximated by ρ ≈ (1 – 1/s)/(1 – 1/sN), the same expression as for the Moran process but with different values of s. For s ≪ 1, Eq. 1 can be approximated by ρ ≈ (sN)N–1e–sN/(N – 1)!, which is the formula for the standard γ distribution.
Second, the opposite extreme is the assumption that the rates of apoptosis of both wild-type and mutant cells are high. Therefore, the probability that cell N is discarded is negligible, p ≈ 0. In this limit, the linear and Moran processes are equivalent. The relative fitness of mutant cells is given by s = [r2/(a2N)]/[r1/(a1N)], the fixation probability is ρ = (1 – 1/s)/(1 – 1/sN), and the accumulation of mutated compartments is described by P(t) = Nρut. Thus, high rates of apoptosis destroy the flow within the linear process and allow the rapid fixation of advantageous mutants. Therefore, chemicals and radiation that induce premature apoptosis are carcinogenic not only by increasing mutation rates but also by inhibiting the cellular flow that otherwise would weed out mutated cells.
Table 2 provides numerical examples. Premature apoptosis of mutated cells reduces the rate of evolution in the linear process. Some mutants that are advantageous in the Moran process are slower than neutral in the linear process. Although premature apoptosis helps to slow down deleterious mutants in the linear process, the best architecture for containing deleterious mutants is given by a Moran process with large compartment sizes.
Table 2. The effect of selective apoptosis.
| Moran
|
Linear
|
|||
|---|---|---|---|---|
| a2N | N = 10 | N = 20 | N = 10 | N = 20 |
| 0 | 5.00 | 10.0 | 0.50 | 0.50 |
| 0.2 | 4.02 | 8.00 | 0.46 | 0.45 |
| 1.0 | 1.00 | 1.00 | 0.29 | 0.27 |
| 2 | 0.088 | 0.003 | 0.14 | 0.094 |
Selective apoptosis, a2, of mutant cells slows down the rate of evolution in the linear and Moran processes. Again the factor that multiplies ut is shown. For the Moran process, it is N ρ(s)/τ with s = r2/[r1(1 + a2N)]. For the linear process, it is Nδ/(2τ0) with ρ given by Eq. 1. We choose r1 = 1, r2 = 2 and τ = τ0 = 1.
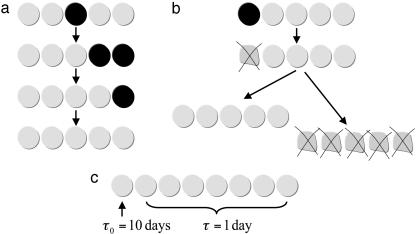
For the linear process, we have assumed that if a cell in position i dies, its function can be taken over by the cell in position i + 1. This is not the case for irreversible differentiation. Suppose the cell in i = 1 is a tissue-specific stem cell, whereas the other cells are irreversibly differentiated. If the cell in position i = 1 undergoes apoptosis, then the whole compartment might die (Fig. 2). If apoptosis is unlikely for wild-type cells but occurs for mutant cells at rate a2, then mutated compartments have an average lifetime of 1/a2. The expected number of mutated compartments rises initially as a linear function of time and then saturates at a steady-state level. If mutated compartments require another mutation for further neoplastic growth, then apoptosis of mutated stem cells and subsequent loss of the compartment is an effective prevention of cancer initiation.
Fig. 2.
The architecture of the linear process facilitates a number of mechanisms that slow down the unwanted somatic evolution leading to cancer. The cell in position i = 1 functions like a stem cell for this compartment. (a) Mutations that do not occur in stem cells are washed out. (b) If mutated stem cells undergo apoptosis, then mutated compartments can become entirely wild-type, given that cells in position i = 2 take over the stem cell function, or the whole compartment might die. Both processes prevent the accumulation of mutated cells. (c) If stem cells divide only once every 10 days, whereas all other cells divide once per day, then the rate of evolution in the linear process is reduced by a factor of 10.
We also can calculate the rate of eliminating tumor suppressor genes (Appendix and Table 3). The number of mutated compartments at a given time is many orders of magnitude lower for the linear process. Thus, the architecture of the linear process is also protective against accumulation of cells with inactivated tumor suppressor genes.
Table 3. Tumor suppressor genes.
| Linear
|
|||
|---|---|---|---|
| N | Moran, τ = 1 | τ0 = 1 | τ0 = 10 |
| 100 | 11127 | 82 | 1 |
| 1000 | 23539 | 82 | 1 |
| 10000 | 180790 | 82 | 1 |
Tumor suppressor genes require inactivation of both alleles for the cell to have an increased net growth rate. Here we show the expected number of mutated compartments at t = 70 years of age in an organ that contains 107 compartments. Parameters are u1 = 10-7, u2 = 10-6, and ρ = 1/2. The linear process leads to a much smaller number of mutated compartments, thereby efficiently delaying cancer initiation.
In summary, we defined a simple stochastic process that captures fundamental properties of evolutionary dynamics within tissues of multicellular organisms. In the basic linear process, mutations in oncogenes or tumor suppressor genes that increase the reproductive rates of cells have the same fixation probability as neutral mutations. In the extended linear process with premature apoptosis, mutations that have an increased net reproductive rate in the Moran process can be fixed more slowly than neutral mutations. Irreversible differentiation, slower cycling time of stem cells, and asymmetric mutation rates in stem cell divisions are additional mechanisms that reduce the rate of evolution in the linear process (Fig. 2). We propose that patterns of cell division in tissues of multicellular organisms have evolved to delay the onset of cancer. The linear process provides a quantitative understanding for how various mechanisms slow down the unwanted somatic evolution that leads to cancer.
Appendix
Fixation Probability in the Linear Process. Consider the linear process with premature apoptosis of mutant cells but not of wild-type cells. We calculate the probability that a single mutant cell starting in position one will reach fixation. The only configurations that can occur have mutant cells in the leftmost positions; a wild-type cell can never be to the left of a mutant cell. The state of the stochastic process is given by the number, i, of mutant cells. We have a birth–death process in the states i = 0,..., N. There are two absorbing states: 0 and N. The reproductive rates of wild-type and mutant cells are given by r1 and r2, respectively. The probability that a mutant cell is chosen for reproduction is bi = r2i/[r1(N – i) + r2i]. The probability that a wild-type cell is chosen for reproduction is 1 – bi. The probability that the cell in position N undergoes apoptosis is given by pi = 1/(1 + a2i). The probability that a mutant cell undergoes premature apoptosis is given by 1 – pi. The transition matrix for the birth–death process is given by
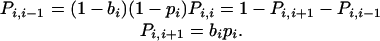 |
[2] |
Denote by xi the probability that the system will be absorbed into state N starting from state i. Solving the recursion xi = Pi,i+1xi+1 + Pi, i xi + Pi,i–1xi–1 leads to Eq. 1 for the probability x1. This expression is the inverse of a generalized hypergeometric function, ρ = 1/F([1,1 – N], [], – 1/sN).
Tumor Suppressor Genes. Denote by u1 and u2 the mutation rates for inactivating the first and second allele of a tumor suppressor gene, respectively. Consider a compartment of N cells. Let N < 1/u1 and u1 < u2. The second mutation can be much faster because of various mechanisms that lead to loss of heterozygosity. In a Moran process, the probability that a cell with two inactivated alleles has reached fixation by time t is given by
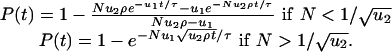 |
[3] |
Here ρ denotes the probability that a single cell with two inactivated alleles reaches fixation, and τ is the cellular generation time. In a linear process with N cells, neglecting premature apoptosis, the corresponding fixation probability is given by
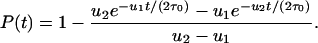 |
[4] |
The generation time of the stem cell (in position one) is given by τ0. The factor 1/2 in the exponent arises from the fact that, in the linear process, the left daughter cell has to receive the mutational hit: If the cell in position one divides, then the left daughter cell goes to position one, and the right daughter cell goes to position two. A mutation in position two will be washed out.
In a tissue with M compartments, the expected number of mutated compartments at time t is given by MP(t).
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Vogelstein, B. & Kinzler, K. W. (1998) The Genetic Basis of Human Cancer (McGraw–Hill, Toronto).
- 2.Knudson, A. G. (2001) Nat. Rev. Cancer 1, 157–162. [DOI] [PubMed] [Google Scholar]
- 3.Weinberg, R. A. (1991) Science 254, 1138–1146. [DOI] [PubMed] [Google Scholar]
- 4.Levine, A. J. (1993) Annu. Rev. Biochem. 62, 623–651. [DOI] [PubMed] [Google Scholar]
- 5.Knudson, A. G. (1993) Proc. Natl. Acad. Sci. USA 90, 10914–10921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lengauer, C., Kinzler, K. W. & Vogelstein, B. (1997) Nature 386, 623–627. [DOI] [PubMed] [Google Scholar]
- 7.Lengauer, C., Kinzler, K. W. & Vogelstein, B. (1998) Nature 396, 643–649. [DOI] [PubMed] [Google Scholar]
- 8.Loeb, L. A. (2001) Cancer Res. 61, 3230–3239. [PubMed] [Google Scholar]
- 9.Boyer, J. C., Umar, A., Risinger, J. I., Lipford, J. R., Kane, M., Yin, S., Barrett, J. C., Kolodner, R. D. & Kunkel, T. A. (1995) Cancer Res. 55, 6063–6070. [PubMed] [Google Scholar]
- 10.Tomlinson, I. P., Novelli, M. R. & Bodmer, W. F. (1996) Proc. Natl. Acad. Sci. USA 93, 14800–14803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nowak, M. A., Komarova, N. L., Sengupta, A., Jallepalli, P. V., Shih, I.-M., Vogelstein, B. & Lengauer, C. (2002) Proc. Natl. Acad. Sci. USA 99, 16226–16231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Michor, F., Iwasa, Y., Komarova, N. L. & Nowak, M. A. (2003) Curr. Biol. 13, 581–584. [DOI] [PubMed] [Google Scholar]
- 13.Komarova, N. L., Lengauer, C., Vogelstein, B. & Nowak, M. A. (2002) Cancer Biol. Ther. 1, 685–692. [DOI] [PubMed] [Google Scholar]
- 14.Michor, F., Frank, S. A., May, R. M., Iwasa, Y. & Nowak, M. A. (2003) J. Theor. Biol. 225, 377–382. [DOI] [PubMed] [Google Scholar]
- 15.Mintz, B. (1971) Symp. Soc. Exp. Biol. 25, 345–370. [PubMed] [Google Scholar]
- 16.Mintz, B. (1977) Adv. Pathobiol. 6, 153–157. [PubMed] [Google Scholar]
- 17.Winton, D. J. & Ponder, B. A. J. (1990) Proc. R. Soc. London Ser. B 241, 13–18. [DOI] [PubMed] [Google Scholar]
- 18.Tannishtha, R., Morrison, S. J., Clarke, M. F. & Weissman, I. L. (2001) Nature 414, 105–111. [DOI] [PubMed] [Google Scholar]
- 19.Turksen, K. & Troy, T. C. (1998) Biochem. Cell Biol. 76, 889–898. [DOI] [PubMed] [Google Scholar]
- 20.Janes, S. M., Lowell, S. & Hutter, C. (2002) J. Pathol. 197, 479–491. [DOI] [PubMed] [Google Scholar]
- 21.Marshak, D. R., Gardner, R. L. & Gottleib, D. (2001) Stem Cell Biology (Cold Spring Harbor Lab. Press, Plainview, NY).
- 22.Moran, P. (1962) The Statistical Processes of Evolutionary Theory (Clarendon, Oxford).
- 23.Kimura, M. (1968) Nature 217, 624–626. [DOI] [PubMed] [Google Scholar]
- 24.Cairns, J. (1975) Nature 255, 197–200. [DOI] [PubMed] [Google Scholar]
- 25.Cairns, J. (2002) Proc. Natl. Acad. Sci. USA 99, 10567–10570. [DOI] [PMC free article] [PubMed] [Google Scholar]