Liquid-Liquid Phase Separation of a Monoclonal Antibody and Nonmonotonic Influence of Hofmeister Anions

Abstract

Liquid-liquid phase separation was studied for a monoclonal antibody in the monovalent salt solutions of KF, KCl, and KSCN under different pH conditions. A modified Carnahan-Starling hard-sphere model was utilized to fit the experimental data, establish the liquid-liquid coexistence curve, and determine antibody-antibody interactions in the form of T_c (critical temperature) under the different solution conditions. The liquid-liquid phase separation revealed the complex relationships between antibody-antibody interactions and different solution conditions, such as pH, ionic strength, and the type of anion. At pH 7.1, close to the pI of the antibody, a decrease of T_c versus ionic strength was observed at low salt conditions, suggesting that the protein-protein interactions became less attractive. At a pH value below the pI of the antibody, a nonmonotonic relationship of T_c versus ionic strength was apparent: initially as the ionic strength increased, protein-protein interactions became more attractive with the effectiveness of the anions following the inverse Hofmeister series; then the interactions became less attractive following the direct Hofmeister series. This nonmonotonic relationship may be explained by combining the charge neutralization by the anions, perhaps with the ion-correlation force for polarizable anions, and their preferential interactions with the antibody.

Introduction

Protein liquid-liquid phase separation (LLPS) is an intriguing thermodynamically driven event, in which a homogenous protein solution separates into a protein-poor top layer and a protein-rich bottom layer as the temperature decreases. Often this event is reversible simply by mixing the two phases and raising the temperature of the solution.

Protein LLPS has wide implications in many biological processes. It has been postulated that the LLPS happens in the cytoplasm, where the protein concentration may reach 350 mg/mL (1). There is abundant experimental evidence that LLPS of a class of lens proteins, the γ-crystallins, is involved in mammalian cataracts (2,3). Furthermore, it has been shown that protein LLPS plays a role in sickle-cell disease (4). Also, it has been demonstrated that protein LLPS is a prerequisite for one of the pathways in protein crystallization (5).

The occurrence of protein LLPS has been attributed to short-range protein-protein interactions, most likely attractive in nature (6). Therefore, the protein-protein interactions can be studied by using the protein LLPS event (7). However, protein LLPS typically occurs at metastable conditions. Experimental data of protein LLPS are sparse and limited to a few small globular proteins, e.g., lysozyme (8,9) and γ-crystallins (10,11).

LLPS of monoclonal antibodies is of special interest to the biopharmaceutical industry because there is a need for developing long-term stable liquid formulations at high antibody concentrations, i.e., >100 mg/mL. LLPS is one of several possible solution behaviors, such as amorphous precipitation, crystallization, and gel formation, for monoclonal antibody solutions at high concentration. However, monoclonal antibody LLPS is still poorly understood. Despite the recent work on LLPS of monoclonal antibodies (12–16), there is a lack of systematic experimental studies to evaluate the effect of pH, ionic strength, and salt type on monoclonal antibody LLPS.

In this article, we studied the LLPS of a recombinant monoclonal antibody, by constructing the liquid-liquid coexistence curves, in the monovalent salt solutions of KF, KCl, and KSCN at low ionic strength under different pH conditions. Our objective was to understand protein-protein interactions qualitatively in relationship to the above solution conditions by charting perturbations of T_c that are indicative of the trends of attractive interactions (becoming stronger or weaker). This approach of using T_c or T_cloud as a relative measurement of protein-protein interactions has been used for studying LLPS of lysozyme in salt solutions (8,9,17,18).

We chose the above three anions because they follow the order of F⁻ > Cl⁻ > SCN⁻ for precipitating proteins according to the (direct) Hofmeister series (19–23). Although the exact interaction mechanisms of the electrolyte ions with proteins are still open to debate (24–27), the above three monovalent anions should impart an effect on LLPS of the antibody because they rank from the strongly hydrated F⁻ to the weakly hydrated SCN⁻ (19–23). Our work may fundamentally help us to understand how the solution conditions affect the LLPS of monoclonal antibodies and extend the current knowledge of protein LLPS beyond the work generally performed on small globular proteins.

Materials and Methods

LLPS experiment

The antibody studied was a humanized IgG₂ with a molecular mass of ∼148 kDa and measured pI of 7.2 (Amgen internal data). A stock solution of the recombinant humanized IgG₂ monoclonal antibody was produced at Amgen. It was exhaustively dialyzed into Milli-Q water (Millipore, Billerica, MA) using 6000–8000 Da molecular mass cutoff Spectra/Por dialysis tubing obtained from Spectrum Laboratories (Carilion-Spectrum, Greensboro, NC). The volume ratio of the protein solution to water was ∼1:100 with three exchanges over a period of 48 h at 2–8°C with constant gentle stirring. The material was then collected and concentrated using a Stir Cell (Amicon, Houston, TX) with a 10,000 Da molecular mass cutoff to obtain a solution at 133 mg/mL. The antibody solution was mixed with Milli-Q water and desired amounts of potassium monophosphate and potassium diphosphate stock solutions to achieve 22 ± 1.5 mM ionic strength at the target pH conditions of 6.1, 6.6, and 7.1, respectively, and a final antibody concentration of 90 mg/mL.

Similarly, appropriate amounts of acetic acid and NaOH were added to achieve the target pH of 5.3 at 22 ± 1 mM ionic strength. The pH of all the above solutions was within ±0.1 of the target values, as measured by an Orion pH meter with a Micro Combination pH electrode (Thermo Scientific, Waltham, MA). High pH, i.e., >8.0 range, was not explored because of potential chemical instability. In the KCl series experiment, the samples were prepared using the above procedure except that the desired amount of the KCl stock solution was added and the volume of water was reduced accordingly to maintain a 90 mg/mL concentration. This approach was also used to prepare the samples for the ionic strength series experiments with KF, KCl, and KSCN. The final volume for each sample was 1.4 mL. All the salt concentrations mentioned in this article were reported as ionic strength, unless specified otherwise. Examples of sample preparation details and calculation of the ionic strength are presented in the Supporting Material.

All samples were placed into clear plastic tubes obtained from Beckman Instruments (Beckman-Coulter, Fullerton, CA) and centrifuged at 6000 rpm (504 × g) using an Allegra 64R centrifuge fitted with a F2402H rotor (Beckman-Coulter). The samples were centrifuged at the desired temperature between −2°C and −12°C for a minimum of 30 min. The temperature was verified externally using a model No. HH21 Microprocessor Thermometer (Omega Engineering, Stamford, CT) fitted with a Type K thermocouple. In the event that phase separation had occurred, the top layer and the bottom layer were sampled using a positive displacement pipette (Gilson, Middleton, WI). If phase separation was not observed, no sample was taken.

Upon phase separation, the antibody concentrations of the top and bottom layers were determined using a UV-vis spectrometer (Agilent, Santa Clara, CA). The absorbance was measured at 280 nm in a 1-cm pathlength cuvette to determine the antibody concentration, using the extinction coefficient of 1.4 mL × mg⁻¹ × cm⁻¹ (Amgen internal data). For the top layer, a 25-μL aliquot was taken and diluted in water by 100-fold. A 50-μL aliquot of the bottom layer was diluted in water by 500-fold. The spectrometer was then blanked against water and the absorbance was measured.

The standard deviation for the antibody concentration measurement was determined for three samples at 22 mM and pH 7.1 at −9°C for both bottom and top layers, as an overall estimation for the standard deviation for all the measurements. For the KCl series experiment, both top and bottom layers were sampled to determine the liquid-liquid coexistence curve. In the ionic strength experiment with KF, KCl, and KSCN, the top layer was sampled for all the temperatures when the LLPS occurred and the bottom layer was sampled only at one temperature. The data set obtained was used to fit the coexistence curve and estimate the T_c for each condition.

The net charge of the antibody at different pH conditions was estimated according to the method developed by Shire (28) (shown in the Supporting Material). The antibody has ∼26, 11, 4, and 0 net positive charges at pH 5.3, 6.1, 6.6, and 7.1, respectively.

Fitting of the liquid-liquid coexistence curve and modeling

The LLPS data was fitted to a coexistence curve derived from the following equation of state for osmotic pressure (Eq. 1) for a modified Carnahan-Starling hard-sphere model (i.e., the CS model), as described by Petsev et al. (29):

$$\frac{\Pi V_{hs}}{kT}=\varphi \frac{1+\varphi +{\varphi }^2-{\varphi }^3}{{\left(1-\varphi \right)}^3}+B_2^{\prime }{\varphi }^2+B_3^{\prime }{\varphi }^3+B_4^{\prime }{\varphi }^4+\dots .$$ (1)

This model implies a reference system of hard-spheres with the repulsive force shown in the first term and with the additional interactions modeled by the first few terms of a virial series. The value ϕ is the volume fraction of the antibody hard-sphere, i.e., ϕ = V_hsn, where n is the number density of the antibody solution and V_hs is the volume of the hard sphere (in our studies, this includes the hydration layer). The value k is the Boltzmann constant. The value T is the absolute temperature and B₂′ is the contribution of an effective two-body interaction outside the hard-sphere to the second virial coefficient, and B₃′ and B₄′ are the third- and fourth-order contributions, respectively. Higher order terms are ignored.

To account for the anisotropic nature of protein-protein interactions, we further modeled the two-body attractive interaction represented by B₂′ using the form of the Flory interaction parameter as in the Flory-Huggins theory of polymer solutions (30),

$$B_2^{\prime }=-A\frac{\theta }{T}+A,$$ (2)

where A is a positive coefficient and θ is the temperature at which the mean field two-body attractive interaction is zero.

The coexistence curve can be obtained by the Maxwell construction on the Π-ϕ diagram, which implies the equality of chemical potentials of the two phases. We can fit the coexistence curve to the LLPS data and extract parameters A, θ, and V_hs. The critical temperature and the concentration (T_c and C_c) can be estimated by the requirement of an inflection point on the Π-V diagram,

$${\left(\frac{\partial \Pi }{\partial \varphi }\right)}_{{\varphi }_c,T_c}=0\text{and}{\left(\frac{{\partial }^2\Pi }{\partial {\varphi }^2}\right)}_{{\varphi }_c,T_c}=0.$$ (3)

By definition, the osmotic second virial coefficient B₂₂ (31,32) can also be calculated from B₂′ as

$$B_{22}=\frac{\left(4+B_2^{\prime }\right)V_{hs}}{M_W^2}\equiv \frac{B_2}{M_w^2},$$ (4)

where M_W is the molecular weight of the antibody molecule and B₂ is the conventionally defined second virial coefficient. B₂₂ is often used to represent the nature and strength of the interaction between two molecules.

To assess the error in the fitted parameters, we have assumed that the error of measured temperature follows a normal distribution with a standard deviation of 0.5 K, and used 100 sets of computer-generated random numbers to simulate this distribution, and hence generated 100 sets of simulated temperature data sets for each measured data set. Although the resulting data might not follow a normal distribution, we used a standard deviation as an estimate for the accuracy of the fitted numbers.

Results

LLPS

It was observed that the antibody solution was slightly opalescent at >70 mg/mL, pH 7.1 (near its pI) and low temperature (near 0°C). Upon cooling the solution below 0°C, the antibody solution became opaque and white, and remained so for at least 6 h if kept statically. As shown in Fig. 1 a, the formation of two transparent layers with a protein-poor top layer and a protein-rich bottom layer after centrifugation at −10°C was observed for the solution conditions of 22, 42, 62, and 82 mM ionic strength. But after centrifugation at −7°C as shown in Fig. 1 b, the phase boundary was not observed for the solution conditions of 62 or 82 mM ionic strength. The solution turned clear and transparent when the two layers were mixed thoroughly through gentle inversion and the temperature was raised to room temperature. These results were very similar to what was reported previously for a few small globular proteins like lysozyme (8,9) and γ-crystallins (10,11). Similarly as with lysozyme (9), it was necessary to centrifuge the antibody solution at low temperature for a period of ∼30 min, to achieve the two distinct layers separated by a clear meniscus. LLPS was observed for the KF series after centrifugation at −9°C at 42 mM and 1272 mM (see the Supporting Material).

Figure 1.

LLPS of the monoclonal antibody was conducted in glass vials to demonstrate the separation. (a) The formation of two transparent layers with a protein-poor top layer and a protein-rich bottom layer after centrifugation at −10°C for the 90 mg/mL antibody solution at pH 7.1 with the following salt conditions: 22 mM potassium phosphate (#1), 22 mM potassium phosphate + 20 mM KCl (#2), 22 mM potassium phosphate + 40 mM KCl (#3), and 22 mM potassium phosphate + 60 mM KCl (#4). (b) The formation of two transparent layers after centrifugation at −7°C can only be seen for the solution conditions of #1 and #2, but not of #3 and #4.

Liquid-liquid coexistence curve

There are two common approaches to establish the coexistence curve for describing protein LLPS: 1), cloud-point measurements; and 2), temperature quenching and centrifugation (9). It has been shown that both approaches give similar coexistence curves. The temperature-quenching and centrifugation approach was used for this work due to the instrumentation capability in our lab and low temperature of LLPS. Shown in Fig. 2 is the coexistence curve for the antibody at pH 7.1 in 22 mM of potassium phosphate fitted by the CS model without B₃′ and B₄′. At T_c and ϕ_c, the total contribution of the third- and fourth-order terms on the right-hand side of Eq. 1 was <3% of that from the second term. Even at the highest volume fraction in our experiment of ϕ = 0.3 and lowest temperature of T = 264 K, this total contribution was still <10% of the second term. Thus, we did not use these two terms in our fit for calculations. As shown in the Supporting Material, there was only a slight difference between the T_c and C_c determined from the two fits. The liquid-liquid coexistence curves plotted in terms of volume fraction are shown in the Supporting Material.

Figure 2.

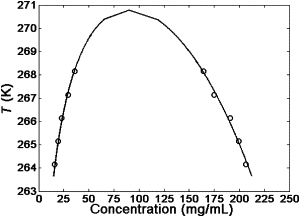
The antibody liquid-liquid coexistence curve at pH 7.1 and 22 mM ionic strength of potassium phosphate. The curve was fitted by the CS model without B₃′ and B₄′ terms. The error bar for the concentration measurement is smaller than the size of the data symbol.

Apparently the coexistence curve has an upper consolute critical point. The critical temperature (T_c) and the critical concentration (C_c) (33) are the two important parameters for describing the coexistence curves. For the solution at pH 7.1 with 22 mM potassium phosphate in Fig. 2, the fitted C_c and T_c are ∼90.1 mg/mL and ∼270.8 K, respectively. The average C_c based on the individual values from the different solution conditions using KCl was 87.1 ± 4.0 mg/mL. Because the temperature-quench and centrifugation approach cannot measure the protein concentration at conditions very close to the critical points, we were not able to confirm the critical temperature and concentration using the centrifugation approach. Instead, using the cloud-point measurement approach (34) as shown in the Supporting Material, the T_c was found to be 268.5 K, which was ∼2.3 K lower than that determined from the CS model. This is consistent with the prediction that the hard sphere model gives higher T_c values due to the implied critical exponent of 1/2 (35). For simplicity and consistency in this article, the T_c from the CS model is used to compare different solution conditions and detect relative trends. Our experimental results from the cloud-point measurement approach (34) in the Supporting Material suggested that 90 mg/mL was near the critical concentration.

T_c-ionic strength relationships at pH 7.1 for KF, KCl, and KSCN

In this LLPS system with an upper consolute critical point, T_c can be an indicator of how the intermolecular forces change, i.e., becoming more attractive or less attractive when the T_c increases or decreases, respectively (8,17,18). In Fig. 3 a, the T_c decreased as the ionic strength initially increased at pH 7.1 for all three salts, suggesting that the overall antibody-antibody interactions became less attractive as the ionic strength increased. The other subtle feature in Fig. 3 a is that there was anion specificity for decreasing the attractive interaction between the antibody molecules. For example at 142 mM, LLPS can still be observed for KF at ∼263 K, but not for KCl and KSCN. Therefore, F⁻ was least effective for decreasing the attractive interactions among the three anions.

Figure 3.

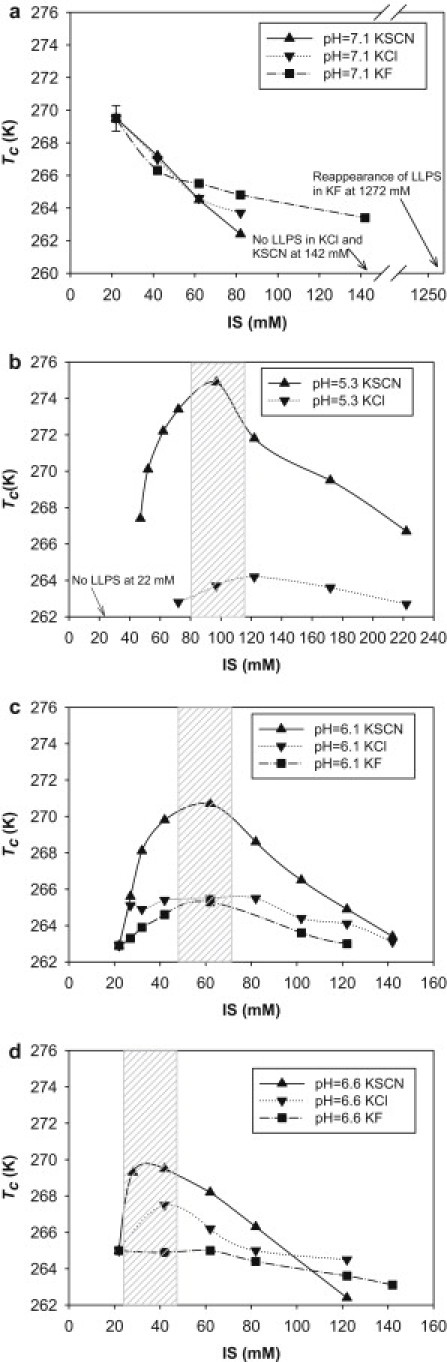
The relationship between T_c and ionic strength in the monovalent salt solutions of KF, KCl, and KSCN. The final antibody concentration was 90 mg/mL. Shown in X axis is the total ionic strength after the addition of the monovalent salt. The lines were drawn to guide the visual evaluation. The shaded box is used to indicate the ionic strength ranges for achieving the T_c maximum in the KSCN series. (a) pH 7.1: the monovalent salts were added into the antibody solution at the pH 7.1 and 22 mM potassium phosphate. The standard deviation of the T_c determination was obtained from three independent experiments at the solution conditions of the 90 mg/mL antibody solution at pH 7.1 and 22 mM of potassium phosphate. Additional experiments including higher ionic strength up to 142 mM for KCl and KSCN did not show LLPS. (b) pH 5.3: the monovalent salts were added into the antibody solution at pH 5.3 and 22 mM sodium acetate. No LLPS was observed at pH 5.3 and 22 mM sodium acetate condition and for the KF series at pH 5.3 up to 200 mM. (c) pH 6.1: the monovalent salts were added into the antibody solution at pH 6.1 and 22 mM potassium phosphate. (d) pH 6.6: the monovalent salts were added into the antibody solution at pH 6.6 and 22 mM potassium phosphate.

It is interesting to note that LLPS could be observed again when the ionic strength reached 1272 mM in the KF series (see the Supporting Material) and at ∼3.0 M, precipitation occurred (data not shown). LLPS was not observed for KSCN and KCl at 1272 mM. This observation agrees with the direct Hofmeister effect typically occurring at high salt concentrations.

T_c-ionic strength relationships at pH below pI for KF, KCl, and KSCN

In Fig. 3, b–d, at pH 5.3, 6.1, and 6.6, there was a nonmonotonic relationship between T_c and ionic strength for KCl and KSCN in general: T_c initially rises, reaches a maximum, and then decreases as the ionic strength increases. This nonmonotonic relationship was less obvious for the KF series at pH 6.6 in Fig. 3 d. For the KF series at pH 5.3, LLPS was not observed despite the addition of KF up to 200 mM.

At pH 5.3, the initial rise of T_c in the KSCN series was steeper than that in the KCl series. For example, the addition of 20 mM KSCN into 22 mM sodium acetate (pH 5.3) increased the T_c to ∼267 K, while the addition of 50 mM KCl only raised the T_c to ∼263 K. Therefore, KSCN is the most effective for increasing the attractive interactions between the antibody molecules up to ∼100 mM. Qualitatively, attractive protein-protein interactions can lead to protein precipitation from a colloidal system point of view. Thus, the above trend follows an inverse Hofmeister effect. Additionally, as indicated by the shaded box area in Fig. 3, b–d, for the KSCN series, the lower the solution pH, the more KSCN was required to achieve the T_c maximum. The T_c maximum at pH 5.3 was achieved in the region of ∼100 mM, followed by the regions of ∼60 mM for pH 6.1 and ∼40 mM for pH 6.6.

As shown in Fig. 3, b–d, after the T_c reached the maximum or plateaued, the T_c began to drop. More specifically shown in Fig. 3 b at pH 5.3, KSCN was more effective at lowering the T_c. The addition of KSCN at 122 mM ionic strength decreased the T_c by >4 K from ∼272 K to ∼267 K at 222 mM while the same addition of KCl only decreased the T_c by <2 K from ∼264 K to ∼263 K. A similar trend could be observed at pH 6.1 and 6.6. Thus, KSCN decreased the antibody-antibody attractive interactions more effectively than KCl at higher ionic strength, following the direct Hofmeister effect.

Another important observation was the behavior of the T_c maximum at the different pH conditions. The value of the T_c maximum in the KSCN series as shown in Fig. 4 was consistently higher than those in the KCl and KF series at the corresponding pH. At pH 6.1, the value of the T_c maximum was ∼270 K for the KSCN series and ∼265 K in the KCl and KF series. Additionally for the KSCN series in Fig. 4, the value of the T_c maximum at pH 5.3 was ∼275 K, significantly higher than those for pH 6.1 (∼271 K) and 6.6 (∼270 K). Conversely, for the KCl series, the value of the T_c maximum of ∼264 K at pH 5.3 was lower than at pH 6.6 (∼267 K).

Figure 4.

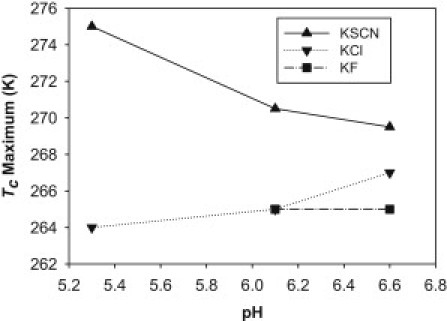
The value of the T_c maximum achieved by the individual salt at pH 5.3, 6.1, and 6.6. For KF, no LLPS can be observed at pH 5.3 up to 220 mM. The lines were drawn to guide the visual evaluation. The magnitude of the T_c maximum for each salt series was estimated from the individual curve in Fig. 3, b–d.

Discussion

Liquid-liquid coexistence curve

The average C_c of 87 mg/mL for this antibody is significantly lower, due to its large hydrodynamic size of 10 nm (measured by dynamic light scattering), than that reported for lysozyme and γ-crystallin, 230 ± 10 mg/mL (9) and 289 mg/mL (10), respectively. This is consistent with the idea that the larger the protein is, the smaller its C_c will be (9).

To justify the use of our CS model to describe short-range interactions, there was a need to introduce a modification that accounts for thermal and orientational dependence in the B₂′ term. For an isotropic interaction, the lowest-order perturbation theory, using the Carnahan-Starling hard-sphere model as the reference system, results in a simple expression for B₂′,

$$B_2^{\prime }=2\pi {\int }_{\sigma }^{\infty }\left(1-\exp \left(-W\left(r\right)/kT\right)\right)r^{2}dr,$$ (5)

where W(r) is the two-body interaction depending only on the distance (r) between the two interacting particles. Equation 5 suggests that at a high temperature limit,

$$W\left(r\right)/kT\ll 1,$$

$$B_2^{\prime }\approx \frac{12}{KT}{\int }_1^{\lambda }W\left(x\right)x^{2}dx,$$

$$\text{where}x=\frac{r}{\sigma },$$

σ is the hydrodynamic diameter, and λ is the range parameter that depends upon the center-to-center distance between the protein molecules. This implies that B₂′ is inversely proportional to temperature. More sophisticated perturbation theories or Monte Carlo simulations also imply this lowest order temperature dependence of B₂′ no matter how many higher order perturbation terms in density are used. This is simply a consequence of the assumption of isotropic interaction.

However, efforts of trying to fit the theoretical coexistence curve directly to experimental data, including ours, are sometimes found unsatisfactory. For example, in the Monte Carlo simulation of Lomakin et al. (36), the authors found good fits to the data by Broide et al. (10) only when a temperature-dependent square-well potential was introduced, or when orientation-dependent interactions were introduced (37).

It is a well-known empirical fact in polymer physics that the Flory-Huggins interaction expression has an enthalpy component and an entropy temperature-independent component which are similar to the first and second terms on the right side of Eq. 2, respectively (38). The second term can indeed be understood as the result of anisotropic interactions which compete with the entropic properties of the solution due to specific orientations of the molecules required for short-range interactions to take place. Truskett et al. (39) have derived this term explicitly using a statistical mechanics model of orientation-dependent interactions. Therefore, we adopted this orientation dependence in the model to determine B₂′ as shown in Eq. 2.

Although our equation of state does not contain explicit information on the microscopic interaction range, we can gain some estimation by comparing our fitted orientation-dependent B₂′ with that in the article of Lomakin et al. (36) as shown in Fig. 5. We found an equivalent potential well range of 1.2 (reduced) and a reduced critical energy (ɛ_c) of 1.54 at the critical temperature. Lomakin et al. (36) has pointed out that mean field theory gives a good estimate for ɛ_c for reduced ranges >∼1.10. Therefore it seems consistent that our system has an estimated reduced range of ∼1.2 and can be fairly well approximated by the mean field term B₂′ only.

Figure 5.

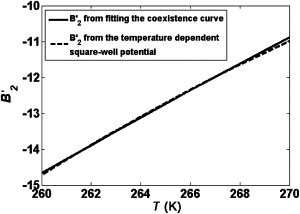
Comparison of B₂′ obtained from our model (solid line) with that (dashed line) from a temperature-dependent square-well potential with the depth at T_c equal to 1.57 kT_c and the range equal to 1.2σ described in Lomakin et al. (36) using Eq. 5.

It is worth noting that in the work of Gast et al. (40), the qualitative change of the liquid-liquid coexistence curve from stable to metastable seems to occur around the reduced range of ∼1.2. From these indications, we can hypothesize that the microscopic reduced range for our antibody molecules in aqueous solution is in the region where the modified CS model equation of state is still a fairly good approximation to describe the phase behavior as long as B₂′ takes into account a corrected function that includes an orientation-dependent interaction term. At the same time, the reduced range is short enough to manifest the metastable liquid-liquid phase separation of the antibody as suggested by the crystallization of the antibody shown in the Supporting Material.

By using the hydrodynamic diameter of ∼10 nm for this antibody, the estimated ϕ_c was 0.19 (see calculation in the Supporting Material). In the CS model it is implied that ϕ_c = 0.13. In fact, ϕ_c can vary from 0.05 to 0.2 for protein systems depending on how it is calculated (see the Supporting Material). Therefore, a limitation exists in using the CS model when ϕ_c may be substantially different from 0.13. This brings into question the validity of the calculated B₂₂ (Eq. 4) because the fitted B₂′ may be affected by ϕ_c. However, despite the limitations of the CS model, the B₂₂ for the solution of pH 7.1 and 22 mM of potassium phosphate at 270 K was calculated to be −6.42 ± 0.04 × 10⁻⁵ mL mol g⁻², which is within the narrow B₂₂ range from −3.5 × 10⁻⁵ to −9.0 × 10⁻⁵ mL mol g⁻², suitable for growing crystals for a large protein (MW = 140,000) (31). In fact, crystal growth was observed for the solution at these conditions when incubated at 2–8 and 25°C for a few days (shown in the Supporting Material), which suggests that the approximation as used does predict a result that is close to our experimental outcome.

T_c-ionic strength relationships at pH 7.1 for KF, KCl, and KSCN

The antibody LLPS at pH 7.1 suggests that the antibody-antibody interactions were attractive. Because the solution pH was near the pI, the antibody was almost charge neutral. Based on the classic Derjaguin, Landau, Verwey and Overbeek (DLVO) theory, the electric double-layer repulsion between the antibody molecules should be small and the net DLVO interaction between them should arise mainly from the attractive van der Waals force. However, the decrease of T_c versus the ionic strength for all three salts in Fig. 3 a suggests that the intermolecular attractive interactions were sensitive to the presence of electrolytes and therefore electrostatic in nature. In our study, the antibody was at high protein concentration and low ionic strength. Thus, the complementary electrostatic interaction (41) between positive-charged patches and negative-charged patches (or ion pairing) becomes more likely.

First, at the condition of 90 mg/mL in our experiment, the distance between the antibody molecules was relatively short with respect to its molecular size. For example, if one assumes a uniform distribution in solution, the estimated average distance between the antibody molecule surfaces is in the range of ∼4.0 nm based on the hydrodynamic diameter of ∼10 nm. The surface distance between the antibody molecules would be less than its diameter. As a result, the molecules in our study could experience short-range interactions at high concentrations. This is especially true when the antibody molecules were charge neutral and could approach each other easily due to the lack of electric double-layer repulsion.

Second, at pH 7.1 there were ∼88, 38, 2, 58, and 70 charged lysine, arginine, histidine, aspartic acid, and glutamic acid residues, respectively, per antibody molecule. The total molar concentration for the positive-charged and negative-charged amino acids was ∼77 mM of each at the antibody concentration of ∼0.6 mM (90 mg/mL). The molar concentration of phosphate and potassium was 9 mM and 20 mM, respectively, at 22 mM ionic strength. Therefore, the antibody was studied under conditions of relatively low ionic strength and the intermolecular complementary electrostatic interaction could occur.

The specificity of the individual anions on weakening the complementary electrostatic interaction at pH 7.1 may be explained through the classic protein-salt preferential interaction theory (22,42). For example, the possible preferential interactions of anions with positive-charged side chains and peptide groups (amide bonds) (19,43) could potentially decrease the antibody solvation free energy and effectively decrease the antibody-antibody attractive interactions, analogous to a salting-in effect. This salting-in effect at low ionic strength is generally observed when the pH is near the pI of the protein based on solubility measurements (44). According to the law of matching water affinities (20,21), both SCN⁻ and Cl⁻ are weakly hydrated while F⁻ is strongly hydrated; SCN⁻ and Cl⁻ should more strongly interact with weakly hydrated ions from the side chains of lysine, arginine, histidine, and peptide groups than F⁻. Thus, SCN⁻ and Cl⁻ should decrease the attractive interactions more effectively than F⁻, as our experimental results suggest. However, our results do not have sufficient evidence to demonstrate the specificity difference between SCN⁻ and Cl⁻, although SCN⁻ is the least hydrated of the two anions.

The appearance of LLPS in the KF solution at 1272 mM indicated that the antibody-antibody interactions became more attractive, but not for KCl and KSCN. This seems to be in agreement with the direct Hofmeister effect. F⁻ is strongly hydrated and may impart a tendency for intermolecular protein interactions due to its hydration properties at high concentrations that have been known to influence water structure and surface tension at the interface between the antibody and bulk solution (23).

T_c-ionic strength relationships at pH below pI for KF, KCl, and KSCN

Far from the pI, at pH 5.3 and 22 mM ionic strength, the electric double-layer repulsion should dominate the antibody-antibody interactions. This is consistent with no observed LLPS at this condition without the addition of KSCN, KCl, and KF. The initial rise of T_c for the three anions as shown in Fig. 3, b–d, may be explained by the binding of the anions and neutralization of the protein net charges (44,45), which decreases the electric double-layer repulsion as described in the DLVO theory. This idea has been suggested for lysozyme LLPS at pH conditions below its pI and an inverse Hofmeister series was used to explain the specificity of the chaotropic anions studied (18).

According to the law of matching water affinities, when a protein has net positive charge, the weakly hydrated (more chaotropic) SCN⁻ binds more strongly to the weakly hydrated side chains of lysine, arginine, and histidine and thus decreases the electric double-layer repulsion more effectively than the strongly hydrated (kosmotropic) anions, such as F⁻ (20,21). Therefore, SCN⁻ being more weakly hydrated should raise the T_c more effectively than Cl⁻ and F⁻ when the same amount of salt is used, which follows the inverse Hofmeister effect. Our experimental results are consistent with the above mechanism. The fact that the T_c maximum in the KSCN series at pH 5.3, 6.1, and 6.6 was reached with ∼100, 60, and 40 mM ionic strength, respectively, may suggest complete charge neutralization by SCN⁻. At pH 5.3, the antibody has a total of ∼+26 net charges, and thus a higher concentration of SCN^- would then be required to neutralize the charges completely than at pH 6.1 and 6.6 with ∼+11 and ∼+4 net charges, respectively.

Our experimental results do not provide sufficient evidence to clearly differentiate the binding strength between F⁻ and Cl⁻ for the antibody under all the pH conditions, although Cl⁻ is more weakly hydrated than F⁻. But at pH 5.3, the T_c and ionic strength relationship might suggest that Cl⁻ more effectively decreases the double-layer repulsion than F⁻. At pH 6.1 and 6.6, the above pattern was less obvious.

If the antibody-antibody interactions are simply affected by charge neutralization, the magnitude of the T_c maximum from the three anions series should be fairly close to each other at complete neutralization at a given pH below the pI. Instead, in the KSCN series the T_c maximum was greater than that in the KCl series as shown in Fig. 4. Furthermore, the value of the T_c maximum within the KSCN series decreased as the pH increased from 5.3 to 6.6. The opposite response was observed for the KCl series.

This might suggest the presence of an additional attractive force, like an ion-correlation force (46), in the KSCN series. This force between two molecules is caused by an attractive van der Waals force between opposing electric double layers, where the mobile counterions could form a polarizable layer (46). This force is augmented by the polarizability of the counterion type in the electric double-layer at small separation distances <4 nm between protein molecules (46). This force becomes more pronounced at high charge densities as would be the case for this antibody at pH 5.3 and should decrease as the pH moves toward the pI. Among the three anions studied, SCN⁻ has the largest polarizability (47) and therefore the ion-correlation force should be greater in the KSCN solution than KCl (44). Indeed, the data seem to agree with this possibility. It remains unknown to us why the opposite effect was observed for the T_c maximum for KCl. Yet, this would suggest that the T_c maximum is perturbed in a fashion consistent with slightly more attractive interactions between the molecules.

For all three anions studied, the T_c began to decrease after it reached a maximum or plateau as the ionic strength was further increased, suggesting that the antibody-antibody interactions become less attractive. What appeared to occur, after charge neutralization, seems to mimic the responses at pH 7.1 where the net charge was approximately zero. Therefore, the effectiveness of the three anions for weakening the attractive protein interactions should follow the direct Hofmeister series of SCN⁻ > Cl⁻ > F⁻. This is consistent with our results as shown in Fig. 3, b–d, for KSCN and KCl, although the effectiveness difference between KCl and KF was subtle.

The nonmonotonic behavior of the T_c (initially rising followed by a decreasing arm) indicates a transition from more attractive to less attractive as ionic strength of the anion increases below the pI. This behavior has been observed for lysozyme with NaSCN at pH 9.4 (below its pI) and 90 mg/mL (∼0.06 mM), where ∼200–300 mM of SCN⁻ was required to achieve complete charge neutralization (18). However, at a pH <9.4, the protein-protein interaction always became more attractive for the monovalent salts tested (8,17,18).

As we mentioned, the transition to the decreasing arm should not occur until the net charge of the protein is completely neutralized. As shown in the Supporting Material, the estimated charge density for lysozyme is ∼0.0276 and ∼0.0511 C/m² at pH 9.4 and 4.1, respectively. At pH 4.1, the highest concentration of SCN⁻ tested was 400 mM, which might not be sufficient to achieve complete neutralization due to the high charge density of lysozyme and thus the plateau was never reached. In addition, the possible presence of an ion-correlation force may have rendered protein-protein interactions more attractive. Nevertheless, the decreasing arm was not observed at pH 4.1 for lysozyme when using SCN⁻.

Conclusions

Liquid-liquid phase separation was studied and the coexistence curve was constructed for a monoclonal antibody in monovalent salt solutions of KF, KCl, and KSCN under different ionic strengths and pH conditions. Using the CS model, we determined and used T_c as a measurement of antibody-antibody interactions. At pH conditions below the pI of the antibody, there was a nonmonotonic relationship between the ionic strength and antibody-antibody interactions. This behavior was characterized by an initial arm of more attractive interactions followed by less attractive interactions upon further increments of ionic strength.

To the best of our knowledge, such nonmonotonic protein LLPS behaviors have seldom been observed experimentally in these monovalent salt solutions at low ionic strength. Based on the theoretical work by Curtis and Lue (22) and preceding discussion, it is proposed that in a monovalent salt system, when the pH is below the pI at low ionic strength, the electric double-layer repulsion dominates the antibody-antibody interactions. Thus, an increase of the ionic strength begins to weaken the double layer repulsion and the antibody-antibody interactions become more attractive. The anion with stronger binding to the positively charged antibody, possibly with an ion-correlation force, decreases the double-layer repulsion more effectively (inverse Hofmeister series). After neutralization, preferential interactions between the anions and antibody result in a decrease in the antibody's solvation free energy. The antibody-antibody interactions then become less attractive, following the direct Hofmeister effect. A similar effect was observed under the pH condition close to the pI.