Abstract
By combining the osmotic stress technique with small-angle x-ray scattering measurements, we followed the structural response of the casein micelle to an overall increase in concentration. When the aqueous phase that separates the micelles is extracted, they behave as polydisperse repelling spheres and their internal structure is not affected. When they are compressed, the micelles lose water and shrink to a smaller volume. Our results indicate that this compression is nonaffine, i.e., some parts of the micelle collapse, whereas other parts resist deformation. We suggest that this behavior is consistent with a spongelike casein micelle having a triple hierarchical structure. The lowest level of the structure consists of the CaP nanoclusters that serve as anchors for the casein molecules. The intermediate level consists of 10- to 40-nm hard regions that resist compression and contain the nanoclusters. Those regions are connected and/or partially merged with each other, thus forming a continuous and porous material. The third level of structure is the casein micelle itself, with an average size of 100 nm. In our view, such a structure is consistent with the observation of 10- to 20-nm casein particles in the Golgi vesicles of lactating cells: upon aggregation, those particles would rearrange, fuse, and/or swell to form the spongelike micelle.
Introduction
Casein micelles are probably one of the most common natural association colloids. They are complex macromolecular assemblies made of four distinct caseins, namely, αs1, αs2, β, and κ, and 8% in mass of phosphate and calcium ions. Casein micelles play a central role in the processing of milk, cheese, and most dairy products, and their structural and physical properties have been studied extensively over the last 50 years. Yet their structure is still a puzzle and is continuously the subject of furious debates among the scientific community (see reviews (1,2)). The problem is indeed difficult for a number of reasons. First, the casein micelles have a wide distribution of sizes: the average micelle has a diameter between 100 and 200 nm (3), but the full range and the exact form of the distribution are still not well established (4). Second, and more important, the internal structure of the casein micelle is made by the assembly of many components that are in complex equilibrium with their environment. Their interactions, and the interactions between the micelles themselves, may vary according to ionic conditions, temperature, and concentration. This makes the micelle a delicate and dynamic object that is not easy to observe in conditions that are representative of the native state. Finally, the assembly process that takes place in the lactating cell cannot be fully reproduced in vitro (1), which makes it difficult to connect the micelle with building blocks from which it assembles.
At this time, it is now well established that the surface of the micelle is essentially made of a brush layer of κ-caseins (5). So the controversy is mainly focused on the internal structure of the casein micelle. Previous scattering and microscopy experiments (small-angle neutron scattering and small-angle x-ray scattering (SAXS), and transmission electron microscopy) have revealed some distinctive features of this internal structure (6–10). However, these features are not always identical and diverse models have been designed to account for the different results. As for now, the following models are still in use: 1), the submicelle model, which describes the micelle as made of closely packed submicelles of ∼15 nm in diameter, either linked together by calcium phosphate (CaP) nanoclusters (11) or containing these nanoclusters (12); 2), the homogeneous model, in which the internal structure is made of a loose and uniform casein matrix with randomly distributed CaP nanoclusters (7); and 3), the core-shell model which still considers a homogeneous casein matrix but suggests that the CaP nanoclusters are preferentially located near the micelle surface (10).
This lack of a consensus indicates that there is a serious need for new and additional information. In this study, we report experiments that consist of examining the SAXS structure of the casein micelle in response to an osmotic stress. The osmotic stress technique makes it possible to concentrate casein dispersions to conditions where the micelles are closely packed and ultimately deform and deswell (13,14). During the concentration process, the chemical potential of all ions can be maintained at their values in the native state, thus preserving the integrity of the micelle. We show that the structural signature of the casein micelle is strongly affected by the change in concentration, and more particularly after close-packing, when the casein micelles are directly compressed and shrink to a lower volume. We then address two crucial questions: can we explain these changes using the models previously proposed for the internal structure of the micelle? If not, are we able to build a model that fits our SAXS data, is physically consistent, and remains realistic from a biological point of view?
Materials and Methods
Proteins and dispersions preparation
Experiments were performed with dispersions made from native phosphocaseinate powder (NPC) dissolved in a solvent made from ultrafiltration of skimmed milk (UF). NPC powder is a serum protein-free milk powder in which the caseins and their associated minerals represent >90% of the total solid content. Such a powder is known to be an adequate model for native milk casein micelles and it has been used as such in a number of recent studies (15–17). The use of UF as solvent ensures that the chemical potentials of all ions are maintained at their values in the native state. In addition, important properties of the casein micelles in NPC + UF dispersions (size distribution, behavior toward pH gelation) are virtually identical to those measured in skimmed milk (18).
The NPC powder was prepared in our laboratory according to a protocol developed by Pierre et al. (19) and Schuck et al. (20) and described in a previous work (14). The UF was prepared through membrane ultrafiltration (5-kDa cutoff) of fresh skimmed milk. Its average ionic composition can be found in Jenness and Koops (21). UF also contains lactose (150 mM) and a few other low-molar-mass molecules such as riboflavin. Thimerosal and sodium azide, both purchased from Sigma-Aldrich (Lyon, France), were added to UF as preservatives at 0.02% and 0.1% (w/w), respectively.
For a casein concentration of up to 150 g/L, the dispersions were prepared by thoroughly mixing the NPC powder in UF for 15 h at 35°C. Dispersions at higher casein concentrations were prepared through osmotic stress, a concentration technique based on water exchange between the sample, i.e., a liquid NPC dispersion, and a reservoir of controlled osmotic pressure. A detailed description of the technique and the materials we used is given in our previous work (14). This technique made it possible to easily prepare ∼1 mm3 homogeneous samples with casein concentrations of up to 400 g/L. The casein concentrations in the prepared samples were accurately determined through drying at 105°C. At 20°C, the pH of all dispersions matched the average pH of milk, i.e., pH 6.7 ± 0.1.
Small-angle x-ray scattering
SAXS measurements were performed at the French national synchrotron facility SOLEIL in Gif sur Yvette, France, in the beam line SWING operating at ∼12 keV photon energy. Each sample, either liquid- or solidlike, was placed in a watertight cell with a cylindrical cavity of diameter 4.5 mm and thickness 2 mm closed by flat mica windows. The scattered intensity was recorded on a detector placed at ∼6.5 m from the sample. For each sample, data were first recorded at short exposure time (typically ∼0.2 s) to avoid any radiation damage (aggregation) that could result in artifacts at low q values. Subsequently, data were recorded at long exposure times (typically ∼15 s) using a larger beam stop to obtain a good signal/noise ratio at high q values without damaging the detector. Intensities recorded at the two exposure times were then radially averaged and combined to get a scattering curve covering a q-range of 1.5 × 10−3 to 1.4 × 10−1 Å−1. In some cases, artifacts due to sample radiation damage were visible in the low-q regions of the data recorded at long exposure times. The corresponding intensities were discarded before the merging procedure was carried out. For each sample, the intensity scattered from the solvent (UF) in the same mica cell was measured and subtracted from the casein sample pattern. The resulting corrected intensity is denoted by I(q). All measurements were performed at room temperature (∼23°C).
Results
General structural features at native concentration
Fig. 1 shows the measured scattering intensities, I(q), for casein micelle dispersions at the average casein concentration of bovine milk, C = 25 g/L. Our results are compared with those of previous studies obtained at the same concentration but with slightly different model dispersions, namely fresh and pasteurized skimmed milk. At native concentration, the volume fraction occupied by the micelles is ϕeff ∼ 0.1 (ϕeff = Cv∗, where v∗ is the specific volume of an undeformed casein micelle, v∗ = 4.4 mL/g (3)). In these conditions, the casein micelles are well separated from each other so that interparticle interactions are weak and do not perturb the structure of the micelles (10).
Figure 1.
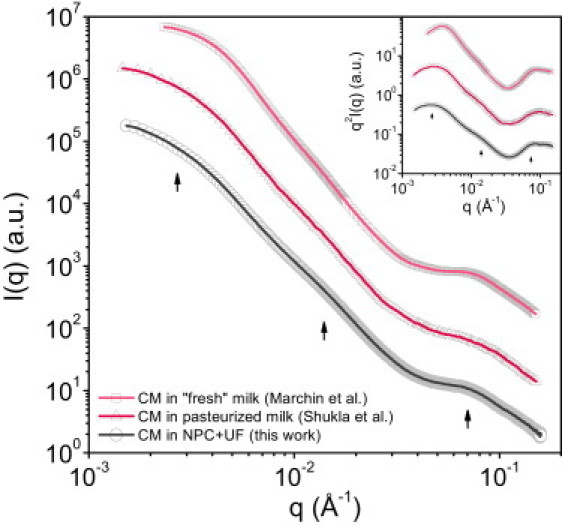
Typical SAXS profiles for the casein micelle at casein concentration ∼25 g/L in fresh milk (squares; data from Marchin et al. (8)), pasteurized milk (triangles; data from Shukla et al. (10)), and NPC + UF (circles; this work). Intensities are in arbitrary units (a.u.) and the data have been shifted along the y-axis for clarity. (Inset) The corresponding Kratky plots in a log-log scale. The lines guide the eye.
The SAXS profile shown in Fig. 1 for NPC powder rehydrated in a milk aqueous phase is practically identical to the profiles obtained from a fresh skimmed milk (8) or from a pasteurized skimmed milk (10). Therefore, the results reported here are representative of a micelle that is close to its native state, and NPC powder is an adequate model for milk casein micelles.
The casein micelle exhibits a SAXS pattern with three characteristic features, numbered 0–2 (Fig. 1, arrows):
-
Level 0:
low q values, up to 6 × 10−3 Å−1, distances >100 nm. In this range, the signal is controlled by the distances between micelles, and by their overall shapes (22). The curvature of the scattering curves corresponds to the scattering expected from repelling polydisperse spheres at low volume fraction. This part of the scattering has been well described by previous authors (8,10,22,23), and it is not the focus of this work.
-
Level 1:
intermediate q values, in the range 6 × 10−3 to 2 × 10−2 Å−1. In this range, a small oscillation is observed around 2π/q ≈ 40 nm. This oscillation shows up better when the data are plotted as I(q) × q2 versus q on a so-called Kratky plot (inset of Fig. 1). This feature has been analyzed according to a core-shell model (10), or, alternatively, as resulting from the presence of a second population of very small casein micelles, called minimicelles (4,15,24,25)
-
Level 2:
high q values, ∼7–8 × 10−2 Å−1. In this range, the variation in I(q) originates from the presence of the ∼4- to 5-nm CaP nanoclusters. This was nicely demonstrated through SAXS experiments with casein micelles depleted in calcium (8,10).
Response to osmotic stress
Fig. 2, A and B, shows the SAXS intensities obtained in the concentration range C = 25–400 g/L. In addition, the results at C ≥ 100 g/L are displayed in Fig. 3 in terms of an effective structure factor, Seff(q), obtained by dividing I(q) by the intensity scattered by the most dilute dispersion (C = 25 g/L). Seff(q) is called effective because it takes into account all changes in shape and size of the micelles that result from the compression at high concentrations (26,27).
Figure 2.
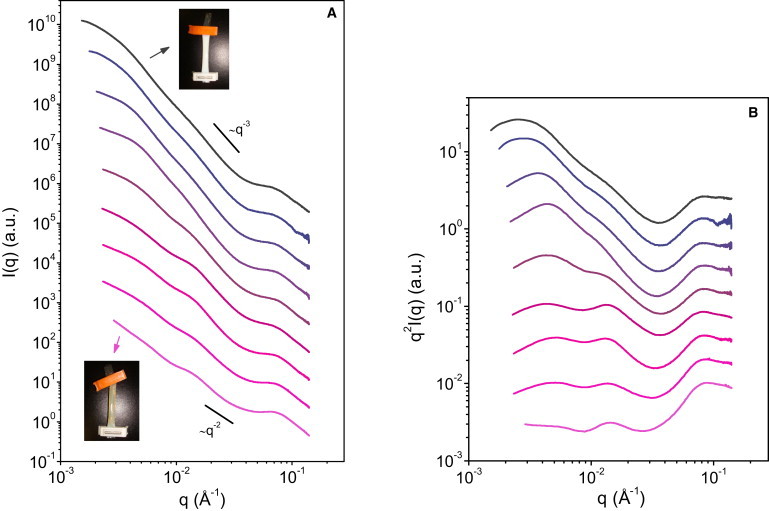
(A) The SAXS intensities of casein micelle dispersions at casein concentrations (top to bottom) 25, 33, 100, 150, 167, 206, 337, 365, and 400 g/L. The data have been shifted along the y-axis for clarity. At 25 g/L, the dispersion is turbid and fluid, whereas it is a nearly transparent gel at 400 g/L. The transition from a fluid to a gel takes place between 150 and 200 g/L of casein. (B) The corresponding Kratky plots in a log-log scale.
Figure 3.
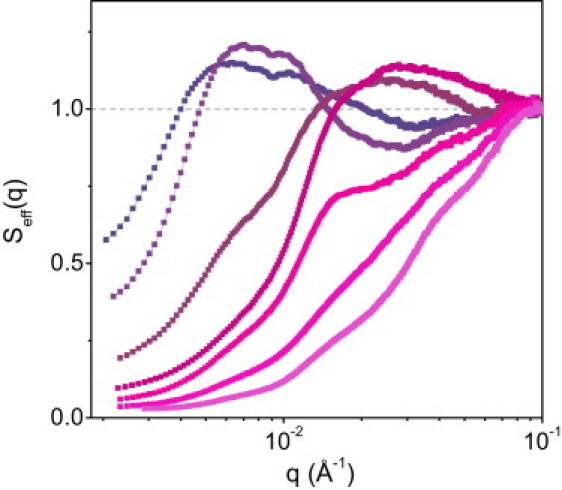
The effective structure factor Seff(q) measured for casein micelle dispersions at concentrations ≥100 g/L. Concentrations (top to bottom at low q values) are 100, 150, 167, 206, 337, 365, and 400 g/L.
In a first concentration regime, i.e., C = 25–150 g/L, the changes in I(q) are restricted to the low-q region where the shoulder that corresponds to distances between micelles shifts toward shorter distances. In this regime, the dispersions are liquid and turbid (Fig. 2 A, upper inset). Viscosity and osmotic pressure measurements indicate that the micelles interact as repelling spheres with free volume between them (13,14). Therefore, only their relative positions are changed by compression. This is confirmed by the structure factor, Seff(q) (Fig. 3), which closely resembles those of concentrated dispersions of hard particles, or those of nanoemulsions (26,28). Hence, there are no changes of internal structure in this regime.
In a second concentration regime, i.e., at C > 150 g/L, corresponding to ϕeff > 0.65, the increase in concentration produces changes that are much more significant. The main change is that the scattering curves clearly flatten as concentration increases: if we roughly approximate each spectrum by a power law , the overall exponent df changes from df ≈ 3 at 150 g/L to df ≈ 2 at 400 g/L (Fig. 2, A and B). Another obvious point is that the I(q) oscillation at intermediate q values becomes more prominent at increasing concentrations, while in the meantime, the shoulder at low q becomes less pronounced (Fig. 2, A and B). Finally, and quite remarkably, the position of the oscillation at intermediate q is not affected at all by the increase in concentration. All these changes in the scattering at intermediate q values must reflect changes in the internal structure of the micelles; they are correlated with major changes in the macroscopic properties of the dispersions. At the beginning of this second concentration regime, i.e., at C = 150–200 g/L, the osmotic pressure increases suddenly as the micelles strongly interact and progressively get into close contact (14). The dispersions then change from liquids to soft solids, as indicated from rheological experiments (13). At still higher concentrations, the micelles are in close packing and then tend to deform and deswell as concentration increases. These dispersions have the rheological properties of viscoelastic gels and show low turbidities (13,14) (Fig. 2 A, lower inset).
Discussion
The aim of this section is to find a structural model for the casein micelle that is deformed under compression in a way that is consistent with the SAXS spectra shown in Fig. 2 A. In a first part, we demonstrate that the deformation of the micelle is of a very peculiar type (nonaffine), and that it cannot be described by any of the structural models previously proposed. We then show that a model that accurately accounts for this atypical behavior is a sponge model with three levels of structure.
A nonaffine deformation
In the first stage of compression, at C ≤ 150 g/L, the micelles are separated from each other (13). The changes of I(q) and Seff(q) are restricted to the low-q part of the scattering curves, and they match the usual behavior of repelling polydisperse hard spheres (26,28). Therefore, the only effect of the rise in concentration is a change in the relative positions of the micelles. This is not the focus of the work presented here.
At concentrations >150 g/L, the SAXS spectra are much more interesting and informative. In this second concentration regime, the micelles are in contact, deform, and deswell as C increases. The changes in the shape of the spectra clearly indicate that the internal structure of the micelles is deformed in a way that is nonaffine with respect to the overall (macroscopic) compression. A first indication of this behavior is the observed flattening (df changes from ∼3 to ∼2 (Fig. 2 A)) of the spectra as C increases from 150 to 400 g/L. Indeed, an affine or homogeneous deformation, where all dimensions are affected through the same linear transformation, would induce an overall translation of the curve along the q-axis instead of a flattening. This first general nonaffine behavior is also seen in Fig. 3 where the depression of Seff(q) becomes very broad at C > 150 g/L and extends to q values that are well within the internal structure of the micelles. If we now consider the details of the spectra, another striking indication that the deformation is nonaffine is the fact that the positions of the I(q) oscillations at intermediate and high q values do not change at all with compression (Fig. 2 B), so although the micelle deforms and shrinks to a smaller volume, the distances that characterize some substructures within the micelles remain constant.
At this point, the question is whether or not the structural models that already exist for the casein micelle can explain this nonaffine behavior. A careful analysis of each model suggests that the answer is no. The main points of this analysis are summarized below. Some additional information and calculations are given in Note S1 in the Supporting Material:
Submicelle model. In this model, the micelle is made of closely packed submicelles of ∼15 nm in diameter (11,12). Upon compression, these submicelles would be forced to interact strongly and would ultimately deform and diminish in size. This would lead to strong and shifting correlation peaks at intermediate q values, which is not observed.
Homogeneous model. In this model, the internal structure is made of a loose and uniform casein matrix with randomly distributed CaP nanoclusters (7,8). A first obvious argument against this model is that it cannot explain the presence of the I(q) oscillation at intermediate q values. In addition, the homogeneous model suggests that the casein micelles behave as some simple unstructured microgel particles upon compression, which is not verified (Note S1-1 in the Supporting Material).
Core-shell model. In this model, the CaP nanoclusters are preferentially located at the periphery of the micelle, thus forming a shell of higher electronic density (10). We have calculated the form factor for such a structure and considered different scenarios regarding its deformation (affine deformation, deformation of the core only, and deformation of the shell only). In each case, the I(q) oscillation at intermediate q values shifts toward higher values and/or does not become more prominent as C increases (Note S1-2 in the Supporting Material).
Presence of minimicelles. In this scenario, a second population of smaller casein micelles is present in the dispersions (4). Because both the micelles and the minimicelles would be forced to interact, the oscillations at low and intermediat q values would change in the same way as C increases; and this is not the case. In addition, the concentration in minimicelles that is necessary to describe the intermediate I(q) oscillation is too high to be realistic (Note S1-3 in the Supporting Material).
Sponge model
A way to explain the nonaffine deformation of the casein micelle is that both hard and soft regions coexist within its structure: under compression, the soft regions lose water and are compressed, whereas the hard regions are pushed closer together. The choice of a model consists of describing what these hard and soft regions are and how they are distributed within the micelle. It is quite obvious that the hard regions characterized by the I(q) oscillation at high q values are the 4- to 5-nm CaP nanoclusters present in the micelle body. Then the central question is the physical meaning of the I(q) oscillation at intermediate q values: what does it tell us about the structure of the micelle? Since the position of this oscillation does not shift when the micelle is compressed, it may correspond to another type of hard region that resists compression. Such regions, made of a number of nanoclusters with adsorbed casein molecules, would be separated or connected by soft regions or voids that collapse under osmotic stress. This would make the casein micelle a sort of sponge, a term used by McMahon and Oomen in a recent publication when discussing transmission electron microscope images of the micelle (9).
The most general model that describes a heterogeneous or spongelike material containing hard and soft components is a cell model where the cells are randomly occupied by either type of component, according to the overall volume fractions of each. This has been used successfully with a cubic lattice or with an array of Voronoi cells to describe microemulsions (29–31). In this model, the intensity scattered by the material is
| (1) |
where ϕ is the volume fraction of occupied cells, vcell the cell volume, Δρ the difference in scattering density between occupied and empty cells, and P(q) the single-cell scattering function. In the simplest nonaffine deformation, the occupancy ϕ changes with C and the form factor P(q) remains unchanged.
At low occupancies (ϕ << 1), this intensity is proportional to ϕ, and at high occupancies, it goes as 1 − ϕ, as it should, since the scattering will be produced by the voids. Moreover, the only characteristic length is the cell size, which is taken into account by the single-cell scattering function P(q). Since there are no correlations between the occupancies of neighboring cells, nor any voids between them, this model does not produce any of the correlation peaks that are observed for systems with repulsive interactions. In this respect, it appears well suited to analyze the scattering curves of casein micelles that show characteristic distances but no correlation peaks even at high volume fractions. For simplicity, we assume that the same description is applicable to the three levels of structure, i.e., the whole micelles (level 0), the hard regions (level 1) and the CaP nanoclusters (level 2). The expression of the scattered intensity then becomes
| (2) |
with
| (3) |
| (4) |
and
| (5) |
This model is identical in its functional form (Eq. 2) to the Beaucage scattering function used by Pignon et al. (22) or the composed form-factor function used by Gebhardt et al. (24). However, it has the advantage that it gives a precise physical meaning to the form factors Pn(q) and to their prefactors a, b, and c. We assume here that Pn(q) can be approximated by the form factors of polydisperse spheres. To calculate them, we use the expressions given by Aragon et al. for a Schulz size distribution of spheres of polydispersity σn and number average diameter dn (32).
To test our model, we first perform a fit of the experimental data to Eq. 2 by simply varying the values of prefactors a–c and the mean diameters d0, d1, and d2 used in the calculation of Pn(q). To minimize the number of free parameters in the fits, we set the polydispersity values to realistic ones, i.e., σ0 = σ1 = 1/3 and σ2 = 0.2. The agreement with the data is excellent at all concentrations (Fig. 4). The parameters obtained from the fits are given in Table S4 in the Supporting Material.
Figure 4.
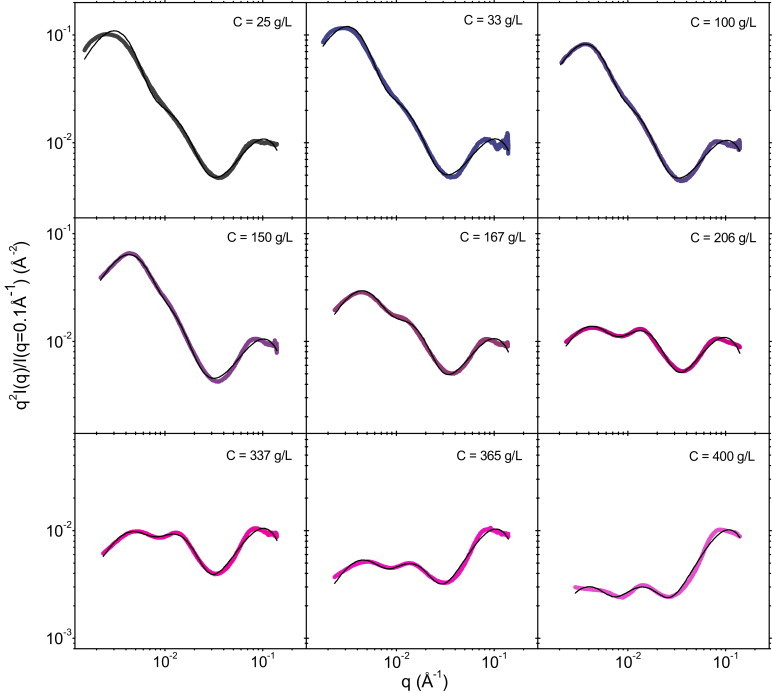
Modeling of the SAXS intensities of compressed casein micelle dispersions. Thick lines are the experimental data and thin black lines are the best fits to Eq. 2 (see text). See Fig. S8 for another representation of these modeling results.
In a second step, we use the concentration dependence of prefactors a–c to check whether the model is physically meaningful. For that purpose, the simplest approach consists in estimating the volume fractions ϕ0, ϕ1, and ϕ2 from those prefactors and in examining the variations of each volume fraction with C. A detailed description of how we make our calculations is given in the Note S2 in the Supporting Material. For simplicity, we consider only the case for which the soft regions are voids filled with solvent and the hard regions contain all the CaP and protein materials. The resulting volume fractions are given in Fig. 5, A and B, as a function of casein concentration.
Figure 5.
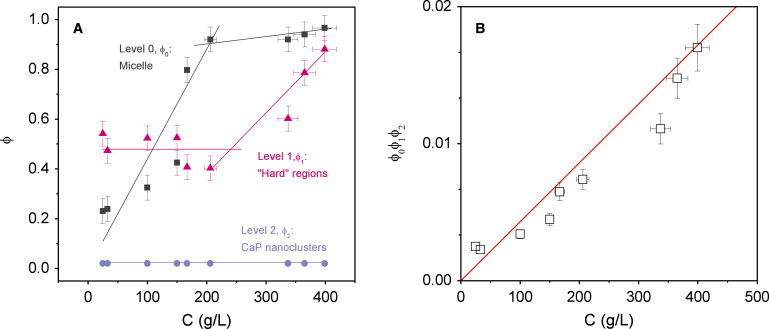
Consistency of the model. (A) The casein concentration dependence of the volume fractions obtained from the best fits of the model to the SAXS data. Those volume fractions characterize the volume occupied by the micelles in the dispersions (ϕ0, squares), the hard regions in the micelle (ϕ1, triangles), and the CaP nanoclusters in the hard regions (ϕ2, circles). The lines guide the eye. (B) The casein concentration dependence of the product (ϕ0ϕ1ϕ2) (open squares). The data agree well with the volume fraction occupied by the CaP nanoclusters in the dispersions, (ϕ0ϕ1ϕ2) ≈ 0.01Cv∗ (solid line).
It is clear that the individual variations of ϕ0, ϕ1, and ϕ2 with C are consistent with a heterogeneous micelle made of hard regions that contain the CaP nanoclusters (Fig. 5 A):
-
Level 0,
whole micelle: at low concentrations, when the micelles are not yet compressed, ϕ0 increases roughly linearly with C, in good agreement with the specific volume of the native micelle, v∗ = 4.4 mL/g (ϕ0 = v∗C (Fig. 5 A)). Then when the micelles are in contact and fill almost all the space in the dispersions, ϕ0 remains about constant at values close to 1.
-
Level 1,
hard regions: as opposed to ϕ0, ϕ1 remains constant at low concentrations where the micelles are not yet compressed. Then, when the micelles are in contact, these hard regions are being pushed closer together as solvent is expelled from the micelle and ϕ1 increases with C. From our estimations, these 10- to 40-nm hard regions make up ∼50% of the volume of the micelle at native concentration, C = 25 g/L. This corresponds to ∼30 of hard regions (between 8 and 500 if we consider their strong polydispersity in size) in a micelle of 100 nm in diameter. At the highest compression (C = 400 g/L), ϕ1 ≈ 0.9, meaning the hard regions occupy nearly the whole micelle volume.
-
Level 2,
CaP nanoclusters: the volume fraction ϕ2 occupied by the CaP in the hard regions is constant at ∼0.02 at all concentrations. This is consistent with hard regions that resist compression and are not yet compressed in the concentration range investigated. The calculated value of ϕ2 ≈ 0.02 indicates that an average hard region of ∼25 nm in diameter contains ∼7 CaP nanoclusters.
An additional and important indication of the consistency of our model is the overall evolution of the product (ϕ0ϕ1ϕ2) with casein concentration (Fig. 5 B). In theory, this product is indeed equal to the CaP volume fraction in the dispersions, a quantity that can be estimated quite simply from the CaP mass fraction in the native micelle (7). Again, the accordance between the (ϕ0ϕ1ϕ2) values calculated from the model and their theoretical variation is very satisfactory.
On a conceptual point of view, our sponge model then appears to be valid. So as a sponge, the casein micelle would be composed of hard regions of a certain characteristic size (10–40 nm) that are connected or partially merged which each other and form a continuous and porous material. Fig. 6 gives a schematic view of the resulting structure (see Fig. S11 for a picture of how this structure is modified upon compression). Compared to previous works, it is clear that this structural model is more complex than the submicelle (11,12), homogeneous (7,8), and core-shell models (10). However, introducing such a complexity is necessary, since none of these models are able to accurately describe the behavior of the micelle under compression. The deformation of the micelle is of a very peculiar type and our sponge model is able to describe it through the collapsing of voids that separate hard regions. On a biological point of view, such a heterogeneous and hierarchical structure is quite consistent with the observation of 10- to 20-nm casein particles in the Golgi vesicles of lactating cells (33): upon aggregation, those casein particles would rearrange, fuse, and/or swell to form the spongelike micelle.
Figure 6.
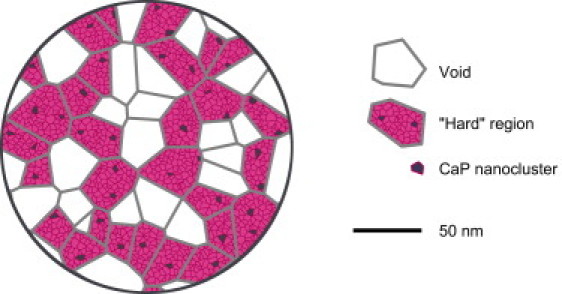
Highly schematic picture of a cross section of a 200-nm casein micelle according to the sponge model. The micelle is made of soft and hard regions represented here as Voronoi cells of ∼25 nm in size. The soft regions are voids filled with solvent and the hard regions contain all the CaP and protein materials. According to our description of the model, the hard regions are also decomposed into cells that contain either one CaP nanocluster (dark cells) or casein molecules and solvent (lighter cells).
Conclusions
Casein micelles are soft objects that respond to changes in their environment. In particular, their structure is deformed by compressive forces such as osmotic stress or the forces exerted in any concentration or filtration process. We have shown through SAXS that this deformation is nonaffine, i.e., some parts of the micelle collapse, whereas other parts resist deformation. None of the structural models previously proposed for the casein micelle can account for the deformations observed through SAXS. However, we show that a model made of random cells, in which some cells are filled and incompressible, whereas others are empty and collapse under pressure, can reproduce this type of deformation. We call this model the sponge model and we show that the spongelike micelle has a triple hierarchical structure (Fig. 6). The lowest level of the structure consists of the CaP nanoclusters that serve as anchors for the casein molecules. The intermediate level consists of hard regions ranging in size from 10 to 40 nm that occupy about half of the micelle volume at native concentration C = 25 g/L. Those regions are connected and/or partially merged with each other, thus forming a continuous and porous material. Each hard region contains an average of around seven nanoclusters, with considerable variation as the width of the distribution of volumes is >50%. The third level of structure is the casein micelle, which contains ∼30 of hard regions, again with a considerable polydispersity.
In future studies, it would be interesting to examine how the structure of the micelle is perturbed when both osmotic pressure and composition of the aqueous phase are changed. Such experiments would help in identifying the nature of the interactions that stabilize the micellar edifice and that are responsible for its peculiar structure.
Acknowledgments
We thank M. Van Audenhaege for her help in the preparation of the samples for SAXS analysis, and J. Léonil and R. Botet for interesting discussions. We are also grateful to J. Fauquant, F. Garnier-Lambrouin, N. Leconte, and P. Schuck from UMR1253 for preparing and providing us with the NPC powder and the UF permeate of skimmed milk.
Footnotes
This is an Open Access article distributed under the terms of the Creative Commons-Attribution Noncommercial License (http://creativecommons.org/licenses/by-nc/2.0/), which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Contributor Information
Antoine Bouchoux, Email: antoine.bouchoux@rennes.inra.fr.
Bernard Cabane, Email: bcabane@pmmh.espci.fr.
Supporting Material
References
- 1.Farrell J., Malin E.L., Qi P.X. Casein micelle structure: what can be learned from milk synthesis and structural biology? Curr. Opin. Colloid Interface Sci. 2006;11:135–147. [Google Scholar]
- 2.Horne D.S. Casein micelle structure: models and muddles. Curr. Opin. Colloid Interface Sci. 2006;11:148–153. [Google Scholar]
- 3.De Kruif C.G. Supra-aggregates of casein micelles as a prelude to coagulation. J. Dairy Sci. 1998;81:3019–3028. [Google Scholar]
- 4.Müller-Buschbaum P., Gebhardt R., Doster W. Effect of calcium concentration on the structure of casein micelles in thin films. Biophys. J. 2007;93:960–968. doi: 10.1529/biophysj.107.106385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.De Kruif C.G., Zhulina E.B. κ-casein as a polyelectrolyte brush on the surface of casein micelles. Colloids Surf. A Physicochem. Eng. Asp. 1996;117:151–159. [Google Scholar]
- 6.Kumosinski T.F., Pessen H., Brumberger H. Determination of the quaternary structural states of bovine casein by small-angle x-ray scattering: submicellar and micellar forms. Arch. Biochem. Biophys. 1988;266:548–561. doi: 10.1016/0003-9861(88)90288-3. [DOI] [PubMed] [Google Scholar]
- 7.Holt C., De Kruif C.G., Timmins P.A. Substructure of bovine casein micelles by small-angle x-ray and neutron scattering. Colloids Surf. A Physicochem. Eng. Asp. 2003;213:275–284. [Google Scholar]
- 8.Marchin S., Putaux J.L., Léonil J. Effects of the environmental factors on the casein micelle structure studied by cryo transmission electron microscopy and small-angle x-ray scattering/ultrasmall-angle x-ray scattering. J. Chem. Phys. 2007;126:045101–045110. doi: 10.1063/1.2409933. [DOI] [PubMed] [Google Scholar]
- 9.McMahon D.J., Oommen B.S. Supramolecular structure of the casein micelle. J. Dairy Sci. 2008;91:1709–1721. doi: 10.3168/jds.2007-0819. [DOI] [PubMed] [Google Scholar]
- 10.Shukla A., Narayanan T., Zanchi D. Structure of casein micelles and their complexation with tannins. Soft Matter. 2009;5:2884–2888. [Google Scholar]
- 11.Schmidt D.G. Association of caseins and casein micelle structure. In: Fox P.F., editor. Developments in Dairy Chemistry. Vol. 1. Elsevier Applied Science; London: 1982. pp. 61–86. [Google Scholar]
- 12.Walstra P. Casein sub-micelles: do they exist? Int. Dairy J. 1999;9:189–192. [Google Scholar]
- 13.Bouchoux A., Debbou B., Cabane B. Rheology and phase behavior of dense casein micelle dispersions. J. Chem. Phys. 2009;131:165106–165111. doi: 10.1063/1.3245956. [DOI] [PubMed] [Google Scholar]
- 14.Bouchoux A., Cayemitte P.E., Cabane B. Casein micelle dispersions under osmotic stress. Biophys. J. 2009;96:693–706. doi: 10.1016/j.bpj.2008.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gebhardt R., Roth S.V., Müller-Buschbaum P. Structural changes of casein micelles in a rennin gradient film with simultaneous consideration of the film morphology. Int. Dairy J. 2010;20:203–211. [Google Scholar]
- 16.Huppertz T., Smiddy M.A., de Kruif C.G. Biocompatible micro-gel particles from cross-linked casein micelles. Biomacromolecules. 2007;8:1300–1305. doi: 10.1021/bm061070m. [DOI] [PubMed] [Google Scholar]
- 17.Metwalli E., Moulin J.F., Müller-Buschbaum P. Hydration behavior of casein micelles in thin film geometry: a GISANS study? Langmuir. 2009;25:4124–4131. doi: 10.1021/la802602g. [DOI] [PubMed] [Google Scholar]
- 18.Famelart M.H., Lepesant F., Schuck P. pH-induced physicochemical modifications of native phosphocaseinate suspensions: influence of aqueous phase. Lait. 1996;76:445–460. [Google Scholar]
- 19.Pierre A., Fauquant J., Maubois J.L. Native micellar casein separation through cross flow membrane microfiltration. Lait. 1992;72:461–474. [Google Scholar]
- 20.Schuck P., Piot M., Maubois J.L. Spray-drying of native phosphocaseinate obtained by membrane microfiltration. Lait. 1994;74:375–388. [Google Scholar]
- 21.Jenness R., Koops J. Preparation and properties of a salt solution which simulates milk ultrafiltrate. Neth. Milk Dairy J. 1962;16:153–164. [Google Scholar]
- 22.Pignon F., Belina G., Gésan-Guiziou G. Structure and rheological behavior of casein micelle suspensions during ultrafiltration process. J. Chem. Phys. 2004;121:8138–8146. doi: 10.1063/1.1800931. [DOI] [PubMed] [Google Scholar]
- 23.Pitkowski A., Nicolai T., Durand D. Scattering and turbidity study of the dissociation of casein by calcium chelation. Biomacromolecules. 2008;9:369–375. doi: 10.1021/bm7006899. [DOI] [PubMed] [Google Scholar]
- 24.Gebhardt R., Burghammer M., Müller-Buschbaum P. Structural changes of casein micelles in a calcium gradient film. Macromol. Biosci. 2008;8:347–354. doi: 10.1002/mabi.200700203. [DOI] [PubMed] [Google Scholar]
- 25.Gebhardt R., Burghammer M., Müller-Buschbaum P. Investigation of surface modification of casein films by rennin enzyme action using micro-beam grazing incidence small angle x-ray scattering. Dairy Sci. Technol. 2010;90:75–86. [Google Scholar]
- 26.Mason T.G., Graves S.M., Lin M.Y. Effective structure factor of osmotically deformed nanoemulsions. J. Phys. Chem. B. 2006;110:22097–22102. doi: 10.1021/jp0601623. [DOI] [PubMed] [Google Scholar]
- 27.Mattsson J., Wyss H.M., Weitz D.A. Soft colloids make strong glasses. Nature. 2009;462:83–86. doi: 10.1038/nature08457. [DOI] [PubMed] [Google Scholar]
- 28.Graves S., Meleson K., Mason T.G. Structure of concentrated nanoemulsions. J. Chem. Phys. 2005;122:134703–134706. doi: 10.1063/1.1874952. [DOI] [PubMed] [Google Scholar]
- 29.Auvray L., Cotton J.P., Taupin C. Concentrated Winsor microemulsions: a small angle x-ray scattering study. J. Phys. France. 1984;45:913–928. [Google Scholar]
- 30.De Gennes P.G., Taupin C. Microemulsions and the flexibility of oil/water interfaces. J. Phys. Chem. 1982;86:2294–2304. [Google Scholar]
- 31.Talmon Y., Prager S. Statistical thermodynamics of phase equilibria in microemulsions. J. Chem. Phys. 1978;69:2984–2991. [Google Scholar]
- 32.Aragon S.R., Pecora R. Theory of dynamic light scattering from polydisperse systems. J. Chem. Phys. 1976;64:2395–2404. [Google Scholar]
- 33.Clermont Y., Xia L., Hermo L. Transport of casein submicelles and formation of secretion granules in the Golgi apparatus of epithelial cells of the lactating mammary gland of the rat. Anat. Rec. 1993;235:363–373. doi: 10.1002/ar.1092350305. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


