Distinguishable Populations Report on the Interactions of Single DNA Molecules with Solid-State Nanopores

Abstract

Solid-state nanopores have received increasing interest over recent years because of their potential for genomic screening and sequencing. In particular, small nanopores (2–5 nm in diameter) allow the detection of local structure along biological molecules, such as proteins bound to DNA or possibly the secondary structure of RNA molecules. In a typical experiment, individual molecules are translocated through a single nanopore, thereby causing a small deviation in the ionic conductance. A correct interpretation of these conductance changes is essential for our understanding of the process of translocation, and for further sophistication of this technique. Here, we present translocation measurements of double-stranded DNA through nanopores down to the diameter of the DNA itself (1.8–7 nm at the narrowest constriction). In contrast to previous findings on such small nanopores, we find that single molecules interacting with these pores can cause three distinct levels of conductance blockades. We attribute the smallest conductance blockades to molecules that briefly skim the nanopore entrance without translocating, the intermediate level of conductance blockade to regular head-to-tail translocations, and the largest conductance blockades to obstruction of the nanopore entrance by one or multiple (duplex) DNA strands. Our measurements are an important step toward understanding the conductance blockade of biomolecules in such small nanopores, which will be essential for future applications involving solid-state nanopores.

Introduction

The use of solid-state nanopores for the detection and study of biological molecules has expanded greatly in recent years (1–3). For example, solid-state nanopores have now been used for the detection of locally bound proteins (4–6) or other molecules (7–9) along DNA, the unzipping of single-stranded DNA hairpins (10), and the discrimination of single- and double-stranded nucleic acids (11,12). In all studies involving solid-state nanopores, charged biological molecules in an electrolyte are driven in or through the nanopore by an electrical field (Fig. 1 a). Upon entry inside the nanopore, these molecules cause a characteristic change in the ionic conductance through the pore, which can serve as a means to detect local structure along the molecule. Although such translocation studies can also be performed with biological pores (1,13), the use of nanopores fabricated in solid-state membranes offers a number of advantages, such as the flexibility to tune their size (14,15), shape (16,17), and surface chemistry (18), and the fact that they can easily be integrated into electronic devices. For solid-state nanopores, the conductance blockade of translocating molecules is well understood for pore sizes much larger than the molecular diameter, and simple models based on the total area or volume blocked by the polymer inside the nanopore provide quantitative agreement with the observed blockades (19). However, when the pore size approaches the size of the translocating molecule, new effects, such as the three-dimensional (3D) shape of the pore, its surface roughness (20), and the overlap of counterion screening layers must be taken into account.

Figure 1.

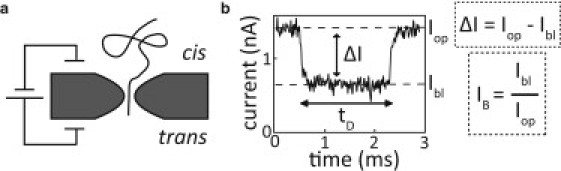
Experimental setup. (a) Schematic of our setup. A nanopore immersed in electrolyte separates two compartments (cis and trans). After DNA is introduced on the cis side, an external bias voltage can thread DNA molecules through the nanopore, causing the ionic current to be partially blocked. (b) Sample trace of the current blockade caused by a DNA molecule in a 3.2 ± 0.5 nm diameter pore at 100 mV bias voltage. For each translocation event we determine the average blockade ΔI = I_op − I_bl as the current in the open state (I_op) minus the current in the blocked state (I_bl), the dwell time t_D as the total duration of the event, and the relative current blockade I_B = I_bl / I_op = 1 − ΔI/I_op.

Here, we study the translocation of double-stranded DNA (henceforth simply referred to as DNA) through solid-state nanopores ranging from 1.8 nm to 7 nm in diameter. We characterize the DNA translocation events by their average conductance change ΔG = ΔI/V, as well as their dwell time t_D (see Fig. 1 b and Materials and Methods). ΔI is defined as the open pore current (I_open) minus the current in the blocked state (I_blocked), resulting in positive values for all experiments presented here. Following Wanunu et al. (21), we also define a relative current blockade I_B = 1 − (ΔI/I_open) = I_blocked/I_open as the current through the nanopore in the blocked state divided by the open pore current (Fig. 1 b). For example, I_B = 1 when no molecule blocks the nanopore, and I_B = 0 in the fully blocked state.

In our results we identify three distinct event populations, each with a characteristic I_B and/or t_D. The first population consists of very short events with very small conductance blockades. Such events have also frequently been observed in larger pores (22,23) and attributed to DNA molecules that skim the entrance of the nanopore but do not translocate through it. To explain how the other two populations can arise from a monodisperse sample of DNA molecules, we investigate how the relative weights of the populations change with pore size and DNA length. First, we show that in the smallest nanopores the majority of events result in a very large blockade whereby the conductance through the nanopore is nearly entirely blocked. When the nanopore size is increased, however, the number of events with this large blockade gradually decreases, whereas more events appear with an intermediate blockade. We then show that in nanopores of 2.5–3 nm diameter, the population associated with the largest blockade increases in weight as the DNA length is increased. These observations suggest that this population is associated with events in which part of the DNA blocks the entrance of the nanopore, since such interactions would be more likely in smaller pores, and for longer DNA. A possible scenario for such an interaction would be the capture of a polymer in a transverse orientation at the nanopore entrance, after which the molecule may (through buckling or sliding one of its ends into the nanopore) or may not translocate.

We then focus on the population of events with intermediate blockades. Experimentally, the magnitude of this intermediate blockade corresponds very well to the conductance blockade observed in larger pores (∼10 nm in diameter) (12) using longer DNA. Furthermore, we demonstrate that the magnitude of this conductance blockade is constant over a large range of pore diameters (2.5–12 nm). We therefore surmise that these events correspond to regular head-to-tail translocations in which the polymer enters the nanopore with one end and is then reeled through the pore in a linear fashion. For such events the magnitude of the conductance blockade is not expected to depend strongly on the pore size, as the total volume of ions blocked by the DNA should be constant.

Of interest, our results deviate somewhat from earlier results obtained in small nanopores by Wanunu and co-workers (21), who also reported the existence of different event populations. They found that the weight of the population with the largest conductance blockade decreased with decreasing nanopore diameter, and concluded that this population must correspond to regular translocations. We observe that the weight of the population with the largest conductance blockade increases with decreasing nanopore diameter. Furthermore, we additionally observe a clearly separable population with an intermediate blockade, and it is this population that we associate with regular translocations. A third population was also inferred from the data of Wanunu et al. by a detailed study of the dwell times, but this population was not clearly separable from its conductance blockade only. We postulate that these differences are a consequence of differences in pore shape or the pore surface roughness, caused by altered nanopore fabrication or storage conditions. In support of this reasoning, we demonstrate that by tuning the transmission electron microscopy (TEM) beam size employed in nanopore fabrication, we can obtain results similar to those of Wanunu et al. (21). Our results therefore indicate that small differences in the nanopore fabrication process can lead to significantly different results for biomolecular translocation. In this light, this work contributes to the understanding of the conductance blockades caused by single molecules in very small nanopores, which will be crucial for the further development of nanopores as single-molecule sensors.

Materials and Methods

Sample preparation

Nanopores were fabricated in 20 nm SiN membranes by means of a highly focused TEM beam as previously described (24), using a typical TEM beam size of 15 nm (full width at half-maximum), and stored in a solution containing 50% ethanol and 50% ddH₂O directly after drilling. The nanopore size was directly determined from the TEM image before storage, and the error bar quoted for each nanopore stems from the determination of the size from the image. The measured ionic resistance through the nanopore was also used to double-check the diameter and stability of the nanopore. In some cases, the nanopore size was also remeasured after the DNA translocation experiments to verify that the nanopores did not change during the course of the experiment (16). Only results obtained in nanopores that exhibited a < 25% change in open pore current during the experiment were used. Before it was used, the chip containing the membrane with the nanopore was rinsed with deionized H₂O, followed by acetone and IPA, and then blown dry. Subsequently, the sample was treated with O₂ plasma at room temperature for 30 s, mounted into the flow cell, and immediately flushed with electrolyte. For each experiment, ∼30 s of conductance traces were recorded and analyzed before addition of DNA to the cis chamber, to ensure that no events were detected in that situation. All experiments were performed in 1 M KCl, 10 mM Tris-HCl (pH 8.0), and 1 mM EDTA.

Analysis

The voltage and current were sampled at 200 kHz bandwidth and subsequently low-pass filtered at 35–70 kHz. For every nanopore, hundreds to thousands of conductance blockade events were collected at 300 mV bias voltage. The typical requirement for the detection of an event was that a minimum of 10 consecutive data points (corresponding to a minimum dwell time of 50 μs) must deviate by > 4.5× the standard deviation from the average current. This criterion ensures that detected events are extremely unlikely to be caused by random fluctuations of the current. After low-pass filtering was completed, conductance blockade events were identified and corresponding histograms were constructed as previously described (12). For each identified event, a dwell time t_d and average conductance blockade (expressed as both ΔG = ΔI/V and I_B; see Fig. 1 b) were determined.

Each individual event was additionally assigned to a type, such as 0, H, or L (see Fig. 2), corresponding to its conductance blockade level. To perform this assignment, we first determined the conductance blockade for each of the three levels (0, H, and L) from Gaussian fits to the current histogram comprised of all the events (see Fig. 2 b). When we report on fitted values, the errors correspond to the standard errors of the means of the Gaussian distributions. Next, we scanned each individual event point by point to determine to which of the three levels (0, H, or L) the blockade value of each point corresponded most closely. When the number of consecutive points closest to the same level exceeded a critical value (typically > 7), the event type was assigned accordingly. Multilevel events in which a single event reached different blockade levels consecutively (such as LH or HL or more complex versions; see Fig. 2 a) were also frequently observed. In these cases, the same minimum number of consecutive points was required for the event to be named accordingly. For example, an LH event must have a minimum of seven consecutive points that are closest to the L level, followed by a minimum of seven consecutive points that are closest to the H level. In the graphs shown in Fig. 4, a and b, where we plot the percentage of L events, we took such multilevel events into account by adding one-half of the percentage of multilevel events to the percentage of L events (and similarly to the percentage of H events; see Fig. S2 a in the Supporting Material). This number is additionally reflected in the size of the error bars for both event types.

Figure 2.

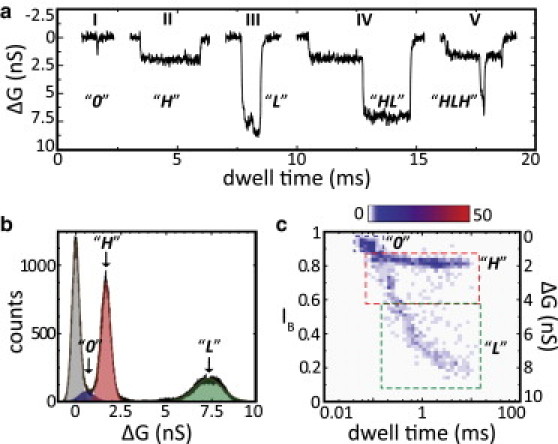
Typical conductance blockade events and corresponding histograms from 3.5 kbp long DNA molecules interacting with a 2.5 ± 0.4 nm diameter nanopore. (a) Representative conductance traces of individual events. Events I–III are single-level events, i.e., they reach a single blockade level and return to the baseline after a while. There are also a smaller number of multilevel events, such as events IV and V. The different blockade levels are labeled 0, H, and L, and are discussed in the main text. (b) Histogram of the conductance traces of all the events (black solid line). The change in conductance is plotted with respect to the open pore conductance. Each event contributes multiple counts to this histogram. A number of peaks can be distinguished, fitted by Gaussian curves and denoted by different colors. The brown solid line is the sum of these fitted Gaussians. (c) 2D histogram of the same set of events, showing the dwell time and relative current blockade I_B for each event. The events cluster into distinct populations (denoted by squares; see Materials and Methods) that correspond to the peaks in the histogram in b.

Figure 4.

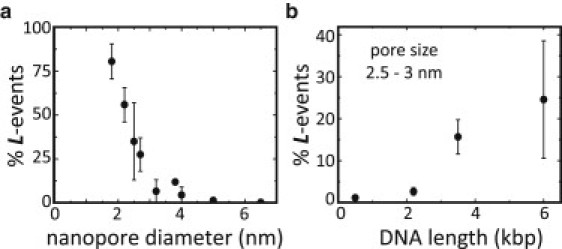
Dependence of L events on pore size and DNA length. (a) Fraction of L events as a function of nanopore diameter for 3.5 kbp DNA at a bias voltage of 300 mV. A clear reduction of the percentage of L events is observed as the pore size increases. (b) Fraction of L events for different DNA lengths (0.5 kbp: 1214 events; 2.2 kbp: 321 events; 3.5 kbp: 2081 events; 6 kb: 2672 events) in nanopores ranging from 2.5 to 3 nm diameter. As the DNA length is increased, the relative amount of L events increases. Multilevel events are included as error bars (see Materials and Methods for a definition of the percentage of L events).

The dotted squares in Figs. 2 and 3 indicating the different event types were attributed by first determining the I_B-values of the 0, H, and L levels (determined from Gaussian fits to the conductance blockade histogram and converting the resulting value of ΔG to I_B). The I_B-values closest to the 0 level were then surrounded by a blue dotted square, those closest to the H level by a red dotted square, and those closest to the L level by a green dotted square. The left and right sides of the squares were determined by the observed minimum and maximum dwell times.

Figure 3.

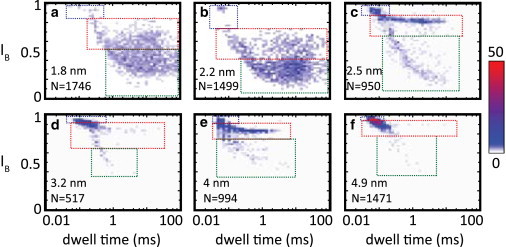
Individual examples of 2D event histograms of dwell time versus relative current blockade I_B for nanopores of different diameters. In all cases, events were recorded using 3.5 kbp long DNA at a bias voltage of 300 mV. The three event populations can be distinguished as before (denoted by dotted squares; see Materials and Methods), but their relative weights vary with pore size. The general trend is that L events are very frequent in the smallest pores, but as the pore size increases, their frequency gradually reduces together with a concomitant increase in H events. The variation in the conductance blockades is further quantified in Fig. S4 and Fig. 5a.

Synthesis of DNA molecules

In our experiments we employed DNA molecules of different lengths, all synthesized from DNA templates via polymerase chain reaction (PCR) amplification. The 3.5 kbp and 2.2 kbp molecules were synthesized as described previously (25). The 500 bp molecule was synthesized by PCR amplification of pBluescript1,2,3,4 using the primers GATCGGTACCTATGGCTGAACCGGTAGG and AAAACTGCAGTACGATCTGCCGTCAGTC, and the 6 kbp molecule was synthesized by PCR amplification of λ-phage (Promega) using the primers AAAAGAATTCAGCCTCAGCTGACCAGCCAGAAAACGACC and GATTTGTTCGTGACCGATATGC.

Results

In Fig. 2 a we show a number of typical events caused by 3.5 kbp DNA molecules in a nanopore of 2.5 ± 0.4 nm diameter (total open pore conductance G = 9.8 ± 0.4 nS). In such a small nanopore, we expect that only a single duplex DNA could occupy the nanopore at any given time, as the diameter of duplex DNA determined via x-ray crystallography is 2.0 nm (26). Since the DNA sample used in this experiment is monodisperse, one might expect to see only a single blockade level, corresponding to the characteristic conductance blockade of a single molecule inside the nanopore. However, the events displayed in Fig. 2 a clearly indicate the existence of multiple levels (here indicated by 0, H, and L). Although the majority (typically ∼85%) of the events are single-level (events I–III; Fig. 2 a), multilevel events (events IV and V; Fig. 2 a) are not uncommon, indicating that an individual molecule alone can produce different conductance blockades in the nanopore.

To analyze the entirety of events, we grouped the acquired events in this nanopore together into a corresponding conductance blockade histogram (N = 950; Fig. 2 b, and Materials and Methods). We can now clearly identify a number of peaks in the histogram (fitted by the sum of multiple Gaussians and colored distinctly) whose different means reflect the different blockade levels observed in the individual events in Fig. 2 a. Examining the conductance blockade histogram from left to right, we can easily attribute the first peak (gray, centered at ΔG = 0 nS) to the baseline (open pore) current, as our event selection algorithm always collects a number of baseline points accompanying individual events. In addition to this baseline conductance peak, we observe a second peak (blue-labeled 0, centered at ΔG = 0.61 ± 0.08 nS), which corresponds to the smallest observed conductance blockade. Next, there are two peaks of similar magnitude corresponding to larger blockades (red, centered at ΔG = 1.66 ± 0.05 nS and labeled H; and green, centered at ΔG = 7.32 ± 0.15 nS and labeled L). We point out that the L-labeled peak with its high ΔG-value is very different from results obtained in a previous study on folded DNA translocations in larger nanopores (23). In that study, multiple peaks ΔG peaks appeared at integer multiples of the first (H) peak, whereas here the L peak appears at a ΔG-value more than fourfold higher than the H peak.

Although the conductance histogram in Fig. 2 b allows us to clearly identify the different possible levels of blockade caused by single DNA molecules, it has the disadvantage that the information it contains cannot be traced back to the individual events. For example, the existence of multilevel events (such as in Fig. 2 a, events IV and V) cannot be deduced from the histogram. Thus, we also plot in Fig. 2 c a two-dimensional (2D) histogram showing for each event the (average) relative current blockade I_B on the vertical axis and its event dwell time t_D on the horizontal axis. This also allows us to investigate whether different conductance blockades are associated with different dwell times. Looking at the 2D histogram, we can distinguish three groups of events that can be related back to the different peaks in Fig. 2 b: the blue peak in Fig. 2 b, corresponding to events with a very small conductance blockade (ΔG = 0.61 ± 0.08 nS; Fig. 2 b), appears as a small group of events at its corresponding value of I_B = 0.94 ± 0.01, denoted by a blue square; the red peak in Fig. 2 b, with ΔG = 1.66 ± 0.05 nS, corresponds to the group of events denoted by a red square (with corresponding I_B = 0.83 ± 0.01; Fig. 2 c). Finally, the green peak in Fig. 2b, with ΔG = 7.32 ± 0.15 nS, corresponds to the group of events denoted by a green square (with corresponding I_B = 0.27 ± 0.02; Fig. 2 c). Since for each event its average value of I_B is plotted, multilevel events (as in Fig. 2 a, events IV and V) will appear somewhere in between the H and L levels in the figure.

Using the combined information from histograms such as those in Fig. 2, b and c, we now investigate the different groups of events to understand their origin. Starting first with the events in the 0 group, we find that these are associated with the shorter dwell times and smallest conductance blockade, both of which approach the limits of our detection. Although the number of events in this group is therefore subject to the precise parameters employed in our analysis (minimum blockade and dwell time), it is nevertheless clear that such events cannot be caused simply by random fluctuation of the current (see Materials and Methods). This is supported by the fact that no such events were observed in control experiments without DNA (see Materials and Methods). Thus, this group of events must derive from a form of interaction of the molecules in the sample with the nanopore. However, given the low magnitude of conductance blockade, it is reasonable to assume that these events do not correspond to molecules passing through the nanopore. In a 2.5 nm pore, the presence of a 2.0 nm diameter DNA molecule would likely block > 6% of the total current (corresponding to the average I_B = 0.94 ± 0.01 for these events) and would likely take longer to translocate (22,23). We therefore propose that these events correspond to molecules that briefly skim the nanopore entrance without actually entering the nanopore itself. As additional evidence in support of this hypothesis, we note that such short events with only a very small blockade have frequently been observed in other translocation studies involving larger nanopores and longer molecules (22,23).

We now turn our attention to the H and L events. First, we investigated the relative magnitudes of these groups of events in nanopores of different sizes and determined their respective characteristic blockade and dwell time. In Fig. 3 we show 2D histograms of I_B versus dwell time for nanopores with diameters varying between 1.8 and 5 nm to roughly indicate the main trends. All measurements in Fig. 3 were performed using 3.5 kbp DNA at a bias voltage of 300 mV. As before, we can identify the three different groups of events in each size of pore (indicated by dotted squares). The dotted squares reflect the I_B range corresponding to each of the three groups as determined from Gaussian fits to the conductance blockade histogram (see Materials and Methods; also see Fig. S4 for a plot of I_B versus pore diameter). The group of 0 events appears to be independent of the nanopore size, in accordance with our hypothesis that these events correspond to molecules that briefly skim the pore entrance. The populations of the other two groups, however, vary with pore size. We find that in the smaller nanopores (Fig. 3, a and b), the H and L events are not very clearly separated visually in the 2D histograms. Nevertheless, for the small nanopores (Fig. 3, a–c), the majority of the events appear to be of type L. As the pore size is increased, however, the fraction of L events decreases, until almost no L events are found in the largest pores. We also see that for the larger nanopores (Fig. 3, e and f), the average event dwell time decreases (see also Fig. S3), and that, while some L events can still be separately identified, the distinction between H and 0 events has become less clearly visible. These last two observations can be readily explained by the fact that in larger nanopores, the translocation time of the DNA is expected to reduce due to decreased interactions with the nanopore. Also, because the total nanopore conductance scales quadratically with nanopore diameter but the conductance blockade itself does not, the I_B of the events will approach one as the nanopore size is increased (recall that I_B = 1 − ΔI/I_open). Thus, in particular, the distinction between the H and 0 events becomes more difficult to see as the nanopore size increases. By using longer DNA and zooming in on I_B in a narrower range (e.g., ranging from I_B = 0.9 to I_B = 1), we can again make such a distinction (Fig. S1).

In the following, we will further quantify these trends. In Fig. 4 a we plot the percentage of L events (see Materials and Methods for a description of the determination of this percentage) relative to the total number of events as a function of pore size, for a fixed DNA length of 3.5 kbp at a bias voltage of 300 mV (for completeness, the corresponding percentages of H and 0 events as a function of pore size are displayed in Fig. S2 a). Clearly, the fraction of L events increases gradually with decreasing nanopore size: while in the nanopores larger than 4 nm, L events are very rare, for the smallest nanopores almost all events are of type L. Since a notable effect of reducing the nanopore diameter is presumably an increased probability that the DNA will transversely approach the nanopore, this result suggests that L events may be events in which the DNA partially obstructs the nanopore entrance. In such a scenario, an increase in L events would also be expected when the DNA length is increased, since longer DNA should also increase the likelihood for obstruction of the nanopore entrance. As can be seen from Fig. 4 b, in which the percentage of L events in 2.5–3 nm pores is plotted for DNA lengths ranging from 500 bp up to 6 kbp in length, at a bias voltage of 300 mV, an increase in the fraction of L events is indeed observed for longer DNA (the corresponding percentages of H and 0 events are shown in Fig.S2 b). Clearly, for the longer DNA molecules, the occurrence of L events is more likely than for shorter DNA molecules. Although experiments with even longer DNA lengths are possible in principle, we found that such results were very difficult to obtain, as the likelihood for permanent clogging of the nanopore increased dramatically with larger DNA lengths in such small nanopores. Nevertheless, a clear increase in L events is visible even in the range up to 6 kb. The observation that L events are more likely to occur when the nanopore size is reduced and when the DNA length is increased strongly suggests that these events are associated with events in which the DNA approaches the nanopore transversely, thus obstructing the entrance of the nanopore with one or more (duplex) strands. We will discuss possible mechanisms for this below (see Discussion).

We now switch our attention to the H events, whose fraction gradually increases with increasing nanopore diameter (Fig. 3). This permits us to compare the magnitude of the conductance blockade of the H events over the pore size range probed here with previous results obtained in larger nanopores. We reported previously that 12.7 kbp long DNA molecules translocating in a head-to-tail fashion through nanopores of ∼10 nm in diameter caused a characteristic conductance blockade of ΔG = 1.68 ± 0.15 nS (at 300 mV bias voltage) (12). This is strikingly close to the blockade level of the H events in the 2.5 nm pore shown in Fig. 2 b, where we found ΔG = 1.66 ± 0.05 nS. Assuming that the conductance change does not depend on the nanopore diameter or DNA length, this similarity suggests that the H events may be of the same type as the translocation events observed in the larger pores involving longer DNA. Furthermore, similar ΔG-values in nanopores down to 3.5 nm in diameter were also found in previous studies, in which DNA molecules tethered to an optically trapped bead were confirmed to enter the nanopores by a commensurate movement of the bead (4,27,28).

It is therefore of interest to probe how the magnitude of the conductance blockade of the H events varies over a wide range of nanopore sizes and DNA lengths. In Fig. 5 a we show the conductance blockade ΔG of the H events (solid symbols) and L events (open symbols) for nanopore diameters varying between 1.8 and 12 nm. The dotted line indicates the DNA helical diameter of 2.0 nm. For the smallest pore diameters (< 2.5 nm), we observe an increase and a large variation in ΔG. For the pores with diameters > 2.5 nm, however, the conductance blockade of the H events appears to be quite independent of nanopore diameter, since the conductance blockade averages ∼1.9 ± 0.4 nS over the entire range (where the error is the standard deviation). In contrast, the L events show a gradual increase with increasing pore size until they almost completely disappear for pore sizes > 5 nm (as discussed above). We further note that Fig. 5 a includes data points for DNA molecules of a number of different lengths. There are several reasons for this. First, we found that experiments involving longer DNA (such as the 12.7 kbp DNA used previously in larger pores (12)) in nanopores < 5 nm in diameter were impractical because the nanopores very quickly became permanently clogged, before enough translocation events could be collected. The smallest nanopores (< 5 nm) therefore required the use of shorter DNA. Second, the shorter DNA could not be used for the larger nanopores (> 5 nm in diameter) because in those cases the translocation time reduced below the limit of detection and the conductance blockades could no longer be properly determined. This raises the question as to whether DNA of different lengths might cause different conductance blockades in a nanopore of given diameter, thereby complicating the interpretation of Fig. 5 a. To address this question, we show in Fig. 5 b the conductance blockade in nanopores of 2.5–3 nm diameter for different DNA lengths ranging from 500 bp to 6 kbp. For completeness, we show both the H events (solid circles) and the L events (open circles). We find that for both populations, the conductance blockade is a constant and is independent of the DNA length. Thus, given the independence of ΔG on DNA nanopore size and DNA length (Fig. 5, a and b, respectively), and the observation that the H events observed in the smaller pores exhibit conductance blockades of similar magnitude as the regular head-to-tail events observed in larger pores, we surmise that the H events must correspond to this type of translocation.

Figure 5.

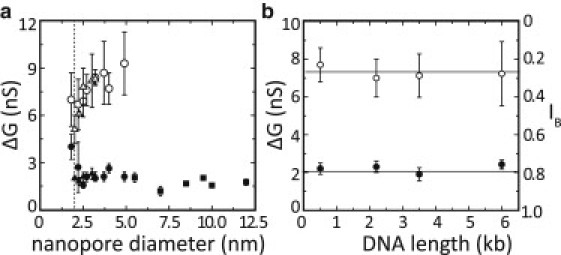
Dependence of the blockade level of the H and L events on nanopore size and DNA length. (a) Conductance blockades of H (solid symbols) and L events (open symbols) as a function of nanopore diameter for DNA molecules of varying lengths (triangles: 500 bp; circles: 3.5 kbp; squares: 12.7 kbp). The dotted line indicates the diameter of DNA. For pores sizes approximately equal to the DNA, we find a large variation in the conductance blockade of the H events and a small increase in the conductance blockade. However, for pores larger than 2.5 nm, we observe an ∼30% variation in the conductance blockade of the H events, but find no obvious dependence on pore diameter, as the pore size is varied ∼5-fold. The conductance blockade of the L events gradually increases, and the L events completely disappear in pores larger than ∼5 nm. (b) Conductance blockades of both H and L events as a function of DNA length in 2.5–3 nm diameter pores. Solid circles correspond to H events, open circles to L events. Solid lines are guides to the eye. On the right, the approximately corresponding I_B is plotted for reference (based on a 2.5 nm pore). Both types of events exhibit no dependence on DNA length for lengths varying between 500 and 6000 bp. The values and error bars for a and b were determined from Gaussian fits to the conductance change histogram (see Fig. 2b).

Discussion

When we examined the interaction of DNA molecules with small solid-state nanopores, we found that we could typically distinguish three groups of events whose relative weight varied with pore size. Below, we expand on the interpretation of these different groups of events.

We start with the H events, for which the straightforward interpretation that these correspond to regular head-to-tail translocations should be examined in light of the magnitude of the relative current blockade I_B measured for these events. Our experiments yield three primary results for the H events: 1), the fraction of H events increases gradually as the nanopore size is increased from ∼2 nm to 5 nm (Figs. 3 and 4 a); 2), for nanopores larger than 2.5 nm the magnitude of the conductance blockade of the H events is independent of both nanopore size and DNA length (Fig. 5, a and b); and 3), the magnitude of the conductance blockade is similar to that of the translocations in larger pores (12,22,23) and measurements involving DNA molecules tethered to optically trapped beads (4,27,28). Such observations would be expected from a simple model in which the conductance blockade is determined only by the exclusion of ions due to the presence of the DNA inside the nanopore. In such a model, the total volume of the DNA occupying the nanopore is constant, regardless of the nanopore diameter or DNA length (provided the membrane thickness is constant and excluding bending or folding of the DNA, in which case multiple duplex DNA strands could occupy the nanopore). The corresponding conductance blockade is thus also expected to be independent of nanopore diameter and DNA length. Since this is exactly what we observe for the H events, and given that the H events gradually disappear when the pore size is reduced below 2 nm, we propose that the H events correspond to regular translocations.

Although this conclusion is compelling on the basis of our presented results, it is nonetheless surprising that the typical I_B-value for our H events (I_B ≈ 0.8) is quite high, even for nanopores as small as ∼2.5 nm in diameter. This means that only ∼20% of the open pore conductance is blocked. If we assume that all the ions in the volume occupied by the DNA are blocked from traversing the pore, a DNA molecule of ∼2.0 nm diameter (corresponding to its crystallographic diameter (26)) would rather be expected to block ∼65% of the current through a cylindrical pore of 2.5 nm diameter (corresponding to an I_B of 0.35). We offer two potential explanations for this discrepancy. First, the DNA is not in actual fact a closed cylinder; rather, it is a highly charged, permeable and flexible structure that attracts counterions, which may be able to move within the DNA helix. Recent molecular-dynamics simulations (29) demonstrated that counterions can indeed penetrate within the DNA helix and remain mobile (albeit less so than in bulk). This implies that part of the ionic current may be carried along the major or minor grooves of the DNA, thus making the DNA less of a restriction for ionic conduction than a solid cylinder would be, and effectively increasing the corresponding value of I_B. Furthermore, the large amount of counterions attracted by the highly charged DNA backbone may increase the ionic conductance through the nanopore (19,20), thus also leading to a higher value of I_B during DNA translocation. Second, it is possible that the low conductance blockade observed for the H events results from the particular 3D shape of the nanopores employed in these experiments. We previously demonstrated that the nanopore shape depends sensitively on the conditions employed during fabrication (16,17). In particular, the shape depends on the size (full width at half-maximum) of the focused electron beam of the TEM: a large beam compared to the nanopore size causes an hourglass shape, whereas a small beam leads to a cylindrical shape (16). The smallest nanopores used in this study were all drilled with a beam size at least three times larger than the nanopore diameter, and thus these pores have an hourglass shape. For such a shape, only a very small section (in z) at the center of the SiN membrane contains the narrowest nanopore constriction. The electrical field at this location is likely higher than that in nanopores with a more cylindrical shape, and this could lead to a stronger stretching force on the DNA, making it more permeable for ions to contribute to the current. Also, the relative volume (with respect to the total volume of the pore) excluded by the presence of the DNA is much smaller for a compressed hourglass shape than for a cylindrical nanopore, which effectively lowers the relative amount of conductance blocked (thus leading to a higher value of I_B). Both explanations, i.e., that the DNA is an open cylinder that is partially permeable to ions, and that the hourglass shape of our nanopores may stretch the DNA at the smallest constriction, making it even more permeable for ionic conduction, may explain why the H events only block 20% of the nanopore conductance.

Another surprising fact is that, although their occurrence is greatly reduced, H events still occur in even the smallest pores studied here, implying that DNA can translocate through nanopores smaller than the DNA diameter. Indeed, it was reported previously that DNA can even penetrate nanopores as small as 0.5 nm (30) (albeit at higher bias voltages), and this finding was supported by molecular-dynamics simulations (20,31). In our experiments, the hourglass shape of our nanopores may further facilitate the translocation of DNA through nanopores slightly smaller than the DNA helical diameter. As discussed above, the electrical field at the narrowest constriction is likely very high, allowing for possible deformation of the DNA, and subsequent translocation through the nanopore.

It is interesting to note that our results deviate from previous results published by Wanunu and co-workers (21). They reported that the weight of the population with the largest conductance blockade decreased as the nanopore diameter was decreased, and concluded that this population corresponded to regular translocations. On the contrary, we observe that the weight of the population with the largest conductance blockade increases as the nanopore diameter is decreased. However, we additionally observe a clearly separable population with an intermediate blockade (H events), and it is this population that we associate with regular translocations. Wanunu et al. (21) also proposed such a third population based on a detailed study of the event dwell times, but this population could not clearly be distinguished from its conductance blockade only. This striking difference could be the result of different procedures used during manufacturing of the nanopore membranes or sample preparation, giving rise to differences in surface roughness or surface charge. Alternatively, this discrepancy with our results may originate from the shape of our nanopores. If the nanopores used by Wanunu et al. were drilled with a significantly smaller TEM beam size than used for our nanopores, we would expect them to be more cylindrical in shape. In accordance with the above arguments, this would increase the conductance blockade of H events (lowering their value of I_B), moving them closer to the blockade level of the L events and rendering a distinction based on their conductance blockade more difficult. To quantitatively investigate whether the nanopore shape influences the event distribution, we performed measurements in 2.5–3 nm diameter pores that were drilled with a small TEM beam size of nominally 2 nm in diameter. A typical example is given in Fig. 6 a, which shows a 2D histogram for a 2.5 ± 0.5 nm diameter pore. For comparison, we show in Fig. 6 b a similar 2D histogram for one of our regular nanopores of 2.5 ± 0.5 nm diameter, drilled with a TEM beam of 15 nm diameter. Indeed, a clear difference is observed for the pore drilled with the smaller beam: no clearly distinguishable population of H events is observed in this case. This demonstrates that a seemingly small difference in the manufacturing conditions (e.g., the TEM beam size) may indeed give rise to very different conductance blockades.

Figure 6.

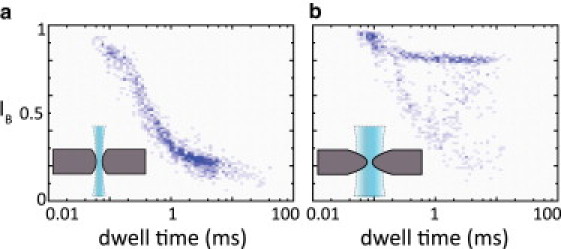
Comparison of results obtained in nanopores drilled with different TEM beam sizes. (a) Results for a 2.5 ± 0.5 nm pore drilled with a TEM beam of 2 nm diameter, smaller than the minimum beam size used for the earlier results. The smaller beam size is expected to give rise to a cylindrical shape (15), as indicated by the picture in the inset. Clearly, the conductance blockade distribution is different from the results obtained in the other nanopores: no clear distinction into H and L events is observed. For comparison, in panel b we show another typical 2D histogram for a 2.5 ± 0.5 nm pore drilled with our typically employed 15 nm beam, where a large population corresponding to the H events is present. In both experiments we used 3.5 kbp DNA at a bias voltage of 300 mV.

An altogether different interpretation of our data is that the L events correspond to actual translocations, whereas the H events correspond to events in which the DNA partially blocks the nanopore but does not translocate. For example, the H events could correspond to instances in which the DNA skims the nanopore, presumably leading to a much smaller conductance blockade than in the case of a translocating molecule. This interpretation would perhaps make it easier to explain the magnitude of the I_B levels of both the H and L events for small nanopores of ∼2–4 nm diameter. Yet it would be very difficult to explain why the fraction of L events decreases so dramatically with increased pore size; in nanopores with diameters exceeding 5 nm, L events are hardly detected at all (Fig. 4 a). The observed increase in the fraction of L events for longer DNA in Fig. 4 b would be similarly difficult to explain. In both cases, one would rather expect the opposite dependence: translocations should be more likely when the nanopore size is increased and less likely when the DNA length is increased, which is precisely the behavior we observed for our H events.

In summary, our results therefore imply that H events correspond to regular translocations, whereas L events correspond instead to a different event type in which the DNA partially obstructs the entrance of the nanopore with one or more (duplex) DNA strands. In the latter case, the DNA most probably approaches the nanopore in a transverse orientation, since this would be increasingly likely for smaller pores or longer DNA. Presumably, given the hourglass shape of our nanopores, the high electrical field in our small nanopores can easily trap transversely oriented molecules at the nanopore entrance without necessarily blocking the central constriction of the nanopore. Once the molecule is trapped in this fashion, several scenarios are possible. For instance, the molecule might move away from the pore through thermal motion, and thus not translocate at all. Alternatively, it might be forced through the pore by buckling or local denaturation (at 300 mV the force on the DNA can be higher than the overstretching limit of 60 pN (27)), or it might ultimately translocate in the regular head-to-tail fashion by slithering one of its ends into the pore through thermal motion. Lastly, the molecule could remain stuck to the pore, clogging it until manual reversal of the bias voltage pushed it back out. Future experiments are expected to shed light on the likelihood of these different scenarios.

Conclusions

We have presented results of DNA molecules translocating through small solid-state nanopores with diameters ranging from 1.8 nm to 7 nm. In contrast to previous results involving small solid-state nanopores (21), we can clearly distinguish different levels of conductance blockade for a single species of DNA molecules. We attribute this separation capability to differences in the nanopore shape caused by small differences in the nanopore fabrication, and demonstrate that we can tune the separation capability by varying the TEM beam size employed during nanopore drilling.

By varying the DNA length and nanopore size, we can assign different interaction mechanisms between the DNA and the nanopore to the different conductance blockade levels. We propose that the largest conductance blockades are caused by obstruction of the nanopore entrance with one or multiple duplex DNA strands, and do not necessarily correspond to translocations. Actual head-to-tail translocations, on the other hand, appear to cause a smaller absolute blockade, even in small nanopores approaching the diameter of the DNA helix. Such an ability to distinguish different modes of translocation by the magnitude of their conductance blockade could potentially be further exploited to detect local structure along DNA molecules. Finally, by demonstrating that small differences in the way nanopores are fabricated may lead to significantly different conductance blockades, our results contribute to the understanding of conductance blockades in nanopores, which will be required for further development of nanopores as single-molecule detectors.