Support for a synaptic chain model of neuronal sequence generation

Summary

In songbirds, the remarkable temporal precision of song is generated by a sparse sequence of bursts in the premotor nucleus HVC (proper name). To distinguish between two possible classes of models of neural sequence generation, we carried out intracellular recordings of HVC neurons in singing birds. We found that the subthreshold membrane potential is characterized by a large rapid depolarization 5–10 ms prior to burst onset, consistent with a synaptically-connected chain of neurons in HVC. We found no evidence for the slow membrane potential modulation predicted by models in which burst timing is controlled by subthreshold dynamics. Furthermore, bursts ride on an underlying depolarization of ~10ms duration, likely the result of a regenerative calcium spike within HVC neurons that could facilitate the propagation of activity through a chain network with high temporal precision. Our results shed light on the fundamental mechanisms by which neural circuits can generate complex sequential behaviours.

Complex behaviours are made possible by the ability of the brain to step through well defined sequences of neural states ¹. Brain processes capable of generating intrinsic sequential activity are thought to underlie motor sequencing ², navigation ^3–4, movement planning ⁵, sensitivity to the timing of sensory stimuli ⁶, and cognitive tasks ⁷. With few exceptions ⁸, however, the biophysical mechanisms by which neural circuits produce sequences are poorly understood.

Songbirds have emerged as an excellent model system for investigating the neural mechanisms of sequence generation. The adult zebra finch song motif consists of a stereotyped pattern of song syllables ⁹. One premotor forebrain area in particular, HVC, is known to play a central role in controlling the temporal structure of birdsong ^10–12. During singing, neurons in HVC projecting to downstream premotor nucleus RA (robust nucleus of the arcopallium) produce only a single highly-stereotyped burst of spikes during each repetition of the song motif ¹³. Different RA-projecting HVC neurons burst at different time points in the song, suggesting that HVC neurons may burst sequentially through the song motif, in turn activating a complex and highly stereotyped pattern of bursts in the downstream nucleus RA ^14–15.

Here we set out to experimentally distinguish among several distinct classes of possible sequence-generating circuits within HVC. First, it has been proposed that sequential states of neural activity may be generated by synaptically connected chains of neurons ^6,16–17. In this view, activity could propagate through the HVC network – like a chain of falling dominoes – forming the basic clock that underlies song timing (Fig. 1a) ^10,18–20. A second, fundamentally different, class of models can allow for sequence generation in the absence of overt feed-forward connections between HVC_(RA) neurons. In these models, oscillatory or other subthreshold dynamics can modulate the excitability of neurons and thus control the timing of their activity ^21–22, like those proposed to control the sequential activation of spikes during hippocampal theta sequences ²³ and within replay events ^3,24. Subthreshold dynamics and rhythmicity on the timescale of song syllables (~100ms) exist within HVC in vitro ²⁵ and could thus play a central role in controlling the timing of HVC bursts on that timescale in the singing bird.

Figure 1.

Two broad classes of models for a sequence generating circuit. a, Neurons could form a feed-forward synaptically-connected chain within HVC such that activity propagates from one group of neurons to the next. b, Alternatively, sequential activity could occur in the absence of directed connections between neurons, from temporal and spatial gradients of excitability. For example, the network could receive a global and gradual ramping-down of an inhibitory input over time (red synapses), producing a sequential activation. The order of activation would be determined by neuronal excitability. In the example model shown here, neurons receive different levels of constant excitatory input (green synapses). The neuron with the largest excitatory input (neuron 1) would be most depolarized and would be the first to reach spiking threshold. The neuron with the smallest constant excitatory input (neuron 8) would be the last to reach threshold. In the model depicted here, the timescale of the sequence produced corresponds to one song syllable (shown above).

Intracellular recording during singing

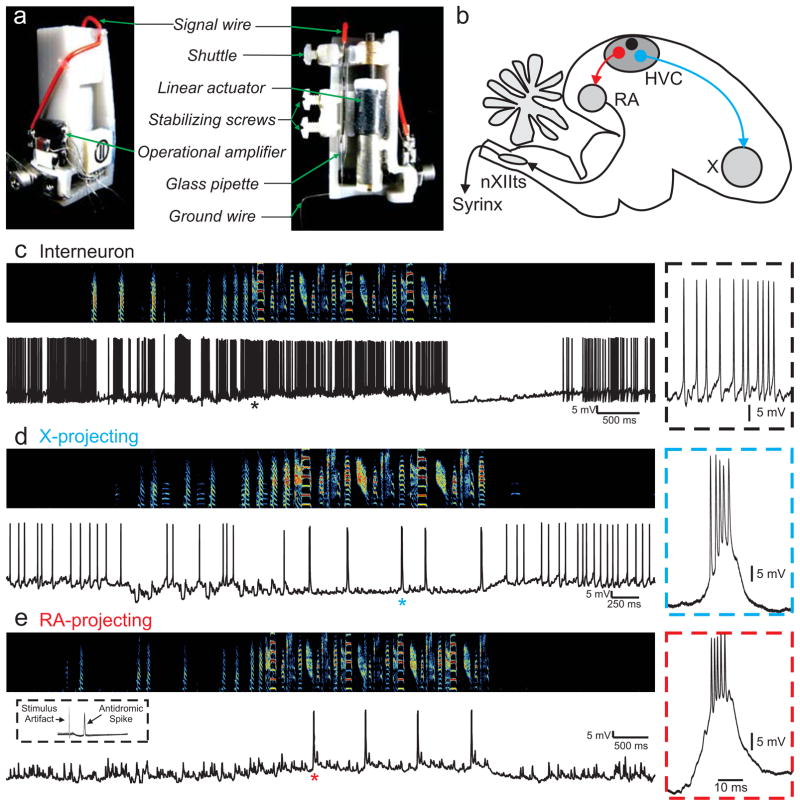
To examine the role of subthreshold dynamics in the control of timing of HVC bursts during singing, we adopted an approach recently introduced for intracellular recordings in the freely moving rat ²⁶. We developed a miniature (1.6 gram) microdrive that allows sharp microelectrode recordings to be performed in singing male zebra finches (Fig. 2a). Birds could move freely in a recording chamber, unrestrained except for a thin, flexible tether. In total, 28 neurons in 12 birds were recorded during singing of all three HVC neuron types, defined broadly by their axonal projections ^27–28 (Fig. 2b).

Figure 2.

A microdrive for sharp intracellular recording in the singing bird. a, The intracellular microdrive incorporates a motor that rotates a threaded rod and advances a shuttle that holds the electrode. b, A schematic of the zebra finch brain, highlighting three cell types in HVC defined by their projections: local circuit interneurons (in black), neurons that project to RA (in red), and neurons that project to basal ganglia-homologue area X (in blue). c, Examples of intracellular records from a putative local circuit interneuron, d, a putative X-projecting neuron, and e, an antidromically-identified RA-projecting neuron. Asterisk indicates the region magnified in the panels at right.

The singing-related spiking patterns of intracellularly recorded neurons closely resembled the previously described patterns in extracellular recordings ^13,29. Putative interneurons (n=3) were identified by a high spontaneous firing rate, and a continuous high firing rate throughout song (Fig. 2c, 117±24.6 Hz singing, 66.3±21.6 Hz baseline). Putative HVC neurons projecting to the basal ganglia homologue area X (n=12) exhibited a low spontaneous spiking rate (<10 Hz) when the bird was not singing, and one or more high-frequency bursts during singing (Fig. 2d). These neurons showed a gradual hyperpolarization during the introductory notes (prior to the first motif in a bout of singing), and were hyperpolarized during song motifs (Fig. 2d, n=12/12, singing: −70.8±3.4 mV, baseline: −67.7±3.1 mV), similar to what has been observed during auditory song playback ^30–31. We did not consider these neurons further in the context of sequence generation because it has been shown that selective ablation of X-projecting HVC neurons in adult zebra finches does not impair song production ³².

HVC neurons that project to RA were identified by antidromic stimulation from RA (Fig. 2e, inset; Supplementary Fig. 1)¹³. HVC_(RA) neurons showed a gradual depolarization prior to the onset of singing (Fig. 2e) and were persistently depolarized during singing (n=13/13, singing: −67.3±3.5 mV , baseline: −75.7±3.5 mV). About half of HVC_(RA) neurons (n=7/13) generated a single burst during each song motif (3.8±0.6 spikes per burst). The remaining HVC_(RA) neurons (n = 6/13 cells) did not spike during song motifs (e.g. Fig. 3d) ¹³.

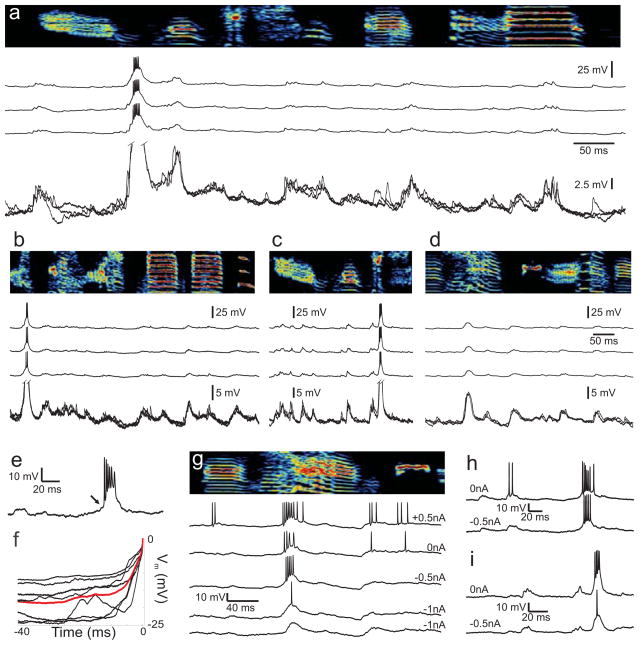
Figure 3.

Intracellular membrane potential of identified HVC_(RA) neurons during singing. a–d, Examples of the membrane potential of four HVC_(RA) neurons recorded during singing. For each cell, activity from three motif renditions is shown aligned to the song (top). Also shown is an overlay of the membrane potential traces (expanded vertical scale, bottom of each panel) e, Expanded view of a burst from another neuron during singing showing the flat membrane potential prior to burst onset (arrow). f, Average membrane potential of seven HVC_(RA) neurons prior to the first spike in the burst (time zero). The population average is shown in red. g–i, The membrane potential of three HVC_(RA) neurons during singing with different holding currents. g, One neuron was held long enough to record with injected currents of +0.5 nA, 0 nA, −0.5 nA and −1.0 nA. h,i, Two other neurons recorded with 0 nA and −0.5 nA hyperpolarizing current. Note that injected current had little effect on burst timing, inconsistent with the predictions of the ramp-to-threshold model.

Chain model vs. ramp-to-threshold model

Recurrent synaptic connections within a network of sequentially active neurons would be expected to produce patterned synaptic inputs; thus previous reports of patterned synaptic inputs have been used as evidence of synaptically-connected chains both in vitro and in vivo ³³. Consistent with this view, we observed a highly stereotyped pattern of fast subthreshold fluctuations widely distributed throughout the song (Figs 2e and 3a–d, Supplementary Fig. 2). For individual neurons, the song-aligned subthreshold fluctuations were highly correlated across song motifs (cross correlation 0.80±0.04, p<10⁻⁹, n=13 neurons).

We now ask whether, as predicted by the ramp-to-threshold model, there was any slow ramping of membrane potential prior to the onset of bursts (Fig. 1b). We first consider the time window from the beginning of the song motif to the burst onset for each neuron. Across all 7 HVC_(RA) neurons that burst during singing, the membrane potential did not change significantly in the period from the beginning of the song motif to the moment 10 ms before the first spike in the burst (−0.47±0.69 mV, p=0.53, t-test, average window duration: 387±92 ms). We next considered a ramp of excitation on the shorter timescale of a song syllable (~100ms). Across all bursting neurons (n=7), the membrane potential did not change during a window from 100ms to 10ms prior to the first spike in the burst (0.31±1.04 mV, p=0.77, t-test). Both of these results are inconsistent with a slow ramp of excitation prior to burst onset, on the timescale of either a song motif or a song syllable. In contrast, bursts of HVC_(RA) neurons were preceded, within the 5ms before the first spike in the burst, by a large depolarization of 10.5±1.9 mV from baseline (Fig. 3e,f, the first spike of the burst initiated at a membrane potential of −52.6±1.7 mV). This result is consistent with a model in which HVC_(RA) neurons are activated by a large synchronous synaptic input from a group of previously active neurons.

The two models described in Fig. 1 give very different predictions for the effect of intracellular current injection on the timing of neural activity. In a model in which the timing of HVC_(RA) bursts is controlled by slow membrane potential dynamics (Fig. 1b), an injected depolarizing current would cause the neuron to burst earlier during the slow depolarizing ramp, assuming that the burst generating mechanism is sufficiently well coupled to the site of current injection (see Supplementary Discussion). In contrast, in the chain model, burst timing is controlled by a synaptic input from a preceding group of neurons (Fig. 1a). Thus, current injection would have a minimal effect on burst timing, perhaps causing the first spike in the burst to appear a few milliseconds earlier during the onset of the synaptic depolarization.

We assessed the effect of intracellular current injection on the timing of bursts in HVC_(RA) neurons during singing in three neurons. Two neurons were recorded with zero holding current and with 0.5nA of hyperpolarizing current. One additional neuron was held long enough to record at four levels of holding current (0.5nA, 0nA, −0.5nA, and -1nA). On average, the resulting membrane potential change was 20.3 mV/nA of injected current. In all cases, hyperpolarizing current was seen to reduce the number of spikes in the burst (Figs 3g–i, average 5 spikes per burst at 0nA compared to 3.3 spikes per burst at −0.5nA), and could suppress spiking completely at the most hyperpolarizing currents (−1.0 nA). Depolarizing current injection increased the number of spikes per burst (Fig. 3g).

Remarkably, the timing of the burst was only weakly affected by injected currents. At a hyperpolarizing holding current of 0.5nA, the burst onset was delayed by an average of only 2.6 ms (n=3). However, the last spike of the burst was advanced by a similar amount such that the center of the burst (midpoint between first and last spikes) was very weakly affected by injected current (1.2ms/nA, Fig. 3g–i). In addition, under conditions at which the spiking was suppressed or nearly suppressed by hyperpolarizing current, a large underlying depolarization at the temporal position of the burst was clearly visible (Fig. 3g,i). These results are consistent with a mechanism in which a given HVC_(RA) neuron is driven by fast synaptic input from a preceding group of neurons.

Cellular mechanisms of burst generation

The broad powerful depolarizations that underlie the bursts of spikes in the HVC_(RA) neurons during singing (Fig. 3) are reminiscent of dendritic calcium spikes observed in many neurons ^34–35. While it is difficult to definitively establish that the singing-related bursts of HVC_(RA) neurons are mediated by calcium spikes, we have carried out in vitro and in vivo whole-cell recordings and pharmacological manipulations that support this view.

While HVC_(RA) neurons have not been observed to generate a burst response to somatic intracellular current injection (Fig. 4a,b) ^27–28,36, dendritic calcium spikes in some neurons may not be observed during somatic current injection ³⁷, but can be unmasked by the intracellular blockade of sodium and potassium channels ³⁸. We carried out whole-cell recordings in brain slices of antidromically-identified HVC_(RA) neurons with QX-314 in the recording pipette. Indeed, current injection resulted in a large depolarizing event in all neurons tested (n=23 cells, Fig. 4c, average amplitude 26.4 ± 5.6 mV, width at half height 4.5 ± 1.0 ms). The depolarizing events had a clear all-or-none response with an initiation threshold at the soma of −36.2 ± 4.4 mV (Fig. 4d, n = 14 cells, compared to a threshold of −40.3 ± 4.3 mV for sodium spikes). In contrast, neurons in nucleus RA did not exhibit all-or-none spikes in the presence of QX-314 ³⁹ (Supplementary Fig. 3). The depolarizing events in HVC_(RA) neurons were completely blocked by the broad spectrum calcium channel antagonist cadmium (100 μM, n = 4 cells), but were unaffected by nickel (100 μM, n = 5 cells), an antagonist of low-threshold voltage-gated calcium channels, suggesting that the depolarizing events might be mediated by a high-threshold calcium channel.

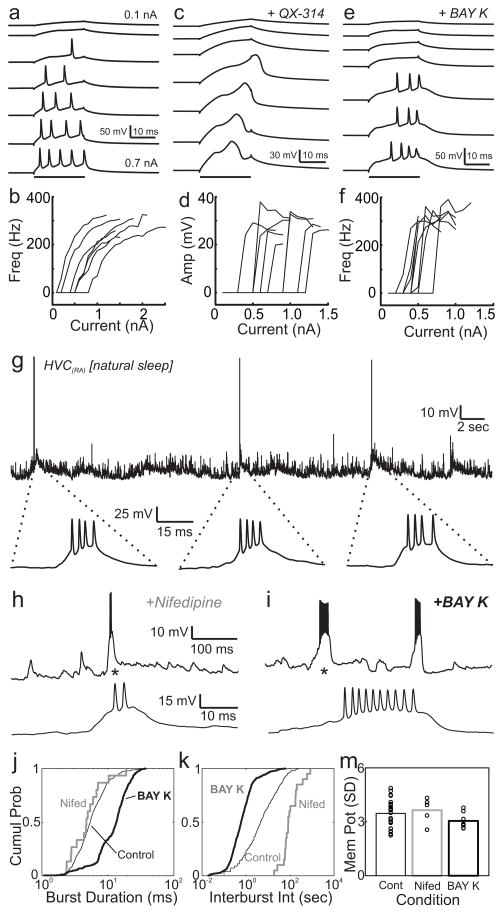
Figure 4.

Evidence that calcium channels contribute to burst events in HVC_(RA) neurons. a, Response of an HVC_(RA) neuron in brain slice to somatically injected current steps (black bar) of different size. b, relationship between injected current and evoked firing rate in a population of 7 HVC_(RA) neurons. Note that somatic current injection does not elicit an all-or-none burst. c, In the presence of intracellular sodium and potassium channel blocker QX-314 (5mM), calcium spikes appear as an all-or-none depolarizing event. d, The amplitude of the depolarizing event (threshold to maximum point) as a function of injected current reveals an all-or-none response (n=8/8 neurons). e,f, HVC_(RA) neurons treated with the L-type calcium channel agonist BAY K 8644 (5–10μM) generate all-or-none spike bursts in response to somatic current injection. g, Segment of a whole-cell recording in a head-fixed bird during natural sleep showing three spontaneous bursts. h,i, Spontaneous bursting activity recorded during sleep following localized injection of L-type calcium channel antagonist Nifedipine (h) or agonist BAY K 8644 (i). Asterisk indicates expanded view below. j, k, Cumulative distribution of burst durations and inter-burst intervals for control, Nifedipine and BAY K 8644 conditions, m, Standard deviation of membrane potential fluctuations is not affected by Nifedipine or Bay K 8644, suggesting that synaptic transmission is not affected by these drugs .

We found that the L-type calcium channel agonist BAY K 8644 could enhance the calcium current sufficiently to evoke a burst response in HVC_(RA) neurons even in the absence of QX-314 (n = 8 cells, Fig. 4e,f, average of 3.4±0.2 spikes, within-burst spike rate 302±14 Hz). These burst responses appeared to have an all-or-none characteristic with a well-defined threshold for injected current (0.50±0.05 nA), and a spike rate within bursts that did not increase at higher currents, (p = 0.60). These in vitro experiments suggest that HVC_(RA) neurons are capable, under some conditions, of generating calcium-based regenerative spikes, possibly mediated by an L-type Ca conductance.

We wanted to more directly examine the role of these calcium conductances under conditions in which HVC_(RA) neurons naturally generate burst sequences, rather than in brain slice. In a form of ‘replay’ of song-like patterns ⁴⁰, HVC_(RA) and RA neurons generate sparse sequential bursts during sleep similar to those produced during singing ^13,41. We have adapted a head-fixed sleeping bird preparation ¹³ and used whole-cell recordings and pharmacological manipulation of HVC_(RA) neurons to study the mechanisms underlying these bursts in naturally sleeping zebra finches (Fig. 4g). Across the population of HVC_(RA) neurons in our dataset (n = 36 cells), nearly half the spikes recorded (49.3±3.5%) formed high-frequency bursts (>100Hz) bursts during sleep (2.74±0.11 sodium spikes, average within-burst rate of 265±13 Hz). Just as during singing, sleep bursts were seen to ride on a prominent underlying depolarizing event (Fig. 4g, 25.2±0.9 mV amplitude, 18.4±1.5 ms width at 2/3 height).

Injections of the L-type calcium channel agonist BAY K 8644 (100 μM, 5–20nL bolus) in the vicinity (<100um) of the whole-cell recording pipette increased the burst size (Fig. 4i, increased number of spikes and total burst duration, p < 10⁻⁵ for both measures, KS-test). In addition, these injections significantly increased the incidence of bursting (Fig. 4k, mean interburst interval 2.0±5.7s with BAY K, compared to 18.4±34.5s control, p < 10⁻⁴, K-S test, n = 6 cells from 5 birds, mean±S.D.). In contrast, injections of the L-type calcium channel antagonist Nifedipine (100 μM) significantly decreased burst incidence (Fig. 4k, mean interburst interval, 171.7±209.6s, greater than control, p<0.0001, K-S test, n = 6 cells from 4 birds, mean±S.D.). The effect of L-type calcium channel modulators could not be explained by changes in the size of synaptic inputs: The magnitude of fluctuations in membrane potential was not altered by BAY K or nifedipine (p>0.05, t-test, Fig. 4m). Taken together, these experiments demonstrate that L-type calcium channels play a role in generating or initiating bursting activity in HVC_(RA) neurons. Such highly nonlinear all-or-none calcium spikes produce a highly stereotyped response to a wide range of synaptic inputs ⁴², and could have implications for the propagation of activity in a synaptically connected chain of neurons.

Burst propagation in a chain network

The stable propagation of bursts in an excitatory chain network is non-trivial; it requires precisely tuned synaptic strengths to avoid runaway excitation or decay ¹⁹. It has previously been shown that an intrinsic neuronal burst mechanism can allow the stable propagation of activity in a chain network ¹⁹, but what about temporal precision and stereotypy? Here we use a simple biophysical model to examine the role that intrinsic bursting might play in achieving precise stereotyped temporal structure in the presence of noise. We also examine how such a mechanism might make the functioning of these networks robust over a wide range of network and synaptic properties.

We studied a network of 70 groups of 30 excitatory HVC_(RA) neurons each, organized in a sequentially connected chain. Recurrent inhibition in HVC ^25,43 was implemented by a population of 300 interneurons with sparse random connections to the excitatory chain (Supplementary Fig. 4a). We began with a non-bursting model of HVC_(RA) neurons, described by a single spiking somatic compartment. (Fig. 5, Supplementary Fig. 4b, see Supplementary Methods). We found that this network did not exhibit the unstable (explosive or decaying) behaviour characteristic of purely excitatory networks ¹⁹, but exhibited stable propagation of burst activity over a wide range of connection probabilities (P = 0.1–1.0) and synaptic strengths between HVC_(RA) neuron groups (G_EE,max from 0.2 to 4.0 mS/cm²). Nevertheless, the activity tended to be non-stationary, particularly at lower connection probabilities (p=0.1, Fig. 5a), exhibiting both dispersion (broadening) and variations in propagation velocity at different points in the network (Supplementary Figs 5 and 6a,b). Furthermore, the network was sensitive to the presence of noise, producing activity that was not stereotyped across multiple trials of the simulation, including large jitter in the speed of propagation through the network (Fig. 5b,e; 1.95±1.38% mean run-time jitter ±S.D.) and large variations in the burst response on different trials (quantified as spikes per burst and burst unreliability, Supplementary Fig. 6c–e). Finally, many characteristics of the propagation (number of spikes per burst, burst duration, and burst jitter) were strongly dependent on the network connection probabilities and connection strengths (Fig. 5, Supplementary Fig. 6). Thus, while the stable propagation of bursts is possible in a chain network of non-bursting neurons, the network does not produce the stereotyped sequences characteristic of real HVC_(RA) neurons.

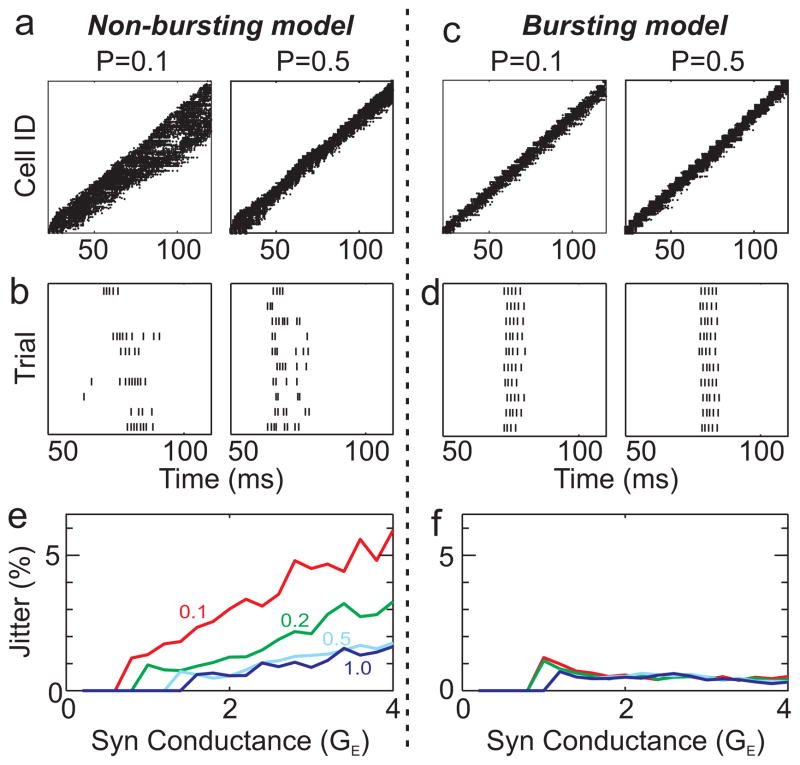
Figure 5.

A simple biophysical model to examine the implications of neuronal bursting on the robustness of HVC network propagation. Two models of a synaptically-connected chain network were compared: one with non-bursting neurons (a,b), the other with bursting neurons (c,d). a, non-bursting model: Spike raster plot for all neurons in the network showing activity as a function of time for two different levels of network connection probability (P=0.1 and 0.5). b, Spike raster of a single neuron during different runs of the network. Note the non-stationarity of propagation and large variability across runs. c, Bursting model: Spike raster plot for all neurons in the network. d, Spike raster of a single neuron during different runs of the network. Note the highly uniform propagation and stereotyped response across runs. e,f, Runtime jitter, plotted as a function of network connectivity and synaptic conductance, is consistently lower in the bursting model than in the non-bursting model. (See Supplementary Figures and Table for further quantification, and Supplementary Methods for model details.)

The situation was markedly different in a model with neurons that have an intrinsic burst mechanism. Bursting HVC_(RA) neurons were modelled with a spiking somatic compartment plus a dendritic compartment containing conductances for generating calcium spikes (see Supplementary Figs 4c,d, 7, 8, 9). Propagation down the chain was stationary, with no broadening or variations in velocity (Fig. 5c, Supplementary Fig. 5). The propagation was also extremely stereotyped, exhibiting small trial-to-trial variations in propagation speed (Fig. 5d, 0.52±0.17% mean run-time jitter ±S.D.). Burst response was much more reliable in the bursting model (see spikes per burst and burst unreliability, Supplementary Fig. 6), similar to what has been observed in singing-related firing patterns of HVC_(RA) neurons ^13,29. Finally, in the bursting model, every characteristic of burst propagation we examined was much more robust to variations is network connection probability and synaptic strength than was the single compartment model (Fig. 5e,f, Supplementary Fig. 6). Similar results were obtained with a simple integrate-and-burst model (Supplementary Fig. 10), Taken together, these results suggest that an intrinsic neuronal burst mechanism, regardless of its biophysical implementation, could serve a fundamental role in allowing synaptically-connected chain networks to propagate in a highly stereotyped manner with low temporal jitter, even in the presence of noise, and over a wide range of network connectivities. Such robustness could also make sequence-generating networks easier to assemble during development ^44–45.

In summary, we have carried out intracellular recording and manipulation of activity in the freely behaving animal in a neural circuit important for the temporal control of behaviour. We observed no ramping or rhythmicity that could contribute to the temporal patterning of HVC_(RA) bursts. In contrast, our recordings reveal a single large postsynaptic potential that immediately precedes the onset of a song-locked burst of spikes. Together our findings are consistent with the idea that the control of song temporal structure is produced by the propagation of calcium-mediated bursts through a synaptically-connected chain of neurons. Temporally precise learned behaviours in other vertebrates could employ similar mechanisms to organize neuronal activity into sequentially active states.

METHODS SUMMARY

Subjects

We used adult (> 120 post hatch days) male zebra finches (Taeniopygia guttata). All animal procedures were reviewed and approved by the MIT committee on animal care.

Intracellular recording during singing

Intracellular recordings were achieved in the zebra finch using a custom microdrive constructed out of 3D printed plastic (AP Proto, Inc) outfitted with a lightweight linear actuator (Smoovy Series 0515, Faulhaber). A preamplifer was mounted at the base of the device which routed signals to a commercially available intracellular amplifier (IR-183, Cygnus Technology, Inc.). Sharp microelectrodes were pulled to a final impedance of 80–110 MΩ and were filled with 3M potassium acetate. Once a stable intracellular recording was obtained, a female bird was presented to elicit directed singing.

Intracellular recording during sleep

During an initial surgical step, a stainless steel headplate was affixed to the skull. A small (~ 200 μm) craniotomy was made over HVC. Whole-cell recordings were made with glass electrodes (5–8 MΩ) using techniques described elsewhere ⁴⁶. Signals were measured using an Axoclamp 2B (Molecular Devices). In some experiments, an injection pipette (20–30 μm opening) was positioned less than 100 μm from the recording site for the injection (Nanoject II, Drummond Scientific) of a small volume (5–20 nL) of 100μM (+/−)BAY K 8644 (A.G. Scientific) or 100μM Nifedipine (Sigma).

Slice preparation

400 μm slices were prepared on a vibrating microtome (Leica VT1000) and placed in ice-cold ACSF (sodium replaced with equimolar sucrose). Slices were then recorded in an interface-style chamber (VB5000, Leica) with standard ACSF (in mM): 126 NaCl, 3 KCl, 1.25 NaH₂PO₄, 2 MgSO₄-7H₂O, 26 NAHCO₃, 10 Dextrose, 2 CaCl₂-2H₂0. QX-314 (5 mM, internal) was used in a subset of these experiments.

All error bars are ±s.e.m. unless otherwise noted. Additional methods details are presented in the Supplementary Methods section.