A Ground Truth Based Comparative Study on Detecting Epistatic SNPs

Abstract

Genome-wide association studies (GWAS) have been widely applied to identify informative SNPs associated with common and complex diseases. Besides single-SNP analysis, the interaction between SNPs is believed to play an important role in disease risk due to the complex networking of genetic regulations. While many approaches have been proposed for detecting SNP interactions, the relative performance and merits of these methods in practice are largely unclear. In this paper, a ground-truth based comparative study is reported involving 9 popular SNP detection methods using realistic simulation datasets. The results provide general characteristics and guidelines on these methods that may be informative to the biological investigators.

1. Introduction

Single-nucleotide polymorphisms (SNPs) are the most common DNA sequence variation, which occurs when a single nucleotide in the genome differs between members of a species (or between paired chromosomes in an individual). The human genome contains millions of SNPs, some of which may either directly cause changes in traits of disease or influence the risk of disease along with other factors [1]. GWAS allows researchers to genotype large number of SNPs from subjects to explore the genetic association between SNP mutations and disease phenotypes [2]. Once new genetic associations are identified, this information can help unveil the disease mechanism and develop better strategies to detect, treat and prevent the disease.

So far, single-SNP analysis is widely performed via the traditional statistical filtering methods (e.g. chi-2 test, Fisher's Exact Test, logistic regression [10]), which perform hypothesis testing on SNPs one by one. Although single-SNP analysis is successful at discovering some novel disease-risk loci with confirmative validation by multiple independent cohorts, the new findings explain only a small fraction (usually less than 20%) of heritability. A frequently cited reason is that most common diseases have complex mechanisms, with the phenotype determined by interactions (also called epistasis effects) between multiple SNPs and other factors [3]. Searching for SNP interactions in high-dimensional SNP data is a daunting computational task, and some unique characteristics of SNP data further prompt challenges for effective detection of informative SNPs.

Driven by goals of efficiency and effectiveness, many methods [4-9] originating from various underlying techniques and assumptions have been developed to detect SNP interactions, while so far, the relative performance and advantages of these methods are largely unknown.

The purpose of this paper is to provide a thorough and objective comparison on the performance of several benchmark SNP epistasis detection methods. As the results, this comparison study reveals the difficulties and existing problems in SNP epistasis detection, and provides guidelines on applying these methods in GWAS. In addition, by analyzing the merits and principles of these methods, we would gain novel insights into the key problems associated with the existing methods and potentially develop more effective methods. In section 2, we first discuss the data characteristics and challenges in GWAS, and then briefly introduce the basic principles of 9 representative SNP detection methods. In section 3, we give experimental comparisons on the performance of these methods using simulation datasets derived from real genotyped data, with synthetically generated (and hence known) ground-truth SNP interactions. Finally, the general characteristics and guidelines in applying these methods are presented.

2. Methods

2.1. Background

We shall first simply discuss the characteristics and unique challenges in detecting interacting SNPs.

1. Huge number of SNPs with limited sample size. Current estimates indicate that there are millions of SNPs in the human genome. To date, more than 900k SNPs have been genotyped by Affymetrix. Numerous SNPs not only increase the demand for computational scalability, but also pose challenges in SNP detection, i.e., problems such as the curse of dimensionality [11] and multiple testing [10] will affect both the accuracy and robustness of SNP detection.

2. Nonlinear and complex SNP interactions. A SNP interaction takes place when multiple SNPs interact with each other to affect the disease risk. In this way, some SNPs with insignificant marginal effects may show relatively strong association to diseases by interacting with other SNPs. However, exhaustive search of SNP interactions presents tremendous computational burden. Additionally, given the fact that the exact forms of SNP interactions are largely unknown, for those nonlinear and complex SNP interactions, traditional linear models or kernel methods [11] are not applicable or effective here.

3. Narrow-ranged and semi-nominal valued data. Practically SNPs are simply referred to as bi-allelic markers [1], i.e., A and B. So SNPs only have 3 statuses: {AA, AB, BB}. The data values are narrowly-ranged and discrete. Moreover, how to encode these 3 statuses depends on the genetic allele model. For example, consider 3 common genetic allele models: dominant model, recessive model and additive model, {AA, AB, BB} mostly resembles nominal values under the dominant and recessive model, while tends to be ordinal under the additive model. The unknown genetic allele model introduces additional uncertainty in identifying the effects of interacting SNPs, adding difficulty in computational algorithms.

4. Confounding Factors & Gene-Environment Interactions. Confounding factors (e.g., gender, age and smoking habit) and environmental factors can also interact with SNPs. The SNP data is discrete, while the confounding and environment measurements are usually continuous. These factors and the hybrid data type pose extra problems in detecting SNP interactions.

5. Linkage Disequilibrium (LD). Linkage disequilibrium is the non-random association of alleles at multiple SNPs. Some statistical models and machine learning methods are based on the assumption of independence among SNPs. These methods will not be effective when applied to the real SNP data. Bonferroni correction which compensates for the multiple testing effects also makes assumption on the independence between SNPs. LD violates this assumption and causes the Bonferroni correction to underestimate statistical significance of SNP interactions.

Facing to the 5 problems mentioned above, two important features in developing methods for detecting epistatic interacting SNPs are:

1. Effective Detection Criterion (How to define a sensitive and specific criterion function which can differentiate the informative SNPs from so many “null” SNPs). The criterion should be comprehensive and can encode SNP interaction effects with complex and unknown mechanism; can deal with narrow-ranged discrete and semi-nominal data values; and is free of the independence assumptions between SNPs.

2. Computational Scalability and Search Strategy. The great amount of SNPs proposes challenges on both time and resource scalability. And the combinatorial search required to find SNP interactions further makes the computational burden formidable. So to define a heuristic search strategy which may retain as many as possible informative SNPs while largely reducing the computational complexity is essential.

2.2. Algorithms being compared

In recent years, many methods have been proposed for detecting informative SNPs. We have tested 9 representative methods originating from different underlying techniques and assumptions.

1. Pearson's chi-square test (Chi-2) evaluates the null hypothesis that the occurrence frequency of observed events follows a specified frequency distribution. Specifically, a contingency table can be constructed for each SNP. The quantity χ² follows a 2 degree of freedom (df) chi-square distribution under the null hypothesis that a SNP and disease status are independent [10].

2. Fisher's exact test (FET) is a statistical test used to determine if there are nonrandom associations between two categorical variables. [10]. The probability of obtaining any such set of values is given by the hypergeometric distribution. Assuming that the alleles of SNPs are coded either by the dominant or recessive model, FET can address the statistical significance for each SNP. The final P value is chosen from the more significant P value obtained from the dominant and recessive model.

3. Logistic Regression. Logistic regression (LR) is a generalized linear model used for binomial regression. Let π(X) denote the probability of getting disease for a subject carrying the genotype X ∈ {0,1,2}. The logit function of π is considered as a linear function of genotypes

   $$\text{log}(\pi (X)/(1-\pi (X)))={\beta }_0+{\beta }_{1}X$$ (1)

   , where β₀ and β₁ are the regression coefficients and can be learned through the maximum likelihood method. By a likelihood ratio test, logistic regression gives statistical significance for each SNP.

4. Full Interaction Model (FIM). In FIM, 3^d dummy variables are constructed for a subset of d SNPs and a logistic regression with 3^d parameters is estimated from the data. Correspondingly, we have a chi-square distribution with 3^d −1 df [4].

5. Information Gain (IG). Consider two SNPs A and B. Let C denote the class label. The information gain (IG) of A, B and C is defined as follows

   $$IG(A,B,C)=I(A;B\mid C)-I(A;B)$$ (2)

   , where I(A;B) is the mutual information between A and B and I(A;B ∣ C) is the conditional mutual information. A large IG is the indication of interaction of A and B [5].

6. Bayesian Epistasis Association Mapping (BEAM) treats the disease-associated markers and their interactions via a Bayesian partitioning model and computes, via Markov chain Monte Carlo (MCMC), the posterior probability that each marker set is associated with the disease [6].

7. Multifactor dimensionality reduction (MDR) is a nonparametric data mining approach designed to identify interactions among discrete variables that influence a binary outcome. MDR uses the prediction accuracy of the multifactor model as the measure of the association between SNPs and the disease risk [7].

8. SNP Harvester (SH) proposes a heuristic search strategy named “PathSeeker” to reduce the computational complexity and detect SNP interactions with weak marginal effects [8]. SH defines multiple paths to detect SNP interactions, based on the χ² values and the heuristic search algorithm.

9. Penalized logistic regression (PLR). Logistic regression typically estimates coefficients by maximum likelihood, while PLR [9] maximizes the log-likelihood subject to an L2-norm constraint on the coefficients. The authors also extend the method to detect high-order SNP interactions via heuristic search.

These 9 methods can be classified into several categories according to different principles.

1. Marginal Effect vs. interaction effect. Statistical filtering methods (chi-2 test, FET, LR) are traditional methods which have been widely applied in GWAS. They focus on the marginal effect of the single SNP. FIM, IG, BEAM, MDR, SH, PLR are newly proposed GWAS methods, and they aim to detect SNP interaction effects.

2. Statistical Significance. Many of the methods proposed hypothesis testing approach to test the statistical significance of SNPs. Among the 9 methods, chi-2 test, FET, LR, FIM, BEAM and SH have well-defined distributions directly linked to the underlying null hypothesis. MDR uses random permutation test to obtain the statistical significance based on prediction accuracy, while IG and PLR does not provide a statistical significance evaluation.

3. Search Strategies. As stated in section 2.1, the efficiency of a GWAS method largely decides its applicability, so the search strategy is an important issue in GWAS. There are 3 main types of search strategies in the 9 methods: the first one is exhaustive search (applied by chi-2 test, FET, LR, FIM, IG, MDR); the second one is stochastic search (applied by BEAM); and the third one is the deterministic heuristic search (applied by SH, PLR).

4. Detection principle. Chi-2 test, FET and SH apply statistical testing based on contingency table; BEAM uses Bayesian inference and MCMC; LR, FIM, PLR are all based on the logistic regression model; IG ranks SNPs according to the quantitative measures from information theory; MDR selects SNPs via testing error by cross validation.

2.3. Evaluation criteria

There are 2 main factors deciding the applicability of these methods: firstly, the sensitivity and the specificity of the criteria function (whether the method makes good use of the data characteristics to provide a sensitive criteria which selects the informative SNPs along with few false positives); secondly, the computation complexity (to detect SNP interactions in large-scale SNP set is even more challenging than other difficulties discussed previously, so only those methods with high computational efficiency have realistic applicability).

In our study, we used the run time of the methods in the same computational environment to evaluate the computational complexity, and used the following two measures to assess the sensitivity and specificity of the detection principles:

1. Sensitivity (the proportion of ground truth SNPs is detected) at 0.5% false positive rate (FPR). Since the number of SNPs is huge, only a small portion of the top-ranked SNPs are meaningful to GWAS. Therefore, we are most interested in the sensitivity at low FPR.

2. The receiver operating characteristic (ROC) curve. ROC shows the sensitivity with different FPR level. Since performance at low FPR is of more interest, we can observe the left-side performance of ROC curve as an intuitive evaluation of the methods.

3. Experiment and Results

3.1. Realistic simulation data

We have constructed 11 simulation datasets for a ground-truth based comparative study. Within each dataset, there are two data which include 100 and 1000 SNPs, respectively. Each data file contains 2000 simulated individuals (about 1000 cases and 1000 controls) which are randomly drawn (with replacement) from the pre-existing human subjects genotyped by the 317K-SNP Illumina HumanHap300 BeadChip from the New York City Cancer Control Project and lupus study. The data retain the basic patterns of linkage disequilibrium and allele frequencies as those observed in the original genome scan data.

Assuming that the disease risk is 100% explained by genetic factors, ground truth SNPs are sampled according to the requirements of the penetrance function in which they participate (randomly within a narrow window of minor allele frequency tolerance) and the remaining SNPs are chosen at random. The disease labels are affected jointly by several penetrance functions of ground truth SNPs. Several 1-way, 2-way, 3-way and 5-way interaction models are defined. Their penetrance functions are built under various models, and those models are set as fully penetrant or incompletely penetrant in order to give a comprehensive comparison. 11 data sets were replicated using penetrance functions given by the following link: http://www.cbil.ece.vt.edu/software/SNP%20Simulation.pdf

3.2. Results

For the first 8 methods on the 11 datasets, we record their run time, the sensitivity at FPR=0.5%, ROC curves, and AUC (not necessary but just give more details). Because of the large computational complexity of PLR (spent 2 days to select top 30 SNPs in the 100-SNP data), we only record its sensitivity at FPR=0.5% on the 100-SNP data.

The parameters are set as close as possible to the default settings in [4-9] or in the related software whenever possible, and we only modify a few parameters in order to control the computational cost and performance within a reasonable range. When testing MDR on 1000-SNP data, we used the heuristic search (100,000 evaluations) instead of exhaustive search because of limited memory and high computational complexity. When testing BEAM, we enlarged the number of Markov chains from 1 to 10, and increased the number of initial tries from 20 to 40 in order to obtain a more complete result.

For statistical filtering methods (chi-2 test, FET and LR), we only detect the marginal effects of each SNP. For FIM, IG and PLR, we detect up to 2-way SNP interactions with exhaustive search. And for MDR and SH, we detect up to 3-way SNP interactions. The run time (including time for loading data) used by the 9 methods to output the full rank of SNPs is recorded in Table 1. All the experiments are run on a desktop with 3GHz CPU and 2GB RAM, OS: WinXP.

Table 1.

Run time (sec) of 9 methods on 100-SNP data and 1000-SNP data. The time for MDR on 1000-SNP data is estimated for exhaustive search.

	FET	chi-2	LR	IG	FIM	MDR	BEAM	SH	PLR
100-SNP	2	2	2	3	4	1120	12	6	>1.7×105
1000-SNP	5	4	5	114	205	1.4×106	855	21	---

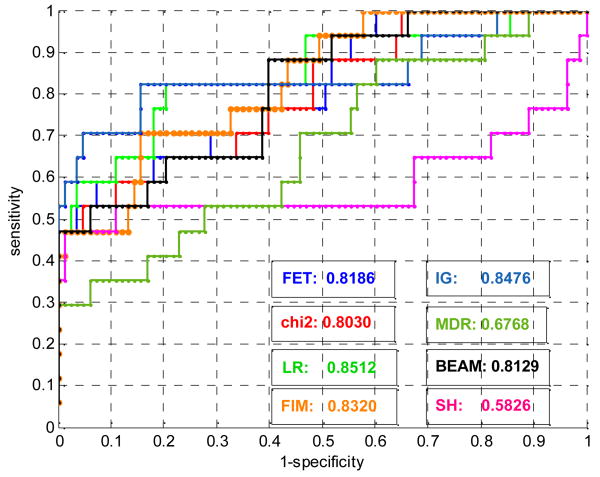
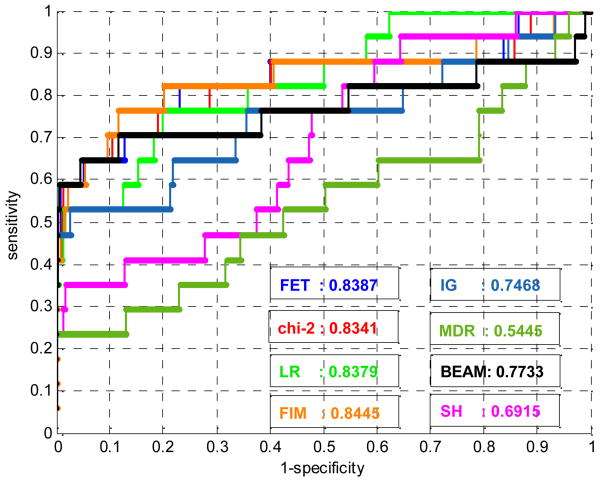
The ROC curves for 100-SNP and 1000-SNP data in the 1st dataset are shown in Fig. 1 and Fig. 2. ROC curves and AUCs are marked by different color shown in the lower right corner of the figures.

Fig. 1. ROCs of 8 methods on 100-SNP data of set 1.

Fig. 2. ROCs of 8 methods on 1000-SNP data of set 1.

For 100-SNP and 1000-SNP data in all of the 11 datasets, AUC and the sensitivity when FPR=0.5% are shown in Table 2∼5. The last row of each table records the mean value of the performance measures across all datasets.

Table 2. Sensitivity when FPR=0.5% of 9 methods on 100-SNP data.

	FET	chi-2	LR	IG	FIM	MDR	BEAM	SH	PLR
Set1	0.47	0.47	0.47	0.53	0.41	0.29	0.47	0.35	0.65
Set2	0.35	0.35	0.4	0.4	0.3	0.25	0.35	0.3	0.4
Set3	0.55	0.4	0.5	0.35	0.4	0.3	0.4	0.1	0.4
Set4	0.25	0.25	0.25	0.35	0.25	0.3	0.25	0.2	0.35
Set5	0.4	0.4	0.35	0.45	0.3	0.25	0.4	0.25	0.5
Set6	0.4	0.4	0.4	0.4	0.4	0.3	0.4	0.2	0.4
Set7	0.35	0.3	0.35	0.35	0.35	0.25	0.3	0.1	0.35
Set8	0.35	0.35	0.35	0.45	0.4	0.25	0.35	0.15	0.45
Set9	0.55	0.45	0.45	0.4	0.35	0.25	0.4	0.25	0.5
Set10	0.5	0.5	0.45	0.35	0.45	0.35	0.5	0.1	0.5
Set11	0.35	0.35	0.4	0.35	0.3	0.3	0.35	0.25	0.4
mean	0.41	0.38	0.40	0.40	0.36	0.28	0.38	0.20	0.45

Table 5. AUC of 8 methods on 1000-SNP data.

	FET	chi-2	LR	IG	FIM	MDR	BEAM	SH
Set1	0.84	0.83	0.84	0.75	0.84	0.54	0.77	0.69
Set2	0.85	0.85	0.81	0.70	0.83	0.63	0.74	0.61
Set3	0.85	0.84	0.80	0.60	0.74	0.53	0.68	0.59
Set4	0.77	0.76	0.79	0.76	0.85	0.76	0.69	0.62
Set5	0.75	0.76	0.73	0.66	0.68	0.54	0.59	0.70
Set6	0.79	0.77	0.80	0.70	0.67	0.62	0.77	0.63
Set7	0.65	0.63	0.68	0.71	0.68	0.61	0.61	0.56
Set8	0.72	0.73	0.71	0.81	0.64	0.71	0.70	0.62
Set9	0.78	0.76	0.84	0.70	0.71	0.61	0.65	0.62
Set10	0.87	0.86	0.86	0.81	0.80	0.69	0.72	0.68
Set11	0.74	0.73	0.72	0.73	0.79	0.63	0.71	0.66
mean	0.78	0.77	0.78	0.72	0.75	0.62	0.69	0.63

From Fig.1∼2, Table 1∼5, we can see that:

Although the global performance (AUCs) of these 9 methods are fairly good, the sensitivities at low FPR are not satisfactory, i.e. only a small part of ground truth SNPs is selected by the 9 methods at FPR=0.5% in most datasets. As stated in section 2.3, the sensitivity with low FPR is more critical than AUCs, the results are actually unsatisfactory. This may be caused by the aforementioned challenges in detecting SNP epistasis effects, or by existing problems or limitations in these methods. For example, statistical filtering methods cannot detect SNP interactions well; chi-2 test and LR are based on asymptotic distributions so that large sample size is required; FET is an exact test but assumes either the dominant or recessive genetic model; FIM has high degrees of freedom, which also requires large sample size and degrades the accuracy of statistical significance; the cross-validation prediction error of multifactor model (MDR) is not sensitive enough to differentiate ground truth SNPs from other SNPs, and etc.

Comparing the relative performance of the 9 methods, we can see that although statistical filtering methods (FET, chi-2, LR) can only detect marginal effects of SNPs, the performance of these methods is relatively good. The methods considering SNP interactions (FIM, IG, MDR, SH, BEAM, PLR) do not gain significantly better sensitivity and ROC compared to statistical filtering methods. From Table 2∼5, we can see that IG, FIM, BEAM have similar but slightly lower mean sensitivity and mean AUC than FET, chi-2 and LR, while MDR and SH have apparently weaker performance. Only PLR has slightly (but not consistently) better sensitivity on 100-SNP data, but its high computational complexity prevents us from further evaluating it on 1000-SNP data.

By looking into the SNP interactions selected by FIM, IG, MDR, SH, BEAM, and PLR, we found that they indeed detect some ground truth SNP interactions which cannot be detected by statistical filtering methods. These methods have their merits by considering the interaction effects, and taking account of nonlinearity and complexity of the SNP interactions. Moreover, some of the methods, such as SH, have explicitly devised principles to detect the SNP interactions with insignificant marginal effects. An interesting observation is: although some of the ground truth SNP interactions are detected, many false positives are also highly ranked by these methods, and the false positive SNPs are usually mistakenly selected as interacting with the ground truth SNPs having strong marginal effects. Therefore, the performance of these methods is heavily weakened by the false positives. The criterion functions of these methods are not sensitive enough to differentiate ground truth SNPs from false positives, due to various reasons, e.g. multiple testing, high degrees of freedom, and the improper underlying model.

As to computational complexity, the run time of statistical filtering methods is quite modest on the 100-SNP data and goes up linearly on the 1000-SNP data. For methods considering interactions, the run time goes up quickly. Among them, SH is the fastest but its efficiency is obtained by paying the price of SNP discovery accuracy. For IG, FIT and BEAM, the computation increases at least quadratically with the number of SNPs. We are questioning their applicability for the real scenario, since with about 500k SNPs, it is estimated to take at least (for IG) 300 days. For MDR and PLR, the computation burden is even heavier, which makes their applicability unrealistic on large datasets. Certainly, the algorithms considering the interactions are still useful and applicable for candidate gene based association studies, alternatively, they can serve as post processing methods after pre-screening the whole SNPs into a manageable size using some other methods such as the statistical filtering methods.

4. Conclusion

Detection of informative SNP markers associated with complex genetic diseases is a challenging task, due to the particular SNP data characteristics and biological facts such as the large number of SNPs and nonlinear and complex SNP interactions of unknown a priori form. Many methods have been proposed in this field trying to enhance both sensitivity and computational efficiency. But so far there have been no studies giving a comprehensive evaluation of methods and guidelines for their applicability. This paper proposed a comparative study on the representative GWAS methods, in which multidimensional performance is measured via run time, ROC, AUC and sensitivity. From the results on simulation data, we see that although the newly proposed methods [4-7] obtain benefits at detecting SNP interactions with weak marginal effects, they do not gain apparently improved performance compared to traditional statistical filtering methods. We realize that the criterion functions need to be sensitive enough to differentiate those true SNP interactions from false positives caused by marginal effects. And the heuristic search strategies needs to be further explored according to data characteristics so that efficiency is achieved without too much sacrifice in performance. The software of MDR, BEAM, SH, and PLR can be found in either the original papers or the authors' websites. For the convenience of peers, we also provide free software on the other 5 methods at: http://www.cbil.ece.vt.edu/ResearchOngoingSNP.htm

Table 3. AUC of 8 methods on 100-SNP data.

	FET	chi-2	LR	IG	FIM	MDR	BEAM	SH
Set1	0.82	0.80	0.85	0.85	0.83	0.68	0.81	0.58
Set2	0.79	0.79	0.81	0.75	0.72	0.72	0.74	0.71
Set3	0.84	0.83	0.83	0.70	0.81	0.58	0.81	0.59
Set4	0.77	0.78	0.73	0.83	0.77	0.59	0.71	0.67
Set5	0.79	0.80	0.76	0.75	0.81	0.70	0.67	0.69
Set6	0.68	0.67	0.67	0.66	0.74	0.68	0.68	0.45
Set7	0.74	0.72	0.72	0.68	0.66	0.58	0.74	0.48
Set8	0.77	0.76	0.72	0.67	0.79	0.70	0.73	0.52
Set9	0.82	0.81	0.82	0.77	0.78	0.65	0.80	0.63
Set10	0.83	0.81	0.80	0.86	0.78	0.73	0.84	0.55
Set11	0.71	0.71	0.72	0.78	0.77	0.70	0.79	0.60
mean	0.78	0.77	0.77	0.75	0.77	0.66	0.76	0.59

Table 4. Sensitivity with FPR=0.5% of 8 methods on 1000-SNP data.

	FET	chi-2	LR	IG	FIM	MDR	BEAM	SH
Set1	0.41	0.41	0.41	0.47	0.41	0.24	0.53	0.24
Set2	0.25	0.3	0.25	0.25	0.3	0.25	0.25	0.2
Set3	0.35	0.3	0.3	0.3	0.3	0.2	0.25	0.05
Set4	0.35	0.3	0.25	0.35	0.35	0.2	0.25	0.15
Set5	0.3	0.3	0.3	0.35	0.3	0.2	0.25	0.25
Set6	0.35	0.4	0.4	0.35	0.35	0.25	0.35	0.15
Set7	0.35	0.35	0.35	0.35	0.35	0.2	0.25	0.2
Set8	0.35	0.35	0.35	0.4	0.35	0.25	0.3	0.15
Set9	0.35	0.35	0.35	0.35	0.35	0.15	0.3	0.3
Set10	0.4	0.4	0.35	0.35	0.4	0.2	0.35	0.3
Set11	0.35	0.35	0.3	0.3	0.35	0.2	0.35	0.25
mean	0.35	0.35	0.33	0.35	0.35	0.21	0.31	0.20