Abstract
This article considers the utility of the bounded cumulative hazard model in cure rate estimation, which is an appealing alternative to the widely used two-component mixture model. This approach has the following distinct advantages: (1) It allows for a natural way to extend the proportional hazards regression model, leading to a wide class of extended hazard regression models. (2) In some settings the model can be interpreted in terms of biologically meaningful parameters. (3) The model structure is particularly suitable for semiparametric and Bayesian methods of statistical inference. Notwithstanding the fact that the model has been around for less than a decade, a large body of theoretical results and applications has been reported to date. This review article is intended to give a big picture of these modeling techniques and associated statistical problems. These issues are discussed in the context of survival data in cancer.
Keywords: Bayesian methods, Biologically based models, Bounded cumulative hazard, Cure models, Hazard regression, Semiparametric inference, Survival data
1. INTRODUCTION
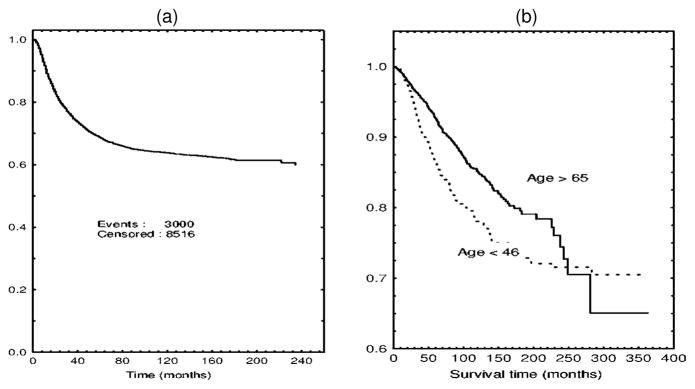
In many clinical and epidemiological settings, investigators observe cause-specific survival curves that tend to level off at a value strictly greater than 0 as time increases. A prominent example of this pattern is shown in Figure 1(a). A well-pronounced plateau in this display of the Kaplan–Meier curve may be thought of as an indication of the presence of a proportion of patients for whom the disease under study will never recur. Alternatively, one can consider such patients to be cured. Clearly, estimating the proportion of cured patients may have important medical implications. In addition, clinical covariates may exert dissimilar effects on the probability of cure and the timing of tumor relapse or other events of interest. This is apparent from Figure 1(b), where two survival curves for patients with localized breast cancer stratified by age are presented. These plots suggest that the two categories of patients are likely to have a similar probability of cure, whereas a short-term effect of age at diagnosis on cancer-specific survival is highly plausible. It is also clear that the commonly used proportional hazards model fails to fit the data shown in Figure 1(b). In Section 3.3 we present a detailed example involving prostate cancer survival that has major biomedical implications. Such an advance would have not been possible to make without invoking the concept of cure. The preceding examples suggest at least two advantages that survival models have for allowing for the presence of cured individuals: (1) They enrich our ability to interpret survival analysis in terms of characteristics that have a clear biomedical meaning; (2) they lead to more general regression models, thereby extending our ability to describe actual data. The latter contention holds whether the probability of cure is significantly separated from 0 (see Sec. 3).
Figure 1.
(a) Relapse-Free Survival for Patients With Hodgkin’s Disease Treated by Radiotherapy. Data from the International Database on Hodgkin’s Disease. (b) Breast cancer specific survival in local stage by age. Data from the Surveillance Epidemiology and End Results Program.
To develop relevant methods of statistical data analysis, one has to provide a rigorous definition of cure rate. In this article, we will proceed from the most widely accepted concept of biological cure. The probability of (biological) cure, variously referred to as the cure rate or the surviving fraction, is defined as an asymptotic value of the survival function Ḡ(t) as t tends to ∞. Let X be the survival time with cumulative distribution function (c.d.f.) G(t) = 1 − Ḡ(t). Under a continuous model the existence of a nonzero surviving fraction, p, is determined by the behavior of the hazard function, λ(t), by virtue of the equality
| (1.1) |
Whenever p > 0 the underlying survival time distribution is said to be improper. Clearly, λ(u) → 0 as u → ∞ if p > 0 and the limit of λ(u) (as u → ∞) exists. Formulated in terms of the marginal failure time distribution, this definition does not imply that the overall survival time may be infinite, because the time to death from other causes (censoring time) is finite with probability 1. Therefore, the distribution of the observed lifetime in the presence of competing risks is always proper, and there is no defiance of common sense.
Boag (1949) and later Berkson and Gage (1952) proposed a two-component (binary) mixture model for the analysis of survival data when a proportion of patients are cured. Since then, the binary mixture-based approach has become the dominant one in the literature on cure models (Miller 1981; Farewell 1982; Goldman 1984; Greenhouse and Wolfe 1984; Gamel, McLean, and Rosenberg 1990; Gordon 1990; Bentzen, Johansen, Overgaard, and Thames 1991; Goldman and Hillman 1992; Kuk and Chen 1992; Laska and Meisner 1992; Maller and Zhou 1992, 1994, 1995, 1996; Sposto, Sather, and Baker 1992; Yamaguchi 1992; Gamel and Vogel 1993; Gamel, Vogel, Valagussa, and Bonadonna 1994; Chappell Nondahl, and Fowler 1995; Taylor 1995; Gamel, Meyer, Feuer, and Miller 1996; Peng and Dear 2000; Sy and Taylor 2000, 2001, to name a few). The main idea behind this approach is that any improper survival function can be represented as
| (1.2) |
where M is a binary random variable taking on the values of 0 and 1 with probability p and 1 − p, respectively, with
and Ḡ0(t) is defined as the survival function for the time to failure conditional upon ultimate failure, that is,
| (1.3) |
When designing regression counterparts of model (1.2), it is common practice to use the logistic regression model for incorporating covariates into the probability p, and proportional hazards regression for modeling the effect of the covariates on the conditional survival function Ḡ0.
An alternative, but equally general, representation of an improper survival time distribution can be obtained by assuming that the cumulative hazard has a finite positive limit, say θ, as t tends to ∞. In this case one can write
| (1.4) |
where F(t) = Λ(t)/θ is the c.d.f. of some nonnegative random variable such that F(0) = 0. In what follows we will call the model given by (1.4) the bounded cumulative hazard (BCH) model.
Within the nonparametric framework it makes no difference whether representation (1.2) or (1.4) is used as a basis for the estimation of p, but the situation is not the same when Ḡ0(t) is parametrically specified. Using definition (1.3), one can represent the survival function (1.4) in the form of formula (1.2), but both p and Ḡ0 become functions of the common parameter θ:
A similar confounding occurs when one represents (1.2) in the form of (1.4). A summary of useful formulas showing the relationship between the two models was given in Chen, Ibrahim, and Sinha (1999).
Although the models given by (1.2) and (1.4) are just two different ways of rescaling the survival function Ḡ(t), it took a long time to realize some virtues of the BCH model (which will be discussed later), which is the main subject matter of the present article. The first move in this direction was due to Haybittle (1959, 1965). The author proceeded from the observation that in some clinical data on cancer survival, an actuarial estimate of the hazard function tends to decrease exponentially with time. If the same property holds for the true hazard, expression (1.4) assumes the form:
| (1.5) |
A comprehensive treatment of this model was given by Cantor and Shuster (1992) who used the following parameterization:
| (1.6) |
where β > 0, but ζ may take either sign. If ζ > 0 the survival function (1.6) corresponds to the proper Gompertz distribution, but if ζ < 0 the distribution is improper with the surviving function equaling eβ/ζ. For this reason the distribution given by (1.6) can be called a generalized Gompertz distribution. In more recent work Cantor (2001) used representation(1.6) to determine the projected variance of estimated survival probabilities in clinical trials. A generalization of the model (1.6) was proposed by Cantor (1997) who suggested approximating a log hazard by a polynomial to obtain an estimate of the cure rate based on formula (1.1).
Clearly, the Gompertz-like model given by formula (1.5) is a special case of formula (1.4) with the function F(t) specified by an exponential c.d.f. with parameter ζ. The representation (1.4) was first introduced in an article of Yakovlev et al. (1993) and discussed later as an alternative to the mixture model by Yakovlev (1994). Interestingly enough, Yakovlev et al. (1993) proceeded from purely biological considerations; the idea of imposing a constraint on the behavior of the hazard function was introduced later in Tsodikov, Loeffler, and Yakovlev (1998b). In fact, the authors proposed a simple mechanistically motivated model of tumor recurrence yielding an improper survival time distribution. Under this model the probability of tumor cure is defined as the probability of no clonogenic tumor cells (clonogens) surviving by the end of treatment. The cell is called clonogenic if it is capable of producing a cell clone, that is, a group of cells that have this cell as their common parent. There is biological evidence that the majority of recurrent tumors are clonal in origin; that is, they arise from a single progenitor cell. In cancer studies the primary endpoint is conventionally the time to failure, referred to as survival time or failure time, X, with the event of failure being either tumor recurrence (disease-free survival) or death caused by the cancer under study (cancer-specific survival). According to the clonal model of posttreatment tumor development proposed by Yakovlev et al. (1993), a recurrent tumor arises from a single clonogenic cell. Every surviving clonogen can be characterized by a latent time (termed the progression time) during which it could potentially propagate into an overt tumor. Let M be the number of clonogens remaining in a treated tumor and ϕM be its probability generating function (p.g.f.). Assuming that progression times for surviving clonogens are independent and identically distributed (i.i.d.) with a common survival function F̄, one can find easily that G(t) = ϕM (F̄(t)), t ≥ 0. This formula suggests that knowledge of the entire distribution of the number of surviving clonogens is critical for developing biologically motivated survival models with cure. In particular, suppose that M is Poisson distributed. Then the survival function Ḡ(t) is given by the BCH model (1.4) with the parameter θ interpreted as the mean number of surviving clonogens.
A more general mechanistic model was considered by Hanin (2001). Suppose a tumor initially comprising a nonrandom number i of clonogenic cells is exposed to a fractionated radiation schedule consisting of n instantaneously delivered equal doses D separated by equal time intervals τ. It is assumed that every cell survives each exposure to the dose D with the same probability s = s(D), given that it survived the previous exposures, and independently of other cells. It is also assumed that the death of irradiated tumor cells is effectively instantaneous. Assuming, in addition, that tumor growth kinetics between radiation exposures can be modeled as a homogeneous birth-and-death Markov process with birth rate λ > 0 and spontaneous death rate ν ≥ 0, Hanin (2001) derived an explicit formula for the distribution of the random variable (r.v.) M; the latter turned out to be a generalized negative binomial distribution. The corresponding p.g.f. is of the form (Hanin 2001):
| (1.7) |
suggesting the following survival function for the time to tumor recurrence
| (1.8) |
where a = 1 − ω − s + sωμn−1; b = s(ωμn−1 − 1), c = 1 − ω − s + sμn−1, d = s(μn−1 −1), α = e(ν−λ)τ, μ = s/α, ω = [λ − να − s(λ − ν)]/[λ(1 − α)], F̄ (t) = 1 − F (t), satisfying the conditions: μ ≠ 1 and λ ≠ ν. The preceding formula may be taken as the starting point for the development of a new class of regression survival models; with this aim in mind, it makes sense to reduce the number of baseline parameters by enforcing the conditions: F (0) = 0 and Ḡ(0) = 1.
Clinically detectable primary tumors are estimated to contain at least i = 105 clonogenic tumor cells ranging up to probably 109 cells or even more (Tucker 1999). On the other hand, the probability, sn, for a cell to survive n fractions is expected to be very low, especially in the total dose range where cures occur frequently. This provides the rationale for exploring limiting distributions associated with model (1.8). As was shown by Hanin (2001), if n is fixed, i → ∞ and s → 0 in such a way that there exists a limit A = limi→∞ isn, 0 < A < ∞, then the distribution of the number of clonogens converges to a Poisson distribution with parameter θ = A/αn−1. This result disproves the conjecture (Tucker, Thames, and Taylor 1990; Tucker and Taylor 1996; Tucker 1999) that, due to cell proliferation occurring between fractions of radiation, the limiting distribution of the number of surviving clonogenic cells may not be Poisson. However, the convergence to the limiting distribution is quite slow, indicating a strong point in the line of reasoning presented by these authors. The rate of convergence was evaluated numerically by Hanin, Zaider, and Yakovlev (2001) in terms of the total variation distance between the exact distribution of the number of clonogens and its Poisson limit. Another useful limiting distribution arises in the subcritical case where μ = s/α < 1. This condition means that the total cell loss due to both causes of cell death (radiation induced and spontaneous) prevails on average over the cell gain owing to the proliferation of tumor cells between fractions of radiation dose. An explicit expression of this distribution was derived by letting i → ∞ and n → ∞ so that iμn → γ, 0 < γ < ∞ (Hanin et al. 2001).
The book by Yakovlev and Tsodikov (1996) presents several applications of (1.4) with a two- or three-parameter gamma distribution for the function F. The authors use the Hjort test (Hjort 1990) for goodness-of-fit testing, which is a natural choice in the parametric analysis of censored data without covariates. In a recent article, Gregori, Hanin, Luebeck, Moolgavkar, and Yakovlev (2002) adopted the Hjort goodness-of-fit test for testing several models of carcinogenesis. Methods of model diagnostics specially designed for different versions of this model have yet to be explored.
In this article, the current state of the art in methodology of statistical inference based on the BCH model is reviewed. The approach under review has emerged from cancer studies, and this fact necessarily reflects on the focus of our discussion. The history of the BCH model is relatively short, and the model has not yet enjoyed applications to other human diseases, to say nothing of nonmedical applications, such as estimation of recidivism rates. However, it should be kept in mind that other possible applications of the BCH model, including those mentioned previously, are every bit as well justified as for the binary mixture model; there is no reason for practitioners to refrain from using the BCH model just because it was originally derived in the context of cancer development.
The BCH model has the following distinct advantages:
It allows construction of a rich class of nonlinear transformation regression models to describe complex covariate effects. The class includes the traditional proportional hazards model as a special case; this structure is lacking in the binary mixture model. This makes the BCH model a natural tool for studying and testing departures from the proportionality of risks.
In some settings the BCH model provides a biologically meaningful interpretation of the results of the data analysis. This feature is especially important for combining statistical inference with other mathematical approaches to biomedical problems, for example, optimization of cancer therapy.
The BCH model offers certain technical advantages when developing maximum likelihood or Bayesian estimation procedures.
Before turning to the discussion of specific methods and results, one important remark is in order here. As is evident from definition (1.1), the probability of cure is essentially an asymptotic notion. However, the period of observation in actual truth is always finite, which is to say that one deals here with a problem of prediction rather than with the usual type of statistical inference. In other words, additional assumptions as to the behavior of Ḡ(t) or λ(t) beyond the period of observation are needed. At the same time a sample of i.i.d. right-censored observations is available, and it is natural that one tries to reduce the problem of prediction to that of estimation.
2. NONPARAMETRIC METHODS FOR A HOMOGENEOUS SAMPLE
As was mentioned in Section 1, formula (1.2) is a general expression for any improper survival time distribution. Proceeding from this representation, Maller and Zhou (1996) developed a theory of nonparametric estimation of the probability p. Suppose that the survival time distribution G(t) is absolutely continuous and let t1 < t2 < · · · < tn be a sample (subject to right censoring) of the ordered observed failure times. Maller and Zhou (1996) suggested estimating p by
| (2.1) |
where is the Kaplan–Meier estimator of the underlying survival function. Then a natural estimator for the conditional survival function Ḡ0(t) is given by
| (2.2) |
For any c.d.f. K(t) define its right extreme τK as τK = inf{t ≥ 0: K(t) = 1}. The consistency question for the estimator p̂n is settled in the following result by Maller and Zhou (1992):
Assume that censoring is independent and 0 < p ≤ 1. Let C̄(t) be the censoring time survival function. Let τH be the right extreme of H (t) = 1 − Ḡ(t)C̄(t) and suppose that the c.d.f. G(t) = 1 − Ḡ(t) is continuous at τH in case τH < ∞. Let G0(t) = 1 − Ḡ0(t) and C(t) = 1 − C̄(t). Then the estimator p̂n is consistent if and only if
| (2.3) |
Under the same conditions the authors showed that the condition τG0 ≤ τC is necessary and sufficient for the convergence in probability of to 0 as n tends to ∞. Assuming the inequality (2.3) and some additional mild conditions, Maller and Zhou also proved that, when p < 1, is asymptotically (as n → ∞) normally distributed with mean 0. Laska and Meisner (1992) showed that the estimator is, in fact, the generalized nonparametric maximum likelihood estimator of the proportion p in the mixture model (1.2).
As discussed previously, the inequality τG0 ≤ τC is both necessary and sufficient for consistency of the Kaplan–Meier estimator of the cure probability p. This inequality may be thought of as a quantification of “sufficient follow-up” (Maller and Zhou 1992). If the condition is not true, then failures may occur after the maximum follow-up period and it is not possible to determine which proportion of the late censored data has actually been cured. Maller and Zhou (1994) suggested a statistical test based on the length of the interval between the largest uncensored failure time and the largest overall failure time tn. Intuitively, if this interval is large, then the last failure has occurred well before the last censoring event so there has been sufficient follow-up. Maller and Zhou showed that, under appropriate regularity conditions, the estimator αn = (1 − Nn/n)n is an approximate p value for a test of τG0 ≤ τC, and αn converges to 0 in probability if and only if τG0 ≤ τC. Here Nn is the number of uncensored failure times in the interval ( ]. This test estimates a significance level rather than controls for it, so that the original version of the test by Maller and Zhou suggests the hypothesis of sufficient follow-up to be rejected whenever the estimated p value exceeds a prespecified critical value, say .05. Later, after conducting computer simulations, Maller and Zhou (1996) came to the conclusion that this test was far too conservative. It is clear that a pertinent test should be based on percentiles of the sample distribution of αn (or the closely related statistic qn = Nn/n) rather than on a fixed p value. Unfortunately, the relevant sample distributions are not known even in large samples. The idea of sufficient follow-up is intuitively compelling and a search for a more general formal definition of this notion (which is not necessarily related to consistency of the corresponding nonparametric estimator) should be continued.
When proceeding from the BCH model, formula (1.1) suggests the following nonparametric estimator of the cure probability: p̃n = exp{−Λ̃n(tn)}, where Λ̃n(tn) is the Nelson–Aalen estimator of the cumulative hazard at the point of last observation. A pertinent nonparametric estimator for F(t) can be proposed in the form:
| (2.4) |
where is the Kaplan–Meier estimator for the survival function Ḡ(t).
It is important to note that the preceding nonparametric estimators yield an estimate of survival probability at the right end T of the observation period. This estimate is all we have to predict the behavior of the survival function beyond the period of observation, and all such predictions are final. If we strictly follow the formal definition of cure rate, we have to recognize that the nonparametric approach implies a straight-line extrapolation of the estimated survival function beyond the period of observation T : Ḡ(t) is set to be equal to a constant value of for all t ≥ T. The same holds true for the semiparametric regression models discussed in Section 3. It should also be noted that the length T of the period of observation is implicitly involved in (2.3). Let us decompose the censoring time survival function as follows: C̄(t) = C̄*(t)[1 − I (t − T)], where I (x) = 0 for x < 0 and I (x) = 1 for x ≥ 0. Then inequality (2.3) is replaced by τG0 ≤ min{τC*, T}. The finiteness of the follow-up period is relevant to large-sample studies, where the value of T should be kept fixed when increasing the sample size; otherwise, ensuring asymptotic properties would imply infinite observation time.
Another feature inherent in the nonparametric approach has to do with the instability (high variance) of the nonparametric estimators. It is a well-known fact that the Kaplan–Meier estimator becomes highly unstable for t close to the end of an observation period in the presence of heavy censoring (Pepe and Fleming 1989; Cantor and Shuster 1992; Tsodikov 2001), which may have a very significant effect on the accuracy of cure rate estimation. The method for testing for sufficient follow-up, proposed by Maller and Zhou (1994, 1996), suffers from the same kind of instability as well. The nonparametric estimator is particularly sensitive to variations of in the denominator. Therefore, it is not recommended to use it in its original form. An improved estimator was proposed in Tsodikov (2001). This is a two-stage estimator. First, Ḡn(tn) is estimated parametrically. Then Ḡ(t) is estimated nonparametrically with Ḡn(tn) constrained to be equal to the corresponding value of the parametric estimate.
3. SEMIPARAMETRIC REGRESSION SURVIVAL MODELS WITH CURE
3.1 Mixture Models and Generalizations
So far we have followed two distinct lines of reasoning in the discussion of cure models: statistical and mechanistic. We now consider more formal relationships between the two aspects of the problem.
A cure model can be formulated by making assumptions about either the hazard or the survival function. For example, making the assumption on the bounded cumulative hazard in a proportional hazards (PH) model, we obtain the so-called improper PH model
| (3.1) |
where β is a vector of regression coefficients, z is a vector of covariates, and θ(β, z) is a known function relating β to z. In what follows we allow for more than one predictor, and for an arbitrary parameterization of regression predictors. However, in the examples the most common exponential parameterization is used, in which θ(β, z) = exp{β′ z}, where β′ is the transposed β vector. The component β0 of the vector β = (β0, β1, …)′ is the intercept term; therefore, z0 = 1 in the vector of covariates z = (z0, z1, …).
A general class of semiparametric regression models, nonlinear transformation models (NTM), was proposed in Tsodikov (2002, 2003):
| (3.2) |
where γ(x|β, z) is some parametrically specified cumulative distribution function in x with support on [0, 1]. Although our discussion allows for any parameterization of γ in terms of β and z, in the examples we assume that γ is parameterized through a set of parameters/predictors θ, η, …, where each predictor is further parameterized using generally different sets of regression coefficients β1, β 2, …, so that . The linear transformation models considered by Cheng, Wei and Ying (1995) represent a subclass of NTM with
| (3.3) |
where p is a tail function (=1− c.d.f.) and q is an inverse of a tail function (not necessarily that of p). Cure models represented by the NTM class were introduced in Tsodikov (2002). To make (3.2) a cure model, the following assumptions are made to enforce the limit Ḡ(t|β, z) → p > 0:
| (3.4) |
The restriction limt→∞ F̄(t) = 0 proposed by Taylor (1995) in the context of the two-component mixture model removes the overparameterization of the description of the baseline cure rate through F and h and the associated estimation and convergence problems for the fitting algorithms. Following the restriction, the estimate is assumed to satisfy . This restriction is also necessary for separation of the long- and short-term covariate effects on survival. The preceding restriction should be observed when parameterizing the model, as discussed in the following examples.
Alternatively, a cure model can be formulated as a two-stage model. First, an unobservable random variable M is postulated with distribution p(m|β, z) that depends on covariates. Second, the observed survival function is formed as
| (3.5) |
where the expectation is taken with respect to M, given z, and the distribution of M depends on β and z. The model (3.5) represents a generalized PH frailty model, which we simply call the PH mixture model, introduced in Tsodikov (2002, 2003), where M is assumed to be an arbitrary nonnegative random variable. In this context M can be interpreted as a missing covariate in a PH model. Obviously, the usual PH frailty model
| (3.6) |
where the distribution of U is independent of covariates, is a particular case of (3.5) with M = Uθ(β, z). Missing variables U dependent on covariates have been considered by several authors (e.g., Wassel and Moeschberger 1993) within the shared PH frailty framework. It should be noted that the PH mixture model (3.5), although at least as general as (3.6) with U = U(β, z), leads to a computationally efficient estimation procedure that we consider in the next section. Because all models considered previously in this article are particular cases of (3.5), an estimation procedure designed for the PH mixture model, or for the NTM subclass (3.2) restricted to (3.4), represents a universal tool for statistical inference with such models.
The discrete mixture model [i.e., (3.5) with a discrete random variable M], which was used in particular forms as a mechanistic model in Section 1, can be linked to the NTM class. Observe that the p.g.f. of a discrete random variable M
is a distribution function in x with the support [0, 1]. Indeed, because the pm are nonnegative, ϕM (x) is increasing in x. Also, . If M is discrete and depends on covariates, (3.5) can be rewritten as an NTM with
With the discrete mixture model, the probability of cure is given by γ (0|z) = ϕM (0|β, z) = p0(β, z).
Alternatively, we may want to write an NTM model as a discrete mixture model. It should be noted that NTM is a wider class than that of mixture models. For an NTM to be a discrete mixture, we may require that γ (x|β, z) be an analytic function of x on [0, 1]. As such, it can be expanded in a power series about x = 0. Additionally, the coefficients of the corresponding power series must be positive. Should this be the case, they can be interpreted as probabilities, and γ as a generating function of some discrete random variable. If γ is a mixture model (discrete or continuous), then ψ(λ) = γ (e−λ) is the Laplace transform of the distribution of the mixing variable M. Generally, a necessary and sufficient condition for γ (x|·) to be a mixture model is that ψ be a completely monotonic function as given by the Bernstein theorem (see Feller 1971). A function ψ(λ) is called completely monotonic if all of the derivatives ψ(n) exist and (−1)nψ(n)(λ) ≥ 0, λ > 0.
We can now represent the cure models discussed earlier in this article as members of the mixture–NTM model family. It should be stressed that such a representation is not unique.
The improper PH model (3.1) corresponds to
| (3.7) |
This is the generating function of the Poisson distribution, and by expanding γ about x = 0, we get a power series with Poisson probabilities as coefficients. This gives us the mechanistic interpretation of the improper PH model discussed in Section 1.
Consider an extension of the improper PH model allowing for dissimilar covariate effects on long- and short-term survival. To construct an extended hazard model (the term was introduced by Etezadi-Amoli and Ciampi 1987), we employ the fact that F̄ is a survival function. Incorporating covariates into F̄, we can add a short-term effect to the improper PH model. The class of extended hazard models
| (3.8) |
where γ̃ is an NTM and β = (β1, β2), βi = (βi0, βi1, …), i = 1, 2, was introduced in Tsodikov (2002). If γ̃ is a mixture model itself, then (3.8) is also a mixture model with γ̃ = exp{− θ[1 − γ̃]}. The mixing variable M that generates the family (3.8) has a well-defined structure of a compound variable
| (3.9) |
where ν is a Poisson random variable, , and the δk are i.i.d. copies of a random variable δ with Laplace transform γ̃(e−λ). The binary distribution for ν gives rise to the two-component mixture class of models
| (3.10) |
Kuk and Chen (1992) proposed a regression model in the form of (3.10) with p being a logistic regression and γ̃ a proportional hazards regression. This model was further studied by Sy and Taylor (2000) and Peng and Dear (2000). The Poisson distribution for ν leads to the bounded hazard family of mixture models. For example, let δ be degenerate (nonrandom): Pr(δ = η(β2, z)) = 1. Then M = η(β2, z)ν, where ν is Poisson with expectation θ(β1, z). Then we have the PHPH model
| (3.11) |
The model (3.11) was proposed by Broët et al. (2001) in the context of two sample score tests for long- and short-term covariate effects.
In the preceding cure models, restriction (3.4) needs to be observed. In models (3.8) considered so far, one predictor (η) was used to describe the short-term effect. To avoid overparameterization of the model, the intercept component of β2 has to be fixed or removed, for example, by setting β20 = 0. With this coding of the model, the intercept term in the first predictor (θ), β10, corresponds to the baseline log cure rate. With an exponential parameterization of the predictors, the baseline survival function takes the form Ḡb(t|β0, z) = exp{− exp(β10)[1 − γ̃(F̄|0)]}, where 0 = (0, 0, …)′ and β0 = ((β10, 0, 0, …), 0)′. As in the Cox model (Cox 1972), the regression coefficients βij, i = 1, 2, j = 1, 2, …, correspond to the relative effects of the covariates zij on the long- and short-term predictor, i = 1, 2, respectively. For example, with the PHPH model, βij, i = 1, 2, j = 1, 2, …, is the log of the hazard ratio in the two PH models of which the PHPH model is composed, corresponding to the long- and short-term effect, i = 1, 2, respectively.
3.2 Estimation Procedures
The issue of the potentially infinite dimension has been the most critical deterrent to the use of maximum likelihood estimation (MLE) in semiparametric regression models. Methods based on the partial likelihood are specific to the proportional hazards model and do not extend to other models. The Newton–Raphson procedure requires taking the inverse of the information matrix, which gets computationally prohibitive and unstable with increasing dimension. Characterizing the future directions in survival analysis in their editorial in Biometrics, Fleming and Lin (2000) pointed out that “it would be highly useful to develop efficient and reliable numerical algorithms for the semiparametric estimation….” In the following sections we review some recent approaches to the problem.
Introduce a set of times ti, i = 1, …, n, arranged in increasing order, with tn+1 = ∞. Associated with each ti is a set of individuals  with covariates zij, j ∈
with covariates zij, j ∈  , who fail at ti, and a similar set of individuals
, who fail at ti, and a similar set of individuals  with covariates zij, j ∈
with covariates zij, j ∈ 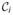 , who are censored at ti. For any function A(t) let Ai = A(ti) and ΔAi = |Ai − Ai−1|. The generalized log-likelihood for an NT model (3.2) can be written as
, who are censored at ti. For any function A(t) let Ai = A(ti) and ΔAi = |Ai − Ai−1|. The generalized log-likelihood for an NT model (3.2) can be written as
| (3.12) |
3.2.1 Conventional Maximization Methods
Consider maximization of the log-likelihood function ℓ(x) with respect to the joint vector of parameters x, representing regression coefficients β and the nonparametrically specified function F. The vector ΔH represents a set of jumps ΔHi of the cumulative hazard function H, which can be used to parameterize F so that x = (β, ΔH). Consider a so-called direction sets method (Press, Flannery, Teukolsky, and Vetterling 1994) constructed as follows:
Given the current iteration vector x(k), find the search direction s(k).
Maximize f (x(k) + ys(k)) with respect to the scalar y.
Set x(k+1) = x(k) = y*s(k), where y* is the solution at the previous step.
Set k = k + 1 and continue to step 1.
The Newton–Raphson method is one example of the direction sets methods. To avoid taking the inverse of the full-model information matrix, the search direction s can be specified according to the Powell method, which uses multiple line maximizations in one dimension to construct a set of conjugate directions (Press et al., 1994).
3.2.2 Profile Likelihood Approach
Assume that we have a method to obtain the global maximum of ℓ with respect to F, given β. We discuss two such methods in the next two sections. We may write the profile log-likelihood as an implicit function of β:
| (3.13) |
where F* is the solution of the problem
| (3.14) |
where 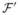 is the class of proper discrete survival functions. A profile algorithm is a straightforward nested procedure:
is the class of proper discrete survival functions. A profile algorithm is a straightforward nested procedure:
Maximize ℓpr(β) by a conventional nonlinear programming method (e.g., a direction sets method).
For any β as demanded in the preceding maximization procedure, solve the problem (3.14) with specified tolerance.
Inference based on the profile likelihood is similar to that based on the partial likelihood for the PH model. However, the classical theory of MLE does not apply to infinite dimensions. Important results have been obtained regarding theoretical justifications for the nonparametric maximum likelihood estimation (NPMLE) method and the profile likelihood for semiparametric models (Murphy 2000). It was shown that profile likelihoods with nuisance parameters estimated out behave like ordinary likelihoods under some conditions. In particular, these results apply to the PH model, the proportional odds (PO) model, the PH frailty model, and presumably to many other models.
3.2.3 Restricted Nonparametric Maximum Likelihood Estimation
Tsodikov (2002) developed the so-called restricted nonparametric maximum likelihood estimation (RNPMLE) algorithm. The RNPMLE method is based on a recurrent structure of the score equations with respect to the nonparametric part of the model (F̄). Earlier variations of the procedure were developed for the PH model (Tsodikov 1998a) and for the proportional odds (PO) model (Tsodikov, Hasenclever, and Loeffler 1998a) and were subsequently generalized for NT cure models (Tsodikov 2002). Although quite computationally intensive, the RNPMLE method is numerically stable and it allows us to avoid taking inverses or approximating the information matrix of the full model.
According to the nonparametric maximum likelihood method, the model can be fitted by maximizing the generalized log-likelihood (3.12) with respect to the regression parameters β and the unspecified survival function F̄ (or the corresponding distribution function F). In doing so, the log-likelihood ℓ is maximized for a step function F with steps at the times of failures.
As discussed earlier we impose the restriction F(tn) = 1. To maximize (3.12) under the restriction F(tn) = 1, we use the method of Lagrange multipliers and obtain the system of score equations
| (3.15) |
| (3.16) |
| (3.17) |
Inference procedures for the regression coefficients β can be obtained from the profile log-likelihood (3.14). The profile log-likelihood is obtained by solving the score equations (3.16) and (3.17) for F simultaneously, given β.
In the RNPMLE method the system of score equations (3.16) is partitioned into a subsystem of the form
| (3.18) |
that can be solved recurrently for F̄2, …, F̄n, given F0 = 0 and F1. Finally, the equation ϕ(F̄1) = 1 is solved, where ϕ is defined as Fn generated recurrently using the subsystem (3.18). The RNPMLE method yields point estimates and confidence intervals for the regression coefficients and the function F (Tsodikov 2002).
3.2.4 EM-Based Methods
The EM algorithm used to fit shared frailty models in survival analysis (Nielsen, Gill, Andersen, and Sørensen 1992) handles H in a numerically efficient way. This is made possible as the M step reduces to the PH model. Estimates are obtained iteratively by maximizing the partial likelihood and computing the Nelson–Aalen–Breslow estimator (Andersen, Borgan, Gill, and Keiding 1993) for the cumulative hazard H. Similar algorithms have been used to fit the two-component mixture model, given by Taylor (1995), Sy and Taylor (2000, 2001), and Peng and Dear (2000).
Recently, Tsodikov (2003) generalized the EM algorithm for the frailty model into a universal “distribution-free” procedure applicable to the general PH mixture model (3.5) and NTM class (3.2). This family of algorithms (quasi-EM, QEM) is a subclass of the so-called MM algorithms based on surrogate objective functions (Lange, Hunter, and Yang 2000). Broadly defined, an MM algorithm substitutes a computationally simpler surrogate objective function for the target function on each step of the procedure (similar to the E step of the EM). Maximizing the surrogate objective function drives the target function in the desired direction. Thus, a difficult maximization problem is replaced by a series of simpler ones. Unfortunately, there is no universal recipe on how to find an appropriate surrogate objective function. The idea of the QEM is to obtain a surrogate objective function by generalizing the one inherent in the EM procedure so that it does not depend on the missing data formulation of the model. Practically, the QEM approach for semiparametric models is based on a derivation of the “distribution-free” E step for the EM algorithm, constructed for the PH mixture model (3.5). More formally, we consider the QEM procedure for cure models. The following statement is the key result underlying the QEM construction.
Proposition 3.1 (Tsodikov 2003)
Let τ be the observed event time under independent censoring and let c be the observed censoring indicator (c = 1, if a failure, and c = 0, otherwise). Under the PH mixture model,
and if F′(τ) > 0, the conditional expectation of M, given the observed event, is given by
where
| (3.19) |
where γ(c)(x|·) = ∂cγ (x|·)/∂xc, c = 0, 1, …, γ(0)(x|·) = γ (x|·).
The preceding result indicates that the E step can be constructed using the first two derivatives of the NTM-generating function γ without any knowledge or even existence of the mixing random variable M. Specification of an algorithm for a particular model requires evaluation of Θ for the model. For example, for the models discussed in the previous section, we have
Improper PH model: From (3.1) or (3.7), Θ(x|·, c) = c + θ(·)x.
PHPH model: From (3.11), Θ(x|·, c) = θ(·)η(·)xη(·) + cη(·).
Cure models require a correction of Θ at the last observation [see (3.21)]. Let cij = 1, j ∈ 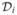 , and cij = 0, j ∈
, and cij = 0, j ∈ 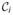 . Let τk, k = 1, …, K, be the time points in ascending order where failures occur (
. Let τk, k = 1, …, K, be the time points in ascending order where failures occur (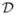 is not empty). Denote by rk the rank of τk in the set {ti}. The ranks rk locate the points τk on the set {ti: τk = trk}. By definition, we set τK +1 = n + 1 and τ0 = 0. Imputation of the mixing variable M using (3.19) results in the score equations for the cumulative hazard H corresponding to F,
is not empty). Denote by rk the rank of τk in the set {ti}. The ranks rk locate the points τk on the set {ti: τk = trk}. By definition, we set τK +1 = n + 1 and τ0 = 0. Imputation of the mixing variable M using (3.19) results in the score equations for the cumulative hazard H corresponding to F,
| (3.20) |
where is the risk set at tk, Dk is the number of failures at tk, and
| (3.21) |
where (·)ij stands for (β, zij). The fact that the contributions of the observations ij to the likelihood as well as Θ at, or after the last failure (i ≥ rK), are different from their counterparts before the last failure (i ≤ rK − 1) is due to the restriction F̄i = 0, i = rK, …, n, representing the fact that F̄ is a proper survival function. This distinction is not made if the model is a general NTM with an unrestricted F.
It is interesting to note that the score equations have the form of the Nelson–Aalen–Breslow estimator for the PH model with the usual predictor replaced by Θ. Because Θ depends on F, an iteration procedure is needed to satisfy (3.20). Given β, iterations with respect to F can be carried out as follows:
At the kth iteration F̄(k), compute Θ(k) for each subject.
Update F(k) by F(k+1) using the Nelson–Aalen–Breslow estimator (3.20).
It can be shown (Tsodikov 2003) that if Θ(x|·) is a nondecreasing function of x, or if γ is a PH mixture model (a stronger assumption), then each iteration described previously improves the likelihood. Also, this assumption makes the preceding procedure a member of the MM family (Lange et al. 2000), and the convergence properties of the algorithm follow from the general MM theory.
There are many ways to build a particular model fitting algorithm based on the principles described previously, and this depends on how the maximization with respect to β is incorporated into the procedure. One way would be to use partial likelihood and a setup similar to the EM algorithm for frailty models (Nielsen et al. 1992). Such an EM algorithm was used in Sy and Taylor (2000) and Peng and Dear (2000) to fit the two-component mixture model. As simple as the setup of the procedure with a binary distribution for M might be, its generalization for a wider family of PH mixture models or NTM’s is problematic. The key to a straightforward setup of the procedure is not to use the EM principle on β, as it would require working with the distribution of M.
We find the profile version of the QEM algorithm particularly easy and straightforward to work with. The profile QEM algorithm outperformed conventional maximization procedures (Sec. 3.2.1) and the frailty EM algorithm based on partial likelihood when used to fit a semiparametric proportional odds (PO) model. Also, it was shown to be faster than a directions set method used to fit a parametric PO model.
3.3 Example: Prostate Cancer Data
The study was carried out using data on 1,100 patients with clinically localized prostate cancer who were treated with three-dimensional conformal radiation therapy at the Memorial Sloan-Kettering Cancer Center (Zaider et al. 2001). The patients were stratified by radiation dose (group 1, <67.5 Gy; group 2, 67.5–72.5 Gy; group 3, 72.5–77.5 Gy; group 4, 77.5–87.5 Gy) and prognosis category [favorable, intermediate, and unfavorable as defined by pretreatment prostate specific antigen (PSA) measurement and Gleason prognostic score]. A relapse was recorded when tumor recurrence was diagnosed or when three successive PSA elevations were observed from a post-treatment nadir PSA level. PSA relapse-free survival was used as the primary endpoint. There were no failures observed in patients with favorable prognosis in dose group 4. For that reason this group of patients is not included in the data analysis.
We applied the PHPH extended hazard model (3.11) with z specified by indicator dummy variables that code the four dose groups and the three prognostic categories. In the unrestricted model dose and summary prognosis may each have an effect on long-term survival through θ(z) and on short-term survival through η(z). The hypothesis of no short-term effect of prognostic category (proportional hazards with respect to prognosis) is not rejected (p = .49) by the likelihood ratio test. This observation justifies the use of the PH model for the effect of the prognostic category. However, the total radiation dose appears to have a significant (p < .0001) short-term effect on survival of patients with prostate cancer, indicating nonproportionality of the effect of dose. Resorting to our mechanistic interpretation of (3.11), we may speculate that the progression time distribution varies with radiation dose while being essentially the same for all prognostic categories. Semiparametric estimates of the mean values for the distributions 1 − γ (F̄|z) are equal to 1,279, 867, 803, and 498 days for dose groups 1, 2, 3, and 4, respectively. Estimates of the hazard ratio for the short-term effect of each dose group,
show a monotonically increasing (with dose) short-term risk: .188 with confidence limits (.038, 1.538) for dose group 1, .415 (.065, .765) for dose group 2, .474 (.024, 1.224) for dose group 3, and 1.000 for dose group 4.
Semiparametric estimates of the probability of cure are given in Table 1. For comparison, we also present parametric estimates obtained with F specified by a two-parameter gamma distribution. It is shown in Table 1 that the two estimates appear to be quite close to each other. This analysis indicates that, in terms of cure rate, dose escalation has a significant positive effect only in the intermediate and unfavorable groups. It is also found that progression time is inversely proportional to dose, which means that patients recurring in higher dose groups have shorter recurrence times, yet these groups have better long-term survival. One possible explanation for this seemingly illogical observation lies in the fact that less aggressive tumors potentially recurring after a long period of time are cured by higher doses and do not contribute to the observed time pattern of tumor relapse. As a result tumors in higher dose groups are less likely to recur; however, if they do, they tend to recur earlier.
Table 1.
Estimates of the Probability of Cure (semiparametric/parametric) and 95% Semiparametric Likelihood Ratio Confidence Intervals (in parentheses) as Estimated Using Multivariate Semiparametric Regression Analysis Based on (3.11).
| Prognostic category | Dose group |
|||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Favorable | .78/.80 | .79/.74 | .88/.87 | 1.00* |
| (.55, .95) | (.68, .92) | (.80, .97) | – | |
| Intermediate | .37/.25 | .53/.51 | .67/.58 | .79/.74 |
| (.21, .55) | (.41, .64) | (.58, .78) | (.68, .87) | |
| Unfavorable | .02/.00 | .35/.27 | .46/.33 | .60/.64 |
| (.00, .11) | (.25, .45) | (.38, .56) | (.45, .74) | |
The estimate of the probability of cure is set equal to 1 because no failures are observed in this group of patients.
4. BAYESIAN INFERENCE
4.1 Parametric Cure Rate Model
Ibrahim, Chen, and Sinha (2001a) presented a comprehensive treatment of Bayesian approaches for the cure rate model
| (4.1) |
We review some of their work here. We let the covariates depend on θ through the relationship θ = exp(x′β), where x is a p × 1 vector of covariates and β = (β1, …, βp) is a p × 1 vector of regression coefficients. Proceeding from the biological interpretation discussed in Section 1, we can now construct the likelihood function (see Chen et al. 1999; Ibrahim et al. 2001a) in a typical setting. Suppose we have n subjects and let Ni denote the number of surviving clonogenic tumor cells for the ith subject. Further, we assume that the Ni’s are i.i.d. Poisson random variables with mean θ, i = 1,2, …, n. We emphasize here that the Ni’s are not observed and can be viewed as latent variables in the model formulation. Further, suppose Zi1, Zi2, …, Zi, Ni are the i.i.d. progression times for the Ni cells for the ith subject, which are unobserved, and all have proper cumulative distribution function F (·), i = 1,2, …, n. We denote the indexing parameter (possibly vector valued) by ψ, and thus write F(·|ψ) and F̄(·|ψ) = 1 − F (·|ψ). For example, if F (·|ψ) corresponds to a Weibull distribution, then ψ = (α, λ)′, where α is the shape parameter and λ is the scale parameter. Let yi denote the survival time for subject i, which may be right censored, and let νi denote the censoring indicator, which equals 1 if yi is a failure time and 0 if it is right censored. The observed data are Dobs = (n, y, ν), where y = (y1, y2, …, yn)′ and ν = (ν1, ν2, …, νn)′. Also, let N = (N1, N2, …, Nn)′. The complete data are given by D = (n, y, ν, N), where N is an unobserved vector of latent variables. Throughout the remainder of this section, we will assume a Weibull density for f (yi|ψ), so that f (y|ψ) = αyα−1 exp{λ − yα exp(λ)}. When covariates are included we have a different cure rate parameter, θi, for each subject, i = 1, 2, …, n. Let denote the p × 1 vector of covariates for the ith subject. We relate θ to the covariates by , so that the cure rate for subject i is , i = 1, 2, …, n. This relationship between θi and β is equivalent to a canonical link for θi in the setting of Poisson regression models. With this relation we can write the complete data likelihood of (β, ψ) as
| (4.2) |
where D = (n, y, X, ν, N), X is the n × p matrix of covariates, f (yi|ψ) is the Weibull density given previously, and .
Chen et al. (1999) discussed classes of noninformative priors as well as the class of power priors for (β, ψ) and examined some of their properties. Consider the joint noninformative prior π(β, ψ) ∝ π(ψ), where ψ = (α, λ)′ are the Weibull parameters in f (y|ψ). This noninformative prior implies that β and ψ are independent a priori and π(β) ∝ 1 is a uniform improper prior. We will assume throughout this section that π(ψ) = π(α|δ0, τ0)π(λ), where π(α|δ0, τ0) ∝ αδ0−1 exp(−τ0α) and δ0 and τ0 are two specified hyperparameters. Although several choices can be made, we will use a normal density for π(λ). With these specifications the posterior distribution of (β, ψ) based on the observed data Dobs = (n, y, X, ν) is given by
| (4.3) |
where the sum in (4.3) extends over all possible values of the vector N. Chen et al. (1999) gave conditions concerning the propriety of the posterior distribution in (4.3) using the non-informative prior π(β,ψ) ∝ π(ψ). This enables us to carry out Bayesian inference with improper priors for the regression coefficients and facilitates comparisons with maximum likelihood. However, under the improper priors π(β, ψ) ∝ π(ψ), the mixture model in (1.2) always leads to an improper posterior distribution for β as shown in Chen et al. (1999).
Ibrahim and Chen (2000) described a general class of informative priors called the power priors for conducting Bayesian inference in the presence of historical data. We now examine the power priors for (β, ψ). Let n0 denote the sample size for the historical data, let y0 be an n0 × 1 of right-censored failure times for the historical data with censoring indicators ν0, let N0 be the unobserved vector of latent counts of clonogenic cells, and let X0 be an n0 × p matrix of covariates corresponding to y0. Let D0 = (n0, y0, X0, ν0, N0) denote the complete historical data. Further, let π0(β, ψ) denote the initial prior distribution for (β, ψ). A beta prior is chosen for a0, leading to the joint power prior distribution
| (4.4) |
where L(β, ψ|D0) is the complete data likelihood given in (4.2) with D being replaced by the historical data D0 and D0,obs = (n0, y0, X0, ν0). We take a noninformative prior for π0(β, ψ), such as π0(β, ψ) ∝ π0(ψ), which implies π0(β) ∝ 1. For ψ = (α, λ)′ we take a gamma prior for α with small shape and scale parameters and an independent normal prior for λ with mean 0 and variance c0. Also, (γ0, λ0) are specified prior parameters. The prior in (4.4) does not have a closed form but has several attractive properties. First, we note that if π0(β, ψ) is proper, then (4.4) is guaranteed to be proper. Further, (4.4) can be proper even if π0(β, ψ) is improper. Chen et al. (1999) characterized the propriety of (4.4) when π0(β, ψ) is improper. In addition, they showed that the power prior for β based on the model (1.2) will always lead to an improper prior as well as an improper posterior distribution.
4.2 Semiparametric Cure Rate Model
In this section we consider a semiparametric version of the parametric cure rate model discussed in the previous section. Following Ibrahim et al. (2001a), Chen, Harrington, and Ibrahim (2001), and Chen and Ibrahim (2001), we construct a finite partition of the time axis, 0 < s1 < ··· < sJ, with sJ > yi for all i = 1, 2, …, n. Thus, we have the J intervals (0, s1], (s1, s2], …, (sJ − 1, sJ], and we assume that the hazard for F(y) is equal to λj for the jth interval, j = 1, 2, …, J, leading to
| (4.5) |
where λ = (λ1, …, λJ)′. We note that, when J = 1, F *(y|λ1) reduces to the parametric exponential model. With this assumption the complete data likelihood can be written as
| (4.6) |
where νij = 1 if the ith subject failed or was censored in the jth interval, and 0 otherwise. The model in (4.6) is a semiparametric version of (4.2) in which the degree of the nonparametricity is controlled by J. Because the estimation of the cure rate parameter θ could be highly affected by the nonparametric nature of F*(y|λ), it may be desirable to choose small to moderate values of J for cure rate modeling. In practice, we recommend doing analyses for several values of J to see the sensitivity of the posterior estimates of the regression coefficients. The semi-parametric cure rate model (4.6) is quite flexible, as it allows us to model general shapes of the hazard function, as well as choose the degree of parametricity in F*(y|λ) through suitable choices of J. Again, because N is not observed, the observed data likelihood, L(β, λ|Dobs), is obtained by summing out N from (4.6) as in the previous section. Also, power priors for this model can be constructed in a similar fashion as in the previous section. We refer the reader to Ibrahim et al. (2001a), Chen et al. (2001), and Chen and Ibrahim (2001) for more details.
4.3 An Alternative Semiparametric Cure Rate Model
A crucial issue with cure rate modeling, and semiparametric survival models in general, is the behavior of the model in the right tail of the survival distribution. In these models there are typically few subjects at risk in the tail of the survival curve after sufficient follow-up; therefore, estimation of the cure rate can be quite sensitive to the choice of the semi-parametric model. Thus, there is a need to carefully model the right tail of the survival curve and allow the model to be more parametric in the tail, while also allowing the model to be non-parametric in other parts of the curve. Ibrahim, Chen, and Sinha (2001b) constructed such a model by defining a smoothing parameter κ, 0 < κ < 1, that controls the degree of parametricity in the right tail of the survival curve and does not depend on the data. Specifically, the prior for λj depends on κ, such that the model converges to a parametric model in the right tail of the survival curve as j → ∞. By an appropriate choice of κ, one can choose a fully nonparametric model or a fully parametric model for the right tail of the survival distribution. Also, κ will allow some control over the degree of parametricity in the beginning and middle part of the survival distribution. A more parametric shape of the model in the right tail facilitates more stable and precise estimates of the parameters. This approach is fundamentally very different from previous approaches for semiparametric Bayesian survival analysis, which primarily focus on specifying a prior process with a mean function and possibly a smoothing parameter, in which the posterior properties of both of them depend on the data.
Let F0(t|ψ0) denote the parametric survival model chosen for the right tail of the survival curve and let H0(t) denote the corresponding cumulative baseline hazard function. Now take the λj’s to be independent a priori, each having a gamma prior distribution with mean
| (4.7) |
and variance
| (4.8) |
where 0 < κ < 1 is the smoothing parameter. As κ → 0, , so that small values of κ imply a more parametric model in the right tail. In addition, as j → ∞, , implying that the degree of parametricity is increased at a rate governed by κ as the number of intervals increases. This property also implies that, as j → ∞, the survival distributionin the right tail becomes more parametric regardless of any fixed value of κ. The properties of this model are attractive. For example, if F0(·|ψ0) is an exponential distribution, then F0(y|ψ0) = 1 − exp(−ψ0y), so that μj = ψ0 and . If F0(·|ψ0) is a Weibull distribution, then F0(y|ψ0) = 1 − exp(−γ0yα0), ψ0 = (α0, γ0)′, so that
Several properties of this model are now given, which are proved in Ibrahim et al. (2001a,b).
Property 4.1
Assume that (sj + sj−1)/2 → t as sj − sj−1 → 0. Then, for any j, according to this prior process, E(λj|ψ0) → h0(t) as sj − sj−1 → 0, where .
For example, if F0(y|ψ0) = 1 − exp(−ψ0y), then E(λj|ψ0) = ψ0 regardless of the choice of s1, s2, …, sJ. If F0(y|ψ0) = 1 − exp(−γ0yα0), then E(λj |ψ0) → γ0α0tα0−1 as sj − sj −1 → 0. This assures that, as j becomes large and sj − sj−1 → 0, this prior process approximates any prior process with prior mean h0(t) defined on the progression time hazard h*(t|λ) corresponding to (4.5).
Property 4.2
Let . Then as κ → 0, where F̄p(y|ψ0) = exp(−θF0(y|ψ0)).
Property 4.3
Let and let denote the corresponding hazard function. Then as κ → 0, where .
We now give joint prior specifications for the semiparametric model in (4.7) and (4.8). We specify a hierarchical model and first consider a joint (improper) noninformative prior distribution for (β, λ, ψ0), given by
| (4.9) |
We take each π(λj|ψ0) to be independent gamma densities with mean μj and variance . If F0(·|ψ0) is an exponential distribution, then ψ0 is a scalar, and we specify a gamma prior for it; that is, , where ζ0 and τ0 are specified hyperparameters. If F0(·|ψ0) is a Weibull distribution, then ψ0 = (α0, γ0)′. In this case we take a prior of the form
| (4.10) |
where ζα0, τα0, ζγ0, and τγ0 are specified hyperparameters. For β we consider a uniform improper prior. Ibrahim et al. (2001a, 2001b) established conditions for the propriety of the joint posterior distribution of (β, λ, ψ0), when using an exponential distribution or a Weibull distribution for F0(·|ψ0). In addition, they developed the power prior for this model.
4.4 Multivariate Cure Rate Model
It is often of interest to jointly model several types of failure time random variables in survival analysis, such as time to cancer relapse at two different organs, times to cancer relapse and death, times to first and second infection, and so forth. In addition, these random variables typically have joint and marginal survival curves that “plateau” beyond a certain period of follow-up; therefore, it is of great importance in these situations to develop a joint cure rate model for inference. There does not appear to be a natural multivariate extension of the mixture model in (1.2). Even if such an extension were available, it appears that a multivariate mixture model would be extremely cumbersome to work with from a theoretical and computational perspective. As an alternative to a direct multivariate extension of (1.2), Chen, Ibrahim, and Sinha (2001) proposed a multivariate generalization of (4.1), called the multivariate cure rate model. This model proves to be quite useful for modeling multivariate data in which the joint failure time random variables have a surviving fraction and each marginal failure time random variable also has a surviving fraction. To induce the correlation structure between the failure times, Chen et al. (2001) introduced a frailty term (Clayton 1978; Hougaard 1986; Oakes 1989), which is assumed to have a positive stable distribution. A positive stable frailty results in a conditional proportional hazards structure (i.e., given the unobserved frailty). Thus, the marginal and conditional hazards of each component have a proportional hazards structure and remain in the same class of univariate cure rate models.
For clarity and ease of exposition, we will focus our discussion on the bivariate cure rate model, as extensions to the general multivariate case are quite straightforward. The bivariate cure rate model of Chen et al. (2001) can be derived as follows. Let Y = (Y1, Y2)′ be a bivariate failure time, such as Y1 = time to cancer relapse and Y2 = time to death, or Y1 = time to first infection and Y2 = time to second infection, and so forth. We assume that (Y1, Y2) are not ordered and have support on the upper orthant of the plane. For an arbitrary patient in the population, let N = (N1, N2)′ denote latent (unobserved) variables for (Y1, Y2), respectively. We assume throughout that Nk has a Poisson distribution with mean θkw, k = 1, 2, and (N1, N2) are independent, given w. The quantity w is a frailty component in the model that induces a correlation between the latent variables (N1, N2). Here we take w to have a positive stable distribution indexed by the parameter α, denoted by w ~ Sα(1, 1, 0), where 0 < α < 1 (see Chen et al. 2001 for more details). Although several choices can be made for the distribution of w, the positive stable distribution is quite attractive, common, and flexible in the multivariate survival setting. In addition, it will yield several desirable properties.
Let Zi = (Z1i, Z2i)′ denote the bivariate progression time for the ith clonogenic cell. The random vectors Zi, i = 1, 2, …, are assumed to be independent and identically distributed. The cumulative distribution function of Zki is denoted by Fk (t) = 1 − F̄k(t), k = 1, 2, and Fk is independent of (N1, N2). The observed survival time can be defined by the random variable Yk = min{Zki, 0 ≤ i ≤ Nk}, where P (Zk0 = ∞) = 1 and Nk is independent of the sequence Zk1, Zk2, …, for k = 1, 2. The survival function for Y = (Y1, Y2)′, given w, and hence the survival function for the population, given w, is given by
| (4.11) |
where P (Nk = 0) = P (Yk = ∞) = exp(−θk), k = 1, 2. The frailty variable w serves a dual purpose in the model—it induces the correlation between Y1 and Y2 and at the same time relaxes the Poisson assumption of N1 and N2 by adding the same extra Poisson variation through their respective means θ1w and θ2w.
The Laplace transform of w is given by E(exp(−sw)) = exp(−sα). Using the Laplace transform of w, a straightforward derivation yields the unconditional survival function
| (4.12) |
It can be shown that (4.12) has a proportional hazards structure if the covariates enter the model through (θ1, θ2). The joint cure fraction implied by (4.12) is F̄pop(∞, ∞) = exp(−[θ1 + θ2]α). From (4.12) the marginal survival functions are , k = 1, 2. Equation (4.12) indicates that the marginal survival functions have a cure rate structure with probability of cure for Yk, k = 1, 2. It is important to note in (4.12) that each marginal survival function has a proportional hazards structure as long as the covariates, x, only enter through θk. The marginal hazard function is given by , with attenuated covariate effect (θk(x))α, and fk(y) is the survival density corresponding to Fk(y). This property is similar to the earlier observations made by Oakes (1989) for the ordinary bivariate stable frailty survival model. The parameter α, 0 < α < 1, is a scalar parameter that is a measure of association between (Y1, Y2). Small values of α indicate high association between (Y1, Y2). As α → 1 this implies less association between (Y1, Y2), which can be seen from (4.12). Following Clayton (1978) and Oakes (1989), we can compute a local measure of dependence, denoted θ*(y1, y2), as a function of α. For the multivariate cure rate model in (4.12), θ*(t1, t2) is well defined and is given by
| (4.13) |
We see that θ*(y1, y2) in (4.13) decreases in (y1, y2). That is, the association between (Y1, Y2) is greater when (Y1, Y2) are small and the association decreases over time. Such a property is desirable, for example, when Y1 denotes time to relapse and Y2 denotes time to death. Finally, we mention that a global measure of dependence such as Kendall’s τ or the Pearson correlation coefficient is not well defined for the multivariate cure rate model (4.12) because no moments for cure rate models exist due to the improper survival function.
The likelihood function for this model based on n subjects can be written as
| (4.14) |
where ψ = (ψ1, ψ2), θ = (θ1, θ2), Nki is the number of clonogens for the ith subject, and fk(yki|ψk) is the density corresponding to Fk(yki|ψk), i = 1, …, n, k = 1,2. Chen et al. (2001) used a Weibull density for fk (yki|ψk), so that fk(y|ψk) = ξkyξk−1 exp{λk − yξk exp(λk)}, where ψk = (ξk, λk), k = 1, 2. To construct the likelihood function of the observed data, we integrate (4.14) with respect to (N, w) assuming an Sα(1, 1, 0) density for each wi, denoted by fs (wi|α), where N = (N11, …, N1n, N21, …, N2n) and w = (w1, …, wn). As before we incorporate covariates for the cure rate model (4.12) through the cure rate parameter θ. Let denote the p × 1 vector of covariates for the ith subject and let βk = (βk1, βk2, …, βkp)′ denote the corresponding vector of regression coefficients for failure time random variable Yk, k = 1, 2. We relate θ to the covariates by , so that the cure rate for subject i is for i = 1, 2, …, n and k = 1, 2. Letting , Chen et al. (2001) showed that the observed data likelihood of (β, ψ, α) can be written as
| (4.15) |
where 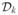 consists of those patients who failed according to Yk, k = 1, 2, Dobs = (n, y1, y2, X, ν1, ν2), X is the n × p matrix of covariates, fk (yki|ψk) is Weibull, and
.
consists of those patients who failed according to Yk, k = 1, 2, Dobs = (n, y1, y2, X, ν1, ν2), X is the n × p matrix of covariates, fk (yki|ψk) is Weibull, and
.
Chen et al. (2001) considered a joint improper prior for (β, ψ, α) = (β1, β2, ψ1, ψ2, α) of the form
where I (0 < α < 1) = 1 if 0 < α < 1, and 0 otherwise. This prior implies that β, ψ, and α are independent a priori, (β1, β2) are independent a priori with an improper uniform prior, α has a proper uniform prior over the interval (0, 1), and (ψ1, ψ2) are independent and identically distributed as π(ψk) a priori. Chen et al. (2001) assumed that π(ξk, λk) = π(ξk|ν0, τ0)π(λk), where
and δ0, τ0, and c0 are specified hyperparameters. Chen et al. (2001) and Ibrahim et al. (2001a) gave a detailed discussion of the computational implementation of this model.
Detailed real data examples for the models discussed in Sections 4.1–4.3 can be found in Ibrahim et al. (2001a). The Gibbs sampler was used to obtained posterior estimates for all models discussed in this section. Details of the Gibbs sampling algorithms and covergence diagnostics can be found in Ibrahim et al. (2001).
5. FUTURE RESEARCH
Future areas of research include expanding the Bayesian model to include covariates in θ as well as F (t). Although not investigated here, this appears to be a natural extension of the Bayesian model presented in Section 4. A more general regression model is currently being investigated. The results reported in Section 3 from the frequentist perspective also encourage this research effort.
The class of models given by expression (1.8) in Section 1 opens a new avenue in parametric (and probably semiparametric; see Section 3) survival regression. For example, by incorporating a predictor into the parameter i we obtain a proportional hazards (PH) model. The quantity i is unobservable, but it is reasonable to assume that i is proportional to the observable tumor volume. If one predictor is incorporated into the parameter i whereas another covariate (e.g., fractional radiation dose) is incorporated into some other parameter(s) of the model, the resulting regression counterpart of (1.8) will no longer be the PH model. From a statistical viewpoint the main advantage of this generalization of the clonal model of tumor recurrence is that it can suggest the structure of new regression models to be further explored by statistical methods. Such models may provide a useful means of searching for better regimens for fractionated radiotherapy.
Another promising idea is to explore possible links between stochastic models proposed for the natural history of cancer and for posttreatment cancer survival; this approach can enrich statistical inference by supplementing the analysis of patients’ survival with additional epidemiological data on cancer detection. We believe that this idea may dramatically change the whole concept of modern parametric survival analysis, by invoking mechanistically motivated models for the joint distribution of covariates at the time of diagnosis.
Methods for model diagnostics especially designed for the semiparametric models in Section 3 remain a very important issue for future methodological research. The same is equally true for the regression counterparts of the two-component mixture model. Justification of asymptotic properties of the estimate represent a serious challenge.
6. SOFTWARE AND DATA ANALYSIS FOR CURE RATE MODELS
Prototype software implementing the estimation procedures of Section 3.2 was programmed in Delphi 6.0 for Windows 95/98/2000/XP, an object-oriented visual development environment based on the Pascal programming language by INPRISE™. This software is available on request from Alex Tsodikov. Implementation of these methods in high-level languages such as R, S, or SAS appears straightforward. In addition, Extensive BUGS software is available for the cure rate and other related models given in the book by Ibrahim et al. (2001a). This software can be easily downloaded from the book’s Web site at http://www.merlot.uconn.edu/mhchen/survbook. BUGS code for several models and datasets is available from this Web site.
In the semiparametric context a cure model can be regarded as a convenient reparameterization of its counterpart in the noncure form [compare the traditional form of the PH model G = F̄θ with its cure form (3.1)]. A display of the Kaplan–Meier estimator for the data may indicate a noncure situation if the curves go to 0 at the end of follow-up. Fitting a cure form model to such data may result in numerical instability as the parameter coding the cure rate would be approaching the border of the parametric space.
Departures from proportionality and an indication for the extended hazard models can be explored using an empirical display of the function F (2.4) or its more sophisticated versions as discussed in Section 2. Similar techniques for model exploration is available for two-component mixture models (Tsodikov 2002). More work is needed to create a toolbox of methods for model building, choice and diagnostics.
7. BIBLIOGRAPHICAL NOTES
Over recent years the BCH model has been developed in many different directions. In particular, the literature on parametric inference based on this model is quite voluminous. The usual practice is to use the two-parameter gamma or the Weibull distribution for the function F(t) in formula (1.4). Maximum likelihood inference without covariates has been discussed in the context of right-censored data under continuous follow-up (Asselain, Fourquet, Hoang, Myasnikova, and Yakovlev 1994;Hoang, Tsodikov, Yakovlev, and Asselain 1995; Yakovlev 1996; Yakovlev and Tsodikov 1996); discrete surveillance design (Tsodikov, Asselain, Fourquet, Hoang, and Yakovlev 1995), and doubly censored data (Kruglikov, Pilipenko, Tsodikov, and Yakovlev 1997). A version of the Hjort goodness-of-fit test for the model (1.4) with F (t) represented by the gamma distribution was described in Gregori et al. (2002). Tsodikov (1998a) studied the asymptotic efficiency of cure rate estimation. Some limiting distributions associated with model (4.1) and their bivariate counterparts were described in the articles by Klebanov, Rachev, and Yakovlev (1993a) and Rachev, Wu, and Yakovlev (1995); the authors also provided estimates of the convergence rates. Parametric and semiparametric regression models allowing for dissimilar effects of covariates on the probability of cure and the timing of the event of interest were extensively explored in several publications (Asselain, Fourquet, Hoang, Tsodikov, and Yakovlev 1996; Tsodikov et al. 1998b; Myasnikova, Asselain, and Yakovlev 2000; Tsodikov 2002). An improper proportional hazards model was studied by Tsodikov (1998a,b) and Chen and Ibrahim (2001). Time-dependent risk factors for the cure probability were introduced in Tsodikov et al. (1997, 1998b) and Tsodikov and Müller (1998). Two-sample score tests for long-term and short-term effects on survival were proposed by Broët et al. (2001). Statistical inference from the Bayesian prospective was discussed by Klebanov, Rachev, and Yakovlev (1993b), Chen et al. (1999, 2001), Ibrahim and Chen (2000), Ibrahim et al. (2001a,b), and Chen, Ibrahim, and Lipsitz, (2002). Ibrahim et al. (2001a) devoted an entire chapter (chap. 5) to the cure rate model and its applications in their book. Moreover, recent books discussing Gibbs sampling for this model and related models are also given in Ibrahim et al. (2001a) and Chen, Shao, and Ibrahim (2000). The model has successfully been applied to various datasets on cancer survival (Yakovlev et al. 1993; Asselain et al. 1994, 1996; Yakovlev 1996; Yakovlev and Tsodikov 1996; Tsodikov et al. 1995, 1997; Tsodikov 1998a, Tsodikov et al. 1998b; Chen et al. 1999; Yakovlev et al. 1999; Myasnikova et al. 2000; Trelford, Tsodikov, and Yakovlev 2001; Tsodikov 2001, 2002; Tsodikov, Dicello, Zaider, Zorin, and Yakovlev 2001; Zaider et al. 2001; Zorin, Tsodikov, Zharinov, and Yakovlev 2001).
Acknowledgments
The authors wish to thank the editor, the associate editor, and three referees for several suggestions and editorial changes which have greatly improved the paper. The research of A. Tsodikov and A. Yakovlev was supported by NIA/NIH grant 1 RO1 AG14650-01A2, NCI/NIH 1U01 CA88177-01, CA97414-01, and DAMD 17-03-1-0034. Dr. Ibrahim’s research was partially supported by NCI/NIH CA 70101, CA 74015, and CA 23318.
Contributor Information
A. D. Tsodikov, Email: atsodikov@ucdavis.edu, University of California, Davis, CA 95616.
J. G. Ibrahim, Email: ibrahim@bios.unc.edu, Department of Biostatistics, University of North Carolina, McGavran-Greenberg Hall, Chapel Hill, NC 27599.
A. Y. Yakovlev, Email: andrei-yakovlev@urmc.rochester.edu, Department of Statistics and Computational Biology, University of Rochester, 601 Elmwood Avenue, Box 630, Rochester, NY 14642.
References
- Andersen PK, Borgan Ø, Gill RD, Keiding N. Statistical Models Based on Counting Processes. New York: Springer-Verlag; 1992. [Google Scholar]
- Asselain B, Fourquet A, Hoang T, Myasnikova C, Yakovlev AYu. Testing the Independence of Competing Risks: An Application to the Analysis of Breast Cancer Recurrence. Biometrical Journal. 1994;36:465–473. [Google Scholar]
- Asselain B, Fourquet A, Hoang T, Tsodikov A, Yakovlev AYu. A Parametric Regression Model of Tumor Recurrence: An Application to the Analysis of Clinical Data on Breast Cancer. Statistics & Probbability Letters. 1996;29:271–278. [Google Scholar]
- Bartoszyński R, Edler L, Hanin L, Kopp-Schneider A, Pavlova L, Tsodikov A, Zorin A, Yakovlev A. Modeling Cancer Detection: Tumor Size as a Source of Information on Unobservable Stages of Carcinogenesis. Mathematical Biosciences. 2001;171:113–142. doi: 10.1016/s0025-5564(01)00058-x. [DOI] [PubMed] [Google Scholar]
- Bentzen SM, Johansen LV, Overgaard J, Thames HD. Clinical Radiobiology of Squamous Cell Carcinoma of the Oropharynx. International Journal Radiation Oncology–Biology–Physics. 1991;20:1197–1206. doi: 10.1016/0360-3016(91)90228-v. [DOI] [PubMed] [Google Scholar]
- Berkson J, Gage RP. Survival Curves for Cancer Patients Following Treatment. Journal of the American Statistical Association. 1952;47:501–515. [Google Scholar]
- Boag JM. Maximum Likelihood Estimates of the Proportion of Patients Cured by Cancer Therapy. Journal of the Royal Statistical Society, Ser B. 1949;11:15–44. [Google Scholar]
- Broët P, Rycke YD, Tubert-Bitter P, Lellouch J, Asselain B, Moreau T. A Semiparametric Approach for the Two-Sample Comparison of Survival Times With Long-Term Survivors. Biometrics. 2001;57:844–852. doi: 10.1111/j.0006-341x.2001.00844.x. [DOI] [PubMed] [Google Scholar]
- Cantor AB. Cure Rate Estimation Using the Polynomial Gompertz Model. The Communication of Statitistics: Exchange and Dissemination; 1997; Spring Meeting of the International Biometric Society, Eastern North American Region, Abstracts; 1997. p. 144. [Google Scholar]
- Cantor AB. Projecting the Standard Error of the Kaplan–Meier Estimator. Statistics in Medicine. 2001;20:2091–2097. doi: 10.1002/sim.856. [DOI] [PubMed] [Google Scholar]
- Cantor AB, Shuster JJ. Parametric Versus Nonparametric Methods for Estimating Cure Rates Based on Censored Survival Data. Statistics in Medicine. 1992;11:931–937. doi: 10.1002/sim.4780110710. [DOI] [PubMed] [Google Scholar]
- Chappell R, Nondahl DM, Fowler JF. Modeling Dose and Local Control in Radiotherapy. Journal of the American Statistical Association. 1995;90:829–838. [Google Scholar]
- Chen MH, Harrington DP, Ibrahim JG. Bayesian Cure Rate Models for Malignant Melanoma: A Case Study of ECOG Trial E1690. Applied Statistics. 2002a;51:135–150. [Google Scholar]
- Chen MH, Ibrahim JG. Maximum Likelihood Methods for Cure Rate Models With Missing Covariates. Biometrics. 2001;57:43–52. doi: 10.1111/j.0006-341x.2001.00043.x. [DOI] [PubMed] [Google Scholar]
- Chen MH, Ibrahim JG, Lipsitz SR. Bayesian Methods for Missing Covariates in Cure Rate Models. Lifetime Data Analysis. 2002b;8:117–146. doi: 10.1023/a:1014835522957. [DOI] [PubMed] [Google Scholar]
- Chen MH, Ibrahim JG, Sinha D. A New Bayesian Model for Survival Data With a Surviving Fraction. Journal of the American Statistical Association. 1999;94:909–919. [Google Scholar]
- Chen MH, Ibrahim JG, Sinha D. Bayesian Inference for Multivariate Survival Data With a Surviving Fraction. Journal of Multivariate Analysis. 2002c;80:101–126. [Google Scholar]
- Chen MH, Shao QM, Ibrahim JG. Monte Carlo Methods in Bayesian Computation. New York: Springer-Verlag; 2000. [Google Scholar]
- Cheng S, Wei L, Ying Z. Analysis of Transformation Models With Censored Data. Biometrika. 1995;82:835–845. [Google Scholar]
- Clayton DG. A Model for Association in Bivariate Life Tables and Its Application in Epidemiological Studies in Familial Tendency in Chronic Disease Incidence. Biometrika. 1978;65:141–151. [Google Scholar]
- Cox DR. Regression Models and Life Tables (with discussion) Journal of the Royal Statistical Society, Ser B. 1972;34:187–220. [Google Scholar]
- Dempster A, Laird N, Rubin D. Maximum Likelihood From Incomplete Data via the EM Algorithm. Journal of the Royal Statistical Society, Ser B. 1977;39:1–38. [Google Scholar]
- Etezadi-Amoli L, Ciampi A. Extended Hazard Regression for Censored Survival Data With Covariates: A Spline Approximation for the Baseline Hazard Function. Biometrics. 1987;43:181–192. [Google Scholar]
- Farewell VT. The Use of Mixture Models for the Analysis of Survival Data With Long-Term Survivors. Biometrics. 1982;38:1041–1046. [PubMed] [Google Scholar]
- Feller W. An Introduction to Probability Theory and Its Applications. Vol. 2. New York: Wiley; 1971. [Google Scholar]
- Fleming T, Lin D. Survival Analysis in Clinical Trials: Past Developments and Future Directions. Biometrics. 2000;56:971–983. doi: 10.1111/j.0006-341x.2000.0971.x. [DOI] [PubMed] [Google Scholar]
- Gamel JW, McLean IW, Rosenberg SH. Proportion Cured and Mean Log Survival Time as Functions of Tumour Size. Statistics in Medicine. 1990;9:999–1006. doi: 10.1002/sim.4780090814. [DOI] [PubMed] [Google Scholar]
- Gamel JW, Meyer JS, Feuer E, Miller BA. The Impact of Stage and Histology on the Long-Term Clinical Course of 163,808 Patients With Breast Carcinoma. Cancer. 1996;77:1459–1469. doi: 10.1002/(SICI)1097-0142(19960415)77:8<1459::AID-CNCR6>3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
- Gamel JW, Vogel RL. A Model of Long-Term Survival Following Adjuvant Therapy for Stage 2 Breast Cancer. British Journal of Cancer. 1993;68:1167–1170. doi: 10.1038/bjc.1993.498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gamel JW, Vogel RL, McLean IW. Assessing the Impact of Adjuvant Therapy on Cure Rate for Stage 2 Breast Carcinoma. British Journal of Cancer. 1993;68:115–118. doi: 10.1038/bjc.1993.296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gamel JW, Vogel RL, Valagussa P, Bonadonna G. Parametric Survival Analysis of Adjuvant Therapy for Stage II Breast Cancer. Cancer. 1994;74:2483–2490. doi: 10.1002/1097-0142(19941101)74:9<2483::aid-cncr2820740915>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Goldman AI. Survivorship Analysis When Cure Is a Possibility: A Monte-Carlo Study. Statistics in Medicine. 1984;3:153–163. doi: 10.1002/sim.4780030208. [DOI] [PubMed] [Google Scholar]
- Goldman AI, Hillman DW. Exemplary Data: Sample Size and Power in the Design of Event-Time Clinical Trials. Controlled Clinical Trials. 1992;13:256–271. doi: 10.1016/0197-2456(92)90010-w. [DOI] [PubMed] [Google Scholar]
- Gordon NH. Application of the Theory of Finite Mixtures for the Estimation of ‘Cure’ Rates of Treated Cancer Patients. Statistics in Medicine. 1990;9:397–407. doi: 10.1002/sim.4780090411. [DOI] [PubMed] [Google Scholar]
- Greenhouse JB, Wolfe RA. A Competing Risk Derivation of a Mixture Model for the Analysis of Survival Data. Communications in Statistics—Theory and Methods. 1984;25:3133–3154. [Google Scholar]
- Gregori G, Hanin L, Luebeck G, Moolgavkar S, Yakovlev A. Testing Goodness of Fit With Stochastic Models of Carcinogenesis. Mathematical Biosciences. 2002;175:13–29. doi: 10.1016/s0025-5564(01)00088-8. [DOI] [PubMed] [Google Scholar]
- Hanin LG. Iterated Birth and Death Process as a Model of Radiation Cell Survival. Mathematical Biosciences. 2001;169:89–107. doi: 10.1016/s0025-5564(00)00054-7. [DOI] [PubMed] [Google Scholar]
- Hanin LG, Zaider M, Yakovlev AY. Distribution of the Number of Clonogens Surviving Fractionated Radiotherapy: A Long-Standing Problem Revisited. International Journal of Radiation Biology. 2001;77:205–213. doi: 10.1080/09553000010007703. [DOI] [PubMed] [Google Scholar]
- Haybittle JL. The Estimation of the Proportion of Patients Cured After Treatment for Cancer of the Breast. British Journal of Radiology. 1959;32:725–733. doi: 10.1259/0007-1285-32-383-725. [DOI] [PubMed] [Google Scholar]
- Haybittle JL. A Two-Parameter Model for the Survival Curve of Treated Cancer Patients. Journal of the American Statistical Association. 1965;60:16–26. [Google Scholar]
- Hjort N. Goodness of Fit Tests in Models for Life History Based on Cumulative Hazard Rates. The Annals of Statistics. 1990;18:1221–1258. [Google Scholar]
- Hoang T, Tsodikov A, Yakovlev AYu, Asselain B. Modeling Breast Cancer Recurrence. In: Arino O, Axelrod D, Kimmel M, editors. Mathematical Population Dynamics: Analysis of Heterogeneity. Vol. 2. Winnipeg: Wuerz Publications; 1995. pp. 283–296. [Google Scholar]
- Hougaard P. A Class of Multivariate Failure Time Distributions. Biometrika. 1986;73:671–678. [Google Scholar]
- Ibrahim JG, Chen MH. Power Prior Distributions for Regression Models. Statistical Science. 2000;15:46–60. [Google Scholar]
- Ibrahim JG, Chen MH, Sinha D. Bayesian Survival Analysis. New York: Springer-Verlag; 2001a. [Google Scholar]
- Ibrahim JG, Chen MH, Sinha D. Bayesian Semi-Parametric Models for Survival Data With a Cure Fraction. Biometrics. 2001b;57:383–388. doi: 10.1111/j.0006-341x.2001.00383.x. [DOI] [PubMed] [Google Scholar]
- Kalbfleisch JD, Prentice RL. The Statistical Analysis of Failure Time Data. New York: Wiley; 1980. [Google Scholar]
- Klebanov LB, Rachev ST, Yakovlev AYu. A Stochastic Model of Radiation Carcinogenesis: Latent Time Distributions and Their Properties. Mathematical Biosciences. 1993a;113:51–75. doi: 10.1016/0025-5564(93)90008-x. [DOI] [PubMed] [Google Scholar]
- Klebanov LB, Rachev ST, Yakovlev AYu. On the Parametric Estimation of Survival Functions. Statistics & Decisions. 1993b;3:83–102. [Google Scholar]
- Klein J. Semiparametric Estimation of Random Effects Using the Cox Model Based on the EM Algorithm. Biometrics. 1992;48:795–806. [PubMed] [Google Scholar]
- Kruglikov IL, Pilipenko NI, Tsodikov AD, Yakovlev AY. Assessing Risk With Doubly Censored Data: An Application to the Analysis of Radiation-Induced Thyropathy. Statistics & Probability Letters. 1997;32:223–230. [Google Scholar]
- Kuk AYC, Chen C-H. A Mixture Model Combining Logistic Regression With Proportional Hazards Regression. Biometrika. 1992;79:531–541. [Google Scholar]
- Lange K, Hunter DR, Yang I. Optimization Transfer Using Surrogate Objective Functions (with discussion) Journal of Computational and Graphical Statistics. 2000;9:1–59. [Google Scholar]
- Laska EM, Meisner MJ. Nonparametric Estimation and Testing in a Cure Model. Biometrics. 1992;48:1223–1234. [PubMed] [Google Scholar]
- Maller RA, Zhou S. Estimating the Proportion of Immunes in a Censored Sample. Biometrika. 1992;79:731–739. [Google Scholar]
- Maller RA, Zhou S. Testing for Sufficient Follow-up and Outliers in Survival Data. Journal of the American Statistical Association. 1994;89:1499–1506. [Google Scholar]
- Maller RA, Zhou S. Testing for the Presence of Immune or Cured Individuals in Censored Survival Data. Biometrics. 1995;51:1197–1205. [PubMed] [Google Scholar]
- Maller RA, Zhou S. Survival Analysis With Long-Term Survivors. Chichester, U.K: Wiley; 1996. [Google Scholar]
- Miller RG. Survival Analysis. New York: Wiley; 1981. [Google Scholar]
- Murphy S. On Profile Likelihood. Journal of the American Statistical Association. 2000;95:449–485. [Google Scholar]
- Myasnikova EM, Asselain B, Yakovlev AYu. Spline-Based Estimation of Cure Rates: An Application to the Analysis of Breast Cancer Data. Mathematical and Computer Modelling. 2000;32:217–228. [Google Scholar]
- Nielsen G, Gill R, Andersen P, Sørensen T. A Counting Process Approach to Maximum Likelihood Estimation in Frailty Models. Scandinavian Journal of Statistics. 1992;19:25–43. [Google Scholar]
- Oakes D. Bivariate Survival Models Induced by Frailties. Journal of the American Statistical Association. 1989;84:487–493. [Google Scholar]
- Peng Y, Dear KBG. A Nonparametric Mixture Model for Cure Rate Estimation. Biometrics. 2000;56:237–243. doi: 10.1111/j.0006-341x.2000.00237.x. [DOI] [PubMed] [Google Scholar]
- Pepe MS, Fleming TR. Weighted Kaplan–Meier Statistics: A Class of Distance Tests for Censored Survival Data. Biometrics. 1989;45:497–507. [PubMed] [Google Scholar]
- Press W, Flannery B, Teukolsky S, Vetterling W. Numerical Recipes in Pascal: The Art of Scientific Computing. New York: Cambridge University Press; 1994. [Google Scholar]
- Rachev ST, Wu C, Yakovlev AY. A Bivariate Limiting Distribution of Tumor Latency Time. Mathematical Biosciences. 1995;127:127–147. doi: 10.1016/0025-5564(94)00043-y. [DOI] [PubMed] [Google Scholar]
- Sposto R, Sather HN, Baker SA. A Comparison of Tests of the Difference in the Proportion of Patients Who Are Cured. Biometrics. 1992;48:87–99. [PubMed] [Google Scholar]
- Sy JP, Taylor JMG. Estimation in a Cox Proportional Hazards Cure Model. Biometrics. 2000;56:227–236. doi: 10.1111/j.0006-341x.2000.00227.x. [DOI] [PubMed] [Google Scholar]
- Sy JP, Taylor JMG. Standard Errors for the Cox Proportional Hazards Cure Model. Mathematical and Computer Modelling. 2001;33:1237–1252. [Google Scholar]
- Taylor JMG. Semi-Parametric Estimation in Failure Time Mixture Models. Biometrics. 1995;51:899–907. [PubMed] [Google Scholar]
- Trelford J, Tsodikov AD, Yakovlev AY. Modeling Post-Treatment Development of Cervical Carcinoma: Exophytic or Endophytic—Does It Matter? Mathematical and Computer Modelling. 2001;33:1439–1443. [Google Scholar]
- Tsodikov A. A Proportional Hazards Model Taking Account of Long-Term Survivors. Biometrics. 1998a;54:1508–1516. [PubMed] [Google Scholar]
- Tsodikov A. Asymptotic Efficiency of a Proportional Hazards Model With Cure. Statistics & Probability Letters. 1998b;39:237–244. 1998. [Google Scholar]
- Tsodikov A. Estimation of Survival Based on Proportional Hazards When Cure Is a Possibility. Mathematical and Computer Modelling. 2001;33:1227–1236. [Google Scholar]
- Tsodikov A. Semiparametric Models of Long- and Short-Term Survival: An Application to the Analysis of Breast Cancer Survival in Utah by Age and Stage. Statistics in Medicine. 2002;21:895–920. doi: 10.1002/sim.1054. [DOI] [PubMed] [Google Scholar]
- Tsodikov A. Semiparametric Models: A Generalized Self-Consistency Approach. submitted to. Journal of the Royal Statistical Society, Ser B. 2003;65:759–774. doi: 10.1111/1467-9868.00414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsodikov AD, Asselain B, Fourquet A, Hoang T, Yakovlev AYu. Discrete Strategies of Cancer Post-Treatment Surveillance: Estimation and Optimization Problems. Biometrics. 1995;51:437–447. [PubMed] [Google Scholar]
- Tsodikov A, Dicello J, Zaider M, Zorin A, Yakovlev A. Analysis of a Hormesis Effect in the Leukemia Caused Mortality Among Atomic Bomb Survivors. Human and Ecological Risk Assessment. 2001;7:829–847. [Google Scholar]
- Tsodikov AD, Hasenclever D, Loeffler M. Regression With Bounded Outcome Score: Evaluation of Power by Bootstrap and Simulation in a Chronic Myelogenous Leukaemia Clinical Trial. Statistics in Medicine. 1998a;17:1909–1922. doi: 10.1002/(sici)1097-0258(19980915)17:17<1909::aid-sim890>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- Tsodikov A, Loeffler M, Yakovlev AYu. Assessing the Risk of Secondary Leukemia in Patients Treated for Hodgkin’s Disease. A Report From the International Database on Hodgkin’s Disease. Journal of Biological Systems. 1997;5:433–444. [Google Scholar]
- Tsodikov A, Loeffler M, Yakovlev AYu. A Cure Model With Time-Changing Risk Factor: An Application to the Analysis of Secondary Leukemia. A Report From the International Database on Hodgkin’s Disease. Statistics in Medicine. 1998b;17:27–40. doi: 10.1002/(sici)1097-0258(19980115)17:1<27::aid-sim720>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
- Tsodikov AD, Müller W. Modeling Carcinogenesis Under a Time-Changing Exposure. Mathematical Biosciences. 1998;152:179–191. doi: 10.1016/s0025-5564(98)10030-5. [DOI] [PubMed] [Google Scholar]
- Tucker SL. Modeling the Probability of Tumor Cure After Fractionated Radiotherapy. In: Horn MA, Simonett G, Webb G, editors. Mathematical Models in Medical and Health Sciences. Nashville: Vanderbilt University Press; 1999. pp. 1–15. [Google Scholar]
- Tucker SL, Taylor JMG. Improved Models of Tumour Cure. International Journal of Radiation Biology. 1996;70:539–553. doi: 10.1080/095530096144743. [DOI] [PubMed] [Google Scholar]
- Tucker SL, Thames HD, Taylor JMG. How Well Is the Probability of Tumor Cure After Fractionated Irradiation Described by Poisson Statistics? Radiation Research. 1990;124:273–282. [PubMed] [Google Scholar]
- Wassel JT, Moeschberger ML. A Bivariate Survival Model With Modified Gamma Frailty for Assessing the Impact of Interventions. Statistics in Medicine. 1993;12:241–248. doi: 10.1002/sim.4780120308. [DOI] [PubMed] [Google Scholar]
- Yakovlev AYu. Letter to the Editor. Statistics in Medicine. 1994;13:983–986. doi: 10.1002/sim.4780130908. [DOI] [PubMed] [Google Scholar]
- Yakovlev AYu. Threshold Models of Tumor Recurrence. Mathematical and Computer Modelling. 1996;23:153–164. [Google Scholar]
- Yakovlev AY, Asselain B, Bardou VJ, Fourquet A, Hoang T, Rochefordiere A, Tsodikov AD. A Simple Stochastic Model of Tumor Recurrence and Its Application to Data on Premenopausal Breast Cancer. In: Asselain B, Boniface M, Duby C, Lopez C, Masson JP, Tranchefort J, editors. Biometrie et Analyse de Donnees Spatio-Temporelles. Vol. 12. Rennes, France: Société Française de Biométrie; 1993. pp. 66–82. [Google Scholar]
- Yakovlev AYu, Tsodikov AD. Stochastic Models of Tumor Latency and Their Biostatistical Applications. Singapore: World Scientific; 1996. [Google Scholar]
- Yakovlev AY, Tsodikov AD, Boucher K, Kerber R. The Shape of the Hazard Function in Breast Carcinoma: Curability of the Disease Revisited. Cancer. 1999;85:1789–1798. [PubMed] [Google Scholar]
- Yamaguchi K. Accelerated Failure-Time Regression Model With a Regression Model of Surviving Fraction: An Analysis of Permanent Employment in Japan. Journal of the American Statistical Association. 1992;87:284–292. [Google Scholar]
- Zaider M, Zelefsky MJ, Hanin LG, Tsodikov AD, Yakovlev AY, Leibel SA. A Survival Model for Fractionated Radiotherapy With an Application to Prostate Cancer. Physics in Medicine and Biology. 2001;46:2745–2758. doi: 10.1088/0031-9155/46/10/315. [DOI] [PubMed] [Google Scholar]
- Zorin AV, Tsodikov AD, Zharinov GM, Yakovlev AY. The Shape of the Hazard Function in Cancer of the Cervix Uteri. Journal of Biological Systems. 2001;9:221–233. [Google Scholar]