The Path-of-Probability Algorithm for Steering and Feedback Control of Flexible Needles

Abstract

In this paper we develop a new framework for path planning of flexible needles with bevel tips. Based on a stochastic model of needle steering, the probability density function for the needle tip pose is approximated as a Gaussian. The means and covariances are estimated using an error propagation algorithm which has second order accuracy. Then we adapt the path-of-probability (POP) algorithm to path planning of flexible needles with bevel tips. We demonstrate how our planning algorithm can be used for feedback control of flexible needles. We also derive a closed-form solution for the port placement problem for finding good insertion locations for flexible needles in the case when there are no obstacles. Furthermore, we propose a new method using reference splines with the POP algorithm to solve the path planning problem for flexible needles in more general cases that include obstacles.

1 Introduction

Flexible needles with bevel tips, which were designed for minimally invasive medical treatments, approximately follow a circular arc when they are inserted into soft tissue without twisting [33]. Based on this physical phenomenon, we can steer a flexible needle; a flexible needle is rotated with the angular speed ω(t) around its tangent while it is inserted with translational speed υ(t) in the tangential direction. These inputs, ω(t) and υ(t), can generate various trajectories of a needle. One of the most important tasks related to flexible needles is controlling them to reach the desired tip pose¹. In other words, we aim to obtain ω(t) and υ(t) that generate the needle trajectory hitting the target pose.

We have reported path planning methods for flexible needles in recent years including [21,22,24]. The method is based on the observation that needle trajectories form an ensemble of paths due to uncertainty in the insertion conditions even when we insert the needle repeatedly with the same inputs. In order to capture the statistical behavior of the needle, a stochastic model for the steering of flexible needles with bevel tips has been developed in [22]. The method in [22] adopts the unicycle nonholonomic kinematic model developed in [33], and includes white noise weighted by coloring constants to capture the nondeterministic behavior of the needle insertion. The stochastic model, which is reviewed in detail in Section 2.2, is modified in such a way that allows for closed-form evaluation of probability densities that describe the time evolution of the distribution of needle tip pose. The benefit of the closed-form method is that it enables fast path planning. In order to estimate the parameters that serve as the input to this closed-form probability density, the kinematic covariance propagation method developed in [31] is used. In [21] we used this probability density function (PDF) with the parameter estimation method in [31] for path planning of the needle. Like the work by Mason and Burdick [20], this path planning algorithm is an extension of the path-of-probability (POP) algorithm presented in [12].

In this paper, we improve our existing computational methods, develop new components, and incorporate them for a better path planning method for flexible needles. First we improve the computational accuracy and efficiency in estimation of the covariance of the probability density function. Second we solve the port placement problem to find the optimal starting pose of the flexible needle. Third, we modify the POP algorithm so that it can be used for feedback control, and demonstrate it using simulation of the needle insertion. Finally, we develop a method to use the POP algorithm with splines that can be applied for more general choice of the target pose of the needle in the presence of obstacles.

A number of recent works have been reported on the motion/path planning of steerable flexible needles [2,10,11]. Alterovitz et al. [2] developed a 2D motion planning algorithm for Dubins cars which have only two steering inputs (left/right turn), and then applied it to steerable needles. Considering uncertainty in needle motion, their method finds the optimal steering plan which gives the maximum probability that the needle will reach the desired target. Duindam et al. [11] presented a path planning method for 3D flexible needle steering. They discretize the control space enabling an analytical expression for the needle trajectory and then find a locally optimal trajectory in a 3D environment with obstacles. An inverse kinematics technique has been applied to the planning problem in [10].

There exist some methods for steering nonholonomic systems [18]. Since some of them use the concept of optimal control, those methods are computationally intensive. Furthermore, since the needle system is not small-time locally controllable [22], small changes in the goal pose can lead to large changes in the optimal path. We also note that Brockett’s theorem says that some nonholonomic systems can not be stabilized to a desired pose using a continuous feedback law [3]. The POP algorithm used for needle path planning in this paper has the following benefits when compared to existing methods based on optimal path following or optimal control: (1) At each time step we can make a choice about what control input to use, independent of the previous step, which means that this control is discontinuous and the limitations imposed by Brockett’s theorem do not apply; (2) The path that we generate is not the path of minimal length, or optimal, and so the solution is not as sensitive to small changes in the desired position as methods based on optimal control. Of course, this means that our paths may be slightly longer, but we believe that they are also more robust to perturbations.

Throughout this paper, a relatively heavy derivation of equations is performed for faster path planning. In this paper, we use the path-of-probability algorithm as a feedback control scheme. Therefore, it is important to compute each intermediate insertion plan without a significant time lag for planning. For fast computation, we use covariance propagation and the closed-form covariance matrix formula. The use of splines also enables the fast computation of baseline trajectories for needle path planning. We verify with simulations that the equations derived in this paper are useful for both path planning and feedback control of flexible needles.

2 Mathematical Methods

2.1 Review of Rigid-Body Motions

The special orthogonal group, SO(3), is the space of rotation matrices contained in ℝ^3×3, together with the operator of matrix multiplication. Any element of SO(3) can be written using the ZXZ Euler angles α, β and γ as [7]

$$R=R_z(\alpha )R_x(\beta )R_z(\gamma ),$$

where 0 ≤ α ≤ 2π, 0 ≤ β ≤ π, and 0 ≤ γ ≤ 2π and

$$R_x(\theta )=\left(\begin{array}{ccc}1& 0& 0\\ 0& cos\theta & -sin\theta \\ 0& sin\theta & cos\theta \end{array}\right),R_z(\theta )=\left(\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right).$$

The Euclidean motion group, SE(3), represents rigid-body motions in 3D space. It is the semi-direct product of ℝ³ with SO(3). The elements of SE(3) can be written as [7]

$$g=\left(\begin{array}{cc}R& \mathbf{t}\\ {\mathbf{0}}^T& 1\end{array}\right),$$ (1)

where R ∈ SO(3), t ∈ ℝ³ and 0^T denotes the transpose of the 3D zero vector.

Given a time-dependent rigid-body motion g(t), the quantity

$$g^{-1}\stackrel{.}{g}=\left(\begin{array}{cc}{R}^T\stackrel{.}{R}& R^T\stackrel{.}{\mathbf{t}}\\ {\mathbf{0}}^T& 0\end{array}\right)\in se(3)$$ (2)

(where a dot represents the time derivative) is a spatial velocity as seen in the body-fixed frame, where se(3) is the Lie algebra associated with SE(3). We identify se(3) with ℝ⁶ in the usual way via the mappings ^∨: se(3) → ℝ⁶ and ^∧: ℝ⁶ → se(3), given by

$$\xi ={(g^{-1}\stackrel{.}{g})}^{\vee }=\left(\begin{array}{c}{(R^T\stackrel{.}{R})}^{\vee }\\ R^T\stackrel{.}{\mathbf{t}}\end{array}\right)=\left(\begin{array}{c}\mathit{\omega }\\ \mathbf{v}\end{array}\right)\in {\mathbb{R}}^6$$

and

$$\widehat{\xi }=\widehat{\left(\begin{array}{c}\mathit{\omega }\\ \mathbf{v}\end{array}\right)}=\left(\begin{array}{cc}\widehat{\mathit{\omega }}& \mathbf{v}\\ {\mathbf{0}}^T& 0\end{array}\right)\in se(3).$$

The mappings ^∨: so(3) → ℝ³ and ^∧: ℝ³ → so(3) are given by

$$\widehat{\mathit{\omega }}=\widehat{\left(\begin{array}{c}{\omega }_1\\ {\omega }_2\\ {\omega }_3\end{array}\right)}=\left(\begin{array}{ccc}0& -{\omega }_3& {\omega }_2\\ {\omega }_3& 0& -{\omega }_1\\ -{\omega }_2& {\omega }_1& 0\end{array}\right)\text{and}{\widehat{\mathit{\omega }}}^{\vee }=\mathit{\omega }.$$

The vector ξ contains both the angular and translational velocity of the motion g(t) as seen in the body-fixed frame of reference.

Let e_i, i = 1, …, 6 denote the standard basis for ℝ⁶. The basis given by a set of matrices E_i = ê_i, i = 1, …, 6 produce elements of SE(3), when linearly combined and exponentiated. Specifically we have [7]

$$\begin{array}{c}{E}_1=\left(\begin{array}{rrrr}\hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);E_2=\left(\begin{array}{rrrr}\hfill 0& \hfill 0& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);E_3=\left(\begin{array}{rrrr}\hfill 0& \hfill -1& \hfill 0& \hfill 0\\ \hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);\\ E_4=\left(\begin{array}{rrrr}\hfill 0& \hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);E_5=\left(\begin{array}{rrrr}\hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right);E_6=\left(\begin{array}{rrrr}\hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right).\end{array}$$

The element of SE(3) can be obtained by the exponential mapping as [7,24]

$$g=g(x_1,x_2,\dots ,x_6)=exp\left(\sum _{i=1}^6{x}_i{E}_i\right).$$

Therefore the vector x = (x₁ x₂ ··· x₆)^T can be obtained from g ∈ SE(3) by

$$\mathbf{x}={(logg)}^{\vee }.$$

If X ∈ se(3) is an arbitrary element of the form

$$X=\left(\begin{array}{cc}\mathrm{\Omega }& \mathbf{v}\\ {\mathbf{0}}^T& 0\end{array}\right),\text{and}\mathbf{x}={(X)}^{\vee }=\left(\begin{array}{c}\mathit{\omega }\\ \mathbf{v}\end{array}\right),$$

then Ad_g (the adjoint) is defined by the expression

$${(gX{g}^{-1})}^{\vee }={Ad}_g\mathbf{x},\text{where}{Ad}_g=\left(\begin{array}{cc}R& 0\\ TR& R\end{array}\right).$$ (3)

The matrix T is skew-symmetric, and T^∨ = t, when g ∈ SE(3) is given as in (1).

2.2 Nonholonomic Stochastic Needle Model

In a reference frame attached to the needle tip with the local z axis denoting the tangent to the “backbone curve” of the needle, and x denoting the axis orthogonal to the direction of infinitesimal motion induced by the bevel (i.e., the needle bends in the y − z plane), the nonholonomic kinematic model for the evolution of the frame at the needle tip was developed in [33] as:

$$\xi ={(g^{-1}\stackrel{.}{g})}^{\vee }={\left[\begin{array}{cccccc}\kappa & 0& \omega (t)& 0& 0& v(t)\end{array}\right]}^T,$$ (4)

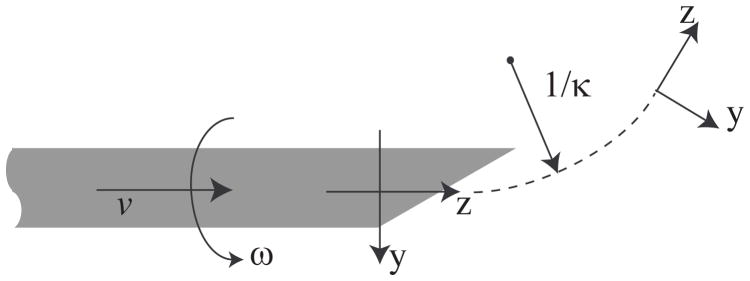
where κ is the curvature of the needle trajectory. The frames, parameters and inputs for the needle are shown in Fig. 1.

Figure 1.

The definition of parameters and frames in the nonholonomic needle model [22,33].

It is useful to note that the needle model (4) is a reachable system [22] and two inputs can control the needle. Inspired by the fact that there may be control errors, we can add uncertainty in the control inputs. This can be simply implemented by adding white noise to the inputs. This addition of white noise in the formulation simultaneously enables us to search the reachable work space with probability, and consider the possible uncertainty that occurs in the actual needle insertion.

In order to reduce the complexity of the model inputs, we set the constant insertion speed as υ(t) = υ₀ ≥ 0. Therefore, the needle is inserted with the constant speed υ₀ ≥ 0 and is rotated with the angular velocity ω(t) simultaneously. The path planning problem, which is the main goal of this paper, is to determine ω(t) so that the needle trajectory reaches the desired pose (position and orientation).

If everything were certain, and if this model were exact, then g(t) could be obtained by simply integrating the ordinary differential equation in (4). However, when we insert the needle repeatedly, we will get trajectories that are sightly different from each other due to uncertainty in the needle insertion system.

One simple way to capture the stochastic phenomenon is to add a noise term to the input as

$$\omega (t)={\omega }_0(t)+\lambda w(t),$$ (5)

where λ is the noise parameter, and w(t) is the Gaussian white noise. Thus, a nonholonomic needle model with noise is

$${(g^{-1}\stackrel{.}{g})}^{\vee }dt={\left[\begin{array}{cccccc}\kappa & 0& {\omega }_0(t)& 0& 0& v_0\end{array}\right]}^{T}dt+{\left[\begin{array}{cccccc}0& 0& \lambda & 0& 0& 0\end{array}\right]}^{T}dW$$ (6)

where dW = W(t+dt) − W(t) = w(t)dt is the non-differentiable increment of a Wiener process W(t). This noise model is a stochastic differential equation (SDE) on SE(3). As shorthand, we write this as

$${(g^{-1}\stackrel{.}{g})}^{\vee }dt=\mathbf{h}(t)dt+Hd\mathbf{W}(t).$$ (7)

Corresponding to this SDE is the Fokker-Planck equation that describes the evolution of the probability density function of the ensemble of tip positions and orientations at each value of time, t [8,22,24]:

$$\frac{\partial \rho (g;t)}{\partial t}=-\sum _{i=1}^6{h}_i(t){\stackrel{\sim }{E}}_i^r\rho (g;t)+\frac{1}{2}\sum _{i,j=1}^6{D}_{ij}{\stackrel{\sim }{E}}_i^r{\stackrel{\sim }{E}}_j^r\rho (g;t)$$ (8)

where $D_{ij}={\sum }_{k=1}^m{H}_{ik}{H}_{kj}^T$ and ρ(g; 0) = δ(g). In (8) the ‘right’ Lie derivative ${\stackrel{\sim }{E}}_i^r$ is defined for any differentiable function f(g) as

$${\stackrel{\sim }{E}}_i^{r}f(g)={\left(\frac{d}{dt}f(g\circ exp({tE}_i))\right)|}_{t=0}.$$ (9)

For a small amount of diffusion, the solution for the Fokker-Planck equation, (8), can be approximated by a shifted Gaussian function [24,30]:

$$\rho (g;t)={(2\pi )}^{-3}\mid det(\mathrm{\sum }(t)){\mid }^{-1/2}exp\left(-\frac{1}{2}{\mathbf{y}}^T\mathrm{\sum }{(t)}^{-1}\mathbf{y}\right),$$ (10)

where y = log(μ(t)⁻¹ ◦ g)^∨, and μ(t) ∈ SE(3) and Σ(t) ∈ ℝ^6×6 are the mean and the covariance of the probability density function, ρ(g; t), respectively. In Section 3, the method for computing the mean and covariance will be proposed. This approximation is based on the fact that for small diffusion the Lie derivative is approximated as [24]

$${\stackrel{\sim }{E}}_i^{r}f(g)\approx \frac{\partial f}{\partial x_i}.$$

Using this, the Fokker-Planck equation (8) becomes a diffusion equation in ℝ⁶. Therefore, we have the solution for the diffusion equation as (10).

We need to carefully deal with the Gaussian expression in (10) when the covariance matrix Σ(t) is close to singular, because (10) needs the inverse of the covariance matrix. In order to overcome this, we smear the Gaussian distribution in (10). In other words, the modified distribution can be obtained by convolving the Gaussian distribution in (10) with a new Gaussian with zero mean. This can be implemented by adding small numbers on the diagonal of the covariance matrix as

$$\mathrm{\sum }^{\sim }(t)=\mathrm{\sum }(t)+\left(\begin{array}{cc}{\epsilon }_1{I}_{3\times 3}& O_{3\times 3}\\ O_{3\times 3}& {\epsilon }_2{I}_{3\times 3}\end{array}\right),$$ (11)

where I_3×3 and O_3×3 are 3 × 3 identity and zero matrices, respectively. ε_i is a small positive number that reflects the amount of smearing.

2.3 Path-of-Probability Algorithm for Flexible Needles

For path planning, we modify the path planning method for needle steering that appeared in [22,24]. This algorithm was adapted from the path-of-probability algorithm introduced in [12]. A similar trajectory planning method can be also found in [20].

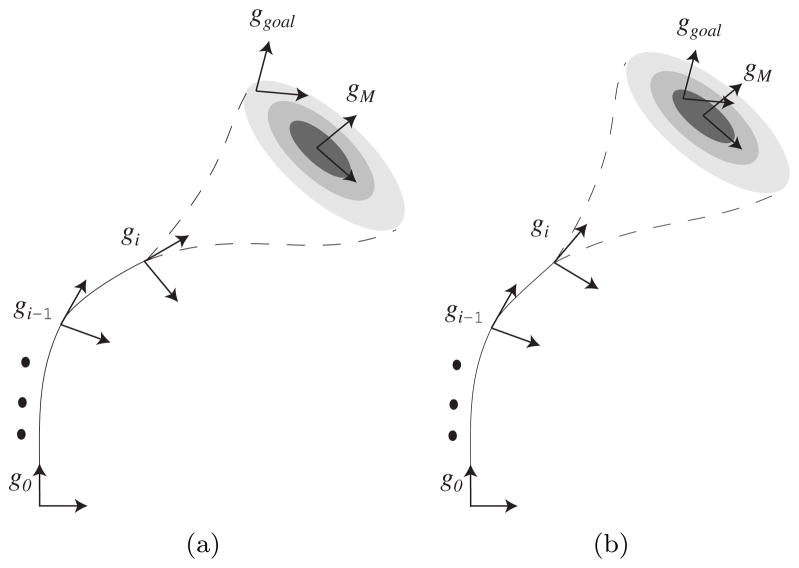
In this algorithm, we find the whole trajectory by serially pasting together several intermediate paths. Fig. 2. shows the concept of this algorithm. We aim to find a path that starts at g₀ = I_4×4 and ends at g_goal using M intermediate steps. The homogeneous transformation matrix, g_i ∈ SE(3) (i = 1, 2, …, M), represents the position and orientation of the i^th frame with respect to the (i − 1)^th frame as shown in Fig. 2. Suppose that the (i − 1) intermediate steps (g₁, g₂, ···, g_i−1 ∈ SE(3)) have already been determined. The intermediate step, g_i is determined to maximize the probability that the remaining steps reach the goal. In Fig. 2, the shaded ellipses depict the probability density functions when we consider the remaining (M − i) steps. In other words, when we consider (M − i) intermediate steps after g_i, the expected final pose will be in the dark area which has higher probability than the bright area. Comparing the two simplified cases in Fig. 2, if the previous intermediate steps (g₁, g₂, ···, g_i−1) are the same for both cases, we should choose g_i shown in Fig. 2(b), because it yields a higher probability that the final pose is the goal pose.

Figure 2.

The path-of-probability algorithm at the ith step. (a) Evaluation of one candidate move, g_i, with low resulting probability of reaching goal, (b) an candidate move, g_i, resulting in high probability of reaching the goal.

The determination of the intermediate steps can be formulated as

$$g_i=\underset{g\in S}{argmax}\rho ({(g_1\cdots g_{i-1}\circ g)}^{-1}\circ g_{\mathit{goal}};{\tau }_i),$$ (12)

where τ_i is the remaining time to hit the goal and S is the set of possible intermediate poses. Now let us adapt this to the needle insertion problem. If t_total is the time spent for the insertion from g₀ to g_goal and we have M intermediate steps with a constant insertion speed, each intermediate step takes Δt = t_total/M. Therefore, we can define τ_i = (M − i)t_total/M in (12). Technically, the formula (12) can not be used for determining the final intermediate step, g_M, because there is no remaining path when we determine g_M. The final step can be determined so that the needle tip position is placed as close to the goal position as possible.

Instead of pursuing a continuous function ω(t) as a steering input, we consider a discretized input in the similar way in [11]. In this strategy we control the flexible needle by alternating pure rotation around the z-axis and pure short insertion along the z-axis. By modifying (12), the rotation angle at the i^th step can be determined by

$${\theta }_i=\underset{\theta \in [02\pi )}{argmax}\rho ({(g_1\cdots g_{i-1}\circ \stackrel{\sim }{R}(\theta )\circ \mu (\mathrm{\Delta }t))}^{-1}\circ g_{\mathit{goal}};(M-i)t_{\mathit{total}}/M),$$ (13)

where

$$\stackrel{\sim }{R}(\theta )=\left(\begin{array}{cc}{R}_z(\theta )& \mathbf{0}\\ {\mathbf{0}}^T& 1\end{array}\right),$$

and μ(Δt) ∈ SE(3) is the sample mean of the SDE (6) at the time t = Δt = t_total/M. When determining θ_i using (13), the i^th insertion actually has not been performed. In order to evaluate the probability density function in (13), we need an estimate for pure short insertion after rotation. Since our needle insertion system has stochastic behavior, the mean path is a reasonable choice for the estimate. Then the theoretical intermediate step can be defined as g_i = R̃(θ_i) ◦ μ (Δt). The whole trajectory will be g = g₀ ◦ g₁ ◦ ··· ◦ g_M.

Generally speaking, path planning is performed off-line, and then a system is controlled based on the path planning results. However, one distinctive feature of the path planning method presented here is that we can use it during feedback control of the needle steering. After having the i^th intermediate insertion plan g_i = R̃ (θ_i) ◦ μ(Δt), the mechanical control system rotates the needle by θ_i and pushes it for t = Δt. The needle may not exactly follow the control input because of uncertainty in the mechanical system and the interaction between the needle and the tissue. Therefore, we need to measure the actual intermediate step $g_i^{\text{m}}$. The modified rotation plan can then be formulated as

$${\theta }_i=\underset{\theta \in [02\pi )}{argmax}\rho ({(g_1^{\text{m}}\cdots g_{i-1}^{\text{m}}\circ \stackrel{\sim }{R}(\theta )\circ \mu (\mathrm{\Delta }t))}^{-1}\circ g_{\mathit{goal}};(M-i)t_{\mathit{total}}/M),$$ (14)

where $g_k^{\text{m}}$ is the actual insertion based on the control input g_k = R̃(θ_k) ◦ μ(Δt).

For the purpose of simulation, we use the model for the actual intermediate step as

$$g_i^{\text{m}}=\stackrel{\sim }{R}({\theta }_i+{\epsilon }_i)\circ h(\mathrm{\Delta }t),$$ (15)

where ε_i is the error in the rotation angle, and h(Δt) is the actual insertion which can be simulated by integrating the SDE (6) up to t = Δt. The integration can be implemented using the numerical method in [14]. Practically, the mean path μ(Δt) can be replaced with the trajectory which can be obtained by integrating (6) with zero noise, λ = 0.

In the case when there are no obstacles, the POP method uses global foresight (i.e., the relative probability of reaching the end goal) to plan local motions, and in this sense it is not greedy. For needle insertion, the nonholonomic constraints are built into the propagation of probability density functions, and decisions are made at each stage to maximize the ability of the remaining moves to reach the goal. It is true that if we use a method that propagates probabilities under the assumption of no obstacles in the case when there actually are obstacles, then this will lead to problems. The full scenario in the presence of obstacles or narrow passages would require us to propagate probabilities while taking into account corresponding obstacle boundary conditions. This is possible in principle, but difficult to do in practice. Therefore, we have sought a middle ground in which obstacles that are relatively sparse compared to the support of the probability density function are considered. In a sense, if the probabilities can propagate without significantly overlapping the obstacles, then the needle never knows/cares that there are the obstacles.

3 Diffusions with Drift and Covariance Propagation

In this section, we consider how the error probability associated with the stochastic differential equation evolves as a function of time. Specifically we derive an equation for the time-varying covariance matrix of the probability density function for the needle tip pose. The covariance matrix is defined in an integral form. We derive the closed-form solution for the covariance matrix for the case of needle trajectories constructed from piecewise circular arcs. For more general cases, we consider the second order propagation formula for the covariance matrix which can be computed faster than the integral form.

3.1 Diffusions with Drift

In addition to (8), we have another expression for the Fokker Planck equation of (7):

$$\frac{\partial \rho (g;t)}{\partial t}=\sum _{i=1}^d{h}_i(t){\stackrel{\sim }{E}}_i^l\rho (g;t)+\frac{1}{2}\sum _{i,j=1}^d{D}_{ij}{\stackrel{\sim }{E}}_i^l{\stackrel{\sim }{E}}_j^l\rho (g;t).$$ (16)

The differential operators ${\stackrel{\sim }{E}}_i^l$ are the Lie derivatives:

$${\stackrel{\sim }{E}}_i^{l}f=\frac{d}{d\tau }{[f(exp(-\tau X_i)\circ g)]}_{\tau =0}.$$ (17)

Our goal here is to obtain an approximate functional form of f(g, t) that is efficient to compute in the case when ||D|| ≪ 1. In the case when D = O, the above SDE becomes the matrix ODE

$$\stackrel{.}{g}=gA\text{where}g(0)=e\text{and}A=\sum _{i=1}^6{h}_i(t)E_i,$$ (18)

with E_i denoting the standard basis for se(3). Let the solution to the above ODE be denoted as m(t) ∈ SE(3). In the case when A is constant, m(t) = exp(At). More generally, if A and its integral commute then the solution can also be written as a matrix exponential:

$$\left[{\int }_0^{t}A(\tau )d\tau ,A(t)\right]=O\Rightarrow m(t)=exp\left({\int }_0^{t}A(\tau )d\tau \right).$$ (19)

However, if the above condition does not hold, then m(t) cannot be written as a single matrix exponential. In practice, if a baseline path is a circular arc or helix, then (19) will hold, because A will be constant.

In order to achieve the goal stated above, it will be useful to convert (16), which has potentially large values of h_i, into an alternative form where all of the coefficients are small. An intuitive way to do this is to seek the new function F(g, t) such that

$$\rho (g;t)=F(m^{-1}(t)\circ g,t).$$ (20)

Here the notation m⁻¹(t) is shorthand for [m(t)]⁻¹. In other words, we will substitute (20) into (16) with the expectation that the large drift term will disappear and what remains can be described as a diffusion in a small neighborhood about m⁻¹(t) ◦ g.

To begin, we observe that the Lie algebra se(3) can be mapped bijectively to IR⁶ using the ∨ operation, where ∨: E_i → e_i. Therefore, it is sometimes convenient to use the notation ${\stackrel{\sim }{E}}_i^l={\stackrel{\sim }{E}}_{{\text{e}}_i}^l$. Note that by the use of various notational substitutions,

$$\sum _{i=1}^6{h}_i{\stackrel{\sim }{E}}_i^l\rho ={\left(\stackrel{\sim }{\sum _{i=1}^6{h}_i{E}_i}\right)}^l\rho ={\stackrel{\sim }{E}}_{{\sum }_{i=1}^6{h}_i{\text{e}}_i}^l\rho .$$ (21)

This means that

$$\begin{array}{l}\sum _{i=1}^6{h}_i{\stackrel{\sim }{E}}_i^l\rho (g;t)=\frac{d}{d\tau }{[F(m^{-1}\circ exp(-\tau A)\circ g,t)]}_{\tau =0}\\ =\frac{d}{d\tau }{[F([m^{-1}\circ exp(-\tau A)\circ m]\circ [m^{-1}\circ g],t)]}_{\tau =0}\\ =\frac{d}{d\tau }{[F([exp(-\tau m^{-1}Am)]\circ [m^{-1}\circ g],t)]}_{\tau =0}\\ ={{[\stackrel{\sim }{m^{-1}Am}]}^{l}F(p,t)|}_{p=m^{-1}\circ g}\end{array}$$ (22)

$$={{\stackrel{\sim }{E}}_{{Ad}_{m^{-1}}\mathbf{h}}^{l}F(p,t)|}_{p=m^{-1}\circ g}$$ (23)

$$={\sum _{i,k=1}^6{h}_i{\mathbf{e}}_k^T{Ad}_{m^{-1}}{\mathbf{e}}_i{\stackrel{\sim }{E}}_k^{l}F(p,t)|}_{p=m^{-1}(t)\circ g}.$$ (24)

Here (22)–(24) are just different ways of writing the same thing, each of which can be convenient in different contexts, where p ∈ SE(3) is a dummy variable, h_i = h_i(t), A = A(t) is defined in (18), and m = m(t). In the case when h_i are all constant, we have m⁻¹ Am = A. Therefore, in that case (22)–(24) can be avoided and

$$\sum _{i=1}^6{h}_i{\stackrel{\sim }{E}}_i^l\rho (g,t)={\sum _{i=1}^6{h}_i{\stackrel{\sim }{E}}_i^{l}F(k,t)|}_{k=m^{-1}\circ g}.$$ (25)

In the general case, the result in (24) can also be used to write

$$\begin{array}{l}{\stackrel{\sim }{E}}_j^l{\stackrel{\sim }{E}}_k^l\rho ={{\stackrel{\sim }{E}}_{{Ad}_{m^{-1}}{\mathbf{e}}_j}^l{\stackrel{\sim }{E}}_{{Ad}_{m^{-1}}{\mathbf{e}}_k}^{l}F|}_{m^{-1}(t)\circ g}\\ ={\sum _{p,q=1}^6\left[{\mathbf{e}}_p^T{Ad}_{m^{-1}}{\mathbf{e}}_j{\stackrel{\sim }{E}}_p^l\right]\left[{\mathbf{e}}_q^T{Ad}_{m^{-1}}{\mathbf{e}}_k{\stackrel{\sim }{E}}_q^l\right]F|}_{m^{-1}(t)\circ g}\\ ={\sum _{p,q=1}^6\left[{\mathbf{e}}_p^T{Ad}_m^{-1}{\mathbf{e}}_j{\stackrel{\sim }{E}}_p^l\right]\left[{\mathbf{e}}_q^T{Ad}_m^{-1}{\mathbf{e}}_k{\stackrel{\sim }{E}}_q^l\right]F|}_{m^{-1}(t)\circ g}.\end{array}$$

Direct substitution and using the fact that the 6×6 identity matrix can be written as $\mathbb{I}={\sum }_{k=1}^6{\mathbf{e}}_k{\mathbf{e}}_k^T$ then gives

$$\sum _{j,k=1}^6{D}_{jk}{\stackrel{\sim }{E}}_j^l{\stackrel{\sim }{E}}_k^l\rho ={\sum _{p,q=1}^6{({Ad}_m^{-1}D{Ad}_m^{-T})}_{pq}{\stackrel{\sim }{E}}_p^l{\stackrel{\sim }{E}}_q^{l}F|}_{m^{-1}(t)\circ g}.$$ (26)

When making the substitution (20) into (16) the left side of the equation becomes

$$\frac{\partial \rho (g,t)}{\partial t}=\frac{\partial F(m^{-1}(t)\circ g,t)}{\partial t}.$$

When m(t) = exp(At) where A ∈ se(3) is constant, it can be shown that for m⁻¹(t) ◦ g near the identity that

$$\frac{\partial \rho }{\partial t}={\frac{\partial F(k,t)}{\partial t}|}_{k=m^{-1}(t)\circ g}+{\sum _{i=1}^6{h}_i({\stackrel{\sim }{E}}_i^{l}F)(k·t)|}_{k=m^{-1}(t)\circ g}.$$ (27)

A detailed derivation of (27) is given in [8]. Substituting (25), (26) and (27) into (16) then gives

$${\frac{\partial F(k·t)}{\partial t}|}_{k=m^{-1}(t)\circ g}=\frac{1}{2}{\sum _{j,k=1}^6{D}_{jk}(t)({\stackrel{\sim }{E}}_j^l{\stackrel{\sim }{E}}_k^{l}F)(k,t)|}_{k=m^{-1}(t)\circ g}\text{where}D(t)={Ad}_m^{-1}{D}_0{Ad}_m^{-T}.$$ (28)

In other words, the drift term can be canceled, and we can study the diffusion (with time-varying diffusion matrix, D(t)) around the identity.

When motions are very close to the identity and m⁻¹(t) ◦ g = exp X, then the exponential coordinates {x_i} are convenient, and ${\stackrel{\sim }{E}}_j^r\approx \partial /\partial x_j$. The SE(3)-covariance defined in [30,31] then is computed as

$$\mathrm{\sum }(t)={\int }_0^t{Ad}_m^{-1}D{Ad}_m^{-T}dt.$$ (29)

3.2 Closed-Form Expression for Σ(t) for Circular Arc Trajectory

In this subsection, for the circular arc trajectory m(t), we derive a closed-form expression for (29). Obviously, the advantage of the closed-form covariance is that we can compute it very quickly at any time of interest.

The circular arc needle trajectory m(t) is given by

$$m(t)=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& cos(\kappa t)& -sin(\kappa t)& (cos(\kappa t)-1)/\kappa \\ 0& sin(\kappa t)& cos(\kappa t)& sin(\kappa t)/\kappa \\ 0& 0& 0& 1\end{array}\right)\equiv \left(\begin{array}{cc}R& \mathbf{p}\\ {\mathbf{0}}^T& 1\end{array}\right).$$

We compute the inverse of m(t) as

$$m^{-1}(t)=\left(\begin{array}{cc}{R}^T& -R^{T}p\\ {\mathbf{0}}^T& 1\end{array}\right)=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& cos(\kappa t)& sin(\kappa t)& (cos(\kappa t)-1)/\kappa \\ 0& -sin(\kappa t)& cos(\kappa t)& -sin(\kappa t)/\kappa \\ 0& 0& 0& 1\end{array}\right)\equiv \left(\begin{array}{cc}{R}^T& \mathbf{q}\\ {\mathbf{0}}^T& 1\end{array}\right).$$

The adjoint matrix is

$${Ad}_{m^{-1}}={Ad}_m^{-1}=\left(\begin{array}{cc}{R}^T& 0_{3\times 3}\\ \widehat{q}{R}^T& R^T\end{array}\right).$$

Since D₀ = HH^T, D₀ can be written as

$$D_0=\left(\begin{array}{cc}{D}_{11}& D_{12}\\ D_{21}& D_{22}\end{array}\right),$$

where D₁₂ = D₂₁ = D₂₂ = 0_3×3 and

$$D_{11}=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& {\lambda }^2\end{array}\right).$$

λ is the noise parameter in (6). Therefore we have

$${Ad}_{m(t)}^{-1}{D}_0{Ad}_{m(t)}^{-T}=\left(\begin{array}{cc}{R}^T{D}_{11}R& -R^T{D}_{11}R\widehat{q}\\ \widehat{q}{R}^T{D}_{11}R& -\widehat{q}{R}^T{D}_{11}R\widehat{q}\end{array}\right)=\left(\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& {\lambda }^2{S}^2& {\lambda }^{2}CS& \frac{{\lambda }^2}{\kappa }S(1-C)& 0& 0\\ 0& {\lambda }^{2}CS& {\lambda }^2{C}^2& \frac{{\lambda }^2}{\kappa }C(1-C)& 0& 0\\ 0& \frac{{\lambda }^2}{\kappa }S(1-C)& \frac{{\lambda }^2}{\kappa }C(1-C)& \frac{{\lambda }^2}{{\kappa }^2}{(1-C)}^2& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right).$$

where C = cos(κt) and S = sin(κt). Therefore, the covariance in (29) can be given as:

$$\mathrm{\sum }(t)={\int }_0^t{Ad}_{m(\tau )}^{-1}{D}_0{Ad}_{m(\tau )}^{-T}d\tau =\left(\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& a& b& e& 0& 0\\ 0& b& c& d& 0& 0\\ 0& e& d& f& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right),$$ (30)

where

$$\begin{array}{l}a=\frac{{\lambda }^2}{2}\left(t-\frac{1}{\kappa }sin(\kappa t)cos(\kappa t)\right),\\ b=\frac{{\lambda }^2}{2\kappa }{sin}^2(\kappa t),\\ c=\frac{{\lambda }^2}{2}\left(t+\frac{1}{\kappa }sin(\kappa t)cos(\kappa t)\right),\\ d=\frac{{\lambda }^2}{{\kappa }^2}\left(1-cos(\kappa t)-\frac{1}{2}{sin}^2(\kappa t)\right),\\ e=\frac{{\lambda }^2}{\kappa }\left(\frac{1}{\kappa }sin(\kappa t)-\frac{1}{2\kappa }sin(\kappa t)cos(\kappa t)-\frac{1}{2}t\right),\\ f=\frac{{\lambda }^2}{{\kappa }^2}\left(\frac{3}{2}t-\frac{2}{\kappa }sin(\kappa t)+\frac{1}{2\kappa }sin(\kappa t)cos(\kappa t)\right).\end{array}$$

3.3 Second Order Error Propagation

Basically, the covariance (29) is the result of the first order error propagation. In this subsection, we compute the covariance using second order error propagation.

If a unique value μ ∈ SE(3) exists for which

$${\int }_{\text{SE}(3)}{[log({\mu }^{-1}(t)\circ g)]}^{\vee }\rho (g;t)dg=\mathbf{0},$$

then μ(t) is called the mean of a PDF ρ(g, t). In addition, the covariance about the mean is defined as [31]

$$\mathrm{\sum }(t)={\int }_{\text{SE}(3)}log{({\mu }^{-1}(t)\circ g)}^{\vee }{[log{({\mu }^{-1}(t)\circ g)}^{\vee }]}^T\rho (g;t)dg.$$

Suppose that for small values of t, the quantities μ(t) and Σ(t) corresponding to ρ(g; t) can be obtained (even if ρ(g; t) is not known in closed form). Then these can be propagated over longer times. In other words, due to the Markovian nature of the above model, solutions can be “pasted together” using the fact that the following convolution equalities hold:

$$\rho (g;t_1+t_2)=\rho (g;t_1)\ast \rho (g;t_2),$$

where convolution on SE(3) is defined as in [6]. Even if these convolutions are too time-consuming to compute explicitly, the fact that these expressions hold means that propagation formulas for the mean and covariance can be used.

Wang and Chirikjian [31] derived the formulas for the second order propagation. If a PDF, ρ_i(g) has mean μ_i and covariance Σ_i for i = 1, 2, then with second order accuracy, the mean and covariance of (ρ₁ * ρ₂)(g) are respectively [7]

$${\mu }_{1\ast 2}={\mu }_1\circ {\mu }_2\text{and}{\mathrm{\sum }}_{1\ast 2}=A+B+F(A,B),$$ (31)

where $A=Ad({\mu }_2^{-1}){\mathrm{\sum }}_{1}A{d}^T({\mu }_2^{-1})$, B = Σ₂ and F (A, B) is given in the appendix. Consequently, we can obtain the mean and covariance for a relatively large t with given mean and covariance for a small t by this propagation formula. These can then be substituted into (10) to obtain a closed-form estimate of the probability density that the needle will reach any particular pose at any value of time.

The covariance propagation (31) requires covariances for short needle insertion as inputs, and returns covariances for long needle insertion as outputs. In the previous work in [21], we sampled needle trajectories and then computed the covariance from the samples in order to obtain the inputs. Using the closed-form covariance in (30), we can calculate the input covariances very fast, because the sampling process is not required and the evaluation of (30) is very quick.

4 Path Planning Using the POP Algorithm

In this section, we use the POP algorithm to generate needle trajectories. We consider two distinct situations. The first situation is that there is no obstacle and we should determine the insertion position and orientation under the assumption that the needle trajectory is close to a perfect circular arc. Second, we consider the case where the insertion position and orientation are given and the needle trajectory may not be close to a circular arc.

4.1 Choosing the Needle Insertion Location and Orientation

The choice of the insertion position and orientation for a flexible needle with a bevel tip can make path planning very simple and fast. It also can influence the amount that the needle needs to be inserted in order to reach a target. This is similar to the port placement problem studied in [1,4,26]

If the tangent to the needle is denoted as the local e₃ direction, the bevel causes the needle to rotate at a rate κυ(t) around the local e₁ axis, where υ(t) is the insertion speed. If υ(t) = 1 and ω(t) = 0, the points on the circular arc needle trajectory will be parameterized in the frame of reference attached at the point of needle insertion as

$$\begin{array}{l}{x}_1(t)=0,\\ x_2(t)=-{\int }_0^{t}sin\left({\int }_0^{\tau }\mathit{kds}\right)d\tau =\frac{1}{\kappa }[cos(\kappa t)-1],\\ x_3(t)={\int }_0^{t}cos\left({\int }_0^{\tau }\kappa ds\right)d\tau =\frac{1}{\kappa }sin(\kappa t),\end{array}$$

where 0 ≤ t ≤ T. Let x(t) = [x₁(t), x₂(t), x₃(t)]^T. A frame of reference at every point on the curve is defined by the pair (R(t), x(t)) where R(t) = R_x(κt).

The needle insertion pose can be chosen such that the initial needle tip position can be any position on the boundary surface of the volume into which the needle is to be inserted, and the orientation is arbitrary except for the constraint that the needle tip must be initially pointing toward the volume into which it is being inserted. For simplicity, it is assumed here that the only bounding surface being considered for insertion is planar. This means that a transformation of the insertion frame will be of the form

$$(A,\mathbf{b})=\left(\begin{array}{cc}A& \mathbf{b}\\ {\mathbf{0}}^T& 1\end{array}\right)\text{where}A=R_z(\alpha )R_x(\beta )R_z(\gamma )\text{and}\mathbf{b}={[b_1,b_2,0]}^T.$$

The allowed range of angles is 0 ≤ α ≤ 2π, 0 < β < π/2, and 0 ≤ γ ≤ 2π. Note that the range of β is half of the usual allowed for Euler angles.

If the needle is angled and its initial position is changed before insertion, then the resulting end pose of the needle tip after pushing in for time t = T, will be

$$(R^{\mathit{tip}},{\mathbf{x}}^{\mathit{tip}})=(A,\mathbf{b})\circ (R(T),\mathbf{x}(T)),\text{or}{R}^{\mathit{tip}}={AR}_x(\kappa T)\text{and}{\mathbf{x}}^{\mathit{tip}}=A\mathbf{x}(T)+\mathbf{b}.$$

This means that

$${\mathbf{x}}^{\mathit{tip}}=R^{\mathit{tip}}{R}_x(-\kappa T)\mathbf{x}(T)+\mathbf{b}.$$ (32)

The pairs (R^tip, x^tip), (A(α, β, γ), b) and (R(T), x(T)) respectively have six, five and one degrees of freedom. Whereas (R^tip, x^tip) is the specified goal (where we might not care about the roll degree of freedom in R^tip), The five insertion pose parameters α, β, γ, b₁, b₂ and the needle insertion time, T, are what we have control over. Therefore, the inverse kinematics problem is determining α, β, γ, b₁, b₂, T for given (R^tip, x^tip). As explained below, this can be done in closed form.

To begin, observe that

$$R_x(-\kappa T)\mathbf{x}(T)=\left(\begin{array}{c}0\\ \frac{1}{\kappa }[1-cos(\kappa T)]\\ \frac{1}{\kappa }sin(\kappa T)\end{array}\right).$$

This means that the third component in the positional equation in (32) can be written as

$$x_3^{\mathit{tip}}=\frac{1}{\kappa }\left(r_{32}^{\mathit{tip}}·[1-cos(\kappa T)]+r_{33}^{\mathit{tip}}·sin(\kappa T)\right).$$ (33)

If we let z = tan(κT/2) then

$$cos(\kappa T)=\frac{1-z^2}{1+z^2}\text{and}sin(\kappa T)=\frac{2z}{1+z^2}$$

and (33) is written as the quadratic equation:

$${az}^2+bz+c=0,$$

where a, b, and c are each functions of κ, $x_3^{\mathit{tip}}$, and $r_{32}^{\mathit{tip}}$. This sort of trick is common in kinematics [19,25,27].

Solving this quadratic equation for z using the above formulas for cos(κT) and sin(κT) together with the two-argument inverse tangent function allows us to recover T as

$$T=\frac{1}{\kappa }\mathit{Atan}2\left(\frac{2z}{1+z^2},\frac{1-z^2}{1+z^2}\right).$$

If we do not care about the roll at the tip, then writing R^tip = R_z(α^tip)R_x(β^tip)R_z(γ^tip) means that

$$r_{32}^{\mathit{tip}}=sin{\beta }^{\mathit{tip}}cos{\gamma }^{\mathit{tip}}\text{and}{r}_{33}^{\mathit{tip}}=cos{\beta }^{\mathit{tip}},$$

where 0 ≤ γ^tip ≤ 2π can be used to parameterize a whole family of solutions to the “position-plus-pointing” problem. In other words, since the desired 3D position and the desired 2D pointing direction are specified, γ^tip is a free variable. In the case when there are no obstacles, we can choose a solution from this one-dimensional set that minimizes T. The optimal value γ^tip = 0 can be obtained based on the geometric observation that the minimum T occurs when the plane on which the circular arc needle trajectory is placed is perpendicular to the x − y plane.

After this solution is obtained, T is known, and back-substitution into the first two components of (32) yields b₁ and b₂. And the needle insertion orientation is calculated simply as

$$A=R^{\mathit{tip}}{R}_x(-\kappa T).$$

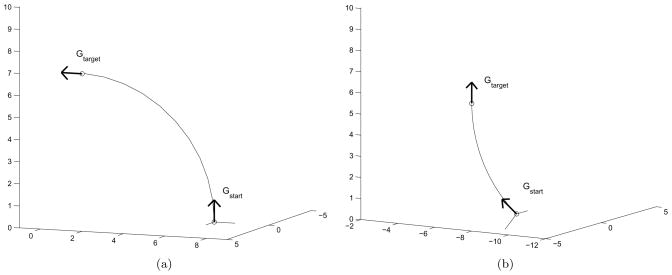
Fig. 3 shows two examples of port placement and the path planning result by the POP algorithm. For a target position and direction which is denoted by G_target, a pair of insertion position and orientation which is denoted by G_start is obtained using the port placement method. If there is no error in the insertion mechanism, the ideal input is ω(t) = 0, because the port placement method was based on the pure insertion without twisting. However, in practice, the error cannot be avoided perfectly. As mentioned in Section 2.3, the POP method deals with this error by reflecting the error from the previous intermediate step to the choice of the current intermediate step during the consecutive determination of intermediate steps. In the simulation shown in Fig. 3, the errors in the rotation angles and the intermediate pure push are assumed to be non-zero. Therefore, the needle tends to get off the path that we aim for, but the POP algorithm keeps correcting the error to have the needle to get back to the planed path. For the examples in Fig. 3, the errors in rotation angles are sampled from the normal distribution whose mean and variance are zero and λ², respectively. This error model is based on the initial setting in (5). The pure push with error is simulated by integrating the SDE (6).

Figure 3.

Two examples of port placement.

We implemented the POP algorithm with 10 intermediate steps. We used κ = 0.157 (cm⁻¹) which corresponds to a circular arc with radius = 6 (cm). We choose this for better demonstration. The noise parameter is set as λ = 0.1, which means the angular speed of needle rotation is perturbed by adding a Gaussian with standard deviation = 0.1 (rad/s). This assumption of small perturbation is consistent with observation of repeated insertion in [33]. The smearing factors are set as ε₁ = 0.001 and ε₂ = 0.0001 in the simulation examples. This implies that the zero-mean artificial distribution for smearing has the rotational standard deviation = 0.032 (rad) and the translational standard deviation = 0.01(cm). These values do not significantly distort the initial distribution because they imply that the corresponding distribution is fairly tightly focused.

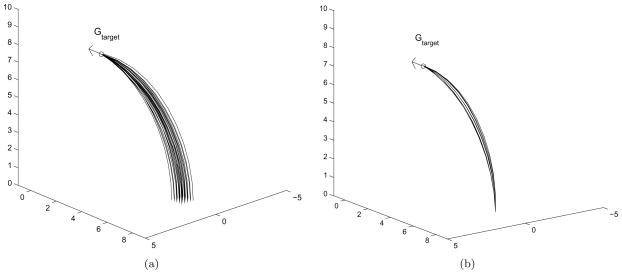
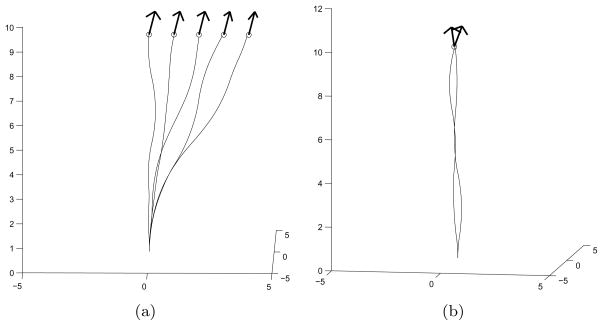
The POP algorithm also works for the case where the actual insertion position and orientation are not exactly the same as the ones planed by the port placement method. The discrepancy will occur because of the uncertainty of the needle positioning system. Fig. 4 shows a few examples. In Fig. 4(a) for various starting positions near the optimal location, the paths generated by the POP algorithm hit the target successfully. Fig. 4(b) shows an example of the POP algorithm handling the cases where there are errors in the orientation at the insertion location. For various starting orientations near the optimal orientation, the POP algorithm produces the paths that hit the target successfully.

Figure 4.

Paths generated by the POP algorithm in the case where there are errors in the insertion pose. (a) Positional errors, (b) orientational errors.

4.2 Path-of-Probability Algorithm with Splines

For convenience, let us define a baseline trajectory as a trajectory that can be obtained by integrating (6) with zero noise, λ = 0. This baseline trajectory plays a crucial role in the path-of-probability algorithm, because this algorithm searches the workspace density around the baseline trajectory using the probability density function in (10). Note that even though the mean path, μ(t) in (10) is not exactly the same as this baseline trajectory, the two paths can be treated as the same in practice when the noise is small.

The POP algorithm shows better performance with target positions and orientations that are close to the baseline trajectory. If we use the port placement method in the previous subsection, the target pose is close to the baseline trajectory that is a circular arc. However this is a very limiting case. In this subsection, we will develop a method for more general cases.

Suppose the start and target poses are given, and the circular arc trajectory by pure insertion is far from the target pose. In order to solve this, we need to start with a new baseline trajectory that is close to the target pose. In other words, we need a better ω₀(t) in (6) so that the baseline trajectory closely reaches the desired pose. Note that the new baseline trajectory does not have to hit the desired pose exactly, because we will apply the POP method to the new baseline trajectory to reach the desired pose accurately.

4.2.1 Generating Baseline Trajectory using Splines

Now we will generate a spline that connects the start and final positions with the given pointing directions at both locations. Then we will obtain a baseline trajectory that roughly follows the spline. We expect that the baseline trajectory will reach the desired pose fairly close.

A polynomial spline can be written as

$$\mathbf{x}(t)=\sum _{k=0}^N{\mathbf{p}}_k{t}^k\in {\mathbb{R}}^3,$$ (34)

where p_k ∈ ℝ³ are the coefficients for the spline and t is the spline parameter. For boundary conditions, we have

$$\mathbf{x}(0)={\mathbf{x}}_0,\mathbf{x}(t_f)={\mathbf{x}}_f,$$

and

$$\stackrel{.}{\mathbf{x}}(0)=u_0{\mathbf{u}}_0,\stackrel{.}{\mathbf{x}}(t_f)=u_f{\mathbf{u}}_f,$$ (35)

where x₀ and x_f are the starting and final positions, respectively, and u₀ and u_f are the unit vectors for the starting and final pointing directions, respectively. ẋ is the derivative of x with respect to the spline parameter t. The magnitudes of the direction vectors, u₀ and u_f, are free parameters, since only the directions are given. Therefore, we need to determine p_k, u₀ and u_f to have a spline.

The Frenet-Serret apparatus, which is defined for an arc-length-parameterized space curve, can be adapted to one that is parameterized by an arbitrary parameter t as:

$$\mathbf{u}(t)=\stackrel{.}{\mathbf{x}}(t)/\left|\right|\stackrel{.}{\mathbf{x}}(t)\left|\right|;\mathbf{b}(t)=(\stackrel{.}{\mathbf{x}}(t)\times \ddot{\mathbf{x}}(t))/\left|\right|\stackrel{.}{\mathbf{x}}(t)\times \ddot{\mathbf{x}}(t)\left|\right|;\mathbf{n}(t)=\mathbf{b}(t)\times \mathbf{u}(t),$$

where u(t), b(t) and n(t) are the tangent, binormal and principal normal vector, respectively. Then R(t) = [b(t); n(t); u(t)] is a rotation matrix that varies along the arclength of the curve constituting the Frenet frames.

Ideally, we need a spline which has a constant curvature κ, because the actual needle trajectory defined by (4), which must have a curvature of κ, will be made to follow the spline as closely as possible. However, it is computationally expensive to compute splines with a constant curvature. Alternatively, we consider the following two cost functions.

$$c_1(\mathbf{p})={\int }_0^{t_f}{\left|\right|\stackrel{.}{\mathbf{x}}(t)\left|\right|}^{2}dt,\text{and}{c}_2(\mathbf{p})={\int }_0^{t_f}{\left|\right|\kappa (t)-\kappa \left|\right|}^{2}dt,$$

where κ(t) = ||ẋ(t) × ẍ(t)||/||ẋ(t)||³ is the curvature of the spline at t, κ is the curvature of the needle trajectory modeled in (4), and p is the vector consisting of each p_k concatenated. By minimizing the first cost function c₁, we have a spline with minimum length. The second cost function will push the needle to have constant curvature, κ. It is ideal to minimize the weighted sum of the two costs. However, it will be computationally costly because c₂(p) is not a quadratic form with respect to p while c₁(p) is. Since it is not a final goal to have an optimal spline with the boundary conditions and the desired curvature, we will try to obtain a “near-optimal” spline with a fast and simple computation and then use it for the POP algorithm.

Minimizing c₁(p) with the boundary conditions is easy, because it is the minimization of a quadratic cost function subject to linear constraints. Stated generally, the cost and constraints can be respectively written as

$$c_1(\mathbf{p})=\frac{1}{2}{\mathbf{p}}^{T}A\mathbf{p}-{\mathbf{a}}^T\mathbf{p},$$

subject to

$$C\mathbf{p}=\mathbf{m}.$$

Note that m is a function of u₀ and u_f. Using Lagrange multipliers, the modified cost becomes

$$c_1^{\prime }(\mathbf{p},\mathbf{\lambda })=\frac{1}{2}{\mathbf{p}}^{T}A\mathbf{p}-{\mathbf{a}}^T\mathbf{p}+{\mathbf{\lambda }}^T(C\mathbf{p}-\mathbf{m}).$$

The solution is the one for which

$$\frac{\partial c_1^{\prime }}{\partial \mathbf{p}}=\mathbf{0}\text{and}\frac{\partial c_1^{\prime }}{\partial \mathbf{\lambda }}=0.$$

This can be written as

$$\left(\begin{array}{cc}A& C^T\\ C& O\end{array}\right)\left(\begin{array}{c}\mathbf{p}\\ \mathbf{\lambda }\end{array}\right)=\left(\begin{array}{c}\mathbf{a}\\ \mathbf{m}\end{array}\right)$$ (36)

or

$$\left(\begin{array}{c}\mathbf{p}\\ \mathbf{\lambda }\end{array}\right)={\left(\begin{array}{cc}A& C^T\\ C& O\end{array}\right)}^{-1}\left(\begin{array}{c}\mathbf{a}\\ \mathbf{m}\end{array}\right).$$

Then we can evaluate c₂(p) with p from (36). This evaluation can be written as

$$c=c_2(\underset{\mathbf{p}}{argmax}{c}_1(\mathbf{p})).$$ (37)

As mentioned earlier, u₀ and u_f in (35) are the free parameters. Therefore, evaluation of (37) requires the given values for u₀ and u_f. In other words, the function c in (37) can be treated as a function of u₀ and u_f. Thus we can minimize the cost with respect to u₀ and u_f. A nonlinear minimization method is required, but the computation is quite fast, because we have only two arguments, and computation of (36) and evaluation of (37) are fast.

4.2.2 POP Method with Splines

Now we will find a baseline trajectory fit to the spline. Basically, we will fit the intermediate positions of the needle trajectory to the corresponding locations on the spline.

Suppose the needle is inserted for time T with the unit insertion speed (υ(t) = 1). Then the insertion length is T. If we consider the M intermediate steps for the POP method, we can divide the spline into M pieces such that all pieces have the same arc length. Using these dividing points on the spline, we make the needle trajectory fit the spline. Specifically, the rotation angle for the i^th joint of the needle trajectory can be obtained by

$${\theta }_i=\underset{\theta \in [02\pi )}{argmax}\left|\right|q_i-r_i(\theta )\left|\right|$$ (38)

where q_i ∈ ℝ³ is the i^th dividing point on the spline and r_i(θ) is the 3D position of the i^th joint on the needle trajectory. Explicitly, r_i(θ) is defined as

$$\left(\begin{array}{cc}{R}_i& r_i(\theta )\\ {\mathbf{0}}^T& 1\end{array}\right)=\stackrel{\sim }{R}({\theta }_1)\circ h(\mathrm{\Delta }t)\circ \stackrel{\sim }{R}({\theta }_2)\circ h(\mathrm{\Delta }t)\cdots \stackrel{\sim }{R}({\theta }_{i-1})\circ h(\mathrm{\Delta }t)\circ \stackrel{\sim }{R}(\theta )\circ h(\mathrm{\Delta }t),$$

where h(Δt) ∈ SE(3) represents pure insertion without twisting for t = Δt = T/M. Using the rotation angles determined here, we can have the needle trajectory coarsely fit the spline. With this baseline trajectory, we apply the POP method to solve the path planning problem.

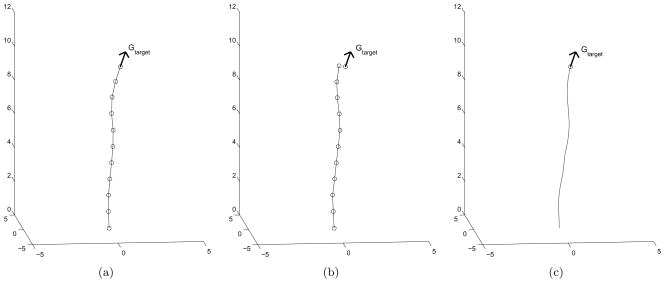
Fig. 5 shows an example of the POP method with a spline. The needle inserted at (0, 0, 0) along the z-axis (upward in the figure). G_target depicts the desired pose. The curve with circles in Fig. 5(a) shows a polynomial spline connecting the start and target positions with the desired pointing directions. The circles on the spline are the reference points from which the baseline trajectory is obtained. The baseline trajectory is shown in Fig. 5(b). Note that the baseline trajectory does not hit the target perfectly, but it reaches close. Finally the POP method gives a path hitting the target as shown in Fig. 5(c). 10 intermediate steps are used for the POP algorithm and the parameter values are κ = 0.157, λ = 0.1, ε₁ = 0.001 and ε₂ = 0.0001 as used in Section 4.1. Fig. 6 shows the additional path planning results when various targets are considered.

Figure 5.

A path produced by the POP algorithm with a spline. (a) A spline, (b) a baseline trajectory, (c) a path generated by the POP algorithm using the baseline trajectory from (b).

Figure 6.

Path planning using the POP algorithm with a spline for several desired targets.

The computation time for each path planning in this simulation is about 1.6 sec. We used a standard PC (Intel Core Duo processor 2.66GHz, 1GB memory) and Matlab programming. Since the whole trajectory consists of 10 intermediate insertions, this path planning can give the each intermediate insertion in about 0.16 sec. This fast computation is possible because of the closed-form formula for covariance matrix, the approximation of probability density function using a Gaussian, and the use of polynomial splines.

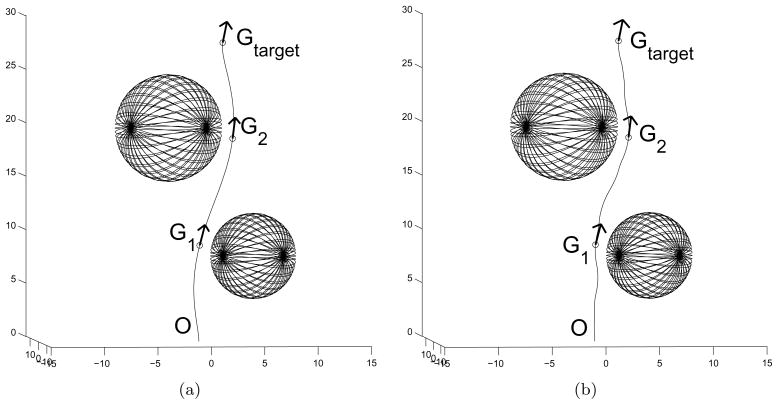
For a long general spline, we can apply the method above in a piecewise fashion. Suppose that we have a desired target (G_target) and two spherical obstacles and that an obstacle-avoiding spline connecting the starting and desired positions with the given pointing directions is obtained in some way as shown in Fig. 7(a). This spline may be a result of path planning for holonomic systems with obstacles or another method for needle path planning, even though we used (34) to generate the spline in this example. Next we choose two poses (G₁ and G₂) that the needle should pass through in order to avoid the obstacles. Then, we can obtain a path from O to G₁ using the POP method with a spline. We repeat it from G₁ to G₂, and from G₂ and G_target. The result is a trajectory from O to G_target via G₁ and G₂ as shown in Fig. 7(b). This example also demonstrates how we can apply our path planning approach to the environment with obstacles.

Figure 7.

(a) A long spline with a target and two obstacles, (b) a path generated by the POP algorithm with a spline in a piecewise fashion.

For more reliable avoidance, we can define obstacles with larger redundant area. Development of the systematic way to find a long spline that avoids obstacles is a subject of its own. We note that there is a huge literature for path planning of holonomic point robots using artificial potential fields or C-space methods among others. In principle, any such method could be used to generate the reference trajectory, and our method could be used on top. Therefore, while our specific implementation used a spline, this can be thought of as one instantiation of a more general approach.

As long as the probability flows along/near the spline without intersecting obstacles, the method works well. In principle, if there were narrow passages, the method would fail. The way around this would be to compute the evolution of probability densities that include obstacle boundaries after each push-twist move. This would be necessary if, for example, there is no port placement that can circumvent narrow passages. While it is possible to generate obstacle-avoiding probability flows for 3D searches (see [32]) that would preserve the non-greedy nature of POP even in cluttered environments, it would be computationally prohibitive for full 6D search. Therefore, we restrict our scope to exclude the case of narrow passages. This justifies the use of the port placement in Section 4.1, which gives significant freedom in the choice of insertion pose.

To see robustness of our algorithm and reflect the most recent stochastic needle model, we try to combine our planning method with the new needle model induced by the observation of real needle insertion. Consider the following needle model [23]:

$${(g^{-1}\stackrel{.}{g})}^{\vee }dt={\left(\begin{array}{cccccc}\kappa v_0& 0& {\omega }_0(t)& 0& 0& v_0\end{array}\right)}^{T}dt+{\left(\begin{array}{cccccc}0& 0& {\lambda }_1& 0& 0& 0\\ \kappa {\lambda }_2& 0& 0& 0& 0& {\lambda }_2\\ {\lambda }_3& 0& 0& 0& 0& 0\end{array}\right)}^T\left(\begin{array}{c}d{W}_1\\ d{W}_2\\ d{W}_3\end{array}\right)$$ (39)

with the parameters

$${\lambda }_1=0.0219,{\lambda }_2=0.04937,{\lambda }_3=0.0043,\kappa =\mathrm{0.062.}$$ (40)

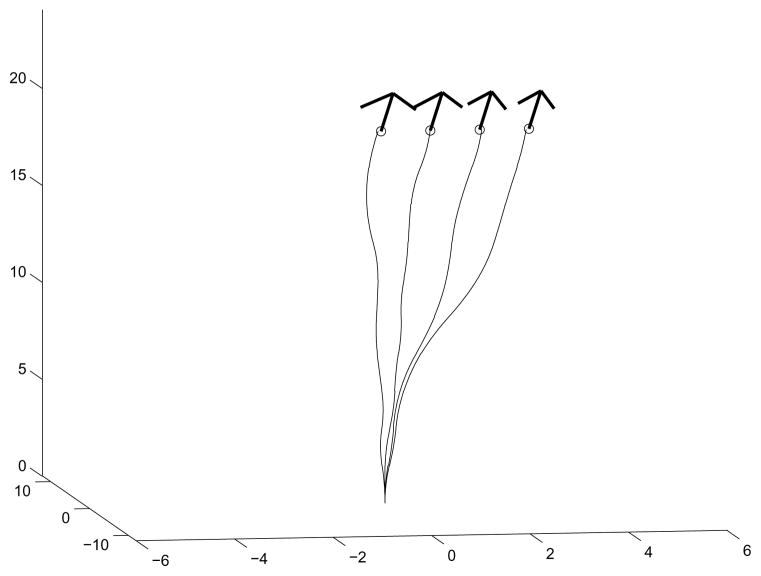
The model with three noise parameters was developed using the 3D position information of 100 needle trajectories that were detected by stereo vision [23]. The parameters were determined so that the needle model (39) best fits the 100 needle trajectories. Fig. 8 shows the path planning results using the needle model (39) and the parameter values (40), when various targets are considered.

Figure 8.

Path planning using the POP algorithm with a spline for several desired targets. In this path planning, the new needle model (39) and parameters (40) from [23] are used.

5 Conclusion

In this work, we proposed a new framework for path planning of flexible needles. This method primarily uses the path-of-probability algorithm with a closed-form probability density function. Based on the stochastic model for needle insertion, we approximate the probability density function for the needle tip pose with a shifted Gaussian distribution and obtain the mean and covariance for the probability density function using the second order error propagation theory. We derived the closed-form expression for the first order error propagation and used it to compute the inputs for the second order error propagation formula. This method enables fast computation of the covariance without sampling.

A nice feature of our planning method is that we can compute the insertion plan for intermediate steps in a serial manner. The insertion plan for the i^th intermediate step can be determined without considering the specific plan for the intermediate steps after the i^th step. This is possible because we consider the probability of the future insertion. For a given insertion plan for the 1^st, 2^nd, ···, (i − 1)^th steps, the insertion plan for the i^th intermediate step can be determined by maximizing the probability that the remaining insertion reaches the target. Using this feature, we demonstrated that the path planning method presented here can be applied to feedback control of the flexible needle. According to the insertion plan for the i^th intermediate step, we insert the needle and then measure the actual insertion that will be slightly different from the planed one. Based on the measured insertion, we move on to the determination of the insertion plan for the next step. In this process, the error in the actual i^th insertion will be corrected in the plan for the (i + 1)^th insertion.

In a simple case where there is no obstacle and we have full freedom to choose the insertion location and orientation, we solved the port placement problem and the POP algorithm provided a needle path. The simulation demonstrated that the planning method works when there are errors in the actual intermediate insertions as well as in the initial pose due to uncertainty. For more general case, a new method to use splines with the POP algorithm was developed. A spline is used to find a baseline needle path which the POP algorithm is applied to.

The computation efficiency is significantly improved compared to the previous work in [21]. In the previous work, one drawback was that we need to perform a 1D search for the roll angle of the target pose. The roll angle of the needle at the moment the needle hits the target is not important, because any roll angle at that moment can be achieved by twisting the needle after hitting the target. However, the mathematical formulation in (10) needs 6D full information including roll angles of the target pose. In this paper, we could avoid this difficulty by determining the reasonable value for the roll angle. In the port placement problem, the roll angle is determined so that the circular arc needle path has shortest length. When we use a spline with the POP algorithm, we can define the spline with the positions and pointing directions at the starting and target locations. Then the Frenet-Serret frame by the spline gives the appropriate roll angles. Therefore we do not need to perform a 1D search for the roll angle. The actual time consumption for the example in Fig. 5 is 1.6 sec, when we use a standard PC (Intel Core Duo processor 2.66GHz, 1GB memory) and Matlab programming. This calculation includes the computation of covariances and a spline as well as path generation by the POP algorithm.

The example in Fig. 7 shows that our method can be extended to the environment with obstacles. Suppose that we prepare a spline that avoids all obstacles. We can do this using classical ways of path planning with obstacle avoidance. Then we pick the important points on the spline which the needle will pass through. The piecewise approach shown in Fig. 7 can make the needle reach the target avoiding the obstacles. As future work, we plan to develop a more systematic method to incorporate obstacle-avoiding splines and the POP algorithm.

In many ways, our approach based on the path-of-probability method is similar to methods that use reachable sets (see e.g. [13]). The level curves of our probability densities can be viewed as boundaries of reachable sets associated with perturbations of each baseline trajectory. As in [13], the whole insertion which we seek is divided into several intermediate insertions. The planner (or controller) determines the intermediate insertions in a serial manner. For given current needle state and goal position, the next intermediate insertion is chosen based on a criterion.

In [13], from a set of proposed trajectories which are helices, one helix is selected that terminates closest to the goal position. A set of deterministic helical paths are considered and an optimal helix is selected. Actual insertion for Δt is performed, and it may be slightly different from the planned trajectory. The feedback controller computes the next insertion considering the actual needle state.

In contrast, our planner chooses an intermediate insertion using probability density functions (PDFs). In this method, we compute the PDF for the possible next insertions. This PDF comes naturally based on our stochastic modeling. The method in [13] assumes the deterministic path and compensates the insertion error after the actual insertion is performed. However, in our method, when the next insertion is considered, the possible noise in the actual insertion is also considered and is reflected in the choice of the next intermediate insertion. Furthermore, in our method, the desired direction of the needle can also be specified. The ability to specify the desired direction of the needle can be useful in medical procedures with flexible needles, although most path planning methods for flexible needles neglect this feature.

Appendix

We review the second order propagation formulas. The entire work including derivation appears in [31].

If a PDF, ρ_i(g), has mean μ_i and covariance Σ_i for i = 1, 2, then to second order, the mean and covariance of (ρ₁ *ρ₂)(g) are respectively [7]

$${\mu }_{1\ast 2}={\mu }_1\circ {\mu }_2\text{and}{\mathrm{\sum }}_{1\ast 2}=A+B+F(A,B),$$

where $A=Ad({\mu }_2^{-1}){\mathrm{\sum }}_{1}A{d}^T({\mu }_2^{-1})$, B= Σ₂. Here

$$F(A,B)=C(A,B)/4+(A^{″}B+{(A^{″}B)}^T+B^{″}A+{(B^{″}A)}^T)/12.$$

A″ is computed as

$$A^{″}=\left(\begin{array}{cc}{A}_{11}-\text{tr}(A_{11})I_3& 0_3\\ A_{12}+A_{12}^T-2\text{tr}(A_{12})I_3& A_{11}-\text{tr}(A_{11})I_3\end{array}\right),$$

where A_ij are 3 × 3 matrices holding

$$A=\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{12}^T& A_{22}\end{array}\right).$$

B″ is defined in the same way with B replacing A everywhere in the expression. The blocks of C are computed as

$$\begin{array}{c}{C}_{11}=-D_{11,11}\\ C_{12}=-{(D_{21,11})}^T-D_{11,12}=C_{21}\\ C_{22}=-D_{22,11}-D_{21,21}-{(D_{21.12})}^T-D_{11,22}\end{array}$$

where D_ij,kl = D(A_ij, B_kl), and the matrix-valued function D(A′, B′) is defined relative to the entries in the 3 × 3 blocks A′ and B′ as

$$\begin{array}{ll}{d}_{11}=-a_{33}^{\prime }{b}_{22}^{\prime }+a_{31}^{\prime }{b}_{32}^{\prime }+a_{23}^{\prime }{b}_{23}^{\prime }-a_{22}^{\prime }{b}_{33,}^{\prime }\hfill & d_{12}=a_{33}^{\prime }{b}_{21}^{\prime }-a_{32}^{\prime }{b}_{31}^{\prime }-a_{13}^{\prime }{b}_{23}^{\prime }+a_{21}^{\prime }{b}_{33}^{\prime }\hfill \\ d_{13}=-a_{23}^{\prime }{b}_{21}^{\prime }+a_{22}^{\prime }{b}_{31}^{\prime }+a_{13}^{\prime }{b}_{22}^{\prime }-a_{12}^{\prime }{b}_{32}^{\prime },\hfill & d_{21}=a_{33}^{\prime }{b}_{12}^{\prime }-a_{31}^{\prime }{b}_{32}^{\prime }-a_{21}^{\prime }{b}_{13}^{\prime }+a_{21}^{\prime }{b}_{33}^{\prime }\hfill \\ d_{22}=-a_{33}^{\prime }{b}_{11}^{\prime }+a_{31}^{\prime }{b}_{31}^{\prime }+a_{13}^{\prime }{b}_{13}^{\prime }-a_{11}^{\prime }{b}_{33}^{\prime },\hfill & d_{23}=a_{23}^{\prime }{b}_{11}^{\prime }-a_{21}^{\prime }{b}_{31}^{\prime }-a_{13}^{\prime }{b}_{12}^{\prime }+a_{11}^{\prime }{b}_{32}^{\prime }\hfill \\ d_{31}=-a_{32}^{\prime }{b}_{12}^{\prime }+a_{31}^{\prime }{b}_{22}^{\prime }+a_{22}^{\prime }{b}_{13}^{\prime }-a_{21}^{\prime }{b}_{23}^{\prime },\hfill & d_{32}=a_{32}^{\prime }{b}_{11}^{\prime }-a_{31}^{\prime }{b}_{21}^{\prime }-a_{12}^{\prime }{b}_{13}^{\prime }+a_{11}^{\prime }{b}_{23}^{\prime }\hfill \\ d_{33}=-a_{22}^{\prime }{b}_{11}^{\prime }+a_{21}^{\prime }{b}_{21}^{\prime }+a_{12}^{\prime }{b}_{12}^{\prime }-a_{11}^{\prime }{b}_{22}^{\prime }.\hfill & \hfill \end{array}$$