Abstract
The cingulate gyri in 37 subjects with and without early dementia of the Alzheimer type (DAT) were studied by using MRI at 1.0 mm3 isotropic resolution. Groups were segregated into young controls (n = 10), age-matched normal controls (n = 10), very mild DAT (n = 8), and mild DAT (n = 9). By using automated Bayesian segmentation of the cortex and gray matter/white matter (GM/WM) isosurface generation, tissue compartments were labeled into gray, white, and cerebrospinal fluid as a function of distance from the GM/WM isosurface. Cortical mantle distance maps are generated profiling the GM volume and cortical mantle distribution as a function of distance from the cortical surface. Probabilistic tests based on generalizations of Wilcoxon–Mann–Whitney tests were applied to quantify cortical mantle distribution changes with normal and abnormal aging. We find no significant change between young controls and healthy aging as measured by the GM volume and cortical mantle distribution as a function of distance in both anterior and posterior regions of the cingulate. Significant progression of GM loss is seen in the very mild DAT and mild DAT groups in all areas of the cingulate. Posterior regions show both GM volume loss as well as significant cortical mantle distribution decrease with the onset of mild DAT. The “shape of the cortical mantle” as measured by the cortical mantle distance profiles manifests a pronounced increase in variability with mild DAT.
Dementia of the Alzheimer type (DAT) becomes increasingly common with advancing age (1). However, there is increasing evidence that DAT represents a disease process that is separable from the process of healthy aging (2). The classical neuropathological signs of DAT include the widespread distribution of amyloid plaques and neurofibrillary tangles within the hippocampal formation and across many regions of the cerebral cortex (3, 4). In a previous neuroimaging study of elder subjects with and without early DAT (5), we found that differing patterns of hippocampal volume loss and shape distortion distinguish early DAT from healthy aging. Changes in the structure of the cerebral cortex have also been associated with both DAT and healthy aging (6–10). As we have shown, the cingulate gyrus seems to be involved in both DAT and healthy aging.
High-resolution MRI now affords an unprecedented opportunity to acquire detailed images of the neuroanatomical configurations and tissue characteristics of the living human brain. Automated methods for the analysis of the cerebral cortex have progressed to the point where several methods for accurate cortical mantle reconstruction via statistical decision methods exist (10–15). Connected subvolumes of the brain such as the deep nuclei (thalamus, hippocampus, ventricles, and others) are appropriately studied as 3D submanifolds. In contrast, the neocortical mantle has a thin laminar structure on the order of 3 mm in thickness with a large surface area, implying that viewing it as a thin shell, rather than as a strict subvolume, provides significant advantages in understanding the “shape of the cortical mantle.”
Methods for automated generation of 2D surface coordinate system on the cortex have improved dramatically as well (16–19). Natural local coordinates useful for studying the neocortex are the 2D submanifold associated with the gray matter/white matter (GM/WM) interface; the natural third dimension is then the normal coordinates measuring distance to the surface submanifold. Distance maps are created profiling the GM cortical mantle indexed by its distance along the normal axis to the GM/WM surface. Cortical “shape and thickness” are quantified via these maps, demonstrating significant sensitivity when used with Wilcoxon function tests for sensing GM volume and GM decrease with the onset of DAT. These distance transforms directly quantify “the thickness of the cortical mantle,” as well as the variability of GM volume as a function of localized coordinates of the neocortex.
Methods
Subjects and Imaging. The elder subjects enrolled in longitudinal studies of healthy aging at the Alzheimer Disease Research Center at Washington University School of Medicine. Members of families with genetic mutations known to be related to DAT, as well as subjects with symptoms of other neuropsychiatric disorders that could have confounded their diagnosis, were excluded. The younger healthy control subjects (YC) in this study (n = 10) were selected from a database of young adult controls that had originally been recruited for a study of schizophrenia. All subjects gave informed consent for their participation in this study after the risks and benefits of participation were explained to them. The elder subjects were assigned to three groups for neuroanatomical comparison: subjects with very mild DAT (n = 8), mild DAT (n = 9), and healthy elders with no evidence of dementia (n = 10). The subjects and available family members were interviewed by using the Clinical Dementia Rating Scale (CDR) (20). A CDR score of 0.5, 1, 2, or 3 indicates very mild, mild, moderate, or severe DAT, respectively; clinical designations have been validated by the neuropathological presence of DAT (21, 22). Subjects with no discernable evidence of dementia on the CDR were designated as healthy elder subjects with CDR 0. The subjects with mild dementia (CDR 1) were slightly older [mean (SD) age = 75.3 (6.1)] than the subjects with very mild dementia [i.e., CDR 0.5; mean (SD) age = 70.5 (2.7)] and the healthy elder subjects [mean (SD) age = 70.8 (1.8)]. The younger healthy subjects had a mean (SD) age of 25.6 (4.6). There were 12 males and 15 females among the elder subjects (with no substantial differences among the three groups), and there were 5 males and 5 females among the younger healthy subjects.
The population was examined by means of high-resolution magnetic resonance (MR) scans, which were acquired by using a turbo-FLASH sequence (repetition time = 20 ms, echo time = 5.4 ms, flip angle = 30°, number of acquisition = 1, matrix 256 × 256, scanning time = 13.5 min) with 1 mm3 isotropic resolution across the entire cranium (23). By using ANALYZE (24), raw MR data were reformatted from signed 16-bit to unsigned 8-bit and interpolated into 0.5 × 0.5 × 0.5-mm3 isotropic voxels by using trilinear interpolation.
Anatomic Definition of Anterior and Posterior Cingulate Gyrus. Delineation of the cingulate is made primarily from MR slices oriented in the coronal plane. The cingulate gyrus is separated into anterior and posterior segments by a plane perpendicular to and bisecting the line connecting the anterior and posterior commissure. For the anterior cingulate gyrus, the anterior limit is defined as the most rostral coronal section through the septum pellucidum; the superior limit is the cingulate sulcus. For the posterior cingulate gyrus, starting at the anterior end of the calcarine sulcus below the splenium, it follows posteriorly the bank of the calcarine until reaching the bifurcation point where the calcarine sulcus branches into the parietal-occipital sulcus. Moving upwards, the posterior cingulate gyrus follows the bank of subparietal sulcus as it traces out a curve parallel to the corpus callosum (see Supporting Text, which is published as supporting information on the PNAS web site).
Segmentation and Surface Generation. A Bayesian segmentation using the expectation-maximization algorithm (11) to fit the compartmental statistics is used to segment voxels as GM, WM, and cerebrospinal fluid (CSF). Surfaces are generated at the GM/WM interface by using isosurface generation algorithms (12, 13). Dynamic programming (25) is used to delineate the boundaries of the anterior and posterior cingulate on the generated surface. By using the distance calculation algorithm (13), the labeled voxel closest to the vertex in the original surface is determined and assigned to the region (anterior or posterior) that the closest vertex corresponds to.
Labeled Cortical Mantle Distance (CMD) Maps. The neocortical mantle is defined by the relatively thin laminar coadjacency of GM voxels (roughly 3 mm) relative to WM and CSF. The laminar shape of the neocortex is quantified by generating labeled cortical mantle distance maps (LCMDMs), labeling every voxel by the tissue type GM, WM, and CSF that it belongs to and its distance to the GM/WM surface. For this result, two natural coordinate systems interact: the coordinates xn ∈ X ⊂ IR3 representing the regular lattice of voxels and the 2D manifold S (Δ) ⊂ IR3 representing the smooth boundary at the GM/WM interface. Associated with S(Δ) is a third axis Ns, s ∈ S(Δ) that is normal to every point s ∈ S(Δ). On this axis are the points that are minimum distance defined by the set distance function d:xn ∈ X → d(xn) ∈ (-max,+max) representing the distance between xn ∈ X and S(Δ):
 |
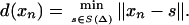[1] |
Positive and negative values along the normal direction of the local surface coordinate system mean distances as measured inside vs. outside of the cortical surface. As described in ref. 13, the distances are real-valued given by the voxel centers to the closest triangle vertex calculated by means of geometry and are used to generate the histograms calculated below.
The LCMDMs form a secondary data structure (separable from the MRI image) of the same dimension as the MRI volume consisting of the labeled pair (d,l):X → IR × {GM, WM, CSF}. The pair d(xn), l(xn) at each voxel xn ∈ X is the distance of the voxel center xn to the triangulated graph coordinate system and the associated compartment type of the voxel.
CMD Profiles. From the LCMDMs direct measures of volume and of cortical GM distribution as a function of position relative to the cortical surface can be calculated via histograms hG(D), D∈[-max,+max] generated by counting the total amount of GM as a function of distance from the surface:
 |
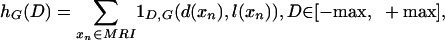[2] |
where the indicator 1D,G(d,l) = 1 if d = D,l = G. The GM volume is simply the total summed histogram GVOL = ΣD hG(D). Normalizing the histograms by GVOL generates a normalized function fG(D); integrating the density gives a distribution function FG(D):
 |
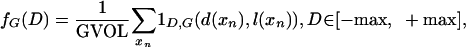[3] |
 |
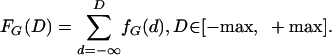[4] |
Wilcoxon Testing on CMDs for Stochastic Ordering. To quantify the change in CMD profiles, statistical testing on all of the stochastic values is performed directly on the CMDs profiling the occurrence of GM as a function of position. The Wilcoxon–Mann–Whitney (26–28) tests the null hypothesis that the distance values for each class of GM CMD profiles come from the same distribution. A random variable X, with cumulative distribution function F, is said to be stochastically larger than random variable Y with cumulative distribution function H if F(x) ≤ H(x) for all x, with strict inequality for at least one x (28). The rank-sum test is a test for stochastic ordering; a significant P value resulting from the Wilcoxon test performed on two cumulative distributions indicates stochastic ordering supporting the hypothesis that the greater percentage of GM voxels occupy smaller distances and corresponds to cortical mantle thinning.
Wilcoxon rank-sum is a nonparametric statistical test; it does not assume data come from a particular distribution as it is based on replacing data by ranks, eliminating distributional assumptions, thereby controlling the influence of extreme values. Samples are compared from two populations under the null hypothesis that the samples come from the same distribution (26); the alternative hypothesis is that the population with the larger CDR score has lower distance values in the CMDs, representing cortical mantle thinning. The data from two populations are ranked together from smallest to largest; the test statistic W is the sum of the ranks of the population hypothesized to have lower distance values. Then W approaches normality as population sizes increase with a mean of μ = [n(n + m + 1)/2], and a variance of σ2 = [nm(n + m + 1)/12], where n is the size of the population with ranks summed to create W, and m is the size of the other population in question. The value (W - μ)/σ can be compared with the unit normal distribution in a one-sided fashion to yield the probability that a sum of ranks with a value W or lower would occur when both populations are from the same distribution. For P ≤ 0.05, the null hypothesis is rejected (29).
For computational reasons, the P values of Wilcoxon tests using the full samples were approximated by performing multiple Wilcoxon tests on subsamples of data from each population. The final P value reported, the average of P values from multiple Wilcoxon tests on data subsamples, is an unbiased estimator of the mean P value for the subsample size and approximates the P value of the Wilcoxon test incorporating all data values.
Automated segmentation is most reliable for the GM close to the WM because of contrast; large distances have higher error rates in the labeling between GM/CSF compartments. Wilcoxon tests were run on censored data: that is, all data values below a set censoring distance. The P values were computed for all combinations with censoring distances in the range 0.25-5mm in intervals of 0.5mm. Censoring distances in the range 3-3.5 mm corresponded to minimum P values, indicating a minimization of both the segmentation error and information loss, and represent a range of optimal censoring distances (30).
Wilcoxon Testing on Cortical Distance Distribution Variation with Disease. To test variability increase with aging, the CMDs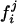 
(i = subject, j = group) are pointwise averaged, yielding a mean CMD normalized profile f̄j for each group YC, CDR 0, CDR 0.5, CDR 1. The censored integrated absolute error
 |
[5] |
yields a scalar measure of the variability of subject i within group j. The Wilcoxon–Mann–Whitney robust one-sided test of location is calculated; the null hypothesis is that the mean of group j variabilities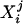 
is equal to the mean of group j′ variabilities 
.
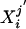Results
Accuracy of LCMDMs. Accuracy of LCMDMs and resulting histograms hG(D) depends on both segmentation labeling and isosurface generation (Fig. 1 A–C). For cingulate subvolumes, segmentation has been validated with classification errors in the range 0.06-0.12 (12), and isosurface generation has been validated in which >75% of surface vertices are within a half voxel of hand-contours (12). Fig. 1D shows how closely the surface follows the GM/WM boundary. Hand and automated LCMDM profiles show virtually identical profiles (Fig. 1D). Almost all of the WM occurs at negative distances (D < 0 mm) except for the partial volume voxels; almost all of the GM voxels occur at D ∈ [0 mm, 3 mm]; the CSF compartment occurs at D ≥ 2 mm.
Fig. 1.
Accuracy of LCMDMs. (A) MRI section of a cingulate gyrus. (B) Segmentation into GM/WM/CSF. (C) Embedded Isosurface. (D) Histogram profiles h(Distance) for hand (dashed) and automated (solid) labeled W (green), G (red), and CSF (blue).
Variability of Cortical Mantle Distance Profiles. The total GM volume is a separate statistic from the CMD profile quantifying the laminar thickness and extent or position of the cortical mantle. The CMD profiles fG, FG, which are normalized by the total volume, provide profiles of GM distribution as a function of distance independent of total GM volume (Fig. 2 A and B). Normalizing the CMD histograms (Fig. 2 B and C) decreases the variability and stabilizes the measure of GM occurrence vs. distance.
Fig. 2.
CMD density and distribution profiles. (A) Normalized CMD profile f(Distance) from a left posterior surface for the YC group. (B) Corresponding CMD distribution F(Distance) representing the percentage of GM as a function of distance from the cortical surface. (C) Nonnormalized histograms h(Distance) for the right anterior in the CDR 0 group. (D) The corresponding normalized CMD profile. Averaged f̄(Distance) shown in thick black line in C and D.
GM Loss in the Anterior and Posterior Cingulate Areas. The LCMDMs are calculated for the subvolumes representing the anatomically defined anterior and posterior regions of the cingulate gyrus. Average LCMDMs gray matter profiles h̄G for the gray matter were generated as a function of distance from the GM/WM surface by averaging the profiles over the group. The averaged GM histogram profiles h̄G generated from the four groups illustrate clear decreases in the GM profile (Fig. 3 A–D). There is a systematic shift in total GM volume from YC to CDR 0, CDR 0.5, and CDR 1 as manifested by the systematic downward shift of the profiles. This shift with onset of aging and abnormal aging is also seen in the total GM volume (Fig. 3 E–H).
Fig. 3.
(A–D) Averages of GM histograms h̄G as a function of distance from the left anterior (A), right anterior (B), left posterior (C), and right posterior (D) surfaces for each of the four groups. (E and F) GM volumes GVOL for corresponding regions.
GM reduction was statistically examined by comparing the cumulative number of GM voxels between groups. One-sided t tests hypothesized that the distribution of GVOL is normal, with the alternative being that the class with a lower CDR would have a greater number of GM voxels. There is no evidence for rejection of the null hypothesis for GM volume differences between the YC and the CDR 0 groups (Fig. 3 and Table 1); there is systematic and consistent evidence for the rejection of the null hypothesis that the volumes are identical between YC-CDR 0 vs. the CDR 0.5 and CDR 1 groups (Table 1).
Table 1. t test for cingulate volumes for YC and CDR 0 groups compared with CDR 0.5 and CDR 1 groups.
| Cingulate area | Class | P value | Class | P value |
|---|---|---|---|---|
| Left anterior | YC vs. 0.5 | 0.6304 | 0 vs. 0.5 | 0.6023 |
| Left posterior | YC vs. 0.5 | 0.0327 | 0 vs. 0.5 | 0.0692 |
| Right anterior | YC vs. 0.5 | 0.0418 | 0 vs. 0.5 | 0.0523 |
| Right posterior | YC vs. 0.5 | 0.0208 | 0 vs. 0.5 | 0.0493 |
| Left anterior | YC vs. 1 | 0.0453 | 0 vs. 1 | 0.0728 |
| Left posterior | YC vs. 1 | 0.0001 | 0 vs. 1 | 0.0006 |
| Right anterior | YC vs. 1 | 0.0073 | 0 vs. 1 | 0.0108 |
| Right posterior | YC vs. 1 | 0.0025 | 0 vs. 1 | 0.0060 |
Cortical Mantle Distance Distributions Change with DAT. The CMD distributions signal cortical volume depletion as a function of distance from the GM/WM surface. When compared with the YC group, cortical mantle distribution in the CDR 1 group decreases with larger distances (Fig. 4 A–D). The horizontal shift of the distributions clearly indicates thinning between these two groups, which is also seen when comparing CDR 0 and CDR 1 subjects (Fig. 4 E–H).
Fig. 4.
Averaged CMD distributions F̄(Distance). (A–D) YC vs. CDR 1; (E–H) CDR 0 vs. CDR 1. Columns correspond to left anterior, right anterior, left posterior, and right F posterior regions, respectively.
The Wilcoxon–Mann–Whitney test on stochastic order was performed several times on the subsamples of the data for each group. Consistent with the volume results, there is no evidence for rejection of the null hypothesis for the YC vs. CDR 0 groups (Table 2). In sharp contrast, there is significant evidence for rejection of the null hypothesis for the YC or CDR 0 vs. CDR 1 groups for the one-sided rank-sum test (Table 2). Stochastic ordering exists between the YC and CDR 1 groups in all four cingulate regions; similar results hold between CDR 0 and CDR 1 groups.
Table 2. One-sided Wilcoxon test for D ≤ 3 mm. Sample sizes of 1,000 chosen without replacement from each population and P values averaged over 50 trials.
| Cingulate area | Class | P value | Class | P value |
|---|---|---|---|---|
| Left anterior | YC vs. 0.5 | 0.2118 | 0 vs. 0.5 | 0.3769 |
| Left posterior | YC vs. 0.5 | 0.4365 | 0 vs. 0.5 | 0.5971 |
| Right anterior | YC vs. 0.5 | 0.0693 | 0 vs. 0.5 | 0.1219 |
| Right posterior | YC vs. 0.5 | 0.2923 | 0 vs. 0.5 | 0.5837 |
| Left anterior | YC vs. 1 | 0.0209 | 0 vs. 1 | 0.0530 |
| Left posterior | YC vs. 1 | 0.0048 | 0 vs. 1 | 0.0070 |
| Right anterior | YC vs. 1 | 0.0009 | 0 vs. 1 | 0.0156 |
| Right posterior | YC vs. 1 | 0.0019 | 0 vs. 1 | 0.0216 |
Cortical Mantle Variation with Disease Onset. The GM CMD distributions signal the result of biological change sensitively with aging. There is disintegration in the regularity of the CMD profile as a function of onset for CDR 1 (Fig. 5, rows 1–3 compared with row 4). By using the Wilcoxon–Mann–Whitney robust one-sided test of location testing the null hypothesis that the mean of the group j variabilities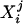 
from Eq. 5 is equal to the mean of the group j′ variabilities 
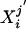, similar trends are found as before. There is no evidence for increased variability with normal aging in the YC vs. CDR 0 groups (Table 3); the null hypothesis is not rejected. In sharp contrast, the null hypothesis is rejected with significance when considering the YC or CDR 0 against the CDR 1 groups (Table 3). Again, greatest sensitivity is manifest in the posterior regions for rejection of the null hypothesis in comparing YC and CDR 0 with the CDR 1 cohort; variability increases as dementia progresses, with strong P value rejection of the null hypothesis.
Fig. 5.
CMD profiles f(Distance) for YC (A–D), CDR 0 (E–H), CDR 0.5 (I–L), and CDR 1 (J–M). Columns, from left to right, correspond to left anterior, left posterior, right anterior, and right posterior regions, respectively. The thick black line f̄(Distance) indicates the averaged profile.
Table 3. One-sided Wilcoxon test D ≤ 3 mm for profile randomness.
| Cingulate area | Class | P value | Class | P value |
|---|---|---|---|---|
| Left anterior | YC vs. 0.5 | 0.1371 | 0 vs. 0.5 | 0.6518 |
| Left posterior | YC vs. 0.5 | 0.4143 | 0 vs. 0.5 | 0.6191 |
| Right anterior | YC vs. 0.5 | 0.3809 | 0 vs. 0.5 | 0.7426 |
| Right posterior | YC vs. 0.5 | 0.4143 | 0 vs. 0.5 | 0.7426 |
| Left anterior | YC vs. 1 | 0.0175 | 0 vs. 1 | 0.3598 |
| Left posterior | YC vs. 1 | 0.0000 | 0 vs. 1 | 0.0007 |
| Right anterior | YC vs. 1 | 0.0001 | 0 vs. 1 | 0.0015 |
| Right posterior | YC vs. 1 | 0.0015 | 0 vs. 1 | 0.0051 |
CMD Distribution Profiles Provide Powerful Discrimination over Volume. The CMD distributions profile complementary information for discrimination of the groups that the volume data alone does not provide. There is no significant difference between the YC and CDR 0 groups. There is a statistically significant difference between the CDR 0.5 and the CDR 1 groups (Table 4). The stochastic ordering clearly discriminates the right posterior region, with P = 0.0242, whereas the volume data does not. The variability testing discriminates left posterior, right anterior, and right posterior regions at P = 0.0039, P = 0.0039, and P = 0.01, respectively (Table 4). The complementary information from these various methods permits visual discrimination between the various groups. The CMD distributions in the CDR 0.5 group (Fig. 5 I–L) vary much less than that in the CDR 1 groups (Fig. 5 M–P).
Table 4. t test volume, one-sided Wilcoxon test on stochastic ordering, and one-sided Wilcoxon test for profile randomness.
| Cingulate area | Volume | Stochastic ordering | Randomness |
|---|---|---|---|
| Left anterior 0.5 vs. 1 | 0.0302 | 0.0811 | 0.1852 |
| Right anterior 0.5 vs. 1 | 0.1845 | 0.1419 | 0.0039 |
| Left posterior 0.5 vs. 1 | 0.0231 | 0.0244 | 0.0039 |
| Right posterior 0.5 vs. 1 | 0.1049 | 0.0242 | 0.0103 |
Discussion
There is rapidly emerging evidence that automated methods can be used for both tracking of and early diagnosis of development and disease onset as manifest in the cortex. The pioneering work of the Massachusetts General Hospital and University of California at Los Angeles groups demonstrates that gross cortical mantle changes during Huntington's disease (31) and DAT (32), respectively, can be measured via methods for computing cortical thickness over the entire cortex. Our methods described here provide complementary information for studying in local coordinates (33) the evolutionarily stable submanifold gyri of the neocortex. The results we have presented demonstrate that using distance transforms to profile separately cortical volumes and cortical mantle distribution as a function of distance from the GM/WM surface provides sensitive metrics for studying the laminar structure of the cortical mantle. Because of the precision and locality of the distance transform, the sharp distinction between normal aging and the mild DAT categories in small samples has been demonstrated. Specifically, we find the following: (i) There is no significant difference between YC and normal aging (CDR 0) as manifest by the GM volume and the CMD distribution. (ii) Cortical GM decreases significantly in all areas of the cingulate studied for very mild DAT (CDR 0.5) compared with YC or normal aging (CDR 0). (iii) CMD profiling demonstrates significant GM decreases with distance as measured by stochastic ordering of the CMDs between the mild DAT (CDR 1) and normal aging (CDR 0) groups. (iv) The shape of the cortical mantle increases in variability with mild DAT compared with YCs and the normal aging group. (v) The CMD distributions are sharp discriminators between populations carrying complementary information to the total GM volume. Stochastic ordering of cortical thinning and stochastic variability are sharply different between the CDR 0.5 and CDR 1 groups.
Interestingly, none of the analyses suggest that healthy aging is associated with a reduction in either the total GM volume or CMD distribution as a function of the cingulate gyrus. Volume quantification in the anterior and posterior segments of the cingulate gyrus showed that the subjects with early DAT (i.e., the CDR 0.5 and CDR 1 groups), but not the nondemented elder subjects, had significant reductions compared with healthy younger subjects. Similar results were obtained by quantifying the CMD distribution profiles.
The cortical distance maps allow for the separate assessment of cortical volumes and cortical mantle density as a function of distance from the GM/WM surface in MR scans collected from living human subjects. The results of this study do not permit us to conclude what types of cellular changes might be associated with losses of cortical volume but not thickness, as was found in the CDR 0.5 subjects. The lack of a significant difference in cortical thickness could have been the result of a type II error, given the relatively small sample size. However, if cortical volume was reduced without a change in thickness, the possibility of a change in the cross-sectional area of the cingulate gyrus should be considered. In DAT, the degeneration of neuronal synapses and neuronal processes, and the shrinkage of neuronal cell bodies of neurons may precede the actual death and elimination of neurons in DAT for a substantial period (4). Based on our findings, it is intriguing to speculate that such sublethal cellular changes may be detectable as cortical volume decreases without thinning, with the ultimate loss of neurons eventually reflected by cortical thinning. Clearly, studies where antemortem and postmortem data are both available in the same DAT subjects and controls will be needed to test this hypothesis.
Finally, changes in cortical volume and CMD distribution may occur separately in other neuropsychiatric disorders. For example, in neurodevelopmental disorders such as schizophrenia and autism, the organization of the cortex may be altered without an overall loss of cortical neurons or volume (34, 35). In such circumstances, a thinning (or thickening) of local regions of the cortex may be present without overall changes in the volume of such regions. Tools, such as the labeled cortical distance maps, will increase our ability to study such phenomena by improving the discrimination between groups of subjects with and without disease, and ultimately by helping to identify the cellular processes underlying specific brain diseases.
Supplementary Material
Acknowledgments
We thank the Mayo Foundation for providing analyze. This work was supported by Public Health Service Grants MH56584 (to J.G.C.), MH/AG 60883 (to J.G.C.), AG03931 (to J.C.M.), GDSGR1 (to J.C.M.), MH62130 (to J.G.C. and M.I.M.), P41 RR15241-01A1 (to M.I.M. and J.T.R.), and P41 RR15241-02S1 (to M.I.M.), and by a Johns Hopkins University Provost Undergraduate Research Award (to A.R.B.).
Abbreviations: CMD, cortical mantle distance; LCMDM, labeled CMD map; DAT, dementia of the Alzheimer type; GM, gray matter; WM, white matter; YC, younger healthy control subjects; CDR, Clinical Dementia Rating Scale; MR, magnetic resonance; CSF, cerebrospinal fluid.
References
- 1.Cummings, J. L & Cole, G. (2002) J. Am. Med. Assoc. 287, 2335-2338. [Google Scholar]
- 2.Morris, J. C. (1999) J. Clin. Invest. 104, 1171-1173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Arnold, S. E., Hyman, B. T., Flory, J, Damasio, A. R. & Van Hoesen, G. W. (1991) Cereb. Cortex 1, 103-116. [DOI] [PubMed] [Google Scholar]
- 4.Price, J. L & Morris, J. C. (1999) Ann. Neurol. 45, 358-368. [DOI] [PubMed] [Google Scholar]
- 5.Csernansky, J. G., Wang, L, Joshi, S, Miller, J. P., Gado, M, Kido, D, McKeel, D, Morris, J. C. & Miller, M. I. (2000) Neurology 55, 1636-1643. [DOI] [PubMed] [Google Scholar]
- 6.Du, A. T., Schuff, N., Amend, D., Laakso, M. P., Hsu, Y. Y., Jagust, W. J., Yaffe, K., Kramer, J. H., Reed, B., Norman, D., et al. (2001) J. Neurol. Neurosurg. Psychiatry 71, 441-447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gosche, K. M., Mortimer, J. A., Smith, C. D., Markesbery, W. R. & Snowdon, D. A. (2002) Neurology 58, 1476-1482. [DOI] [PubMed] [Google Scholar]
- 8.Baron, J. C., Chetelat, G, Desgranges, B, Perchey, G, Landeau, B, de la Sayette, V & Eustache, F. (2001) NeuroImage 14, 298-309. [DOI] [PubMed] [Google Scholar]
- 9.Good, C. D., Johnsrude, I. S., Ashburner, J, Henson, R. N., Friston, K. J. & Frackowiak, R. S. (2001) NeuroImage 14, 21-36. [DOI] [PubMed] [Google Scholar]
- 10.Sowell, E. R., Peterson, B. S., Thompson, P. M., Welcome, S. E., Henkenius, A. L. & Toga, A. W. (2003) Nat. Neurosci. 6, 309-315. [DOI] [PubMed] [Google Scholar]
- 11.Joshi, M., Cui, J., Doolittle, K., Joshi, S., van Essen, D. C., Wang, L. & Miller, M. I. (1999) NeuroImage 9, 461-476. [DOI] [PubMed] [Google Scholar]
- 12.Miller, M. I., Massie, A., Ratnanather, J. T., Botteron, K. N. & Csernansky, J. G. (2000) NeuroImage 12, 676-687. [DOI] [PubMed] [Google Scholar]
- 13.Ratnanather, J. T., Botteron, K. N., Nishino, T, Massie, A. B., Lal, R. M., Patel, S. G., Peddi, S, Todd, R. D. & Miller, M. I. (2001) NeuroImage 14, 1058-1069. [DOI] [PubMed] [Google Scholar]
- 14.Teo, P. C., Sapiro, G & Wandell, B. A. (1997) IEEE Trans. Med. Imaging 16, 852-863. [DOI] [PubMed] [Google Scholar]
- 15.Fischl, B., Salat, D. H., Busa, E., Albert, M., Dieterich, M., Haselgrove, C., van der Kouwe, A., Killanay, R., Kennedy, D., Klaveness, S., et al. (2002) Neuron 33, 341-355. [DOI] [PubMed] [Google Scholar]
- 16.van Essen, D. C., Drury, H., Joshi, S. & Miller, M. I. (1998) Proc. Nat. Acad. Sci. USA 95, 788-795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fischl, B, Sereno, M. I., Tootell, R. B. H. & Dale, A. M. (1999) Human Brain Mapping 8, 272-284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hurdal, M. K., Bowers, P. L., Stephenson, K., Sumners, D. L., Rehm, K., Schaper, K. & Rottenberg, D. A. (1999) in In: Lecture Notes in Computer Science, eds. Taylor, C. & Colchester, A. (Springer, Berlin), pp. 279-286.
- 19.van Essen, D. C., Lewis, J. W., Drury, H. A., Hadjikhani, N. A., Tootell, R. L., Bakircioglu, M. & Miller, M. I. (2001) Vision Res. 41, 1359-1378. [DOI] [PubMed] [Google Scholar]
- 20.Morris, J. C. (1993) Neurology 43, 2412-2414. [DOI] [PubMed] [Google Scholar]
- 21.Berg, L, McKeel, D. W., J, Miller, J. P., Storandt, M., Rubin, E. H., Morris, J. C., Baty, J., Coats, M., Norton, J., Goate, A. M., et al. (1998) Arch. Neurol. 55, 326-335. [DOI] [PubMed] [Google Scholar]
- 22.Morris, J. C., Storandt, M., Miller, J. P., McKeel, D. W., Price, J. L., Rubin, E. H. & Berg, L. (2001) Arch. Neurol. 58, 397-405. [DOI] [PubMed] [Google Scholar]
- 23.Venkatesan, R. & Haacke, E. M. (1997) Int. J. Imaging Syst. Technol. 8, 529-543. [Google Scholar]
- 24.Robb, R. A., Hanson, D. P., Karwoski, R. A., Larson, A. G., Workman, E. L. & Stacy, M. C. (1989) Comput. Med. Imaging. Graph. 13, 433-454. [DOI] [PubMed] [Google Scholar]
- 25.Khaneja, N., Grenander, U. & Miller, M. I. (1998) Pattern Anal. Machine Intell. 20, 1260-1264. [Google Scholar]
- 26.Wilcoxon, F. (1945) Biometrics Bull. 1, 80-83. [Google Scholar]
- 27.Mann, H. B & Whitney, D. R. (1947) Ann. Math. Stat. 18, 50-60. [Google Scholar]
- 28.Lehmann, E. L. (1998) Nonparametrics (Prentice-Hall, Englewood Cliffs, NJ).
- 29.Bradley, J. V. (1968) Distribution-Free Statistical Tests. (Prentice-Hall, Englewood Cliffs, NJ).
- 30.Barker, A. R. (2003) Masters thesis (The Johns Hopkins University, Baltimore, MD).
- 31.Rosas, H. D., Liu, A. K., Hersch, S., Glessner, M., Ferrante, R. J., Salat, D. H., van der Kouwe, A., Jenkins, B. G., Dale, A. M. & Fischl, B. (2002) Neurology 58, 695-701. [DOI] [PubMed] [Google Scholar]
- 32.Thompson, P. M., Hayashi, K. M., de Zubicaray, G., Janke, A. L., Rose, S. E., Semple, J., Herman, D., Hong, M. S., Dittmer, S. S., Doddrell, D. M. & Toga, A. W. (2003) J. Neurosci. 23, 994-1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ratnanather, J. T., Barta, P. E., Honeycutt, N. A., Lee, N., Morris, H. M., Dziorny, A. C., Hurdal, M. K., Pearlson, G. D. & Miller, M. I. (2003) NeuroImage 20, 359-377. [DOI] [PubMed] [Google Scholar]
- 34.McGlashan, T. H & Hoffman, R. E. (2000) Arch. Gen. Psychiatry 57, 637-648. [DOI] [PubMed] [Google Scholar]
- 35.Piven, J., Berthier, M. L., Starkstein, S. E., Nehme, E., Pearlson, G. & Folstein, S. (1990) Am. J. Psychiatry 147, 734-739. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.