Abstract
Mechanical cues are known to regulate tissue differentiation during skeletal healing. Quantitative characterization of this mechano-regulatory effect has great therapeutic potential. This study tested an existing theory that shear strain and interstitial fluid flow govern skeletal tissue differentiation by applying this theory to a scenario in which a bending motion applied to a healing transverse osteotomy results in cartilage, rather than bone, formation. A 3-D finite element mesh was created from micro-computed tomography images of a bending-stimulated callus and was used to estimate the mechanical conditions present in the callus during the mechanical stimulation. Predictions regarding the patterns of tissues—cartilage, fibrous tissue, and bone—that formed were made based on the distributions of fluid velocity and octahedral shear strain. These predictions were compared to histological sections obtained from a previous study. The mechano-regulation theory correctly predicted formation of large volumes of cartilage within the osteotomy gap and many, though not all patterns of tissue formation observed throughout the callus. The results support the concept that interstitial fluid velocity and tissue shear strain are key mechanical stimuli for the differentiation of skeletal tissues.
Keywords: Mechanobiology, Finite element analysis, Mechanical stimulation, Mesenchymal stem cell, Bending motion, Pseudarthrosis
1 Introduction
Mechanical stimulation of a bone fracture can alter the course of tissue differentiation (Cullinane et al. 2002; Goodship and Kenwright 1985; Hente et al. 2004). Quantitative characterization of this mechano-regulatory effect has great therapeutic potential. Mechano-regulation theories are already being applied to the design of tissue engineering scaffolds (Byrne et al. 2007; Kelly and Prendergast 2006; Lacroix et al. 2006). These theories also inform investigation of the effects of early versus delayed weight bearing on bone healing (Bailon-Plaza and Van der Meulen 2003). Identification of the mechanical stimuli that control the differentiation of skeletal tissue could also help elucidate the molecular mechanisms by which mesenchymal stem cell fate is determined. Thus, study of the effect of mechano-regulation on skeletal tissue differentiation during fracture healing may lead to enhanced understanding of stem cell mechanotransduction as well as improved treatment of orthopedic injuries and bone and joint degeneration.
Several mechano-regulation theories of skeletal tissue differentiation have been developed that predict many aspects of bone healing under various mechanical conditions. Early theories were proposed by Perren and Cordey (1980), Carter et al. (1988), and Blenman et al. (1989). More recently, Prendergast et al. (1997) proposed that combinations of interstitial fluid velocity and octahedral shear strain govern the course of tissue differentiation (Prendergast et al. 1997). Carter et al. (1998) and Claes and Heigele (1999) put forth mechano-regulation theories based on hydrostatic stress and tensile strain. For axial loading of a transverse osteotomy, these latter three theories predicted very similar patterns of tissue formation, and these patterns that were in general agreement with histological observations (Carter et al. 1998; Claes and Heigele 1999; Isaksson et al. 2006b; Lacroix and Prendergast 2002). Further, in comparing these latter three theories, Isaksson et al. (2006b) demonstrated that an algorithm based solely on shear strain resulted in predictions very similar to those of the Prendergast theory (Isaksson et al. 2006b). However, a subsequent study that investigated torsional loading of a transverse osteotomy indicated that the Prendergast theory yielded much more accurate predictions than those resulting from theories based on hydrostatic stress and tensile strain or on shear strain alone (Isaksson et al. 2006a). The Prendergast theory has also been applied to distraction osteogenesis, healing of an osteochondral defect, and healing at a bone-implant interface (Isaksson et al. 2007; Kelly and Prendergast 2005; Prendergast et al. 1997). However, to our knowledge, the ability of this theory to describe impairment of bone healing via mechanical loading has yet to be explored. This type of investigation is important in that it would gauge how comprehensive the mechano-regulation theory is over the wide spectrum of skeletal healing responses.
The goal of this study was to test the Prendergast mechano-regulation theory in a scenario in which mechanical stimulation is used to inhibit bone healing. Previous work has demonstrated that cyclic bending motion applied to an osteotomy gap results in formation of cartilage, rather than bone, within the gap (Cullinane et al. 2002, 2003). Thus, the first objective of this study was to use the Prendergast theory to simulate the effect of the bending motion on healing and to compare the simulation results to existing experimental observations. The second objective of this study was to investigate the individual contributions of the two stimuli—octahedral shear strain and fluid velocity—to the course of tissue differentiation that results from the bending stimulation.
2 Materials and methods
A 3-D finite element model was created to simulate the in vivo mechanical conditions within a rat femoral fracture callus during bending stimulation. The left femur that the model was based on had undergone production of a 1.5 mm, full-thickness transverse osteotomy followed by stabilization with an external fixator, a ten-day latency period, and four weeks of mechanical stimulation. The stimulation protocol consisted of ±30° bending in the sagittal plane about the center of the osteotomy at 1 Hz for ten minutes per day, five days a week for four weeks. Details regarding the surgical procedure have been published elsewhere (Salisbury et al. 2005).
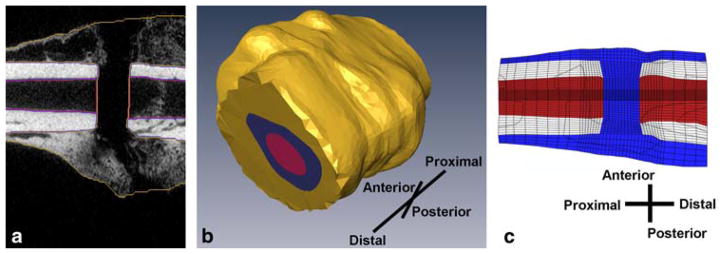
The 3-D FE model was created from micro-computed tomography (μCT) scans of the fracture callus after four weeks of mechanical stimulation. The boundaries of the cortex, callus, and medullary tissue were identified on stacks of individual, 2-D, transverse, μCT tomograms (Fig. 1a). Three-dimensional surfaces were created that represented the boundaries of each tissue (Amira 4.1, Mercury Computer Systems, Chelmsford, MA) (Fig. 1b). A 3-D, cylindrical finite element mesh was then created (TrueGrid 2.2, XYZ Scientific, Livermore, CA) with a higher element density (characteristic element size ~0.11 mm) within and near the osteotomy gap and a lower element density (characteristic element size ~0.64 mm) remote to the gap, resulting in a total of 81,920 elements (Fig. 1c). Results of an ancillary convergence study indicated that a 20% change in the number of elements resulted in less than a 10% change in the maximum values of fluid flow and maximum principal strain.
Fig. 1.
a Cortical bone, medullary tissue, and callus are labeled on μCT cans of a sample rat fracture callus. The orientation of the callus is the same as in part c. b 3-D surfaces of the cortical bone, medullary canal, and fracture callus are extrapolated from the labeled images. c The finite element mesh is then contoured to conform to the tissues’ surfaces and scaled. Pictured is a cross section of the finite element model of the fracture callus prior to bending stimulation. Cortical bone is light blue, bone marrow is dark blue, and callus tissue is red
The size of the model was then scaled down in order to match the callus size that exists at the end of the latency period, just prior to the onset of mechanical stimulation, rather than at the end of the stimulation timecourse. It was determined from histological measurements that the diameter of the callus approximately doubles from the end of the latency period to the end of the four-week stimulation period when the bending motion consists of ±30° bending. Accordingly, the outer eight layers of elements were removed from the mesh in order to reduce the diameter of the callus by a factor of two (Fig. 1c). The resulting mesh consisted of 61,440 elements.
The Prendergast mechano-regulation theory was implemented in each element of the fracture callus (Kelly and Prendergast 2005; Lacroix and Prendergast 2002; Prendergast et al. 1997). Briefly, the entire callus was assumed to consist of granulation tissue at the start of the stimulation regimen (Fig. 1c). Stem cells were assumed to originate from the periosteum, the outer cortical surface, and the medullary canal. To simulate the diffusion of stem cells throughout the callus, a diffusion coefficient was chosen to predict 99% stem cell coverage six weeks after surgery (Kelly and Prendergast 2005). In a previous study, bony bridging was shown to occur by five weeks in control (continuous rigid fixation) animals (Cullinane et al. 2002). Differentiation of the granulation tissue in a given element towards fibrous tissue, cartilage, or bone was then determined by the stimulus factor (S):
where γ is the octahedral shear strain, ν is the fluid velocity, and a (3.75%) and b (3 μm/s) are the scaling factors for each stimulus. For S > 3 the mechano-regulation theory predicts fibrous connective tissue, for 1 < S < 3 it predicts cartilage, for 0.53 < S < 1 it predicts immature woven bone, for 0.01 < S < 0.53 it predicts mature woven bone, and for 0 < S < 0.01 the theory predicts bone resorption (Kelly and Prendergast 2005; Prendergast et al. 1997). Poroelastic material properties were updated according to a rule of mixtures that considers the concentration of cells in a given element (nc) and the volume fractions (φj) and material properties of granulation tissue and j types of differentiated tissues in that element. For example, the Young’s modulus (E) for a given element was calculated as
where Egranulation is the Young’s modulus of granulation tissue, Ej is the Young’s modulus of the jth type of differentiated tissue in that element (Table 1), and is the maximum concentration of cells permitted in any given element. The volume fraction φj of given type of differentiated tissue was calculated as the fraction of the last ten iterations for which that differentiated tissue type was predicted in the element. This allowed the material properties to change gradually and prevented instability in the algorithm (Lacroix and Prendergast 2000). The number of tissue types predicted in the element over the last ten iterations was nt. Each material property was calculated for each element with this formula using a custom MATLAB script (The Mathworks, Inc., Natick, MA). Twenty-four iterations were performed in order to simulate six days per week of stimulation for four weeks. The three day latency period and the one day of rest each week were accounted for with the diffusion of the stem cells. For purposes of graphing and visualization the distribution tissues throughout the mesh, elements were assigned the tissue type with the largest volume fraction.
Table 1.
Material properties used in the simulations (Lacroix and Prendergast 2002)
| Young’s modulus (MPa) | Permeability (mm4/Ns) | Poisson’s ratio | Bulk modulus of the solid (MPa) | Bulk modulus of the fluid (MPa) | |
|---|---|---|---|---|---|
| Granulation tissue | 0.2 | 1e-14 | 0.167 | 2300 | 2300 |
| Fibrous connective tissue | 2 | 1e-14 | 0.167 | 2300 | 2300 |
| Cartilage | 10 | 5e-15 | 0.167 | 3400 | 2300 |
| Immature bone | 1000 | 1e-13 | 0.3 | 13920 | 2300 |
| Mature bone | 6000 | 3.7e-13 | 0.3 | 13920 | 2300 |
| Bone marrow | 2 | 9.81e-8 | 0.167 | 2300 | 2300 |
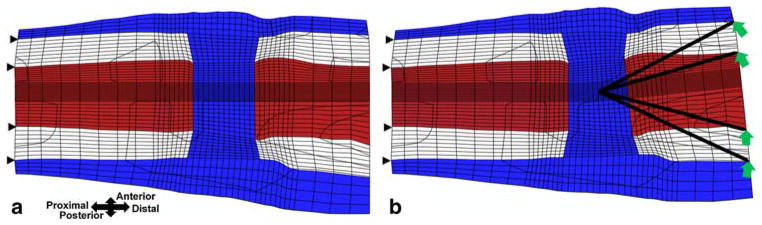
Displacement boundary conditions were chosen to correspond to previous in vivo experiments which applied ±6° of bending in the sagittal plane (Cullinane et al. 2002, 2003). The nodes of the cortical bone on the proximal end of the model were fixed, and the nodes of the cortical bone on the distal end were displaced to simulate ±6° bending about the center of the osteotomy gap in the sagittal plane over the course of one second (Fig. 2). All finite element analyses were performed using ABAQUS 6.5 (Abaqus, Inc., East Providence, RI). In order to reduce the compute time, the cortical bone was modeled as a linear elastic material with a Young’s modulus and Poisson’s ratio of 15750 MPa and 0.325 respectively (Isaksson et al. 2006b). Each model thus consisted of 244,772 degrees of freedom and required approximately 14 CPU hours on an IBM pSeries 655 system.
Fig. 2.
Finite element mesh bent a 0° and b +6° about the center of the osteotomy gap in the sagittal plane. The (displacement) boundary conditions are shown
Due to the oscillatory nature of the applied bending motion, multiple values of octahedral shear strain and fluid velocity occur in each element over the course of one bending cycle. It was assumed that the values of octahedral shear strain and fluid velocity that direct tissue differentiation in a given element would be the maximum values that occurred in that element over one cycle. In an effort to reduce computational time, it was investigated whether it was necessary to simulate the entire cycle in order to identify the maximum values of the stimuli. The maximum values predicted by quarter cycles (0° → 6° or 0° → −6°) were compared to the maximum values predicted by the entire cycle. First, the maximum values of octahedral shear strain and fluid velocity in each element during a quarter cycle (0° → 6° and 0° → −6°) were compared. The values were found to be significantly different. However, the values predicted in each element after a quarter cycle (0° → 6°) were very similar to those predicted after three quarters of a cycle (0° → −6° → 0° → 6°). Thus, only two quarter cycles (0° → 6° and 0° → −6°) were simulated, and this reduced the computational time required to run the simulation by more than half.
The simulation results were compared to histology from Cullinane et al. (2003). In that study, four rat femora underwent production of a transverse osteotomy and ±6° bending stimulation for up to six weeks. Histological sections from femora harvested after four weeks were reexamined. The size, shape, and location of various tissue types were compared to the simulation’s predictions. For this ±6° stimulation regimen, no change in callus size was observed at the end of the six-week timecourse; hence, no mechanism for callus growth was incorporated into the simulation algorithm.
3 Results
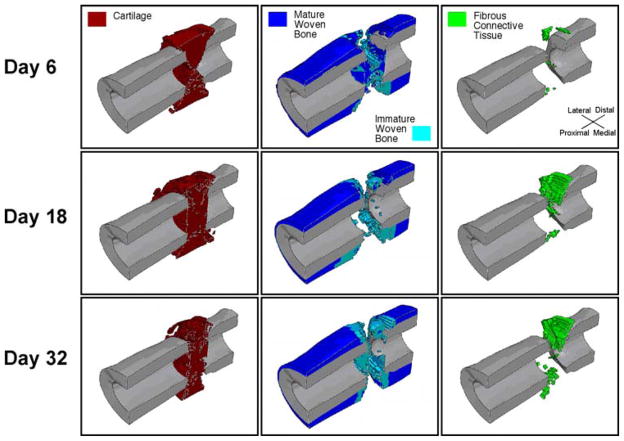
A heterogeneous distribution of cartilage, bone and fibrous connective tissue was predicted to form in the osteotomy gap (Fig. 3). A continuous mass of cartilage was predicted to span the gap with small quantities of bone and fibrous connective tissue scattered throughout the cartilage mass. Platforms of immature woven bone were predicted at the osteotomized ends of the medullary canals, partially capping the ends of the cortical fragments. Immature woven bone was also predicted adjacent to the periosteum of the cortex just proximal and distal to the osteotomy. A wedge-shaped mass of immature woven bone was also predicted in the anterior-most portion of the gap. Mature woven bone was predicted to form exclusively adjacent to the cortical fragments and the periosteum, proximal and distal to the immature woven bone. Smaller pieces of fibrous connective tissue were also present tangent to the posterior and anterior corners of the osteotomized surfaces of the cortex. Small quantities of immature woven bone and fibrous connective tissue were scattered throughout the osteotomy gap.
Fig. 3.
Sagittal cross-section of the predicted distributions of cartilage, bone and fibrous connective tissue at three time points. The cortex is shown in gray. The first time point corresponds to the latency period plus three days of bending stimulation. The second time point is the end of the second week of stimulation, and the final time point is the end of the fourth week of stimulation
Asymmetry in the predicted patterns of tissue differentiation was notable in the sagittal, coronal, and transverse planes. Specifically, more fibrous connective tissue was predicted on the anterior side of the osteotomy (Fig. 4a,b). In the coronal plane, more cartilage was predicted on the medial side of the callus and more bone was predicted on the lateral side of the callus.
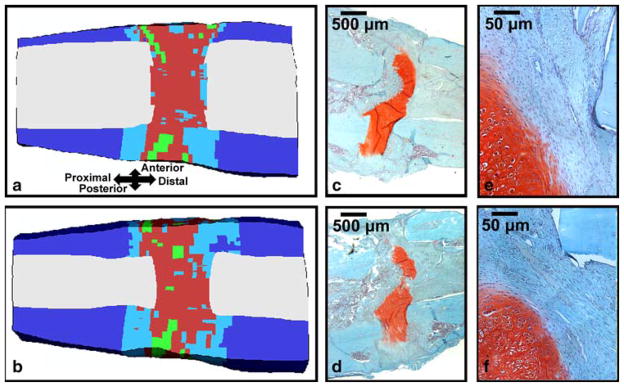
Fig. 4.
a Mid-sagittal and b para-sagittal cross sections of the predicted tissue distribution after four weeks of bending stimulation; the color key is the same as in Fig. 4. c Mid-sagittal and d para-sagittal histology slides (20x magnification) from a specimen from Cullinane et al. (2003) that underwent four weeks of bending stimulation. Regions of (e) and (f) that are adjacent to a cortical fragment and that contain fibrous connective tissue are shown in e and f, respectively (200x magnification). The tissue has been stained with Safranin-O (coloring cartilage red) and Fast Green (coloring bone blue-green)
The predicted tissue distributions were consistent with the histology results. In two of the four histological specimens (Fig. 4c,d), the osteotomy gap was dominated by a continuous band of cartilage, and these bands of cartilage often took on an arched appearance (Cullinane et al. 2003). In the other two cases, the gap contained large masses of fibrous connective tissue with smaller masses of cartilage, adjacent to the cortical fragments. New bone formation was also observed along the periosteal surface of the cortical fragments as well as scattered in small quantities along the proximal and distal boundaries of the gap. Regions of fibrous connective tissue were observed tangent to the corner of a cortical fragment and on the posterior side of the external callus adjacent to the osteotomy gap (Fig. 4e,f). These histological sections also showed asymmetry in the distribution of cartilage and fibrous connective tissue within and surrounding the osteotomy gap.
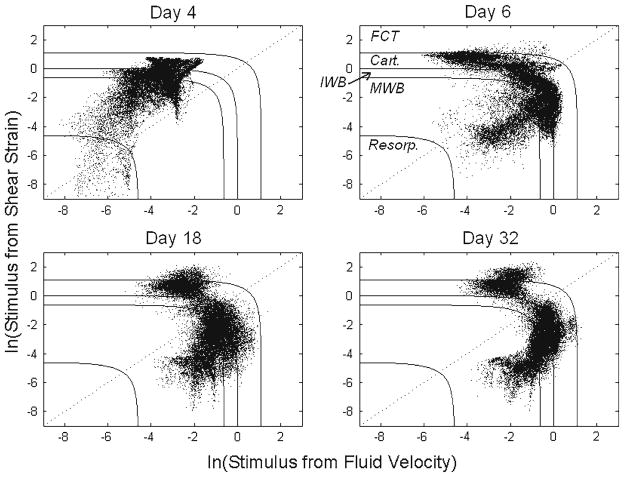
The respective contributions of the two stimuli, octahedral shear strain and fluid velocity, to the stimulus factor were observed to change over time (Fig. 5). In the first iteration, discrimination among predicted tissue types based on the value of the stimulus factor S was due almost entirely to octahedral shear strain. Interstitial fluid velocity did not affect the course of tissue differentiation until the second iteration. From the second iteration onward, the elements within the callus began to diverge into two groups (Fig. 5); one group dominated by the fluid velocity portion of the stimulus factor and one dominated by the octahedral shear strain portion of this factor. Each group of tissue was nearly continuous (Fig. 6). The group dominated by shear strain formed an hourglass-shaped mass spanning the osteotomy gap and oriented along the anterior posterior direction as well as a ring around the exterior of the callus adjacent to the gap. The group dominated by fluid flow filled the rest of the callus.
Fig. 5.
Distribution of the stimulus factor S for each element on the first and third days of bending stimulation (Days 4 and 6, respectively), and at the ends of the second and fourth weeks of stimulation (Days 18 and 32, respectively). Solid lines define boundaries between regions of different predicted tissue types or tissue resorption), according to Prendergast et al. 1997. Resorp. = resorption, MWB = mature woven bone, IWB = immature woven bone, Cart = cartilage, FCT = fibrous connective tissue. The dotted line is used to investigate the respective contributions of the two stimuli, as shown in Fig. 6
Fig. 6.
Distribution of elements for which the predicted tissue type is determined largely by fluid flow (left) or shear strain (right) after four weeks of stimulation. Elements for which the stimulus factor S falls to the bottom right of the dotted line in Fig. 5 are shown in the left figure, and elements for which the stimulus factor S falls to the top left of the line are shown in the right figure
4 Discussion
To date, the Prendergast mechano-regulation theory has been applied to a number of different scenarios of skeletal healing and has shown tremendous promise as a theory that could accurately describe the course of mesenchymal tissue differentiation in response to a wide spectrum of mechanical conditions. Our goal in this study was to carry out a robust test of this theory by applying it to a scenario in which mechanical loading is used to dramatically alter the bone healing response. Application of a cyclic bending motion to a healing osteotomy was simulated, and the results were compared to pre-existing histological sections obtained from calluses that had undergone the bending stimulation regimen. Our results indicated that the Prendergast theory correctly predicted non-union as a result of the bending stimulation. The band of cartilage across the osteotomy gap, the bony caps across the ends of the medullary canal, the fibrous connective tissue tangent to the cortical bone, and the lack of bony bridging were all consistent with the patterns of tissue formation observed in the histological sections. The only notable disagreement was the prediction of a bony wedge on the anterior aspect of the osteotomy gap. Thus, the Prendergast mechano-regulation theory was highly successful at duplicating most of the patterns of tissue formation produced by the applied mechanical simulation. Subsequent investigation of the individual contributions of fluid flow and shear strain indicated that both stimuli were important for directing tissue differentiation when the entire four-week timecourse of stimulation was considered. The success of an algorithm based solely on octahedral shear strain and fluid velocity provides strong evidence for the importance of these stimuli in directing the differentiation of mesenchymal stem cells.
A strength of the design of this study was that it tested the mechano-regulation theory in a scenario very dissimilar from the ones that have typically been used to investigate mechano-regulation of fracture healing. Many prior computational studies on the mechanobiology of fracture healing have investigated only physiological axial loads, whereas an angular displacement of 6° is outside the range of expected physiological displacements. Moreover, the applied bending motion results in a very different healing outcome than that which occurs with more rigid fixation or with axial dynamization. The different mechanical conditions at the osteotomy site and the different distributions of tissues that result together created a robust test condition for the theory that shear strain and fluid flow govern differentiation of mesenchymal tissue. In addition, this study evaluated the accuracy of the simulation results by comparison to histological sections from specimens subjected to the same experimental conditions as those that were simulated in the FE analysis.
There are also several limitations to this study. First, the FE mesh of the callus is only a simplified model of the geometry and mechanical behavior of an in vivo callus. The boundaries of the tissues were determined from the μCT tomograms with some user guidance, the mesh was created of one specimen only, and the material properties were based on approximations of the properties of developing tissues, on a simple rule of mixtures, and on assumptions regarding stem cell diffusion. Future studies could use experimentally measured tissue properties as input in order to address this limitation. Second, proliferation and apoptosis for different cell types were not accounted for as was done in other studies (Bailon-Plaza and Van der Meulen 2003; Kelly and Prendergast 2005). Third, the study assumed that one iteration of the algorithm was representative of one day of healing. Fourth, because of the geometric differences between the bending-stimulated callus that was used as a template for the FE mesh and the bending-stimulated calluses in the histology the comparison of the predictions and the histology is limited to gross morphology. Sample-specific FE models would be needed to carry out a point-by-point comparison of the algorithms predictions and histology. Finally, because histology from only one time point was examined, it is also unknown whether the simulation accurately predicts tissue differentiation patterns at earlier time points. Additional computational and in vivo studies are needed to compare the tissue distribution and material properties predicted at earlier time points to those observed in vivo. Improvements such as these would allow us to increase the accuracy and precision of the model for possible clinical applications, including the design of custom implants or identifying cases in which fractures are unlikely to heal.
Previous computational studies have reported that when the callus tissue is modeled as spatially homogenous, the fluid flow stimulus does not significantly affect tissue differentiation (Epari et al. 2006). This study supports those findings. However, we also found that as soon as spatial heterogeneity in material properties developed, the interstitial fluid velocity became a determining factor. In a previous study testing the Prendergast mechano-regulation theory, Lacroix and Prendergast (2002) also observed elements diverging into two groups, one group dominated by shear strain and one by fluid flow. These prior and current observations, together with the close agreement between simulation and experiment found in the present study, support the inclusion of both fluid velocity and shear strain as stimuli in a mechano-regulation algorithm and suggest that deviatoric stimuli are highly significant to the cell fate of mesenchymal stem cells. Additionally, the results highlight the importance of considering how the patterns of tissue differentiation and respective contributions of fluid flow and shear strain evolve over the time course of the stimulation regimen rather than simply investigating what tissue distributions are predicted initially. The contribution of fluid flow would have been overlooked in the present study if only the first iteration had been considered.
Prior studies have also suggested that tissue differentiation in the endosteal regions near the fracture gap or osteotomy gap is dominated by chemical signaling and not by mechanical factor (McKibbin 1978). However, in the current study, the predicted distributions of tissues in these regions were generally accurate. The bony caps that were predicted at the ends of the medullary canals as well as the band of cartilage across the osteotomy gap were consistent with what was observed in the histological sections, suggesting that mechano-regulation concepts can be applicable to stem cell differentiation in this region.
The results of this study also provide some insight into the possible advantages of using an anatomically accurate mesh geometry with respect to the asymmetry that can develop naturally in fracture calluses (Gerstenfeld et al. 2006). The mesh that was used in the current study was asymmetric along the anterior-posterior axis, and to a lesser extent, along the medial-lateral and proximal-distal axes, resulting primarily in a smaller callus radius on the anterior as compared to posterior aspect. Localized strain concentrations resulted on the anterior aspect, which in turn led to asymmetric patterns of tissue differentiation. The asymmetry in both the predicted and experimentally observed tissue distributions, despite the symmetry in the applied displacements, indicates that even moderate irregularities in callus shape can affect the tissue differentiation patterns. For example, the differences between the shape of the finite element mesh and the shape of the physical specimens could explain the appearance of the bony wedge in the predictions but not in histology. This finding regarding the effects of asymmetric geometry further emphasizes that simplification of FE model geometry can substantially affect the predictions, and it indicates that anatomically accurate models may provide greater insight into the effects of the local mechanical environment on the healing process.
The results of this study may have important implications for cartilage tissue engineering and stem cell mechano-transduction. Mechanical stimulation of cartilage explants and scaffolds seeded with chondrocytes or mesenchymal stem cells via application of dynamic compression or fluid perfusion has been shown to facilitate extracellular matrix production and to bring the mechanical properties of the tissue engineered constructs closer in line with those of healthy articular cartilage (Angele et al. 2004; Davisson et al. 2002a,b; Hung et al. 2004; Mauck et al. 2007; Sah et al. 1989). However, the optimal type, frequency, and magnitude of stimulation are still unknown. The success of the Prendergast mechano-regulation theory at predicting an equilibrium population of chondrocytes and cartilage in the present study suggests that this theory could be applied to develop in vitro loading protocols that result in improved functional outcome. While the optimal stimulation regimen may differ between in vivo and in vitro conditions, the design of loading protocols based on target magnitudes of octahedral shear strain and interstitial fluid velocity should nevertheless provide a valuable starting point. The present results regarding the importance of deviatoric stimuli for mesenchymal stem cell differentiation are also relevant for mechanotransduction studies. Previous studies have demonstrated that uniaxial compression (which creates nonzero octahedral shear strain) and fluid flow affect the expression of chondrogenic markers, signaling molecules, and extracellular matrix components in mesenchymal stem cells (Angele et al. 2004; Knippenberg et al. 2005; Mauck et al. 2007; Riddle et al. 2006). Together with the data from this study, these results suggest that further investigation into the cellular and molecular response of mesenchymal stem cells to deviatoric strain and fluid flow may provide valuable insight into the mechanotransduction pathways in skeletal tissue differentiation. The identification of these pathways responsible will also aid in the engineering of skeletal tissue.
Acknowledgments
Funding for this study was provided by NIH AR053353 (EFM) and S10-RR021072-01. The IBM pSeries 655 system was made available through the Boston University Scientific Computing Facility.
Contributor Information
Lauren Nicole Miller Hayward, Email: lnmh@bu.edu, Department of Mechanical Engineering, Boston University, 110 Cummington Street, Boston, MA 02215, USA, Department of Biomedical Engineering, Boston University, 44 Cummington Street, Boston, MA 02215, USA.
Elise F. Morgan, Department of Mechanical Engineering, Boston University, 110 Cummington Street, Boston, MA 02215, USA, Department of Biomedical Engineering, Boston University, 44 Cummington Street, Boston, MA 02215, USA
References
- Angele P, Schumann D, Angele M, Kinner B, Englert C, Hente R, Fuchtmeier B, Nerlich M, Neumann C, Kujat R. Cyclic, mechanical compression enhances chondrogenesis of mesenchymal progenitor cells in tissue engineering scaffolds. Biorheology. 2004;41(3–4):335–346. [PubMed] [Google Scholar]
- Bailon-Plaza A, Van der Meulen MC. Beneficial effects of moderate, early loading and adverse effects of delayed or excessive loading on bone healing. J Biomech. 2003;36:1069–1077. doi: 10.1016/S0021-9290(03)00117-9. [DOI] [PubMed] [Google Scholar]
- Blenman PR, Carter DR, Beaupre GS. Role of mechanical loading in the progressive ossification of a fracture callus. J Orthop Res. 1989;7(3):398–407. doi: 10.1002/jor.1100070312. [DOI] [PubMed] [Google Scholar]
- Byrne DP, Lacroix D, Planell JA, Kelly DJ, Prendergast PJ. Simulation of tissue differentiation in a scaffold as a function of porosity, Young’s modulus and dissolution rate: application of mechanobiological models in tissue engineering. Biomaterials. 2007;28(36):5544–5554. doi: 10.1016/j.biomaterials.2007.09.003. [DOI] [PubMed] [Google Scholar]
- Carter DR, Beaupre GS, Giori NJ, Helms JA. Mechanobiology of skeletal regeneration. Clin Orthop Relat Res. 1998;355(Suppl):S41–S55. doi: 10.1097/00003086-199810001-00006. [DOI] [PubMed] [Google Scholar]
- Carter DR, Blenman PR, Beaupre GS. Correlations between mechanical stress history and tissue differentiation in initial fracture healing. J Orthop Res. 1988;6(5):736–748. doi: 10.1002/jor.1100060517. [DOI] [PubMed] [Google Scholar]
- Claes LE, Heigele CA. Magnitudes of local stress and strain along bony surfaces predict the course and type of fracture healing. J Biomech. 1999;32(3):255–266. doi: 10.1016/S0021-9290(98)00153-5. [DOI] [PubMed] [Google Scholar]
- Cullinane DM, Fredrick A, Eisenberg SR, Pacicca D, Elman MV, Lee C, Salisbury K, Gerstenfeld LC, Einhorn TA. Induction of a neoarthrosis by precisely controlled motion in an experimental mid-femoral defect. J Orthop Res. 2002;20(3):579–586. doi: 10.1016/S0736-0266(01)00131-0. [DOI] [PubMed] [Google Scholar]
- Cullinane DM, Salisbury KT, Alkhiary Y, Eisenberg S, Gerstenfeld L, Einhorn TA. Effects of the local mechanical environment on vertebrate tissue differentiation during repair: does repair recapitulate development? J Exp Biol. 2003;206(Pt 14):2459–2471. doi: 10.1242/jeb.00453. [DOI] [PubMed] [Google Scholar]
- Davisson T, Kunig S, Chen A, Sah R, Ratcliffe A. Static dynamic compression modulate matrix metabolism in tissue engineered cartilage. J Orthop Res. 2002a;20:842–848. doi: 10.1016/S0736-0266(01)00160-7. [DOI] [PubMed] [Google Scholar]
- Davisson T, Sah RL, Ratcliffe A. Perfusion increases cell content and matrix synthesis in chondrocyte three-dimensional cultures. Tissue Eng. 2002b;8(5):807–816. doi: 10.1089/10763270260424169. [DOI] [PubMed] [Google Scholar]
- Epari DR, Taylor WR, Heller M, Duda GN. Mechanical conditions in the initial phase of bone healing. Clin Biomech (Bristol, Avon) 2006;21:646–655. doi: 10.1016/j.clinbiomech.2006.01.003. [DOI] [PubMed] [Google Scholar]
- Gerstenfeld LC, Alkhiary YM, Krall EA, Nicholls FH, Stapleton SN, Fitch JL, Bauer M, Kayal R, Graves DT, Jepsen KJ, et al. Three-dimensional reconstruction of fracture callus morphogenesis. J Histochem Cytochem. 2006;54(11):1215–1228. doi: 10.1369/jhc.6A6959.2006. [DOI] [PubMed] [Google Scholar]
- Goodship AE, Kenwright J. The influence of induced micromovement upon the healing of experimental tibial fractures. J Bone Joint Surg Br. 1985;67(4):650–655. doi: 10.1302/0301-620X.67B4.4030869. [DOI] [PubMed] [Google Scholar]
- Hente R, Fuchtmeier B, Schlegel U, Ernstberger A, Perren SM. The influence of cyclic compression and distraction on the healing of experimental tibial fractures. J Orthop Res. 2004;22:709–715. doi: 10.1016/j.orthres.2003.11.007. [DOI] [PubMed] [Google Scholar]
- Hung CT, Mauck RL, Wang CC, Lima EG, Ateshian GA. A paradigm for functional tissue engineering of articular cartilage via applied physiologic deformational loading. Ann Biomed Eng. 2004;32(1):35–49. doi: 10.1023/B:ABME.0000007789.99565.42. [DOI] [PubMed] [Google Scholar]
- Isaksson H, Comas O, van Donkelaar CC, Mediavilla J, Wilson W, Huiskes R, Ito K. Bone regeneration during distraction osteogenesis: mechano-regulation by shear strain and fluid velocity. J Biomech. 2007;40(9):2002–2011. doi: 10.1016/j.jbiomech.2006.09.028. [DOI] [PubMed] [Google Scholar]
- Isaksson H, van Donkelaar CC, Huiskes R, Ito K. Corroboration of mechanoregulatory algorithms for tissue differentiation during fracture healing: Comparison with in vivo results. J Orthop Res. 2006a;24(5):898–907. doi: 10.1002/jor.20118. [DOI] [PubMed] [Google Scholar]
- Isaksson H, Wilson W, van Donkelaar CC, Huiskes R, Ito K. Comparison of biophysical stimuli for mechano-regulation of tissue differentiation during fracture healing. J Biomech. 2006b;39(8):1507–1516. doi: 10.1016/j.jbiomech.2005.01.037. [DOI] [PubMed] [Google Scholar]
- Kelly DJ, Prendergast PJ. Mechano-regulation of stem cell differentiation and tissue regeneration in osteochondral defects. J Biomech. 2005;38(7):1413–1422. doi: 10.1016/j.jbiomech.2004.06.026. [DOI] [PubMed] [Google Scholar]
- Kelly DJ, Prendergast PJ. Prediction of the optimal mechanical properties for a scaffold used in osteochondral defect repair. Tissue Eng. 2006;12(9):2509–2519. doi: 10.1089/ten.2006.12.2509. [DOI] [PubMed] [Google Scholar]
- Knippenberg M, Helder MN, Doulabi BZ, Semeins CM, Wuisman PIJM, Klein-Nulend J. Adipose tissue-derived mesenchymal stem cells acquire bone cell-like responsiveness to fluid shear stress on osteogenic stimulation. Tissue Eng. 2005;11(11/12):1780–1788. doi: 10.1089/ten.2005.11.1780. [DOI] [PubMed] [Google Scholar]
- Lacroix D, Chateau A, Ginebra MP, Planell JA. Micro-finite element models of bone tissue-engineering scaffolds. Biomaterials. 2006;27(30):5326–5334. doi: 10.1016/j.biomaterials.2006.06.009. [DOI] [PubMed] [Google Scholar]
- Lacroix D, Prendergast PJ. A homogenization procedure to prevent numerical instabilities in poroelastic tissue differentiation models. Eighth annual symposium: computational methods in orthopaedic biomechanics.2000. [Google Scholar]
- Lacroix D, Prendergast PJ. A mechano-regulation model for tissue differentiation during fracture healing: analysis of gap size and loading. J Biomech. 2002;35(9):1163–1171. doi: 10.1016/S0021-9290(02)00086-6. [DOI] [PubMed] [Google Scholar]
- Mauck RL, Byers BA, Yuan X, Tuan RS. Regulation of cartilaginous ECM gene transcription by chondrocytes and MSCs in 3D culture in response to dynamic loading. Biomech Model Mechanobiol. 2007;6:113–125. doi: 10.1007/s10237-006-0042-1. [DOI] [PubMed] [Google Scholar]
- McKibbin B. The biology of fracture healing in long bones. J Bone Joint Surg B. 1978;60-B(2):150–162. doi: 10.1302/0301-620X.60B2.350882. [DOI] [PubMed] [Google Scholar]
- Perren M, Cordey J. The concept of interfragmentary strain. In: Uhthoff HK, editor. Current concepts of internal fixation of fractures. Springer; Berlin: 1980. pp. 63–77. [Google Scholar]
- Prendergast PJ, Huiskes R, Soballe K. ESB Research Award 1996. Biophysical stimuli on cells during tissue differentiation at implant interfaces. J Biomech. 1997;30(6):539–548. doi: 10.1016/S0021-9290(96)00140-6. [DOI] [PubMed] [Google Scholar]
- Riddle RC, Taylor AF, Genetos DC, Donahue HJ. MAP kinase and calcium signaling mediate fluid flow-induced human mesenchymal stem cell proliferation. Am J Physiol Cell Physiol. 2006;290:C776–C784. doi: 10.1152/ajpcell.00082.2005. [DOI] [PubMed] [Google Scholar]
- Sah RL, Kim YJ, Doong JY, Grodzinsky AJ, Plaas AH, Sandy JD. Biosynthetic response of cartilage explants to dynamic compression. J Orthop Res. 1989;7(5):619–636. doi: 10.1002/jor.1100070502. [DOI] [PubMed] [Google Scholar]
- Salisbury KT, Einhorn TA, Gerstenfeld LC, Morgan EF. Compendex. Vail, Colorado: 2005. Mechanobiological regulation of molecular expression and tissue differentiation during bone healing; pp. 1530–1531. [Google Scholar]