Measuring the Osmotic Water Permeability of the Plant Protoplast Plasma Membrane: Implication of the Nonosmotic Volume

Abstract

Starting from the original theoretical descriptions of osmotically induced water volume flow in membrane systems, a convenient procedure to determine the osmotic water permeability coefficient (P_os) and the relative nonosmotic volume (β) of individual protoplasts is presented. Measurements performed on protoplasts prepared from pollen grains and pollen tubes of Lilium longiflorum cv. Thunb. and from mesophyll cells of Nicotiana tabacum L. and Arabidopsis thaliana revealed low values for the osmotic water permeability coefficient in the range 5–20 μm · s⁻¹ with significant differences in P_os, depending on whether β is considered or not. The value of β was determined using two different methods: by interpolation from Boyle-van’t Hoff plots or by fitting a solution of the theoretical equation for water volume flow to the whole volume transients measured during osmotic swelling. The values determined with the second method were less affected by the heterogeneity of the protoplast samples and were around 30% of the respective isoosmotic protoplast volume. It is therefore important to consider nonosmotic volume in the calculation of P_os as plant protoplasts behave as nonideal osmometers.

Introduction

Since the discovery of the first aquaporins (AQPs) in the 1980s (Denker et al., 1988), the number of identified AQPs has increased almost exponentially due to progress in molecular biology techniques (Quigley et al., 2001). AQP sequences from plants have been reported too, and their water transport activity was demonstrated by the usual functionality test developed for animal AQPs (Zhang, Logee & Verkman, 1990; Zhang & Verkman, 1991; Preston et al., 1992), e.g., expression of the AQP mRNA in Xenopus laevis oocytes (Maurel et al., 1993; Daniels, Mirkov & Chrispeels, 1994; Kamerloher et al., 1994).

Due to the growing interest in the identification and physiological characterization of plant AQPs in their natural environment, protoplast swell assays were performed similar to the oocyte swell assay to determine the value of the water permeability coefficient (P_os) of the plasma membrane. Besides molecular biological experiments (overexpression, knockout), P_os and Arrhenius activation energy are among the few experimentally measurable, physical parameters that indicate the contribution of AQPs to water transport, thus playing an important role in the debate about the physiological function of specific AQPs in plant cells and their regulation (Chaumont, Moshelion & Daniels, 2005; Hill, Shacher-Hill & Shacher-Hill, 2004). Therefore, a precise determination of the P_os value is necessary.

For plant cells, mainly two strategies to determine P_os were used: (1) volume changes of membrane vesicles or of whole protoplasts were recorded until a steady state was reached, and the whole transient, V_t, was used to fit the experimental data to a theoretical function or approximated forms of it (membrane vesicles: Niemietz & Tyerman, 1997; Maurel et al., 1997; protoplasts: Suga et al., 2003; Moshelion, Moran & Chaumont, 2004); (2) measurements on isolated protoplasts were performed over short time periods, assuming that during the initial phase of osmotic swelling the volume changes are linear (“initial rate” approach), and P_os was calculated according to Zhang et al. (1990).

In most reports (see references in Table 1), P_os of individual protoplasts was determined by the second method, essentially similar to that used for Xenopus oocytes, assuming an instantaneous exchange of bath solutions of different osmolalities and a neglectable nonosmotic volume, meaning that the total volume of the protoplast is osmotically active. A problem with the first assumption is the effect of the unstirred layers (Dainty, 1963), which introduces a temporal delay in the exchange of solutions with different osmolalities. This effect depends on the cell size and is not significant for oocytes but could “mask” or bias the initial phase of the volume change of plant protoplasts, leading to underestimation of P_os (Ramahaleo et al., 1999; Moshelion et al., 2004). On the other hand, there is no general agreement about the optimal duration of the measurements, which also depends on the cell properties (e.g., size, water permeability) and on the particular experimental conditions (e.g., magnitude of the osmotic step). For instance, the swelling of oocytes takes a couple of minutes, which enables the sampling of sufficient experimental data points for a reliable linear plot of the volume vs. time. Plant protoplasts are usually smaller and often have higher P_os values than oocytes; therefore, they swell much faster and the duration of the linear volume increase is just several seconds. Additionally, to our knowledge, the nonosmotic volume of plant protoplasts (as well as that of oocytes) has never been considered in calculations of P_os. However, the theoretical function used to describe the time course of water volume fluxes, and thus for calculating P_os, was initially developed by Kedem & Katchalsky (1958) starting from “a thermodynamic description of non-equilibrium systems in which two solutions of the same solvent and solute are separated by a membrane.” The solution of this equation considers only the osmotically active volume of the two compartments, whereas the total measured volume of a cell, especially in plant cell protoplasts, consists of the osmotic and nonosmotic volumes (Wiest & Steponkus, 1978; Dowgert & Steponkus, 1983).

Table 1.

Osmotic water permeability coefficient (P_os) values for different plant tissues. Note that the calculation method predominantly used is the initial rate method

Organism, tissue	Pos (μm s−1)	Range (μm s−1)	Method	Reference
Arabidopsis thaliana, leaf	10.8 ± 2.1		Initial rate	Kaldenhoff et al., 1998
Allium cepa, leaf	1 0 ± 7		Initial rate	Ramahaleo et al., 1999
Brassica napus, hypocotyls	400 ± 150
Brassica napus, root	330 ± 140	1–640
Petunia hybrida, leaf	–	1–330
Phaseolus vulgaris
Bending zone epidermis	40	5–300	Initial rate	Comparot et al., 2000
Terminal part epidermis	36
Bending zone parenchyma	62
Concave part epidermis and parenchyma	46	5–300
Convex part
Epidermis and parenchyma	51	6–380
Graptopetalum paraguayense,	2.8 (swelling)		Initial rate	Ohshima et al., 2001
Leaf mesophyll	6.2 (shrinking)
Radish hypocotyls	13 (swelling)
	23 (shrinking)
Samanea saman, leaf, motor cells	3.3 ± 0.2 (noon)		Initial rate	Moshelion et al., 2002
	5.2 ± 0.3 (morning)
Linum usitatissimum, root	485 ± 159		Initial rate	Morillon and Lassalles, 2002
Brassica napus, root	582 ± 100
Triticum turgidum, root	6.3 ± 3.5
Triticum aestivum, root	–	2.2–720
Nicotiana tabacum, root	27.12 ± 1.8	4–128	Initial rate	Siefritz et al., 2001
Raphanus sativus, root cortex	365 ± 90		Time course fit	Suga et al., 2003
Raphanus sativus, root endodermis	323 ± 96
Nicotiana tabacum, leaf	70 ± 12		Initial rate	Ding et al., 2004
Arabidopsis thaliana, leaf		1.25 – 540	Initial rate	Morillon and Chrispeels, 2001

Following the reflections above, there is a need for a new, accurate method to calculate the water permeability of plant protoplasts considering their specific properties, e.g., size and nonosmotic volume.

In this study, starting from the original theoretical descriptions of osmotically induced water flow across a membrane system (Kedem & Katchalski, 1958; Dainty, 1963), a convenient procedure to calculate simultaneously both P_os and the nonosmotic volume of individual protoplasts from the time course of their total volume change is presented and the effect of the nonosmotic volume in the calculation of P_os is discussed.

Materials and Methods

Isolation of Plant Protoplasts

Protoplasts from pollen grains and tubes from Lilium longiflorum Thunb. were isolated as described previously (Griessner & Obermeyer, 2003). For preparing mesophyll protoplasts, upper leaves from healthy greenhouse Arabidopsis thaliana and Nicotiana tabacum L. plants were used. Strips, 1 mm wide, were cut and vacuum-infiltrated with isolation medium containing 10 mM KCl, 1 mM CaCl₂, 10 mM morpholinoethanesulfonic acid and 500 mM mannitol adjusted to pH 5.5 with tris(hydroxymethyl)aminomethane (TRIS). The strips were then incubated for up to 2 h at room temperature in a medium of the same composition as above, containing cell wall-digesting enzymes: cellulase (1%, w/v) and pectinase (0.02%, w/v). The protoplasts were released by gently shaking the tissue strips after replacing the digestion medium with cold isolation medium adjusted to pH 6 and collected manually by aspiration with a Pasteur pipette. They were subsequently washed three times by centrifugation (80 × g, 5 min) in isolation medium and kept on ice. Only protoplasts of a spherical shape with randomly distributed chloroplasts and cytoplasmic streaming were used for measurements.

Determination of Nonosmotic Volume by Boyle-van’t Hoff Plots

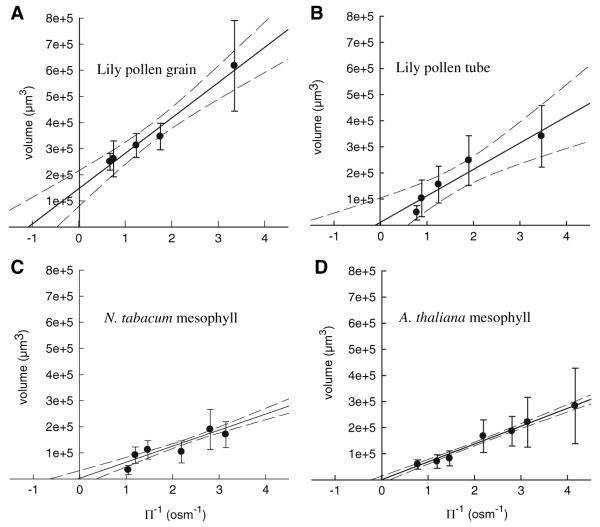
Lily pollen grain and pollen tube protoplasts were incubated for 20–30 min at room temperature in isolation medium (Griessner & Obermeyer, 2003) with osmolalities in the range 288–1,483 mOsm adjusted with mannitol. For each osmolality value, the diameter of 15–80 protoplasts was measured with an inverted microscope equipped with a video system and the corresponding volume was calculated assuming that the protoplasts had a spherical shape. For monitoring the equilibrium volume of mesophyll protoplasts, aliquots of each protoplast sample were resuspended in the isolation medium with various amounts of mannitol, giving an osmolality range of 240–1,280 mOsm. After 20–30 min, the diameters of 12–113 protoplasts were measured for each osmolality value. A freezing point osmometer (OSMOMAT 030; Gonotec, Berlin, Germany) was used to measure the osmolality of the media. The average protoplast volumes were plotted vs. the corresponding reciprocal of the external osmolalities. A straight line was fitted to the data points using the least-square fit method (SigmaPlot; Jandel Scientific, Erkrath, Germany, Corte Madera, CA), and the nonosmotic volume was taken as the intercept of the regression line with the volume axis.

Swelling Experiments and Image Acquisition

Transient volume changes of single protoplasts exposed to hypoosmolar solutions were monitored in a measuring chamber mounted on the stage of an inverted microscope (Axiovert 135; Zeiss, Oberkochen, Germany) equipped with a video camera (CCD-IRIS; Sony, Tokyo, Japan) and a Zeiss 40 × 0.6 Achroplan objective lens. Two identical measuring chambers with a volume of 500 μl each were mounted in parallel, adjacent to each other on the stage of an inverted microscope. One chamber contained a protoplast suspension in isoosmotic medium and the other, a hypoosmotic solution. After a single protoplast was chosen and its initial diameter (D₀) was measured, it was transferred with a microcapillary (200–250 μm tip diameter, nanoliter injector; WPI, Berlin, Germany) into the other chamber containing the hypoosmotic solution. Before releasing the protoplast, the microscope was focused on the tip of the microcapillary near the bottom of the chamber so that the subsequent focusing of the protoplast itself could proceed immediately. Image capture was started simultaneously by releasing the protoplast into the hypotonic solution. The osmolality change in the hypotonic medium was negligible since the amount of isotonic medium released with the protoplast was less than 500 nl. In order to insure that the protoplast kept its spherical symmetry during the measurements, the ratio of two perpendicular diameters was measured at the beginning and at the end of the experiment. Only protoplasts with a constant ratio of the diameters were accepted for analysis. All experiments were performed at room temperature.

Images were acquired every 3 s and digitized using a frame grabber (MV Sigma; Matrix Vision, Oppenweiler, Germany). For each protoplast, 150 frames were recorded, resulting in a volume transient of 450 s. The focal plane was manually adjusted if necessary. The 150 frames corresponding to a swelling protoplast were merged into a single file and analyzed using Image Compact 4.0 software (Matrix Vision), which allows measurement of cell diameter (D). The brightness and contrast of the digitized two-dimensional images were adjusted off-line in order to increase the sharpness of the protoplast contour. The scaling factor was 3 pixels · μm⁻¹; thus, the precision of the measurements was 0.33 μm. The corresponding protoplast volumes were calculated as V = (π D³)/6.

Calculation of P_os and β from Single-Cell Volume Transients

In order to calculate P_os, the following data-processing steps were applied. First, the value of the relative nonosmotic volume, β, was calculated from relation (10) (see below). $V_f^{measured}$ is the value where the volume relaxation curve reaches a steady maximum. Calculation of β allowed the transformation of the measured volume into the osmotic volume using relation (9). Subsequently, the calculated values of the osmotic volume were fitted with Eq. 4 and the regression parameter k was used to calculate the osmotic water permeability coefficient P_os with relation (5).

Statistical comparisons between different samples were performed using Student’s t-test, whereby a value of p < 0.05 was considered statistically significant. All data transformation, fitting routines and statistical analyses were performed using SigmaPlot version 8.0 software.

Results

Theory

Basic theoretical assumptions

When protoplasts behave as linear osmometers within a given range of osmolalities, the following relation (Boyle-van’t Hoff) is fulfilled:

$$\Pi =\left(\mathrm{nRT}\right)∕(V-b)=\mathrm{RTc}$$

which is equivalent to

$$c{V}^{\mathrm{os}}=n$$

where Π is the osmotic pressure; n and c are the mole number and the concentration of the impermeant solutes in the cell, respectively; and V is the protoplast volume, which consists of an osmotically responsive part (V^os) and an osmotically inactive part, the nonosmotic volume (b).

$$V=V^{\mathrm{os}}+b$$

It is further assumed that at equilibrium there is no difference in osmotic as well as hydrostatic pressures across the plasma membrane and that the protoplasts have a spherical shape. According to Kedem & Katchalsky (1958), the bulk flow of water across the plasma membrane of a protoplast suddenly transferred from a solution c₀ to a solution with an osmolality c_f ≠ c₀ can be described by the following equation:

$$\frac{d{V}^{os}\left(t\right)}{dt}=-P_{os}\cdot V_{\mathcal{w}}\cdot A\cdot [c_f-c\left(t\right)]$$ (1)

with c₀V^os₀ = c(t)V^os(t) = c_fV^os_f. V^os(t) and c(t) are the time-dependent values of the osmotic volume and internal osmolality, respectively; c₀ and $V_0^{os}$ are the protoplast initial (t = 0) internal osmolality and osmotic volume, respectively; $V_f^{os}$ is the final (equilibrium) osmotic volume, A is the surface area at t = 0 and V_w is the molar volume of water (18 cm³ · mol⁻¹). It should be kept in mind that in the original theoretical derivation of Eq. 1 (Kedem & Katchalsky, 1958) the volume flux of water across a surface or membrane area A, which in a first approximation was taken to be constant (Dainty, 1963), is described. Using Eq. 1 for the description of volume changes of protoplasts upon hypoosmolar shock therefore presupposes a constant water permeability coefficient and a constant surface area that contribute to the water flux. However, the total surface area of a protoplast will change during the volume increase; but with the assumption that the initial surface area contributing to the water flux (“osmotic active surface”)¹ stays constant or that the fraction of the “new” surface area contributes much less to the water flux (in other words, that the osmotic permeability coefficient P_os is constant during the osmotic swelling and, thus, independent from the increase in surface), Eq. 1 can still be used for the description of volume transients of protoplasts and, thus, for the calculation of P_os (see also Discussion).

Rearranging the above equation results in the following differential equation for V^os(t):

$$\frac{d{V}_{os}\left(t\right)}{d\left(t\right)}=-P_{os}\cdot V_{\mathcal{W}}\cdot A\cdot c_f\cdot \left[1-\frac{V_f^{os}}{V^{os}\left(t\right)}\right]$$ (2)

This equation can be integrated, giving the following expression:

$$\text{In}\frac{V^{os}\left(t\right)-V_f^{os}}{V_0^{os}-V_f^{os}}+\frac{V^{os}\left(t\right)-V_0^{os}}{V_f^{os}}=-\frac{P_{os}{V}_{\mathcal{W}A}}{V_0^{os}}\cdot \frac{c_f^2}{c_0}\cdot t$$ (3)

During the last three decades, several equivalent forms of Eq. 3 have been reported (Terwilliger & Solomon, 1981; Mlekoday, Moore & Levitt, 1983; van Heeswijk & van Os, 1986; Olbrich et al., 2000).

In order to simplify the mathematical expressions, we introduced the following notations:

$$\frac{c_0}{c_f}=\frac{V_f^{os}}{V_0^{os}}=\alpha$$

$$\frac{V^{os}\left(t\right)}{V_0^{os}}=V_{rel}^{os}\left(t\right)$$

$$k=\frac{P_{os}\cdot V_{\mathcal{W}}\cdot A\cdot c_f}{\alpha \cdot V_0^{os}}$$

Eq. 3 now becomes

$$\text{In}\frac{\alpha -V_{rel}^{os}\left(t\right)}{\alpha -1}+\frac{V_{rel}^{os}\left(t\right)-1}{\alpha }=-k\cdot t$$ (4)

By fitting experimental values of $V_{rel}^{os}\left(t\right)$ and t with Eq. 4, the parameter k can be determined and P_os can be calculated as follows:

$$P_{os}=\frac{k\cdot \alpha \cdot V_0^{os}}{V_{\mathcal{W}}\cdot A\cdot c_f}$$ (5)

A single exponential function is not appropriate for calculating correct P_os values

Equation 4 obviously does not have a simple mathematical form; therefore, it would be reasonable to look for an “easier to manage” equivalent expression. For this purpose, a function of the “exponential rise to maximum” type would seem to be a good candidate:

$$V_{rel}^{os}\left(t\right)=\alpha -(\alpha -1)\cdot e^{-Kt}$$ (6)

This phenomenological function fits well the experimental data from a typical osmotic swelling experiment; however, it has to be clarified how the time constant K in function (6) relates to k in equation (4), and eventually one should be able to interpret K in terms of P_os. As an approximated form of Eq. 4, the following function was proposed (van Heeswijk & van Os, 1986), which is practically equivalent to the phenomenological function (6):

$$\text{In}\frac{\alpha -V_{rel}^{os}}{\alpha -1}=-K\cdot t$$ (7)

with K = αk (k and α as previously defined; van Heeswijk & van Os, 1986, denoted K as k_e). Consequently, P_os was calculated as follows:

$$P_{os}=\frac{K\cdot V_0^{os}}{V_{\mathcal{W}}\cdot A\cdot c_f}$$ (8)

However, the following example demonstrates that although function (7) can be used to fit experimental data, the calculated water permeability coefficient deviates considerably from the true value. In Figure 1, data points corresponding to a hypothetical protoplast with a diameter of 40 μm and a P_os of 14.9 μm · s⁻¹ exposed to an osmolality change from 600 to 300 mOsm were generated with Eq. 4. The corresponding rate constant for this simulation was k = 0.006. The simple exponential function (6) was fitted to these data, and the value obtained for the fit parameter K was 0.0093, giving for P_os a value of 23.13 μm · s⁻¹, which means an overestimation of the true P_os by >50%. Supposing now the rate constant is defined as K = αk (van Heeswick & van Os, 1986), k takes the value 0.00465 and consequently P_os (calculated with relation [8]) is 11.56 μm · s⁻¹, a value that underestimates the true P_os by 23%. Function (7) proves thus to be a poor approximation for function (4), and calculation of P_os with relation (8), on the basis of a k value derived from function (7), can lead to erroneous values.

Fig. 1.

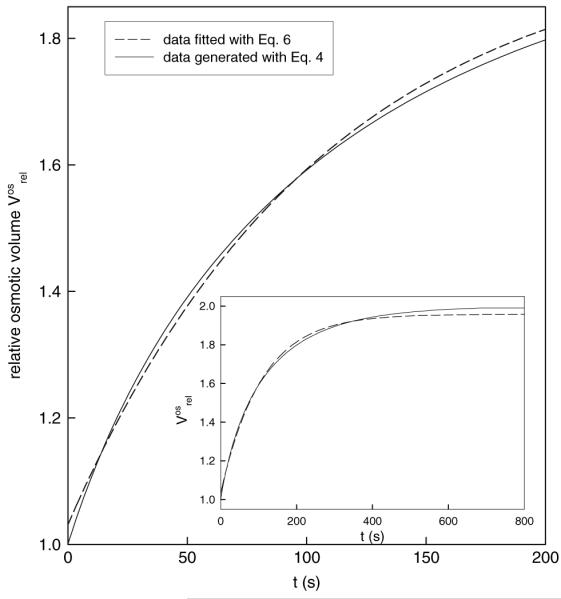
Single exponential functions do not describe adequately the osmotic swelling data. The plot shows the first 200 s from a simulated 800 s volume transient. The entire transient is shown in the inset. Continuous line represents data simulated with theoretical function (4), using a rate constant of k = 0.006 corresponding to Pos = 14.9 (μm · s⁻¹; further parameters used were α = 2, D = 40 μm, cf = 300 mOsm. Dashed line represents the regression curve obtained by fitting the data points with a single exponential function (Eq. 6). The fit parameter K has the value 0.0093, which gives a Pos of 23.13 μm · s⁻¹, according to relation (5). If the rate constant is defined as proposed by van Heeswijk & van Os (1986) as K = αk, then k takes the value 0.00465 and consequently Pos (calculated with relation 8) is 11.56 (μm · s⁻¹)

To sum up, although functions (6) and (7) describe roughly the experimental data, there is no theoretically founded, straightforward relationship between K and P_os as defined in Eq. 1. Therefore, the most accurate method for determining P_os is to fit function (4) to the measured data and finally to calculate P_os with relation (5) using the fit parameter k.

The nonosmotic volume

It is commonly accepted that just a part of the cell volume (the so-called osmotic volume, V^os) responds to an external osmotic challenge and that within a cell there are osmotically inactive components such as cell solids or other cell contents (endomembranes, starch grains, lipid drops, etc.), representing the nonosmotic volume, b. Very frequently, b is normalized to the isoosmotic volume, V_iso, giving the fractional nonosmotic volume β (β = b/V_iso). The value of β depends on the cell type and on the physiological state of the cell (Dowgert & Steponkus, 1983; Reed et al., 1987). In plant cells and algae, β values range from ca. 8% (nonacclimated rye protoplasts: Dowgert & Steponkus, 1983) to 60–80% (Dunaliella parva: Rabinowitch, Grover & Ginzburg, 1975), whereas in animal cells β values from 14% (J774 macrophages: Echevarria & Verkman, 1992) to 57% (Madin-Darby canine kidney [MDCK] cells: Zelenina & Brismar, 2000) have been reported. In the field of cryopreservation research, the importance of considering nonosmotic volume was recognized very early (see review by Steponkus, 1984). It seems necessary to take β into consideration in protoplast swelling experiments, too, since it is the osmotic volume, V^os, and not the entire cell volume that obeys the theoretical Eq. 1. Therefore, corrections are needed to the measured cell volume in order obtain a correct value for P_os.

Starting from the definition of β and assuming V₀ = V_iso, a mathematical expression can be found that relates the relative osmotic volume to the relative measured volume:

$$V_{rel}^{os}\left(t\right)=\frac{V_{rel}^{measured}\left(t\right)-\beta }{1-\beta }$$ (9)

with

$$V_{rel}^{measured\left(t\right)}=\frac{V^{measured}\left(t\right)}{V_0^{measured}}$$

and

$$V_{rel}^{os}\left(t\right)=\frac{V^{os}\left(t\right)}{V_0^{os}}$$

In practice, by introducing β in relation (9), the measured volume data $V_{rel}^{measured}$ can be transformed into osmotic volume data $V_{rel}^{os}$, which can then be fitted with function (4), in order to determine the rate constant k and eventually to calculate P_os.

There are two possibilities to infer the value of the nonosmotic volume b (and consequently β) for a certain cell type: (1) the standard procedure of measuring the steady-state volume of the cell at several external osmolalities and interpolate b as the volume at infinite osmolality from the Boyle-van’t Hoff linear plot and (2) monitoring a single transient volume increase upon a hypoosmotic challenge (β > 1) on a time scale which is long enough to allow the cell to reach the final steady-state value V_f^measured. The following formula can then be used to calculate β:

$$\beta =\frac{\alpha -\frac{V_f^{measured}}{V_0^{measured}}}{\alpha -1}$$ (10)

Relation (10) is easily derived from relation (9), considering initial and final values for the protoplast volume and using the usual notations. An equivalent expression was used in osmotic water permeability experiments on MDCK cells, giving a β of 57% (Zelenina & Brismar, 2000).

Experimental Determination of P_os and β

After isolation from their respective tissues, the protoplasts were incubated in an appropriate isoosmolar medium and their diameters determined. Usually, the majority of lily pollen grain protoplast diameters ranged from 40–60 μm, with a peak around 80 μm, at an osmolality of ca. 800 mosmol · kg⁻¹. At the same osmolar conditions, the size of pollen tube protoplasts showed a wider distribution of 45–85 μm, peaking at around 60 μm. The peak diameter of the size distribution of mesophyll protoplasts was around 50 μm for N. tabacum (range 45–70 μm) and ca. 60 μm for A. thaliana (range 50–80 μm) in an isoosmolar medium of ca. 450 mosmol · kg⁻¹.

Determination of nonosmotic volume from Boyle-van’t Hoff plots

Incubation of protoplasts under non-isoosmolar conditions resulted in a change of the protoplast volume (Fig. 2). Using the intercepts of the regression lines in the Boyle-van’t Hoff plots (Fig. 2a–d), values for b were determined. For lily pollen grain protoplasts, b was 146,000 μm³, corresponding to a relative nonosmotic volume β of 42%; for lily pollen tube protoplasts, b was 11,600 μm³, corresponding to β of 4.7%. Mesophyll protoplasts showed much lower values for b: for N. tabacum protoplasts, the Boyle-van’t Hoff plot gave a nonosmotic volume of 3,214 μm³, and for A. thaliana protoplasts, b was 643 μm³. The corresponding β values were 1.7% and 0.4%. Note that at lower osmolalities the range covered by the measured volumes was in all samples wider than at higher osmolalities. Consequently, the standard deviations from the mean values were considerably higher at lower osmolalities, limiting the accuracy of the fit with a regression line, from which eventually the value of the nonosmotic volume, b, was extrapolated.

Fig. 2.

Boyle-van’t Hoff plots for protoplasts isolated from (a) Lilium longiflorum pollen grains and (b) tubes and protoplasts from mesophyll cells of (c) Nicotiana tabacum and (d) Arabidopsis thaliana show that these protoplasts behave as linear osmometers in the osmolality range investigated. Dashed lines define the limits of the 95% confidence region of the linear regression

Simultaneous determination of the osmotic parameters P_os and β

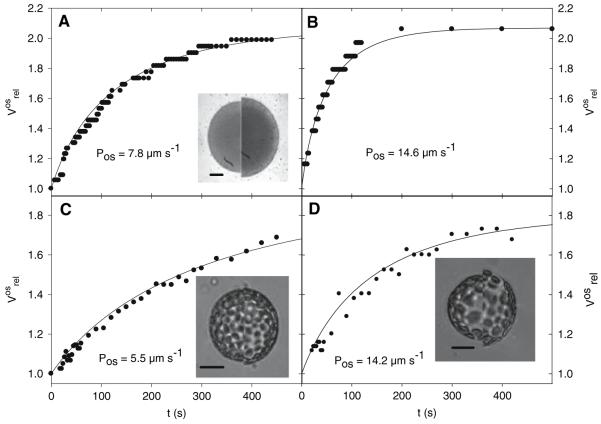
Starting from isoosmotic conditions, single protoplasts were exposed to hypoosmotic solutions that gave α values (α = c₀/c_f) ranging 1.38–1.89 for N. tabacum, 1.41–1.81 for A. thaliana, 1.7–2.3 for lily pollen grains and 1.88–2.1 for lily pollen tube protoplasts. In order to establish an optimal sampling rate, we adapted the image acquisition speed to the swelling speed of the protoplasts, considering our resolution limits. We noticed that in the most rapid phase of volume change the protoplasts increased their volume by ca. 20% within the first 30–60 s. A 20% volume increase corresponds to a 6.3% increase in protoplast diameter. For a representative protoplast with a diameter of 60 μm, this means an increase of 3.78 μm, which on a digital image gives 10 pixels (our scaling factor was 3 pixels · μm⁻¹). It follows that acquiring one frame every 3 s gives a reasonable sampling rate. A whole volume transient extended over 450 s.

The first step of the data processing was to use the swelling curve for the calculation of the relative nonosmotic volume, β. The raw volume data (V^measured) were then transformed into osmotic volume data (V^os), giving a corrected swelling curve which was fitted with Eq. 4 in order to calculate the osmotic water permeability coefficient P_os. Thus, the parameters β and P_os were determined from the volume transient of the same protoplast, reflecting the osmotic properties of this single protoplast. In Figure 3, typical swelling curves (volume transients) are shown for the different protoplast types. Note that the Arabidopsis protoplast in Figure 3d has a lower initial swelling rate than the lily pollen tube protoplast, although their P_os values are practically equal. In addition, the initial swelling rates of the Arabidopsis and the pollen grain protoplasts look very similar, though the P_os value of the pollen grain protoplast (Fig. 3a) is only half that of the Arabidopsis protoplasts (Fig. 3d). These apparent discrepancies can be explained if one writes Eq. 1 for the relative osmotic volume $V_{rel}^{os}$ at t = 0, which gives the initial protoplast swelling rate:

$${\phantom{\mid }\frac{d{V}_{rel}^{os}}{dt}\mid }_{(t\to 0)}=-P_{os}\frac{6}{D_0(1-\beta )}{V}_{\mathcal{W}}{\Delta }_c$$

where D₀ is the initial diameter of the protoplast and Δc = c_f − c₀ is the osmotic step, with the other symbols as described in the theory section. It can be seen that besides the value of the osmotic permeability coefficient P_os, also the initial size of the protoplast, the relative nonosmotic volume β and the height of the osmotic step determine the rate of volume change in the initial phase of the swelling process.

Fig. 3.

Typical volume transients measured for protoplasts isolated from lily pollen grains (a), pollen tubes (b), Nicotiana tabacum mesophyll (c) and Arabidopsis thaliana mesophyll (d). Measured data were fitted with the theoretical function (4), and the resulting Pos values are indicated on the corresponding plot. Insets show superimposed images of selected protoplasts at the beginning (left half of picture) and end (right half of picture) of the measurements. Bar = 20 μm. Further data necessary for calculation of Pos are given. Lily pollen grain protoplast: initial diameter D₀ = 73 μm, osmotic step Δc = −365 mOsm, β = 0.43 and α = 2.16. Lily pollen tube protoplast: D₀ = 46 μm, Δc = −361 mOsm, β = 0.35, α = 2.07. Tobacco mesophyll protoplast: D₀ = 47 μm, Δc = −259 mOsm, β = 0.13 and α = 1.89. Arabidopsis mesophyll protoplast: D₀ = 78 μm, Δc = −234 mOsm, β = 0.15 and α = 1.8

More than 90% of the protoplasts survived the hypoosmotic challenge and reached an equilibrium size. A small percentage of the protoplasts burst within the first 100 s of the recordings and were not analyzed, whereas analysis of protoplasts that burst shortly before reaching an equilibrium (t = 300–400 s) revealed an abnormally high P_os, usually one order of magnitude higher than in individuals from the same sample and species that did not burst until the end of the measurements. These bursting protoplasts were excluded from further processing; yet, it is interesting to note that measurements over shorter time spans (<100 s) would have most probably included contributions from such protoplasts, which would have considerably broadened the range of the calculated P_os values. Our reason to exclude these protoplasts from further processing was the assumption that the integrity of their plasma membrane was affected at a submicroscopic level undetectable by light microscopy, rather than having higher membrane permeability. In our experiments, the samples were exposed to relatively moderate osmotic stress, which most of the protoplasts survived. Therefore, the bursting protoplasts were rejected and not treated as individuals with high water permeability coefficients of physiological relevance.

The mean values of the osmotic parameters β and P_os for different protoplast preparations are listed in Table 2. For lily pollen grain protoplasts, we obtained P_os values ranging 2.2–10.4 μm · s⁻¹, whereas for pollen tube protoplasts the values were twice as large, 7.6–21 μm · s⁻¹. The difference between these two samples is statistically significant (p < 0.05, Student’s t-test). N. tabacum protoplasts showed values in the range 4.0–13.9 μm · s⁻¹; values obtained for A. thaliana protoplasts extended over a broader range, 3.8–20.6 μm · s⁻¹.

Table 2.

Values of the osmotic parameters Pos and β obtained for different protoplast types. The water permeability coefficient was calculated by three methods: (a) fitting the transient osmotic volume with Eq. 4, (b) using the “initial rate” method and (c) using uncorrected values for the protoplast volume neglecting the non-osmotic volume and fitting the raw volume data with Eq. 4

Protoplast source	Pos (μm s−1)			β
	Fit with Eq. 4	“Initial rate” method	Non-osmotic volume ignored	fit with Eq. 4	Boyle-van’t Hoff plot (upper limit of 95% confidence)
Lilium longiflorum pollen grain	6.59 ± 2.26	4.87 ± 1.68*	5.31 ± 2.22	0.27 ± 0.12	0.420 (0.520)
Lilium longiflorum pollen tube	15.74 ± 5.05	12.12 ± 6.00	6.59 ± 3.17*	0.29 ± 0.08	0.047 (0.403)
Nicotiana tabacum mesophyll	5.75 ± 2.89	3.94 ± 1.13*	4.23 ± 2.52*	0.27 ± 0.13	0.017 (0.210)
Arabidopsis thaliana mesophyll	11.31 ± 6.04	8.15 ± 4.63*	6.45 ± 3.23*	0.32 ± 0.11	0.004 (0.144)

^*Significantly different results (p < 0.05) obtained with methods (b) and (c) compared to method (a). The relative non-osmotic volume β was calculated from individual volume transients using Eq. 10 or by interpolation from Boyle-van’t Hoff plots with the upper limit of the 95% confidence in parentheses (Fig. 2)

The same experimental data were also used to determine P_os by two other methods: the “initial rate” method and by fitting Eq. 4 to volume data which were not corrected for the nonosmotic volume. Both analysis strategies resulted in P_os values which were lower than those obtained by fitting osmotic volume data to Eq. 4 (Table 2). In addition, a difference between the values of β can be observed depending on the method used to obtain them. β values can be calculated from the single volume transients that were also used to calculate P_os of the same protoplast or by interpolation from the Boyle-van’t Hoff plots, giving lower values for the respective protoplast, except for the pollen grain protoplasts (Table 2).

In Figure 4, the calculated P_os value (Eq. 4) was plotted against the relative increase in the surface area ([S_final − S₀]/S₀) for all individual protoplasts measured in this study. No significant correlation between P_os and the corresponding surface increase was noticed (r² values of regression lines <0.5, data not shown) for the different protoplast species, indicating that a large surface increase is not caused by a high P_os. On the other hand, a positive correlation of P_os with surface enlargement would indicate an active contribution of the new membrane area to the water transport, e.g., by incorporation of AQPs into the plasma membrane during swelling. Therefore, the data of Figure 4 do not contradict the prerequisite of a constant water permeability coefficient of the Kedem-Katchalsky model or our assumption of a constant “osmotically active” surface.

Fig. 4.

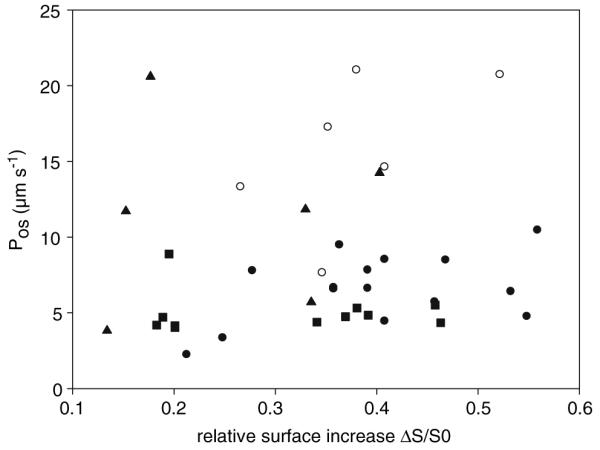
Scatter plot of individual Pos values of all four protoplast types were plotted against the respective relative surface increase. Each data point in the plot represents a single protoplast, with P_os and ΔS/S₀ calculated from its volume transient. Pollen grain protoplasts (●), pollen tube protoplast (○), tobacco mesophyll cell protoplasts (▲) and Arabidopsis thaliana mesophyll cell protoplasts (■)

Discussion

This theoretical and experimental study shows that the accuracy of calculating the protoplast osmotic water permeability P_os can be considerably improved by taking into account the nonosmotic volume and by analyzing the whole swelling curve.

Previous reports on water channels in plant cells used stopped flow measurements on membrane vesicle suspensions (Niemietz & Tyerman, 1997; Maurel et al., 1997), heterologous expression in oocytes (e.g., Maurel et al., 1993; Daniels et al., 1994; Kamerloher et al., 1994; Chaumont et al., 1998) and measurements on whole isolated protoplasts (see Table 1 for references). For the calculation of P_os, most authors have used a method based on the “initial rate” of volume change and reported values that largely ranged 1–500 μm · s⁻¹, depending on the tissue type and age of the plants used. In contrast to experiments that were performed only during the initial linear phase of the volume increase, we used volume transients from the onset of the swelling until a steady state was reached and the volume data were corrected for the contribution of the nonosmotic volume. This is, in our opinion, a necessary step since the theoretical Eq. 1 that describes the time course of the volume change applies only to the osmotic volume (Kedem & Katchalski, 1958).

Using the described approach for the calculation of P_os, the values of the water permeability coefficient of mesophyll protoplasts are within the range common for cells of similar origin (see Table 1 and Table 1 in Chaumont et al., 2005), 5–20 μm · s⁻¹. These rather low values may indicate a lower AQP expression level in leaf mesophyll cells than in other parts of the plant, a lower activity of AQPs or both. The osmotic water permeability coefficient for lily pollen grains showed values in the same range as for mesophyll cells. Interestingly, the values corresponding to the pollen tube protoplasts were twice as high as those for pollen grains, suggesting a possible physiological role of AQPs in water uptake during pollen tube elongation. The data of Table 2 clearly show that the values of the osmotic water permeability coefficient are underestimated when they are calculated with the “initial rate” method or when the nonosmotic volume is ignored. Note that no significant differences in the water permeability coefficient were observed between pollen grains and tubes when neglecting the nonosmotic volume.

The Nonosmotic Volume

We determined the nonosmotic volume of protoplasts by two different methods: (1) by interpolation from linear Boyle-van’t Hoff plots and (2) by fitting whole volume transients measured during osmotic swelling. The values obtained with the first method are lower than those calculated with the second one, except for pollen grain protoplasts. However, when the upper limit of the regression line at 95% confidence is considered in the Boyle-van’t Hoff plots, the discrepancies are less considerable. For the tobacco protoplasts, the intercept of the upper regression line (upper dotted line in Fig. 2) gives a value of 35,000 μm³, which yields a β of 21%, which is not very different from the calculated value using the second method (Table 2). For Arabidopsis protoplasts, the same procedure gives an upper estimate of the nonosmotic volume of 15,000 μm³, indicating a β of 14.4%, also closer to the calculated β value in Table 2. For pollen grain protoplasts, the upper estimate of β gives 52% and for pollen tube protoplasts, 40.3%. To obtain V^os from the measured volume transients (V^measured), the β value determined from the volume transient of the same, single protoplast, also used to calculate P_os, was used. These β values are much less affected by the size heterogeneity of the protoplast population as indicated by the standard deviation (graphs in Fig. 2). In addition, the regression line in the Boyle-van’t Hoff plots can be biased by the less reliable value at the lowest medium osmolality, probably leading to underestimated β values. In general, β is thought to be correlated with different cell structures such as organelles, starch grains, hydration water, etc. (Zimmermann, 1978); and β values in the same range have been measured in other organisms, e.g., 40–50% for the freshwater alga Ochromonas malhamensis (Zimmermann, 1978) and 60–80% for the halophilic alga Dunaliella parva (Rabinowitch et al., 1975). Changes in the relative nonosmotic volume are considered to be a possible mechanism of adaptation to water stress. For example, in Platymonas subcordiformis, the absolute value, b, of the nonosmotic volume is reported to be constant over a large range of salinities, β being found to be shifted from 45% at low salinity to 80% at high salinity (see Zimmermann, 1978, and references therein). Furthermore, the osmoregulation in cotton in response to water stress has been correlated to a starch content-induced increase in the cellular nonosmotic volume (Ackerson & Hebert, 1981).

The relative homogeneity in the β values of our samples is not easy to interpret, given the important structural differences between mesophyll protoplasts, which have a large central vacuole with osmotically active solutes, and pollen protoplasts, which lack a central vacuole but contain many starch grains, liposomes and large generative or sperm cells. One would expect that mesophyll cells have a lower β than pollen protoplasts. Nevertheless, for Commelina communis guard cells, where the vacuoles dominate the cell volume, high values for the relative nonosmotic volume, up to 45%, were reported (Weyers & Fitzsimons, 1982) and it was hypothesized that a large proportion of the guard cell β is due to chloroplast starch. Also, algae, although having a vacuole, show large values of the nonosmotic volume (see citations above). One may, therefore, speculate that not only do specific cellular structures contribute to β but β includes all cell properties accounting for the nonideal osmotic behavior of protoplasts (e.g., stiffness of membrane, rigidity of cytoskeleton) as suggested to explain the resistance in the volume reduction of the hardy dogwood parenchymal cells (β = 48%) at high external osmotic pressures (Williams & Williams, 1976). The detection of deviations from the ideal osmometer behavior depends on the chosen experimental conditions, e.g., the height of the osmolality step and the precision in detecting protoplast volume changes. Using the notations introduced here and the Boyle-van’t Hoff law, we remind that for ideal osmometers c_fV_f = c₀V₀, whereas for real protoplasts c_fV_f − c₀V₀ = b(c₀ − c_f). Let us suppose that a protoplast with a nonosmotic volume b = 0.3V₀ (corresponding to β = 30%) experiences a small osmotic step of just 10% (c₀ − c_f = 0.1c₀). The deviation from an ideal osmometer is then c₀V₀ − c_fV_f = 0.03c₀V₀, or, rearranging, c_fV_f = 0.97 c₀V₀. This 3% deviation from the expected value of the volume corresponds to a deviation of 1% in the diameter of the protoplast (e.g., 0.5 μm for diameters of 50 μm). This is definitely too small to be detectable in a swell assay under such experimental conditions.

The Osmotic Active Surface

In the Kedem-Katchalsky model, the water permeability coefficient is a constant and, in a first approximation, the assumption of a constant surface area, A, is made (Dainty, 1963). In our study, in particular we suggested an “osmotic active” surface area of the protoplast plasma membrane that does not change during the measurement, although the whole membrane surface area changes along with the volume. The assumption of a constant “osmotic active” surface area is fulfilled if the new incorporated membrane material contributes much less to the water transport properties of the membrane than the already existing membrane, also meaning a constant osmotic permeability coefficient, P_os, during the swelling of the protoplast. Typically, the intrinsic elastic stretching of the protoplast membrane can only account for a 2% increase in surface area (Wolfe, Dowgert & Steponkus, 1986), which is completed in usually <10 s. Further changes in the membrane area occurring during a swelling episode do not conserve the amount of material in the membrane. It is hypothesized that in plant protoplasts the plasma membrane exchanges material with an internal membrane reservoir in order to maintain a certain resting tension (Wolfe et al., 1986) and that this is a general mechanism used by animal and plant cells to regulate their surface area (Raucher & Sheetz, 1999; Morris & Homann, 2001). In guard cell protoplasts, it was shown that osmotically induced changes in the surface area are accomplished by reversible incorporation of membrane material during shrinking or stretching (Shope, DeWald & Mott, 2003), more precisely by fission and fusion, respectively, of vesicles from a preplasma membrane pool (Homann, 1998; Kubitscheck, Homann & Thiel, 2000). The question if the additional membrane material has the same characteristic composition as the actual plasma membrane, in other words if new transporters are incorporated or not during swelling, is still open. Some information concerning ion transporters comes from patch-clamp measurements in the whole-cell configuration. By doing simultaneous capacitance and conductance measurements, it was shown that in guard cell protoplasts K⁺ channels are added to the plasma membrane during swelling (Hurst et al., 2004), while addition of membrane material in maize coleoptile protoplasts was not accompanied by incorporation of new ion transporters (Thiel, Sutter & Homann, 2000). However, one cannot extrapolate easily these results to the actual situation in intact swelling protoplasts since patched cells were shown to swell considerably more than intact cells do because they are internally dialyzed against the filling solution of the patch pipette (Doroshenko, 1999). There are also reports showing that AQPs cycle between cellular internal membrane compartments during osmotic and salt stress in ice plant (Kirch et al., 2000; Vera-Estrella et al., 2004), and the picture that emerges is that under stress conditions the tonoplast AQPs are redistributed to endosomal compartments, while plasma membrane-located AQPs are not. Owing to its higher water membrane permeability compared to the plasma membrane (e.g., 100 times higher in tobacco suspension cells: Maurel et al., 1997), the vacuole buffers the cytoplasm rapidly against damaging, large volume changes (Tyerman et al., 1999). It is therefore intuitively reasonable to assume that for efficient cell homeostasis, in a hypoosmotic milieu more AQPs would be incorporated in the tonoplast and not in the plasma membrane, even if its area increases. The data of Figure 4 show no correlation between P_os and the increase in membrane area for the individual protoplasts investigated, implying that additional membrane material does not necessarily mean increased water permeability of the membrane. We remind that P_os reflects a whole-membrane property, being actually a measure of the speed of water movement across the plasma membrane (its measuring unit is μm · s⁻¹). Therefore, one might assume that the total amount of active AQPs depends upon the size of P_os and not their density. Considering that the new membrane incorporated during protoplast swelling would have contained additional water transport units (AQPs), P_os would increase continually and proportionally to the surface increase. This has at least two immediate consequences: (1) function (4) fails to fit the experimental data because in the Kedem-Katchalski model P_os is constant and (2) if one still calculates P_os on the basis of the Kedem-Katchalski model despite a “bad fit,” the resulting P_os values would be high for those protoplasts that experienced a high relative surface increase. In other words, one could notice a positive correlation between ΔS/S₀ and P_os, which is not seen in Figure 4.

Recently, Moshelion et al. (2004) reported water permeability measurements on whole protoplasts isolated from cultured maize cells and evidenced dynamic changes of plasma membrane water permeability occurring upon swelling. They used a numerical solution of the theoretical equation describing the volume transients and tested several models of surface area increase. For their data, the best fit was achieved by a model in which membrane surface area increase is paralleled by an increase of P_os. We cannot confirm such dynamic changes of P_os since our data on pollen and mesophyll protoplasts could be well fitted by function (4) with the assumption that the osmotic active surface area and the water permeability coefficient stay constant during the swelling.

In conclusion, when experimental protoplast swelling data are fitted by a function based on the Kedem-Katchalsky model, the prerequisites of the model (osmotic active volume and a constant water permeability coefficient) have to be taken into account or at least one has to be aware of its limitations. Considering the nonosmotic volume of plant protoplasts was crucial for correct calculation of P_os in whole protoplast swell assays when using the equation derived by Kedem & Katchalsky (1958). Otherwise, an incorrect calculation of P_os may mask differences with physiological relevance as shown between the water permeability coefficients of pollen grain and tube protoplasts.