Modular and Hierarchically Modular Organization of Brain Networks

Abstract

Brain networks are increasingly understood as one of a large class of information processing systems that share important organizational principles in common, including the property of a modular community structure. A module is topologically defined as a subset of highly inter-connected nodes which are relatively sparsely connected to nodes in other modules. In brain networks, topological modules are often made up of anatomically neighboring and/or functionally related cortical regions, and inter-modular connections tend to be relatively long distance. Moreover, brain networks and many other complex systems demonstrate the property of hierarchical modularity, or modularity on several topological scales: within each module there will be a set of sub-modules, and within each sub-module a set of sub-sub-modules, etc. There are several general advantages to modular and hierarchically modular network organization, including greater robustness, adaptivity, and evolvability of network function. In this context, we review some of the mathematical concepts available for quantitative analysis of (hierarchical) modularity in brain networks and we summarize some of the recent work investigating modularity of structural and functional brain networks derived from analysis of human neuroimaging data.

Introduction

Many biological, social, and technological systems, comprised of multiple elements interacting with each other, can be represented as networks. A network viewpoint emphasizes that the behavior of a complex system is shaped by the interactions among its constituents (Newman, 2003) and offers the possibility to analyze systems of a very different nature within a unifying mathematical framework. The identification of common topological properties across many superficially different systems corroborates the hypothesis that their evolution has been driven by universal selection criteria, such as high efficiency of information transfer for low physical connection cost (Bullmore and Sporns, 2009; Sporns, 2010).

The brain can be seen as a network of inter-connected components whose architecture supports the emergence of adaptive behavior and cognition.

The application of complex network tools to neuroscience and neuroimaging datasets has recently led to major advances in understanding the way the brain works at a system level. Several recent reviews (Bassett and Bullmore, 2006; Reijneveld et al., 2007; Bullmore and Sporns, 2009; He and Evans, 2010; Rubinov and Sporns, 2010; Wang et al., 2010; Bullmore and Bassett, 2010) have focused on the data analytic methods that can be used to extract complex networks from structural and functional neuroimaging datasets and to quantify their topological organization.

Complex network theory provides a mathematical framework to identify generic organizational principles behind the architecture of nervous systems. Several aspects of brain network organization are typical also of a wide range of non-neural or non-biological complex networks. For example, brains share several properties such as small-worldness, over-representation of hub nodes, and modularity, with many other complex networks (Stam, 2004; Achard et al., 2006; Achard and Bullmore, 2007; He et al., 2007; Bassett et al., 2008). The small-world property is characterized by a relatively short minimum path length on average between all pairs of nodes in the network (sometimes also described as a short diameter of the network), together with a high clustering coefficient or transitivity (Watts and Strogatz, 1998). Highly clustered physical networks thus have a regular, lattice-like organization which is dominated by short distance connections and is highly economical on wiring costs. The existence of a relatively few long-distance topological short-cuts reduces path length, and increases global efficiency of information processing in brain networks, at the expense of more than minimal wiring costs (Kaiser and Hilgetag, 2006; Bassett et al., 2010).

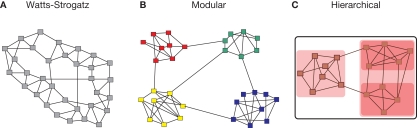
Although small-worldness summarizes key properties of complex networks at global (diameter) and local (triangle) levels of topological description, it does not provide any information about the intermediate scale of network organization, which is more completely described by the community structure or modularity of the network. The modules of a complex network, also called communities, are subsets of nodes that are densely connected to other nodes in the same module but sparsely connected to nodes in other modules. Because nodes within the same module are densely intra-connected, the number of triangular motifs in a modular network is larger than in a random graph of the same size and connection density, while the existence of a few links between nodes in different modules plays the role of topological short-cuts in a small-world formulation of network architecture. Modular systems thus naturally tend to be small-world networks, with high clustering and short path length (Pan and Sinha, 2009), although the converse is not always true: some small-world networks, such as the original Watts–Strogatz model, are not modular (Figure 1).

Figure 1.

Modular systems are small-world but not all small-world systems are modular. Many complex systems can be represented as graphs where the nodes correspond to the constitutive elements (people, websites, neurons, etc), and the links or edges to some type of interaction between nodes (friendships, hyper-links, synapses, etc.). The use of networks across disciplines allows for the formulation of generic organization principles, such as the small-world property. The small-world property is defined as the combination of high clustering and short path length and has originally been illustrated by the Watts–Strogatz model (A). Complex networks also have a tendency to exhibit a modular topology, where links are concentrated within modules (B). Another key type of organization is hierarchical or multi-scale modularity (C), where modules themselves are modular, thus leading to a nested or fractal topological hierarchy.

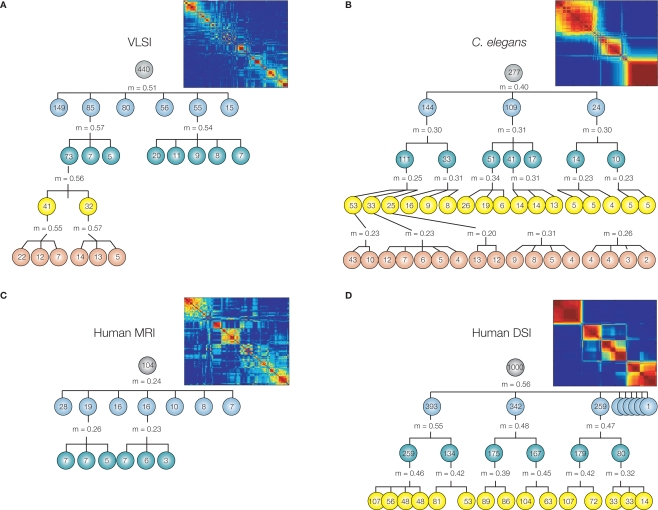
In many systems it seems that modularity does not exist only at a single organizational scale, but rather that each module can be further partitioned into a set of sub-modules, and within each sub-module there may be sub-sub-modules, etc. In other words, many systems have the fractal property of hierarchical modularity, multi-scale modularity or “russian doll” modularity (Figure 2). In biological systems like the brain, self-similarity is statistical rather than exact so the modular community structure brain networks is approximately (not perfectly) invariant over a finite number of hierarchical levels.

Figure 2.

Many information processing networks have a fractal community structure of modules-within-modules. Dendrograms displaying significant modular and sub-modular structure for (A) a very large-scale integrated circuit, (B) Caenorhabditis elegans, (C) the human anatomical network estimated using MRI data on 259 normal volunteers, and (D) the human cortical network estimated using diffusion spectrum imaging (DSI) data on an independent sample of five volunteers. The modularity, m, at each level was estimated using the method of Blondel et al. (2008). The insets demonstrate hierarchical modularity in terms of the co-classification matrix of each system. Reproduced with permission from Bassett et al. (2010).

Here, we discuss different aspects of modularity and hierarchical modularity in relation to brain networks generated from neuroscience and neuroimaging data. We first detail the advantages theoretically provided by a modular topology and review the recognized importance of modularity in models of brain, mind, and information processing systems generally. We then focus on mathematical tools, drawn mainly from graph theory, that can be used to measure and visualize the modular organization of complex systems, and review their recent application to functional and structural brain networks.

Why are Brain Networks Expected to be Modular?

For many years, researchers have been fascinated by the ubiquity of modularity and hierarchical modularity across social, technological, and biological systems, and have searched for dynamic, adaptive, or economical constraints informing the evolution of networks toward a modular architecture. One of the earliest and most influential ideas was formulated by Simon (1962, 1995) who argued that a “nearly decomposable” system built of multiple, sparsely inter-connected modules allows faster adaptation or evolution of the system in response to changing environmental conditions. Modular systems can evolve by change in one module at a time, or by duplication and mutation of modules, without risking loss of function in modules that are already well adapted. Well-adapted modules thus represent stable intermediate states such that further evolution of other modules does not jeopardize function of the entire system. This robustness represents a major advantage for any system evolving under changing or competitive selection criteria, and this may explain the widespread prevalence of modular architectures across a very wide range of information processing systems. In his original article, Simon illustrated his idea by an intuitive parable about two watchmakers, called Hora and Tempus:

“The watches the men made consisted of about 1,000 parts each. Tempus had so constructed his that if he had one partly assembled and had to put it down – to answer the phone say – it immediately fell to pieces and had to be reassembled from the elements. The better the customers liked his watches, the more they phoned him, and the more difficult it became for him to find enough uninterrupted time to finish a watch. The watches that Hora made were no less complex than those of Tempus. But he had designed them so that he could put together subassemblies of about ten elements each. Ten of these subassemblies, again, could be put together into a larger subassembly; and a system of ten of the latter subassemblies constituted the whole watch. Hence, when Hora had to put down a partly assembled watch in order to answer the phone, he lost only a small part of his work, and he assembled his watches in only a fraction of the man-hours it took Tempus.” (Simon, 1962, p. 470)

The implication is that a system with a hierarchically modular design will be more rapidly and robustly assembled. This idea has since been developed more rigorously to identify several evolutionary and computational mechanisms which are likely to favor the emergence of modularity in information processing systems:

• Modular networks have the property of small-worldness which is advantageous for nervous system design because the high clustering of connections between nodes in the same module will favor locally segregated processing (with low wiring cost) of specialized functions such as visual motion detection, while the short path length will support globally integrated processing of more generic functions such as working memory (Sporns et al., 2004).

• Modular network topology is associated with a rich non-linear dynamical behavior that has been described in various ways. Modular networks tend to produce time-scale separation, i.e., fast intra-modular processes and slow inter-modular processes (Pan and Sinha, 2009), or high dynamical complexity (Sporns et al., 2000) due to the coexistence of both segregated and integrated activity (Shanahan, 2008; Pan et al., 2010), or transient “chimera” states (Shanahan, 2010) where synchronization and de-synchronization coexist across the network. The presence of modules allows some neuronal activity to remain locally encapsulated and to maintain dynamical balance (Kaiser et al., 2007; Kaiser and Hilgetag, 2010), i.e., dynamical activity is maintained between the extremes of rapidly dying out and invading the whole network. Hierarchical modularity specifically also enhances dynamical reconnectability (Robinson et al., 2009), as marginally stable networks can be combined or divided while preserving stability. Other benefits of a hierarchically modular organization include an enhanced stability of echo state networks (Jarvis et al., 2010), and dynamical re-connectivity between different transient dynamic behaviors (Müller-Linow et al., 2008; Hütt and Lesne, 2009).

• Plausible mechanisms for brain network development are associated with the formation of modules. This is the case in dynamical systems where network structure and function coevolve (Gross and Blasius, 2008). Models with adaptive rewiring, such as coupled maps with variable coupling strength (Rubinov et al., 2009), typically incorporate a reinforcement of links between synchronized units and a pruning of links between asynchronized ones. This feedback between structure and dynamics, similar to synaptic plasticity in neuronal dynamics, naturally drives the emergence of inhomogeneities and modules in networks.

• Another possible explanation for the origin of modular networks is their optimality at performing tasks in a changing environment (Kashtan and Alon, 2005). In situations where different goals share basic sub-problems, evolutionary pressure produces networks where modules specialize in these sub-problems and where rapid adaptation to each of the different goals is enhanced. This mechanism intuitively describes the natural selection of organisms evolving in a environment where a certain set of basic functions are required and where a combination of these “building functions” is needed to solve complex tasks.

In addition to these general arguments in favor of a modular topology for any economical, adaptive, dynamic system there are also a number of other more specifically neuroscientific reasons to expect brain networks to be topologically modular. For example, in the developmental formation of the nervous system, regular, sometimes metameric, patterns of genetic co-expression can be used to identify modules of spatially localized cells that will share the same developmental fate, maturing to adulthood as a specialized ensemble of cells relatively sparsely connected to cells derived from different histogenetic modules (Redies and Puelles, 2001).

There is massive evidence for anatomical localization of some specialized functions in adult brain. Early studies of anatomical connectivity between major cortical and subcortical regions identified clustering of anatomically and/or functionally related brain regions (Sporns, 2010). Several multivariate methods based on hierarchical clustering, principal component analysis (PCA) or independent component analysis (ICA) have confirmed that functional neuroimaging data, recorded “at rest” or during performance of an experimentally controlled task, can generally be decomposed into sub-systems of functionally connected brain regions (Salvador et al., 2005; Calhoun et al., 2008; Van den Heuvel et al., 2008; Smith et al., 2009).

In the psychological literature, the central principle of phrenology or faculty psychology has been that mental function can be somehow sub-divided into part-functions or mental modules (Fodor, 1983). Modular processes, like color vision, have been described as automatic, effortless, informationally encapsulated, and anatomically localized (Zeki and Bartels, 1998). More consciously effortful tasks, like working memory, have been proposed to demand access to a more globally integrated processing system – a workspace of synchronized neurons oscillating coherently over large physical distances across the whole brain (Varela et al., 2001; Buzsáki and Draguhn, 2004). The emergence of workspace architectures due to conscious effort is therefore expected to “break modularity” of neurocognitive systems (Dehaene et al., 1998). In short, there are strong prior reasons to believe that brain networks are formed and function as modular systems.

Measuring Modularity

The last few years have witnessed a major interdisciplinary effort to develop community detection methods, namely methods for uncovering in an automated way the modules and sub-modules that may be present in networks, and for quantifying how modular the network is. Literally hundreds of methods have been proposed (Porter et al., 2009; Fortunato, 2010), differing in their time complexity and their notion of what a community is. For instance, certain methods aim at uncovering non-overlapping communities while others allow for overlaps, such that nodes have the possibility to belong to several communities (Palla et al., 2005). Partitioning is a popular class of community detection methods which involves finding an optimum partition of the nodes into communities, i.e. each node is assigned to one and only one community. At the core of partitioning methods, there is a mathematical quantity defining what is thought to be a good partition. The widely used modularity metric defined by Newman and Girvan (2004) measures if links are more abundant within communities than would be expected on the basis of chance, but other quality functions have also been proposed, such as the information-theoretic map equation of Rosvall and Bergstrom (2008). Once a quality function has been specified, the network is partitioned heuristically to maximize the chosen quality function. Modularity can be optimized without the need to specify a priori either the number or size of the modules.

As most of the algorithms used for modularity analysis will produce a modular decomposition on random networks (Guimerà et al., 2004), it is always necessary to compare the results obtained from analysis of a brain network with the modularity of appropriate “null model” networks, such as classical Erdös–Renyí graphs, or randomly rewired versions of the observed brain networks (Bullmore and Bassett, 2010). Statistical approaches for handling modularity measurements on several different individual networks (Meunier et al., 2009a), or for comparing modularity between two or more groups of networks (Alexander-Bloch et al., 2010), have been introduced. Alternative and related approaches have been developed for modular decomposition, such as the concept of stability which is based on the persistence of information flows within modules over time (Delvenne et al., 2010). However, there is much active methodological development ongoing for analysis of modular brain networks and this area is likely to advance further in future. In particular, we expect that there will be increasing interest in how the modularity of brain networks – a topological property – relates to their physical instantiation or embedding in space – a geometrical property. In such systems, spatial constraints are known to have a strong effect on connectivity, mainly because of the greater cost associated with longer-distance links. Preponderance of short-ranged interactions has significant consequences for the modular organization of the brain as topological modules tend to be spatially compact and to correspond to anatomically neighboring regions. A better understanding of the principles shaping neuronal organization thus requires future research on the effect of spatial constraints on brain connectivity and the development of appropriately weighted network metrics to fully explore the trade-offs between connection cost and topological efficiency that have been selected in formation of brain networks.

The Community Role of Network Nodes

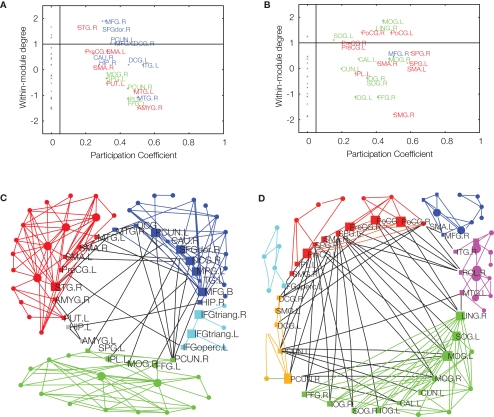
Once an optimally modular partition has been found, it is possible to assign roles to the individual nodes which characterize their significance for intra- and inter-modular transfer of information (Guimerà and Amaral, 2005). The node roles are defined by two parameters. The participation coefficient of a given node is the proportion of edges linking it to nodes in other modules. If a node has zero or only a few inter-modular connections, it is classified as a provincial (or peripheral) node; if its participation coefficient is high, indicating a substantial proportion of inter-modular edges, it is classified as a connector node (Figure 3). The second parameter is a measure of the intra-modular connectivity of the node, namely a Z-score of its intra-modular degree when compared to the degrees of other nodes in the same module. If the degree of a node is higher than that of other nodes in the same module, it is called a hub; otherwise, a non-hub. In the original definition, Guimerà and Amaral (2005) define seven different node roles, depending on specific cut-off values of the participation coefficient and intra-modular degree: ultra-peripheral, peripheral, connector and kinless non-hubs, and provincial, connector and kinless hubs. Connector nodes are naturally of special importance for communication between modules.

Figure 3.

Age-related effects on modularity and topological roles of cortical regions in brain functional networks. Upper panel: intra-modular degree versus participation coefficient for each of the regional nodes in major posterior, central, and frontal modules of fMRI networks in younger (A) and older (B) participants. Connector nodes have large participation coefficients. Lower panel: topological representation of the average young (C) and older (D) brain networks with connector nodes located in a central ring to highlight their key role in inter-modular connectivity. Reproduced with permission from Meunier et al. (2009b).

Hierarchical Modularity

Modularity optimization has been shown to produce useful and relevant partitions in a number of systems (Newman, 2006). Unfortunately, it has also been shown to suffer from several limitations, partly because it produces one single partition, which is not satisfactory when dealing with multi-scale systems. Different methods have been proposed to go beyond modularity optimization (Lambiotte, 2010). A first set of methods searches for local maxima of the modularity landscape in order to uncover partitions at different resolutions (Sales-Pardo et al., 2007; Blondel et al., 2008). Another class of methods introduces multi-scale quality functions, where a resolution parameter is incorporated to tune the characteristic size of the modules and thus to uncover modules at the intrinsic scale of organization of the system, i.e., not at a scale imposed by the method. The most popular multi-scale quality function is the spin-glass modularity (Reichardt and Bornholdt, 2004) whose optimization reveals modules of different characteristic sizes when its resolution parameter is adjusted.

The detection of hierarchies in networks is an active field of research where a broad range of techniques is currently being developed. In addition to generalizations of modularity, let us also mention methods aiming at uncovering hierarchies made of overlapping communities by partitioning the links of the network (Evans and Lambiotte, 2009; Ahn et al., 2010), as well as methods based on the likelihood of hierarchical random graphs to have generated the system in question (Clauset et al., 2008).

Modularity of Anatomical Brain Networks

Several articles studying modular organization at the anatomical level are based on publically available databases of cat or macaque whole brain anatomical connectivity, obtained by fiber tracing and described by Hilgetag et al. (2000). Using these data on brain anatomical networks, Hilgetag et al. (2000) applied an algorithm looking at partitions, with a quality function aiming at maximizing the number of intra-modular edges and minimizing the number of inter-modular edges. They obtained a partition consisting of four subnetworks, that were classified as visual, auditory, somatosensorimotor, and frontolimbic. Zhou et al. (2006) used a modularity metric (Newman and Girvan, 2004) to quantify the optimality of this partition. By simulating dynamics using the anatomical networks, they showed that different dynamics correspond to a hierarchy of modular organization, and provided new insight about the relation between structure and function in brain networks. Sporns et al. (2007) were interested in finding the nodes playing the roles of hub regions in these mammalian anatomical networks. Hubs were defined using several of the many possible criteria, including node roles. Based on the same dataset, Zamora-Lopez et al. (2010) showed the existence of a hierarchy between the different modules: using the notion of betweenness centrality (Freeman, 1979), they showed that the most central nodes of each module constitute a “super-module,” hierarchically on top of the low-level modules.

Modularity in human anatomical networks has been established by Chen et al. (2008). Using correlations across subjects between thickness of gray matter in different cortical regions defined by a previously parcellated template image, an anatomical network was constructed and partitioned. The results show a community structure reproducing some functionally localized areas, such as visual, auditory/language, central (somatosensorimotor), and superior parietal modules. Hagmann et al. (2008) used DTI to uncover a structural core of human anatomical networks. The modules in this network included unilaterally localized areas, such as posterior and frontal lateralized modules, as well as bilateral medial parietal areas and bilateral occipital areas. They define the “structural core of the network” as regions mostly localized in the medial part of the brain, and involving cingulate cortex and precuneus.

Modularity in Functional Brain Networks

The modular organization of the brain functional network in rats was analyzed on the basis of fMRI data, and the influence of pharmacological challenge on the modular structure of functional resting-state networks was investigated (Schwarz et al., 2009), using techniques introduced by Guimerà and Amaral (2005).

Three different studies used very similar methodologies to study the modular partitions of resting-state fMRI networks in humans (Fair et al., 2009; He et al., 2009; Meunier et al., 2009b) (Figure 3). Two of these studies investigated the influence of normal aging on the modular structure: Meunier et al. (2009b) focused on the adult period (healthy controls from 25- to 65-years old); whereas Fair et al. (2009) focused on adolescence and early adulthood (healthy controls from 7- to 31-years old). He et al. (2009) studied a population of healthy young adults (21- to 25-years old).

Two of the studies (He et al., 2009; Meunier et al., 2009b) used similar algorithms and cortical parcellation templates to study modular decomposition, and showed consistent results for the young adult age range (20–25 years) included in both samples. Both studies reported posterior (occipital) and central (sensorimotor) modules, as well as a default-mode module comprising precuneus, cingulate, and medial prefrontal cortex. Valencia et al. (2009) looked at modular organization in human resting-state networks, this time at the voxel level. They showed a similar organization at a finer grain, including visual, central-auditory, default-mode, and subcortical modules.

In keeping with this degree of consistency between studies, there is evidence for reliability of modular decomposition across a range of networks – from sparsely to more densely connected graphs – obtained from the same neuroimaging data by applying different thresholds to define binary graphs from a continuous association matrix (Bullmore and Bassett, 2010). Meunier et al. (2009a) used a stability analysis to assess the reproducibility of the results when applying different thresholds to compute adjacency matrices. They showed that as long as the resulting networks were sparse, the similarity between modular decompositions obtained for different thresholds was very high. He et al. (2009) showed the results of modular decomposition for different thresholds, and once again, for a range of thresholds leading to sparse networks, the modular decompositions were almost the same.

In several of these articles, node roles have been defined to characterize the different functions played by nodes with respect to a given modular partition. Even if using somewhat ad hoc definitions for the different node roles, all the different studies, both in structural and functional neuroimaging (Chen et al., 2008; Meunier et al., 2009a,b; He et al., 2009; Valencia et al., 2009) are quite consistent. It appears that most of the connector nodes (i.e., nodes joining modules together) are located at the junctions between anatomically segregated cortices (occipito-parietal, occipito-temporal, parieto-central, and fronto-central junctions), and are often in regions of multimodal association cortex; whereas the provincial hubs (i.e., nodes mostly linked with nodes of the same modules) are located within functionally specialized areas of cortex (primary or unimodal association areas).

Human brain functional networks obtained from EEG/MEG sensor recordings have also been shown to have small-world and modular properties. Chavez et al. (2010) have shown that EEG networks show differences in modular organization between healthy controls and epileptic patients.

Hierarchical Modularity in Brain Networks

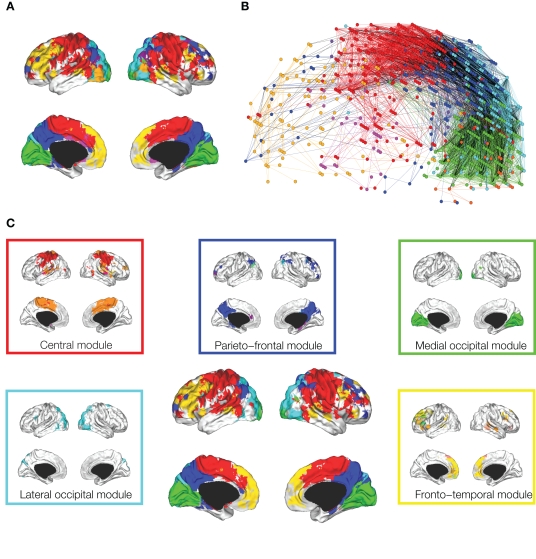
Meunier et al. (2009a) studied the hierarchical organization of human fMRI networks using the greedy method of Blondel et al. (2008) (Figure 4). At the highest level of the hierarchy, where there were fewer and larger modules, occipital, central and default-mode modules were again indentified. However, at lower levels of the hierarchy, each of these major modules was decomposed into a set of sub-modules (or sub-sub-modules). For example, the central module was decomposed into lateral and medial sub-modules. The posterior module could only be decomposed into a few sub-modules, whereas a fronto-temporal module could be decomposed into several small sub-modules. Ferrarini et al. (2009) have also reported that resting state fMRI datasets can be decomposed into a hierarchy of modular communities of functionally related brain regions.

Figure 4.

Hierarchical modularity of a human brain functional network. (A) Cortical surface mapping of the community structure of the network at the highest level of modularity; (B) anatomical representation of the connectivity between nodes in color-coded modules. The brain is viewed from the left side with the frontal cortex on the left of the panel and occipital cortex on the right. Intra-modular edges are colored differently for each module; inter-modular edges are drawn in black; (C) sub-modular decomposition of the five largest modules (shown centrally) illustrates, for example, that the medial occipital module has no major sub-modules whereas the fronto-temporal module has many sub-modules. Reproduced with permission from Meunier et al. (2009a).

Bassett et al. (2010) measured hierarchical modularity of the cellular connectome of the nematode Caenorhabditis elegans and compared this nervous system to whole brain anatomical networks in human MRI and DTI data. They showed that human and nematode networks both demonstrated clear evidence of hierarchical modularity. This organization was also found in the wiring diagram of a high-performance computer chip (or very large-scale integrated circuit). It was argued that hierarchical modularity is expressed consistently across such different information processing systems because it represents an economical wiring diagram for embedding topologically complex systems in a relatively low-dimensional physical space.

Future Questions

One important general problem for the future will be to understand more directly how the topological modularity of large-scale brain networks is related to other aspects of modularity, namely the physical, developmental, pathological, or psychological aspects of the modularity of nervous systems.

The physical geometry of the brain's modularity remains to be elucidated completely. Brain regions belonging to the same topological module are also often neighbors in anatomical space; or, to put it another way, the constituent nodes of topological modules are often anatomically co-localized in the brain (Figure 4). This arrangement seems likely to be advantageous in terms of minimizing the connection distance or wiring cost of intra-modular edges. It also implies that inter-modular connections are likely to be relatively long distance and expensive in terms of wiring cost. There is some evidence that (hierarchical) modular networks represent an economical way of embedding topologically complex systems in relatively low-dimensional physical space (Bassett et al., 2010). However, further work is needed to understand the modularity of brain systems in relation to their anatomical embedding as spatial networks (Barthélemy, 2010).

A related issue concerns the growth of a modular adult brain network: is this developmentally determined in some way by histogenetic modules of the embryonic brain? This could be regarded as further characterization of genetically driven developmental changes in modularity – so-called modularization – that have already been suggested by early studies of normal human brain network maturation and aging (Fair et al., 2009; Meunier et al., 2009b). Moreover, normal processes of modularization might be disrupted in the pathogenesis of neuropsychiatric disorders such as autism or schizophrenia, supporting abnormal modularity of brain network organization as a diagnostic biomarker. In support of this expectation, some evidence for dysmodularity, or abnormal modular organization, has already been reported in the brain functional networks of patients with childhood-onset schizophrenia (Alexander-Bloch et al., 2010).

Since one of the fundamental drivers of human cognitive neuroscience is to understand the brain basis for mental functions, it will also be important to explore how topological modularity of large-scale brain networks might be related to concepts of psychological modularity. For example, Fodor (1983) built on prior ideas from phrenology and faculty psychology to argue that some, relatively low-level, cognitive, or perceptual processes – such as visual perception of motion – can be described as psychologically modular because they are domain-specific, informationally encapsulated, fast, automatic, and anatomically localized. Whereas relatively high-level, integrated, effortful, and conscious cognitive processes have often been linked to an anatomically distributed, neuronal workspace architecture, which may emerge by “breaking modularity” of background processing systems (Dehaene et al., 1998). These and other theoretical ideas suggest that modularity (or non-modularity) of brain network organization might be related to the kind of unconscious/specialized (or conscious/general) cognitive processing that it can support. For example, one might predict that brain functional networks measured serially over time would show dynamic changes in modularity as a function of experimentally controlled changes in demand for psychologically modular cognitive processing.

Clearly there are many questions to address, and theoretical predictions to test, in future experimental studies of modularity and hierarchical modularity of human brain networks.

Conflict of Interest Statement

Edward T. Bullmore is employed half-time by the University of Cambridge and half-time by GlaxoSmithKline; he holds shares in GSK; GSK has no commercial interest in this work.

Key Concept

Modularity

A topologically modular or nearly-decomposable network can be broken down into component modules, each of which comprises a number of nodes that are densely intra-connected to each other but sparsely inter-connected to nodes in other modules.

Path length

A path is a series of edges connecting two nodes in a graph. The path length is the number of edges in a path. Out of all possible paths between two nodes, the shortest path length corresponds to the path made up of the fewest edges. Path length is inversely related to the efficiency of information transfer in a network (Latora and Marchiori, 2001).

Clustering

A high clustering coefficient means that the nearest neighbors of a given node have a high probability to be connected with each other to form the topological motif of a triangle. Small-world networks have higher clustering, but approximately equivalent path length, compared to a random network.

Graph

A graph is a mathematical object, composed of a set of nodes, and a set of edges between pairs of the nodes. In a graphical model of a brain network, the nodes represent (sub)cortical regions or neurons, and the edges represent anatomical or functional connections. Edges can be weighted or unweighted, directed or undirected, and are often defined by thresholding a continuous measure of association between nodes.

Fractal

A fractal object shows approximately the same organization over multiple scales of measurement, so-called scale invariance or self-similarity. For biological fractals like the brain, self-similarity between scales is statistical or approximate rather than exactly perfect as it can be for mathematical fractals like the Sierpinski triangle (Bullmore et al., 2009). Hierarchical modularity (modules-within-modules) is fractal or statistically self-similar in the sense that roughly the same kind of community structure is expressed repeatedly at different hierarchical levels or topological scales of the network.

Heuristics

Finding the optimally modular community structure in a network, according to some quantitative definition of modularity, cannot be solved exactly for large networks. Heuristics or heuristic algorithms thus have to be used to find approximate solutions in non-prohibitive computing times.

Connector nodes

In a modular system, some nodes may have a special role to play in mediating the relatively sparse connections between different modules. In brain networks, cortical regions (e.g., precuneus) with greater inter-modular connectivity are called connector nodes in contrast to other regions (e.g., calcarine cortex) which are called provincial nodes because they may have high connectivity but almost exclusively with other nodes in the same module.

Biography

Edward T. Bullmore studied medicine at the University of Oxford, and St Bartholomew's Hospital in London, before training in psychiatry at the Maudsley Hospital, London. As a Wellcome Trust (Advanced) Research Training Fellow, he was awarded a PhD in statistical analysis of MRI data at the Institute of Psychiatry, London. In 1999, he was appointed Professor of Psychiatry in the University of Cambridge and since 2005 he has been Clinical Director of the Behavioural & Clinical Neuroscience Institute, and Vice-President, Experimental Medicine, for GlaxoSmithKline. He has published more than 260 research articles, mainly on aspects of neuroimaging, and is a Fellow of the Academy of Medical Sciences.