Education And Gender Bias in the Sex Ratio At Birth: Evidence From India

Abstract

This article investigates the possible existence of a nonlinear link between female disadvantage in natality and education. To this end, we devise a theoretical model based on the key role of social interaction in explaining people’s acquisition of preferences, which justifies the existence of a nonmonotonic relationship between female disadvantage in natality and education. The empirical validity of the proposed model is examined for the case of India, using district-level data. In this context, our econometric analysis pays particular attention to the role of spatial dependence to avoid any potential problems of misspecification. The results confirm that the relationship between the sex ratio at birth and education in India follows an inverted U-shape. This finding is robust to the inclusion of additional explanatory variables in the analysis, and to the choice of the spatial weight matrix used to quantify the spatial interdependence between the sample districts.

Access to prenatal sex-detection technologies in areas of the world with rooted son preference has attracted a great deal of attention over recent years. This type of technology enables a person to control family sex-composition by practicing sex-selective abortions. Accordingly, the spread of these technologies might help to explain why atypically high numbers of male births (relative to the number of female births) have become habitual in various countries. The question was first brought up by the work of Johansson and Nygren (1991) and Zeng et al. (1993) in the case of China. Since then, gender bias in natality has been well documented for other countries, such as Korea (Park and Cho 1995) and India (Arnold, Kishor, and Roy 2002; Sudha and Irudaya Rajan 1999).

When there is no access to prenatal sex-detection technology, preferring boys over girls leads parents to focus on an ideal number of sons. That is, regardless of the number of daughters in the family, fertility is completed as soon as the couple has their ideal number of sons (Arnold et al. 2002; Clark 2000). For the aggregate demographic outcomes, this behavior causes inflated fertility ratios, although it does not give rise to female disadvantage at birth. By contrast, controlling family sex-composition through selective abortions decreases the relative number of female births. Therefore, female disadvantage in natality is more likely to arise in those areas of the world that combine the existence of a system of values that give priority to sons over daughters and the availability of prenatal sex-detection technologies.

Education plays a key role in reducing the magnitude of gender inequality (Clark 2000; Murthi, Guio, and Drèze 1995). Nevertheless, various works to date that have examined the relationship between education and female disadvantage in natality in countries characterized by strong son preference have produced inconclusive results. (See the extensive debate that arose from Das Gupta’s [1987] work for the case of India, and the simulation results by Kim [2005] for Korea.) Bearing this in mind, this article aims to delve more deeply into the analysis of the theoretical mechanisms linking education and gender bias in natality. In that respect, education affects a person’s “freedom and power to act” and “freedom and power to question and reassess the prevailing norms and values” (see Drèze and Sen [2002] and Dee [2004] for a similar discussion). In particular, abundant evidence shows that educational gains mean that people are more likely to develop values that give no particular priority to either sex (Bhat and Zavier 2003; Clark 2000). Accordingly, education may be considered an instrument of preference change, which would be supported by the enhancement of freedoms and power to question and reassess the prevailing son preference. Based on efficiency considerations, however, various authors have pointed out that educated parents’ behavior is biased toward the use of sex-selective abortion technologies (Bose and Trent 2005; Das Gupta 1987). This suggests that education can be interpreted alternatively as an instrument of technological-constraint-change because it increases individuals’ freedom and power to access to prenatal sex-detection technologies.

The two effects described above work in opposite directions (Bhat 2002; Clark 2000). Hence, to determine the final impact of education on gender bias in natality, we need to know the magnitude of both effects, which may depend in the final instance on the level of education registered by the society. This suggests the possible presence of a nonmonotonic relationship between education and female disadvantage at birth. Nevertheless, as far as we are aware, this issue has not been considered in any of the works that have so far examined the influence of education on gender bias in natality; see the aforementioned studies. This article fills that gap by presenting for the first time a theoretical model that justifies the existence of a nonlinear relationship between education and female disadvantage at birth. The model is inspired by the literature on cultural transmission, such that particular attention is paid to social interaction and its role in explaining cultural change (Bowles 1998, 2004; Boyd and Richerson 1985).

Using district-level data, we examine the empirical validity of the proposed model for India. Numerous studies have highlighted the influence of cultural and social factors on demographic behavior in India (see the pioneering work by Dyson and Moore [1983] and more recent findings by Rahman and Rao [2004]). This suggests that the geographical location of the various districts may play a relevant role in explaining the spatial distribution of female disadvantage in natality in India. Bearing this in mind, and to investigate in greater detail the importance of spatial effects in this context, we use spatial econometric techniques in our empirical analysis. Most previous work on demographic outcomes in India has tended to ignore the potential relevance of spatial effects,1 which may affect the validity of the results (Anselin 2001).

THE MODEL

In this section, we describe a model that provides various insights into the relationship between education and female disadvantage in natality. Our main assumptions are grounded in empirical evidence on the question under study and the literature on cultural transmission. To start, we consider a population of heterosexual couples in which the husband and wife have identical preferences regarding the sex of their offspring. In turn, each couple lives a single period and then is replaced by their offspring. For simplicity, we assume that population in each generation is of size n, which allows us to eliminate the influence of changes in the population size over time.

A couple modifies the sex of their future child when the following two conditions are satisfied: (1) they have access to the technology that enables them to determine the child’s sex, (2) and they have values (i.e., beliefs and preferences) that lead them to use this technology. As mentioned in the introduction of this article, a wide range of empirical studies describe education as one of the principal predictors of how likely a person is to satisfy each of these conditions. Remember that education is thought of as an instrument that enables access to prenatal sex-detection (Bhat 2002; Das Gupta 1987) but also as an instrument that advocates values that give no priority to any particular gender (Bhat and Zavier 2003; Clark 2000).

We measure education as an exogenous shock that turns a randomly selected portion of the population into educated individuals. In other words, the shock divides the n individuals into two groups: educated and noneducated. Let n^e denote the size of the educated group and n⁰ the size of the noneducated group, where n ≡ n^e + n⁰. Thus, the size of the educational shock is measured by the share of educated population n^e / n. We extend our analysis to the study of infinitesimal increases in education at the end of this section (Result 3).

Prevalence of Son Preference

Regarding the offspring’s gender, an individual either has no preference for any particular sex (unbiased preferences) or has a biased preference toward one particular sex. A nontrivial problem in this context is that biased preferences all run in the same direction, which in turn captures the idea that a portion of the information available to an individual determining his or her preferences suggests that gender does in fact matter: for instance, payoffs associated with raising sons are greater than those associated with raising daughters in many areas of the world (see, e.g., the study by Rosenzweig and Schultz [1982] on rural India).

Without loss of generality, the label female is given to a person with the disadvantageous gender and son preference refers to the biased preferences. In contrast, unbiased preferences are supported by a different body of information, leading people to welcome sons and daughters equally. The idea that several different bodies of information might exist simultaneously means that in acquiring son preference, cultural reasons may be differentiated from alternative ones, such as the payoffs associated with results (Dyson and Moore 1983; Rahman and Rao 2004).

To simulate the effect of education on preferences, we assume that education determines the mechanism through which people acquire preferences. Specifically, we consider that while noneducated people typically acquire their parent’s preferences, education provides individuals with the ability to question and reassess their parents’ preferences. An appealing aspect of this assumption is that education may be said to increase the probability that a person will reevaluate his or her values, preferences, and beliefs in light of a larger informational set (Dee 2004).

We go on to impose some structure on the effects of people gaining the ability to question and reassess their parent’s attitudes toward preferences. At this point, it is worth raising the importance of social interaction. A wide range of theoretical and empirical analyses from different disciplines document a relationship between the aggregated outcomes of individual behavior and the individual behavior itself as a response to the importance of social interaction (Bowles 1998). With that relationship in mind, our model relies on the following nonstandard but highly intuitive assumption: if the size of the educational shock is small enough, people learn from current evidence that replicating values is a best response (Boyd and Richerson 1985; Castelló-Climent 2008).

Our assumption implies that the share of education matters in explaining the effects of education. Recent studies have tested this assumption. In her study explaining the effects of education on the sustainability of democracy, Castelló-Climent (2008) showed that the share of education matters more than average schooling years. In our scenario, the intuitive idea underlying this assumption might be that breaking with family values (or otherwise regarding groups, such as friends) implies facing social costs, which decrease with the shock size (which is to say, “enough people might do the same as one does”); eventually, educated people become encouraged to break with family values, hence switching to unbiased preferences.

Moreover, the idea of relating the acquisition of behavioral traits and the prevalence of the traits in the society is reminiscent of arguments explaining behavior in terms of conformism (see the pioneering work by Boyd and Richerson 1985). Thus, let ρ⁻ be the portion of the population with son preference before the educational shock, ρ^e be the portion of the population in the educated group that develops son preference, and ρ⁰ be the same portion in the noneducated group. Moreover, in line with the conformism models (see the aforementioned literature), let k ∈ [0,1] be a parameter capturing the change benchmark by individuals. Then, we assume that

$${\rho }^e<{\rho }^{-} \text{if} \frac{n^e}{n}\ge k,$$ (1a)

$${\rho }^e={\rho }^{-} \text{otherwise}.$$ (1b)

Expressions (1a) and (1b) together capture the idea that education might act as instrument of preference change. Furthermore, it reflects that the group—rather than the individual—triggers such a change. The structure imposed by (1a) and (1b) does not imply that a person has to develop an identity as a member of a group (the educated group). In order to break with prevailing values, the person has to be aware that a sufficient percentage of “others” might change in a certain direction—in this case, in the direction of unbiased preferences. Because our concern here is to provide as simple an illustrative model as possible, we compare the benchmark k with the educational shock (the portion of educated population). Similar intuitive approaches might well be abstracted from models that compare k with more elaborated functions.

Moreover, only educated people may question and reassess their parents’ preferences, ρ⁰ = ρ⁻. Thus, expressions (1a) and (1b) together mean that ρ^e ≤ ρ⁰ = ρ⁻. The latter implies a weak negative relationship between education and son preference, which is not an overly demanding constraint. A great deal of empirical evidence would support a strict negative relationship between education and son preference (Bhat and Zavier 2003; Clark 2000). We opt to consider that invariant preferences might exist. In contexts of rooted female disadvantage, it is quite possible that education alone does not ensure that people are encouraged to break with prevailing norms and values (see Drèze and Sen [2002] for an in-depth discussion of natality inequality and agency issues).

Access to Technologies

As already stated, our model also captures the role played by education as an instrument that increases the probability of access to prenatal sex-detection technologies. Thus, let σ⁻ ∈ (0,1) be the portion of the population with access to prenatal sex-detection technologies before the educational shock, while σ^e and σ⁰ denote the share of the population with access in each corresponding group. The expression σ⁻ ∉ {0,1} is for mathematical purposes alone and does not imply any change in meaning of theoretical results. We assume that σ^e > σ⁰ = σ⁻.

This assumption implies a strictly positive relationship between education and access to technology. Education is generally considered a key instrument in the enhancement of freedom and power to achieve opportunities that are open to all (Drèze and Sen 1989, 2002). When accounting for the nature of this technology, specifically in the context of female disadvantage in natality, education is presented as an instrument of technological-constraint change (Bose and Trent 2005; Das Gupta 1987).

Theoretical Results

Our concern here is to describe the conditions under which the probability of female disadvantage in natality (represented as changes in the proportion of sons born from one generation to the next) is larger (or smaller) than this probability conditional on being noneducated conditional on being educated versus noneducated. For a sufficiently large population, the result of multiplying ρ^e and σ^e can be taken as the probability that an educated parent will act to switch an offspring’s gender. The same probability, but conditional on being a noneducated individual, is obtained by multiplying ρ⁰ and σ⁰. Hence, our model shows the following:

Result 1. If $\frac{n^e}{n}<k$, then educated people are more likely than noneducated people to cause female disadvantage in natality.

Proof. The proof of Result 1 is straightforward. If $\frac{n^e}{n}<k$, then ρ^e = ρ⁰. Indeed, we get ρ⁻ = ρ⁰ by definition, and ρ^e = ρ⁻ by expression (1b). Meanwhile, by definition, σ^e > σ⁻ = σ⁰. As a consequence, the probability that an educated person controls family sex-composition is larger than the probability that a noneducated person does: ρ^eσ^e = ρ⁰σ^e > ρ⁰σ⁰.

Result 1 explains why, at certain points when the share of education increases in a place, one may obtain the counterintuitive finding that female disadvantage in natality and education positively correlate (Bhat 2002; Das Gupta 1987). Nevertheless, Result 1 says nothing if the spread of education surpasses the benchmark given by k. According to our model, once education triggers preference change, any increment in education is associated with two effects of different sign: ρ^e < ρ⁰, while σ^e > σ⁰. Thus, one might find that the aforementioned positive relationship turns negative, a phenomenon supported by a large body of the literature (Bhat and Zavier 2003; Clark 2000). Let ${\rho }_{MIN}^e$ be the share of educated people who have a son preference if $\frac{n^e}{n}\ge k$. This value is, indeed, the minimum taken by this variable.

Result 2. Consider that $\frac{n^e}{n}\ge k$ holds true. Educated people are less likely to cause female disadvantage in natality if and only if $d>\frac{t{\rho }_{MIN}^e}{{\sigma }^0}$, where $d={\rho }^{-}{\rho }_{MIN}^e$, and t = σ^e – σ⁻.

Proof. The proof of Result 2 is straightforward. By expression (1a), if $\frac{n^e}{n}\ge k$, then ${\rho }^e={\rho }_{MIN}^e$. Thus, ρ^eσ^e < ρ⁻σ⁻ ⇔ (ρ⁻ – d)(σ⁻ + t) < ρ⁻σ⁻ ⇔ ρ⁻t – σ⁻d – td < 0. It is convenient to rewrite [ρ⁻t – σ⁻d – td] as [ $t{\rho }_{MIN}^e-{\sigma }^{-}d$]. Thus, $t{\rho }_{MIN}^e-{\sigma }^{-}d>0\iff d>\frac{t{\rho }_{MIN}^e}{{\sigma }^0}$. Recall that ρ⁻ = ρ⁰ and σ⁻ = σ⁰ by definition. Thus, given $\frac{n^e}{n}\ge k$, ${\rho }^e{\sigma }^e<{\rho }^0{\sigma }^0\iff d>\frac{t{\rho }_{MIN}^e}{{\sigma }^0}$.

Result 2 concludes that if education triggers preference change, this preference change decreases the probability that educated people will cause female disadvantage in natality if and only if there is a large enough decrease in the share of the educated population that has son preference. Here, the decrease in son preference will be large enough if it compensates the fact that by gaining education, educated people who still have son preferences have more chance to act in accordance with their preferences than the noneducated population.

At this point, it is interesting to characterize the effect of infinitesimal increases of education on female disadvantage in natality. To do so, we proceed as follows. Let ɛ be an infinitesimal increase in the share of educated population (which might be interpreted as a second educational shock). This leads to the following result.

Result 3. Assume that $d>\frac{t{\rho }_{MIN}^{e+\epsilon }}{{\sigma }^0}$ holds true. Then for the whole society, the relationship between female disadvantage in natality and education has the following pattern.

(a) If $\frac{n^{e+\epsilon }}{n}<k$ , the increment of education in ɛ is associated with more female disadvantage in natality.

(b) If $\frac{n^e}{n}$, $\frac{n^{e+\epsilon }}{n}>k$, the increment of education in ɛ is associated with reduced levels of female disadvantage in natality.

(c) If, $\frac{n^e}{n}$, $\frac{n^{e+\epsilon }}{n}\approx k$, female disadvantage in natality remains invariant despite the spread of education.

Proof. Patterns (a) and (b) follow from n ≡ n^e + n⁰. Thus, an increment in the educated population in Δn^e = ɛ implies a decrease of the same size in the noneducated population Δn⁰ = –ɛ. These population sizes are expressed in the notation as n ≡ n^{e + ɛ} + n^{0 − ɛ}.

The latter makes the proof of (a) straightforward. As the condition in Result 1 holds, Δn^e = ɛ means the increment of the population that is more likely to switch its offspring’s gender, and hence the increments in female disadvantage in natality.

As far as (b) is concerned, as $\frac{n^e}{n}\ge k$ is upheld, by expression (1a) we arrive at ${\rho }^{e+\epsilon }={\rho }_{MIN}^{e+\epsilon }<{\rho }^{-}$. Meanwhile, by definition, ρ⁰ = ρ⁻. Thus, the condition $d>\frac{t{\rho }_{MIN}^e}{{\sigma }^0}$, by Result 2, implies that the probability that an educated person will switch an offspring’s gender is smaller than the probability that a noneducated person will do so. Thus, for the whole population, Δn^e = ɛ means the increment of the population that is less likely to switch its offspring’s gender, and hence the decrease in female disadvantage in natality. Moreover, it is straightforward to show (c). From (a) and (b), we learn that infinitesimal changes close to k reflect the slope change in the relationship between education and female disadvantage in natality.

Result 3 implies an inverted V-shaped link between education and female disadvantage in natality provided that k ∈ (0, 1). The change in the slope arises as soon as the size of educated population equals the benchmark k: that is, $\frac{n^e}{n}=k$. Our model includes the linear relationship between the two variables—commonly assumed by this literature—as a particular case. If parameter k takes value zero, by gaining education, a person switches to unbiased preferences regardless what the others do. In this case, according to Result 3 (b), we find a negative relationship between education and female disadvantage in natality. In contrast, parameter k may take a value of 1. It implies invariant preferences over educational groups, given that education opens access to sex-selective technology, and according to Result 3 (a), education has a positive impact on the relative number of male births. Note that the latter case is also implied by dropping the condition $d>\frac{t{\rho }_{MIN}^e}{{\sigma }^0}$.

EMPIRICAL ANALYSIS: THE CASE OF INDIA

The theoretical model introduced in the preceding discussion suggests a possible relationship between female disadvantage in natality and education that follows a nonlinear pattern (see Result 3). In this section, we aim to test empirically the validity of our model for the case of India. Research has been conducted in past decades concerning the links between education and demographic outcomes in that country (e.g., Clark 2000; Das Gupta 1987; Murthi et al. 1995), the results of which has failed to achieve a consensus. However, as far as we are aware, no study to date has formally examined the existence of a nonlinear relationship between education and female disadvantage in natality.

To measure the degree of female disadvantage in natality, we employ the sex ratio at birth, defined throughout this article as the ratio of male to female children born in a specific period. In most human populations, more boys than girls are born as a result of a biological phenomenon (Waldron 1985). In an analysis based on different countries with complete and reliable data, Visaria (1971) found that in the absence of intervention, the number of male births per 100 female births ranged between 103 and 107. Nevertheless, during the past two decades, studies have shown anomalously high sex ratios at birth in Asian countries characterized by a long-standing tradition of son preference, such as China or Korea (e.g., Johansson and Nygren 1991; Park and Cho 1995). In these areas, couples are increasingly succeeding in avoiding the birth of girls while ensuring the birth of boys. This raises the possibility that prenatal sex-selection techniques are substituting in these countries for postnatal methods used traditionally to determine the family composition (Goodkind 1996, 1999).

The historical preference for male children in India is well documented in the literature (e.g., Bhat and Zavier 2003; Rosenzweig and Schultz 1982), which suggests that this country is an interesting case study in this context. However, it is difficult to obtain the Indian sex ratio at birth because of incomplete national vital registration data (Griffiths, Matthews, and Hinde 2000; Swamy 1995). Three data sources can be employed by researchers—the Indian census, the Sample Registration System (SRS), and the National Family Health Survey (NFHS)—each of which raises different problems (Bhat 1995; Swamy 1995), such as underenumeration of children (particularly female children), low quality of age reporting, and the presence of sampling errors. In view of these issues, caution must be exercised when comparing the sex ratios at birth obtained from different data sources. Nevertheless, it is interesting to note that the findings of various studies based on data drawn from these three data sources suggest that the Indian sex ratio at birth has tended to increase since the beginning of the 1980s (Arnold et al. 2002; Sudha and Irudaya Rajan 1999). This increasing trend has been particularly relevant in several states located in North-Northwest India, a region traditionally characterized by strong female disadvantage (Miller 1981). Specifically, the most recent data provided by the SRS show that Punjab and Haryana were the two states with the highest sex ratios at birth in India during the period 2004–2006, with values of 124 and 119 boys born per 100 girls, respectively. These figures contrast with the values below the national average (112) observed in several states situated in the South and the East, which confirms the importance of regional differences in the sex ratio at birth across the Indian states.

According to Sudha and Irudaya Rajan (1999), female disadvantage in natality was generally greater in urban areas at the beginning of the 1980s. Nevertheless, the empirical evidence provided by these authors showed that the number of rural zones with anomalously high sex ratios at birth increased considerably throughout the following 10 years.2 As Sudha and Irudaya Rajan (1999) mentioned, this pattern is consistent with the process of spread of a medical technological innovation. Taking into account that there is no reason to attribute the observed trend to an increase in the underenumeration of girls over time, this result suggests the rising employment of prenatal sex-selection techniques and sex-selective abortions in India (Arnold et al. 2002).

Data

The empirical analysis carried out in this section is based on district-level data taken from the 1991 Indian census (Registrar General of India 1991). Specifically, our sample consists of 377 districts for which detailed statistical information is available. These districts belong to the states of Andhra Pradesh, Assam, Bihar, Gujarat, Himachal Pradesh, Karnataka, Kerala, Madhya Pradesh, Maharashtra, Orissa, Punjab, Rajasthan, Tamil Nadu, Uttar Pradesh, and West Bengal, which together accounted for about 90% of India’s population in 1991.

Although the census of India does not publish the sex ratio at birth at the district level, it includes the necessary information to estimate this statistic, applying a reverse-survival technique (e.g. Sudha and Irudaya Rajan 1999; United Nations 1983). The specific procedure used to obtain the sex ratio at birth is based on the idea that the population for age group (0–x) is made up of the survivors from the births that were recorded during the current and the past x years. In particular, from the sex ratio at a certain age cohort, it is possible to obtain the sex ratio at birth in the past x years, given that separate estimates exist for males and females on the probability of dying from birth to each age in the relevant cohort. In our calculations, we use the most recent estimates of the probability of dying from birth to various ages (1, 2, 3, and 5 years) provided by the Registrar General of India (1997). These estimates are based on census questions on the number of children ever born and the number of children surviving.3 Because these probabilities were not available for the 2001 Indian census at the time of this writing, we use the 1991 census in our analysis. This limitation is not particularly important in this context because, as pointed out by Sudha and Irudaya Rajan (1999), prenatal sex-selection techniques had already been introduced in India by 1991 (Arnold et al. 2002). Despite this fact, in the early 1990s, there were still relatively important differences in the access to these techniques, especially in rural areas (Sudha and Irudaya Rajan 1999). This situation is perfectly compatible with the framework outlined in the theoretical model described in the previous section. In any event, as mentioned earlier, the aim of this section is exclusively to test empirically the validity of our theoretical model. Accordingly, we are not interested in explaining the evolution of the sex ratio at birth over time in India.4 The model described in the preceding section does not consider the existence of time effects. Our model is based on the idea that social interaction— not time—is the key factor to understand the relationship between education and female disadvantage in natality.

District-level data, rather than other potential alternatives, were chosen for various reasons. In particular, the district is the basic administrative unit in India and, moreover, the smallest level at which territorially disaggregated information on demographic features is available. Accordingly, the use of district-level data enables us to maximize the number of observations employed in the econometric analysis. This issue is particularly important to justify the adequacy of the methodological approach applied in this section. In fact, the reduced sample size derived from a state-level analysis is clearly inadequate to allow us to employ the various statistical techniques used in our study. Additionally, using state-level data means that existing differences in the sex ratio at birth within the various states are not taken into account, leading to a relatively important loss of information. In particular, according to our estimates, within-state variation explains about 50% of total dispersion in the sex ratio at birth in India, which is consistent with the information provided by, for example, Murthi et al. (1995) and Dharmalingan and Morgan (2004). All these arguments reinforce the need to employ the census data in this context, given that this is the only source that can support a district-level analysis. Furthermore, there are numerous studies on demographic outcomes in India based on this level of territorial disaggregation (e.g. Bhattacharya 2006; Murthi et al. 1995; Rosenzweig and Schultz 1982), which will facilitate any future comparisons of our findings with those previously obtained by other authors.

Econometric Analysis

In view of the implications arising from the theoretical model described in the previous section, our empirical research begins with a preliminary analysis on the possible nonlinearity of the link between the sex ratio at birth and education in India. To this end, the level of education of the population of the sample districts is measured by the literacy rate,5 which is a widely used variable in the literature because of the lack of other alternative indicators at this level of spatial disaggregation (Bhattacharya 2006; Murthi et al. 1995). The literacy rates of the sample districts differ considerably, which confirms the importance of regional disparities in this context.

In the first step of our study to investigate the shape of the relationship between female disadvantage in natality and literacy in India, we seek to impose as little structure on the functional form as possible. A nonparametric approach is advisable in this context because such techniques do not require any prior specification of a particular functional form to capture the relationship between the two variables under analysis. The methodology we employ is locally weighted scatterplot smoothing (lowess).6

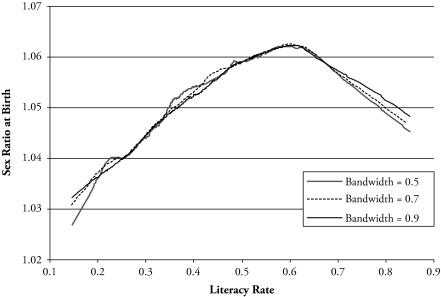
Figure 1 displays the fitted curves obtained when this smoothing method is applied to our sample. The weighting scheme employed in the estimates is based on the tricube weighting function proposed by Cleveland (1979). Accordingly, decreasing weights are attached to observations that are further away from the observation in question. The amount of smoothing depends directly on the number of observations that are used in each regression (the so-called bandwidth). For this reason, we repeat the estimates using different bandwidths in each case. The information provided by Figure 1 suggests that the empirical relationship between the sex ratio at birth and the literacy rate in the sample districts of India is clearly nonmonotonic. Moreover, it appears to follow an inverted U-shape, which is in principle consistent with the theoretical arguments laid down in the preceding section. In fact, this conclusion is robust to the bandwidth employed to obtain the estimates.

Figure 1.

Estimated Sex Ratio at Birth and Literacy Rate in India: Locally Weighted Scatterplot Smoothing

However, several reasons suggest that this finding should be treated with some caution. For example, the nature of the analysis carried out thus far does not allow us to establish a causal link between literacy rate and sex ratio at birth. Likewise, it is very likely that the degree of female disadvantage in natality registered in the sample districts does not depend exclusively on their literacy rates. This suggests that additional explanatory variables should be included in the analysis. Finally, and in relation to the latter, the lowess method used prevents any attempt to control for spatial specific factors relating, for example, to social or cultural features, the importance of which has been repeatedly stressed in the Indian context by numerous authors (Dyson and Moore 1983; Rahman and Rao 2004). In view of these issues, and taking into account that Figure 1 provides strong support for the existence of a quadratic relationship between the sex ratio at birth and literacy rate, we shall now consider the estimation of the following parametric model:

$$SR{B}_i=\alpha +\beta LI{T}_i+\delta LI{T}^2{}_i+\mathbf{\phi }{\mathbf{\text{X}}}_i+{\nu }_i,$$ (2)

where SRB_i is the sex ratio at birth of district i, LIT_i is the literacy rate, X_i is a vector of variables that control for other factors that are assumed to influence the dependent variable, and ν_i is the corresponding disturbance term.

Before discussing several technical issues in relation to the estimation of the regression in Eq. (2), we describe the series of variables that make up the vector X (see Table 1 for further details). Although the choice of the selected variables is well grounded in the literature on the subject, it ultimately depends on the availability of reliable statistical data for the level of spatial disaggregation on which the study is focused.

Table 1.

Variable Definitions and Sample Descriptive Statistics: India 1991

Variable	Definition	Mean	SD
Sex Ratio at Birth	Number of male births per 100 female births	105.17	0.032
Literacy Rate	Percentage of population that is literate	40.91	0.134
Female Literacy Rate	Percentage of female population that is literate	29.83	0.154
Male Literacy Rate	Percentage of male population that is literate	51.18	0.122
Female Labor Force	Percentage of female population categorized as main workers	16.90	0.106
Rural Population	Percentage of population that lives in rural areas	79.67	0.140
Medical Facilities	Percentage of villages that has a medical facility	38.52	0.309
Scheduled Castes	Percentage of population that belongs to a scheduled caste	16.35	0.075
Scheduled Tribes	Percentage of population that belongs to a schedule tribe	10.04	0.163
Agricultural Workers	Percentage of main workers categorized as agricultural workers	24.51	0.129
Poverty Index	Regional incidence of poverty measured in the interval [0,1]	0.518	0.255
East	Dummy variable = 1 for districts in Bihar, Orissa, and West Bengal	0.188	0.391
Northwest	Dummy variable = 1 for districts in Himachal Pradesh, Punjab, and Rajasthan	0.135	0.342
South	Dummy variable = 1 for districts in Andhra Pradesh, Karnataka, Kerala, and Tamil Nadu	0.201	0.402

Sources: Registrar General of India (1998) for medical facilities; Planning Commission of India (2003) for the poverty index. The remaining variables are calculated from the 1991 Indian census (Registrar General of India 1991, 1997).

We begin by considering the role played in this framework by female labor force participation, measured as the percentage of main workers in a district’s female population. A main worker is defined in the Indian census as a person who worked for 183 days or more in the preceding year. The literature has paid increasing attention to the link between demographic outcomes and a factor that is referred to as “women’s agency” (Sen 1984) or “women’s autonomy” (Dyson and Moore 1983), understood as women’s power to exercise choice in their actions regardless of the constraints imposed by social structures. Female labor force participation is a relevant factor in this context (Bhattacharya 2006; Rahman and Rao 2004). Nevertheless, it is difficult to determine beforehand the possible effect of this variable on the sex ratio at birth. On the one hand, women who work outside the home increase family income. Accordingly, a high level of female labor force participation may enhance the value attached to females, thus reducing son preference (Dyson and Moore 1983; Rosenzweig and Schultz 1982). On the other hand, outside employment means greater social interaction, which may favor wider access to prenatal sex-detection technologies. These effects work in opposite directions. Empirical research is therefore key to understanding the nature of the relationship between female labor force participation and our dependent variable.

In addition, it is worth investigating the extent to which the link between the sex ratio at birth and education is the same in rural and urban zones of India. In fact, a wide range of empirical evidence documents that fewer girls than boys are born in Indian urban areas than in rural zones, which might have to do with the existence of greater access opportunities to sex-selective abortion technologies in urban areas than in rural ones (Sudha and Irudaya Rajan 1999). In the light of these considerations, we calculate the proportion of the population in each district that lives in rural areas and include this variable among the regressors in our empirical model.

Furthermore, we take into account the role of family planning services in this context. The Indian Government has a long tradition of promoting family planning programs at the national level (Bose and Trent 2005). This may be relevant in our framework because districts that have traditionally offered professional advice on family planning decisions are likely to be home to a higher portion of the population that is prepared to use prenatal sexselection techniques. Accordingly, the availability of medical facilities can exert a direct effect on the sex ratio at birth through the provision of family planning services. For this reason, the share of villages in a district with access to medical facilities is included in the set of control variables that are used to explain the observed differences in the sex ratio at birth in our sample.

Additionally, the demographic features of Indian districts may depend on the relative importance of the less-advantaged social groups because different social norms may affect the behavior of people in these groups. Bearing this in mind, we calculate the share of a district’s population that integrates two minority social groups: scheduled castes and scheduled tribes. This allows us to illustrate possible contrasts in this context between these two social categories and other sections of the population, which is of particular interest in the Indian case (Luke and Munshi 2007; Mitra 2008). The scheduled castes, which make up about 16% of the country’s population, include various Hindu groups belonging to the lowest scale in the caste hierarchy. Despite the fact that discrimination on the basis of caste is illegal according to the Indian constitution, members of this social group suffer from discrimination in large parts of the country. In turn, the scheduled tribes include the majority of tribal and indigenous communities living in India.

Furthermore, because the demographic features of the Indian districts may depend on their level of economic development and modernization, we should control our estimations for these factors. This is not an easy task at this level of territorial disaggregation, since district-specific indicators of income or expenditure are not available in India. To overcome this important limitation, we use the share of agricultural workers among all main workers in a district as a proxy for its level of economic development. The relevance of the agricultural sector in terms of output and employment decreases as advances are made in the economic development process because of the shift of productive resources toward manufacturing activities and services (Kuznets 1966). According to this argument, it may reasonably be supposed that the districts with greater percentages of agricultural workers tend to register lower levels of economic development. Two of the above-mentioned control variables—the share of rural population and the degree of access to medical facilities—can be also used to approximate the level of economic development and the degree of modernization of the various districts object of analysis (Bhattacharya 2006).

Another issue of interest in this context is the potential link between poverty and the sex ratio at birth (Edlund 1999). Because the Indian census does not gather data on the degree of poverty registered within the sample districts, we employ in our analysis the poverty estimates provided by the Planning Commission of India (2003) and based on the 55th round of the National Sample Survey (NSS). The use of these data is not problem free. In particular, the sample size in the NSS for many districts is very small, which makes it impossible to estimate reliable poverty indicators at this level of territorial disaggregation. Therefore, a different territorial unit is used as a reference. Specifically, the poverty estimates employed in our analysis refer to the different regions defined by the NSS according to socioeconomic and agroclimatic criteria. These regions are inter mediate spatial units between the district and the state. Accordingly, the use of these poverty estimates in our empirical model implies some loss of information because it involves the implicit assumption that intraregional differences in poverty are relatively small. In addition, the inclusion of this additional control variable obliges us to reduce the sample size to 330 districts because of the lack of data. In the light of these considerations, we estimate an alternative version of the regression in Eq. (2) that includes the poverty indicator in order to compare the results with those obtained from the original sample.

Finally, we include three regional dummy variables to identify possible regional patterns and reduce the potential impact on the results of the omitted-variable bias: East for districts in Bihar, Orissa, and West Bengal; Northwest for districts in Himachal Pradesh, Punjab, and Rajasthan; and South for districts in Andhra Pradesh, Karnataka, Kerala, and Tamil Nadu. The control region is integrated by the districts in the remaining states. These three regional dummy variables have been defined by taking our estimates of the sex ratio at birth into account, as well as the findings of the literature on gender bias in India (e.g. Bose and Trent 2005; Dyson and Moore 1983).

Table 2 presents the main results of our empirical study. As shown in the first two columns of the table, we begin by estimating Model (2) by ordinary least squares (OLS). The OLS estimator is based on the assumption that the error terms are independently and identically distributed. However, a simple inspection of the estimated sex ratio at birth values suggests that this variable is not randomly distributed across space in India. This finding points to the possible presence of spatial dependence in our sample,7 which would affect the properties of the OLS estimator. To investigate this issue more deeply, we calculate five tests for spatial dependence from the OLS residuals: the Moran’s I test (Cliff and Ord 1972), the Lagrange multiplier tests for the spatial error model (LMERR), and the spatial lag model (LMLAG) proposed by Burridge (1980) and Anselin (1988a), plus their robust versions (R-LMERR and R-LMLAG; Anselin et al. 1996). Before performing these tests, we must specify a spatial weight matrix to capture the degree of interdependence between each pair of districts i and j. Within this framework, it is important to stress that the spatial weights should be exogenous to the model to avoid the identification problems raised by Manski (1993). For this reason, we use pure geographical distance, which in itself is strictly exogenous. Specifically, the spatial weight matrix we use, W, is based on the inverse geographical distance between the centroids of the sample districts. This matrix is row-standardized, which means that relative—not absolute—distance is what matters. In addition, as is usual in the literature, when defining W, we consider a cutoff parameter above which spatial interactions are assumed to be negligible. In our analysis the critical cutoff is determined by the first quartile of the distance distribution.8

Table 2.

Estimated Sex Ratio at Birth: Results of the Regression Analysis

Variable	OLS	OLS	ML	ML
Constant	1.045*** (0.016)	1.000*** (0.016)	0.289*** (0.088)	0.381*** (0.106)
Literacy Rate	0.187*** (0.046)	0.267*** (0.043)	0.184*** (0.042)	0.233*** (0.042)
Literacy Rate, Squared	−0.170*** (0.049)	−0.242*** (0.045)	−0.165*** (0.044)	−0.211*** (0.043)
Female Labor Force	−0.063*** (0.015)	−0.088*** (0.015)	−0.060*** (0.012)	−0.058*** (0.016)
Rural Population	−0.046*** (0.009)	−0.007 (0.010)	−0.032*** (0.008)	−0.005 (0.009)
Medical Facilities	0.010* (0.005)	0.001 (0.005)	0.002 (0.004)	0.001 (0.004)
Scheduled Castes	−0.003 (0.017)	−0.016 (0.017)	−0.025 (0.015)	−0.024 (0.016)
Scheduled Tribes	−0.033*** (0.007)	−0.038*** (0.008)	−0.031*** (0.007)	−0.038*** (0.007)
Agricultural Workers	0.051*** (0.010)	0.080*** (0.021)	0.051*** (0.009)	0.072*** (0.020)
Poverty Index		0.027*** (0.005)		0.018** (0.006)
East	−0.028*** (0.004)	−0.028*** (0.003)	−0.014*** (0.003)	−0.012** (0.004)
Northwest	0.042*** (0.005)	0.035*** (0.005)	0.023*** (0.005)	0.020*** (0.005)
South	−0.017*** (0.004)	−0.025*** (0.004)	−0.011*** (0.003)	−0.017*** (0.004)
Spatial Lag of SRB (λ)			0.713*** (0.082)	0.593*** (0.100)
Log-Likelihood	918.835	838.476	947.140	854.696
Akaike’s Information Criterion	−1,813.670	−1,650.952	−1,866.279	−1,679.393
Moran’s I	12.177***	8.070***
LMERR	51.955***	17.019***
R-LMERR	10.251***	1.270
LMLAG	81.354***	41.327***
R-LMLAG	39.650***	25.578***
Wald Test for λ = 0			74.693***	34.860***
LM Test for λ = 0			81.354***	41.327***
Number of Observations	377	330	377	330

Notes: The dependent variable in all cases is the sex ratio at birth, defined as the ratio of male to female births. Robust standard errors are in parentheses (White 1980, 1982).

^*p < .05;

^**p < .01;

^***p < .001

According to the information provided by Table 2, the results of the various tests for spatial dependence lead to the rejection of the null hypothesis of absence of residual spatial dependence, despite the fact that Model (2) includes different regional dummies. This may result from the influence of unobserved cultural and social factors on the sex ratio at birth (Murthi et al. 1995; Rahman and Rao 2004). To decide the most appropriate specification in this context, we follow the classical approach adopted in the spatial econometric literature. Specifically, given that in all cases, the values of the LMLAG and R-LMLAG tests are greater than those for the LMERR and R-LMERR tests, we selected the spatial lag model as the best specification in this context (Anselin and Rey 1991). Accordingly, the spatial lag of the dependent variable, WSRB_i, must be included in the list of regressors. Consequently, we should estimate the following model:

$$SR{B}_i=\alpha +\beta LI{T}_i+\delta LI{T}_i^2+\mathbf{\phi }{\mathbf{\text{X}}}_i+\lambda \mathbf{\text{W}}SR{B}_i+{\nu }_i,$$ (3)

where λis the spatial autoregressive parameter.

Nevertheless, the estimation of Model (4) by OLS is inconsistent because of simultaneity induced by the spatial lag. Maximum likelihood (ML) estimators have been proposed to provide consistent estimates (Anselin 1988b).9 In view of this, the third and fourth columns in Table 2 show the ML estimates of the spatial lag Model (3). Following the suggestion of White (1982), reported standard errors come from the heteroskedasticity-consistent estimator of the covariance matrix of the ML parameters.

The different measures of goodness-of-fit included in Table 2 (the value of the maximized log likelihood and the Akaike’s information criterion) reveal that the spatial lag model estimated by ML provides an increased explanatory power. As can be observed, the spatial autoregressive parameter is significant and positive in all cases. In fact, the internal coherence of the spatial lag model is strengthened if we take into account the results of the Wald test and the Lagrange multiplier test for λ = 0. All this clearly shows that the sex ratio at birth in the neighboring districts has a positive effect when one attempts to explain the variability of the dependent variable.

As stated earlier, the main objective of our empirical analysis is to investigate the relationship between female disadvantage in natality and education. In this respect, the estimated coefficients from the spatial lag model yield interesting results. Table 2 shows that the coefficients of the literacy rate and the square of the literacy rate are in all cases statistically significant. Specifically, their signs show the presence of an inverted U-shaped link between the sex ratio at birth and education in the Indian case, thus confirming the preliminary evidence provided by the lowess method. Therefore, as the share of the literate population increases, the sex ratio at birth tends at first to increase. Nevertheless, this relationship does not continue indefinitely, and beyond levels of literacy situated at around 55% of the total population, our analysis reveals a negative correlation between education and the sex ratio at birth. When we weigh the relevance of this finding, our results are consistent with the conclusions derived from the theoretical model discussed in the previous section.

Table 2 also provides information on the role played by the remaining explanatory variables when explaining the variation of the sex ratio at birth across the Indian districts. The analysis indicates that higher levels of female labor force participation decrease the sex ratio at birth, confirming the relevance of women’s agency in reducing female disadvantage in India (Bhattacharya 2006). This finding is indeed obtained after we control for the level of economic development and the degree of poverty within the sample districts. Similarly, earlier studies have identified the positive impact of female labor force participation on the reduction of the extent of gender bias in child survival in India (e.g., Murthi et al. 1995).

Additionally, our estimates indicate that the proportion of the population that is rural is negatively correlated with the dependent variable. This suggests that female disadvantage at birth seems to be lower in rural areas, where access to prenatal sex-detection technologies is generally more difficult than in urban zones (Bose and Trent 2005; Sudha and Irudaya Rajan 1999). Nevertheless, this result should be treated with caution, given that the coefficient associated with the degree of urbanization is not statistically significant when the poverty indicator is included in the list of regressors (fourth column in Table 2).

Another issue of interest is that according to our estimates, the availability of medical facilities has no effect on female disadvantage at birth. When interpreting this result, remember that efficiency in the functioning of health services is at least as important as their availability (Murthi et al. 1995). In fact, many studies have highlighted the poor functioning of public health services in India (e.g., Das and Hammer 2007).

Furthermore, from among the variables included in the analysis to control for the role played by specific social groups, only the proportion of the total population that is in scheduled tribes is statistically significant. Therefore, the share of scheduled castes has no influence on the sex ratio at birth. This is not particularly surprising given that the magnitude of the differences in the gender relations between the scheduled castes and the rest of the population have narrowed considerably in past decades (Luke and Munshi 2007). The situation is different with the proportion of scheduled tribes, however. Our estimates show that relatively high values of this variable lead to a decline in the sex ratio at birth. In fact, the effect still holds after we control for female labor force participation, which tends to be greater among this social group than in the population as a whole. This finding suggests that tribal societies have specific features that contribute to reduce discrimination against females at birth (Mitra 2008). Although further research is required to study this issue more deeply, particular attention should be paid to the characteristics of kinship systems and property rights in this social group (Murthi et al. 1995).

A higher proportion of agricultural workers is positively correlated with our dependent variable. According to this result, the process of structural change that characterizes the advances in the development process leads to a decline in female disadvantage at birth. The degree of poverty registered within the sample districts has a positive impact on the sex ratio at birth, which suggests the possibility that gender bias in natality may be stronger among the less-privileged social classes. Nevertheless, the different problems raised by the inclusion of the poverty indicator in the list of regressors should not be overlooked, for which reason further studies are required to confirm this finding.

Finally, the three regional dummy variables included in our model are statistically significant even after we control for the remaining variables, which highlights the presence of relevant spatial differences in this context. Accordingly, the geographical location of the various districts plays an important role in explaining the variability of the sex ratio at birth. Despite some exceptions, the sex ratio at birth is relatively higher in the Northwest compared with the control region. These areas have a long tradition of social systems in which exogamous marriages, dowries, and the seclusion of women play an important role (Dyson and Moore 1983; Rahman and Rao 2004). On the contrary, discrimination against females at birth is less relevant in the southern states and the rice-cultivating eastern zone of the country. The south of India has been characterized historically by more liberal social structures than other parts of the country in relation to marriage customs, kinship, and inheritance patterns (see Dyson and Moore 1983; Rahman and Rao 2004).

The variable we used to capture the level of education of the population living in the sample districts—the overall literacy rate—does not take into account existing differences between male and female literacy rates. This issue, however, may be of particular relevance in this context because of the relatively high degree of gender inequality in access to education in India. For this reason, and to complete our earlier findings, we repeat the estimations using the male and female literacy rates as an alternative to the overall literacy rates employed in the preceding analysis. The information provided by Tables 3 and 4 indicates that the results are in all cases very similar to those we already discussed. The most relevant issue is that the bell-shaped relationship observed previously between education and the sex ratio at birth still holds when the male and female literacy rates are employed, thus confirming our earlier findings with overall literacy rates.

Table 3.

Robustness Analysis 1: The Role of Male Literacy Rate

Variable	OLS	OLS	ML	ML
Constant	1.030*** (0.021)	0.983*** (0.021)	0.282** (0.090)	0.325** (0.104)
Male Literacy Rate	0.205** (0.065)	0.282*** (0.060)	0.208*** (0.058)	0.258*** (0.056)
Male Literacy Rate, Squared	−0.156** (0.061)	−0.219*** (0.055)	−0.162** (0.055)	−0.203*** (0.052)
Female Labor Force	−0.064*** (0.015)	−0.086*** (0.016)	−0.061*** (0.012)	−0.056*** (0.015)
Rural Population	−0.048*** (0.009)	−0.014 (0.010)	−0.035*** (0.008)	−0.010 (0.009)
Medical Facilities	0.009 (0.005)	0.001 (0.004)	0.001 (0.004)	0.000 (0.004)
Scheduled Castes	−0.000 (0.017)	−0.013 (0.017)	−0.024 (0.016)	−0.024 (0.016)
Scheduled Tribes	−0.032*** (0.008)	−0.037*** (0.008)	−0.030*** (0.007)	−0.036*** (0.007)
Agricultural Workers	0.053*** (0.011)	0.087*** (0.021)	0.052*** (0.009)	0.078*** (0.020)
Poverty Index		0.030*** (0.006)		0.020*** (0.006)
East	−0.029*** (0.004)	−0.026*** (0.004)	−0.015*** (0.003)	−0.010* (0.004)
Northwest	0.041*** (0.005)	0.033*** (0.005)	0.022*** (0.005)	0.019*** (0.005)
South	−0.018*** (0.004)	−0.026*** (0.004)	−0.012*** (0.003)	−0.018*** (0.004)
Spatial Lag of SRB (λ)			0.705*** (0.083)	0.629*** (0.098)
Log-Likelihood	917.778	833.373	945.199	851.679
Akaike’s Information Criterion	−1,811.557	−1,640.746	−1,862.398	−1,673.359
Moran’s I	11.535***	9.253***
LMERR	47.029***	24.537***
R-LMERR	8.390**	2.945
LMLAG	78.393***	48.056***
R-LMLAG	39.755***	26.464***
Wald Test for λ = 0			71.171***	41.028***
LM Test for λ = 0			78.393***	48.056***
Number of Observations	377	330	377	330

Notes: The dependent variable in all cases is the sex ratio at birth, defined as the ratio of male to female births. Robust standard errors are in parentheses (White 1980, 1982).

^*p < .05;

^**p < .01;

^***p < .001

Table 4.

Robustness Analysis 2: The Role of Female Literacy Rate

Variable	OLS	OLS	ML	ML
Constant	1.071*** (0.012)	1.033*** (0.013)	0.297*** (0.087)	0.424*** (0.107)
Female Literacy Rate	0.114*** (0.030)	0.183*** (0.028)	0.118*** (0.027)	0.155*** (0.028)
Female Literacy Rate, Squared	−0.122*** (0.037)	−0.194*** (0.035)	−0.123*** (0.034)	−0.164*** (0.034)
Female Labor Force	−0.059*** (0.015)	−0.086*** (0.015)	−0.056*** (0.012)	−0.005 (0.016)
Rural Population	−0.048*** (0.010)	−0.007 (0.011)	−0.032*** (0.009)	−0.005 (0.010)
Medical Facilities	0.010* (0.005)	0.001 (0.005)	0.002 (0.004)	0.001 (0.004)
Scheduled Castes	−0.001 (0.017)	−0.013 (0.017)	−0.033*** (0.015)	−0.021 (0.016)
Scheduled Tribes	−0.036*** (0.007)	−0.042*** (0.008)	−0.031*** (0.007)	−0.041*** (0.007)
Agricultural Workers	0.048*** (0.010)	0.069*** (0.021)	0.048*** (0.009)	0.063*** (0.019)
Poverty Index		0.026*** (0.006)		0.017** (0.006)
East	−0.028*** (0.004)	−0.029*** (0.003)	−0.014*** (0.004)	−0.013*** (0.004)
Northwest	0.042*** (0.005)	0.035*** (0.005)	0.022*** (0.005)	0.020*** (0.005)
South	−0.018*** (0.004)	−0.025*** (0.004)	−0.012*** (0.003)	−0.018*** (0.004)
Spatial Lag of SRB (λ)			0.727*** (0.082)	0.580*** (0.101)
Log-Likelihood	916.605	838.109	945.904	853.352
Akaike’s Information Criterion	−1,809.210	−1,650.219	−1,863.808	−1,676.703
Moran’s I	12.888***	7.968***
LMERR	57.748***	16.136***
R-LMERR	12.439***	1.375***
LMLAG	84.304***	37.950***
R-LMLAG	38.995***	23.189***
Wald Test for λ = 0			79.260***	32.678***
LM Test for λ = 0			84.304***	37.950***
Number of Observations	377	330	377	330

Notes: The dependent variable in all cases is the sex ratio at birth, defined as the ratio of male to female births. Robust standard errors are in parentheses (White 1980, 1982).

^*p < .05;

^**p < .01;

^***p < .001

CONCLUDING REMARKS

In this article, we investigate the possible existence of a nonlinear relationship between female disadvantage in natality and education. In a first stage, we devised a theoretical model that justifies the existence of a nonmonotonic link between both variables. As is usual in the literature on cultural transmission, our framework stresses the relevance of social interaction when explaining cultural change. Specifically, the final impact of education on gender inequality in natality in our model depends in the final instance on the magnitude of two effects that work in opposite directions. These two effects are based on the double role played by education in this context: as an instrument of preference change and as an instrument of technological-constraint change.

In a second stage, we examined the empirical validity of the proposed model in the context of India, a country characterized by a long-standing tradition of son preference. To do so, we estimated the sex ratio at birth of the Indian districts by applying a reverse survival method. Following the common practice in the literature, we proxied the level of education of the various districts by their literacy rate. To avoid potential misspecification problems, our empirical study paid special attention to the role played in this context by spatial effects, for which reason we employed a methodological approach based on spatial econometric techniques. This is particularly advisable in the present framework because the calculations of the various spatial dependence tests indicate the need to include the spatial lag of the sex ratio at birth in the list of regressors (spatial lag model). Our estimates reveal that the relationship between the sex ratio at birth and the literacy rate follows an inverted U-shape, which confirms the conclusions derived from the theoretical model proposed in the article. In fact, this finding is obtained after including various additional explanatory variables in the analysis such as female labor force participation, the share of rural population, the proportion of villages in a district with access to medical facilities, the relevance of scheduled castes and scheduled tribes, the share of agricultural workers, the degree of poverty registered within the sample districts, and regional dummy variables.