Multivariate Analysis of Parity Progression–Based Measures of the Total Fertility Rate And Its Components

Abstract

This article describes a methodology for applying a discrete-time survival model—the complementary log-log model—to estimate effects of socioeconomic variables on (1) the total fertility rate and its components and (2) trends in the total fertility rate and its components. For the methodology to be applicable, the total fertility rate (TFR) must be calculated from parity progression ratios (PPRs). The components of the TFR are PPRs, the total marital fertility rate (TMFR), and the TFR itself as measures of the quantum of fertility, and mean and median ages at first marriage and mean and median closed birth intervals by birth order as measures of the tempo or timing of fertility. The focus is on effects of predictor variables on these measures rather than on coefficients, which are often difficult to interpret in the complex models that are considered. The methodology is applicable to both period and cohort data. It is illustrated by application to data from the 1993, 1998, and 2003 Demographic and Health Surveys (DHS) in the Philippines.

In this article, we develop methodology for applying a multivariate discrete-time survival model—the complementary log-log model—to estimate effects of socioeconomic predictor variables on the total fertility rate (TFR) and on the trend in the total fertility rate.1 The methodology requires individual-level survey data and is applicable to both period and cohort measures of the TFR. The analysis of effects of socioeconomic variables on the trend in the TFR is based on two or more surveys of the same population at different times.

The TFR is usually defined as the number of births that a woman would have by age 50 if she lived through her reproductive years and experienced the age-specific fertility rates (ASFRs) that prevailed either in a particular time period (e.g., the five-year period before survey) or over the lifetime experience of a particular cohort (e.g., women aged 40–49 at time of survey). The TFR so defined is calculated by summing ASFRs (births per woman per year at each age) between the ages of 15 and 50. For the methodology in this article to be applicable, however, the TFR must be calculated from parity progression ratios (PPRs) for either a particular period or a particular cohort. A woman’s parity is defined in the usual way as the number of children she has ever borne, but with parity zero subdivided into two states: never married with no children and ever married with no children. PPRs are the fractions of women who ultimately progress from their own birth to first marriage, from first marriage to first birth, from first birth to second birth, and so on. The PPRs so obtained are aggregated to a total marital fertility rate (TMFR) as well as a TFR. (TMFR is actually a total ever-marital fertility rate, but for simplicity it is referred to here as a total marital fertility rate.)

TFR, TMFR, and PPRs are measures of the quantum of fertility. The methodology is also applicable to period and cohort measures of the tempo or timing of first marriages and births, as measured by mean and median ages at first marriage and mean and median closed birth intervals by birth order. In this article, these tempo measures are referred to generically as mean and median failure times, where a failure is either a first marriage or a next birth. As defined here, the components of the TFR include PPRs, TMFR, and mean and median failure times.

We focus on the TFR calculated from PPRs (TFR_ppr) instead of the TFR calculated from ASFRs (TFR_asfr) for two main reasons. First, a multivariate method for analyzing factors affecting TFR_asfr calculated from individual data has already been developed and applied by Schoumaker (2004), who used Poisson regression for this purpose. Second, from an explanatory point of view, age-specific fertility rates are not ideal measures of the components of the total fertility rate. A woman’s decision about whether to have a next birth does not depend primarily on her age. More important considerations are her marital status, time elapsed since marriage if she is married but does not yet have any children, time elapsed since her last birth if she already has children, and the number of children she already has. The TFR calculated from PPRs takes all these considerations into account. Henceforth in this article, except for a few instances where clarity of exposition demands the use of subscripts, TFR and TMFR refer to the total fertility rate and the total marital fertility rate calculated from PPRs, whether for periods or cohorts.

We use the complementary log-log (CLL) model to model parity progression, with a separate model for each parity transition. Because the CLL model was originally developed for application to cohort data, its additional application here to period data, which yields a multivariate analysis of the period TFR and its components, is methodologically one of the more innovative aspects of the article. A second innovative aspect is the focus on predicted values of aggregate-level demographic measures (TFR or one of its components) instead of coefficients, which are often difficult to interpret in the complex model specifications considered here. This aspect of the analysis entails estimation of the effects of one predictor variable on TFR or one of its components while holding other predictor variables constant. Typically, the main predictor variable is a categorical variable, so this amounts to tabulating predicted values of the TFR or one of its components by categories of the main predictor while holding other predictors constant—simple enough in concept but somewhat complicated in terms of calculation, as will be shown later. Effects on TFR and TMFR are of particular interest because they represent effects on a woman’s ultimate number of births, which is often the principal fertility measure of interest. Tests of statistical significance of these effects are calculated using the jackknife method.

The utility of the methodology is demonstrated by applying it to both period data and cohort data from three demographic and health surveys (DHS) undertaken in the Philippines in 1993, 1998, and 2003. The application is illustrative, not an in-depth analysis. Period measures of TFR and its components are estimated for the five-year period before each of the three surveys. Cohort measures are based on the earlier marital and reproductive experience of women aged 40–49 at the time of each survey.2 A 10-year age cohort is used instead of a 5-year age cohort, such as women aged 40–44 or 45–49, in order to base the cohort analysis on a larger number of cases. In the analysis of the trend in the TFR and each of its components, which utilizes pooled data from all three surveys, three 5-year cohorts of women aged 40–44 are used, one from each survey.

In the Philippines surveys, some regions were oversampled, so weights must be used to restore representativeness. The oversampled regions were more rural than average, so that, in effect, the surveys oversampled rural areas. The design of the three surveys is described in more detail in the basic survey reports, which include questionnaires and information about sampling procedures (Philippines National Statistics Office and Macro International 1994; Philippines National Statistics Office and ORC Macro 2004; and Philippines National Statistics Office, Philippines Department of Health, and Macro International 1999).

METHODOLOGY

Cross-Sectional Analysis

The core of the methodology is a multivariate discrete-time survival model of parity progression applied to either period data or cohort data.3 The models for the various parity transitions yield multivariate discrete-time hazard functions, from which multivariate life tables of parity progression are calculated. Multivariate PPRs and mean and median failure times (mean and median ages at first marriage and mean and median closed birth intervals by birth order) are calculated from these multivariate life tables. The multivariate PPRs are aggregated to a multivariate TFR and a multivariate TMFR.

The particular form of discrete-time survival model that we use is the complementary log-log (CLL) model, although we could have used the discrete-time logit model. As noted by Allison (1982, 1995), an advantage of the CLL model over the discrete-time logit model is that the discrete-time CLL model is derived from the continuous-time Cox proportional hazards model (Cox 1972; Prentice and Gloeckler 1978) and is therefore itself a proportional hazards model. It follows that coefficients of predictor variables in the CLL model have the same interpretation as in the continuous-time Cox proportional hazards model—namely, that a one-unit increase in a predictor variable multiplies the underlying continuous-time hazard by exp(b), where b is the coefficient of the predictor variable and exp(b) is the relative risk. By contrast, the discrete-time logit model is a proportional odds model, which means that a one-unit increase in a predictor variable multiplies the odds of failure (rather than the probability of failure) by exp(b), which is an odds ratio instead of a relative risk. The estimates of the coefficient b accordingly differ between the two models. The proportional odds model approximates a proportional hazards model when failure probabilities are small, but they are not always small in the present application to parity progression. In practice, when fitted to data, the CLL model and the discrete-time logit model often yield rather similar results in terms of predicted values of the hazard function, and this is true also in the present application.4

The choice between the two models then hinges on which of the two assumptions, proportional hazards or proportional odds, better fits the data. Ascertaining which model fits better is not easy, however, because there is no generally accepted measure of goodness of fit with which to compare the two models. Various measures are available, but they sometimes lead to different conclusions (Allison 1995). In the end, we chose the CLL model because relative risks are conceptually simpler than odds ratios. This is in keeping with a general goal of modeling, which is to capture the essential features of reality in the simplest way possible.

The continuous-time Cox model itself, from which the CLL model is derived, is not suitable for our purposes because it is estimated by partial likelihood, yielding estimates of coefficients but not an estimate of the baseline hazard function, which, as will be seen shortly, is needed for the methodology presented here. By contrast, the CLL model is estimated by maximum likelihood, yielding estimates of both coefficients and baseline hazard function.5

The CLL model, like other discrete-time survival models, is applied not to the original “person sample” but instead to an “expanded sample” of person-year observations created from the original person observations. The expanded sample makes it easy to include time-varying predictor variables. For example, if a person moves from a rural to an urban area, some of the person-year observations created for that person are coded as rural and some are coded as urban. The CLL model, like other survival models, can also handle time-varying effects of predictor variables by interacting socioeconomic variables with life table time or some function of life table time. In this article, life table time is equivalent to duration in parity.

Discrete-time survival models, such as the CLL model, easily handle both left-censoring and right-censoring, thereby enabling application of the model to period data. One simply treats person-year observations before and after the period of interest as censored. Otherwise the application of the model is the same as in the cohort case. The only difference is how the expanded person-year data set is constructed.6

As already mentioned, the CLL model can be viewed as a multivariate life table, inasmuch as the response variable is a hazard function evaluated at particular values of the predictor variables, from which a complete life table can be calculated. In our illustrative analysis using Philippines DHS data, the multivariate life table for the transition from birth to first marriage (B–M) is truncated at 30 years of duration in parity (the difference between the beginning and ending life table ages of 10 and 40), whereas for each higher-order transition, it is truncated at 10 years of duration in parity. In the former case, the terminating event or “failure” in the life table is a first marriage, and in the latter case it is a next birth. First marriages after age 40 and next births after 10 years of duration in parity are rare and are ignored. Other cutoffs could also be used, but the cutoffs of 40 and 10 are appropriate for our illustrative application to Philippines data.

Two socioeconomic predictor variables are included in the illustrative analysis using Philippines data: urban-rural residence (specified by a dummy variable U, representing urban, with rural as the reference category) and education (specified by dummy variables M and H, representing medium and high education, with low education as the reference category) as assessed at the time of the survey. These variables are treated as time-invariant in the absence of adequate information on their values in earlier years before each of the three Philippines surveys.

In the case of the birth-to-first-marriage (B–M) transition, our specification of the CLL model, fitted to the expanded sample, is

$$\begin{array}{l}\text{log}[-\text{log}(1-P)]=a+b_1{T}_1+b_2{T}_2+\dots +b_{29}{T}_{29}+U(c+dt+e{t}^2)\\ +M(f+gt+h{t}^2)+H(j+kt+m{t}^2),\end{array}$$ (1)

where P is the predicted probability of failure (also called the discrete hazard) in a life table time interval; T₁, ..., T₂₉ are 29 dummy variables representing the first 29 of 30 life table time intervals, with the 30th interval as the reference category; t is a counter variable (equal to 1, 2, ..., 30) that also denotes life table time interval; a is an intercept term (implying that P = 1 – exp[−exp(a)] for the 30th life table time interval, when all predictors equal zero); and b₁, ..., b₂₉, c, d, e, f, g, h, j, k, and m are coefficients to be fitted, along with the intercept a, to the data.

Solving Eq. (1) for P yields an alternative form of the model:

$$\begin{array}{l}P=1-\text{exp}\{-\text{exp}[a+b_1{T}_1+b_2{T}_2+\dots +b_{29}{T}_{29}+U(c+dt+e{t}^2)\\ +M(f+gt+h{t}^2)+H(j+kt+m{t}^2)]\}.\end{array}$$ (2)

When all of the socioeconomic predictors (U, M, and H) are set to zero, Eq. (2) yields the baseline hazard function (30 values of P for the 30 life table time intervals, denoted more compactly as P_t).

Nonproportionality can occur because of time-varying predictor variables, time-varying effects of predictor variables, or both. In Eqs. (1) and (2), nonproportionality occurs because of time-varying effects of the predictor variables. For example, in Eq. (1), the effect of a one-unit change in U on log[−log(1 – P)] is the time-varying “coefficient” c + dt + et². In the model that the computer sees and fits, however, the term U(b + ct + dt²) appears as bU + cZ₁ + dZ₂, where, following procedures recommended by Allison (1995), Z₁ and Z₂ are new variables defined as Z₁ = Ut and Z₂ = Ut². The terms M(f + gt + ht²) and H(j + kt + mt²) appear in analogously altered form. Rewritten in this way, the model that the computer sees and fits has the form of a proportional hazards model, which is fitted in the usual way.

Although the birth histories in the Philippines DHS surveys are specified by month, we aggregate months into years. This is done because monthly data sometimes result in empty cells (e.g., there are no births in the second month after a previous birth), in which case the maximum-likelihood estimation procedure for fitting a discrete-time survival model does not converge to a solution.7

Even when life table time is specified in years, nonconvergence can still be a problem at higher-order transitions, where numbers of cases are smaller. Sometimes this problem can be solved by using a quadratic specification in place of a dummy-variable specification of the basic life table time variable, and we do this when nonconvergence becomes a problem. In this case, the terms b₁T₁ + b₂T₂ + ... + b₂₉T₂₉ in Eqs. (1) and (2) are replaced with the terms b₁t + b₂t². Where even the quadratic specification results in nonconvergence, higher-order parities are grouped into an open-ended parity interval.

A time-varying specification of the effect of U on the probability of first marriage is necessary because the effect of urban residence, relative to rural residence, is to lower the probability of first marriage at younger ages and increase it at older ages, insofar as urban marriages are postponed to later ages. Thus, the effect of urban residence on the risk of progression to first marriage, relative to rural residence, is not constant (i.e., not proportional) over life table time. The effect of education is also modeled as time-varying because more education also tends to result in postponement of marriage. For similar reasons, at higher-order parity transitions, the effects of U, M, and H on the probability of next birth are modeled as time-varying, again with a quadratic specification. An additional reason for modeling effects as time-varying at higher-order transitions is that mean and median closed birth intervals can remain constant or change little, while parity progression ratios fall dramatically (Pathak, Feeney, and Luther 1998), a pattern that cannot be modeled with time-invariant effects of the socioeconomic predictor variables.

The set of estimated values of P (one failure probability for each life table time interval, as calculated from Eq. (2)) is called the discrete hazard function, which is a multivariate hazard function specified for particular values of the socioeconomic predictor variables. From the discrete hazard function for a particular parity transition, it is a simple matter to calculate the rest of the life table, which is also multivariate, as are all quantities calculated from this life table. A PPR is calculated from the life table as one minus the proportion “surviving” (not yet having experienced failure) at the end of the life table.

It is also straightforward to calculate mean and median failure times from the multivariate life table. In the case of the B–M transition, the mean and median failure times, when added to 10 (age at the start of the life table), are mean and median ages at first marriage. In the case of higher-order transitions, mean and median failure times are mean and median closed birth intervals by birth order. (The medians so calculated are true medians. By contrast, because of the problem of age truncation at time of survey in the case of cohort estimates, DHS survey reports define medians differently as the duration in parity by which half of the original cohort experience failure.)

Unadjusted and adjusted estimates of TFR (or one of its components) by categories of a predictor variable are calculated using the logic of what is sometimes referred to as multiple classification analysis (MCA) (Andrews, Morgan, and Sonquist 1969; Retherford and Choe 1993). In MCA, unadjusted means “without controls” and adjusted means “with controls.”

For a particular parity transition, unadjusted estimates of the discrete hazard function by urban/rural residence, for example, are calculated from a CLL model that includes U as the sole socioeconomic predictor variable. In the case of Eqs. (1) and (2) for the B–M transition, this means dropping the last two terms containing M and H before fitting the model to the data. The unadjusted discrete hazard function for urban is then calculated by setting U = 1 in the fitted model equation (Eq. (2) above), and the unadjusted discrete hazard function for rural is calculated by setting U = 0 in the fitted model equation. Unadjusted urban and rural life tables are then calculated from the unadjusted urban and rural discrete hazard functions, and unadjusted urban and rural values of PPR and mean and median ages at first marriage are calculated from the unadjusted urban and rural life tables. Unadjusted estimates of PPR and mean and median age at first marriage by categories of education are similarly calculated, with education represented by M and H as the sole socioeconomic predictor variable in the CLL model.

Adjusted estimates of the discrete hazard function by urban/rural residence for the B–M transition are calculated from Eq. (2) with all of the predictor variables U, M, and H included in the fitted model equation. M and H, representing education, are viewed as control variables. To obtain the adjusted discrete hazard function for urban, one sets U = 1 and M and H equal to their interval-specific mean values in the fitted model equation. In this context, interval means life table time interval (i.e., duration in parity). Each parity transition has its own set of interval-specific mean values of M and H derived from the person-year data set for that parity transition. To obtain the adjusted discrete hazard function for rural, one sets U = 0 and M and H equal to the same interval-specific mean values that were used to calculate the adjusted discrete hazard function for urban. In this way, M and H are held constant, or “controlled,” when U is varied from 0 to 1 (i.e., from rural to urban) in the fitted model equation. Adjusted urban and rural life tables are then calculated from the adjusted urban and rural discrete hazard functions, and adjusted urban and rural values of PPR and mean and median ages at first marriage are calculated from the adjusted urban and rural life tables.

Adjusted values of PPR and mean and median age at first marriage by education are similarly calculated, with the control variable U held constant at its interval-specific mean values, and (M, H) set alternatively to (0, 0), (1, 0), and (0, 1) in order to obtain adjusted values for low, medium, and high education.

Unadjusted and adjusted values of PPR and mean and median failure times (i.e., mean and median closed birth intervals by birth order) by residence and education for higher-order parity transitions are calculated in a similar manner. Eqs. (1) and (2) retain the same form as before, except that the terms b₁T₁ + b₂T₂ + ... + b₂₉T₂₉ are replaced with the terms b₁T₁ + b₂T₂ + ... + b₉T₉. As explained earlier, at higher-order parity transitions, when nonconvergence becomes a problem, a quadratic specification of life table time is used in place of a dummy variable specification of life table time.

In the above procedure for computing adjusted values of PPRs and mean and median failure times, interval-specific means are used instead of overall means of the predictor variables in order to fit the data more precisely. It is especially important to do this in the period analysis because the use of overall means results in younger women being treated as less educated than they really are and older women being treated as more educated than they really are.

We use a separate model for each parity transition, rather than a combined repeated-events model for all the transitions, for two reasons. First, a repeated-events model is not applicable to period data, especially when the period is very short. Second, pertaining to applications to both period and cohort data, effects of the predictor variables vary from one parity transition to the next. For example, in the transition from first birth to second birth, the effect of education on parity progression is small because almost all women who have a first birth go on to have a second birth, regardless of level of education. By contrast, in the transition from second to third birth, the effect of education is typically much larger because the proportion of women who go on to have a third child typically declines sharply as education increases. This implies that a combined model for all transitions would not only have to include an additional variable for parity but also would have to interact each predictor variable with parity. Such a model would have to include not only two-way interactions but also a large number of three-way interactions and would be very complicated. A simpler way to handle interactions with parity is simply to run a separate model for each parity transition, which is the modeling strategy adopted here.

Basic notation for PPRs and parity transitions is as follows:

• p_B = PPR for the transition from a woman’s own birth to her first marriage (B–M)

• p_M = PPR for the transition from first marriage to first birth (M–1)

• p₁ = PPR for the transition from first to second birth (1–2)

• p₂ = PPR for the transition from second to third birth (2–3)

• p₃ = PPR for the transition from third to fourth birth (3–4)

• p₄ = PPR for the transition from fourth to fifth birth (4–5)

• p₅ = PPR for the transition from fifth to sixth birth (5–6)

• p₆₊ = PPR for the transition from sixth or higher-order birth to next higher-order birth (6+ to 7+).

For purposes of exposition, the open parity interval is specified here as 6 or more, even though open parity intervals as high as 13 or more are used later in the illustrative analysis using Philippines DHS data.

We assume in the illustrative analysis that no births occur before first marriage. This works in the Philippines application because the Philippines DHS surveys treat nonformalized unions as marriages. In the case of the small number of births that occur before first marriage or first nonformalized union (we refer to such births simply as premarital births), date of first marriage or date of first nonformalized union is coded or recoded back to date of first premarital birth. In the case of twins or higher-order multiple births, birth orders are arbitrarily assigned.

TFR is calculated from the PPRs as

$$\begin{array}{l}\text{TFR}=p_B{p}_M+p_B{p}_M{p}_1+p_B{p}_M{p}_1{p}_2+p_B{p}_M{p}_1{p}_2{p}_3+p_B{p}_M{p}_1{p}_2{p}_3{p}_4\\ +p_B{p}_M{p}_1{p}_2{p}_3{p}_4{p}_5+p_B{p}_M{p}_1{p}_2{p}_3{p}_4{p}_5{p}_{6+}/(1-p_{6+}).\end{array}$$ (3)

The term p_B p_M is the expected number of first births, the term p_B p_M p₁ is the expected number of second births, and so on. As explained by Feeney (1986), the term p₆₊ / (1 – p₆₊) is obtained by assuming that p₆ and all higher-order PPRs equal p₆₊ and pulling out a geometric series. (Recall that, if r is a positive number less than 1, the geometric series r + r² + r³ + ... = r / (1 – r).) The formula for TMFR is the same as the formula for TFR in Eq. (3), except that p_B is set equal to 1.

Unadjusted values of TFR by residence or education are calculated from Eq. (3) using unadjusted PPRs by residence or education. Adjusted values of TFR by residence or education are calculated from Eq. (3) using adjusted PPRs by residence or education. Unadjusted and adjusted values of TMFR are similarly calculated from Eq. (3) but with p_B set equal to 1.

Trend Analysis

In the multivariate analysis of trend in TFR or one of its components, the expanded data sets for a particular parity transition are pooled over the three surveys.

In the case of trend in the period TFR or one of its components, periods are again defined as the five-year period before each of the three Philippines DHS surveys, which were taken five years apart. The first step in the trend analysis is to pool the three person-year samples for the five-year period preceding each of the three surveys, pertaining to a particular parity transition. Each person-year observation in each of the original three person-year samples has a value of a variable called CALTIME attached to it. The value of CALTIME indicates the calendar year in which the person-year observation is located. New variables PERIOD2 and PERIOD3 are defined, based on each person-year observation’s value of CALTIME. In the pooled sample, (PERIOD2, PERIOD3) = (0, 0) for person-year observations in the earliest five-year period, (1, 0) for person-year observations in the second five-year period, and (0, 1) for person-year observations in the third five-year period.

To calculate unadjusted period estimates of the trends in, for example, p_B and mean and median ages at first marriage, based on the pooled data set, we estimate a CLL model for progression to first marriage that includes (in addition to the 29 dummy variables indicating the 30 life table time intervals) only PERIOD2 and PERIOD3 as predictor variables, with quadratic specifications of their time-varying effects (where, as before, “time” is life table time, not calendar time). Time-varying effects are specified because part of the effect of time period, as specified by PERIOD2 and PERIOD3, may be to delay first marriage. An unadjusted discrete-time hazard function is then estimated for each of periods 1, 2, and 3 by setting (PERIOD2, PERIOD3) alternatively to (0, 0), (1, 0), and (0, 1) in the fitted model. Unadjusted life tables for the three periods are then calculated from the three unadjusted discrete hazard functions. Unadjusted values of p_B and mean and median ages at first marriage for the three periods are then calculated from the three unadjusted life tables. These are the unadjusted trends in these measures.

Adjusted trends in p_B and mean and median ages at first marriage are similarly calculated, the only difference being that the underlying CLL model is expanded by adding residence and education to the set of predictor variables, with quadratic specifications of their time-varying effects. Estimates of trend in p_B and mean and median ages at first marriage are calculated from the fitted model in the same way as in the unadjusted case, but this time with U, M, and H held constant at their interval-specific mean values in the pooled data set of person-year observations for the B–M transition when (PERIOD2, PERIOD3) is set alternatively to (0, 0), (1, 0), and (0, 1). Coefficients of the socioeconomic predictors are assumed to be the same for all three 5-year time periods, so that only one set of coefficients of these predictors is estimated when using the pooled data set. If the adjusted values of p_B (or mean or median age at first marriage) are found to be the same for the three periods, so that the trend in p_B disappears, we would provisionally conclude that changes in population composition by residence and education explain the trend in p_B (provisionally because there are other predictor variables that affect first marriage that are not included in the model).

Unadjusted and adjusted trends in PPRs and mean and median failure times for higher-order transitions are similarly calculated. Unadjusted and adjusted trends in TFR and TMFR over the three periods are then calculated from the unadjusted and adjusted PPRs for the three periods. If adjustment results in disappearance of the trend in any of these measures, we provisionally conclude that changes in population composition by residence and education explain the trend in that measure.

The approach is similar in the cohort analysis, in which cohorts are defined as women aged 40–44 in each survey. In the pooled cohort data set, the three cohorts are specified by two dummy variables, COHORT2 and COHORT3. The analysis proceeds in the same way as in the period case, except that PERIOD2 and PERIOD3 are replaced with COHORT2 and COHORT3.

The logic of the trend analysis, as explained above, makes clear why controls are introduced using interval-specific mean values of the control variables (referred to here as the interval-specific means approach) instead of observed values of the control variables at the level of individual person-year observations (the individual-level observed values approach). Using the fitted model for P for a particular parity transition, the individual-level observed values approach, in a cross-sectional analysis based on a single survey, first computes an adjusted value of the progression probability P for each person-year observation in the expanded sample. For example, adjusted values of P for urban and rural for the B–M transition are computed for a particular person-year observation from Eq. (2) by setting U alternatively to 1 or 0 (regardless of the actual value of U for that person-year observation) while holding life table time t and the control variables M and H, representing education, constant at their observed values for that person-year observation. Aggregate-level adjusted values of P_t for urban and rural for the particular value of t are then computed by averaging the individual-level adjusted values of P for urban and rural over only those person-year observations with the particular value of t. Once the aggregate-level adjusted values of P_t for urban and rural are calculated for each value of t, the analysis proceeds as before.

Our tests using data from the Philippines 2003 DHS indicate that the individual-level observed values approach for introducing controls yields adjusted values of PPRs and mean and median failure times for categories of residence and education that are very close to those derived by the interval-specific means approach used in this article. Differences occur only in the second and higher decimal places. The maximum difference is (for one of the mean failure times) 0.05, with most of the differences being much smaller than this. Differences tend to be larger for mean and median failure times (especially mean failure times, which are more affected than median failure times by extreme values at the individual level) than for PPRs. The maximum difference in a PPR is 0.02.

Notwithstanding the similarity of results between the two approaches, the individual-level observed values approach seems more precise and therefore better than the interval-specific means approach. The individual-level observed values approach, however, does not work in the trend analysis because the individual-level observed values approach always uses individual-level observed values of the control variables, thereby making it impossible to control for changes over the three surveys in population composition by the control variables. By contrast, in the interval-specific means approach, it is possible to control for changes in population composition because different sets of interval-specific mean values of the control variables are used in the cross-sectional analysis (separate set of interval-specific means for each time period or each cohort) and the trend analysis (common set of interval-specific means for periods or cohorts derived from the pooled sample).

The analysis would unnecessarily become more complicated if we were to use the individual-level observed values approach in the cross-sectional analysis and the interval-specific means approach in the trend analysis. We therefore use the interval-specific means approach throughout.

As already mentioned, the original three Philippines DHS samples are weighted samples. Appendix A describes how weights are incorporated in both the cross-sectional analysis and the trend analysis.

Standard Errors of the Estimates

Standard errors of the estimates of PPRs, mean and median failure times, TFR, and TMFR are estimated by the jackknife method, as explained in Appendix B.

ILLUSTRATIVE APPLICATION TO THE THREE PHILIPPINES DHS SURVEYS

The Philippines Data

Table 1 shows the distribution of the original Philippines survey samples for 1993, 1998, and 2003 by residence and education. Distributions are shown for women aged 10–49 in the period analysis, and for women aged 40–49 in the cohort analysis, based on each of the three surveys considered separately.

Table 1.

Percentage Distribution of Women by Urban/Rural Residence and Education: 1993, 1998, and 2003 DHS Surveys, Philippines

Survey Year	Education	Women Aged 10–49			Women Aged 40–49
		Urban	Rural	Total	Urban	Rural	Total
1993	Low	18	27	45	21	34	56
	Medium	20	16	35	14	10	24
	High	14	6	20	15	6	21
	Total	51	49	100	50	50	100
	N			19,586			2,741
1998	Low	14	29	43	15	34	49
	Medium	18	18	36	14	13	26
	High	14	7	22	18	7	25
	Total	46	54	100	47	53	100
	N			17,857			2,693
2003	Low	14	23	37	15	26	42
	Medium	22	18	40	18	13	32
	High	16	7	24	19	8	27
	Total	52	48	100	52	48	100
	N			17,515			2,884

Notes: Low education is less than secondary education; medium is some or completed secondary education; and high is more than secondary education. The samples for which the distributions are shown include single women as well as ever-married women. Numbers in this table incorporate sample weights. The weighted N equals the unweighted N for each of the six samples shown in the table.

Expanded samples of person-year observations for the period analysis and the cohort analysis, shown in Table 2, are created from the two groups of women in Table 1. The sample sizes in Table 2 indicate numbers of person-year observations in the data sets to which CLL models are fitted. For each of the three surveys, two separate data sets, one for the period analysis and one for the cohort analysis, are created for each of 16 parity transitions (B–M, M–1, 1–2, …, 14–15), for a total of 96 data sets. When fitting CLL models for open parity intervals, some of these person-year data sets are combined. The cutoff parity for the open parity interval varies depending on the parity at which nonconvergence problems arise.

Table 2.

Expanded Sample Sizes: 1993, 1998, and 2003 DHS Surveys, Philippines

Parity Transition	Period Analysis			Cohort Analysis
	1993	1998	2003	1993	1998	2003
B–M	45,172	40,504	30,418	37,010	36,800	39,348
M–1	4,794	4,761	5,209	6,806	6,585	7,300
1–2	8,025	7,520	8,589	9,192	9,364	10,668
2–3	8,210	7,545	7,995	9,905	10,065	11,386
3–4	7,536	6,942	6,524	10,096	9,927	11,038
4–5	6,085	5,461	4,922	8,999	8,431	9,087
5–6	4,333	3,924	3,376	6,951	6,518	6,155
6–7	3,078	2,810	2,353	4,988	4,757	4,427
7–8	2,188	1,916	1,692	3,751	3,418	2,969
8–9	1,695	1,238	1,058	2,667	2,078	1,890
9–10	1,027	876	636	1,697	1,429	1,093
10–11	652	585	471	1,099	852	708
11–12	352	327	250	534	433	354
12–13	221	155	96	316	201	156
13–14	82	72	37	121	99	63
14–15	27	47	27	43	48	45

Notes: Expanded sample sizes are numbers of person-year observations. Each cell in the table corresponds to a separate data set, for which the sample size (number of person-year observations) is shown. There are 96 data sets. For each data set, weighted and unweighted sample sizes are the same. B–M denotes the transition from a woman’s own birth to first marriage, and M–1 denotes the transition from first marriage to first birth. In the period analysis, periods are the five-year period before each survey. In the cohort analysis, cohorts are defined as women aged 40–49 at the time of the survey. The B–M expanded sample size for the 2003 period analysis is relatively small because the B-M period life table starts at age 12 instead of age 10 as a consequence of empty-cell problems at ages 10 and 11.

Findings From the Cross-Sectional Analysis

In the cross-sectional analysis, each of the three surveys is analyzed independently of the other two. For each survey, we hold control variables constant by setting them equal to their interval-specific mean values in that particular survey. In other words, when we compute adjusted values of TFR and its components, sample composition by residence or education is held constant within surveys but not across surveys, thereby muddying the interpretation of trends. This problem is overcome later in the multivariate analysis of trends.

The cross-sectional analysis begins with CLL models that include as predictor variables only those variables representing life table time (e.g., the variables T₁, T₂, ..., T₂₉ in Eqs. (1) and (2)). This initial analysis yields, for each survey, a basic period life table and a basic cohort life table for each parity transition, pertaining to all persons regardless of their socioeconomic characteristics. PPRs, mean and median failure times, TFR, and TMFR are calculated from these basic life tables, as shown in Table 3. PPRs and mean and median failure times are shown only up to the 9–10 transition, but TFR and TMFR are calculated using a higher cutoff (in each case, as high as possible without running into non convergence problems) and an open parity interval beyond the cutoff.

Table 3.

Period and Cohort Estimates of Parity Progression Ratios (PPR), Mean and Median Ages at First Marriage (A_m), Mean and Median Closed Birth Intervals (CBI), TFR, and TMFR, Derived From CLL Models in Which the Only Predictor Variables Are the Variables Representing Life Table Time Intervals: 1993, 1998, and 2003 DHS Surveys, Philippines

Parity Transition and Life Table Measure	Period Analysis			Cohort Analysis
	1988–1992	1993–1997	1998–2002	1993	1998	2003
B–M
PPR (pB)	0.89	0.91	0.94	0.94	0.92	0.95
Mean Am	23.5	23.4	22.7	21.6	21.9	22.0
Median Am	23.0	23.2	22.4	21.4	21.6	21.6
M–1
PPR (pM)	0.98	0.97	0.96	0.96	0.97	0.96
Mean CBI	1.2	1.2	1.3	1.4	1.4	1.4
Median CBI	1.5	1.5	1.5	1.6	1.6	1.6
1–2
PPR (p1)	0.91	0.89	0.86	0.95	0.92	0.91
Mean CBI	2.6	2.7	2.9	2.3	2.4	2.5
Median CBI	2.7	2.7	2.8	2.5	2.6	2.6
2–3
PPR (p2)	0.85	0.82	0.77	0.90	0.86	0.86
Mean CBI	2.9	3.0	3.3	2.6	2.7	2.8
Median CBI	2.9	2.9	3.3	2.7	2.7	2.8
3–4
PPR (p3)	0.78	0.70	0.68	0.84	0.79	0.77
Mean CBI	3.0	3.0	3.4	2.8	2.8	2.9
Median CBI	3.0	2.9	3.2	2.8	2.9	2.9
4–5
PPR (p4)	0.72	0.70	0.63	0.77	0.75	0.71
Mean CBI	2.9	3.1	3.3	2.8	2.9	3.0
Median CBI	2.9	3.1	3.3	2.8	2.9	3.0
5–6
PPR (p5)	0.75	0.70	0.65	0.77	0.76	0.74
Mean CBI	3.0	3.0	3.2	2.8	2.9	2.9
Median CBI	3.0	3.0	3.3	2.9	3.0	2.9
6–7
PPR (p6)	0.74	0.69	0.72	0.79	0.75	0.74
Mean CBI	2.9	3.0	3.2	2.7	2.9	3.0
Median CBI	2.9	3.0	3.2	2.8	2.9	3.0
7–8
PPR (p7)	0.76	0.68	0.64	0.79	0.70	0.73
Mean CBI	2.7	2.9	2.9	2.8	2.8	2.9
Median CBI	2.8	2.9	3.0	2.9	2.9	3.1
8–9
PPR (p8)	0.72	0.66	0.70	0.76	0.75	0.72
Mean CBI	3.0	2.9	3.3	2.8	2.7	2.9
Median CBI	3.4	3.0	3.3	2.9	3.0	3.0
9–10
PPR (p9)	0.63	0.67	0.67	0.70	0.71	0.73
Mean CBI	2.5	2.8	2.7	2.5	2.9	2.8
Median CBI	2.7	2.8	3.2	2.7	2.9	2.9
TFR	4.21	3.76	3.44	5.17	4.48	4.42
TMFR	4.71	4.12	3.65	5.50	4.84	4.65

Notes: In the period analysis, the time periods are the five-year period before each of the 1993, 1998, and 2003 surveys. Separate CLL models are calculated for the five-year period before each survey, using data from only that survey. In the cohort analysis, three cohorts are defined as women aged 40–49 at the time of each of the three surveys. Separate CLL models are calculated for the cohort from each survey, using data from only that survey. The CLL models use a dummy variable specification of the basic life table time variable up to the parity transition where nonconvergence first occurs, after which a quadratic specification is used until nonconvergence again occurs, up to a cutoff, which is chosen as high as possible. An open-parity interval is used after the cutoff. In this table, the cutoffs are 12+ for all three surveys. Results for parity transitions higher than 9–10 are not shown, but TFR and TMFR are calculated using PPRs from transitions higher than 9–10, including the PPR for the open-parity interval 12+. In this table and in all subsequent tables, births of order 16 and above are ignored.

In the period analysis in Table 3, an unexpected finding is that p_B rose and mean and median ages at first marriage fell across the three surveys. By contrast, in the cohort analysis p_B hardly changed, and mean and median ages at first marriage rose slightly. The difference occurs because the cohort estimates of mean and median ages at first marriage pertain to marriages that occurred roughly two decades before survey interview, when age at first marriage was slowly rising rather than falling. As previously mentioned, however, the trends in this table do not control for changes in population composition by residence and education across the three surveys.

In period analyses, falling mean and median ages at first marriage cause a compression of marriages in calendar time (Bongaarts and Feeney 1998), thereby contributing to a temporary rise in the period estimate of p_B. This “tempo effect” may be part of the reason for the rise in the period estimate of p_B in Table 3. Supporting evidence for this tentative conclusion is that residence and education explain neither the upward trend in p_B nor the downward trends in mean and median ages at first marriage, as will be seen later in the multivariate analysis of trends, in which population composition by residence and education is controlled.

Tempo effects, however, are only part of the story. Another, perhaps more important cause of not only the upward trend in the period estimate of p_B but also the downward trends in the period estimates of mean and median ages at first marriage is the rising prevalence of nonformalized unions. Mean age at first union (calculated directly from reported first unions occurring in the five-year period before each survey) was about two years younger for nonformalized unions than for formalized marriages in all three surveys, while the proportion of all unions that were nonformalized unions increased across the three surveys. At ages 15–19, this proportion was 35% in the 1993 survey, 36% in the 1998 survey, and 55% in the 2003 survey; and at ages 20–24, it was 13% in the 1993 survey, 16% in the 1998 survey, and 25% in the 2003 survey. The biggest increases in these proportions and the biggest declines in the period estimates of mean and median ages at first marriage both occurred between the second and third surveys, a pattern that also suggests a causal effect of prevalence of nonformalized unions on mean and median ages at first marriage and p_B.

Table 3 also shows that both period and cohort estimates of p_M hardly changed over the three surveys and that p₁ declined only modestly. As expected, both period and cohort estimates of p₂, p₃, …, p₇ declined more substantially. PPRs at higher-order transitions also declined in most cases, but less regularly. Birth intervals between first marriage and first birth are very short, reflecting the fact that many first births within first marriage were conceived shortly before first marriage. Our recoding of date of first marriage back to age at first birth in cases where the first birth was a premarital birth also contributes to the short intervals between first marriage and first birth, but not by very much; only 6%–8% of births were recoded in this way. Mean and median closed birth intervals tended to increase over the three surveys, more so in the period case than in the cohort case. In the period case, the increases again occurred mainly between the second and third surveys.

Also in Table 3, mean age at first marriage always exceeds median age at first marriage. This pattern occurs because distributions of first marriages are skewed toward higher ages. The pattern is reversed in the case of the M–1 transition, where mean closed birth intervals are shorter than median closed birth intervals. The reversal occurs because the distribution of M–1 intervals is skewed toward shorter birth intervals, as a result of premarital pregnancies leading to many first births shortly after first marriage. At higher-order birth intervals, the pattern is less consistent, with mean and median closed birth intervals usually being very close to each other. Exceptions occur mainly at very high birth orders, where numbers of cases are smaller and results are more affected by sampling variability.

The period estimates of TFR_ppr at the end of Table 3 are close to the estimates of TFR_asfr for the five years before the survey in the published DHS reports: 4.21 compared with 4.11 for the 1993 survey, 3.76 compared with 3.78 for the 1998 survey, and 3.44 compared with 3.58 in the 2003 survey. Because of the very different ways that TFR_ppr and TFR_asfr are calculated, perfect agreement is not expected.

Similar comparisons cannot be made for the cohort estimates of TFR_ppr at the end of Table 3 because the DHS program does not calculate cohort TFRs. Our cohort estimates of PPRs, mean and median failure times, TFR_ppr, and TMFR_ppr are virtually identical, however, to comparable estimates calculated from Kaplan-Meier (product-limit) life tables (Retherford et al. 2009). This latter comparison is not possible with period estimates because the Kaplan-Meier method of constructing life tables cannot be applied to period data.

Tables 4 and 5 show unadjusted and adjusted estimates of PPRs and mean and median failure times by residence and education. For reasons of space, these are shown only for the B–M and 3–4 transitions. Eq. (2) is the basic CLL model for the B–M transition. The CLL model for the 3–4 transition is the same as that for the B–M transition, except that the dummy variables T₁, T₂, ..., T₂₉ are replaced with T₁, T₂, ..., T₉.

Table 4.

Unadjusted and Adjusted Estimates of Parity Progression Ratios (PPR) and Mean and Median Ages at First Marriage (A_m) for Progression From Birth to First Marriage (B–M): 1993, 1998, and 2003 DHS Surveys, Philippines

Variable	Life Table Measure	Period Analysis			Cohort Analysis
		1988–1992	993–1997	1998–2002	1993	1998	2003
Unadjusted Estimates
Residence
Urban	PPR (pB)	0.87**	0.87**	0.92**	0.92**	0.90**	0.94
	Mean Am	24.3**	24.2**	23.4**	22.2**	22.4**	22.5**
	Median Am	23.9**	24.3**	23.2**	22.1**	22.2**	22.3**
Rurala	PPR (pB)	0.93	0.97	0.97	0.96	0.95	0.96
	Mean Am	22.3	22.1	21.5	21.0	21.2	21.3
	Median Am	21.9	22.0	21.1	20.7	20.9	20.9
Education
Lowa	PPR (pB)	0.94	0.93	0.98	0.96	0.95	0.96
	Mean Am	21.5	21.0	19.8	20.3	20.3	20.3
	Median Am	20.6	20.3	19.5	20.0	19.9	19.9
Medium	PPR (pB)	0.91	0.92	0.96*	0.94	0.93	0.97
	Mean Am	22.7**	22.6**	21.8**	21.7**	21.7**	21.6**
	Median Am	22.2**	22.3**	21.5**	21.7**	21.4**	21.4**
High	PPR (pB)	0.84**	0.90	0.91**	0.90**	0.88**	0.90**
	Mean Am	25.5**	25.2**	24.8**	25.0**	24.9**	25.0**
	Median Am	25.4**	25.3**	24.8**	25.1**	24.8**	24.9**
Adjusted Estimates
Residence
Urban	PPR (pB)	0.86*	0.86**	0.91**	0.92*	0.90*	0.94
	Mean Am	24.5**	24.4**	23.7**	22.4*	22.6	22.8
	Median Am	24.1**	24.5**	23.5**	22.3*	22.3	22.6
Rurala	PPR (pB)	0.91	0.96	0.96	0.95	0.93	0.95
	Mean Am	23.1	22.8	22.5	22.0	22.7	22.5
	Median Am	22.8	22.8	22.2	21.8	22.4	22.2
Education
Lowa	PPR (pB)	0.93	0.91	0.97	0.95	0.94	0.96
	Mean Am	21.9	21.4	20.2	20.4	20.3	20.4
	Median Am	20.9	20.7	19.7	20.1	19.9	20.0
Medium	PPR (pB)	0.91	0.91	0.95	0.94	0.93	0.97
	Mean Am	22.8*	22.8**	21.9**	21.7**	21.7**	21.6**
	Median Am	22.3**	22.5**	21.6**	21.7**	21.4**	21.4**
High	PPR (pB)	0.84**	0.90	0.91**	0.90**	0.88**	0.91**
	Mean Am	25.4**	25.2**	24.8**	25.0**	24.9**	25.0**
	Median Am	25.4**	25.3**	24.7**	25.0**	24.8**	24.9**

Notes: One or more asterisks after a quantity indicate that the quantity differs significantly from the corresponding quantity in the reference category. All tests of statistical significance are two-tailed tests.

^aReference category.

^*p ≤ .05;

^**p ≤ .01

Table 5.

Unadjusted and Adjusted Estimates of Parity Progression Ratios (PPR) and Mean and Median Closed Birth Intervals (CBI) for Progression From Third Birth to Fourth Birth (3–4): 1993, 1998, and 2003 DHS Surveys, Philippines

Variable	Life Table Measure	Period Analysis			Cohort Analysis
		1988–1992	1993–1997	1998–2002	1993	1998	2003
Unadjusted Estimates
Residence
Urban	PPR (p3)	0.75**	0.64**	0.64**	0.80**	0.72**	0.71**
	Mean CBI	3.1	3.1	3.4	2.8	2.8	3.0*
	Median CBI	3.0	2.9	3.2	2.8	2.9	2.9
Rurala	PPR (p3)	0.82	0.76	0.73	0.87	0.85	0.84
	Mean CBI	2.9	2.9	3.4	2.7	2.8	2.8
	Median CBI	3.0	2.9	3.2	2.8	2.8	2.9
Education
Lowa	PPR (p3)	0.85	0.79	0.78	0.91	0.87	0.88
	Mean CBI	2.9	2.9	3.4	2.6	2.6	2.8
	Median CBI	3.0	2.9	3.3	2.7	2.8	2.8
Medium	PPR (p3)	0.75**	0.72*	0.69*	0.79**	0.76**	0.75**
	Mean CBI	3.0	2.9	3.3	2.9**	2.9**	3.0*
	Median CBI	2.9	2.8	3.2	2.9**	2.9*	3.0*
High	PPR (p3)	0.69**	0.56**	0.55**	0.66**	0.60**	0.59**
	Mean CBI	3.4*	3.1	3.6	3.2**	3.2**	3.1*
	Median CBI	3.2	2.9	3.2	3.1*	3.1*	3.0
Adjusted Estimates
Residence
Urban	PPR (p3)	0.75	0.65*	0.65	0.82	0.74**	0.72**
	Mean CBI	3.1	3.0	3.4	2.7	2.8	3.0
	Median CBI	3.0	2.9	3.2	2.8	2.8	2.9
Rurala	PPR (p3)	0.80	0.73	0.70	0.84	0.81	0.80
	Mean CBI	2.9	2.9	3.4	2.8	2.9	2.9
	Median CBI	3.0	2.9	3.2	2.9	2.9	2.9
Education
Lowa	PPR (p3)	0.85	0.77	0.77	0.90	0.86	0.86
	Mean CBI	2.9	3.0	3.4	2.6	2.6	2.8
	Median CBI	3.0	2.9	3.3	2.7	2.8	2.8
Medium	PPR (p3)	0.75**	0.72	0.69*	0.79**	0.76**	0.75**
	Mean CBI	3.0	2.9	3.3	2.9**	2.9**	3.0*
	Median CBI	2.9	2.8	3.2	2.9**	2.9*	3.0
High	PPR (p3)	0.69**	0.57**	0.56**	0.67**	0.61**	0.60**
	Mean CBI	3.3*	3.0	3.6	3.2**	3.3**	3.1*
	Median CBI	3.2	2.9	3.2	3.1*	3.2**	3.0

Notes: One or more asterisks after a quantity indicate that the quantity differs significantly from the corresponding quantity in the reference category. All tests of statistical significance are two-tailed tests.

^aReference category.

^*p ≤ .05;

^**p ≤ .01

In Table 4, pertaining to the B–M transition, unadjusted and adjusted estimates of p_B tend to be higher for rural than for urban areas and higher for those with less education. Unadjusted and adjusted estimates of mean and median ages at first marriage tend to be lower for rural than for urban areas and lower for those with less education. Differences in p_B and mean and median ages at first marriage by urban/rural residence are affected little by the introduction of controls for education, and differences in p_B and mean and median ages at first marriage by education are affected little by the introduction of controls for residence. In other words, education explains little of the effects of residence, and residence explains little of the effects of education. The effects of both residence and education on mean and median ages at first marriage are strong, indicating that much of the effects of urban residence and more education are to delay marriage. In Table 4, most of the effects of residence and education on p_B and mean and median ages at first marriage, whether unadjusted or adjusted, are statistically significant at the 5% level or better. The main exceptions are that, in both the period and cohort analyses, the effects of medium education on p_B are mostly not significant; in the cohort analysis, the adjusted effects of residence on mean and median ages at first marriage are mostly not significant. When measuring level of significance, rural residence and low education are taken as the reference categories.

Table 5, pertaining to the 3–4 transition, shows that for each period and each cohort, PPRs tend to be higher and birth intervals shorter for rural than for urban areas, and PPRs tend to decrease and birth intervals to increase as education increases. PPRs tend to be lower and birth intervals longer in the period analysis than in the cohort analysis, reflecting the long-term downward trend in p₃ and upward trend in the interval between third and fourth birth. Differences in p₃ by residence are substantially reduced when education is controlled, but differences in p₃ by education are reduced only slightly when residence is controlled. In other words, education explains a good deal of effects of residence on p₃, but residence explains very little of the effects of education on p₃. Effects are stronger for p₃ than for mean and median closed birth intervals—that is, the main effect of urban residence and more education is to reduce the likelihood of having a fourth child, rather than to increase the birth interval between the third and fourth child; this is especially true in the period analysis, in which the effects of residence and education on birth interval are almost never statistically significant.

The pattern of effects of residence and education (though not necessarily their statistical significance) for the other parity transitions (results not shown) is for the most part similar to that for the 3–4 transition (Retherford et al. 2009).

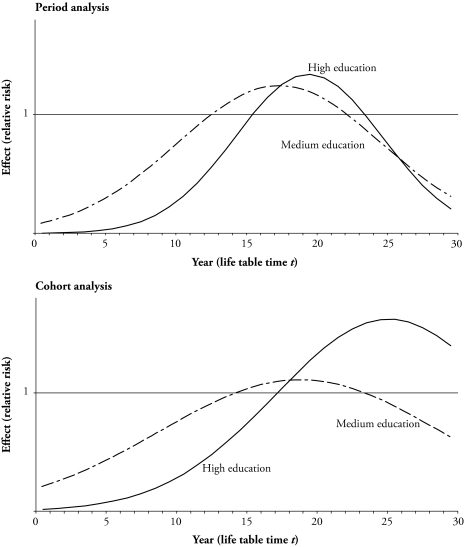
Figure 1, pertaining to the B–M transition, validates the earlier argument that the effects of residence and education on the hazard of first marriage are not proportional and must be modeled as time-varying, as shown earlier in Eqs. (1) and (2). The figure uses data from the 1993 survey to graph the relative risks exp(f + gt + ht²) and exp(j + kt + mt²) against t to show how much the quadratic specifications of the time-varying effects of medium and high education on the continuous-time hazard of first marriage, relative to the effect of low education, depart from the time-invariant (i.e., proportional) specifications of these effects. If the effects were proportional, the graphs would be horizontal lines, so the comparison amounts to assessing the extent to which the graphs depart from horizontal lines.

Figure 1.

The Effect of Medium Education, exp(f + gt + ht²), and the Effect of High Education, exp(j + kt + mt²), on Progression From Birth to First Marriage, Based on the 1993 Survey

Notes: Effects of medium and high education, which are multiplicative, are relative to low education. Effects less than 1 reduce the hazard, and effects greater than 1 increase the hazard.

The first graph in Figure 1 is based on period data pertaining to the five-year period before the 1993 survey, and the second graph is based on cohort data pertaining to women aged 40–49 at the time of the 1993 survey. Both graphs indicate postponement of marriage with more education, inasmuch as the relative-risk curves start out below 1, rise above 1, and then fall, usually to values that are again below 1, and inasmuch as the curve for high education is shifted to the right relative to the curve for medium education. Both graphs show that the effects of education vary substantially as t increases, indicating major departures from proportionality. Similar graphs of the effect of urban/rural residence, which are not shown, also indicate the need for a time-varying specification of the effect of residence. Also not shown are similar graphs for higher-order parity transitions, which also indicate the need for time-varying specifications of the effects of residence and education on the hazard of a next birth.

Table 6 shows unadjusted and adjusted estimates of TFR and TMFR, calculated from unadjusted and adjusted PPRs, where the cutoff for the open parity interval is at as high a parity as possible without running into nonconvergence problems. TFR and TMFR are always higher for rural than for urban areas and are always lower for women with more education. In each of the three surveys, both TFR and TMFR differentials by residence are substantially reduced when education is controlled, and both TFR and TMFR differentials by education are substantially reduced when residence is controlled. The effects of residence and education on TFR and TMFR are all statistically significant, in almost all cases at the 1% level.

Table 6.

Unadjusted and Adjusted Values of the Total Fertility Rate and the Total Marital Fertility Rate, Calculated From Unadjusted and Adjusted Parity Progression Ratios (PPR): 1993, 1998, and 2003 DHS Surveys, Philippines

Variable	Type of Estimate	Period Analysis			Cohort Analysis
		1988–1992	1993–1997	1998–2002	1993	1998	2003
Total Fertility Rate
Residence
Urban	Unadjusted	3.66**	3.02**	2.92**	4.49**	3.66**	3.73**
	Adjusted	3.69**	3.05**	2.95**	4.58**	3.77**	3.78**
Rurala	Unadjusted	4.93	4.69	4.14	5.97	5.44	5.27
	Adjusted	4.53	4.39	3.80	5.45	4.97	4.79
Education
Lowa	Unadjusted	5.37	4.67	4.42	6.25	5.63	5.52
	Adjusted	5.18	4.30	4.20	6.12	5.36	5.31
Medium	Unadjusted	4.19**	3.73**	3.53**	4.62**	4.28**	4.24**
	Adjusted	4.18**	3.69**	3.50**	4.64**	4.30**	4.25**
High	Unadjusted	2.76**	2.81**	2.59**	3.09**	2.84**	2.96**
	Adjusted	2.79**	2.88**	2.63**	3.16*	2.95**	3.03**
Total Marital Fertility Rate
Residence
Urban	Unadjusted	4.20**	3.47**	3.19**	4.86**	4.05**	3.97**
	Adjusted	4.28**	3.55**	3.23**	4.98**	4.20**	4.04**
Rurala	Unadjusted	5.30	4.85	4.25	6.22	5.74	5.48
	Adjusted	4.96	4.56	3.94	5.76	5.33	5.05
Education
Lowa	Unadjusted	5.70	5.02	4.51	6.54	5.94	5.73
	Adjusted	5.55	4.74	4.32	6.42	5.68	5.52
Medium	Unadjusted	4.61**	4.05**	3.69**	4.92**	4.59**	4.37**
	Adjusted	4.62**	4.04**	3.67**	4.94**	4.62**	4.38**
High	Unadjusted	3.28**	3.12**	2.85**	3.43**	3.23**	3.27**
	Adjusted	3.31**	3.19**	2.90**	3.49*	3.34**	3.34**

Notes: One or more asterisks after a quantity indicate that the quantity differs significantly from the corresponding quantity in the reference category. All tests of statistical significance are two-tailed tests.

^aReference category.

^*p ≤ .05;

^**p ≤ .01

Findings From the Trend Analysis

Results of the multivariate trend analysis based on pooled data from the three Philippines surveys are shown in Tables 7 and 8. In the period analysis, the unexpected upward trend in p_B and downward trend in age at first marriage, observed earlier in Table 3, persist after adjustment for residence and education, as shown in Table 7. The changes in both the unadjusted and the adjusted period estimates of p_B and mean and median ages at first marriage are statistically significant between the first and third periods but not between the first and second periods. In the cohort analysis, the changes between the first and third cohorts in both the unadjusted and the adjusted estimates of p_B and mean and median ages at first marriage are not statistically significant.

Table 7.

Unadjusted and Adjusted Trends in TFR and Its Components (pooled data analysis)

Transition	Measure	Period Analysis			Cohort Analysis
		1988–1992a	1993–1997	1998–2002	1993a	1998	2003
B–M	PPR (pB)
	Unadjusted	0.89	0.91	0.94**	0.95	0.92*	0.95
	Adjusted	0.88	0.90	0.93**	0.93	0.91*	0.94
	Mean Am
	Unadjusted	23.4	23.4	22.7**	21.8	21.7	21.9
	Adjusted	24.1	23.9	23.1**	22.7	22.4	22.4
	Median Am
	Unadjusted	23.1	23.1	22.4**	21.5	21.5	21.6
	Adjusted	23.9	23.7	22.9**	22.5	22.2	22.2
M–1	PPR (pM)
	Unadjusted	0.98	0.97	0.96**	0.97	0.97	0.96
	Adjusted	0.97	0.97	0.96**	0.97	0.97	0.96
	Mean CBI
	Unadjusted	1.2	1.2	1.3**	1.4	1.3	1.4
	Adjusted	1.2	1.2	1.3**	1.4	1.3	1.4
	Median CBI
	Unadjusted	1.5	1.5	1.5	1.6	1.6	1.6
	Adjusted	1.5	1.5	1.5*	1.6	1.6	1.6
1–2	PPR (p1)
	Unadjusted	0.91	0.89	0.86**	0.95	0.92*	0.91**
	Adjusted	0.91	0.89	0.86**	0.94	0.92*	0.91**
	Mean CBI
	Unadjusted	2.6	2.7	2.9**	2.3	2.4	2.6**
	Adjusted	2.6	2.7	2.9**	2.4	2.4	2.6**
	Median CBI
	Unadjusted	2.7	2.7	2.8**	2.5	2.6	2.6*
	Adjusted	2.7	2.7	2.8**	2.5	2.6	2.6
2–3	PPR (p2)
	Unadjusted	0.85	0.82	0.77**	0.90	0.87*	0.87*
	Adjusted	0.83	0.82	0.77**	0.89	0.86	0.86*
	Mean CBI
	Unadjusted	2.9	3.0	3.3**	2.6	2.8	2.9**
	Adjusted	2.9	3.0	3.3**	2.7	2.8	2.9**
	Median CBI
	Unadjusted	2.9	2.9	3.2**	2.8	2.8	2.9*
	Adjusted	2.9	2.9	3.2**	2.8	2.8	2.9
3–4	PPR (p3)
	Unadjusted	0.78	0.70**	0.68**	0.83	0.76**	0.77**
	Adjusted	0.77	0.69**	0.68**	0.81	0.75**	0.76**
	Mean CBI
	Unadjusted	3.0	2.9	3.4**	2.8	2.9	3.0
	Adjusted	3.1	2.9	3.4**	2.9	2.9	3.0
	Median CBI
	Unadjusted	3.0	2.9	3.2**	2.8	2.9	2.9
	Adjusted	3.0	2.9	3.2**	2.9	2.9	2.9
4–5	PPR (p4)
	Unadjusted	0.72	0.70	0.63**	0.74	0.74	0.69*
	Adjusted	0.71	0.68	0.62**	0.73	0.72	0.68
	Mean CBI
	Unadjusted	2.9	3.1	3.3**	2.7	3.0*	2.9*
	Adjusted	2.9	3.1	3.3**	2.7	3.0*	2.9
	Median CBI
	Unadjusted	2.9	3.1	3.3**	2.8	3.0*	3.0
	Adjusted	2.9	3.1	3.3**	2.8	3.0*	2.9
5–6	PPR (p5)
	Unadjusted	0.76	0.70*	0.65**	0.77	0.72	0.74
	Adjusted	0.73	0.68*	0.64**	0.76	0.70*	0.73
	Mean CBI
	Unadjusted	3.0	3.0	3.2*	2.8	2.9	2.8
	Adjusted	3.0	3.0	3.2	2.8	2.8	2.8
	Median CBI
	Unadjusted	3.0	3.0	3.3*	2.9	3.0	2.9
	Adjusted	3.0	3.0	3.2	2.9	3.0	2.9
6–7	PPR (p6)
	Unadjusted	0.74	0.69	0.72	0.81	0.74*	0.79
	Adjusted	0.73	0.68	0.71	0.78	0.74	0.77
	Mean CBI
	Unadjusted	2.9	3.0	3.2*	2.9	2.7	3.4**
	Adjusted	2.8	3.0	3.1*	2.8	2.7	3.3**
	Median CBI
	Unadjusted	2.9	3.1	3.1	2.9	2.8	3.3**
	Adjusted	2.9	3.0	3.1	2.9	2.8	3.3*
7+–8+	PPR (p7+)
	Unadjusted	0.71	0.66*	0.64*	0.82	0.79	0.78
	Adjusted	0.70	0.65*	0.64*	0.82	0.78	0.77
	Mean CBI
	Unadjusted	2.8	2.8	3.0	3.0	2.8	3.1
	Adjusted	2.8	2.8	3.0	3.0	2.8	3.0
	Median CBI
	Unadjusted	2.9	2.9	3.0	3.0	2.9	3.1
	Adjusted	2.9	2.9	3.0	3.0	2.9	3.1
TFR	Unadjusted	4.20	3.77**	3.43**	5.47	4.81	4.48**
	Adjusted	3.97	3.63**	3.34**	5.15	5.28	4.41**
TMFR	Unadjusted	4.71	4.12**	3.65**	5.78	5.23	4.73**
	Adjusted	4.53	4.02**	3.58**	5.52	5.81	4.69**

Notes: Adjusted trends control for both urban/rural residence and education. A_m denotes age at first marriage, and CBI denotes closed birth interval. The calculation of TFR and TMFR utilizes not only the PPRs shown in the table (except for p₇₊, which is not used) but also higher-order PPRs that are not shown (see the footnote to Table 3). One or more asterisks after a quantity indicate that the quantity differs significantly from the corresponding quantity in the reference category. All tests of statistical significance are two-tailed tests.

^aReference category.

^*p ≤ .05;

^**p ≤ .01

Table 8.

Percentages of the Unadjusted Changes in Parity Progression Ratios (PPR), Mean and Median Failure Times, TFR, and TMFR Between the 1993 and 2003 Surveys That Are Explained by Residence and Education (pooled data analysis)

Transition	Measure	Period Analysis, Five-Year Period Before Each Survey	Cohort Analysis, Women Aged 40–44 at Each Survey
B–M	PPR (pB)	−14.1*	−175.6
	Mean Am	−33.1	434.9
	Median Am	−45.2	1,075.9
M–1	PPR (pM)	0.7	−5.8
	Mean CBI	−6.4	−124.7
	Median CBI	−20.8	−46.5
1–2	PPR (p1)	7.7	3.2
	Mean CBI	13.6*	9.3
	Median CBI	11.5*	15.6
2–3	PPR (p2)	8.8	8.1
	Mean CBI	11.9**	21.0*
	Median CBI	13.7**	26.7*
3–4	PPR (p3)	9.0	24.4*
	Mean CBI	4.3	28.5
	Median CBI	4.0	24.0
4–5	PPR (p4)	7.2	18.4
	Mean CBI	8.5	9.7
	Median CBI	9.9*	12.5
5–6	PPR (p5)	7.3	16.0
	Mean CBI	15.2	−359.1
	Median CBI	12.4	439.4
6–7	PPR (p6)	−5.7	31.8
	Mean CBI	14.3	5.6
	Median CBI	16.8	6.0
7+–8+	PPR (p7+)	6.4	−8.3
	Mean CBI	12.8	32.9
	Median CBI	4.1	20.3
TFR		18.4**	25.4
TMFR		11.1**	22.0

Notes: Percentages in this table are calculated using more exact values than shown in Table 7. One or more asterisks after a percentage indicate that the percentage differs significantly zero (see Appendix B). All tests of statistical significance are two-tailed tests.

^aReference category.

^*p ≤ .05;

^**p ≤ .01

The trends in higher-order PPRs are mostly downward, the trends in mean and median closed birth intervals are mostly upward, and the trends in TFR and TMFR are both downward. The unadjusted and adjusted changes in PPRs and mean and median closed birth intervals between the first and third periods are usually statistically significant in the period analysis but less often in the cohort analysis. In most cases, adjusting for residence and education makes little difference in the trends. Adjustment for residence and education makes more of a difference in the trends in TFR and TMFR than in each PPR separately, for reasons to be discussed shortly.

The extent to which residence and education explain the trends in the various measures is examined in more detail in Table 8, which is calculated from Table 7 using values that are more exact than those shown in Table 7. In Table 8, trends are measured by unadjusted changes in TFR or one of its components between the first and third surveys. Percentage explained refers to the percentage by which the introduction of cross-survey controls for residence and education reduces the unpercentaged change. Percentage explained is calculated as {[(unadjusted change) – (adjusted change)]/(unadjusted change)} × 100.

In the case of the B–M and M–1 transitions, some of the “percentages explained” are negative. Negative percentages occur when p_B or p_M increases or when mean or median failure time decreases. In these cases, urbanization and rising levels of education partially offset the change by reducing p_B or p_M or by increasing mean or median failure time. Removing these offsetting effects of urbanization and rising levels of education by controlling for residence and education across surveys causes p_B or p_M to rise even more and mean or median failure time to fall even more in the adjusted case than in the un adjusted case.

In the cohort analysis in Table 8, the unadjusted changes in PPRs and mean and median failure times for the B–M and M–1 transitions between the first and third surveys are very small, so that in the expression {[(unadjusted change) – (adjusted change)]/(unadjusted change)} × 100, the numerator is percentaged on a very small denominator, sometimes resulting in a very large “percentage explained.” A small denominator occurs because of offsetting effects (effects of residence and education and effects of other factors operating in the opposite direction) that are both large compared with the total change. In such cases, the very large “percentage explained” is not statistically significant.

For the B–M and M–1 transitions, the only “percentage explained” that differs significantly from zero is the one pertaining to the period estimate of p_B. For transitions 1–2 and higher, very few of the “percentages explained” are statistically significant, the main exceptions being those pertaining to mean and median closed birth intervals for the 1–2 and 2–3 transitions. In the 1–2 and higher-order transitions, the percentage of change that is accounted for by residence and education is usually greater for mean and median closed birth intervals than it is for PPRs. A possible explanation of this pattern is that declines in PPRs reflect not only effects of residence and education at the individual level but also across-the-board effects of other factors, such as promotion of smaller families by the family planning program. Quite plausibly, these other factors, and especially the family planning program, have had larger effects on PPRs than on birth intervals. If so, the additional effects of these other factors on PPRs tend to reduce the percentage of the downward change in a PPR that is due solely to urbanization and rising levels of education.

Table 8 also shows that, overall, residence and education account for 18% of the change in the period TFR and 25% of the change in the cohort TFR between the first and third surveys. The percentages for TMFR are lower, at 11% and 22%. The “percentages explained” pertaining to changes in the period TFR and TMFR are statistically significant, but the “percentages explained” pertaining to changes in the cohort TFR and TMFR are not significant.

The percentage contributions of residence and education to changes in TFR and TMFR may seem inconsistent with the percentage contributions of residence and education to changes in the individual PPRs from which TFR and TMFR are calculated. For example, in the period analysis, the percentage contributions of residence and education to changes in individual PPRs are all less than the percentage contributions of residence and education to changes in TFR and TMFR. These seeming inconsistencies, which are not real, occur at least partly because of the way that TFR and TMFR are calculated from PPRs in Eq. (3), where, within each term on the right side of the equation, a number of PPRs are multiplied together. Because of the cumulative multiplicative nature of the calculation, small percentage changes in individual PPRs within a term, if all such changes are in the same direction, can result in a much larger percentaged change in the term as a whole and, ultimately, in TFR and TMFR.

CONCLUSION

The multivariate methodology developed in this article focuses on model-predicted values of TFR and its components (PPRs, mean and median ages at first marriage, mean and median closed birth intervals by birth order, and TMFR) instead of coefficients. Though somewhat complicated in its internal details, the methodology ultimately results in simple bivariate tables that show how model-predicted values of these measures vary across categories of each predictor variable with other predictor variables held constant. An advantage of this approach is that the simple bivariate tables that are ultimately produced are much more easily understood than the multiplicity of coefficients in the underlying CLL models. Perhaps the most innovative aspect of the methodology is the chaining together of the multivariate PPRs from the various parity transitions, each of which is modeled separately, to yield multivariate estimates of TFR and TMFR. The methodology has the added advantage of being applicable to not only the cohort TFR and its components but also the period TFR and its components. The application to the period TFR is of particular interest because the period TFR is the fertility measure most commonly used by demographers, population policy makers, and family planning program managers.

Another advantage of the methodology is that it is based on individual-level data, which means that it can be based on data for a single country. Many previous multi variate analyses of the TFR have taken countries (or other geographic areas) as the units of analysis, in which case the predicted value of the TFR for a particular country depends on what other countries are included in the aggregate-level data set to which the multivariate statistical model is fitted (see, e.g., Gauthier and Hatzius 1997). Other advantages of the application to individual-level data include avoidance of ecological fallacy, easier assessment of the direction of causality, and calculation of an integrated set of unadjusted and adjusted values of not only the TFR but also its various components. The methodology is also easily extended to a multivariate analysis of trends in the TFR and its components. We do not know of any aggregate-level multivariate analysis of the TFR that yields such a comprehensive and integrated set of results.

The illustrative application of the methodology to three demographic and health surveys in the Philippines illustrates that the methodology works quite well. Although this application was not meant to be an in-depth analysis, it has brought to light a previously unnoticed and unexpected increase over calendar time in the model-predicted period estimate of the PPR for progression to first marriage and a decrease in the model-predicted period estimates of mean and median ages at first marriage that are not explained by changes in population composition by residence and education. On the contrary, controlling for residence and education accentuates these trends because urbanization and rising levels of education have effects in the opposite direction that tend to slow down the trends.

APPENDIX A: INCORPORATION OF WEIGHTS INTO THE CALCULATIONS

The three Philippines DHS survey samples for 1993, 1998, and 2003 are weighted samples. In each survey, sample weights are normalized so that the weighted number of cases equals the unweighted number of cases in the full DHS data set. In other words, the weights sum to the total survey sample size.

In our analysis, when the expanded data sets are created, the original weight for a woman carries over to the person-year observations created for that woman—that is, the same weight is attached both to the original woman record and to each person-year record created from the original woman record. However, each time a CLL model is fitted to an expanded data set (recall that we have 96 such data sets), it is important that the weights attached to the person-year records are renormalized so that the renormalized weights sum to the number of unweighted person-year observations in the particular expanded data set.

When calculating renormalized weights for person-year observations in the expanded data set for a particular parity transition, we use the following notation pertaining to the particular expanded data set:

• N = the number of unweighted person-year observations in the data set; w_i is the original weight attached to the ith person-year observation in the data set;

• W = the sum of the w_i over the person-year observations in the data set;

• $w_i^{*}$ = a renormalized weight for the ith person-year observation in the data set.

We would like the weighted data set to sum to N (i.e., the renormalized weights should sum to N). Renormalized weights are accordingly calculated as

$$w_i^{*}=w_i(N/W).$$ (A1)

When the $w_i^{*}$ are summed over person-year observations in the data set, the result is W(N / W) = N, as desired.

In the case of the data set for the open parity interval, for example 9+ to 10+, the renormalization of weights is done in the following way. One first creates the expanded data subsets for parity transitions 9–10, 10–11, ..., 14–15. One then pools these data subsets. Finally, one renormalizes the weights in this pooled data set using Eq. (A1). For the merge to be done properly, all variables carried over into the merged data set must have the same names in each and every data subset.

In the trend analysis, the three expanded data sets (one from each survey) for a particular parity transition (period or cohort) are pooled. Each of the three expanded data sets already incorporates renormalized weights. No further renormalization is needed when pooling the three expanded data sets.

APPENDIX B: JACKKNIFE ESTIMATES OF STANDARD ERRORS

Following the approach used in DHS surveys for calculating standard errors of complex measures, such as the TFR, we use the jackknife method, which is recommended when the original sample is a multistage cluster sample, as is the case in all DHS surveys. DHS surveys apply the jackknife by taking repeated samples from the original sample, each time omitting one primary sampling unit (PSU) from the original sample. The number of repeated samples is therefore the same as the number of PSUs.

PSUs typically are rural villages (or segments of villages in the case of large villages) and urban blocks. In the application to Philippines data, the number of PSUs is 744 in the 1993 survey, 752 in the 1998 survey, and 819 in the 2003 survey. In the cross-sectional analysis, in which each of the three Philippines surveys is analyzed separately, the number of repeated samples and the number of jackknife iterations are the same as the number of PSUs in the original sample pertaining to the particular survey under consideration. In the trend analysis, based on pooled data, the number of iterations is the sum of the numbers of PSUs over all three surveys.

Jackknife estimates of standard errors are approximations that are more accurate for some measures than for others (Sarndal, Swensson, and Wretman 1992:437–42). Our measures are unadjusted and adjusted PPRs, mean and median failure times, TFR, and TMFR by residence and education. The calculation of these measures is complex. The jackknife estimates of standard errors of these measures are approximations. The degree of bias in these approximations is unknown.

We did eight runs of our jackknife program—one for period estimates and one for cohort estimates for each of the three Philippines DHS surveys separately and for the pooled sample comprising all three surveys. In any given run of the program, each of N iterations (where N equals the number of PSUs) creates the various expanded samples, renormalizes weights, and calculates unadjusted and adjusted estimates of PPRs, mean and median failure times, TFR, and TMFR by residence and education. In the case of the two runs based on the pooled sample, estimates of the percentages shown in Table 8 are also calculated for each jackknife iteration. The N iterations yield N estimates of each measure, from which standard errors of the estimates are calculated.

The standard error of any particular measure X derived by the jackknife method is calculated as

$$\text{SE}(X)={[\text{Var}(X)]}^{0.5}={\{[(N-1)/N][\Sigma {(X_i-\overline{X})}^2]\}}^{0.5},$$ (B1)

where X_i denotes the value of X in the ith iteration (as calculated from the sample with one PSU removed), X̄ denotes the mean of the X_i over the N iterations, and the summation ranges from 1 to N.

We also calculate standard errors of pairwise differences in the value of each measure between categories of a predictor variable. For example, in the case of the adjusted TFR by education (low, medium, high), we calculate X = TFR_M – TFR_L for each of the N iterations and then use Eq. (B1) to compute the standard error of X = TFR_M – TFR_L. The calculation is repeated for X = TFR_H – TFR_L. We then form the test statistics z_M = (TFR_M – TFR_L) / SE(TFR_M – TFR_L) and z_H = (TFR_H – TFR_L) / SE(TFR_H – TFR_L). z_M and z_H are assumed to be normally distributed, thereby enabling tests of whether TFR_M and TFR_H differ significantly from TFR_L. In these comparisons, low education is considered as the reference category. All tests of significance are two-tailed tests.