Three Measures of Longevity: Time Trends and Record Values

Abstract

This article examines the trend over time in the measures of “typical” longevity experienced by members of a population: life expectancy at birth, and the median and modal ages at death. The article also analyzes trends in record values observed for all three measures. The record life expectancy at birth increased from a level of 44 years in Sweden in 1840 to 82 years in Japan in 2005. The record median age at death shows increasing patterns similar to those observed in life expectancy at birth. However, the record modal age at death changes very little until the second half of the twentieth century: it moved from a plateau level, around age 80, to having a similar pace of increase as that observed for the mean and the median in most recent years. These findings explain the previously observed uninterrupted increase in the record life expectancy. The cause of this increase has changed over time from a dominance of child mortality reductions to a dominance of adult mortality reductions, which became evident by studying trends in the record modal age at death.

The aging of populations is a fact that is observed in many Western societies. Evidence for this process includes the acceleration in the rise of the numbers of older (aged 85 and over) persons (Waite 2004), the increase in the numbers and percentages of centenarians and supercentenarians (Robine and Paccaud 2005), the steady rise in the maximum recorded life span (Wilmoth et al. 2000), and the uninterrupted long historical rise in life expectancy (Oeppen and Vaupel 2002; White 2002). These facts have contributed to an increased interest in the ancient question on the possible causes of long life.

Longevity is the capability to survive beyond the species-specific average age of death (De Benedictis and Franceschi 2006). This definition involves not only the individual ability to achieve old age but also the population-level mortality, measured in this case by the mean age at death of the population. Alternative definitions of longevity refer to the period between birth and death of an individual, but expressed in a cohort measure (Carey and Judge 2001). Median and modal ages at death are seldom proposed as measures to study longevity. The mean age at death, or life expectancy, is generally preferred. However, all three measures of central tendency are important. They supplement one another with information on the “center” of the distribution of deaths. Therefore, in an analysis of trends of mortality over time, it is relevant to include all three measures of central tendency to understand the dynamic of these most representative values.

The record values of the three central tendency measures are the main focus of this research. Previous studies demonstrated that the trend over time of the record life expectancy is a measure of the continuous progress in mortality that has, on a regular pace, kept improving (Oeppen and Vaupel 2002). The different time-trends in the mean, median, and mode have previously been shown for specific countries (Cheung and Robine 2007). Looking at the record measures of longevity enables us to understand the strong impact of the continuous progress in mortality and, as explained below, of the ages at which these improvements are occurring.

Survivorship improvements and mortality reductions dictate the changes in the measures of central tendency: mean, median, and mode. In the past centuries, these changes in survivorship and mortality resulted from developments in public health, medicine, economic development, nutrition, education, and household conditions (Riley 2001). As long as the decline in mortality continues (and it does not worsen at other ages), all three measures of “typical” longevity should keep their upward trend. Yet, the pace of these trends is dependent on the ages at which improvements are occurring (Wilmoth 2000). A second motivation for this research is to study the age-specific changes in mortality and their contribution in the measures of central tendency.

The present research on the effect of age-specific mortality changes in the time trends of the record measures of longevity is divided into seven sections. The following section introduces the calculations needed to obtain the measures of central tendency, and the third section illustrates their application with the case of Swedish data. Next, these concepts are expanded to analyze time trends on a global level by looking at record measures of longevity. The age-contribution to the change in longevity measures and the record holding countries of the measures of central tendency are presented in the subsequent two sections. The final section is the conclusion.

CALCULATIONS

To simplify many of the mathematical developments presented here, let the radix of the period life table at time t be equal to 1: ℓ(0,t) = 1. The life table density function describing the distribution of deaths (i.e., life spans) is denoted as d(x,t) at age x and time t. From this distribution, life expectancy at birth is calculated as the mean age at death:

$$e^0(t)=\underset{0}{\overset{\omega }{\int }}xd(x,t)dx,$$ (1)

where ω is the highest age attained, and the denominator of this measure is equal to 1,

$$\underset{0}{\overset{\omega }{\int }}d(x,t)dx=1.$$

The median age at death, Md(t), is the age when half of the population has died: that is, when the survival function is equal to one half, ℓ(Md,t) = 0.5. When the value of Md(t) is found between two complete single ages X and X + 1, its value needs to be interpolated as Md(t) = X + γ, where γ is a function of the survival function at ages X and X + 1.

Finally, the modal age at death is the age when most deaths occur, M(t) = {x | max[d(x,t)]}. Two modes should be distinguished in the life table distribution of deaths: one at age 0, when people die soon after birth, and a late mode found at older ages. Given the interest in changes over time in the measures of central tendency, the focus here is on the late modal age at death. In some countries, the increase in young adult mortality has created local modal ages at death: for example, the reversal in mortality in Russia in the 1990s. Nevertheless, these local modal ages have not passed the higher level of mortality concentration at older ages. In the rest of the text, I refer to this latter measure as the modal age at death,

$$M(t)=\{x|\text{max}[d(x,t)] \text{for} x>5\}.$$ (2)

To obtain a mode with decimal-point precision, it is necessary to calibrate the value, and Kannisto’s (2001) proposal of modal age is used for this purpose. Given an initial single age X with the highest number of deaths, the modal age at death is found as M(t) = X + δ, with δ giving the desired decimal-point precision. The quantity δ is a measure of the distance of death counts at ages adjacent to X, which is resultant of fitting a quadratic curve to the values around the mode (Canudas-Romo 2008). Appendix A includes the precise calculations carried out for the median and the modal age at death to obtain decimal precision.

The Human Mortality Database (2009) provides detailed mortality and population data for industrialized countries. For my purpose, period life table data for all available years from 1840 until 2005 were retrieved from this database (up to 2006 for Sweden in Figure 2).

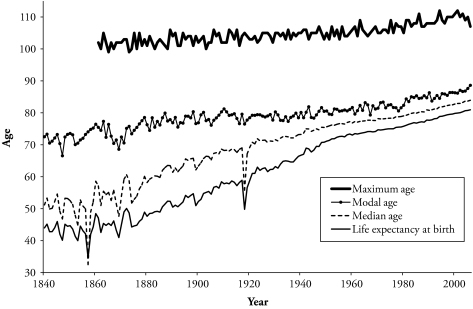
Figure 2.

Maximum, Modal, and Median Ages at Death, and Life Expectancy at Birth for Swedish Total Population, 1840 to 2006

Source: Human Mortality Database (2/4/2009).

Note: Maximum age is calculated from 1861 to 2006.

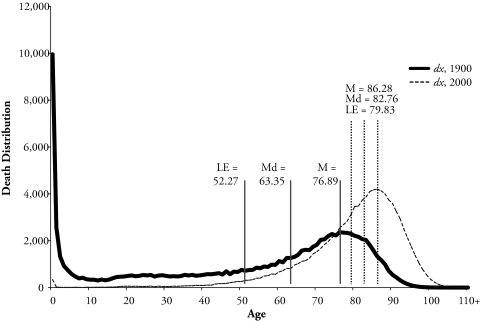
The choice of the mean, median, and mode depends on the purpose that the measure is to serve. For a description of the distribution of deaths, the mode with its easily identified value, after the distribution is plotted, denotes where most of the deaths are concentrated. For example, Figure 1 shows the death distribution for Sweden in 1900, where a bimodal distribution is clearly found at age 0 and around age 77. Figure 1 also displays the death distribution for the Swedish population at the end of the twentieth century. At this time, the distribution has moved toward older ages, and the three measures are close to one another.

Figure 1.

Mode (M) and Median (Md) Ages at Death, and Life Expectancy (LE) for the Life Table Age Distribution of Deaths for Swedish Total Population in 1900 and 2000

Source: Human Mortality Database (2/4/2009).

Life expectancy portrays a mortality situation best when the distribution of deaths is relatively symmetrical. Although the death distribution never was symmetrical during its change from being bimodal to unimodal, demographers have used life expectancy for describing its dynamic. This preeminence comes from the fact that life expectancy is the expected value of the distribution. Predictions and inferences based on the mean have fewer total errors, or smaller standard deviations, than predictions based on the other values. However, as shown in this analysis, a more complete understanding of mortality trends can be reached when the three measures are included.

DYNAMIC OF MEASURES OF LONGEVITY

It is informative to observe the trend over time in the three measures of central tendency for a single country. Figure 2 shows the three measures for the Swedish population during the period 1840–2006. Also included in Figure 2 is the maximum age at death attained from 1861 to 2006 in Sweden (as calculated in Wilmoth et al. [2000] and Wilmoth and Lundström [1996]).

All the measures of longevity increase over time, although at a different pace and level. The upward trend observed in the maximum age at death is similar to that of the modal age at death, while median and mean of the distribution have comparable patterns. Other measures that capture the mortality trend at old ages, such as the senescent life expectancy (Bongaarts 2006), also present a similar trend as the maximum age at death and the modal age. The rise observed in the maximum and modal age accelerates in the second half of the twentieth century, and the median and life expectancy increase at a slower pace over the last decades of the studied period.

The increase in the maximum age at death in the second half of the twentieth century is explained by Wilmoth et al. (2000) as a combination of larger cohorts surviving to old ages, and to improvements in survival after these ages. Of these two components, reduction in mortality above age 70 is the main cause for the increase. In most recent years, this factor accounts for 95% of the rise (Wilmoth et al. 2000). This suggests that the understanding of changes in the different longevity measures hinges on the contribution by age to changes in mortality. This is addressed in a later section of this article.

Life expectancy and the median age at death increased with a more regular and slower pace in the second half of the twentieth century. Similar patterns of change in the pace of life expectancy increases are observed in other industrialized countries (White 2002). Nevertheless, the trend of the record life expectancy is of nearly constant increase (Oeppen and Vaupel 2002). Given that my interest is in using the measures of central tendency to study longevity, in the next section, I analyze the record of all these measures in every year.

RECORD MEASURES OF LONGEVITY

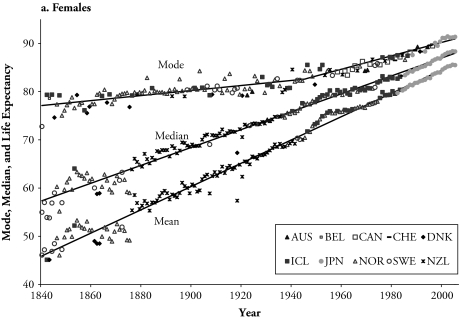
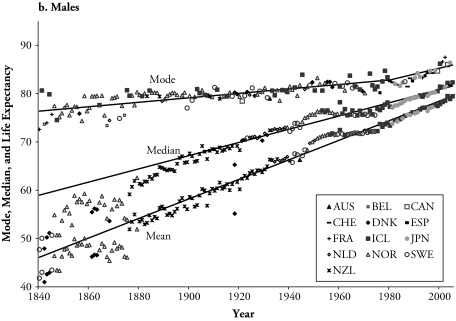
Panels a and b of Figure 3 show the record life expectancy at birth, and record median and modal ages of the death distribution from 1840 to 2005, for females and males, respectively. Each record is calculated independently, which explains why different countries can hold the record mode and median ages at death, and life expectancy in any given year. The focus on trends over time of the record life expectancy was introduced by Oeppen and Vaupel (2002). Figure 3 updates their list of record life expectancies from 1840 to 2005. Furthermore, Figure 3 compares the results of the record life expectancy with the other two measures of central tendency.

Figure 3.

Countries Holding the Record Modal and Median Ages at Death and the Record Life Expectancy at Birth (1840–2005), and the Best-Fitting Lines

Source: Human Mortality Database (2/4/2009).

Note: AUS = Australia, BEL = Belgium, CAN = Canada, DNK = Denmark, FRA = France, ICL = Iceland, JPN = Japan, NLD = the Netherlands, NOR = Norway, NZL = New Zealand, ESP = Spain, SWE = Sweden, CHE = Switzerland.

The mode is above the median, and life expectancy has the lowest values during the entire observed period. The mode stagnated at levels around age 80, with minor increases until the mid-1940s for females and the end of the 1970s for males. During this time, the female record median and life expectancy increased rapidly from levels of 55 years for the median and 46 years for life expectancy in 1840 to 77 and 72 years in the mid-1940s, respectively. For the male population, the record median and life expectancy increased from levels of 48 years for the median and 42 years for life expectancy in 1840 to 77 and 73 years at the end of the 1970s, respectively. Since then, the three measures have increased at a similar pace, with slowly narrowing gaps between the mode and median (average since 1990 of 3.3 years for females and 4.5 years for males), and between the median and life expectancy (average gap of 2.9 for both).

Figure 3 also includes fitted regression lines for the three record measures of longevity. A two-phase linear regression model was used for the record modal age at death that best described the change in pace of increase in this measure. The estimated rates of increase (slopes of the lines) in the record median and mean, respectively, are 0.19 and 0.24 for the females and 0.14 and 0.20 for males (above R² = .94 for all). Here, it should be noted that the fitted lines for males only correspond to the period from 1900 until the most recent year. The mode increases initially at a pace of 0.5 of a year every 10 years for both females and males, changing in the mid-1940s to 1.4 years every 10 years for females and at the end of the 1970s to 1.2 years for males (R² = .96 for females, and R² = .83 for males). For females, the trend in median age and life expectancy decelerated, and the mode accelerated in the last decades of the twentieth century and the first years of the new century. The pace of increase in the three measures of longevity was augmented in this period for males. For the three measures to be equal, the death distribution would be required to become not only unimodal but also perfectly symmetrical.

AGE CONTRIBUTION TO THE CHANGE IN LONGEVITY MEASURES

As discussed in previous sections, reductions in death rates at different ages have different impacts on the measures of longevity. During the more than 160 years analyzed in this study, the overall trend in the record-holding countries has been a decline in mortality at all ages, despite yearly fluctuations. For simplicity, only reductions or stagnation in mortality are discussed, not increases.

The age contribution to the change in life expectancy has been studied extensively using decomposition methods (Canudas-Romo 2003). As shown in Eq. (1), all ages are included when calculating life expectancy and, thus, change at any age has an impact on the change of this measure. This stands in contrast to the case for the other two measures. The median age at death has been examined by methods of decomposition (Horiuchi, Wilmoth, and Pletcher 2008). By definition, this measure is dependent on the number of survivors up to the age at which half of them are left. If reductions in mortality occur before the age where the number of survivors is equal to half, the median will increase. However, there are no changes in the median age if mortality remains the same until the age at which the number of survivors is equal to half. This is the case even when great reductions in mortality are present at ages older than the median age.

The age contribution to changes in modal age at death has yet to be studied exhaustively. To assess this, two situations are analyzed: when changes in mortality occur at ages younger than the modal age, and when the changes are present at older ages than the modal age. As earlier, let M be the modal age at death. The modal age at death is obtained by comparing the number of deaths at all ages. Respectively, the number of deaths at any age is the product of survivors arriving to that age and their death rates. If reductions in mortality occur only at ages younger than M, then the number of deaths found at any age before M, compared with those at age M, will still be lower. A simple argument to illustrate this is that while more survivors arrive at age M, more deaths will also be present at this age, maintaining M as the mode. When changes in mortality take place at ages older than M, this could make the modal age change to older ages. However, enough survivors have to arrive to this older age in order to obtain a greater number of deaths than at M. These transformations of the measures of central tendency are analytically demonstrated in Appendix B.

To assess intuitively the dynamics of the three longevity measures observed in Figure 3, I examine them by using a simple mortality model. For the first years (units of time) of this model, let reductions in mortality occur mainly at young ages. In these first years, an increase in median and mean ages at death will be observed, but very modest change is observed at the mode. The slow trend in the mode is due to small changes in mortality at older ages. Later, more noticeable mortality improvements become present at older ages, and the three measures change over time. A mortality model proposed by Canudas-Romo and Schoen (2005) combines the model used by Siler (1979) and parameters that account for reductions in mortality over time. In the remaining text, I refer to this model as the “Siler mortality change model.” This model can return unrealistic results if used for projections, but here it is used only for illustrating the dynamic of the three measures of longevity.

Let the force of mortality at age a and time t be denoted as μ(a,t) and be defined under the Siler mortality change model as

$$\mu (a,t)=e^{{\alpha }_1-{\rho }_{1}t-{\beta }_{1}a}+e^{{\alpha }_2-{\rho }_{2}t}+e^{{\alpha }_3-{\rho }_{3}t+{\beta }_{3}a},$$ (3)

where three constant terms reflect the value of infant mortality μ(0,0) = e^α₁ + e^α₂ + e^α₃; the parameters β₁ and β₃ are fixed rates of the mortality decline and increase over age, respectively, accounting for infant and senescent mortality; and the parameters ρ₁, ρ₂, and ρ₃ are constant rates of mortality decrease over time. The α and β parameters stem from the Siler model, and the ρ parameters are used in Gompertz models with a continuous rate of decline (Schoen, Jonsson, and Tufis 2004; Vaupel 1986). The parameter values used for the present illustration are e^α₁ = 0.17, e^α₂ = 0.005, e^α₃ = 0.0003, β₁ = 1, and β₃ = 0.65. At time 0, the modal age at death at advanced ages is 80.5, the median age at death is 54.9, and life expectancy is 47.6. These values are comparable with those observed in populations with historical data. For example, the observed record values for females in 1842 are 79, 54, and 45 years for the modal and median ages and life expectancy, respectively (see Figure 3, panel a). For the pace of mortality improvement, I have chosen ρ₁ = 0.015 and ρ₂ = ρ₃ = 0.01. More on the selected parameter values can be seen in Canudas-Romo (2008).

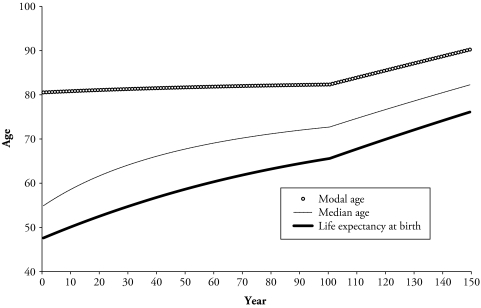
Figure 4 shows the results of the Siler mortality change model for 150 units of time, here set as years. In the first 100 years, the improvement in mortality at adult ages ρ₃ is set to 0. For the subsequent 50 years, mortality improvements at adult ages are present at a level rate of ρ₃ = 0.01. The patterns of the three measures of longevity in Figure 4 resemble those observed for the record measures in Figure 3. That is, during the first 100 years, there is a very slow increase in the modal age at death, which is nearly stagnant around age 80, and the other two measures increase rapidly from values around age 50 years to more than 70 years. For the remaining 50 years, the three measures increased, although at different paces, while keeping the same ranking of highest for the modal age and lowest for life expectancy. These changes are related to the reduction in mortality, which in the first 100 years, occurred mainly at younger ages—that is, below the observed modal age at Time 0 of 80.5 years. In the last 50 years, when mortality also changed at ages older than the modal age, the modal age shows an upward trend.

Figure 4.

Modal and Median Ages at Death, and Life Expectancy Under a Siler Mortality Change Model

The results of this section are summarized in Table 1, which shows the dynamic in the median, modal, and mean ages at death depending on the age at which the change in mortality occurs. If changes occur at ages younger than the modal age, there are no effects in this measure, as opposed to the median and mean that will change with reductions at ages younger than them. Inversely, the median shows no perturbations if changes occur at ages older than the median, but the mode and mean do change for this case. Life expectancy is the only measure that changes regardless of the age at which the reduction in mortality occurs. This could be considered a drawback of the mean’s ability to inform of the origin of the change, but the mode and median complement this information.

Table 1.

Effects on the Measures of Longevity of Changes in Mortality

Measure	Changes at Ages Below the Measure	Changes at Ages Above the Measure
Modal Age at Death	No	Yes
Median Age at Death	Yes	No
Life Expectancy	Yes	Yes

COUNTRIES HOLDING THE RECORD MEASURES OF LONGEVITY

As shown by Oeppen and Vaupel (2002), only few countries have held the record life expectancy at birth over time. As shown in this section, the number of countries having held the record median and modal ages at death is also a small number. Figure 3 displays the record-holding countries for the modal and median ages and life expectancy, and Tables 2 and 3 present the frequency distribution of the records by country.

Table 2.

Frequency Distribution of Records in Modal and Median Ages at Death and Life Expectancy by Country^a

Country	Females				Males
	Mode	Median	Life Expectancy	Total Record	Mode	Median	Life Expectancy	Total Record
Australia	6	2		8	2		1	3
Belgium	1			1	3			3
Canada	12	1		13	3			3
Denmark	11	3	4	18	10	10	7	27
France					6			6
Iceland	25	33	21	79	35	28	26	89
Japan	11	21	23	55	9	16	10	35
The Netherlands					4	13	7	24
Norway	63	40	41	144	60	40	35	135
New Zealand	12	52	66	130	4	45	58	107
Spain					3			3
Sweden	15	13	11	39	17	13	22	52
Switzerland	4	1		5	6	1		7
Total	160	166	166	492	162	166	166	494

Notes: Belarus emerges as the holder of several records in the 1960s, but the Human Mortality Database warns that Belarusian data for 1959–1969 are of poor quality. Thus, Belarus is not included in Figure 3 or Table 2.

Source: Human Mortality Database (2/4/2009).

^aOnly countries that have held more than any three record measures are included. The lower number of “total record” modes comes from the fact that some countries held the record modal ages at death only in one or two years.

Table 3.

Record-Holding Countries of All Three Measures (1840–2005) and Years When This Occurred in the Twentieth Century, by Gender

Country	Female	Male	Both	Year
Demark		1
Iceland	4	7	1	1979
Japan	11	4
New Zealand	2	4
Norway	17	23	12	1947
Sweden	2
Total	36	39	13

Note: The other 11 years when Norway held all the records for females and males occurred in the nineteenth century.

Source: Human Mortality Database (2/4/2009).

It should be noted that Figure 3 and Tables 2 and 3 present only those countries that have held more than any three record measures. For more than 60 years, the record modal age at death was held by Norway, followed by Iceland. The record median and life expectancy are also held by Norway at the beginning of the time series, although New Zealand (excluding the Maori population) is the record-holding country for these latter measures from the 1880s up to the 1940s, after which the records are held by Norway and Iceland. The long range of years that the record life expectancy and median age at death were held by New Zealand might be resultant from a healthy migration effect that this country experienced during the end of the nineteenth and beginning of the twentieth century (Vallin and Meslé 2009). In the latest years of the twentieth century and first years of the new century, Japan has held the record for all three measures for females, but this started much earlier for the median and life expectancy than for the modal age at death. For males, the record median and mean is held by Japan and Iceland, but it is more difficult to identify a sole country for the mode.

Table 2 shows that some countries holding record measures of longevity for males do not hold any records for females. The extreme case of this is the Netherlands, with 24 male records and none for females. On the contrary, during the twentieth century, there were only 2 years when a single country held all three records of longevity for both females and males: 1947 for Norway and 1979 for Iceland (see Table 3).

DISCUSSION

The pace of increase in the record modal and median ages at death and life expectancy at birth shows no signs of reduction over the examined period. However, the reasons for these time trends have varied over time. A simple decomposition of the effect in the measures of longevity of reductions in mortality before and after these measures helps explain the trend. The initial increase in two of these measures is explained by the strong decline in infant and child mortality. As mortality in the first years of life reached low levels, the explanation of increase in median and life expectancy at birth were found at adult ages. When significant mortality improvements were present at older ages, an increase in the modal age at death was observed. Therefore, the increasing modal age at death illustrates a change from a dominance of child mortality reductions to a dominance of adult mortality reductions. This process has been described as a shifting mortality process in which the bulk of a bell-shaped distribution of deaths around the modal age at death moves toward older ages (Bongaarts 2005; Canudas-Romo 2008; Wilmoth and Horiuchi 1999).

The increase in the late modal age at death over the twentieth century has been observed in several countries (Cheung et al. 2005; Cheung and Robine 2007; Kannisto 2001; Robine 2001). The discontinuity in its trend during the second half of the century has also been previously noted (Robine 2001). Nevertheless, findings from the analysis reported here provide important information about what is happening on a global level by looking at the record modal age. Furthermore, to my knowledge, this is the first analytical demonstration of how the changes in the modal age at death, as well as the other measures of longevity, are related to the age contribution of reductions in mortality (see Appendix B).

The series of record measures of longevity, 1840–2005, show the similarity between the median and mean ages at death in both the time trends and the countries holding these record measures. The record modal age at death differs greatly in both time trends and record-holding countries from the other measures and justifies further research on this measure of longevity.

The record measures of longevity are relevant for the current debate of projected mortality trends because national mortality forecasting should be viewed and compared in a larger international context (Oeppen and Vaupel 2006; Lee 2006). Similarly, the mortality situation of a country should be characterized by more than one measure of longevity. Not doing this could hide interesting transformations occurring in the age pattern of mortality. This is especially relevant at times when technology transfers play an important role in reductions in mortality (Oeppen 2006), which could lead to further changes in the measures of longevity. For countries with high survival, the modal age at death will play a central role because this measure is highly sensitive to changes at older ages.

APPENDIX A. THE MEDIAN AND MODAL AGES AT DEATH

For countries with available data, the median and mode were calculated as explained in this appendix.

The median age at death was calculated by using values of the survival function at two contiguous ages of the value of ℓ(Md,t) = 0.5. Let x and x + 1 be the ages of the interval in which ℓ(Md,t) = 0.5 is located. Assuming linearity in this interval, the age Md is located as

$$Md(t)=x+\frac{[0.5-\ell (x,t)]}{[\ell (x+1,t)-\ell (x,t)]}.$$ (A1)

The modal age at death was calculated by using Kannisto’s (2001) proposal of modal age with decimal precision. Let x be the age with the highest number of deaths in the life table at time t, d(x,t). The two contiguous ages x – 1 and x + 1 and the number of deaths at these ages are used to fit a quadratic polynomial to the function describing the death distribution (for more details, see Canudas-Romo 2008). In terms of the ages and distribution of deaths, the expression of the modal age at death is

$$M(t)=x+\frac{[d(x,t)-d(x-1,t)]}{[d(x,t)-d(x-1,t)]+[d(x,t)-d(x+1,t)]},$$ (A2)

where x is the age with the highest number of deaths in the life table at time t, d(x,t).

APPENDIX B. EFFECTS OF CHANGES IN MORTALITY ON THREE MEASURES OF “TYPICAL” LONGEVITY

Definitions

Mean:

$e^0={\int }_0^{\infty }xd(x)dx={\int }_0^{\infty }\ell (x)dx={\int }_0^{\infty }{e}^{-{\int }_0^x\mu (a)da}dx$

Median:

x͂ = x such that ℓ(x) = 0.5

Mode:

M = x such that x > 5 and d(x) > d(a) for all a > 5

Theorem

Let the force of mortality at Times 1 and 2 be denoted as μ₁(x) and μ₂(x). Let these functions be nonnegative, continuous functions with finite derivatives for all x ≥ 0. Suppose in all cases that μ₁(x) ≥ μ₂(x) for all x.

1. If μ₁(x) > μ₂(x) for some x, then $e_1^0<e_2^0$.

2. If μ₁(x) = μ₂(x) for all x ≤ x͂₁, then x͂₁ = x͂₂; but

   if μ₁(x) > μ₂(x) for some x ≤ x͂₁, then x͂₁ < x͂₂.

3. If μ₁(x) = μ₂(x) for all x ≥ M₁, then M₁ = M₂;

   if μ₁(x) > μ₂(x) for M₁ < x ≤ y such that d₂(y) > d₁(M₁), then M₁ < y ≤ M₂.

Proof

For the three parts of the theorem:

a. Since μ₁(x) ≥ μ₂(x) for all x and μ₁(x) > μ₂(x) for some x, it follows that

$${\int }_0^x{\mu }_1(a)da>{\int }_0^x{\mu }_2(a)da.$$

Therefore

$$e_1^0={\int }_0^{\infty }{e}^{-{\int }_0^x{\mu }_1(a)da}dx<{\int }_0^{\infty }{e}^{-{\int }_0^x{\mu }_2(a)da}dx=e_2^0.$$

b. Since μ₁(x) ≥ μ₂(x) for all x and μ₁(x) > μ₂(x) for some x ≤ x͂₁, it follows that

$${\int }_0^{{\tilde{x}}_1}{\mu }_1(a)da>{\int }_0^{{\tilde{x}}_1}{\mu }_2(a)da.$$

Therefore,

$${\ell }_2({\tilde{x}}_1)>{\ell }_1({\tilde{x}}_1)=\frac{1}{2}.$$

Since ℓ₂(x) is a monotonically decreasing function of x with a lower limit of 0, it follows that $\ell (x)=\frac{1}{2}$ for some x > x͂₁, and thus x͂₁ < x͂₂.

On the other hand, if μ₁(x) = μ₂(x) for all x ≤ x͂₁, then ${\ell }_2({\tilde{x}}_1)={\ell }_1({\tilde{x}}_1)=\frac{1}{2}$. Therefore, in this case, x͂₁ = x͂₂.

c. This proof is divided into two parts for changes below and above the mode: by definition of the mode, d₁(M₁) > d₁(x), or equivalently, μ₁(M₁)ℓ₁(M₁) > μ₁(x)ℓ₁(x) for all x (i.e., x > 5).

c1. Changes below the modal age:

Case x ≥ M₁, since μ₁(x) = μ₂(x) for all x ≥ M₁, it follows that $\frac{{\ell }_1(x)}{{\ell }_1(M_1)}=\frac{{\ell }_2(x)}{{\ell }_2(M_1)}$ in this range of x. Therefore,

$${\mu }_2(M_1)={\mu }_1(M_1)>{\mu }_1(x)\frac{{\ell }_1(x)}{{\ell }_1(M_1)}={\mu }_2(x)\frac{{\ell }_2(x)}{{\ell }_2(M_1)},$$

or equivalently, d₂(M₁) > d₂(x) for all x ≥ M₁.

Case x < M₁, since μ₁(x) ≥ μ₂(x) for all x < M₁, it follows that $\frac{{\ell }_1(M_1)}{{\ell }_1(x)}\le \frac{{\ell }_2(M_1)}{{\ell }_2(x)}$ in this range of x. Therefore,

$${\mu }_2(M_1)\frac{{\ell }_2(M_1)}{{\ell }_2(x)}={\mu }_1(M_1)\frac{{\ell }_2(M_1)}{{\ell }_2(x)}\ge {\mu }_1(M_1)\frac{{\ell }_2(M_1)}{{\ell }_1(x)}>{\mu }_1(x)\ge {\mu }_2(x),$$

or equivalently, d₂(M₁) > d₂(x) for all x < M₁. Since d₂(M₁) > d₂(x) for both x ≥ M₁ and x < M₁, it follows that M₂ = M₁.

c2. Changes above the modal age:

Case x ≤ M₁, since μ₁(x) = μ₂(x), it follows that $\frac{{\ell }_1(M_1)}{{\ell }_1(x)}=\frac{{\ell }_2(M_1)}{{\ell }_2(x)}$ in this range of x.

Therefore,

$${\mu }_2(M_1)\frac{{\ell }_2(M_1)}{{\ell }_2(x)}={\mu }_1(M_1)\frac{{\ell }_1(M_1)}{{\ell }_1(x)}>{\mu }_1(x)={\mu }_2(x),$$

or equivalently, d₂(M₁) > d₂(x) for all x ≤ M₁.

If μ₁(x) > μ₂(x) for y ≥ x > M₁ are such that d₂(y) > d₁(M₁) = d₂(M₁) and y > M₁, then since d₂(M₁) ≥ d₂(x) for x ≤ M₁ and d₂(y) > d₂(M₁) for y > M₁, then d₂(y) > d₂(x) for any x ≤ y, and it follows that M₂ ≥ y > M₁.