Biodemographic Modeling of the Links Between Fertility Motivation and Fertility Outcomes in the NLSY79

Abstract

In spite of long-held beliefs that traits related to reproductive success tend to become fixed by evolution with little or no genetic variation, there is now considerable evidence that the natural variation of fertility within populations is genetically influenced and that a portion of that influence is related to the motivational precursors to fertility. We conduct a two-stage analysis to examine these inferences in a time-ordered multivariate context. First, using data from the National Longitudinal Survey of Youth, 1979, and LISREL analysis, we develop a structural equation model in which five hypothesized motivational precursors to fertility, measured in 1979–1982, predict both a child-timing and a child-number outcome, measured in 2002. Second, having chosen two time-ordered sequences of six variables from the SEM to represent our phenotypic models, we use Mx to conduct both univariate and multivariate behavioral genetic analyses with the selected variables. Our results indicate that one or more genes acting within a gene network have additive effects that operate through child-number desires to affect both the timing of the next child born and the final number of children born, that one or more genes acting through a separate network may have additive effects operating through gender role attitudes to produce downstream effects on the two fertility outcomes, and that no genetic variance is associated with either child-timing intentions or educational intentions.

Recent behavioral genetic and molecular genetic evidence indicates that both the motivational precursors to fertility and the fertility outcomes themselves have genetic determinants (Kohler et al. 2006; Rodgers, Hughes, et al. 2001). The behavioral genetic line of research, in particular, has suggested that both the motivational precursors to fertility, such as desired family size, and the corresponding fertility outcomes, such as final family size, have significant heritability (Kohler and Christensen 2000; Pasta and Miller 2000; Rodgers and Doughty 2000; Rodgers, Hughes, et al. 2001).

These findings raise three important questions. First, are the genes and their networks that affect the motivational precursors to fertility the same as those that affect the fertility outcomes? Rodgers, Kohler, et al. (2001) have shown a small but significant overlap in the genetic variance of age at first proception (trying to conceive; Miller 1986) and the genetic variance of completed family size. Presumably, proceptive behavior reflects precursor fertility motivations, but research that examines the motivations themselves, and not just the age at which a certain behavior occurs, would answer this question more directly.

Second, through which specific motivational precursor do genes and their networks affect fertility outcomes? Rodgers and Doughty’s (2000) work with expected and completed family size suggests that one answer could be child-number desires. However, a behavioral genetic study by Rodgers, Bard, and Miller (2007) suggested that there are different sources of genetic variance for the number of children born before age 20 compared with the number of children born between the ages of 20 and 30. This finding suggests that another answer could be child-timing desires. Finally, the findings of Pasta and Miller (2000) that both positive and negative childbearing motivations have significant heritability suggests that yet another answer could be the trait-like factors lying antecedent to desires in the motivational process (Miller 1994).

Third, how much of the genetic variance that is observed in fertility outcomes is attributable to the genetic variance affecting their motivational precursors? Such genetic variance may be passed through to fertility outcomes but may contribute to the genetically determined variance of those outcomes anywhere from substantially to only slightly. A temporally ordered biometric design could help sort out the magnitude of the genetic links between fertility motivations and fertility outcomes.

These questions, and the previous research that suggested them, shape and motivate the design of our study. Using a theoretical framework articulated by Miller (1994), and considering the data available from the National Longitudinal Survey of Youth 1979 (Center for Human Resource Research 2003), we develop a time-ordered, seven-variable model that links a sequence of antecedent fertility motivations with two subsequent fertility outcomes: the timing of the first/next child born and the final number of children born. We then use a structural equation model (SEM) analysis to test that model on the National Longitudinal Survey of Youth (NLSY) data. Having confirmed the hypothesized time-ordered relationships, we then use this SEM as the phenotype whose genetic determinants we wish to examine. To this end, we conduct a biometric analysis of the fertility motivation to fertility outcome sequence, using a multivariate Cholesky model to identify genetic influences on all variables in that sequence.

THEORETICAL FRAMEWORK

We posit two developmental phases during the life course for the motivations that promote childbearing in humans. During growth and development, biologically based, largely hereditary characteristics of the individual interact with the individual’s childhood and adolescent social environments (Belsky 2000; Miller 1992), leading to the formation of a motivational substrate for childbearing (Miller and Pasta 2002). This process culminates at about the time that the individual’s body becomes physiologically fully capable of reproduction. Beginning in the adolescent and early adult periods and extending across the life course until the end of the individual’s reproductive career, the childbearing motivations that arise from this substrate find expression in conscious desires and intentions, in behavior, and ultimately in the occurrence or avoidance of fertility events (Miller 1994). These events, in turn, have a feedback effect on the underlying motivational substrate and the forms of its conscious expression (Miller and Pasta 1995a).

In order to understand how the motivational substrate leads to childbearing, we turn to the Traits-Desires-Intentions-Behavior (TDIB) theoretical framework developed by Miller (1994). The ideas that underlie this framework are fairly simple. There is a three-step motivational sequence, in which traits that dispose the individual toward or away from bearing and caring for children are activated into conscious desires for or against having a child. These desires are, in turn, transformed through some decision-making process into intentions to have or not to have a child. Finally, the individual’s intentions are implemented through behaviors that lead either to the achievement or to the avoidance of conception and subsequent childbearing.

Many elements of this framework have been present in the fertility research literature for a number of decades. Demographers commonly use variables that reflect numbers of children intended, expected, desired, and considered ideal by survey respondents, and much is known about their properties. For example, Ryder and Westoff (1971) showed that responses to the intended and expected number of children were “virtually indistinguishable” and that the pattern of answers to survey questions showed a “well-ordered sequence” from ideal to desired to intended to current parity. On the other hand, there is evidence that these measures have limitations as predictors of actual fertility (Morgan 1982; Trent 1980; Westoff and Ryder 1977). Morgan (2001) pointed out that some measures, such as completed parity intentions, tend to change over time, making their usefulness depend on the time period over which they are projected and highlighting the potential importance of timing desires and intentions in fertility prediction (Rindfuss, Morgan, and Swicegood 1988). However, our own work (Miller and Pasta 1995b) has demonstrated successful prediction with this group of variables, and our framework will incorporate both child-number and child-timing measures to indicate the basic conscious pathway along which we believe underlying motivational traits are channeled into behavior.

We hypothesize that two types of precursor traits are sufficiently laden with affective force to motivate fertility behavior: domain-specific motivational traits, such as the positive and negative childbearing motivations measured by Miller’s (1995) Childbearing Questionnaire; and more general attitudinal traits, such as the traditional and modern sex role orientations measured by Scanzoni (1975). Both types of traits act as a primary source of the three types of fertility desires—namely, childbearing, child-number, and child-timing desires—corresponding to the three major issues that childbearing poses to the individual—namely, whether to have a child (or another child), how many (or how many more) to have, and how soon to have the first (or the next) child. Because of limitations in the NLSY data set, we focus here on child-number and child-timing desires. These two issues are, of course, not independent of each other. Prior research (Miller and Pasta 1994) indicates that child-number desires are causally antecedent to child-timing desires (i.e., the more children one wants, the sooner one wants to start having them).

As a result of individual and couple decision-making, desires are transformed into intentions. Desires represent what people would like, whereas intentions represent more practical goals of what is realistic and can be agreed upon. Intentions may be divided according to the same three issues that childbearing poses, and child-number and child-timing intentions are causally related to each other in the same way as their corresponding desires.

The three-step motivational sequence leads to conception-oriented behavior, including proceptive behavior, which is oriented to the achievement of conception (Miller 1986), and contraceptive behavior, which is oriented to the prevention of conception. Together, these two types of behavior result in the occurrence or avoidance of fertility events. Of course, sexual behavior is implicit in and entangled with both of these conception-oriented behaviors. For this reason, and because motivations and desires commonly drive human behaviors in less than fully conscious ways, and also because even well-motivated contraceptive behavior is often less than fully effective, unplanned fertility outcomes are relatively frequent. If such events result in live births, they typically have a feedback effect on the underlying motivations and desires, thereby changing the course of future childbearing.

HYPOTHESIZED PHENOTYPIC MODEL

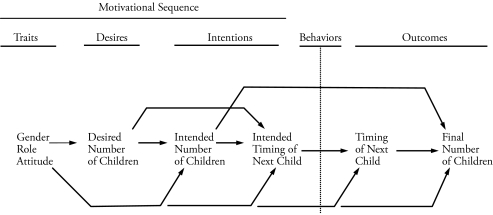
Figure 1 depicts the hypothesized model that was derived from our theoretical framework with the available NLSY variables in mind. It has two main components. On the left are four variables that represent the motivational or traits-desires-intentions (TDI) part of our framework. On the right are two fertility outcome variables. Between these two components are those behaviors that affect the occurrence of fertility. The model is a simple causal one, focused on main effects and not interaction effects. It is linearly time-ordered and does not include any feedback effects of outcomes on the motivational sequence. This is because we are interested in how the elements of that sequence, as measured early in an individual’s reproductive career, affect fertility events extending across the remainder of that career. Once this model has been fitted to the NLSY data, it will represent the phenotype that will be examined with biometric analysis.

Figure 1.

The Hypothesized Fertility Motivation and Outcome Model That Was Fitted to the NLSY Data

As suggested by the theoretical framework, we expect number desires to predict number intentions and—acting through the unmeasured construct of timing desires—to predict timing intentions. We expect number intentions to predict timing intentions and the final number of children born. We expect timing intentions to predict the timing of the next child. Finally, we expect the timing of the next child born to predict the final number born (the sooner one has a child, the more children one is likely to have).

We have selected gender role attitudes as the best available trait predictor in the motivational sequence. Research has shown that both motivations for childbearing and motivations for female education, work, and other aspects of a modern lifestyle are embedded within the gender role attitudes construct. Scanzoni (1975) showed that for wives aged 18–29, sex role modernity (as opposed to traditionalism) not only predicted lower birth intentions, lower parity, and higher effectiveness of contraceptive use, but was also positively associated with greater education and predicted greater work force participation and higher income. Miller (1981) found that a traditional gender role attitude was strongly associated with both positive and negative childbearing motivations in women (r = .59 and –.46, respectively). These findings, together with the trait-like nature of our measure, suggest that gender role attitudes will predict all the downstream variables shown in Figure 1, especially among women. The overall result is a well-ordered, generally linear series of predictions, extending from gender role attitudes to the final number of children born.

Because of the complexity of the behaviors that affect fertility outcomes, we have constructed a model that focuses on the motivational part of our theoretical framework. Thus, we have not included explicit behavioral variables in the model but rather have indicated their ongoing occurrence in Figure 1 with a vertical dotted line placed after the antecedent motivational sequence. We assume that the consequent fertility outcomes represent imperfect indicators of intervening behaviors.

Various social science theorists have conceptualized fertility decision-making as a one-stage process (Becker 1981; Willis 1973), a two-stage process (Fawcett, Albores, and Arnold 1972; Namboodiri 1974), or a multistage process (Bulatao 1981). When considering most modern, developed societies, we are inclined to conceptualize fertility decision-making as occurring one birth at a time, a process that has been called conditional (McClelland 1983), successive (Fawcett 1983), or sequential (Namboodiri 1983) decision-making. This conceptualization does not mean that we think of each successive birth as resulting from a decision to have a child but rather that, both before and after each pregnancy during the reproductive life course, individuals and couples make decisions about their sexual, contraceptive, and proceptive behaviors and that these decisions reflect their child-number and child-timing motivations.

The consequence of this sequential conceptualization is that the hypothesized model shown in Figure 1 can be applied to any single birth, whether it is the first, second, and so on. We wanted to focus here on the predictive validity of fertility motivations, both for short-term fertility outcomes and for fertility outcomes that address entire fertility careers. Thus, we have selected two fertility outcomes that are distinct but related: the timing of the first/next birth and the final number of children born, as shown in our hypothesized model.

Up to this point, we have focused exclusively on motivations within the behavioral domain of reproduction. However, other sources of motivation can affect childbearing and further inform our modeling efforts. One such source is motivation for education, which derives from the behavioral domain that Miller and Rodgers (2001) have called exploration/mastery. Education has a complex, multipathway effect on fertility, one that is predominantly, but not exclusively, negative in the sense that it tends to delay childbearing and reduce the overall number of children born (Cochrane 1979; Kohler and Rodgers 2003). We use a trait-like measure of educational intentions to model the motivation for education and expect this measure to be negatively related to all parts of the childbearing motivational sequence as well as to the fertility outcomes. Because we believe traditional gender role attitudes to be positively related to fertility outcomes but also negatively associated with educational expectations, especially in women, we anticipate that the educational expectations and gender role attitudes variables will to some extent reduce each other’s explanatory power. Further, we anticipate that they should do this in a way that partials the educational motivation effects out of the overall gender role effects. As a result, the latter effects in the presence of an educational expectations variable should reflect primarily the unique childbearing motivational aspect of the gender role attitudes construct.

METHODS: PHENOTYPIC MODEL

Design

The data to which we fitted our hypothesized model were collected as part of the National Longitudinal Survey of Youth (NLSY), beginning in 1979 and ending in 2002, the most recent year prior to starting data analysis. Beginning in 1979, a national probability sample of young men and women was surveyed annually through 1994 and thereafter biennially. We used data collected during the 1979–1982 period to measure the motivational sequence leading to childbearing to predict prospectively the two fertility outcome variables of interest, which were measured beginning after 1982 and continuing through 2002.

Participants

The NLSY79 began with a sample of 6,111 youths representative of the United States as a whole, a military sample of 1,280 youths, and an oversample of 5,295 minority and economically disadvantaged youths, for a total of 12,686 youths. However, because some members of the economically disadvantaged and military samples were dropped from the survey after 1985 and 1990, the sample size from which we could actually draw our participants was 5,022 males and 4,942 females. As a result of attrition during the 23 years of data collection, data were available for the entire 1979–2002 period from 3,683 males and 3,883 females (retention rates of 73.3% and 78.6%, respectively).

The male and female youths who participated in the NLSY79 were born in 1957–1964, making them 14–22 years old in 1979 and 37–45 years old in 2002. This means that child-bearing for this cohort was largely complete, especially for women, and that problems with selection bias caused by fertility timing differences across educational and socioeconomic strata had been substantially resolved. Selected background characteristics of the study participants are shown in Table 1. We report their values as of 1982, when the motivational sequence stage of our model ends and the fertility outcome stage begins. Mean age in 1982 was 20.5 (SD = 2.3).

Table 1.

Frequency Counts for Selected Background Variables, Separately by Sex

	Males (n = 3,683)		Females (n = 3,883)
Variable	Frequency	Column %	Frequency	Column %
Race/Ethnicity, 1979
Hispanic	676	18.4	721	18.6
Non-Hispanic black	1,126	30.6	1,192	30.7
Non-Hispanic, nonblack	1,881	51.1	1,970	50.7
Religious Affiliation, 1982
Protestant	1,969	53.6	2,186	56.5
Roman Catholic	1,168	31.8	1,249	32.3
Other	86	2.3	100	2.6
None	448	12.2	334	8.6
Highest Grade Completed, 1982
8th grade or less	183	5.0	163	4.2
9th–11th grade	1,277	34.8	1,133	29.3
12th grade	1,385	37.7	1,511	39.1
1 or 2 years of college	547	14.9	741	19.2
3 or 4 years of college	252	6.9	305	7.9
Graduate school	29	0.8	16	0.4
Employment Status, 1982
Employed	2,167	58.8	2,030	52.3
Unemployed	571	15.5	526	13.6
Out of labor force	683	18.5	1,303	33.6
Armed services	262	7.1	24	0.6
Marital Status, 1982
Never married	3,035	82.4	2,639	68.0
Married	560	15.2	1,003	25.8
Separated, divorced, or widowed	87	2.4	240	6.2
Number of Children Ever Born, 1982
0	3,097	84.1	2,600	67.0
1	416	11.3	781	20.1
2	135	3.7	376	9.7
3+	34	1.0	126	3.3

Note: The number of missing cases in a variable column ranges from 0 to 14.

Measures

We used 10 variables from the fertility domain to estimate the model shown in Figure 1. All of these variables were based on single questions asked in the course of the annual or biennial survey interviews. These questions included what the participant thought was the ideal number of children for a family, how many children the participant wanted altogether, how many children the participant expected to have, when the participant expected to have the first/next child, whether the participant had given birth to a child since the previous interview, and how many total children the participant had borne. Questions that included the terms “want” and “expect” were considered to be good proxy measures of the constructs of desires and intentions, respectively.

An exception to using single questions to construct variables involved the two gender role attitudes variables from 1979 and 1982. Each of these was based on five of the eight attitudinal statements read to the participants, which they were asked to rate on a strongly agree, agree, disagree, or strongly disagree scale. The five statements we selected, which were strongly intercorrelated, included “A woman’s place is in the home, not the office or shop,” “A wife with a family has no time for outside employment,” “Employment of wives leads to more juvenile delinquency,” “It is much better if the man is the achiever outside the home and the woman takes care of the home and family,” and “Women are much happier if they stay home and take care of children.” Responses to these five questions were then combined additively for each year. Cronbach’s coefficient alpha for males and females, respectively, was .75 and .76 in 1979 and .81 and .81 in 1982.

Three additional variables from the education domain were also used in the model estimation. Each of these was based on the same question asked in 1979, 1981, and 1982 and concerned the highest grade the participant thought he/she would actually complete. For more complete information regarding the fertility, gender role, and education questions and question sequencing, see chapter 3 in the NLS Handbook (Center for Human Resource Research 2003).

Table 2 provides descriptive statistics, separately by sex, for all 13 of the above variables, as well as two reciprocal forms of the timing variables. A suffix indicates the year in which each variable was measured. Variables with a 2002 suffix should be interpreted as indicating the respondents’ fertility status as of that date and represent good approximations of the two fertility outcome variables, given that a very small proportion of participants will bear a child (or another child) after 2002. Two variables, the expected and the actual timing of the next child, were coded in years and fractions of years. In order to achieve a more normal distribution for these two variables and to reduce outlier effects, each score was transformed using a reciprocal transformation. Although these reciprocal variables are the ones actually used in the analyses and in all subsequent discussion, we include the original variable for comparison purposes in Table 2. One consequence of using the reciprocal variables was that their correlations with all fertility variables in the model were expected to be positive.

Table 2.

Means and Standard Deviations (SD), Minimum (Min.) and Maximum (Max.) Values, and Numbers of Missing Cases of All Variables Used in the Structural Equation Modeling,^a Separately by Sex

	Males (n = 3,683)					Females (n = 3,883)
Variable	Mean	SD	Min.	Max.	Missing Cases	Mean	SD	Min.	Max.	Missing Cases
Gender Role Attitudes, 1979	2.36	0.54	1.00	4.00	7	2.09	0.56	1.00	4.00	4
Gender Role Attitudes, 1982	2.21	0.54	1.00	4.00	1	1.97	0.55	1.00	4.00	2
Ideal Number of Children, 1979	3.01	1.33	0	10	15	2.95	1.29	0	10	10
Desired Number of Children, 1979	2.58	1.41	0	10	38	2.49	1.48	0	10	16
Ideal Number of Children, 1982	2.72	1.11	0	10	21	2.65	1.07	0	10	46
Desired Number of Children, 1982	2.49	1.32	0	10	31	2.36	1.28	0	10	15
Expected Number of Children, 1982	2.42	1.24	0	10	23	2.33	1.23	0	10	16
Expected Timing of Next Child, 1982	6.21	5.61	0.08	20	167	6.91	6.69	0.08	20	180
Reciprocal, Expected Timing of Next Child, 1982	0.47	1.17	0.05	12	167	0.55	1.41	0.05	12	180
Timing of Next Child, 2002	11.45	9.18	0.00	25	0	10.33	9.34	0.00	25	0
Reciprocal, Timing of Next Child, 2002	0.23	0.29	0	1.00	0	0.29	0.33	0	1.00	0
Final Number of Children, 2002	1.83	1.46	0	10	0	2.05	1.42	0	11	0
Expected Years of Education, 1979	13.78	2.39	3	18	32	13.78	2.32	1	18	30
Expected Years of Education, 1981	13.77	2.41	1	18	56	13.86	2.29	3	18	55
Expected Years of Education, 1982	13.84	2.40	3	18	9	13.92	2.31	3	18	13

^aAlthough not used in the modeling, the nonreciprocal form of the expected and actual timing variables are included in the table for purposes of comparison with the inverse form.

We adopted special coding conventions for certain variables in order to avoid outlier effects. For the four ideal and desired number of children variables, we set all values greater than 10 to 10. For the expected timing of the next child variable, we set all responses greater than “20 years from now” to 20. We adopted additional coding conventions in order to keep participants in the sample when their responses were categorically different from the continuous variable but we believed their position on the continuum could reasonably be approximated. Thus, for the variable representing the expected timing of the next child, we set all those who expected no (or no more) children and the few who were unable to say what their expectations were to 20, indicating the most extreme expectation score possible within our coding scheme. We kept those who were pregnant at the time of the 1982 interview in the sample and coded how soon they expected to give birth. Thus, the minimum of 0.08 for the expected timing variable in Table 2 represents participants who expected to give birth in one month. For the variable representing the actual timing of the next child, we arbitrarily set all those who had not yet had a first/next child in 2002 to 25, and for the reciprocal of that variable, we arbitrarily set those same participants to 0 (i.e., a slightly rounded version of the reciprocal of 25).

Data Analysis

We estimated the hypothesized phenotypic model shown in Figure 1 using the latent variable and the linear structural equation capabilities of LISREL (Joreskog and Sorbom 1996). We analyzed separate covariance matrices for males and females but tested the null hypothesis of no sex differences in both the measurement and the structural equation models. Therefore, we constrained parameter estimates to be equal across the two sex subsamples, relaxing those constraints only when it significantly improved overall model fit, beginning with those having the largest modification indices and progressing downward. Once no further statistically significant improvement in fit could be accomplished by removing constraints, we dropped pathways with nonsignificant coefficients and added new pathways where modification indices suggested that doing so would significantly improve model fit. In order to maximize the number of cases, and because of the proportionally small number of missing cases (see Table 2), the covariance matrices used in the LISREL analysis were based on the pairwise missing option.

Measurement model. An important consideration in testing our SEM was to reduce measurement error wherever possible through the use of latent variables. Because the important variables of ideal and desired number of children were measured only twice, in 1979 and 1982, and because analyses indicated that all four were strongly intercorrelated, we created a single latent variable to represent child-number desires using these four indicators. We also created a latent variable of gender role attitudes using the 1979 and 1982 measures and a latent variable representing motivation within the domain of education based on expected years of education as measured in 1979, 1981, and 1982.

Structural model. The connections hypothesized for the fertility motivational sequence were measured in the 1979–1982 period and predicted the two fertility outcomes, which were measured beginning in 1983 and continuing until the survey of 2002. Because we did not wish to model the relationships between the trait of gender role attitudes and the trait of expected years of education, these two latent variables were treated as exogenous and allowed to correlate freely with each other and to predict the remaining variables.

Testing variants of the base model. We conducted three substudies that addressed the potential effects of sample attrition, whether the age spread in the base sample obscured developmental differences in model fit, and whether previous childbearing affected model fit. The results are discussed in a companion paper (Miller, Rodgers, and Pasta forthcoming). None of the results materially detracted from the validity of the model used here for our current purposes.

RESULTS: PHENOTYPIC MODEL

With 110 degrees of freedom, the chi-square of the base model was 353.08, the root mean square error of approximation (RMSEA) was 0.024, and the p value for a test of close fit (RMSEA < 0.05) was 1.00. These fit indicators indicate a good fit to the data. Most of the poor-fitting parts of the model occurred between indicators for different latent variables and, largely, between indicators that were measured in the same year. These findings indicate both a small within-indicators measurement effect and somewhat larger within-years measurement effect that were not completely accounted for in the overall model.

The Measurement Model

Table 3 presents the standardized parameter estimates and t values for all indicators in each of the overall model’s three latent variables. For all three latent variables, male and female equality constraints remained in place, with the exception of the desired number of children in 1979. That indicator had a significantly larger parameter estimate among females, suggesting they placed a slightly greater emphasis than males on desires relative to ideals in 1979.

Table 3.

The LISREL Measurement Model, Showing Unstandardized Parameter Estimates and t Values for all Indicators of Latent Variables, Separately by Sex

	Males		Females
Latent Variable	Parameter Estimates	t Value	Parameter Estimates	t Value
Ideal/Desired Number of Children
Desired number of children, 1982	1.00		1.00
Ideal number of children, 1982	0.57	61.24	0.57	61.24
Desired number of children, 1979	0.45	24.38	0.58	30.72
Ideal number of children, 1979	0.35	26.47	0.35	26.47
Gender Role Attitudes
Gender role attitudes, 1982	1.00		1.00
Gender role attitudes, 1979	0.92	29.88	0.92	29.88
Expected Education
Highest grade expected, 1982	1.00		1.00
Highest grade expected, 1981	1.01	93.58	1.01	93.58
Highest grade expected, 1979	0.89	81.07	0.89	81.07

The Structural Equation Model

We present the results for the structural equation model in Table 4. We show the standardized parameter estimates and t values for all the variables predicting each outcome variable, starting with the predictors for the final number of children and moving backward to the predictors of the ideal/desired number of children. The strongest predictor in each of the first four equations is shown in bold and is the one hypothesized in Figure 1 as part of the four-step sequence from desired number of children to final number of children.

Table 4.

The LISREL Structural Equation Model, Showing Unstandardized Parameter Estimates and t Values for All Prediction Pathways and R² for Outcome Variables, Separately by Sex

	Males			Females
Outcome Variable	Parameter Estimate	t Value	R2	Parameter Estimate	t Value	R2
Final Number of Children			.29			.31
Timing of next child	2.69	37.01		2.04	32.45
Expected timing of next child	–0.10	–8.62		–0.10	–8.62
Expected number of children	0.14	8.62		0.24	15.52
Gender role attitudes	0.24	4.66		0.24	4.66
Expected education	0.03	2.44		–0.08	–7.05
Timing of Next Child			.17			.21
Expected timing of next child	0.09	36.91		0.09	36.91
Ideal/desired number of children	0.02	5.84		0.02	5.84
Gender role attitudes				0.06	3.84
Expected education	–0.02	–10.68		–0.02	–10.68
Expected Timing of Next Child			.02			.02
Expected number of children	0.10	8.18		0.10	8.18
Expected education	–0.05	–4.90		–0.08	–6.88
Expected Number of Children			.84			.80
Ideal/desired number of children	0.95	18.51		0.95	18.51
Expected education				–0.02	–3.82
Ideal/Desired Number of Children			.02			.02
Gender role attitudes	0.48	8.73		0.48	8.73
Expected education	0.08	8.21		0.08	8.21

There are essentially no sex differences in these primary pathways. Expected education has unanticipated positive effects on ideal/desired number of children and on the final number of children in males. In addition, there were two unanticipated effects of interest involving the motivational antecedents: first, ideal/desired number of children has a direct positive effect on the actual timing of the next child rather than on its expected timing; second, the expected timing of the next child has a direct negative effect on the final number of children. We discuss these unanticipated findings more fully in Miller et al. (forthcoming). The R² values for three of the equations are substantial, but they are relatively small for predicting the expected timing of the next child and the ideal/desired number of children.

DISCUSSION: PHENOTYPIC MODEL

The findings of this study demonstrate appreciable power in the prediction of fertility events from antecedent fertility motivations across the life course of both male and female youths. The predictive power obtains even in the face of the major impact that unplanned pregnancy and subfecundity inevitably have on fertility plans. The predicted events include both the timing of the next child born and the final number of children born, two aspects of childbearing that are causally related in our model and provide a framework linking both the early and late phases of each participant’s fertility career. The major predictive pathways of the hypothesized phenotypic model demonstrate essentially no sex differences. None of the nonhypothesized pathways gives us serious reason to question the suitability of the phenotypic model for biodemographic analysis.

METHODS: BIOMETRIC MODEL

Design

The overall pattern in the phenotypic model is of a left-to-right flow that matches the temporal structure of the model. The one major exception to this generalization is that gender role attitudes and expected years of education are neither hypothesized nor modeled as antecedent, one to the other. This structure suggests that biometric analysis be applied to two separate, six-variable sequences: one beginning with gender role attitudes and extending through to final number of children, and the other beginning with expected years of education and extending to the same end point. Although the overlap between these two models is great, comparing similarities and differences between them will be informative not only with respect to the genetic influences (if any) on the behavioral domain encompassed by fertility desires, expectations, and their outcomes, but also with respect to whether gender role attitudes have any genetic basis that influences the fertility domain (as hypothesized) and whether expected education, and the distinct behavioral domain that it represents, has any genetic basis that influences fertility desires or expectations and their outcomes.

Participants

In order to fit biometrical analyses, it is necessary to have kinship information that allows the investigator to make assumptions about the degree of genetic relatedness between respondents. Although no questions were originally included in the NLSY that directly address that requirement, Rodgers (1996) developed and validated a kinship-linking algorithm that allows kinship relatedness to be calculated for a large majority of the eligible kinship pairs in the NLSY 1979 database.1 Using this algorithm, we identified 2,940 males and females from the entire SEM study sample who belonged to one of five categories of kinship pairs. Those categories, with the numbers of sample individuals in parentheses, are as follows: cousins (74), half siblings (48), ambiguous siblings (382), full siblings (2,400), and twins (36). Ambiguous siblings are those that could not be distinguished between full and half siblings. All twins are of unknown zygosity. Although the numbers of kinship pairs from our sample falling in these categories are disproportionate, they approximately reflect the distribution of such kinship pairs within the population of U.S. households with adolescents in 1979, providing a form of representative validity for use in our analysis. In terms of the sex distribution of kinship pairs, there were 393 male pairs, 370 female pairs, and 707 mixed-sex pairs.

Analyses

We used the Mx software (Neale et al. 2003; Neale and Cardon 1992) to conduct univariate and multivariate analyses of the kinship data, stipulating the raw data option and the full information maximum likelihood estimation procedure. In addition, we used the raw maximum likelihood as implemented in Mx to handle missing values. Mx allows for the estimation of kinship group differences in covariance structure. Using quantitative genetic theory (e.g., Falconer 1979), we constrained latent additive genetic influences on each kinship group’s phenotype to correlate at the following theoretical averages: cousins = 0.125, half siblings = 0.25, ambiguous siblings = 0.375, full siblings = 0.50, and twins = 0.75. The value for twins represented the average of identical twins (= 1.00) and fraternal twins (= 0.50). The value for ambiguous siblings represented the average of half and full siblings.2 In addition, because all related kin in these analyses lived in the same household environments for at least part of their childhood and adolescence, common environmental influences on phenotypic outcomes were estimated in Mx by constraining correlations among latent shared environment sources of variability to be 1.00. Finally, Mx estimated both nonshared sources of phenotypic variability and measurement error together in one category.

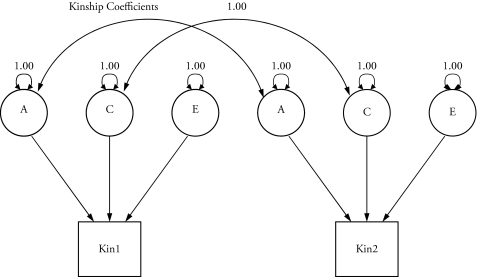
In our initial analyses, we fit standard univariate biometric models to each of the seven variables contained in the phenotypic SEM model reported above. Figure 2 is a graphic representation of an ACE model for a kinship pair in which A indicates the additive genetic source of variance, C indicates the common environmental source of variance, and E indicates the combined unique environmental and measurement error sources of variance (Neale et al. 2003). The two large bidirectional arrows in the figure show that the co variance between the additive genetic component of Kin 1 and Kin 2 is constrained to be equal to the kinship coefficients just discussed, and the covariance between the common environment component of Kin 1 and Kin 2 is constrained to be 1.00 because of the equal home environments assumption. The small circular arrows show that the covariance of each of the three ACE components with itself is set to 1.00 for both kin.

Figure 2.

A Univariate ACE Model

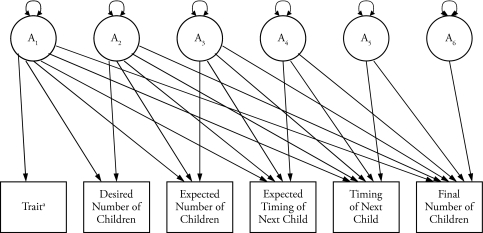
Finally, we fit multivariate Cholesky models to each of the two time-ordered sequences derived from the phenotypic SEM, one beginning with the gender role attitudes variable and the other beginning with the expected years of education variable. Statistically, Cholesky models involve the decomposition of symmetric positive-definite variance-covariance matrices and their transposes. Conceptually, this is equivalent to defining an ordering of the latent variables within the multivariate model. This is especially useful when there is a temporal ordering. In Figure 3, we schematize the genetic part (A) of the two models derived from the phenotypic SEM for one member of a kinship pair only. The two beginning variables are represented in the figure as an unspecified trait. Not schematized are the six bidirectional arrows representing the covariance between the additive genetic components of Kin 1 and Kin 2, as well as the identical schematic for the other kin. Also not schematized are the similarly constructed common environment (C) and unique environment/measurement error (E) parts of these two models. Other notations and the handling of constraints are similar to that described for the univariate model.

Figure 3.

A Six-Variable Multivariate Cholesky Model of the Additive Genetic Component (A) for One Member of a Kinship Pair.

Notes: In addition to the additive genetic component of the Cholesky model, there is also a component reflecting the shared environmental component (C), and another reflecting the nonshared environment/measurement error (E). Across the two members of the kinship pair, the relevant latent variables are connected, and the coefficients are fixed in relation to the source of variance and the kind of kinship pair. For the additive genetic component, full siblings are connected and the coefficient fixed at R = .50, for half-siblings it is fixed at R = .25, etc. For the shared environmental component, those sharing a common family environment are connected, and the associated coefficient is fixed at 1.0.

^aTrait refers either to gender role attitudes or expected education.

Figure 3 represents a decomposition of the additive genetic variance-covariance matrix (A) into six latent variables, A₁ through A₆. The arrows represent the genetic influence that each latent variable has on the six indicator variables from each of the two time-ordered sequences. Because of the structure of the Cholesky model, all of the genetic influences associated with the beginning trait are channeled through A₁, all the remaining influences associated with the desired number of children are channeled through A₂, and so on. In this way, the structure takes into account the causal effects implicit in the time-ordered sequence of the phenotypic SEM. This means that the same network of genes that contributes to any variation in the trait variable may also be said to drive any related variation observed in its five downstream variables; similarly, the same network of genes that contributes to any remaining variation in the desired number of children variable may be said to drive any related variation observed in its four downstream variables, and so on. (For additional discussion of Cholesky modeling, see Rodgers et al. 2007).

RESULTS: BIOMETRIC MODEL

Univariate Results

We fit the univariate ACE model shown in Figure 2 to each of the seven variables used in the phenotypic SEM model. The standardized parameter estimates for h², c², and e² are shown for each of these variables in Table 5. These estimates were standardized by calculating for each variable the proportion of total covariance between kin accounted for by each of the A, C, and E components. Thus, each row sums to 1.00, excepting rounding error. There are major differences in the relative sizes of these three parameters for the seven variables. Heritability (h²) is quite large for the desired number of children and moderately large for the expected number of children and for gender role attitudes, but it is essentially zero for expected education, expected timing of the next child, and actual timing of the next child. The shared family environment effect (c²) is large for expected education, moderate for gender role attitudes, and small to zero for the remaining variables.

Table 5.

Standardized Parameter Estimates for Univariate ACE Model Components of the Seven Variables in the Phenotypic SEM Model

SEM Model Variables	h2	c2	e2
Gender Role Attitudesa	0.34	0.20	0.47
Expected Years of Educationa	0.01	0.54	0.45
Desired Number of Childrena	0.70	0.13	0.16
Expected Number of Children	0.40	0.05	0.55
Expected Timing of Next Child	0.00	0.00	1.00
Timing of Next Child	0.00	0.11	0.89
Final Number of Children	0.16	0.00	0.84

^aThese are latent variables.

In order to determine whether the data had sufficient identifying power to estimate the ACE model components shown in Table 5, we calculated standard errors for all the parameter estimates. Except for two variables, these model components appear to be well estimated. For the expected years of education, the heritability estimate had a large estimated standard error, indicating possibly poor estimation. Similarly, for the expected timing of the next child, both the heritability and common environment estimates had estimated standard errors that were larger than is typical, indicating that the data may not have sufficient power to adequately estimate the components of the ACE model for this variable.

Multivariate Results

In the two multivariate analyses, we constrained all parameters in the A matrix to zero where doing so improved the overall fit of the Cholesky model, using Akaike’s Information Criterion (AIC; Akaike 1987), which indicates an increase of at least 2 in the −2 log likelihood. We left the C and E matrices saturated in order to be conservative and avoid the possibility of forcing the formation of nonzero elements into the A matrix, our primary interest in the analyses reported here, through the use of constraints. Such a step is particularly important with respect to the C matrix, which is potentially confounded with the A matrix because several genetic categories of sibling pairs commonly share a common family environment. The results are shown in Table 6 for the six-variable model beginning with gender role attitudes and in Table 7 for the six-variable model beginning with expected years of education. All the parameter estimates are standardized so that each indicates the proportion of total variation in any given variable listed in the left-hand vertical column accounted for by the latent genetic or environmental variables listed in the column heading. Only the A and C matrix results are shown. The totals for the E matrix coefficients, the great majority of which occur in the diagonal of that matrix, can be inferred by subtracting the total of each variable in matrices A and C from 1.00.

Table 6.

Standardized Parameter Estimates for Cholesky Model Components A and C After Constraining the A Matrix Indicators to Zero If Doing So Improved Model Fit: Gender Role Attitudes Model

SEM Variables	Standardized A Matrix
	A1	A2	A3	A4	A5	A6
Gender Role Attitudes	0.21
Desired Number of Children	––a	0.63
Expected Number of Children	––a	0.38	––a
Expected Timing of Next Child	––a	––a	––a	––a
Timing of Next Child	––a	––a	––a	––a	––a
Final Number of Children	––a	0.02	––a	––a	––a	––a
	Standardized C Matrix
	C1	C2	C3	C4	C5	C6
Gender Role Attitudes	0.26
Desired Number of Children	0.04	0.13
Expected Number of Children	0.01	0.00	0.05
Expected Timing of Next Child	0.01	0.00	0.00	0.01
Timing of Next Child	0.07	0.01	0.02	0.02	0.00
Final Number of Children	0.06	0.00	0.01	0.00	0.00	0.00

^aA dash indicates that the parameter is constrained to 0.

Table 7.

Standardized Parameter Estimates for Cholesky Model Components A and C After Constraining the A Matrix Indicators to Zero If Doing So Improved Model Fit: Expected Years of Education Model

SEM Variables	Standardized A Matrix
	A1	A2	A3	A4	A5	A6
Expected Education	––a
Desired Number of Children	––a	0.65
Expected Number of Children	––a	0.43	––a
Expected Timing of Next Child	––a	––a	––a	––a
Timing of Next Child	––a	0.05	––a	––a	––a
Final Number of Children	––a	0.06	––a	––a	––a	––a
	Standardized C Matrix
	C1	C2	C3	C4	C5	C6
Expected Education	0.55
Desired Number of Children	0.00	0.16
Expected Number of Children	0.00	0.00	0.04
Expected Timing of Next Child	0.01	0.01	0.00	0.01
Timing of Next Child	0.04	0.00	0.00	0.01	0.04
Final Number of Children	0.01	0.00	0.01	0.03	0.00	0.00

^aA dash indicates that the parameter is constrained to 0.

Table 6 shows a somewhat smaller coefficient for the gender role attitudes indicator of A₁ than the univariate h² for gender role attitudes shown in Table 5. There are no other sources of additive genetic variation shown for the A₁ latent variable. The A₂ latent variable has large coefficients associated with child number desires and expectations and a small coefficient associated with the final number of children indicator. The results shown in Table 7 are different in that there is no additive genetic variation shown for the expected years of education indicator of A₁, which is similar to the univariate results for that variable, and none shown for any of the other five A₁ indicators. All the additive genetic variation in the Cholesky model of Table 7 is shown to go through four of the five indicators of A₂, including—in contrast to Table 6—some variation associated with the timing of the next child.

DISCUSSION: BIOMETRIC MODEL

Our univariate results show substantial additive genetic variance in three of the five motivational precursors to fertility included in our phenotypic model and a smaller amount of additive genetic variance in one of the two fertility outcomes. The remaining three variables appear to have little or no such variance, subject to some uncertainty about the power of the data to satisfactorily estimate the two of these that are motivational precursors. These findings confirm earlier research results from other sources (Kohler et al. 2006; Rodgers, Hughes, et al. 2001).

We turn to the multivariate analyses in order to address our primary research questions. Comparing the univariate and multivariate results, we find broadly similar patterns of heritability across the seven variables. However, within that broad similarity are informative differences. One difference involves a reduction in the size of some heritability coefficients in the multivariate analyses compared to the univariate ones, such as the change in the gender role attitudes coefficient from 0.34 to 0.21 and in the final number of children coefficient from 0.16 to 0.06 in the expected education model. These kinds of changes are familiar to those doing behavioral genetic analysis. Two common explanations include (1) better measurement in the multivariate analysis akin to the changes seen in a factor analysis as additional indicators of a latent variable are added to an original single-item factor; and (2) correction for missing data as new kinship pairs not included in the univariate analysis are added in the jump to the multivariate approach. Although these considerations may apply, we suspect that there are also as yet not fully understood explanations having to do with the matrix decomposition procedure itself (Carey 2005).

Second, a more substantive difference observed between the univariate and multivariate findings involves changes that result from the linear, time-ordered restrictions imposed by the Cholesky modeling procedure, thereby allowing causal inferences. There are two such differences in our results: (1) the presence of heritability for the timing of the next child in the expected education model; and (2) the considerably reduced heritability of the final number of children in the gender role attitudes model. These two differences, together with the overall patterns both within and across our two multivariate models, are the most informative with respect to the three questions we posed in the introduction.

Our discussion of these questions begins with an examination of Table 7. Expected education, as represented by the latent variable A₁, has no genetic variance at all. All the additive genetic variance in the model is associated with the desired number of children variable and the other variables situated downstream from it. The lack of additive genetic variance for educational intentions is somewhat surprising because Kohler and Rodgers (2003) found an overlap between genetic variance in education and fertility outcomes. Perhaps it is having education, and not the intentions to have it, that accounts for the difference between the two studies. Almost two-thirds of the desired number of children’s variance is accounted for by genetic influence, a remarkably large proportion. The first variable downstream from this desires variable is the corresponding intentions variable. Not only do these intentions have a large proportion of additive genetic variance, but because all of the values in the A₃ column are 0, this variance is completely shared with the desires variable. This means that there is no additive genetic influence on fertility intentions above and beyond the desires that drive them. Thus, there is no additive genetic variance related to the decision-making, planning, and commitment parts of intentions that makes them distinct from desires.

Timing intentions, like educational intentions but unlike number intentions, have no additive genetic variance. This finding can be explained in two ways. First, the results for our phenotypic model (see Table 4) indicate that number intentions, the precursor immediately upstream to timing intentions, have very little effect on timing intentions. As a result, relatively little of the additive genetic variance of the number intentions variable gets passed through to timing intentions. Second, and more fundamentally, timing intentions depend to a large degree on situational factors in the individual’s and couple’s life (Miller and Pasta 1994), leading us to infer that practical matters such as educational pursuits, employment, income, and health, together with vagaries of the marriage market, all tend to overwhelm any genetic influence on timing intentions that may get passed through from timing desires (which are unmeasured in the NLSY79).

The next two downstream variables in the A₂ column of Table 7 are both fertility outcomes. Why does the actual timing of the next child have a statistically significant level of additive genetic variance when the expected timing does not? The likely explanation lies in our phenotypic model results (see Table 4), which shows that child-number desires have a direct effect on the timing of the next child, thereby enabling that motivational precursor to pass through some of its additive genetic variance to the fertility timing outcome. If we had only the univariate results, we would have no clue that the timing of the next child had any genetic variance associated with it. The variance of child-number desires is also passed through to the fertility number outcome, although in this case (as Table 4 again shows) indirectly through child-number intentions.

The overall conclusion from Table 7 is that there is one source of additive genetic variance that affects the desired number of children of our sample, which is then passed downstream to affect both fertility timing and number outcomes. Although we believe that this part of the story is by and large correct, the findings shown in Table 6 suggest a somewhat more nuanced, although also more inferential, interpretation. The Table 6 model differs from that shown in Table 7 in two major respects. First, gender role attitudes, unlike expected education, are shown to have a modest amount of additive genetic variance. Second, the coefficients for the two number-motivational precursors and the two fertility outcomes are all reduced, only slightly in the case of the precursors but substantially in the case of the outcomes, even to the point of nonsignificance for the timing outcome variable. Table 6 suggests that there is a second source of additive genetic variance affecting gender role attitudes, one that is separate from the source seen in Table 7 affecting child-number desires and three of its downstream variables. This second source appears to have some association with downstream variables, large enough at least to reduce the size of the coefficients representing the first source but not large enough to become significant in the A₁ column of the model. In other words, including gender role attitudes in the model acts in a way that is akin to a partialing out of some of the effects associated with the first source.

In the theoretical framework, we argued that a component of gender role attitudes was motivation for childbearing and that the effect of this component could be identified when other lifestyle-associated components, such as motivation or desires for education and—especially for women—occupational pursuits, were separately taken into account in the model. We speculate here that the second source of additive genetic variance affecting gender role attitudes may represent that childbearing motivation component. This would account for the impact that the presence of gender role attitudes in the Table 6 model has on the outcome variables. The absence of any significant effects of their own on downstream variables in the model suggests that gender role attitudes may represent a diluted version of childbearing motivations.

Regarding the question of how much of the relatively large genetic influence shown in Tables 6 and 7 to affect child-number desires is passed through to the fertility outcomes, several issues must be kept in mind. First, the multivariate models are actually more restricted than the univariate models because in the former, we are forcing all the h² variation to come through a few limited motivational antecedents. It is likely that only a fraction of the fertility outcomes’ h² variation is shared with these measures and that other fractions are shared with unmeasured fertility motivations.

Second, a fertility outcome, such as number of children, has many different sources of genetic influence operating on it other than those associated with precursor fertility motivations. Some sources act through biological variables, such as age at menarche, age at menopause, and fecundability during the ages between menarche and menopause (Kirk et al. 2001; Rodgers, Kohler, and Christensen 2002). Other sources act through behaviors that affect exposure to the risk of childbearing, such as sexual behavior, contraceptive behavior, and marital union behavior (Miller and Pasta 2000; Rodgers, Rowe, and Buster 1999; Trumbetta, Markowitz, and Gottesman 2007). And yet other sources act through behaviors that compete with childbearing and large family size, such as educational and occupational pursuits (Kohler and Rodgers 2003; Rodgers et al. 2007).

Third, the influence of precursor fertility motivations on outcomes can shift over time within any given society. Udry (1996) argued that where culture maintains a high normative control over reproduction, as in natural-fertility regimes typical of preindustrial, agrarian societies, there is relatively little opportunity for individuals to express motivationally based genetic variance in their fertility. However, where those normative controls are relaxed and individuals have some choice over their fertility, as in most modern, contracepting societies, genetic influence on fertility related to its motivation precursors can be expressed. Indeed, in a twin study of Danish fertility over a 100-year period, Kohler, Rodgers, and Christensen (1999) found that the amount of genetic influence on fertility rose during each of two distinct 20-year periods of fertility transition and then dampened back down over time. Further, these kinds of changes are not confined to historic periods. In another Danish twin study of the level of early fertility among females, Kohler, Rodgers, and Christensen (2002) showed that genetic effects on that fertility outcome went from zero in the 1945–1952 birth cohort to over 50% in the 1961–1968 birth cohort. Thus the expression of genetic variance in motivational precursors on fertility outcomes must be looked at in terms of what level of expression is possible in the normative context of the population under consideration.

CONCLUSIONS

The behavioral genetic analyses of the two six-variable time-ordered sequences taken from our phenotypic model of fertility motivations and their outcomes provide evidence that one or more genes and their network have additive effects on the number of children desired and that these effects are passed downstream in the sequence to the number of children expected, the timing of the next child, and the final number of children born. It also provides evidence that one or more other genes and their network may have additive effects on gender role attitudes and that some of this effect may be passed downstream to the child-timing and child-number outcomes. The behavioral genetic analyses also indicate that there are no genetic sources of variation associated with either educational or child-timing expectations. Because the biometric findings indicate that all the genetic variation associated with child-number intentions is passed through from child-number desires, the overall conclusion is that intentions are not associated with genetic influences other than those associated with their domain-specific precursor desires. Finally, the magnitude of the genetic influence passed through from the fertility motivation precursors to the fertility outcomes appears appreciable but must be considered in light of all the other genetic effects that may be acting to affect fertility outcomes.