Fetuin-A Is a Mineral Carrier Protein: Small Angle Neutron Scattering Provides New Insight on Fetuin-A Controlled Calcification Inhibition

Abstract

Clinical studies and animal experiments have shown that the serum protein fetuin-A is a highly effective inhibitor of soft tissue calcification. This inhibition mechanism was elucidated on the basis of an in vitro fetuin-A-mineral model system. In a previous study, we found that in a two-stage process ∼100-nm sized calciprotein particles (CPPs) were formed whose final stage was stabilized by a compact outer fetuin-A monolayer against further growth. Quantitative small-angle neutron scattering data analysis revealed that even at a fetuin-A concentration close to the stability limit, only approximately one-half of the mineral ions and only 5% of the fetuin-A were contained in the CPPs. To uncover the interplay of the remaining supersaturated mineral ion fraction and of the 95% non-CPP fetuin-A, we explored the fetuin-A monomer fraction in solution by contrast variation small-angle neutron scattering. Our results suggest that the mineral ions coalesce to subnanometer-sized clusters, reminiscent of Posner clusters, which are stabilized by fetuin-A monomers. Hence, our experiments revealed a second mechanism of long-term mineral ion stabilization by the fetuin-A that is complementary to the formation of CPPs.

Introduction

According to a popular paradigm in biomineralization, mineral growth is governed by matching topologies at the protein-mineral interface. This effect may result in particular mineral morphologies or pronounced growth inhibition. Soluble inhibitors in the extracellular space either work by crystal poisoning like pyrophosphates which occupy phosphate positions in the lattice and thus interfere with a regular crystal growth (1), by mineral ion complexation like serum albumin (2), or by shielding crystals from further growth. Regarding the latter principle, a diffusion barrier around the mineral core is formed by adsorption of highly mineral specific proteins. For example, Tamm-Horsfall protein and osteopontin inhibit calcium oxalate crystal growth in the renal system of mammals (3). Other proteins inhibit ice-crystal growth in arctic fish (4). Likewise, the plasma protein fetuin-A/α₂ HS-glycoprotein inhibits calcium-phosphate deposition in the soft tissue of mammals. This was demonstrated in fetuin-A knockout mice (5) and subsequently shown in clinical studies for patients with low fetuin-A serum level (6).

Despite the enormous progress in biomineralization research over the last decade, some basic principles of calcification inhibition and serum protein guided mineralization remained enigmatic. In previous investigations, a transiently stable colloidal fetuin-A-mineral composite has been identified, denoted as calciprotein particle (CPP) or fetuin-mineral complex. Using a broad range from biochemical to physical methods like small-angle scattering of neutrons (SANS) and x-rays (SAXS), dynamic light scattering, and transmission electron microscopy (TEM), two CPP populations have been detected time-dependently reflecting a two-step aging process (7–11). Primary CPPs were spheres with a diameter of roughly 500 Å. After a few hours at room temperature, a transformation to elongated particles of approximately twice the initial size was observed (7,9,10). SANS revealed that the long-term stability of the secondary CPPs was due to a dense fetuin-A monolayer covering the mineral core (9).

Quantitative SANS analysis revealed that CPPs contained only 3–5% of the total (2.5 mg/mL, ∼47 μM) fetuin-A content and approximately one-half of the total mineral content (10 mM CaCl₂, 6 mM Na₂HPO₄). The CPPs consisted of ∼25% fetuin-A in volume fraction while the remaining volume was filled with calcium phosphate (9).

This result prompted two observations:

• 1.If the long-term inhibition of mineral deposition was based solely on CPP formation, ∼2.4 μM fetuin-A (5% of 47 μM) would be sufficient for a long-term stability of the mineral solution. This however, was in contrast to other experiments proving that at least 7 μM fetuin-A was necessary for long-term stability ((12) and A. Heiss, V. Pipich, W. Jahnen-Dechent, and D. Schwahn, unpublished).
• 2.The remaining non-CPP mineral ion fraction (roughly 50%) would be still far beyond the solubility limit (a supersaturation of σ ≈ 32 is estimated in the next section) and thus should result in mineral sedimentation (9,13). A further reduction of mineral ion supersaturation by fetuin-A sequestration of calcium ions cannot contribute to stabilization on theoretical grounds: Suzuki et al. (14) determined that one fetuin-A molecule could bind up to six calcium ions, i.e., fetuin-A monomers could only bind up [∼95% of 47 μM fetuin-A] × [6 calcium binding sites] ≈ 0.27 mM calcium ions. Hence, according to this approximation, a reduction of ∼5 mM Ca²⁺ (non-CPP calcium) by ∼0.27 mM would barely have an impact on the supersaturation.

After these considerations, we concluded that an additional mechanism to inhibit calcium-phosphate deposition must exist. This prompted the present SANS study focusing on the fraction of monomeric fetuin-A (95%) at high Q values. In detail, we determined the scattering-length density of the bovine fetuin-A (BF) molecules during CPP ripening and analyzed their scattering relying on the underlying scattering laws. The variation of scattering contrast is based on changes in the D₂O/H₂O ratio in the mineralization mix. Our study revealed previously unnoticed small-yet-significant changes in the scattering of the free BF molecules (also in comparison to native BF), suggesting that the BF is associated with tiny calcium-phosphate clusters, most likely in the form of 7–9 Å sized Posner clusters Ca₉(PO₄)_6, which have been proposed as mineralization precursors and building blocks of amorphous calcium phosphate (15,16).

Further clarification of the mechanisms of BF-mediated mineralization inhibition may help to develop diagnostics and therapeutic regimens against ectopic calcification in renal disease patients. Moreover, it may provide new strategies for the application of biomineralization in bionanotechnology.

Materials and Methods

The in vitro model system

The methods of protein purification and sample preparation have been described previously (7,9). In short, bovine fetuin-A (BF; Sigma, St. Louis, MO) was purified by gel permeation chromatography in Tris-buffered saline. Next, the isolated monomer was concentrated by ultrafiltration using 30-kDa cutoff filter cartridges (Centriprep; Millipore, Billerica, MA). The concentration was assessed by ultraviolet spectrometry relying on an extinction coefficient of 5.3 (17). All stock solutions used were filtered through a 0.2-μm membrane.

Five samples S0–S4 were freshly prepared according to the parameters in Table 1. The saline buffer control S0 was used for a correct determination of the neutron scattering background. By assessing the change in scattering contrast of the calcium-free sample S1 and calcium-containing sample S2, the calcium ion binding capacity of the protein was quantified. In samples S3 and S4, the mineralization process was initiated by CaCl₂ addition and immediate vigorous vortexing. A similar high-concentration BF sample like S3 had already been studied previously by SANS, but not in the high Q range (9). Sample S4 is a low-concentration BF sample close to the stability limit of the mineralization mix (12).

Table 1.

Samples of the in vitro model system

Sample	Bovine BF [mg/mL]	10 mM CaCl2	6 mM Na2HPO4	50 mM Tris pH 7.4, 140 mM NaCl
S0	−	−	−	+
S1	2.5	−	−	+
S2	2.5	+	−	+
S3	2.5	+	+	+
S4	0.5	+	+	+

All samples contained a saline buffer and were measured at room temperature.

The supersaturation σ can be written as σ = ln(I/K_sp) with the ion product

$$I=a{\left(\mathrm{C}{\mathrm{a}}^{2+}\right)}^{5}a{\left(\mathrm{P}{\mathrm{O}}_4^{3-}\right)}^{3}a\left(\mathrm{O}{\mathrm{H}}^{-}\right),$$

the ion activity a = γc and the activity coefficients at physiologic ionic strength γ(Ca²⁺) = 0.36, γ(PO₄³⁻) = 0.06, and γ(OH⁻) = 0.72 (18).

The solubility product K_sp of hydroxyapatite is K_sp(Ca₅(PO₄)₃OH) = 2.35 × 10⁻⁵⁹ M⁹ (19). At pH 7.4, the phosphate concentration is

$$\sim 4.5\times {10}^{-8}\mathrm{M}\mathrm{and}\mathrm{pOH=14-7}\mathrm{.4=6}\mathrm{.6}\mathrm{.}$$

Hence, the ion product for S3 and S4 is

$$I={\left(0.36\times 0.01\mathrm{M}\right)}^5,{\left(0.06\times 4.5\times {10}^{-8}\mathrm{M}\right)}^3,$$

$$\left(0.72\times {10}^{-6.6}\right)=2.15\times {10}^{-45},$$

resulting in a supersaturation of σ ≈ 32.

Small-angle neutron scattering experiments

Probing with neutrons is a popular technique in materials science because of the inherent wave property, neutral charge, and interaction with the atomic nuclei. Neutrons deeply penetrate the material, and their element-dependent scattering, determined by the scattering length, even allows a discrimination of isotopes. The latter property is relevant for this article, because the coherent scattering-length densities of an aqueous solution can be adjusted over a large range by H₂O-D₂O exchange. Contrast variation SANS is a nondestructive method used to probe particle size and composition—making it a valuable tool for monitoring time-dependent inorganic-organic interactions like biomineralization processes.

All neutron scattering experiments were performed at the KWS2 diffractometer of the FRM II research reactor located in Garching near Munich, Germany (http://www.jcns.info/jcns_instruments). The sample/detector distances were varied from 8 to 2 m for 7 Å neutrons to overlap the scattering vector Q interval from 10⁻² to 0.3 Å⁻¹. Furthermore, by using 8 m sample/detector distance and 19 Å neutrons, the Q range could be extended to ∼4 × 10⁻³ Å⁻¹. The neutron wave lengths were adjusted with 20% half-width of maximum.

A separation of coherent, i.e., Q-dependent scattering resulting from particles such as proteins and minerals, from the incoherent scattering (constant over Q) was crucial for this study. The data were corrected for background scattering, sensitivity of the individual detector channels, and finally evaluated in absolute scale by calibration with a secondary standard. The scattering of the saline buffer was analyzed in absolute units and then used for corrections of the incoherent background.

Scattering theory

We determined the intensity of the scattered neutrons as a function of the wave vector Q, which according to

$$Q=\left(4\pi /\lambda \right)\sin \left(\delta /2\right)$$

is proportional to the scattering angle δ and inversely proportional to the wavelength λ. The scattered intensity is given by the macroscopic cross-section dΣ/dΩ(Q) in units of cm⁻¹. The scattering law can be expressed as (21)

$$\frac{d\Sigma }{d\Omega }\left(Q\right)=\frac{d\Sigma }{d\Omega }\left(0\right)\cdot F\left(Q\right).$$ (1)

The scattering at Q = 0,

$$\frac{d\Sigma }{d\Omega }\left(0\right)=\Phi V\Delta {\rho }^2,$$ (2)

depends on the parameters Φ, V, and Δρ² representing the particle volume fraction, its volume, and the scattering contrast between particle and solvent, respectively. The analysis of the scattering experiment relies on a sufficiently good scattering contrast. In fact, Eq. 1 neglects interfering effects from other particles. However, these can be safely neglected in our experiment, because the volume fraction of the calcium-phosphate particles is ∼10⁻⁴. The form factor F(Q) describes size and shape of the particles. Theoretical expressions are known for relatively simple forms. Approximate expressions of F(Q) exist within the limits of small and large Q with respect to the inverse size of the particles. For small Q values, i.e., < 1/R_g, Guinier's approximation

$$F\left(Q\right)=\text{exp}\left(-R_g^2{Q}^2/3\right)$$ (3)

is valid, and the radius of gyration R_g can be derived.

For ellipsoidal particles,

$$R_g=\sqrt{\left(a^2+b^2+c^2\right)/5}$$

is valid, whereas, for spherical particles (R = a=b=c), the equation is simply

$$R_g=\sqrt{3/5}R.$$

In the high Q range, i.e., >1/R_g, a power law according to

$$\frac{d\Sigma }{d\Omega }\left(Q\right)=P_{\alpha }{Q}^{-\alpha }$$ (4)

is often observed. The exponent α is equal to 4, 3, 2, or 1 for compact three-dimensional particles, porous three-dimensional particles, plates, and rods, respectively. In this investigation, the scattering from the mineral colloid showed an exponent of −4, according to Porod's law indicating compact particles with sharp interfaces. The amplitude

$$P_4=2\pi S_t\Delta {\rho }^2$$

is proportional to the total particle surface S_t per unit volume. The approximate scattering laws at low and large Q are both combined in Beaucage's form

$$\frac{d\Sigma }{d\Omega }\left(Q\right)=\frac{d\Sigma }{d\Omega }\left(0\right)\text{exp}\left(-u^2/3\right)+P_{\alpha }{\left[{\left(\text{erf}\left(u/\sqrt{6}\right)\right)}^3/Q\right]}^{\alpha },$$ (5)

with u = R_gQ (22). The erf(u) accounts for the validity of the underlying approximations in their Q ranges. Another important parameter is the so-called integrated intensity Q², which, according to

$$Q^2={\int }_0^{\mathrm{\infty }}{Q}^{2}d\Sigma /d\Omega \left(Q\right)dQ=2{\pi }^2\Phi \left(1-\Phi \right)\Delta {\rho }^2,$$ (6)

allows an assessment of the volume fraction Φ of the scattering particles. The scattering contrast Δρ = (ρ–ρ_S) is given by the difference in the coherent scattering-length density ρ of the solute and the solvent ρ_S. The coherent scattering-length density of a colloidal particle or a molecule is given by

$$\rho =\sum b{}_i/V_{Comp}$$

with the coherent scattering length b_i of the element i and the volume of the corresponding atomic complex V_Comp. The values of b are tabulated in Sears (23).

Ultrafiltration

Ultrafiltration was employed to assess the concentrations of non-CPP fetuin-A molecules and of ionized calcium. After incubation at room temperature for 1 h (i.e., while primary CPP exists) or overnight (secondary CPP), the samples were ultrafiltrated by centrifugal force. The 3-kDa molecular mass cutoff (MMCO) unit (Millipore, Billerica, MA) was centrifuged at 12,000 g whereas the 300 kDa MMCO unit (Sartorius, Göttingen, Germany) was centrifuged at 2000 g. The total calcium ion concentration in the filtrates was assessed by a colorimetric cresolphtalein-dye based assay (Randox, Crumlin, County Antrim, UK).

The filtrates were diluted fourfold (no differences were observed between dilutions in water and 1% HCl) to match the calcium concentration to the range of the calibration curve. Next, 500 μL reaction-buffer and 500 μL dye solution were added to 25 μL of the diluted filtrate. After 10 min, the optical density at 570 nm was measured. Likewise, a colorimetric Bradford-like assay (Carl Roth, Karlsruhe-Rheinhafen, Germany) was used for protein quantification against a BF standard in the filtrate. The absorption was measured at 590 and 450 nm.

Experimental Results

SANS contrast variation on colloidal biocomposites

Fig. 1 depicts a typical SANS scattering pattern of a sample containing CPPs and BF monomers (S3, see Table 1) with a bimodal particle size distribution. Comparably large particles like the CPPs scatter at low values of the scattering vector Q (small scattering angles) whereas smaller particles like fetuin-A molecules scatter at high Q values (large scattering angles).

Figure 1.

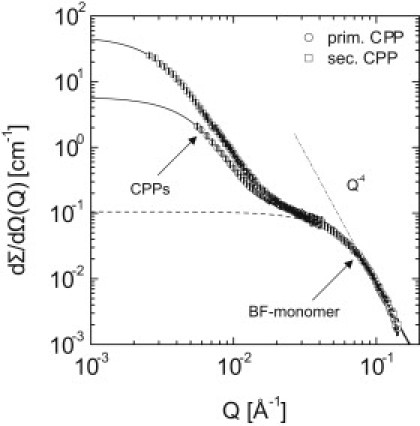
SANS patterns, represented as scattered intensity dΣ/dΩ versus scattering vector Q, of CPP ripening in D₂O (2.5 mg/mL bovine BF, 10 mM CaCl₂, and 6 mM PO₄ in D₂O). The patterns show a bimodal shape reflecting CPP scattering at low Q values and BF scattering at high Q values. Initial CPPs (i.e., primary CPPs, open circles) were only transiently stable. Extensive structural rearrangements lead to a second transiently stable state (secondary CPPs, open squares).

While previous investigation by SANS contrast variation explored the CPPs scattering at low Q values, we focused here on the high Q range where the scattering of the bovine fetuin-A (BF) monomer is detected, which accounts for almost 95% of the total BF concentration in the sample (i.e., roughly 5% of the total BF were bound to the CPPs). To this end, we determined the scattering-length density of the BF monomers during CPP mineralization and analyzed their scattering according to the underlying scattering laws. The variation of scattering contrast is based on changes in the D₂O/H₂O ratio in the mineralization mix.

In Fig. 2, the coherent scattering length densities ρ of solvent and sample components are plotted against the D₂O volume fraction. Because of the very different scattering lengths of hydrogen (b_H = −3.7423 × 10⁻¹³ cm) and deuterium (b_D = 6.674 × 10⁻¹³ cm), the resulting scattering-length density of the solvent strongly correlates with the D₂O content, i.e., from pure H₂O with −0.561 × 10¹⁰ cm⁻² to pure D₂O with 6.39 × 10¹⁰ cm⁻² (solid blue line). According to Eq. 2, a component in the solution becomes transparent to neutrons when Δρ = 0. Thus, SANS contrast variation is a convenient method to determine the mean scattering-length density and also the internal structure of colloidal particles (24). The coherent scattering-length density of BF (sample S1) is depicted as solid circles. The corresponding regression line shows a shallow slope (for more details, see also Table S1 in the Supporting Material). Proteins are generally characterized by quite similar scattering length densities that match the scattering of water at ∼44% D₂O (25). We found that the scattering ρ_BF of S1 is matched at Φ_D2O = 0.447 (see also Table S3). The scattering-length density of two relevant calcium-phosphate mineral polymorphs was evaluated from the chemical structure and molar volume, as depicted as green dashed lines (see also Table S1). The contrast of the mineral phase was matched at 74% D₂O aqueous solution.

Figure 2.

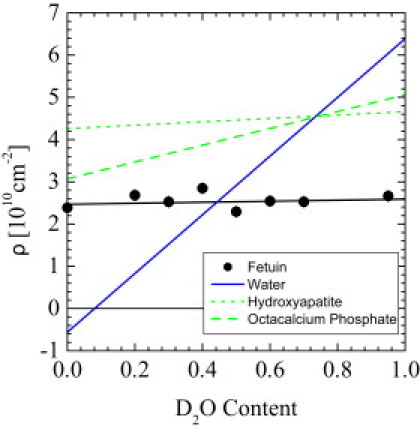
Coherent scattering-length density of water, bovine fetuin-A, and the two putative polymorphs of calcium phosphate. Fetuin-A is matched at Φ_D2O = 0.448.

Calcium-binding capacity of fetuin-A

To assess the calcium ion binding capacity of BF, two BF-containing (2.5 mg/mL) samples were compared. Sample S1 was calcium-free whereas S2 contained 10 mM CaCl₂. SANS was measured in 100% H₂O and the resulting scattering patterns are depicted in Fig. 3 A. Despite the weak BF scattering, which is only 3–10% above the intensity of the buffer sample (S0), a slight increase in scattering intensity was observed for the CaCl₂-containing sample. From the fitted Guinier law, depicted as solid lines, a radius of gyration of 27 Å for S1 and of 29 Å for S2 was derived (Eq. 3, Table S3). In Fig. 3 B, the extrapolated scattering cross section at Q = 0 is plotted against the D₂O content. Next, the average scattering-length density was assessed by fitting the scattering cross section by a parabola, according to Eq. 2 (solid lines). The scattering minima of the calcium-free (S1) and the calcium-supplemented BF sample (S2) were at 45% and 46% D₂O content, respectively (see Fig. 3 B for the exact values including errors). This slightly enhanced coherent scattering-length density in combination with an increased intensity indicated binding of the calcium cations to the acidic BF.

Figure 3.

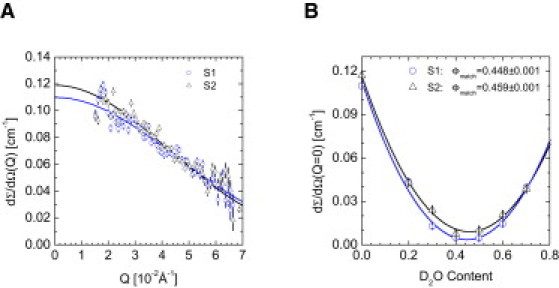
The calcium binding capacity of BF. Contrast variation experiment of the calcium free sample S1 and the calcium supplemented sample S2. (A) Scattering was measured in H₂O. (B) Extrapolated scattering intensity at Q = 0 as a function of the D₂O content. The minimum indicates the point where the scattering length densities of BF and solvent are matched.

Calcium-phosphate binding capacity of fetuin-A

Samples identical to S3 have been investigated previously by SANS, albeit at lower Q values (9). Sample S4 contained a five-times lower BF concentration compared to S3, i.e., 0.5 mg/mL (Table 1), which was close to the stability limit of the system. Nevertheless, both samples were free of mineral deposition for at least two days (9,12). The averaged scattering cross sections plotted versus the D₂O content of S4 and S3 in both CPP stages are depicted in Fig. 4, A and B. After subtraction of the scattering arising from the buffer sample S0 (Fig. S1 in the Supporting Material), the scattering was averaged within the Q interval from 0.03 to 0.06 Å⁻¹. In Fig. S3, A and B, the upturn below Q = 0.03 Å⁻¹ is due to an increasingly dominant scattering from the CPPs.

Figure 4.

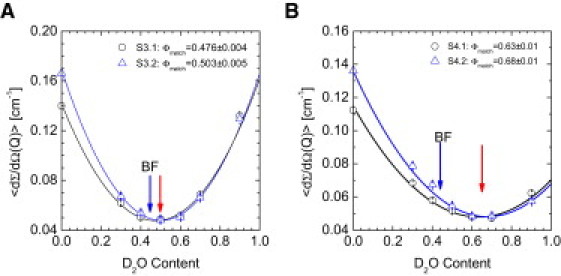
CPM detection by SANS contrast variation. Averaged scattering cross section of the samples S3 (A) and S4 (B) in the presence of primary or secondary CPPs (Fig. S3, A and B), respectively, versus D₂O content. The abbreviations S3.1/S4.1 and S3.2/S4.2 represent the stages of primary and secondary CPPs, respectively. The cross sections were averaged within the interval 0.03 < Q [Å⁻¹] < 0.06. Below Q = 0.03 Å⁻¹, scattering from the CPPs becomes relevant. Scattering from the corresponding buffer solutions was subtracted. (Blue arrow) Minimum in the fitted mean scattering-length density of BF in buffer (S1). (Red arrow) Minimum of the BF monomers in the calcium phosphate containing samples S3 and S4. The shift suggested an uptake of mineral clusters by the BF molecules. Moreover, the higher scattering-length density of S4 reflected a markedly higher total mineral load. Mineral-laden BF molecules are denoted here as CPMs.

The averaged intensity turned out to be the most reliable parameter, inasmuch as it was insensitive to scattering from other components and no data fitting was involved. The corresponding minima of the samples S3 and S4 during the first and second CPP stage (marked by the red arrows in Fig. 4) were found at ∼50 and 65% D₂O concentration, respectively. Hence, both samples showed an appreciably larger scattering contrast than pure and Ca²⁺-loaded BF (Fig. 3 and blue arrows in Fig. 4), indicating that BF monomers were, in fact, loaded with calcium phosphate. Furthermore, we observed that lowering the BF concentration resulted in an increasing fraction of BF-associated mineral. Likewise, the transformation from primary to secondary CPPs was accompanied by a slight increase in the mineral load of the BF molecules. In analogy to the considerably larger calcium-phosphate-fetuin-A colloids called calciprotein particles (CPP), we termed the monomeric, mineral-laden BF molecules “calciprotein monomers” (CPM).

Ultrafiltration analysis

We scrutinized the validity of our SANS results by subjecting the samples to another quantitative analysis. Ultrafiltration proved to be a convenient method for the separation of colloidal protein-mineral aggregates (8). Our approach relied on membranes with 300- and 3-kDa MMCOs, respectively, to separate CPPs, BF monomers and mineral ions, and subsequent quantitative analysis of the filtrates. The concentration of BF and calcium ions in the filtrates, i.e., not trapped in CPPs, was measured in three independent experiments (two experiments for sample S4). Table 2 lists the concentrations of BF and calcium ions demonstrating that:

• 1.During the first CPP stage, the 300-kDa MMCO filtrate contained 78 ± 11% of the initial 1 mg/mL BF and 63 ± 8% when the initial BF concentration was 0.35 mg/mL. In both cases, the filtrate contained roughly 65% of the initial calcium ions. Unlike the 3-kDa MMCO filtrates (see below), the 300-kDa MMCO filtrates were stable for hours despite nominal supersaturation. Irrespective of the initial BF concentration (samples S3 and S4), the 3-kDa MMCO filtrates showed a comparably high calcium concentration like the 300-kDa filtrates, but no BF as expected. Within a few minutes, increasing turbidity in the 3-kDa filtrate indicated the formation of mineral aggregates and subsequent sedimentation.
• 2.The transformation to secondary CPPs had no major affect on the filterable BF fraction, whereas generally a reduction of calcium ions by roughly 50% was detected in all samples, indicating an increase in the CPP mineral fraction.

Table 2.

Photometric quantification in the filtrate after ultrafiltration of samples after an incubation time of 1 and 12 h during stage 1 and 2 of the CPPs, respectively

Cutoff		300 kDa		3 kDa
Centrifugation		2000 g, 4°C,Flow direction toward the top		12,000 g, 4°C,Flow direction toward the bottom
CPP		−		−
BF/CPM		+		−
Mineral ions/clusters		+		+
Initial concentration
BF [mg/mL]		1	0.35	2.5 (S3)	0.5 (S4)
Ca2+ [mM]		10	10	10	10
Filtrate analysis after incubation
t ≈ 1 h	BF [mg/mL]	0.78 ± 0.11	0.22 ± 0.05	−	−
	Ca2+ [mM]	6.3 ± 0.6	6.3 ± 1.0	6.5 ± 0.6	7.0 ± 0.3
t ≈ 12 h	BF [mg/mL]	0.83 ± 0.10	0.16 ± 0.02	−	−
	Ca2+ [mM]	2.9 ± 0.3	2.8 ± 0.1	3.5 ± 0.8	3.2 ± 0.4

Samples were ultrafiltrated by centrifugation with 300-kDa (column 2 and 3) and 3-kDa (column 4 and 5) MMCO membranes. Primary and secondary particles are formed after 1 and 12 h of incubation time, respectively. The radius of a primary CPP is at least ∼10 times larger than the radius of a fetuin-A molecule (10). Therefore a 300-kDa membrane retains any CPPs while the ions and BF molecules pass. Only ions and tiny aggregates can pass a 3-kDa membrane while CPPs and BF molecules are retained. Concentrations of the samples: 10 mM CaCl₂, 6 mM NaH₂PO₄, 50 mM Tris pH 7.4, 140 mM NaCl, and 0.35, 0.5, 1, or 2.5 mg/mL BF.

SANS data analysis

Calcium binding versus calcium-phosphate binding capacity of fetuin-A

The parameters derived from contrast variation SANS with respect to the BF monomers are compiled in Table S3. The first row lists the D₂O concentrations at the scattering minima. At these points, the known mean scattering-length density of the solvent matches the mean coherent scattering-length density ρ_CPM of the calciprotein monomers (Eq. 2). In rows 2 and 3, the corresponding scattering length densities ρ of the CPMs and BF (Table S1) are listed. Rows 4–7 list structural parameters derived from the scattering patterns in Fig. S3, A and B. The radius of gyration R_g of BF ranged from 27 to 29 Å, confirming previous studies (7,9). Regarding the scattering at Q = 0, dΣ/dΩ(0), the amplitudes P₄ according to Porod's law and the second moment Q₂ of S3 and S4 differed by nearly one order of magnitude. This is mainly due to the fivefold difference in BF concentration as well as the lower CPM scattering contrast in 90% D₂O. Due to the higher CPM mineral fraction, the scattering-length density ρ_CPM was larger in sample S4 than in S3. Errors were estimated from the statistical errors of the SANS data. These errors were considered in the nonlinear fits.

The calcium-binding capacity of BF was assessed by comparing the scattering minima of the Ca²⁺ free reference S1 and the Ca²⁺-supplemented sample S2 (Fig. 3). A slight shift of the scattering minimum in S2 was observed, indicating the binding of Ca²⁺ ions to the BF monomers. The Ca²⁺ binding was quantified by assessing BF volume changes based on the known parameters dΣ/dΩ(0) and the corresponding scattering-length density ρ (Table S3). Because the number density n = Φ/V of BF is known from the initial weight, Eq. 2 was rewritten as

$$d\Sigma /d\Omega \left(0\right)=n{V}^2\Delta {\rho }^2.$$

Ca²⁺ addition (S1 vs. S2) lead to increase in the molecular volume, V, of BF by 1 ± 0.5% corresponding to (15 ± 7) Ca²⁺ ions per BF molecule (see also Table S1). This value is compatible with the amount of six Ca²⁺ ions binding to one BF molecule determined by equilibrium dialysis (14).

The parameters describing the calcium-phosphate binding capacity of the BF monomers in sample S3 and S4 are compiled in Table 3. These data were derived from the data in Table S3. The first two rows list the volume fractions based on the initial weight of BF and calcium phosphate. The volume of the CPM in row 3, determined from the ratio of dΣ/dΩ(0) and Q₂ (Eqs. 2 and 6), was 40–60% larger than the corresponding volume of BF in pure buffer (6.66 × 10⁻²⁰ cm³). R_g compiled in row 5 of Table S3 proved to be insensitive to an increase in CPM volume. This observation might indicate anisotropically shaped CPMs, which become more isotropic as the mineral uptake increases (see expression of R_g for ellipsoids in context with Eq. 3). It should be stressed that R_g depends on atomic distribution, which is inhomogeneous for glycoproteins.

Table 3.

CPM analysis

	Sample	S3.1	S3.2	S4.1	S4.2
1	ΦBF (initial weight) [10−3]	1.9	1.9	0.38	0.38
2	ΦMin (initial weight) [10−3]	0.314	0.314	0.314	0.314
3	VCPM [10−20 cm3]	9.7	11.7	10.7	10.8
4	ΦCPM [10−3]	1.90 ± 0.02	1.98 ± 0.03	0.58 ± 0.02	0.64 ± 0.03
5	ΦBF (CPM) [10−3]	1.80	1.80	0.36	0.36
6	ΦMin (CPM) [10−3]	0.10 ± 0.02	0.18 ± 0.02	0.22 ± 0.02	0.28 ± 0.03
7	ΦMin = ΦMin/ΦMin (initial weight)	0.32 ± 0.07	0.57 ± 0.07	0.70 ± 0.07	0.89 ± 0.10
8	CMin (CPM) [%]	5.3 ± 1.1	9.1 ± 1	38 ± 4	44 ± 5

Referring to a previous study, we assumed that ∼95% of the total BF is not involved in CPP formation (9).

Row 4 represents the CPM volume fraction evaluated from Q₂ in 90% D₂O and the scattering length densities of CPM and BF (see Table S3). These values compared well with the corresponding values in rows 1 and 2. The experiments presented here yielded no direct information about the exact composition and structure of the mineral in the CPM. However, the CPP analysis published previously indicated that ∼95% of the total BF remained in solution as a monomer (rows 5 and 6) (9). The difference between the experimental CPM and BF monomer volume fractions corresponds to the absolute and relative mineral volume fractions listed in rows 7 and 8, respectively. This analysis suggests that the BF-associated mineral has a volume fraction of 5–9% for S3 and of 38 to 44% for S4, which is qualitatively consistent with the increase in the CPM volume. With

$${\rho }_{Min}={\rho }_{BF}+\left({\rho }_{CPM}-{\rho }_{BF}\right)/C_{Min}$$

and considering the mineral volume fractions C_Min of all samples, we evaluated an averaged scattering-length density for the mineral of

$${\rho }_{Min}=\left(6.3\pm 0.3\right)\times {10}^{10}{\text{cm}}^{-2}.$$

Thus, the scattering-length density of the CPM-associated mineral phase is considerably larger than the ones of hydroxyapatite and octacalcium phosphate, two mineral phases commonly found in CPPs. Intriguingly, the corresponding value for Posner clusters, which have been proposed as precursors in calcium-phosphate mineralization is very similar (Table S1); based on their chemical composition Ca₉(PO₄)₆ and their diameter of 8.3 Å, we derived a theoretical scattering-length density of

$${\rho }_{Pos}=6.99\times {10}^{10}{\text{cm}}^{-2}$$

(15,16). The measured

$${\rho }_{Min}=\left(6.3\pm 0.3\right)\times {10}^{10}{\text{cm}}^{-2}$$

translates into Posner clusters of 8.6 ± 0.2 Å diameter, which is in good agreement with the theoretical value given above.

Sample S4 (0.5 mg/mL BF) with a CPM mineral volume fraction of ∼40% (Table 3) is close to the lower limit of stability in our model system (10 mM calcium and 6 mM phosphate). Samples with even lower BF concentrations are prone to early mineral sedimentation (12). The following rough estimate may help to explain this limit. Taking the volumes of a BF molecule and Posner cluster (Table S1) and assuming a spherically shaped CPM, roughly 120 ± 20 mineral units should be attached to the surface of one BF monomer. Roughly, this amount of Posner cluster would form a dense layer covering the protein. This amount of calcium phosphate per fetuin-A molecule represents the capacity limit, i.e., an exceeding mineral ion load per BF molecule would lead to cluster aggregation and sedimentation.

In summary, we have refined and extended the concept of BF-mediated inhibition of calcium-phosphate mineral deposition that has been attributed previously to CPP formation. This first-time quantitative analysis of the role of BF monomer suggests that BF monomers also participate in the inhibition of mineral deposition by sequestering calcium-phosphate entities similar or identical to Posner clusters.

Discussion and Conclusion

Fetuin-A is an essential inhibitor of pathological calcification in vertebrates. Numerous investigations by us and others on the principles of fetuin-A-mediated mineral stabilization using various in vitro and in vivo model systems and analytical methods have been published (7–10,12,26–28). For our experiments, a simple and well-established model system was chosen where all parameters were tunable with high precision. This is an important precondition, because the mechanism is very complex on the (sub-) nanometer scale. CPP mineralization proceeds via a two-stage process. Initial CPPs are spherical and have a diameter of ∼500 Å. After a few hours at room temperature, the primary CPPs are subjected to a fundamental structural rearrangement. The resulting secondary CPPs have roughly doubled in size and show an elongated shape. These CPPs are stable for several days without any further structural changes.

Contrast variation SANS analysis indicated that the exceptional stability of the secondary CPPs is due to a compact BF monolayer covering the mineral core (9). Furthermore, SANS data analysis revealed that only a few percent of the BF and approximately one-half of the mineral was trapped in the CPPs. Hence, despite the withdrawal of mineral ions by immobilization within the CPPs, the solution remained strongly supersaturated. Even at low BF concentrations close to the limit of long-term stability, i.e., no mineral sedimentation for at least two days, this inhibitory effect is only partially attributed to CPP formation ((12) and A. Heiss, V. Pipich, W. Jahnen-Dechent, and D. Schwahn, unpublished). This observation strongly suggested that the BF monomers, which have been ignored so far, in fact play a crucial role in the stabilization of the mineral ion load.

To this end, we extended the contrast variation SANS studies into the high Q range, where the BF monomer scatters. First, we assessed the calcium ion binding capacity of BF. Calcium caused a weak increase in coherent scattering-length density as well as in volume of BF (Fig. 3), corresponding to (15 ± 7) Ca²⁺ ions associated with the protein monomer (or ∼0.7 mM of 10 mM), which is in reasonable agreement with literature values (14). Next we explored the calcium-phosphate-binding capacity of BF (Fig. 4, Fig. S3, Table S3, and Table 3). The comparatively pronounced increase in coherent scattering-length density of the BF molecules reflected the binding of calcium and phosphate, most likely aggregated to subnanometer-sized clusters. We called these mineral-cluster-laden BF molecules “calciprotein monomers” (CPM), representing a second equivalent principle of mineral ion buffering in analogy to the calciprotein particles (CPP). Table 3 shows that the amount of calcium phosphate associated with the CPMs was inversely proportional to the BF concentration and that it increased during CPP ripening.

Because we did not have any information about the mineral polymorph, one crucial parameter to determine the total amount of mineral in the CPMs was missing. However, because we knew that ∼95% of the total BF remains monomeric (9) we could estimate the volume fractions Φ_BF (CPM) and Φ_Min (CPM). Fig. 5 depicts the BF and mineral volume fractions of CPM and CPP, at low and high BF concentration, respectively. The very good agreement between the experimental BF and mineral contents and their initial weights (Table 3) strongly supports our CPM model. On the downside, our analysis is likely flawed with systematic error concerning the absolute calibration of the scattering patterns (∼±5%) and the integration procedure of Q₂. These errors might explain the slight overestimation of the mineral content, in particular regarding sample S4. We evaluated the scattering-length density of the CPM-associated mineral

$${\rho }_{Min}=6.39\times {10}^{10}{\text{cm}}^{-2}.$$

This value is notably larger than the corresponding values for hydroxyapatite and octacalcium phosphate but indeed is close to

$${\rho }_{Pos}=6.99\times {10}^{10}{\text{cm}}^{-2}$$

estimated for Posner clusters (Table S1). Posner clusters (Ca₉(PO₄)₆) are slightly smaller than 10 Å in diameter and are thought to be putative precursor particles and building blocks of amorphous calcium phosphate, respectively (Fig. S4, A and B) (15,16). The computer graphics in Fig. S4 were generated using VESTA (29), VMD (30), and APBS (31).

Figure 5.

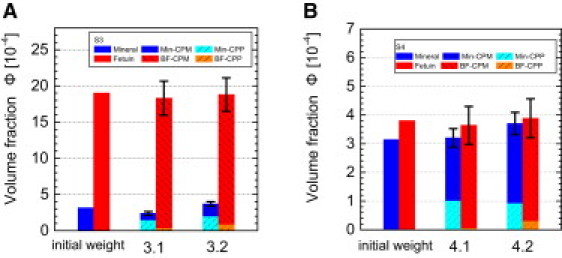
BF (red, orange) and mineral (blue, cyan) volume fractions in CPPs and CPMs of the samples S3 (A) and S4 (B) (Table 3 and Table S2). The data are based on the SANS parameters Q₂, the coherent scattering-length density ρ_CPM, and the volume fraction of the BF monomer (Table S3, Eq. 6). The mineral content in the CPPs was taken from earlier measurements (see values in brackets in Table S2). For the sake of completeness, the volume fractions resulting from the initial weights of mineral and BF have been prefixed to the experimental results.

Hence, we suggest that Posner clusters are the mineral entities which are stabilized by BF molecules. Recent investigations support these results. Calcium-phosphate nucleation and growth within the first second was studied by stopped-flow synchrotron SAXS (11). It was shown that the calcium-phosphate nucleation is not affected by BF. However, the subsequent growth and aggregation of the mineral particles of ∼200 Å size were controlled by the protein. CPM detection by SAXS was not feasible because of the very low protein SAXS scattering contrast and a Q range (Q_max = 0.08 Å⁻¹) too small to be sensitive to tiny particles like Posner clusters. In a cryo-TEM study on calcium carbonate nucleation, cluster formation (prenucleation center) with sizes between 6 and 11 Å was detected (32). Within a few minutes, the clusters aggregated to amorphous calcium carbonate colloids of ∼300 Å before coming into contact with the system's organic interface. Further evidence of CaCO₃ prenucleation clusters was provided on the basis of equilibrium thermodynamic considerations about solvent, individual hydrated ions, and hydrated clusters (33). These calcium-carbonate clusters were transiently stable and may well correspond to Posner clusters in calcium-phosphate systems. Hence, these studies suggested that the first stages of nucleation were neither initiated nor affected by the organic interface. Consistently, however, the interface subsequently mediated cluster aggregation to larger entities.

Ultrafiltration experiments support our SANS results (Table 2). We assessed that, in a fresh mineralization mix, approximately two-thirds of the total Ca²⁺ ions were not enclosed in the (primary) CPPs, whereas in an aged mineralization mix (containing secondary CPPs), the Ca²⁺ was reduced by roughly 50%. Furthermore, we found a weak binding between the BF molecule and the mineral clusters. Fetuin-A is well known for its high affinity for the basic crystalline calcium phosphates like hydroxyapatite and octacalcium phosphate (34). However, this raises the question whether this also applies to the Posner calcium-phosphate prenucleation clusters. The assumption in classical nucleation theory that a nucleus has the same uniform physicochemical properties as the bulk phase has been challenged by evidence from experiments and simulations (35–37). Hence, the comparably weak interaction between BF and the Posner clusters is likely due to their structural properties (38). In conclusion, ultrafiltration and SANS results were qualitatively consistent; a high mineral fraction associated with the CPMs (Table 3) and a rise in CPP volume fraction by 30% was detected (Table S2). Moreover, they are in fair agreement with a previous chemical analysis used in a similar model system and a 10-kDa MMCO membrane (8).

Molecular modeling and activity tests of fetuin-A deletion mutants suggested that the inhibition of calcium-phosphate deposition is chiefly mediated by the dense array of acidic residues on the β-sheet of the amino-terminal cystatin-like domain 1 of fetuin-A (Fig. S4 C) (7). According to our estimate, CPMs consisted of one fetuin-A molecule and up to 120 ± 20 Posner clusters. The sketch presented in Fig. S4 D shows that the β-sheet cannot accommodate this number of clusters without noticeable changes in size and shape. Thus, while we maintain that the β-sheet plays a crucial role in the initial steps of CPP and CPM formation (7), we suggest that the Posner clusters become immobilized at acidic residues spanning the entire surface of fetuin-A, thereby resulting in a random distribution around the protein's core.

In recent works, Price and co-workers (39,40) have shown that BF mediates the infiltration and calcification of a collagenous matrix from a supersaturated solution, possibly by formation of tiny (<6 kDa) mineral crystals. This calcification effect is mirrored by our finding that Posner prenucleation clusters are stabilized by low affinity binding to fetuin-A. Future studies will verify the contribution of these protein-stabilized mineral clusters to controlled ossification in vivo and to high volume mineral transport across barrier tissues including the clearing of mineral in the kidney.