Mechanical Response and Conformational Amplification in α-Helical Coiled Coils

Abstract

α-Helical coiled coils (CCs) are ubiquitous tertiary structural domains that are often found in mechanoproteins. CCs have mechanical rigidity and are often involved in force transmission between protein domains. Although crystal structures of CCs are available, information about their conformational flexibility is limited. The role of hydrophobic interactions in determining the CC conformation is not clear. In this work we examined the mechanical responses of typical CCs and constructed a coarse-grained mechanical model to describe the conformation of the protein. The model treats α-helices as elastic rods. Hydrophobic bonds arranged in a repeated pattern determine the CC structure. The model is compared with molecular-dynamics simulations of CCs under force. We also estimate the effective bending and twisting persistence length of the CC. The model allows us to examine unconventional responses of the CC, including significant conformational amplification upon binding of a small molecule. We find that the CC does not behave as a simple elastic rod and shows complex nonlinear responses. These results are significant for understanding the role of CC structures in chemoreceptors, motor proteins, and mechanotransduction in general.

Introduction

α-Helical coiled coils (CCs) are a common rope-like protein motif found in gene regulation (1), muscle contraction (2), and molecular motors and cell signaling (3). The number of unique CC structures identified in the Protein Data Bank (PDB) is currently 941 (4). How these ubiquitous protein motifs mechanistically contribute to diverse biological functions is not clear. In this work, we explored the conformational flexibility of the CC and developed a coarse-grained mechanical model to explain its response to external perturbations. The model captures the essential features of CC mechanics. We find that the CC does not behave as a simple rod-like structure. In some cases, a dramatic amplification of local conformational changes is observed. The complex response to external loads may explain the roles of CC motifs in a variety of proteins found in the cell.

The basic CC structure is a homodimer where residues in each α-helix contain a sequence pattern called the heptad repeat, typically denoted alphabetically as abcdefg (a and d are the hydrophobic residues that form the hydrophobic core that binds the helices together). Because there are 3.64 residues per turn in the α-helix, the a and d residues form a helical arrangement on the surface of the α-helix. To maintain hydrophobic contact in the CC, the α-helices must twist and bend around each other (Fig. 1) in a fashion that Crick (5) first described as knobs-into-holes. Other interhelical interactions are also important; for example, e- and g-type residue interactions provide specificity to the structure (6), although they are generally weaker than a-a- and d-d-type interactions. Interhelical residue interactions are also the basis of larger and more complex α-helical bundles, such as the recently found heptameric structure (7). Therefore, a mechanistic understanding of these α-helical bundles requires quantitative models of residue side-chain interactions.

Figure 1.

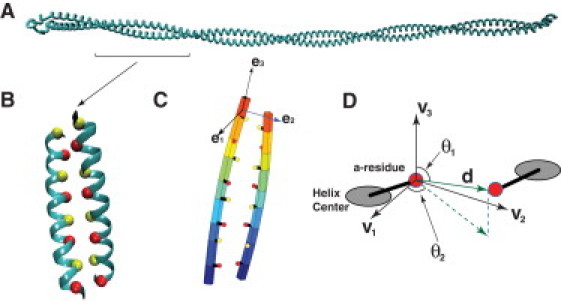
Coarse-grained mechanical model of the CC. (A) Tropomyosin is a prototypical CC. Here, the crystal structure (PDB ID: 2tma) is displayed. (B) A section of the CC, with red and yellow beads representing a- and d-type residue C_α-values, respectively. (C) The CC model represents each α-helix as a slender rod described by the rod position and local material frames $\left({\mathbf{e}}_1\left(s\right),{\mathbf{e}}_2\left(s\right),{\mathbf{e}}_3\left(s\right)\right)$ (see Materials and Methods). The locations of the hydrophobic residues are uniquely defined with respect to these parameters. (D) The interaction between hydrophobic residues is defined by the vector between the residues, d, and the vector between the helix centers, R. For detailed definitions, see Materials and Methods.

An important structural aspect of the CC that is experimentally observable is its pitch. Because of residue sequence irregularities, it is sometimes necessary to define the local and global pitch values. The pitch of perfect CC homodimers is 12–14 nm. For trimeric or tetrameric structures, the upper limit of the pitch value becomes closer to 20 nm (8,9). Several studies have also discussed how the pitch is related to α-helix properties based on geometric arguments (10,11). Recently, Wolgemuth and Sun (12) developed a model (hereafter termed the WS model) to relate the CC pitch to the mechanical properties of the α-helix and the geometric pattern of hydrophobic residues. The model assumes a continuous interaction between helices and treats the hydrophobic interactions as a constraint. Wolgemuth and Sun (12) showed that the CC under small deformation is rod-like, and the bending and twisting stiffness of the CC can be estimated starting from the properties of the α-helices. The mechanical model raises the possibility of understanding conformational properties of the CC and how the CC responds to external forces. Several studies along these lines have appeared (13). Using normal-mode analysis (NMA) and molecular-dynamics (MD) simulations, researchers have investigated the bending and stretching stiffness and unfolding of a CC (14,15). On the basis of NMA and MD data, Lakkaraju and Hwang (16) recently suggested that conformations of longer CCs (>70 nm) could be influenced by a critical buckling length longer than the persistence length. CC conformational studies have also suggested that CCs have an allosteric potential and could be used as nanoswitches (17,18). Additional conformational changes in CCs, such as sliding of an individual helix with respect to another, were shown to have biological relevance (19,20).

Here, we propose a simple scalable coarse-grained model for the CC and α-helical bundles. Specifically, we introduce a discrete interaction potential to model the hydrophobic contact between a- and d-type residues. We use this model to predict the mechanical response of a dimeric CC under force and compare the results with MD simulation results and thin rod theory (21). We find that the hydrophobic contacts provide both distance and angular constraints between the helices in the CC. Under small forces, some of the mechanical response of the CC can be described by a rod. However, depending on how the forces are applied, a complex mechanical response is seen. In some cases, small local conformational changes in the CC are amplified by many fold over long distances. These responses can have important implications for the biological functions of the CC.

Materials and Methods

CC kinematics

The elements of the CC model are depicted in Fig. 1, C and D. Each α-helix is represented by a slender rod whose centerline is denoted as $\mathbf{r}\left(s\right)$, where s is the unstretched arc length along the helix. For points along the helix, a material frame $\left({\mathbf{e}}_1\left(s\right),{\mathbf{e}}_2\left(s\right),{\mathbf{e}}_3\left(s\right)\right)$ also describes the local orientation of the residues. This material frame satisfies the Frenet equation:

$$\frac{\partial {\mathbf{e}}_i}{\partial s}=-\sum _{j,k}{\mathit{\epsilon }}_{ijk}{\mathbf{e}}_j{\omega }_k$$ (1)

where ε_ijk is the antisymmetric tensor; ${\omega }_{1,2}$are the rates of torsion, and ${\omega }_3\left(s\right)$ is the rate of twist for the α-helix. With these parameters, $\left(\mathbf{r}\left(s\right),{\omega }_1\left(s\right),{\omega }_2\left(s\right),{\omega }_3\left(s\right)\right)$, the unstretched configuration of the helix is completely defined. In particular, the positions of all residues can be written with respect to these quantities. We define the position of the CA atom in the m-th residue as

$${\mathbf{h}}_m=\mathbf{r}\left(s_m\right)+r_0{\mathbf{e}}_2\left(s_m\right)$$ (2)

where s_m is the arc-length position of the m-th residue. In the unstretched helix, the helix rise per residue is 0.15 nm; therefore $s_m-s_{m-1}=0.15$ and the arc-length distance between neighboring a-residues is 1.05 nm; the radius r₀ is taken to be 0.23 nm.

Because the residues form a helical pattern in the α-helix and the helix is intrinsically straight if there are no other influences, for an isolated helix the intrinsic torsion and twist of the Frenet frame are defined as

$${\Omega }_1={\Omega }_2=0$$

$${\Omega }_3=\frac{-\pi +\mathrm{mod}\left(\alpha p+\pi ,2\pi \right)}{p{h}_0}$$ (3)

where $h_0=0.15$nm is the helical rise per residue along the centerline, p is the hydrophobic periodicity, and α is the angle between each residue.

In addition to the residue positions, it is also necessary to define the parameters that specify the hydrophobic bonds. The bond vector between the m-th hydrophobic pair is

$${\mathbf{d}}_m={\mathbf{h}}_m-{\mathbf{h}}_m^{\prime }$$ (4)

where the prime denotes the complementary second helix in the CC, and ${\mathbf{h}}_m^{\prime }={\mathbf{r}}^{\prime }\left(s_m^{\prime }\right)+r_0{\mathbf{e}}_2^{\prime }\left(s_m^{\prime }\right)$ is the CA position of the second helix. The distance between helix centerlines is

$${\mathbf{R}}_m=\mathbf{r}\left(s_m\right)-{\mathbf{r}}^{\prime }\left(s_m^{\prime }\right).$$ (5)

In our definitions, we treat the hydrophobic residues as attached rigidly to the helix material frame. Thus, the interaction potential between hydrophobic residues is, in principle, defined by the relative orientations of the helix frames $\left({\mathbf{e}}_1\left(s_m\right),{\mathbf{e}}_2\left(s_m\right),{\mathbf{e}}_3\left(s_m\right)\right)$ and $\left({\mathbf{e}}_1^{\prime }\left(s_m^{\prime }\right),{\mathbf{e}}_2^{\prime }\left(s_m^{\prime }\right),{\mathbf{e}}_3^{\prime }\left(s_m^{\prime }\right)\right)$. To make the definitions simple, we define a triad centered around the m-th hydrophobic residue $\left({\mathbf{v}}_1\left(m\right),{\mathbf{v}}_2\left(m\right),{\mathbf{v}}_3\left(m\right)\right)$, as shown in Fig. 1 D. The orthogonal vectors are as follows:

$${\mathbf{v}}_{\mathbf{3}}\left(m\right)=\frac{1}{2}\left[{\mathbf{e}}_3\left(s_m\right)+{\mathbf{e}}_3^{\prime }\left(s_m^{\prime }\right)\right]$$ (6)

$${\mathbf{v}}_{\mathbf{2}}^{\prime }\left(m\right)=\frac{{\mathbf{R}}_m}{\left|{\mathbf{R}}_m\right|}$$ (7)

$${\mathbf{v}}_1\left(m\right)={\mathbf{v}}_2^{\prime }\left(m\right)\text{×}{\mathbf{v}}_3\left(m\right)$$ (8)

$${\mathbf{v}}_2\left(m\right)={\mathbf{v}}_3\left(m\right)\text{×}{\mathbf{v}}_1\left(m\right)$$ (9)

The orientation of the hydrophobic bond vector with respect to this frame is shown in Fig. 1 D. We define two angles, ${\theta }_{1,m}$ and ${\theta }_{2,m}$, for the m-th residue between two helices as

$$\cos \left({\theta }_{1,m}\right)=\frac{{\mathbf{d}}_m·{\mathbf{v}}_3\left(m\right)}{\left|{\mathbf{d}}_m\right|}$$

$$\cos \left({\theta }_{2,m}\right)=\frac{{\mathbf{d}}_m·{\mathbf{v}}_1\left(m\right)}{\left|{\mathbf{d}}_m\right|}$$ (10)

Geometrically, we see that ${\theta }_{1,m}$ gives the amount of sliding of a helix along the CC centerline, whereas ${\theta }_{2,m}$ is the angle of rigid body rotation of one helix with respect to the other. In our model, the conformational energy of the CC is thus completely defined by the six parameter helix configurations $\left(\mathbf{r}\left(s\right),{\omega }_1\left(s\right),{\omega }_2\left(s\right),{\omega }_3\left(s\right)\right)$ and $\left({\mathbf{r}}^{\prime }\left(s^{\prime }\right),{\omega }_1^{\prime }\left(s^{\prime }\right),{\omega }_2^{\prime }\left(s^{\prime }\right),{\omega }_3^{\prime }\left(s^{\prime }\right)\right)$, and the hydrophobic bond parameters $\left({\mathbf{d}}_m,{\mathbf{R}}_m,{\theta }_{1,m},{\theta }_{2,m}\right)$.

CC conformational energy

Having defined the kinematic variables, we can write the total conformational energy of the CC as a sum of the conformational energy of the helices and bond energies of the hydrophobic contacts:

$$E=E_0\left[\mathbf{r},{\omega }_1,{\omega }_2,{\omega }_3\right]+E_0\left[{\mathbf{r}}^{\prime },{\omega }_1^{\prime },{\omega }_2^{\prime },{\omega }_3^{\prime }\right]+\Delta E$$ (11)

where E₀ is the conformational energy of the α-helix, and $\Delta E$ is the energy of hydrophobic contact between helices. Studies of the conformational dynamics of the α-helix have shown that the helices are rod-like and the bending and twisting stiffness of the helices is relatively sequence-independent. Thus, one may write the helix conformational energy as

$$E_0={\int }_0^L\left[\frac{1}{2}A\left({\omega }_1^2\left(s\right)+{\omega }_2^2\left(s\right)\right)+\frac{1}{2}B{\left({\omega }_3\left(s\right)-{\Omega }_3\right)}^2\right]ds+{\int }_0^L\frac{1}{2}\frac{C}{\sqrt{g}}{\left(\sqrt{g}-1\right)}^{2}ds$$ (12)

where L is the length of the helix. Here, the first line represents the bending and twisting energy of the helix. The second line is the stretching energy. The amount of stretch of the helix or the metric is defined as

$$g={\left|\frac{\partial \mathbf{r}\left(s\right)}{\partial s_0}\right|}^2$$ (13)

where s₀ is the initial arc length of the helix without any other influences; A and B are the bending and twist moduli of the helix, respectively; and C is the stretch modulus. Previous MD studies showed that $A/B\approx 2$, and $A=k_{\text{B}}T{l}_p$, where $l_p=90$nm is the persistence length and $k_{\text{B}}T=4.2$pNnm (22). The parameters used in the model are described in Table 1.

Table 1.

Parameters in our coarse-grained mechanical model

Parameter	Symbol	Value
Intrinsic α-helical twist†	Ω3	−0.6 nm−1
Intrinsic α-helical bending torsion	${\Omega }_{1,2}$	0.0
Helical rise per residue	h0	0.15 nm
Hydrophobic periodicity	p	7
Angle between residues	α	97.7°
Helix bending persistence length	lp	90 nm
Helix twist persistence length	lt	45 nm
Helix stretching modulus	C	3600 pN
Hydrophobic bond length∗	D0	0.45 nm
Hydrophobic bond elevation angle∗	Θ1	π/2 rad
Hydrophobic bond azimuth angle∗	Θ2	1.25 rad
Centerline distance parameter∗	R0	0.92 nm
Energy scale	$k_{\text{B}}T$	4.2 pNnm
Bond distance stiffness∗	$k_1$	70 pNnm−1
Bond angular stiffness∗	$k_2$	200 pNnm
Hardcore repulsion parameter∗	$k_3$	50 pNnm

The values are for cortexillin CC, which has P = 12 nm. Several parameters are established properties of the CC and α-helices, and are not fitted.

^∗Fitted parameters.

^†This value is used for the cortexillin structure used in the MD study. The intrinsic twist for typical helices, such as in the leucine zipper, is closer to −0.46 nm⁻¹.

The hydrophobic interaction energy depends on the distance between the hydrophobic residues, $d_m=\left|{\mathbf{d}}_m\right|$. In our model, we specify the bond energy as

$$\begin{array}{l}\Delta \mathit{E=}\sum _{m=1}^N\frac{1}{2}{k}_1{\left(\left|{\mathbf{d}}_m\right|-D_0\right)}^2+\frac{1}{2}{k}_2{\left({\theta }_{1,m}-{\Theta }_1\right)}^2+\frac{1}{2}{k}_2{\left({\theta }_{2,m}-{\Theta }_2\right)}^2+k_3\exp \left[-{\left(\left|{\mathbf{R}}_m\right|/R_0\right)}^{16}\right]\end{array}$$ (14)

where N is the number of hydrophobic residue pairs in the CC. Of interest, after some trial and error, we found that all four terms in the bond energies are necessary, which suggests that the hydrophobic interactions between residues are complex and contain both distance and angular constraints. The first term is the bond energy that depends on the distance between the hydrophobic residues, $\left|{\mathbf{d}}_m\right|$. This distance can be defined with respect to the CA atom of the residue, as we have done, or with respect to other atoms in the residue. This choice does not influence the final results, as long as the most favorable distance, D₀, is defined properly. The second and third terms constrain the relative angle of the hydrophobic bond with respect to the CC helices. We found that this term is necessary to reproduce the correct force response. Without this term, the helices will tend to twist and slide with respect to each other when forces are applied. This is not seen in MD simulations. Finally, the last term represents the hardcore repulsion between the helices, which prevents the helices from physically penetrating each other.

When forces are applied to the CC (e.g., at one end of the dimer), the conformational energy becomes

$$E=E-\mathbf{F}·\left[\frac{\mathbf{r}\left(l\right)+{\mathbf{r}}^{\prime }\left(l\right)}{2}\right]$$ (15)

where E is the same energy as Eq. 11. Equation 15 implies that the force is applied at the midpoint between two helices, or the force is shared equally. The bending displacement u is therefore the difference in $\left(\mathbf{r}\left(l\right)+{\mathbf{r}}^{\prime }\left(l\right)\right)/2$ before and after the application of force. There are other situations where the force is only applied to one helix, which can be similarly modeled.

Computation of mechanical equilibrium configurations

Formally, in the presence of an external force, the equilibrium configuration of the CC can be computed by force and torque balance, which is equivalent to finding the minimum energy configuration of Eq. 15. The variables are the centerline curves $\left(\mathbf{r}\left(s\right),{\mathbf{r}}^{\prime }\left(s^{\prime },\right)\right)$ and the generalized torsions $\left({\omega }_i\left(s\right),{\omega }_i^{\prime }\left(s^{\prime },\right)\right)$. The minimum energy configurations are solutions of the following equations:

$$\begin{array}{l}\frac{\delta E}{\delta \mathbf{r}\left(s\right)}=0,\frac{\delta E}{\delta \mathbf{r}\left(s\right)}=0\\ \frac{\delta E}{\delta {\omega }_i\left(s\right)}=0,\frac{\delta E}{\delta {\omega }_i^{\prime }\left(s^{\prime }\right)}=0\end{array}$$ (16)

In practice, the calculations are carried out by discretizing $\left(s,s^{\prime }\right)$ into points $\left(s_k,s_{k^{\prime }}^{\prime }\right)$ with $\Delta s=s_k-s_{k-1}=h_0=0.15$nm. The solutions of Eq. 16 comprise a set of vectors with components labeled by k or $k^{\prime }$. The solutions are obtained by using a conjugate gradient search method. Gradients of the energy are computed numerically using the fourth-order finite difference. Multiple initial starting configurations are chosen to test the validity of the solutions.

MD simulations of CCs under force

We use the CC dimer domain of cortexillin I (PDB ID:1D7M) for our MD studies. This is a relatively stiff CC with P = 12 nm. By deleting residues starting from the C-termini, we modify the length of the CC such that we obtain a 12.6 nm (13-heptad) and 8.4 nm (9-heptad) CC. In VMD (23) the structures are submersed in TIP3 water and the overall electrical charge is neutralized with Cl⁻ and Na⁺ ions. The MD simulations are performed using NAMD (24) with CHARMM27 (25) force-field parameters. Particle mesh Ewald (PME) (26) is used for electrostatics calculations. The NPT ensemble and periodic boundary conditions with a rectangular box are applied. For the 9-heptad CC, the system size is 4.5×12×4.5 nm and there are 20,000 atoms. For the 13-heptad CC, the system size is 4.5×16×4.5 nm and there are 27,000 atoms. The temperature (310 K) and pressure (1 atm) in the simulations are kept constant using Langevin dynamics. Initial energy minimization is done with the conjugate gradient method. Equilibration is done for 60 ps by heating up the system from 0 K to 310 K, followed by 20 ns production (bending/twisting) runs. During the production runs, to emulate the clamped boundary condition on one end, the positions of the first eight N-termini C_α atoms on both chains are fixed (Glu²⁴³-Met²⁴⁴-Ala²⁴⁵-Asn²⁴⁶-Arg²⁴⁷-Leu²⁴⁸-Ala²⁴⁹-Gly²⁵⁰ on the A and B chains). The time step for the simulations is 2 fs. The trajectories are sampled at 10-ps intervals. We use MATLAB (The MathWorks, Natick, MA) to analyze the MD trajectories. The simulations are carried out in a Linux-based cluster with eight nodes.

The bending responses of CCs to three different constant forces (7, 11, and 15 pN) are studied using MD simulations. The bending forces are applied at the instantaneous Cartesian coordinates of the C-termini residue C_α atoms on both chains (i.e., residues Glu³⁰⁵–AB for the short CC and residues Ala³³³–AB for the longer). The force magnitude on the two atoms is half the total bending force magnitude. The forces are defined orthogonal to the plane spanned by two vectors: the initial centerline vector of the CCs and the vector defined by the difference between the initial positions of the C-termini C_α atoms of chains A and B. The instantaneous bending displacement is calculated as the tip-to-tip distance between the bent (instantaneous) structure and the initial structure. Statistics are collected on the fluctuating structures for 15 ns, discarding the initial 5 ns.

For the CC twist calculations, we do not apply any torque to the structures. Instead, we gather statistics on the twist angle ϕ of Eq. 19. To calculate the angle ϕ, we first define triads along the centerline of the CC in a manner similar to that described by Choe and Sun (22). Then, from the relative rotation of these local frames, the probability distributions of ϕ along the centerline are histogrammed for 15 ns. By fitting the probability distributions of ϕ, we find the twist persistence length, ${\Lambda }_t$, as a function of the CC length.

Results

CC pitch

The pitch of the CC dimer is directly measurable from x-ray structures. The mechanical model presented here can compute the pitch by finding the mechanical equilibrium configuration without external forces. We define the pitch based on the twist and bending of α-helix local frames (Fig. 1 C) in the mechanical equilibrium configuration. Using Eq. 1, which gives generalized torsions on these local frames, the pitch P is

$$P=\frac{2\pi w_3}{w_1^2+w_2^2+w_3^2}$$ (17)

In general, because of the discrete hydrophobic residues in our model, ω_i is a function of the arc length s. Here, we report the pitch value averaged over the length of the CC in Fig. 2.

Figure 2.

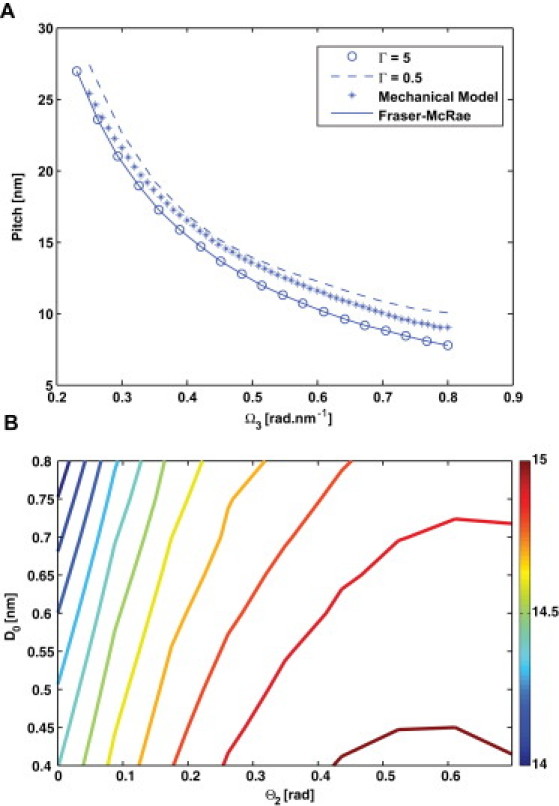
Pitch of the CC. (A) Pitch is plotted as a function of the intrinsic twist of the hydrophobic residues in the α-helices, Ω₃. Wolgemuth and Sun's (12) prediction with $\text{Γ}=l_t/l_p=5$ (circles), $\text{Γ}=0.5$(dashed line) is shown. The solid line shows the solution to the Fraser-MacRae equation (10). The crosses are the mechanical model predictions for a 13-heptad repeat CC. (B) The dependence of the CC pitch on the geometric parameters D₀ and Θ₀. The pitch varies by <10%, which suggests that mechanical constants k₁ and k₂ have a negligible effect on the geometrical properties of the CC.

The pitch strongly depends on the value of the helix intrinsic twist, Ω₃. For historical reasons and simplification purposes, the angle between hydrophobic residues α is taken to be $\alpha =2\pi /3.6={100}^{\circ }$. In fact, as Phillips (9) and Chothia et al. (27) pointed out, there are an average of 3.64 residues in every α-helix turn, thus yielding $\alpha ={98.9}^{\circ }$. This small difference may seem insignificant, but it has a profound influence on the CC pitch because Ω₃ changes from 0.33 rad/nm to 0.46 rad/nm. Fig. 2 A shows the predicted pitch as a function of Ω₃. We see that the pitch changes by 50% as α changes by $2^{\circ }$. For most α-helices, Ω₃ ranges from −0.2 to −0.9 (27).

In our CC model, the hydrophobic bond energy is defined by additional parameters: k₁ and k₂ are the bond distance stiffness and bond angle stiffness, respectively; D₀ is the equilibrium hydrophobic bond length; and ${\Theta }_{1,2}$ are the equilibrium hydrophobic bond angles (see Materials and Methods). We find that in general, the choice of stiffness parameters has a small effect on the CC pitch; however, the geometric parameters D₀ and Θ₂ have a more pronounced effect (Fig. 2 B). As the hydrophobic bond length and contact angles are varied, the pitch varies by roughly 10%. Θ₂ also has a more pronounced effect than Θ₁. These parameters, along with sequence inhomogeneity, will contribute to the diversity of CC pitches observed in protein structures.

CC bending and buckling

CCs often serve as mechanical linkages between protein domains. It is therefore important to address the response of the CC to external force. Here we examine the bending property of the CC and ask whether it can be effectively modeled as a thin rod. Using our coarse-grained mechanical model and Eq. 15, we compute the response of the CC under forces ranging from 5 to 15 pN (Fig. 3). The computed bending displacement, u, is compared with MD simulations of real protein structures in explicit solvent under a constant force. Fig. 3 shows the molecular structures of the CC under force and the observed deflections. MD simulations are performed on two different CCs (8.4 and 12.6 nm long) and three different forces (7, 11, and 15 pN). After equilibration is completed, we collect statistics on the fluctuating structure for 15 ns. The shown structure is the average equilibrium structure of the CC. Superimposed on the MD results are the results of our coarse-grained mechanical model. The model has no free parameters except for stiffnesses k₁, k₂, and k₃. The best-fit results are shown in Fig. 3. The model suggested by Wolgemuth and Sun (12) constrains the distance between helices and does not allow the helices to slide with respect to each other, which can be thought of as $k_1=k_2=\mathrm{\infty }$ in our model. We see that both models compare well with the MD results, although the WS model is significantly worse for short CCs. Because it allows finite stiffness, our current model is better matched with the MD results. The MD results also show additional complex behavior that is not captured by our model. Perhaps additional long-range interactions, as suggested by Lakkaraju and Hwang (16), could improve the model predictions.

Figure 3.

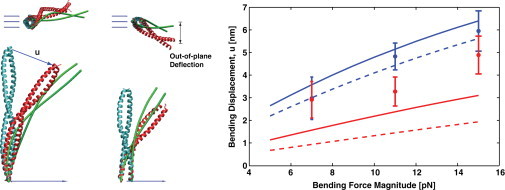
Bending response of the CC model compared with MD simulations. The bottom end of the CC is clamped (both the position and orientation of the material frame are fixed). The applied force is directed to the right (vectors). The average MD structures before (cyan) and after (red) application of the bending force are shown along with the coarse-grained mechanical model (green lines). Views from the side and top are shown. The right plot shows the magnitude of the bending displacement, $\left|\mathbf{u}\right|$, versus the magnitude of the applied force for 8.4 nm (red) and 12.6 nm (blue) CCs. The lines represent the predictions of the mechanical models: current model (solid lines) and Wolgemuth and Sun's (12) prediction with $\text{Γ}=0.5$ (dashed lines). The MD results (symbols) with error bars are compared with model predictions (lines). Both the MD simulation and the CC model show a significant bending response perpendicular to the applied force direction (out-of-plane deflection), although our model shows a smaller out-of-plane deflection (0.5 nm) compared to the MD result (2.0 nm) at 15 pN bending force.

Both the MD simulation and the mechanical model show responses to the applied force that are not replicated by a slender rod. For example, when a slender rod is subjected to a force at one end with the other end held fixed, the deformation of the rod is confined within the plane spanned by the force vector and the opposite end. For the CC, we observe a substantial deflection in the out-of-plane direction (Fig. 3). This is because the α-helices are not confined to the bending plane, and thus there is a significant component of the torque in the direction perpendicular to the deflection plane. The complete problem requires consideration of the bending response of helical rods, which is beyond the scope of this work. Nevertheless, the MD simulation and our model show similar qualitative out-of-plane movement.

By examining the bending response of the CC, we also can estimate the effective bending persistence length (bending modulus) of the CC. There are several ways to obtain this estimate. Fig. 4 A shows the Euler buckling response of the CC. The position and orientation of the CC are fixed at one end. The other end is subjected to a vertical downward force. The critical buckling force is compared with the rod theory prediction:

$$F_b=\frac{{\pi }^2{l}_p{k}_{\text{B}}T}{4L^2}$$ (18)

where L is the length of the CC and $k_{\text{B}}T=4.2$ pNnm. The coarse-grained mechanical model behaves quite similarly to the rod theory. The best fit that gives the effective bending persistence length of the CC is $l_p=$200 nm, although a range of persistence lengths from 160–200 nm can explain the observed buckling force. However, when a horizontal force is applied that bends the CC, the response is again somewhat different from the slender rod model with $l_p=200$ nm (Fig. 4 B). Aside from the observed out-of-plane bending, the net displacement as a function of the CC length is also consistently less than predictions of the rod model with $l_p=200$ nm, suggesting that the CC may be slightly stiffer than the effective rod prediction. The length dependence of the bending displacement also behaves differently compared to that of a standard rod. Therefore, describing the CC as a rod with a single bending constant is problematic. Bathe et al. (28) predicted that the bending response of parallel bundles will have a component that depends on the stretching of the transverse bonds. The overall bending constant of the bundle is also length-dependent (mode-dependent bending). This is consistent with our model, which shows a length-dependent bending modulus and demonstrates that CCs cannot be described as simple rods with a fixed mechanical bending modulus. This result has important implications for the mechanics of motor proteins where force transmission between motor domains is carried out by CCs (29).

Figure 4.

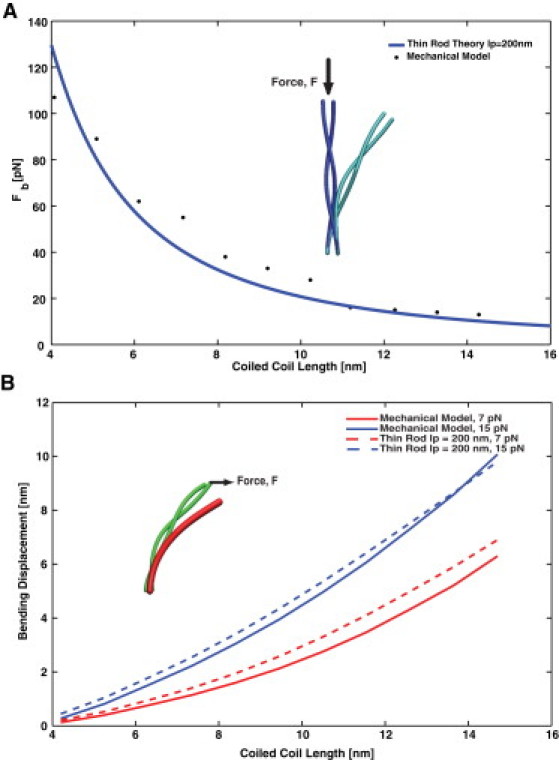
Bending response of the CC compared with that of a slender rod. (A) A vertical force is applied to buckle the CC structure. Our model shows that the critical buckling force as a function of the CC length (points) is well described by buckling of the slender rod (solid line) in Eq. 18. The fitted CC persistence length $l_p=$200 nm. However, the bending response of the CC is not completely described by the slender rod. Panel B shows a comparison between our model and the slender rod bending response with rod $l_p=$200 nm.

CC twist

Twisting of CCs is a common deformation encountered in proteins. The connection between cargos and molecular motors is often made of CCs, and the processive (walking) motion of the motor introduces torsion into the CC domain. To obtain an estimate of the twist modulus of the CC, we examined MD simulation results and our coarse-grained model predictions. For a straight rod only undergoing twist deformations, the conformational energy is

$$E=\frac{1}{2}{\int }_0^L{l}_t{k}_{\text{B}}T{\left({\omega }_3-{\Omega }_3\right)}^{2}ds=\frac{1}{2}\frac{{\Lambda }_t}{L}{k}_{\text{B}}T{\varphi }^2$$ (19)

where L is the rod length, ${\Lambda }_t$ is the twist persistence length, and ϕ is the twist angle at the end of the rod. In the MD simulations we examined the conformational fluctuation of the CC and obtained the probability distribution of the twist angles. From the probability distributions, which are roughly Gaussian functions of ϕ, we obtained the twist persistence length, ${\Lambda }_t$, as a function of the CC length (Fig. 5). We compared the simulation results with those obtained with our coarse-grained model, which we used to examine the response of the CC to an applied torque. The comparison shows that the CC has a twist persistence length of ∼100 nm. However, the twist persistence length depends on the length of the CC, which implies nonlinear behavior. Our model agrees with the MD results for CC lengths of ∼10–12 nm. For shorter lengths, the applied torque generates twist by twisting the individual α-helices. For longer lengths, the applied torque bends the α-helices and reduces the CC pitch. The prediction of the WS model (see Appendix) suggests a slightly higher twist persistence length, presumably because the angular springs characterizing the hydrophobic bond are flexible in reality. The WS model assumes a completely rigid interaction in the hydrophobic bond.

Figure 5.

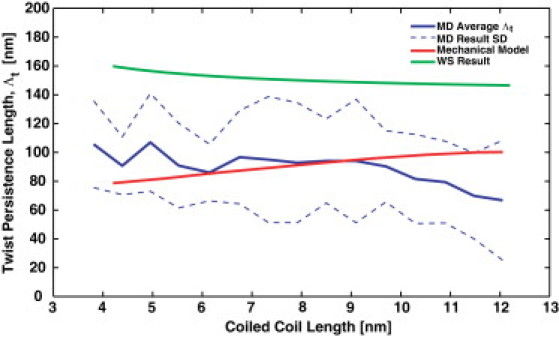
Twist persistence length, ${\Lambda }_t$, of the CC. From MD simulations, the twist persistence length (blue line) can be estimated from the angular fluctuations of the CC twist, in a manner similar to that described by Choe and Sun (22). The model prediction (red line) is obtained by applying a known torque to the CC structure and computing the twist response. Also shown is Wolgemuth and Sun's (12) prediction with $\text{Γ}=0.5$ (green line). The results show that the twist persistence length of the CC is ∼100 nm, although there is some length dependence.

Conformational amplification

So far, we have focused on the overall mechanical behavior of the CC. We have compared the CC response with that of rod-like objects. However, the CC has more complicated mechanical responses that are biologically important. For example, the microtubule-binding domain of dynein appears to undergo a deformation whereby one helix is shifted with respect to the other (19,20). Small molecules can also bind the CC and induce a small local conformational change. The Tar receptor of Escherichia coli binds an aspartate molecule at one end of the CC. Upon binding, this molecule shifts one helix with respect to the other and introduces a piston motion along the centerline of the CC of ∼1.6 Å (30). We find that our model predicts a significant amplification of this type of conformational change, defined as $m_2/m_1$, where m₁ is the magnitude of the pistoning displacement and m₂ is the bending displacement at the distal end (Fig. 6). For example, for a 40 nm long CC, $m_1=1.6$ Å translates to a bending movement of $m_2=5$ nm, a 30-fold amplification. Note that the free energy needed to introduce the small piston displacement is quite small and can derive from the binding free energy of the small ligands (Fig. 6). The amount of amplification depends on the length of the CC. Along the same lines, if a small twist at the end of one of the helices is introduced, a bending motion also can occur in the distal end. A twist of 90° in one of the helices can translate into a small bending movement at the distal end, although the degree of amplification will be significantly smaller.

Figure 6.

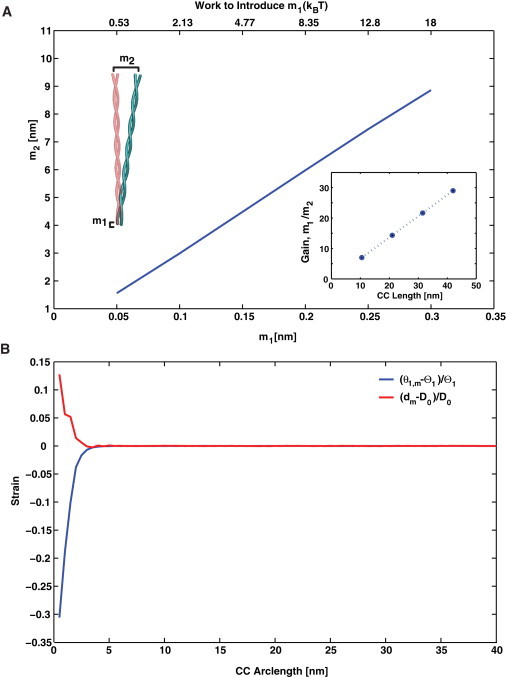
Conformational amplification in the CC. (A) At one end of the CC, we introduce a small conformational change into one of the α-helices while keeping the other helix fixed. A small piston displacement or vertical movement of size m₁ translates to a bending motion of size m₂ at the distal end. The top axis shows the amount of mechanical work needed to introduce the m₁ movement. The inset shows the conformational gain as a function of CC length. (B) The strain in ${\theta }_{1,m}$ and d_m as a function of the CC arc length, s. A piston movement of 0.3 nm is introduced into a 40 nm CC at $s=0$. Most of the strain is concentrated near the position of movement.

Fig. 6 B shows the strains in the hydrophobic bonds in a 40 nm CC with an initial piston movement of 0.3 nm. Most of the significant strains occur within the first 5 nm of the CC. There are also significant bending strains in the α-helices. In an experiment such as that described by Kon et al. (20), in which the α-helices are artificially tied together by disulfide bonds, the overall bending of the CC can be prevented.

This suggests that the elasticity of protein structures can transmit and amplify conformational signals over long distances, and may explain the action of small ligands binding to CC structures. In the Tsr receptor, the distal end of the receptor contacts other signaling proteins and neighboring receptors, leading to cooperativity between receptors. Our model suggests that the cooperativity arises from the intrinsic mechanical properties of α-helical bundles. This mechanism is in contrast to the wedge mechanism proposed by Yu and Koshland (31), which invokes a series of bond rearrangements to explain the propagation of small conformational changes. Since proteins are mechanical structures, a more plausible mechanism would involve large-scale flexible movements based on a geometrical arrangement of the protein components.

Discussion

In this work we explored the conformational properties of the CC in response to applied forces and torques, and developed a coarse-grained mechanical model to describe the conformational dynamics. The model treats the CC motif as two elastic α-helices bonded together by a regular pattern of hydrophobic bonds. The model is able to quickly compute the conformational response of long CCs without resorting to costly atomistic simulations. We compared the results of our model with those obtained in MD simulations for short CCs. Our model is able to reproduce most of the bending and twist response observed in MD simulations, suggesting that the model is a reasonable representation of the actual protein structure. Of course, there are other ways to parameterize the model and the hydrophobic bonds, but it is clear that the model must consider angular constraints provided by the hydrophobic interactions. Our model can also be made more quantitative by considering the sequence dependence of the hydrophobic interaction, which can be added by introducing sequence dependence into the parameters listed in Table 1. Additional factors, such as possible long-range interactions, are not considered here, but could be important for longer CCs.

Although the elastic properties of the α-helix are reasonably simple, we find that the CC shows more complex mechanical properties. For example, by examining the buckling properties of CCs, it is possible to estimate the CC bending persistence length as ≈200 nm, which is approximately two times the persistence length of the α-helix. Experimental measurements of CC persistence length are available in the literature (32–34). However, different measurement techniques seem to yield significantly different results. Part of the reason for this could be the length dependence of the CC mechanical response and the way external forces are applied in the measurements. We also find that CCs are more complex, and a simple rod model does not explain all of the bending responses. For instance, the bending displacement has a component that is out of the plane of the bending force. The bending persistence length also appears to be slightly length-dependent. The twist persistence length shows a similar complexity and length dependence. CCs are often domains in motor proteins that connect the motor to the cargo. In single-molecule experiments, the motion of the cargo is tracked and observed. Our study shows that because of the complex response of the CC domain, the cargo motion is not a direct reflection of the motion of the motor.

For real proteins, if sufficient forces are applied, the hydrophobic bonds will eventually break, leading to possible unfolding of the structure. Indeed, studies suggest that the hydrophobic bond energy is roughly 10$k_{\text{B}}T$. In our model, the spring-like interaction potential does not allow the bonds to break. To introduce structures that can fail, we can define the interaction potential by introducing a cutoff. If the total energy of the bond, $\Delta E$, exceeds the cutoff, the bond will fail. With this, we find that CCs can withstand significant forces before failing, although the direction of the applied force and the length of the CC are important. For example, for perpendicularly applied bending forces such as those shown in Fig. 3, the 13 nm structure can withstand 100 pN of force before breakage of the hydrophobic bonds is observed. In biologically relevant situations, molecules rarely experiences forces of such magnitude. For example, molecular motors often exert forces of <10 pN. Therefore, we expect that CCs function mostly as a folded and intact structure during common deformations.

CC domains in proteins are often involved in mechanotransduction and chemical signaling. Our model suggests that these functions can be explained within one unified picture. The CC structure responds to externally applied forces and changes conformation over long distances. We also find that the CC structure responds to local and small perturbations, and amplifies them over long distances. The amplification depends on the length of the CC, and may explain why the bacterial chemoreceptor is nearly 40 nm long. The amplification also suggests that the cooperative properties of receptor arrays may be mechanical in origin, and the mechanical properties of proteins are an important aspect of elucidating protein function in general.

Appendix: Twist Persistence Length Estimate from the Ws Model

The WS model can be thought of as our current model with $k_1=k_2=\mathrm{\infty }$. In this limit, the arc lengths of the helices become identical and the helices cannot slide with respect to each other. Consider twisting a CC about its centerline. We assume that the CC remains straight (i.e., with no buckling) and that the force applied to the ends of the CC is zero. From Wolgemuth and Sun (12), we find that the moment about the tangent vector of the CC can then be written as

$$\frac{M_3}{k_{\text{B}}T{l}_p}=-\frac{R_0^2}{2g^{5/2}}\frac{{\partial }^2{\omega }_3}{\partial s^2}+\frac{R_0^4{\omega }_3}{4g^{5/2}}{\left[\frac{\partial {\omega }_3}{\partial s}\right]}^2+\frac{R_0^4{\omega }_3^3}{4g^{5/2}}+\frac{2\text{Γ}}{g^{5/2}}\left({\omega }_3-g{\Omega }_3\right)\left(1-\frac{R_0^2{\omega }_3^2}{4}\right)$$ (20)

where s is the arc length along the CC centerline, l_p is the bending persistence length of the α-helices, R₀ is the distance between helix centerlines, and $g=\sqrt{1+R_0^2{\omega }_3^2/4}$ is the metric of the α-helix arc length. Here ω₃ is not the torsion of the helices, rather it is the torsion of the material frame along the CC centerline. See Wolgemuth and Sun (12) for detailed definitions.

The twist persistence length of the CC can be calculated as the average value of the deviation in ω₃ from the unstressed twist, O₃, when a moment of magnitude $k_{\text{B}}T$ is applied about the tangent vector. Therefore, we consider ${\omega }_3=O_3+\mathit{\epsilon }$, and solve Eq. 20 when $M_3=k_{\text{B}}T$. The twist persistence length is then defined to be $1/\mathit{\epsilon }$. The boundary conditions for Eq. 20 are that at one end the α-helices are held in their unstressed configuration; i.e., ${\omega }_3=O_3$. The other end of the CC is free, which implies that $\partial {\omega }_3/\partial s=0$.

To derive an analytic expression for the twist persistence length, we assume that the twist deviation ε is small and linearize Eq. 20. The result is

$$\frac{R_0^2}{2}\frac{{\partial }^2\mathit{\epsilon }}{\partial s^2}\approx \left(A-BM\right)\mathit{\epsilon }-\left(1+\frac{R_0^2{O}_3^2}{2}\right)M$$ (21)

where the constants are

$$A=3R_0^2{O}_3^2+2\text{Γ}\left(1-R_0{\Omega }_3{O}_3+R_0^2{O}_3^2/4\right)$$

$$B=\frac{5}{4}{R}_0^2{O}_3{\left(1+\frac{R_0^2{O}_3^2}{4}\right)}^{3/2}$$

$$M=\frac{M_3}{k_{\text{B}}{Tl}_p}$$ (22)

The solution to Eq. 21, consistent with the boundary conditions, is

$$\epsilon =\frac{M\left(1+R_0^2{O}_3^2/4\right)}{A-BM}\left(1+\tanh kL\sinh ks-\cosh ks\right)$$ (23)

where $k=\sqrt{2\left(A-BM\right)/R_0^2}$ and L is the centerline length of the CC. The average value of ε is

$$\langle \mathit{\epsilon }\rangle =\frac{1}{L}{\int }_0^L\mathit{\epsilon }ds=\frac{M\left(1+R_0^2{O}_3^2/4\right)}{A-BM}\left(1-\frac{\tanh kL}{kL}\right)$$ (24)

Using the values $R_0=0.92$ nm, ${\Omega }_3=-0.6$ nm⁻¹, $O_3=-0.58$ nm⁻¹, $l_p=90$ nm, and $\text{Γ}=0.5$, we have $A=1.65$, $B=-0.69$ nm, and $M=0.011$ nm⁻¹; and $k=1.95$ nm⁻¹. The twist persistence length of the CC is therefore

$${\Lambda }_t=\frac{1}{\langle \mathit{\epsilon }\rangle }\approx \frac{a}{\left(1-\frac{\tanh kL}{kL}\right)}$$ (25)

with $a=140$ nm. The solution as a function of CC length is shown in Fig. 5.