Quantitative Analysis of Ligand Migration from Transition Networks

Abstract

In this work we use transition network analysis for the first time to investigate ligand migration in truncated hemoglobin (trHbN) and obtain kinetic information about the docking-site dynamics in the protein. A comparison with explicit water molecular dynamics simulations (100 ns in total) shows that the rate constants derived from the network analysis are realistic. The transition network analysis provides 1) The time-resolved connectivity network in the protein; 2) The half-lives of the docking sites; 3) The transition timescales between two given docking sites; and 4) The extent of population transfer among different docking sites of the protein as a function of lag time. We investigate the role of the Tyr³³ and Gln⁵⁸ residues in ligand migration by studying ligand migration in four mutants of trHbN. The mutation study suggests that residues Tyr³³ and Gln⁵⁸ stabilize the NO ligand in the Xe2 docking site of trHbN, thus facilitating the efficiency of the NO detoxification reaction.

Introduction

The difficulty of characterizing long-timescale dynamics in complex systems that exhibit several states is a fundamental problem in chemistry and biology. With the increasing availability of computational facilities, it is now routine to generate multiple extended (multi-nanosecond) trajectories for large macromolecules in explicit solvent and to explore the fundamental dynamic nature of biomolecular processes, including protein folding, enzyme catalysis, signal transduction, posttranslational modifications, and ligand binding. It is therefore of considerable importance to formulate methods to harvest these trajectories and analyze the spatial and temporal evolution of the system dynamics.

The dynamical processes by which a system moves from one state to another, and, more importantly, when transitions can follow multiple pathways, can be studied with the use of a transition network analysis (TNA), also known as Markov state modeling (1–4). TNs are discrete representations of states or clusters and contain information about the possible pathways between the states. In graph theoretical terms, the conformational states are represented by nodes or vertices, whereas the transitions between them correspond to the edges. The kinetics between the nodes can be recovered with the use of master-equation dynamics (1) or kinetic Monte Carlo (KMC) methods (5–9). KMC is particularly suitable for situations in which the timescale separation between different motions of interest is large, such as in protein folding. TNs have found several applications in protein folding (10–18), enzyme catalysis (19,20), and studies of electron spin resonance (21). In this work, we employ TNs to quantitatively analyze the dynamics of ligand migration in truncated hemoglobin (trHbN) of Mycobacterium tuberculosis.

M. tuberculosis is responsible for human tuberculosis, which causes about 2 million deaths every year and latently persists in more than a billion individuals worldwide, ∼10% of whom are likely to develop active tuberculosis at a later stage of their life (22). M. tuberculosis evades macrophage killing by neutralizing toxic agents, such as nitric oxide (NO). The trHbN of M. tuberculosis has been shown to oxidize NO to nitrate at least an order of magnitude faster than sperm-whale myoglobin (23,24). Efficient NO detoxification in trHbN has been attributed to the presence of an almost continuous tunnel through the protein that ensures rapid NO transfer to the active site, where the heme-bound dioxygen oxidizes NO to produce free nitrate, which is then transported away from the active site (25–27). This is an important example of the direct involvement of ligand migration in a physiologically relevant process.

The tunnels in trHbN consist of two orthogonal branches connecting the heme distal pocket to the protein surface at two distinct sites (26). Studies using molecular dynamics (MD) simulations have established that in addition to the opening of the two tunnel branches, trHbN also possesses ligand exit channels situated between helices E and F (28) and helices C and F (29). The crystal structure of trHbN with Xe atoms under pressure revealed five distinct docking sites along the two branches of the tunnel (27) (see Fig. 1). Recent atomistic MD simulations of NO dynamics in trHbN have provided a structural and spectroscopic characterization of the protein by using NO as a probe (30). The resulting connectivity network provided additional insight into the ligand migration pathways and exit channels. However, a mechanistic understanding of the underlying dynamics of the connectivity network has remained elusive.

Figure 1.

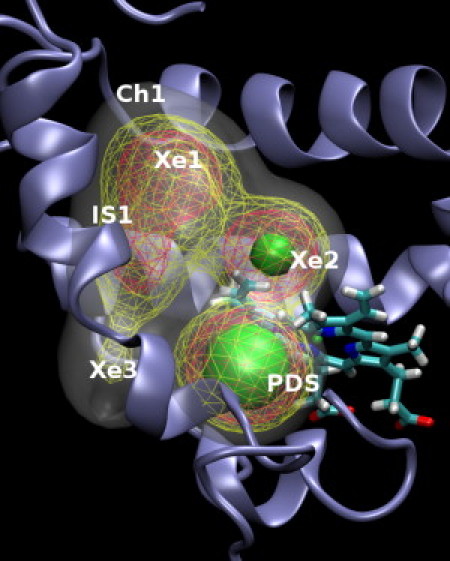
Distribution of NO ligand density in trHbN. The protein is shown in ribbon, and heme is shown in stick representation. The ligand density is shown as an isocontour mesh, with increasing ligand density reflected by gray, yellow, orange, and green colors.

In this work, we used TNA to investigate the dynamics and kinetics of ligand migration in trHbN of M. tuberculosis. Multiple MD trajectories for NO migration inside trHbN were run and the ligand density was partitioned into discrete states corresponding to ligand docking sites. We constructed transition matrices (TMs) by monitoring ligand transitions between the clusters. The results of the analysis describe the kinetics of ligand migration in the protein.

Materials and Methods

Simulation setup

The initial structure was the x-ray crystal structure (Protein Data Bank entry 1IDR) (26), and only monomer A of the homodimeric protein is considered here. The protein contains 131 amino acid residues, a prosthetic heme group, the Fe-bound O₂ ligand, and a free NO ligand. The protein was solvated in a water box (with dimensions $62.1\times 52.8\times 68.3$ ų) and MD simulations were carried out with the CHARMM22 force field (31) and the CHARMM program (32). Nonbonded interactions were truncated at a distance of 14 Å by using a shift function for the electrostatic terms and a switch algorithm for the van der Waals terms (33). All bonds involving hydrogen atoms were kept fixed by using SHAKE (34). The system was slowly heated to 300 K and equilibrated for at least 300 ps before free dynamics was performed at a constant temperature (NVT) of 300 K. For the NO molecule, we used a three-point fluctuating charge model to accurately represent electrostatic interactions (35). For further information concerning the force field parameters, see Ref. (30). Simulations were started from six different structures with the NO ligand in one of the Xe1–Xe5 pockets and in the proximal docking site (PDS). The initial structures were obtained from an equilibration simulation starting with NO in the Xe2 pocket, and the corresponding snapshots were collected when the ligand appeared in one of the docking sites. This method for selecting initial structures avoids perturbation and bias introduced by manual docking of the ligand. Four trajectories of 2 ns duration each were initiated from each of the six snapshots, giving a total of 24 trajectories. Snapshots were collected every 10 fs, and a total of 480,000 frames and 11,458 transitions were analyzed.

Clustering of ligand density and construction of TMs

The frames were then partitioned into clusters corresponding to Xe1, Xe2, Xe3, Xe4, Xe5, PDS, intermediate states between G and H helices (IS1), E and F helices (IS2), and C and F helices (IS3), and the entrance of channel 1 (Ch1). Ligand density that escaped the protein into the solvent was grouped into a separate cluster and referred to as WAT. Thus, the entire data set was divided into 11 clusters. (See the Supporting Material for additional details on the clustering method.) The overall distribution of ligand density obtained from all simulations in trHbN protein is shown in Fig. 1.

The spatial distribution of ligand density provides useful information about ligand docking sites. To characterize the time evolution of ligand density distributions, we constructed transition count matrices, $C\left(\tau \right)$, whose elements C_ij represent the number of observed transitions from state i to state j within time τ. Ideally, for equilibrium sampling, the transition count matrices should be symmetric to satisfy detailed balance, i.e., $C_{ij}\left(\tau \right)=C_{ji}\left(\tau \right)$. However, in practice, due to the finite simulation time, these matrices are only nearly symmetric (2,15,36). From the transition count matrices, we determine the so-called TMs, $T\left(\tau \right)$, via

$$T_{ij}\left(\tau \right)=\frac{C_{ij}\left(\tau \right)}{{\sum }_j{C}_{ij}\left(\tau \right)}.$$ (1)

The matrix elements, $T_{ij}\left(\tau \right)$, provide the probability that the ligand will be found in state j at a time $t+\tau$ given that it was in state i at time t (1). From Eq. 1, it is clear that T is row-stochastic, i.e.,

$$\sum _j{T}_{ij}\left(\tau \right)=1.$$ (2)

The diagonal elements of $T\left(\tau \right)$ represent the population density of the associated state at time τ.

Results and Discussion

A prominent structural feature of trHbN is a continuous tunnel through the protein matrix with two perpendicularly placed channels (Ch1 and channel 2 (Ch2)) that connect the heme active site to the solvent. The residues that define the tunnel entrances and their inner surface are apolar in nature. Ch1 contains pockets Xe1 and Xe5, whereas pockets Xe2, Xe3, and Xe4 are located along the shorter channel (Ch2) (27). In addition to these five Xe pockets, previous simulations (30) revealed the presence of an additional stable docking site (the PDS) situated at the proximal side of the heme group in trHbN. Furthermore, ligand density is also found in intermediate sites between helices G and H (IS1), E and F (IS2), and C and F (IS3), and the entrance of Ch1. Docking sites Xe4, IS2, IS3, and Ch1 are spatially close to the solvent (30).

Ligand migration network in trHbN

The TMs calculated with Eq. 1 are shown in Fig. 2 for a range of lag times (τ = 1, 10, 50, 100, 200, and 500 ps, where τ is defined as the time interval between two subsequent observations of the system). The black squares along the diagonal of the TM at τ = 1 ps show that little density transfer occurs within this period of time, with the exception of Xe3 → IS1 and Ch1 → Xe1. It was previously reported that ligand transfer from the Xe3 pocket is very rapid (30). Also, the entrance of Ch1 is a metastable state that is spatially connected to the Xe1 pocket (see Fig. 1).

Figure 2.

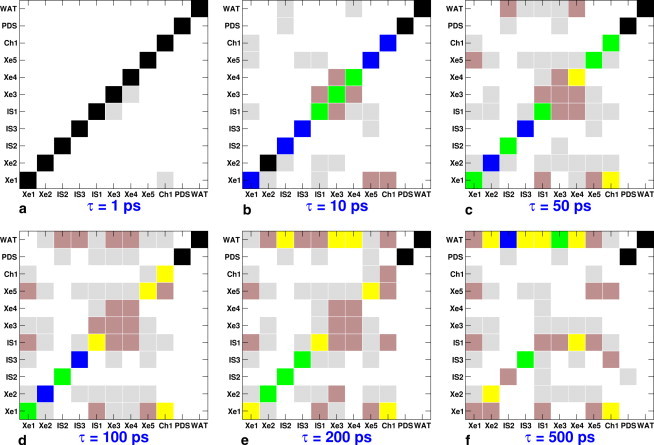
TMs for NO migration within the docking sites of trHbN for different lag times τ. The matrix elements are color-coded, with black, blue, green, yellow, brown, gray, and white for T_ij > 0.9, 0.9–0.7, 0.7–0.5, 0.5–0.3, 0.3–0.1, 0.1–0.01, and <0.01, respectively. The diagonal elements represent the population density of the concerned docking site, and the off-diagonal elements represent transitions between a docking site in a row and a docking site in a column.

A significant number of transitions between the docking sites within 10 ps of simulations is apparent from the increased intensity in the off-diagonal matrix elements of T_ij at τ = 10 ps (see Fig. 2 b). The ligand density is depleted from all of the docking sites except for Xe2 and PDS. The depletion of density is substantial for the Xe3, Xe4, and IS1 docking sites. From Xe3 most of the density is transferred to Xe4 and IS1 docking sites, and only a small fraction migrates to Xe2. For the Xe4 pocket, density flows to the Xe3 and IS1 docking sites, and toward bulk solvent. On the other hand, the probability density from IS1 is transferred primarily to Xe3 and Xe1 docking sites and a small fraction of the density also flows to the Xe5 docking site. The other notable ligand migration on the 10 ps timescale is between Xe5 ↔Xe1 and Ch1 ↔Xe1. Ligand migration between Xe1 and Xe5 pockets has been shown to be controlled by residue Phe⁶², which exists in two conformations that close or open the migration pathway between Xe1 and Xe5 (26,27,30). Thus, the fastest ligand migration occurs within Ch1 and Ch2 of trHbN and the pathway via IS1. It is also seen that a small fraction of ligand density from IS2 is lost to bulk water within 10 ps. The ligand in this case escapes the protein via the extratunnelar pathway located between helices C and F of trHbN, as previously shown (29,30).

The TM at lag times of 50 ps is shown in Fig. 2 c. The populations of pockets Xe3 and Xe4 are <50% of their initial density, suggesting that the ligand has a smaller half-life period in these pockets. Fig. 3 shows the population density of the docking sites as a function of time, which is essentially the time evolution of the diagonal elements of the TM. The time needed for the population density of a given docking site to reduce to half of its initial value represents the half-life period of the ligand in a particular docking site, which is shown in Fig. 3. A large portion of ligand density from Ch1 is transferred to Xe1. Additionally, some of the density flow Ch1 →Xe1 is further transferred to IS1 and Xe5. Therefore, the transition probabilities shown as Ch1 →Xe5 and Ch1 →IS1 are essentially Ch1 →Xe1 →Xe5 and Ch1 →Xe1 →IS1. The majority of the transitions within 50 ps are primarily restricted to within the protein tunnel and the pathway via the Xe1 docking site. Within 50 ps, we can see a significant population loss from IS2 and Xe4 to bulk water. Additionally, the IS1, IS3, and Xe3 docking sites also lose ligand to bulk water. To escape from the Xe3 and Xe4 docking sites, the ligand uses the opening of Ch2, whereas escape from IS3 occurs via the exit pathway located between helices E and F of trHbN (28,30).

Figure 3.

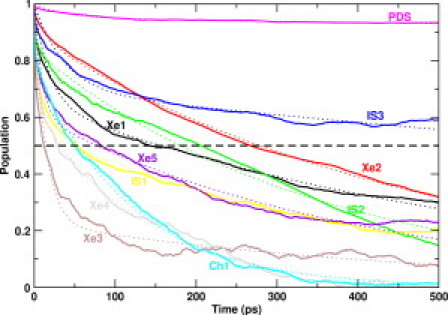
Population decay of the docking sites as a function of time. The horizontal line at population density 0.5 determines the half-life period of the ligand in a given docking site. The fitted double exponential functions are shown as dotted lines. See Table 1 for associated time constants.

At $\tau =100$ ps, ∼30% of the ligand density of the Xe3, Xe4, IS2, and IS3 docking sites has been lost to bulk water, whereas ∼10% of the ligand density of Xe2, Xe5, Ch1, and IS1 has escaped the protein. The escape from sites Xe2, Xe5, Ch1, and IS1 is primarily indirect, since the ligand first migrates to one of the Xe4, IS2, and IS3 sites before leaving the protein. The last column of the TM (Fig. 2) represents ligand migration from bulk water to any of the protein docking sites. This column always remains empty because our simulations are not sufficiently long to capture the reentrance of the ligand from bulk to protein. Furthermore, the column corresponding to PDS also remains blank because once the ligand enters the PDS, it remains there for the rest of the simulation. By 200 and 500 ps (Fig. 2, e and f), a significant fraction of ligand density from all of the protein docking sites has been lost to the bulk solvent.

To extract the time constants associated with the population decay shown in Fig. 3, we fit the population profiles to exponential decay functions. We found that for most of the population profiles (except for PDS), a double exponential form was necessary for a satisfactory fit. Thus, the ligand population density was fit to

$$p\left(t\right)=a_1\exp \left(-t/{\tau }_1\right)+\left(1-a_1\right)\exp \left(-t/{\tau }_2\right)$$ (3)

where $p\left(t\right)$ is the ligand population density in a specific docking site at time t, and ${\tau }_{1,2}$ are the corresponding time constants with coefficients a₁ and $1-a_1$, respectively. The time constants and corresponding coefficients for all docking sites are summarized in Table 1. The time constants associated with rapid transitions between docking sites are often a few tens of picoseconds, whereas those for slower transitions are an order of magnitude larger. This is reminiscent of NO migration in myoglobin, where the rebinding kinetics of photolyzed NO has been associated with time constants of 5.3 and 133 ps (37), and similar time constants have also been reported (38,39). The decay in docking sites PDS and Xe2 has a small fast component $\left(a_1\le 0.1\right)$ that reflects the ligand stability in these two docking sites. In contrast, the Xe3 site has a large coefficient for rapid transitions (${\tau }_1=14$ ps), suggesting that the docking site is metastable. The diffusion coefficients of the ligand in different docking sites vary between 0.05 and 1 Å²/ps, which compares reasonably well with the diffusion coefficient (0.21 Å²/ps) of O₂ in water at 298 K (40) and typical traveling times in the ballistic regime. The largest diffusion coefficients (≈1 Å²/ps) correspond to diffusion within the Xe4 pocket, which also reflects the rather rapid escape of NO toward the solvent observed in the TN analysis.

Table 1.

Double exponential fit of the population density in the docking sites

Docking site	τ1	$a_1$	τ2	$a_2$
Xe1	585	0.65	18	0.35
Xe2	487	0.90	13	0.10
IS2	350	0.80	2	0.20
IS3	2248	0.70	36	0.30
IS1	417	0.55	7	0.45
Xe3	14	0.85	475	0.15
Xe4	106	0.60	4	0.40
Xe5	390	0.60	10	0.40
Ch1	120	0.80	1	0.20
PDS	>6000	1.00

The time constants τ_1,2 are in picoseconds.

To validate the population dynamics obtained by TNA, we analyzed additional MD simulations (50 trajectories of 60 ps each) starting from a snapshot with the ligand in the Xe3 site. The distance between the heme-Fe atom and the ligand center of mass for all trajectories are shown in Fig. 4 a as a function of simulation time. It can be seen that the ligand rapidly leaves the Xe3 pocket and migrates to the Xe2 pocket (small Fe-ligand distance in the figure) or the Xe4, IS1, and Xe1 docking sites (larger Fe-ligand distance in the figure). Reentrance of the ligand from the Xe2 docking site to the Xe3 docking site is a rare event compared to that from other docking sites (Fig. 4 a). Fig. 4 b shows the fraction of trajectories with ligand in the Xe3 docking site as a function of simulation time (shown as black circles). The solid line in Fig. 4 b shows the population density of the Xe3 docking sites obtained from the TNA of long trajectories, which is also the brown curve in Fig. 3. We see excellent agreement between the population densities obtained from the two methods for short times, and deviations at longer times. Nonetheless, the agreement is satisfactory and improves with an increasing number of independent trajectories (see the comparison of population densities in Fig. 4 b).

Figure 4.

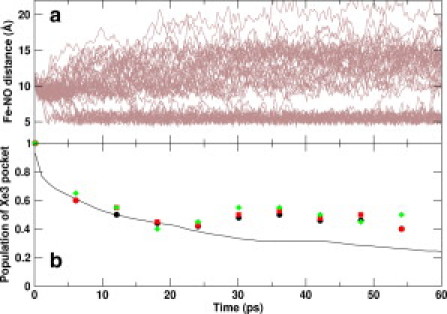
Migration of NO ligand in 50 short trajectories started from a snapshot with the ligand in the Xe3 pocket. (a) Distance between the Fe atom of heme and the center of mass of the NO ligand plotted against the simulation time for 50 trajectories. (b) Fraction of trajectories with NO in Xe3 against simulation time (shown as diamonds, squares, and circles for 30, 40, and 50 trajectories, respectively). The solid line represents the time evolution of the ligand density in Xe3 pocket obtained from the TNA of long trajectories (also shown as a brown curve in Fig. 3).

Using the above information, we constructed a connectivity network (Fig. 5) in which the nodes represent the docking sites and the edges represent the transition between them. Furthermore, the edges are color-coded according to the transition time. This connectivity network is dynamic in nature, in the sense that it provides temporal information about ligand migration in addition to spatial information.

Figure 5.

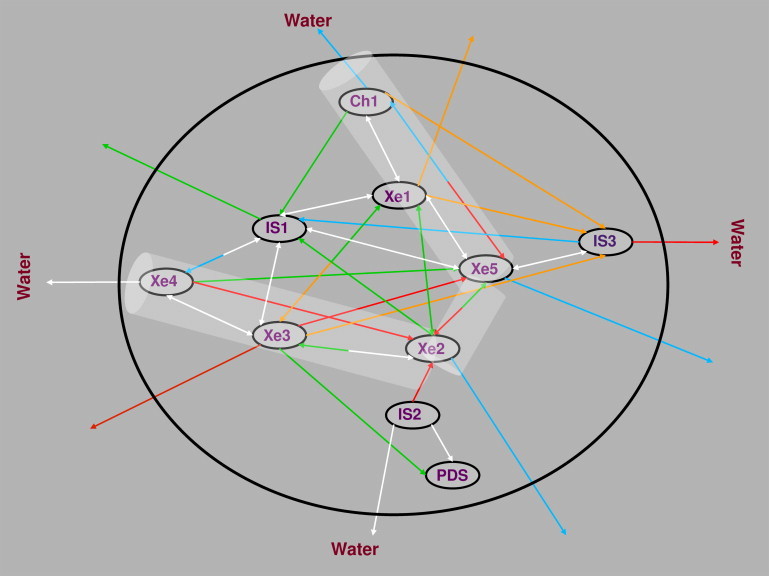
Time-resolved connectivity network between the ligand docking sites in trHbN. The white, red, green, blue, and orange arrows represent ligand transitions faster than 10 ps; within 10–50 ps, 50–100 ps, and 100–200 ps; and slower than 200 ps, respectively. The escape of ligand to bulk water is represented by arrows to water. The protein and surrounding bulk water are demarcated by the black sphere. The tunnels in trHbN are outlined as a mesh.

It can be seen that the fast transitions (white arrows) primarily occur between pockets within one of the two channels. In addition to these transitions, the IS1 site is found to be an important hub. From Fig. 5, it appears that IS1 is an important docking site for ligand migration that provides a connection between Ch1 and Ch2. Transitions between Xe1 ↔Ch1 and Xe5 ↔IS3 are also fast, since Ch1 and IS3 sites are to some extent extensions of Xe1 and Xe5 pockets, respectively. In contrast to the fast transitions, the slower transitions often involve intertunnelar or indirect ligand migration. The indirect migration involves transitions between two docking sites that are not directly (spatially) connected to each other, but instead have a common connecting docking site. For example, ligand migration between Xe5 and Ch1 always occurs via Xe1. As expected, these indirect transitions are comparatively slow. The timescale needed to explore the network (several hundreds of picoseconds) emerging from this analysis is in the range of the overall second-order NO detoxification rate constant ($k=7.5\times {10}^8$ M⁻¹s⁻¹) observed in oxy-trHbN. Such a rate corresponds to processes on the pico- to nanosecond timescale, and involves both ligand migration to the Xe2 docking site and the subsequent oxidation reaction (24,41).

Another feature that emerges from Fig. 5 is the nature of a hub or node. Depending on the type of incoming and outgoing transitions from the docking sites, we can divide the nodes into three types: 1), nodes where in- and outflow occurs rapidly; 2), outflow is faster than inflow; and 3), inflow is faster than outflow. Docking sites IS1 and Xe4 are good examples of type 1 nodes with fast ligand migration. An example of a type 2 node is IS3, which is an outlying ligand hub that has low connectivity to other docking sites and is adjacent to bulk water. Upon entering IS3 from Xe5, the ligand rapidly leaves the protein via the exit pathway located between helices E and F. Type 3 nodes, such as Xe2 and PDS, are stable sites. Ligand migration to PDS is unidirectional, since upon entering the PDS, the ligand does not leave the pocket for the rest of a particular trajectory (Fig. 2). It is also found that ligand migration from Xe3, Xe4, and Xe5 to Xe2 is highly probable, whereas the reverse process has a lower probability (Fig. 5). Note that the incoming and outgoing arrows from the Xe2 pocket represent different timescales. This nature of the Xe2 pocket makes it a stable ligand docking site toward ligand outflow, which has been attributed to the presence of ligand stabilizing Tyr³³ and Gln⁵⁸ residues (see discussion of mutants below).

In our simulations, ligand escape to bulk water is a frequent process. The docking sites with close access to the entrance of Ch2 (e.g., Xe3 and Xe4 pockets) have a high probability of losing the ligand to water. In addition to the opening of Ch2, the exit pathways located between helices E and F (via IS3) and helices C and F (via IS2) are also preferred routes for ligand escape to the bulk. The IS2 and IS3 sites are located close to bulk water and act as gates (bottleneck) for ligand escape. Residues Pro⁷¹, Tyr⁷², Pro¹²¹, and Thr⁴⁹ line the exit pathways and the IS2 and IS3 docking sites, and are favored escape pathways for charged or polar ligands (28–30). On the other hand, a nonpolar ligand such as O₂ prefers the openings of the two channels of the tunnel that are surrounded by nonpolar residues. Thus, NO represents the intermediate situation in which both nonpolar and polar exit pathways are operative (30). Fig. 5 allows us to determine the sequence of docking sites with increasing probability for NO migration to bulk water, as follows: PDS, Xe1, Xe2 ∼ Xe5 ∼ Ch1, IS1, IS3, Xe3 ∼ Xe4 ∼ IS2.

Markov model for ligand migration

An even more compact representation of a TN is that of a Markov model, which, given a particular TM T, would allow one to capture the temporal evolution of the entire system. Thus, we constructed a Markov model to describe ligand migration in trHbN. Various methods can be used to investigate the Markovianity of a process (2–4,15,18,42,43). Here, we use characteristic timescales (also known as “implied timescales”) associated with the decay of an eigenmode i given by (15):

$${\tau }_i^{\ast }=-\frac{\tau }{\ln {\lambda }_i},$$ (4)

where $\lambda \left(i\right)$ is the ith eigenvalue of T at lag time (τ). For a Markovian process, τ^∗ is constant (43). The implied timescales for the eigenmodes of T for a range of lag times (τ) show that τ^∗ continues to increase only moderately after ≈100 ps (Fig. 6 a). However, no real plateau for τ^∗ was found (note the logarithmic scale in Fig. 6 a).

Figure 6.

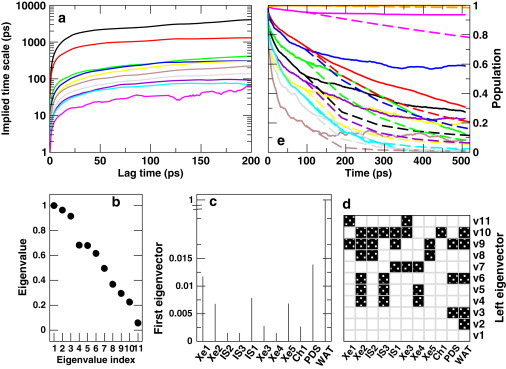
(a) Implied timescale (see Eq. 4) obtained from the TM (T) of ligand migration in trHbN as a function of lag time (τ). (b) Eigenvalue spectrum, (c) the first (left) eigenvector, (d) all eigenvectors of the TM at τ = 100 ps. The solid and open boxes indicate whether the eigenvector component is negative or positive, respectively. (e) Population dynamics of the docking sites obtained from TNA (solid lines) and the Markov model (dashed lines); see Eq. 3. The color-coding is identical to that in Fig. 3.

For further analysis of Markovianity, Fig. 6 b shows the eigenvalue spectrum of the TM at τ = 100 ps. The first eigenvalue is unity, followed by two eigenvalues that are somewhat separated from the rest of the eigenvalues indicating the number of metastable states. The first (left) eigenvector of T provides the stationary state distribution (Fig. 6 c). At equilibrium, the population is primarily concentrated in water (note the large intensity of water in Fig. 6 c). This indicates, in agreement with the simulations, that ligand escape from the protein is the dominating process at longer timescales. The ligand population in the docking sites of the protein is minimal at equilibrium (Fig. 6 c).

The first eigenvector provides the equilibrium properties, whereas the sign structure of other eigenvectors partitions the state space into several metastable states. The eigenvectors of T at τ = 100 ps is given in Fig. 6 d, where the negative component of an eigenvector is shown by a solid box and the positive components are represented by open boxes. The first eigenvector has all positive components. The second eigenvector has one negative component, which corresponds to the ligand density in water. The third eigenvector has two negative components corresponding to the water and PDS docking sites. The higher eigenvectors represent the transition modes among the metastable states, which in this case represent the ligand docking sites of trHbN.

The second and third eigenvectors suggest particular partitions of the state space. The first partition (given by the second eigenvector) divides the state space into intra- and extra-protein states (bulk water). The next partition (given by the third eigenvector) is between the PDS and the other docking sites. This agrees with the TNA, which showed that the PDS is an isolated docking site with infrequent ligand migration in and out of it. On the other hand, ligand migration occurs quite frequently between the remaining docking sites.

Although the implied timescales and the decomposition of eigenvalue spectrum are essential indicators of Markovianity, a comparison of the relaxation dynamics from MD simulation and Markov model prediction remains the quintessential test for Markovianity. For a Markov process, we can express the population of the states at some time t + nτ by applying the transfer matrix n times to a population at a previous time t, i.e.,

$$p\left(t+n\tau \right)=p\left(t\right)T^n\left(\tau \right).$$ (5)

Fig. 6 e compares the population dynamics of the docking sites obtained from the TNA with the relaxation dynamics predicted by Markov state model using Eq. 5, where the initial population distribution was that at τ = 100 ps. The comparison suggests that the Markov model predicts population decay in a qualitative manner. The predictability of the Markov model can be improved by using a TM at larger τ. It is also established that one can construct better Markov models by partitioning the state space into metastable states in such a way that a minimal lag time is achieved (15,18). However, in the case presented here, where state space is divided into different docking sites of trHbN, the qualitative agreement between TNA and the Markov model is satisfactory.

Ligand migration in trHbN mutants

The ligand-stabilizing residues Tyr³³ and Gln⁵⁸ have been proposed to play an important role in the NO detoxification reaction in trHbN (24,44,45). Residues surrounding the Xe2 pocket restrict the movement of free NO by hydrogen bonding (45). To study the role of Tyr³³ and Gln⁵⁸ in NO migration from the Xe2 docking site, we ran 10 trajectories (each for 1 ns) for four mutants of trHbN: 1), Y33F; 2), Y33A; 3), Y33F + Q58A; and 4), Y33A + Q58A. In contrast to the simulations in wild-type (wt) trHbN, where several trajectories were run with NO in different docking sites, trajectories for the mutants were run with NO only in the Xe2 pocket, which is surrounded by Tyr³³ and Gln⁵⁸ residues.

The number of trajectories with NO in the Xe2 docking site is shown in Fig. 7 a at intervals of 100 ps. After 1 ns, in five of the 10 trajectories for the wt, the ligand is still in the Xe2 pocket (circles in Fig. 7 a). On the other hand, for all four mutants, a smaller number of trajectories (two for Y33A + Q58A, and three for the other three mutants) contain the ligand in the Xe2 site. This indicates that NO is stabilized in the Xe2 site in the wt protein. By comparing the single mutants with the corresponding double mutants, we found that the ligand exhibits more rapid migration away from the Xe2 pocket when neither of the two stabilizing residues are present. From Xe2 the ligand migrates to different docking sites, such as Xe3, Xe4, and Xe1. Also, the return of NO to the Xe2 pocket is seen in these trajectories. This is reflected by the increase in the number of trajectories with ligand in the Xe2 pocket (Fig. 7 a). The distribution of ligand density along the Fe-N_NO coordinate is shown in Fig. 7 b for the wt trHbN as well as its four mutants. The peaks at ∼6 Å of Fe-N separation correspond to the ligand in the Xe2 docking site. The peaks at larger Fe-N separations correspond to the Xe3, Xe1, and Xe5 docking sites (30). The distribution profiles can also be translated to the residence time of the ligand in different docking sites by multiplying the normalized population by the total simulation time (10 ns). Fig. 7 b shows that the probability of finding the ligand in the Xe2 docking site is significantly larger for the wt compared to its mutants. The strong and sharp peak of ligand distribution at an Fe-N distance of 6 Å for the wt clearly shows the role of the Tyr³³ and Gln⁵⁸ residues in stabilizing the ligand and restricting its movement. This peak decreases for single mutants and more so for the double mutants (see Fig. 7 b), suggesting the absence of ligand-stabilizing residues in the Xe2 docking site. The observed asymmetry in transition times (discussed above) may be evolutionary, since the stability of the ligand in this docking site influences the NO detoxification reaction occurring inside the Xe2 active site of the protein. Facile ligand inflow and delayed outflow due to ligand-stabilizing residues Tyr³³ and Gln⁵⁸ provide sufficient time for efficient NO detoxification (23,24).

Figure 7.

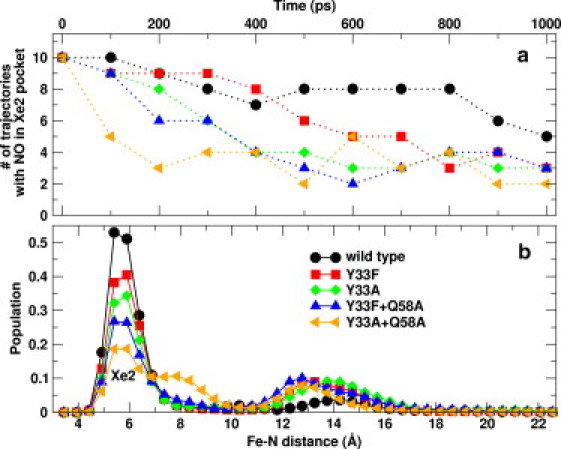
(a) Number of trajectories with NO in the Xe2 docking site for 1 ns of MD simulation. (b) Probability distribution of NO ligand in wt trHbN (black) and its four mutants: Y33F (red), Y33A (green), Y33F + Q58A (blue), and Y33A + Q58A (orange).

Conclusions

This work provides a novel and quantitative analysis of the dynamics of ligand migration in proteins based on TNs. We constructed TMs by clustering the ligand density into different docking sites and monitoring the transitions between them as a function of time. In comparison with protein folding (10–14), the definition of a state is less ambiguous in the case presented here because well-defined internal pockets provide a structural definition. Furthermore, these states can also be probed experimentally (46,47). Our results provide a detailed picture of the probability flux between all accessible metastable states, and the logic behind a ligand-migration network in space and time. Most of the transitions occur on the subnanosecond timescale, which should make them accessible to time-resolved experiments together with spectroscopic techniques (48–51). Also, it is shown that harvesting trajectories from many different initial states leads to a kinetic model in close agreement with explicit long-duration simulations. This makes TNA a relevant and robust technique for treating related problems.

With recent advances in time-resolved crystallography and vibrational spectroscopy, it is now possible to obtain snapshots in time of ligand migration between different docking sites (49,52,53). However, such methods are not used routinely to investigate complicated migration networks with several docking sites and multiple migration pathways, and rapid ligand migration between the docking sites. Although experimental snapshots taken at different times allow us to investigate the population decay of particular docking sites, they do not provide direct insight into the migration pathways and hence the transition rates between the sites. Under such circumstances, computational studies provide an attractive alternative to characterize migration pathways between docking sites. Below, we compare our findings with the available experimental data:

• 1.The timescale of ligand migration found here (tens to hundreds of picoseconds) is commensurate with the timescale for NO detoxification in trHbN (rate constant = 7.5 × 10⁸ M⁻¹s⁻¹) (23,24), which involves ligand migration to the active site and the oxidation reaction of NO.
• 2.The time constants associated with the population decay of the Xe2 docking site (which is the active site for ligand binding and ligand oxidation) obtained in this work (13, 487 ps; see Table 1) are comparable to the NO rebinding timescale in MbNO, which ranges from (27.6, 279.3 ps) (39) to (5.3, 133.0 ps) (37) determined from experiment and from (3.1, 18.9 ps) (38) to (3.6, 373.0 ps) (54) from atomistic simulations with and without dedicated force fields for the Fe-NO interaction, respectively.
• 3.The faster ligand inflow and slower outflow from the Xe2 pocket found here is a physiological requirement for efficient ligand oxidation in the Xe2 pocket.
• 4.The ligand migration studies of the Y33 and Q58 trHbN mutants corroborate previous experimental studies that suggested a stabilization of the NO-ligand by residues Y33 and Q58 (24,44). Furthermore, the TNA reproduced the findings from atomistic simulations, including faster migration between the pockets in the tunnel and the relative stability of the ligand in different docking sites.

The above discussion suggests that a combination of experiments, atomistic simulations, and TNA can lead to a complete understanding of the structural and kinetic aspects of ligand migration in proteins. Finally, we note that processes on the ≈100 ps timescale observed in explicit MD simulations are quantitatively captured by a TNA (see Fig. 4 b). On the other hand, MD simulations have been shown to provide near-quantitative agreement with experimental data for NO and CO migration in Mb (38,55). In MbCO, the experimental rebinding times in wt and the L29F mutant have been correctly reproduced via a combination of MD and stochastic simulations (55). Taken together, our results, as well as the fact that experimental studies of ligand kinetics between neighboring sites in a protein are extremely difficult to perform (47,51, G. U. Nienhaus, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, personal communication, 2010) and probably can be applied to only a few select proteins in the near future, suggest that the approach discussed in this work is a promising step forward in characterizing ligand migration in proteins at an atomistic level.