Single-Molecule Adhesion Forces and Attachment Lifetimes of Myosin-I Phosphoinositide Interactions

Abstract

Phosphoinositides regulate the activities and localization of many cytoskeletal proteins involved in crucial biological processes, including membrane-cytoskeleton adhesion. Yet little is known about the mechanics of protein-phosphoinositide interactions, or about the membrane-attachment mechanics of any peripheral membrane proteins. Myosin-Ic (myo1c) is a molecular motor that links membranes to the cytoskeleton via phosphoinositide binding, so it is particularly important to understand the mechanics of its membrane attachment. We used optical tweezers to measure the strength and attachment lifetime of single myo1c molecules as they bind beads coated with a bilayer of 2% phosphatidylinositol 4,5-bisphosphate and 98% phosphatidylcholine. Adhesion forces measured under ramp-load ranged between 5.5 and 16 pN at loading rates between 250 and 1800 pN/s. Dissociation rates increased linearly with constant force (0.3–2.5 pN), with rates exceeding 360 s⁻¹ at 2.5 pN. Attachment lifetimes calculated from adhesion force measurements were loading-rate-dependent, suggesting nonadiabatic behavior during pulling. The adhesion forces of myo1c with phosphoinositides are greater than the motors stall forces and are within twofold of the force required to extract a lipid molecule from the membrane. However, attachment durations are short-lived, suggesting that phosphoinositides alone do not provide the mechanical stability required to anchor myo1c to membranes during multiple ATPase cycles.

Introduction

Phosphoinositides regulate the activities and localization of scores of cytoskeletal proteins that function in numerous cell processes, including cell migration, membrane trafficking, cell morphology, and cytoskeleton-membrane adhesion (1,2). Remarkably little is known about the mechanical properties of peripheral membrane proteins or phosphoinositide-protein interactions, specifically. Understanding the mechanical properties of membrane-binding proteins is of particular importance when considering force-generating motor proteins that attach directly (3–6) or indirectly (7) to membranes.

Class-I myosins are single-headed, membrane-associated members of the myosin superfamily that are found in nearly all eukaryotic cells (8). Myosin-Is comprise the largest unconventional myosin family found in humans (eight genes), and the large size and expression profile of the family distinguishes it as one of the most diverse. Myosin-Ic (myo1c) is a widely-expressed isoform that associates directly with cellular membranes, where it functions in a variety of cellular processes, including exocytosis (9,10), endocytosis (11), and mechano-signal transduction (12,13). A pleckstrin-homology (PH) domain in the C-terminal tail region of myo1c interacts with phosphoinositides, and this interaction is required for localization of myo1c to the plasma membrane (4,6,14). Recent experimental work with other vertebrate myosin-I isoforms also point to the importance of this PH domain in membrane localization (14,15). However, regions outside of the PH domain also contribute to membrane binding (14,16,17). Myosin-I has been implicated in generation of membrane tension (18), and exciting new work has shown that myosin-I functions as a mechanical linker where it stabilizes adhesion between the cytoskeleton and the plasma membrane (19). The mechanical elements that mediate adhesion have not been identified, but they include interactions between the PH-containing tail and anionic phospholipids (4).

The goals of this study are to:

• 1.Establish an assay for measuring the mechanical properties of the bonds between a membrane and a peripheral-membrane protein.
• 2.Determine the adhesion strength and force-dependent lifetime of myo1c- phosphoinositide interactions with the ultimate goal of understanding the role of membrane binding in myosin-I function.

Materials and Methods

Proteins and reagents

A construct (myo1c^IQ-tail) that contains the tail and regulatory domains of mouse myo1c (residues 690–1028) and N-terminal poly-His and avitag (20) sequences was coexpressed with calmodulin in Sf9 cells using a Baculovirus expression system and purified as described (17,21). The lysine in the avitag sequence was specifically biotinylated using 20 μg/mL BirA (Avidity, Denver, CO) at 30°C for 1 h. Biotinylated myo1c^IQ-tail was dialyzed overnight against HNa100 (10 mM HEPES, pH 7, 100 mM NaCl, 1 mM EGTA, and 1 mM DTT), flash-frozen in liquid nitrogen, and stored at −80°C.

Preparation of lipid-coated hydroxylated polystyrene beads

Hydroxylated polystyrene beads were coated with membranes containing 2% PtdIns(4,5)P₂ and 98% DOPC or 100% DOPC. Briefly, multilamellar and small unilamellar vesicles were prepared as described in Galneder et al. (22) with modifications. DOPC (1,2-Dioleoyl-sn-glycero-3-phosphocholine; Avanti Polar Lipids, Alabaster, AL) was mixed with 2 mol % of PtdIns(4,5)P₂ (L-α-phosphatidylinositol-4,5-bisphosphate, Porcine Brain-Triammonium salt; Avanti Polar Lipids) in a 50-mL round-bottom flask. The solution was thermally equilibrated in a water bath at 35°C for 5 min and dried rapidly (∼1 min) in a rotary evaporator. The lipid film was kept under hard vacuum overnight to remove chloroform. Multilamellar vesicles were formed by vortexing the flask for 2 min after adding 1 mL of HNa100 (5 mM total lipid concentration).

The lipid mixture was tip-sonicated for 13 min on ice in bursts of 10 s followed by 30 s of no sonication. The small unilamellar vesicles were ultracentrifuged at 100,000 ×g for 30 min in polycarbonate tubes to remove multilamellar vesicles and any other insoluble particles. The upper two-thirds of the supernatant was mixed with 6 μL hydroxylated polystyrene beads (1 μm diameter, 4.55 × 10¹⁰ particles/mL; Polysciences, Warrington, PA) that were freshly washed in water. The mixture was vortexed for 5 min and incubated at room temperature for 4 h. Finally, beads were resuspended and washed twice with HNa100. Beads were kept on ice and used within two days. Coating of beads with membranes containing 2% PtdIns(4,5)P₂ was verified by fluorescence microscopy with lipid doped with 0.5% 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-n-(lissamine rhodamine B sulfonyl) (ammonium salt) (Fig. 1). The same procedure was used for beads coated with 0.5% 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-n-(Cap Biotinyl)-99.5% DOPC or 100% DOPC.

Figure 1.

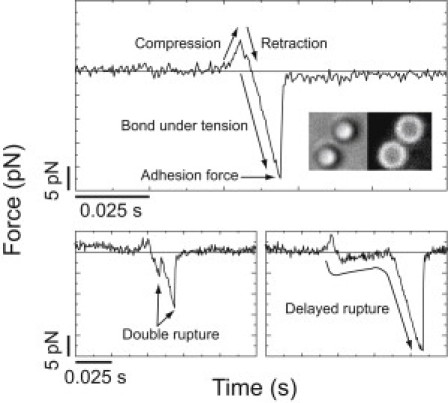
Representative examples of ramp-load rupture events. (Top) The three characteristic regions are: compression of the bead on the pedestal, retraction of the bead in the opposite direction until the compressive force reaches zero, and bond under linearly increasing tension until rupture. (Inset) Transmitted and fluorescence micrographs showing 1-μm-diameter beads coated with 2% PtdIns(4,5)P₂, 97.5% DOPC, and 0.5% LRPE (1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-n-(lissamine rhodamine B sulfonyl)). (Bottom, left) Double rupture and (bottom, right) delayed rupture events made up <10% of interactions and were excluded from the analysis.

Ramp force measurements

A diagram of the experimental geometry is provided in Fig. S1 in the Supporting Material. Nitrocellulose-coated chambers containing 2.5-μm-diameter silica pedestals (Bangs Laboratories, Fishers, IN) were prepared as described (23). All proteins and reagents were prepared in HNa100. During attachment of biotinylated myo1c^IQ-tail and in all subsequent steps, 5 μM calmodulin was included in the buffers to ensure the IQ motifs of myo1c^IQ-tail remained calmodulin-saturated (24). Solutions were added to the chamber in the following sequence:

• 1.0.01 mg/mL neutravidin (Sigma, St. Louis, MO) for 5 min.
• 2.2 mg/mL glutathione-S-transferase as a nitrocellulose blocking agent for 5 min.
• 3.0.2–2.5 nM biotinylated myo1c^IQ-tail, 2 mg/mL glutathione-S-transferase, 5 μM calmodulin for 5 min.
• 4.Three chamber volumes 5 mg/mL casein (made from 10 mg/mL stock solution and filtered to remove solids; Sigma), 5 μM calmodulin.

Lipid-coated beads were diluted 100-fold in HNa100 that contained casein and 5 μM calmodulin, and were injected to one side of the chamber. Although we found casein to be an effective nitrocellulose blocking agent that minimizes nonspecific interactions, it was used after myo1c^IQ-tail was attached to neutravidin due to biotin contaminants in the casein. The chamber was sealed with silicon vacuum grease (Dow Corning, Midland, MI). Chambers were used for <60 min after preparation.

Optical trap instrumentation was as described in Takagi et al. (23) with a water instead of oil objective. The trap stiffness and the force calibration coefficient (pN/V) were determined by the power spectrum of the thermal motion of a trapped bead (25). Data were collected for each lipid-coated bead for 1–2 min against 4–5 different pedestals. LabVIEW software (National Instruments, Austin, TX) was used for data collection and data analysis.

Ramp force measurements were performed as described (26). Briefly, the trap position was oscillated in a triangular waveform. Lipid-coated beads were compressed against immobilized pedestals while formation and subsequent rupture of bonds upon retraction of the bead appeared as negative peaks in the data traces (Fig. 1). Data were digitized with a 2 kHz sampling rate, amplified, and filtered at 1 kHz. The nominal rate at which load was exerted on membrane-myo1c^IQ-tail attachments (loading rate) was set by controlling the frequency and amplitude of the triangular oscillation and the trap stiffness. The average trap stiffness in ramp force experiments for myo1c^IQ-tail and PtdIns(4,5)P₂ was 0.12 ± 0.01 pN/nm. The oscillation amplitude was ∼0.55 μm and the oscillation frequencies were 1.0, 3.5, and 7.0 Hz, which correspond to loading rates of 260 ± 19, 950 ± 46, and 1900 ± 87 pN/s . The concentration of myo1c^IQ-tail added to the flow chamber was twofold lower when performing experiments at 950 and 1900 pN/s because of the higher occurrence of interactions and double peaks at these rates. For lipid extraction experiments, stiffness was changed to 0.2 pN/nm and oscillation frequency was 2 Hz, which correspond to a nominal loading rate of 1100 ± 31 pN/nm.

Compliance in the membrane-bead attachment resulted in variability of the actual loading rate, so we selected events with actual loading rates within 20% of the nominal rate. Actual loading rates were calculated based on linear fits of the segment between the point where the compressive force becomes zero upon retraction and the rupture point (Fig. 1). We report the loading rates based on this selection (Fig. 2). Selection of events with a more stringent tolerance (10%) did not result in a change in the shape of the adhesion force distributions. Errors in the frequency distributions of rupture events per oscillation cycle were calculated by the bootstrap method (1000 calculated data sets) (27). After subtraction of the nonspecific interactions, the distributions were normalized with respect to the size of the bin and the total number of events to give the probability density, such that

$$\sum _i{h}_i\Delta b=1,$$

where h_i is probability density (pN⁻¹). The probability density distributions, p(F), were fitted to Bell-Evans model for a single transition state (28),

$$p\left(F\right)=k\left(F\right)S\left(F\right)/r\left(F\right),$$ (1)

where the dissociation rate as a function of force (k(F)) is given by Bell's model (29),

$$k\left(F\right)=k_{\text{o}}{e}^{\frac{F{d}_{\text{tr}}}{k_{\text{B}}T}},$$ (2)

where k_o is the dissociation rate in the absence of force (F), d_tr is the distance to the transition state, k_B is Boltzmann's constant, and T is the temperature in Kelvin. The survival probability (S(F)) is

$$S\left(F\right)=e^{\left\{\frac{k_{\text{o}}{k}_{\text{B}}T}{r{d}_{\text{tr}}}\left(1-e^{\frac{F{d}_{\text{tr}}}{k_{\text{B}}T}}\right)\right\}},$$ (3)

and the loading rate (r) is

$$r\left(F\right)=\frac{dF}{dt},$$ (4)

where t is time.

Figure 2.

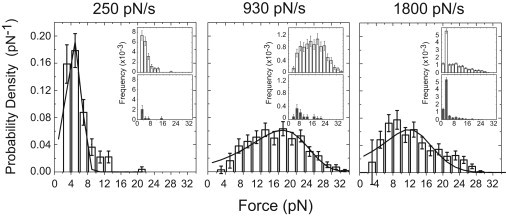
Probability density distributions of forces required to dissociate myo1c^IQ-tail from supported lipid membranes containing 2% PtdIns(4,5)P₂ at loading rates of 250 ± 29, 930 ± 120, and 1800 ± 230 pN/s (standard deviation). The corrected distributions in the main panels were obtained by subtracting (inset, bottom) frequency distributions (per contact cycle) obtained in the absence of myo1c^IQ-tail from (inset, top) uncorrected frequency distributions. (Solid lines) Best fits of the distributions to a model for a single transition barrier (Eq. 1). The fitting results are presented in Table 1, and information regarding numbers of cycles and interactions are presented in Table S1. Errors are standard deviations calculated from bootstrap data sets.

Assuming that the rupture peaks are due to either a single bond or two independent bonds that fail simultaneously, the total rupture probability density (p_tot) can be approximated as Gu et al. (30)

$$p_{\text{tot}}\left(F\right)=Ap\left(F\right)+\left(1-A\right)S\left(F/2\right)p\left(F/2\right),$$ (5)

where A is the fraction of single bonds.

The force dependence of dissociation rate (k_dis) was calculated from the probability density distribution of rupture forces as described in Dudko et al. (31),

$$1/k_{dis}\left(F_{\text{0}}+\left(k-1/2\right)\Delta F\right)=\tau \left(F_{\text{o}}+\left(k-1/2\right)\Delta F\right)=\left(h_k/2+{\sum }_{i=k+1}^N{h}_i\right)\Delta F/\left(h_{k}r\right),$$ (6)

where h_i is the magnitude of the i^th bin, N the number of bins, ΔF the width of the bin, F₀ the force value where binning starts, and r is the loading rate. Because of the large relative errors at the extremes of the probability density distributions, only the central regions of distributions (with <30% relative error) were used in the transformation.

Constant force measurements

Attachment durations under constant tensile force between pedestal-immobilized myo1c^IQ-tail and PtdIns(4,5)P₂ on the lipid-coated beads were measured using a force-clamp scheme similar to that described by Takagi et al. (23), but for a single laser beam instead of two. Briefly, a command square-wave signal (dashed trace, see Fig. 4 A) was applied to a summing junction with the trap force signal, which was fed to a feedback amplifier whose output moved the trap using the acousto-optic deflector. The negative amplitude of the square pulse corresponds to compression of the trapped bead on the pedestal and the positive amplitude to retraction of the bead from the pedestal (see Fig. 4 A). The amplitudes of the square pulse were set to the desired compressive and separating force. When the bead is in mechanical equilibrium (under compression or upon tension if a bond has been formed), the feedback loop settles and the beam is displaced relative to the center of the bead to produce the appropriate compressive or separating force.

Figure 4.

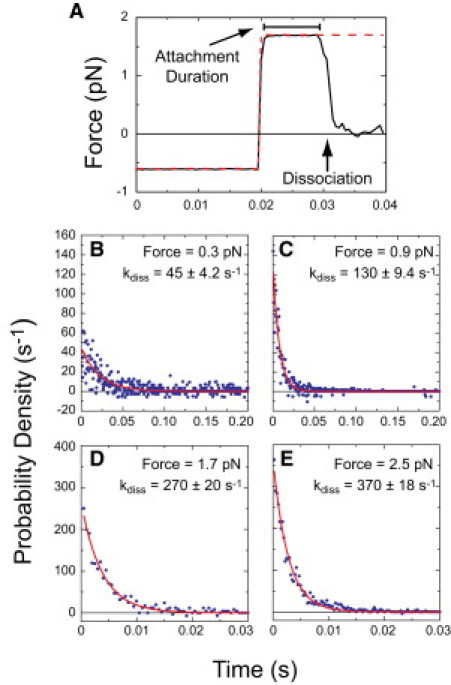
Measurement of myo1c^IQ-tail-membrane dissociation rates under constant tension. (A) The attachment duration of a single attachment under 1.7 pN of load. A square pulse (dashed trace) is the command to drive compression and retraction of the membrane-coated bead. Positive forces on the bond (solid trace) are recorded during attachments. When a bond is formed between the membrane-coated bead and the myo1c^IQ-tail, a constant separating force is maintained via a feedback loop until the bond ruptures. (B–E) Normalized survival probability density of the bond as a function of attachment duration under constant tension is plotted. (Solid lines) Fitting curves of the survival probability densities to Eq. 7. Information regarding number of cycles and interactions are presented in Table S2.

The measurement accuracy of attachment duration was limited by the rate of data acquisition which was necessary to sufficiently sample the distribution of durations at each force. Data points were recorded every 0.5 ms for forces in the range 0.3–1.7 pN and every 0.25 ms for 2.5 pN. In the case of 2.5 pN, we increased the laser trap stiffness (by raising the laser power) from 0.1 to 0.2 pN/nm, to decrease the response time of the feedback circuit and be able to record the very short-lived attachments. Errors in the frequency distributions of attachment-duration per oscillation cycle were calculated by the bootstrap method (1000 calculated data sets) (27). As in the ramp force measurements, after subtraction of the nonspecific interactions, the distributions were normalized with respect to the time width of the bin or equivalently the time resolution and the total number of events to give the probability density. Dissociation rates were determined by fitting the probability density distributions to the exponential distribution:

$$k_{dis}{e}^{(-k_{dis}t)}.$$ (7)

Results

Mechanical strength of myo1c^IQ-tail interaction with supported lipid membranes containing 2% PtdIns(4,5)P₂ under a ramp-load

We measured the forces required to dissociate a truncated construct consisting of the myo1c tail and regulatory domain (myo1c^IQ-tail) from beads coated with 2% phosphatidylinositol 4,5-bisphosphate (PtdIns(4,5)P₂) and 98% phosphatidylcholine (DOPC) (Fig. 1). Experiments were performed with 2% PtdIns(4,5)P₂, because it binds to myo1c^IQ-tail tightly and is the predominant phosphoinositide in the plasma membrane. Myo1c^IQ-tail was site-specifically attached to immobilized pedestals (see Materials and Methods) at a low surface density, such that fewer than 10% of the pedestal-bead contacts resulted in interactions. Three types of ramp-load rupture events were observed: single peak, double peak, and delayed peak (Fig. 1). Double and delayed peaks made up fewer than 10% of the interactions and were not included in our analysis, as they represent multiple-molecule interactions and membrane tethers, respectively.

The forces required to rupture myo1c^IQ-tail-PtdIns(4,5)P₂ interactions were determined at three different loading rates (Fig. 2). Contributions of nonspecific interactions were removed from adhesion-force frequency distributions by subtracting the frequency distribution of forces acquired in experiments performed in the absence of myo1c^IQ-tail (Fig. 2, inset). Frequency distributions of nonspecific interaction forces were also determined by performing experiments with

• 1.100% DOPC-coated beads interacting with pedestal-bound myo1c^IQ-tail, or
• 2.2% PtdIns(4,5)P₂-coated beads interacting with pedestal-bound myo1c^IQ-tail in the presence of 100 μM InsP₆, which competitively inhibits the PtdIns(4,5)P₂-myo1c^IQ-tail interaction (4,17).

The force distributions of rupture events for all three control experiments were similar, with the average forces below 4 pN (Fig. S2).

Probability density distributions of myo1c^IQ-tail-PtdIns(4,5)P₂ adhesion forces were obtained by normalizing the data with respect to the force-width of the bin and the total number of events (Fig. 2). The average forces at the three loading rates ranged between 5.5 and 16 pN, without a clear correlation with the loading rate (Table 1). Fits of the data to the Bell-Evans model (Eq. 1; Fig. 2, solid line) for a reaction with a single transition state yielded k₀ and d_tr values that were different at each loading rate (Table 1).

Table 1.

Parameters obtained from fits of ramp-force probability density distributions to the Bell-Evans model (Eq. 1)

Loading rate (pN/s)	k0 (s−1)	dtr (nm)	Faverage (pN)
Myo1cIQ-tail-2% PtdIns(4,5)P2 dissociation
250 ± 29	9.4 ± 2.4	2.2 ± 0.35	5.6 ± 0.33
930 ± 120	11 ± 1.8	0.64 ± 0.051	16 ± 0.43
1800 ± 230	43 ± 9.6	0.61 ± 0.13	13 ± 0.89
Lipid extraction
1100 ± 130	12 ± 3.9(8.7 ± 3.7)∗	0.33 ± 0.083(0.45 ± 0.085)∗	27 ± 1.6

Errors are obtained from a bootstrap analysis.

^∗Parameters from fits assuming that the rupture peaks are due to either a single bond or two independent bonds that fail simultaneously (Eq. 5). The fraction of single bonds is A = 0.6 ± 0.1.

To ensure that the myo1c^IQ-tail- PtdIns(4,5)P₂ rupture events were not due to the extraction of lipids from the membrane, we determined the force required to extract a lipid molecule. Beads coated with 0.5% biotinylated lipid and 99.5% DOPC were brought into contact with pedestal-attached neutravidin, and adhesion forces were determined at a loading rate of 1100 ± 130 pN/s (Fig. 3). The average force required to extract a lipid was 27 ± 1.6 pN, which is substantially higher than found for the myo1^IQ-tail-PtdIns(4,5)P₂ interaction at a similar loading rate (Table 1) and is similar to previous measurements (32). Despite the low probability of an interaction (4.6%), the resulting force distribution was bimodal, suggesting the presence of double-bond rupture events, which is likely due to the multivalency of the neutravidin. The predominant distribution is well described by the Bell-Evans model assuming a single bond (Eq. 1; Table 1) or a mixture of single and double bonds (Eq. 5; Table 1) with values that are consistent with previous measurements (32).

Figure 3.

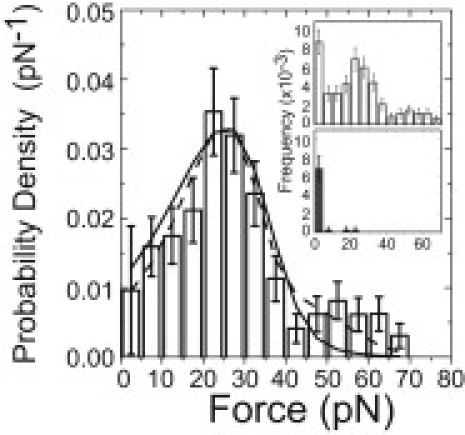
Probability density distribution of forces required to extract a biotinylated-lipid from supported lipid membranes using neutravidin-coated pedestals at a loading rate of 1100 ± 130 pN/s (standard deviation). The corrected distribution was obtained by subtracting (inset, bottom) the frequency distribution acquired in control experiments that did not contain neutravidin from (inset, top) the uncorrected frequency distribution. (Solid lines) Best fit of the distribution to a model for a single transition barrier (Eq. 1). (Dashed line) Best fit of a model that assumes the rupture peaks correspond to single or simultaneous double-bond ruptures (Eq. 5). The fitting results are presented in Table 1. Errors are standard deviations calculated from bootstrap data sets.

Lifetime of myo1c^IQ-tail attachment to lipid membranes containing 2% PtdIns(4,5)P₂, under constant force

We used a force feedback system to measure the lifetime of attachment of 2% PtdIns(4,5)P₂-coated beads with myo1c^IQ-tail at constant force (Fig. 4). A square waveform was applied to the laser beam bringing the lipid-coated bead into contact with the pedestal for 0.2 s under a constant compressive force of 0.5–0.6 pN. The bead was retracted, and if a bond was formed, a constant tensile force was applied until the bond ruptured (Fig. 4 A). Dissociation events that took place in two steps were recognized by the two-step character of the feedback loop output trace, and consisted ≤10% of the interaction events.

We detected attachments that survived for longer than 0.25–0.5 ms (see Materials and Methods) at tensile forces of 0.3–2.5 pN (Fig. 4). This range is similar to the unitary forces generated by myosin-I (33,34). Protein concentrations were the same as above, such that <10% of the pedestal-bead contacts resulted in specific interactions (Fig. S3). The contributions of nonspecific interactions were removed from the distributions using the controls described above, and the data were normalized with respect to the duration of the bin width and total number of events to obtain survival probability densities (Fig. 4, B–E). Survival probability densities at each force were well fit to a single exponential (Eq. 7) to yield dissociation rates (k_dis) (Fig. 4, B–E). Surprisingly, the force dependence of k_dis has a linear force dependence for the range of tested forces (Fig. 5).

Figure 5.

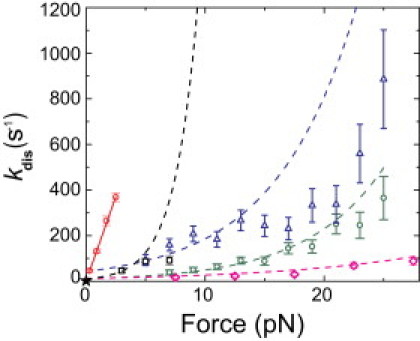
Plot of the dissociation rate of myo1c^IQ-tail from 2% PtdIns(4,5)P₂-containing membranes as a function of applied separating force (open, red circles). The dissociation rate of myo1c^IQ-tail measured at zero force via stopped-flow experiments (17) is shown as a star. A weighted linear fit (solid, red line) gives a slope of 150 ± 10 s⁻¹ pN⁻¹ and a y intercept of 0.45 ± 2.7 s⁻¹ (correlation coefficient = 0.998). Force-dependences of dissociation rates were calculated (Eq. 6) from ramp force histograms obtained at loading rates of (open, black squares) 250, (open, green circles) 930, and (open, blue triangles) 1800 pN/s. The force dependence of the rate of lipid extraction from the membrane at loading rate of 1100 pN/s was also calculated (open, magenta diamonds) from the ramp force distribution. Force-dependent dissociation rates derived from parameters obtained from the best-fits of the corresponding ramp-load experiments (Table 1) are plotted (dashed curves of the corresponding color) using Eq. 2.

Discussion

Mechanics and kinetics of the myo1c^IQ-tail-membrane bond

We measured the mechanical properties of the interaction between single molecules of myo1c^IQ-tail and PtdIns(4,5)P₂ under tensile loads. The experiments predominantly report interactions between pairs of single-molecules, because:

• 1.Fewer than 10% of bead-pedestal contacts resulted in attachments (Fig. 2).
• 2.Two-step dissociation events were rare.
• 3.The survival probability of attachments at constant force are well described by a single exponential decay (Fig. 4 (26)).

However, contributions from two bonds that rupture simultaneously cannot be excluded, especially since a single myo1c^IQ-tail can bind to multiple PtdIns(4,5)P₂ molecules (17).

The average adhesion force is relatively insensitive to the loading rate, and ranges between 5.5–16 pN (Table 1). These forces are greater than the force required to stall the motor activity of myosin-I (∼1.5 pN (33,34);), but are less than the force required to extract a phospholipid from the membrane (Fig. 3). It is interesting to note that these forces are in the range of those required to pull membrane tethers from a cell (35) or giant unilamellar vesicle (36), which is consistent with observed compliance in the bond and our ability to pull tethers from some supported membranes (Fig. 1).

The membrane dissociation rate in the presence of load is surprisingly fast and is linearly related to force (Fig. 5). A linear fit to the data yields a y intercept (0.45 ± 2.7 s⁻¹; Fig. 5) that is not significantly different from the rate of myo1c^IQ-tail dissociation from large unilamellar vesicles composed of 2% PtdIns(4,5)P₂ measured via stopped-flow (2 ± 0.3 s⁻¹ (17)). The Bell model for the force dependence of dissociation has an exponential rate-force relationship (Eq. 2 (29)), and it does not yield reasonable values of k_o and d_tr when applied to these data.

The adhesion-force distributions (Fig. 2) obtained at differing loading rates could not be fit with a unique Bell-Evans model (Eq. 1). Fits of the data with the model yield values of k_o and d_tr that depend on the loading rate (Fig. 2; Table 1). A simple, model-free transformation of ramp force data, into force-dependent dissociation rates (Eq. 6 of (31)), allows a direct comparison of the ramp-force and constant force measurements (Fig. 5). This transformation does not require a priori assumption of the exact analytic expression for k(F) and is applicable if the dissociation kinetics under constant force exhibit single exponential behavior, which is the case for our constant-force measurements (Fig. 4).

The overall trend is that dissociation rates increase with increasing loading rates (Fig. 5). It is especially clear that the dissociation rates determined from the constant force experiments, which have the highest effective loading rates, have the fastest dissociation rates. These results suggest that the forced unbinding of myo1c^IQ-tail from PtdIns(4,5)P₂-containing membranes is nonadiabatic, i.e., the pulling rate, even at the lower rates, is faster than the relaxation of the system in the unruptured state (31). This result may also explain the loading rate dependence of the fitting parameters k₀ and d_tr of the adhesion-force distributions (Table 1). Force-dependent dissociation rates derived from k₀ and d_tr are plotted (Fig. 5).

The apparent nonadiabatic, non-Bell-like character of the myo1c^IQ-tail-membrane interaction may be the result of attachment heterogeneity during pulling (37). This heterogeneity could be the result of loading-rate dependent changes in membrane structure (e.g., formation of small tethers), which may change the geometry or accessibility of the myo1c^IQ-tail binding site. Alternatively, or additionally, the ability of myo1c^IQ-tail to interact with multiple PtdIns(4,5)P₂ molecules via delocalized electrostatic interactions (17) may also depend on the loading rate. Given the dynamics and heterogeneity of peripheral protein-membrane interactions, we propose that this nonadiabatic behavior will be a common trait of protein-membrane interactions.

Biological implications

Adhesion between the plasma membrane and the cytoskeleton is mediated, in part, by the interaction of cytoskeletal proteins with phosphoinositides (2,38). These interactions have been proposed to be dynamic and weak to allow for rapid membrane remodeling. We found the adhesion force of phosphoinositide-myo1c^IQ-tail interactions to be within approximately twofold of the force required to extract a lipid from the membrane (Table 1), but the attachment lifetimes are highly force-dependent. Given the similarity of the affinities of myo1c^IQ-tail with other characterized membrane-binding proteins (39,40), we expect other cytoskeletal proteins to have similar membrane adhesion forces and kinetics. Thus, an ensemble of proteins with these mechanical and kinetic properties may be appropriate links to mediate membrane-cytoskeleton adhesion (2).

Is PtdIns(4,5)P₂ alone a suitable anchor for a molecular motor? The adhesion forces of myo1c^IQ-tail to PtdIns(4,5)P₂ are greater than the stall force of myosin-I (33,34), but the attachment lifetimes are substantially shorter than the ATPase cycle time of the motor (24). Thus, our results indicate that the interaction between myo1c^IQ-tail and PtdIns(4,5)P₂ alone does not provide the mechanical stability required to act as an anchor for the force-generating activity of the myo1c. Thus, it is also unlikely that myo18A or myo6 are anchored solely via phosphoinositide binding (5,7). For myosins to generate force normal to the plane of the membrane (e.g., to pull membrane tethers in the Golgi (7)), additional anchoring molecules are necessary.

A second membrane binding site on myo1c has been shown to bind anionic phospholipids via delocalized electrostatic interactions (4,14,17,41), and inclusion of additional anionic phospholipids into the membrane decreases the unloaded dissociation rate ∼80-fold (17). However, given the sharp dependence of the dissociation rate on force (Fig. 5), it is unlikely that electrostatic membrane attachments are suitable anchors for myosins undergoing multiple ATPase cycles under load. Further experiments are required to identify and characterize the role of putative myo1c binding proteins in the mechanics of membrane attachment (42–44).