Abstract
Optical trapping experiments reveal details of molecular motor dynamics. In noisy data, temporal structure within the power stroke of motors can be analyzed by ensemble averaging, but this obscures infrequent subcategories of events. We have here developed an analysis method that uses Kalman filtering of measurements, model-based estimation of the power strokes produced by the motor head, and automatic event classification to discriminate between different types of motor events. This method was applied to optical trap measurements of power strokes of the Drosophila kinesin-14 ncd in a three-bead geometry. We found the majority of events to be consistent with the previously discovered minus-end directed power stroke of ncd, occurring with ATP binding. Unexpectedly, 30% of apparent power strokes were plus-directed and 6% of binding events did not terminate in a discernible stroke. Ensemble averaging for each event category revealed that plus- and minus-directed strokes have different size and occur at different instants within the ncd-MT attachment sequence.
Introduction
Within the kinesin superfamily of microtubule (MT) motors, a variety of dynamics are found (1–4). Kinesins differ in speed, directionality, reaction to applied forces (5–10), and processivity, i.e., the number of kinetic cycles a motor performs per attachment. All motor proteins undergo conformational changes and transmit those in such a way that force is exerted on their cargos. When part of the molecule acts as a lever arm, these conformational changes are dubbed power strokes. Processive motors (most often dimeric) alternate power strokes to always maintain contact of one of their monomers to the track and thus perform steps along the track.
Step sizes have been measured for processive motors (11). The experimental problem is to achieve a sufficient signal/noise ratio to detect nm-displacements. At limiting ATP concentrations, motors slow down enough to directly observe step distances by low-pass filtering the noisy signals (11–13). Ensemble averaging of processive events of kinesin-1 has also been used to resolve fine details of the motor's kinetic cycle, such as possible substeps within the 8-nm step (14).
Nonprocessive motors, such as myosin-2 (15) or ncd (16,17), perform a power stroke and then detach from the track. Several myosin subtypes (15,18,19) and ncd (20), have been studied with optical traps in a three-bead geometry (Fig. 1 A). An ingenious method to characterize substructure in the power strokes of nonprocessive motors was developed by Veigel et al. (21), using ensemble averaging of events synchronized by attachment and detachment instants. This worked well with myosins that attach rigidly to nitrocellulose surfaces (18).
Figure 1.
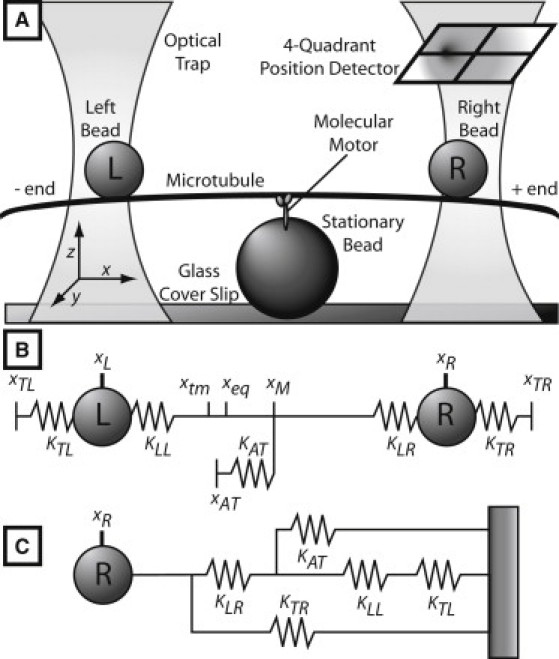
(A) Experimental setup. (B) Two-bead model. Refer to Table S1 in the Supporting Material for the nomenclature and the definition of all variables. (C) Single-bead model.
Less is known about the power strokes of nonprocessive kinesins. Ncd is a slow minus-end directed kinesin (22). Ensemble averaging of optical trap data showed that ncd performs a power stroke of ∼9 nm before releasing from the MT, after binding ATP (20,23). This was later confirmed by electron microscopy (24). Though ncd and kinesin, both homodimers with two motor domains and a coiled-coil stalk, have opposite stroke directions, they are structurally similar (25). Within the motor domain, the neck region is thought to primarily determine power-stroke (25,26). Modifications affect power stroke direction and speed (27,28). Some kinesins step backward under load in 8-nm steps in an ATP-dependent manner (10,29). Load also affects power-stroke amplitude according to the elasticity of the lever arm as observed for myosin 2 (30). This may also be anticipated for ncd.
Here we use model-based Kalman filtering to reanalyze the three-bead optical trapping data with full-length ncd described in deCastro et al. (20). Model-based filtering utilizes first-principles or phenomenological models to produce estimates of the states of the system, conditional upon measurements. This utilization of a priori information allows estimating variables that cannot be measured directly and helps in suppressing noise. For ncd, the method allowed us to analyze motor events before ensemble averaging and detect infrequent event types which are obscured by indiscriminate ensemble averaging. The results indicate the existence of previously undetected variations of the ncd power stroke.
Methods
Three-bead motility assays
The experimental data used in this work were produced by deCastro et al. (20). A biotin-labeled MT (∼4.3-μm-long) was suspended between two streptavidin-coated silica beads of 1-μm diameter, which were trapped by two optical tweezers (Fig. 1 A). The bead/MT structure was then lowered onto a third bead (2-μm diameter), which was immobilized and sparsely coated with ncd molecular motors, to create the three-bead geometry. Low concentration of motors on the surface of the stationary bead ensures that a single motor is interacting with the MT.
Thermal fluctuations and the ncd-MT interactions displace the two 1-μm beads, arbitrarily labeled as right, R, and left, L. The position x of the right bead in the direction connecting the two beads and parallel to the MT was measured by back-focal-plane interferometry (31,32) using a quadrant photo diode. The y-displacement orthogonal to the optical axis and the x direction was also measured. The measurement drift (∼0.1 nm/s) was removed using the following procedure: 90-s data segments were detrended by subtracting a second order polynomial fit. Because the average duration of a motor attachment is ∼2 s, a small fraction of which corresponds to a power stroke, such detrending has a negligible effect on the results.
Four data sets (20), obtained with different beads, MTs, and motors, totaling ∼1.5 h of measurements (sampling rate 5 kHz) were used in the analysis. Two sets were produced with an ATP concentration of 2 μM, the other two with 5 μM ATP. All experiments were conducted at room temperature.
The direction of the predominant power stroke in each data set was used to determine the orientation of +/− ends of the MT. The predominant stroke in the first data set was opposite to the orientation observed in sets 2–4. Therefore, the sign of the raw data in Data Set 1 was reversed.
Kalman filtering
Model-based filtering is widely used in engineering and utilizes first-principles or phenomenological models and the available measurements to estimate the states of the system. The utilization of a priori information in the form of a model allows one to estimate variables that cannot be measured directly, such as the molecular motor head displacement, xAT, in the two-bead model of optical trap experiments, shown in Fig. 1 B. In the model of Fig. 1 B, the motor is attached to the MT and the force balance on the R and L handle beads and the MT is given by the following system of Langevin-like stochastic differential equations of motion for the beads and the MT (33):
| (1) |
| (2) |
| (3) |
Thermal fluctuations are modeled by additive Brownian forces wFR, wFL, and wFM, which are assumed to be white Gaussian processes; β-values are drag coefficients and m values are masses; x is the displacement from the equilibrium; and the subscripts are used to identify right (R) and left (L) beads, right (RT) and left (LT) optical traps, and the MT (M). MT displacement in the x-axis, xM, is caused by the interaction with the motor, the optical trap forces translated to the MTs through biotin-streptavidin links, and by thermal fluctuations. Before ncd attachment, the MT fluctuates around a mean position xM = 0 and E[xM] = 0, where E is the expectation operator.
When masses are small and the Reynolds number is low (as in our case), the inertial terms in Eqs. 1–3 may be ignored without substantially altering the results. However, in the following analysis, the full-scale model is kept to maintain the generality of the presentation and its applicability to the cases in which inertial terms cannot be neglected.
In the above model, the optical trap forces are modeled by Hooke's law with spring constants KTR and KTL, the values of which can be independently altered by varying the laser power. The biotin/streptavidin connections between the MT and the handle beads are modeled as springs with constants KLL and KLR. Because beads are attached laterally to the MTs, the effective spring constant includes bending of the MTs and is in fact highly nonlinear (34). We here assume local linear response, which is a good approximation given that the power stroke amplitudes are small. The MT-ncd interaction is described by the force FAT = −xATKAT, where KAT is the spring constant of the flexible motor-MT attachment. The motor-head displacement xAT is the displacement of the MT during ncd attachment relative to the mean position of the unattached MT. Another interpretation is to view xAT as the relative ncd-MT displacement needed to produce FAT, which explains the measured change in the right bead positions. Such relative displacement is caused by either the tension, introduced when ncd attaches to the MT that is thermally shifted from its mean position, or the ncd power stroke. To differentiate between the two causes, we say that the attachment tension is the source of the equilibrium displacement, whereas the motor action (power stroke) causes terminal displacement. The right bead displacement in x axis, xR, is the only measured state of the model, Eqs. 1–3. The right bead motion in the y axis is also measured and can be similarly modeled.
Because the diameter of the handle beads is much larger than the cross section of the MT, we ignore the drag force on the MT and assume it reaches its steady-state position instantaneously in response to changes in xR, xL, or xAT. With this assumption,
| (4) |
We also assume constant optical trap positions (xTR = xTL = 0), and equal compliances of biotin-streptavidin connections (KLL = KLR = KL). The values of KL and KAT were set to constants identified experimentally, as described below. The only remaining unknown parameter in the resulting model is xAT, which describes the equilibrium displacement caused by ncd attachment to a MT which was thermally displaced from the equilibrium position xM = 0, and/or the displacement due to the motor's power stroke. The estimation of xAT is obtained recursively by continuously adjusting the estimate of xAT for each new measurement, and assuming the following dynamic model,
| (5) |
where wAT is a zero-mean white Gaussian process of a selected intensity. Such a parameterization is fairly standard and implies that without random disturbances, xAT is constant. In our specific application, this is a justifiable assumption if either the motor head position is slowly varying, or intermittent changes in xAT are so fast that we can assume that a new steady-state value of xAT is reached instantaneously. The case of rapid intermittent changes in xAT is assumed to describe the ncd-MT interactions.
To apply Kalman filtering, the two-bead model must be written in the so-called state-space form—as a system of first-order differential equations describing the dynamics of the system states x (now including positions and velocities) plus an algebraic measurement model, relating states x to the available measurements y. Note that y here is unrelated to the bead displacement y in the direction orthogonal to the MT axis. Rather, in the state space form, measurements of any kind are typically denoted by a vector y. With the above assumptions and parameterization of xAT, the state-space model representation of Eqs. 1–3 has the following form,
| (6) |
| (7) |
where the augmented state vector is
the vector of the model noises is
and the vector of known external inputs, e.g., movements of the traps, u is zero if the traps are held steady. Comparison of Eqs. 1–3 with Eq. 6 leads to the system matrix A describing the system response, which is equal to
| (8) |
Random thermal noise enters through the process noise intensity matrix G, which is given as
| (9) |
The measured right-hand bead position y is related to the state vector x by Eq. 7, where
and measurement noise, v, is assumed to be a zero-mean Gaussian process with known variance. This equation gives the measurement model in the state space form, which in our case simply becomes y = xR + v, i.e., the measured value is the position of the right bead plus noise.
The problem is now to estimate the state vector x, which would give us the filtered measurements of xR and, most importantly, the estimated values of the motor-head displacements, xAT. The specific state estimate that we seek is the mean of x(t), conditional upon measurements y(t); that is, the desired estimate is
where E[·] is the expectation operator. The solution of this problem is given by Kalman filtering theory (35,36). Note that in the linear Gaussian case of Eqs. 6 and 7, it is known that the state estimate found as E[x(t)|y(t)] also fulfills the least-mean-squares and maximum-likelihood estimation criteria.
In addition to the described two-bead model, which we use to determine the power strokes, a simplified model of Fig. 1 C is used to detect the exact time points of ncd-MT attachments in the data tracks. This model assumes a single-mass-on-a-single-spring representation (single-bead model) of the experimental system, where the single total spring constant, Ktotal, depends on the springs depicted in Fig. 1 B as
| (10) |
Ktotal characterizes the cumulative effect of optical traps, chemical linkages/MT bending, and ncd-induced forces on the position of the monitored right bead. Because motor binding adds another spring, KAT, to the system, the ncd attachment events correspond to elevated values of Ktotal. Therefore, by analyzing the identified Ktotal(t), the ncd attachment and detachment instants can be estimated.
The single-bead model of Fig. 1 C can be obtained from Eqs. 1–3 by assuming that xL and xM achieve their equilibrium positions instantaneously. If, similarly to Eq. 5, we assume
the state space description of the single-bead model is obtained in the state-space form of Eqs. 6 and 7 with the state vector
and the system matrix
| (11) |
where and depend on the mass and radius of the beads in the two-bead model.
The obtained single-bead model is nonlinear in Ktotal. This makes it necessary to use the so-called extended Kalman filter (37), which is a standard approach to state estimation of nonlinear systems. We take a sudden increase in the estimated value of Ktotal as an indication of the ncd-MT attachment; the return of Ktotal to the preattachment value indicates ncd detachment. A similar approach to event detection was used in the literature (15,20), where Ktotal was estimated using equipartition as
| (12) |
where the variance 〈x2R〉 was calculated using the data in a sliding window.
Filter validation
The performance of our Kalman filters was tuned in simulations. The primary tuning parameters were the variances of the model noises, w, which were selected to compromise between rapid response of the Kalman filter to changes in the measurements due to motor events and reduced sensitivity to thermal noises. The higher the variance of w, the higher is the filter bandwidth. An aggressive Kalman filter with a high bandwidth will provide little filtering and will produce high variance in the estimated xAT as a function of time. A sluggishly tuned filter (which corresponds to lower variance of w) reduces the variance of the results at the expense of slower response that may result in a biased estimation of xAT when rapid changes occur.
To find an optimal tradeoff between fast response and high variance of the results, we constructed synthetic data. These were generated using the two-bead model (Eqs. 1–3) with
(mass of the silica bead with 1 μm radius),
and
To obtain the values of KTR and KTL, separate experiments were conducted to measure the position of an unattached bead in an optical trap. Using the variance of the measured position, the trap constants were calculated assuming equipartition (Eq. 12). With the known trap constants, KL was calculated from the variance of the measured position of a single bead attached to a surface-immobilized MT. Ktotal was calculated using Eq. 12, and the corresponding KAT was obtained from Eq. 10.
In the simulations, the change in the motor head position, xAT, was produced by random ncd-MT attachments leading to equilibrium displacements, random durations of the attachment events, a randomly chosen power stroke direction (positive or negative), and the size of the power stroke occurring just before detachment. A sequence of motor head displacements generated in this way is shown in Fig. 2.
Figure 2.
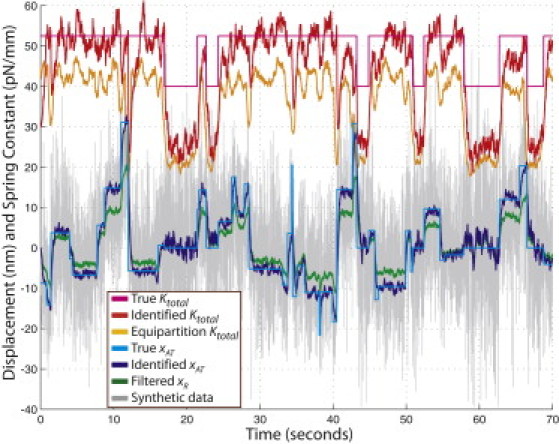
Validation of the Kalman filters in simulations. The time series of true motor head displacements was used in the two-bead model to produce synthetic measurements, y, of the right bead position (shown in gray). Ktotal, identified by the single-bead Kalman filter, is shown in red. Orange line shows Ktotal identified using Eq. 12. The identified xAT and the filtered xR (green line) were obtained using the two-bead Kalman filter (Filter 1 in Fig. S1).
Simulated right bead position, corresponding to randomly generated xAT, was obtained using the two-bead model with the additive Gaussian disturbances, wFR and wFL, representing the effect of Brownian forces. The variances were set to
With this choice, the variances of the simulated and measured right bead positions were equal. Theory predicts a smaller variance equal to 1.3 × 10−25 N2 (38). Within the range of interest, the identification of Ktotal was only slightly affected by assuming the theoretical value, and the identified motor-head position was unaffected.
Synthetic data were filtered with the single-bead Kalman filter to test its ability to identify Ktotal. The gain of this filter depends on second moments of the zero-mean Gaussian process and measurement noises, w and v, and was calculated assuming
and
The measurement noise was set to have a variance
The variances of wFR and wtotal were treated as filter tuning parameters and were set to much higher values than used to produce synthetic data to reflect the higher model uncertainty inherent in the single-bead approximation.
The identified Ktotal was compared with its true value. Ktotal was most accurately identified when in Eq. 11 was twice the corresponding ratio of the two-bead-model. Thus, the mass and drag of the two-bead MT complex is double that of what would be experienced with a single bead, which is an expected result.
The same synthetic data were used as input to the two-bead Kalman filter, the gain matrix of which was calculated using the above specified variances of the process and measurement noises. The performance of the two-bead filter was tested to characterize the accuracy of the identified motor-head displacements. The maximum steady-state identification error in identifying a constant value of xAT was found to be ∼1 nm after 3 s (15,000 samples) of data were used. After a step change in the motor-head position, the identified xAT reaches a new steady state in <200 ms. For a motor-head displacement of 10 nm, persisting for 200 ms or longer, the filter reports the stroke amplitude with <20% error, indicating adequate resolution for most ncd attachment events. Power strokes of ∼10 nm, persisting for <200 ms, may be underestimated in size and those persisting for <50 ms may not be detected.
Synthetic measurements of xR and the corresponding results of the Kalman filtering are shown in Fig. 2. The comparison of the identified and the true values shows the filter's ability to accurately identify and characterize most motor events. Specifically, the values of xAT, identified by the two-bead Kalman filter, closely agree with the true motor head displacements used to produce the synthetic data. Identification errors for Ktotal are higher, but qualitatively correct, showing an elevated Ktotal during attachments, which justifies the use of Ktotal to detect the ncd-MT attachments. It was found that Ktotal, estimated using Eq. 12, has consistently higher estimation errors. Note that with the recursive data processing by the Kalman filter, large motor-head displacements cause a rapid reduction in the identified Ktotal. Such an artifact is not unexpected because large changes in the bead position may be explained by the reduction in the total spring constant. A similar behavior is observed for Ktotal estimated using Eq. 12 when 〈x2R〉 is calculated from the measurements in a relatively narrow data window.
Data analysis
Fig. S1 (Supporting Material) summarizes the developed filtering, identification, and characterization methods used to analyze the ncd-MT interactions. We have used two model-based approaches and one model-independent approach as a control.
In the first approach, a Kalman filter, based on the two-bead model of Fig. 1 B, was used to filter the measured xR and estimate the motor-head displacement xAT as a function of time. At the same time, an extended Kalman filter, based on the single-bead model of Fig. 1 C (Filter 2), was used to identify Ktotal. Binding event detector in Fig. S1 implements a Shewhart control chart (39,40)—a standard thresholding method which we used to detect an increase and decrease in the value of Ktotal. A MT-motor attachment time point was set when Ktotal exceeded a selected value (3.75 × 10−5 N/m); when Ktotal dropped below that value, a detachment time point was set. Estimated attachment and detachment time points were further refined using the decrease in the variance of the measured right bead position, xR, in a narrow window. This segments the identified motor-head position, xAT, into ncd-MT attachment events. Each attachment event, i, was further segmented into motor-head displacements,
with corresponding displacement values, di,j. The difference between the last two displacements before ncd's detachment is the estimate of the power stroke for each attachment event. The average of all power strokes is reported in Table 1. All attachment events were then automatically classified into different event types using a syntactic classification procedure (Fig. S1). The estimated power-stroke values were then grouped into different event types and averaged. The average stroke for each group is reported in Table 1, where the results of the syntactic event classification (frequency of different events as a percent of total) are also listed.
Table 1.
Results based on two-bead Kalman filter and syntactic classification
| All | Set 1 | Set 2 | Set 3 | Set 4 | |
|---|---|---|---|---|---|
| ATP (μM) | 2 | 5 | 2 | 5 | |
| Direction of predominant terminal displacement | −x | +x | +x | +x | |
| Detected events | 675 | 48 | 147 | 253 | 227 |
| Events with positive equilibrium displacements | 322 (48%) | 20 (42%) | 64 (44%) | 112 (44%) | 118 (52%) |
| Events with negative equilibrium displacements | 353 (52%) | 28 (58%) | 83 (56%) | 141 (56%) | 109 (48%) |
| Average equilibrium displacements (nm) | −0.8 | −1.7 | −2.1 | −2.5 | 1.3 |
| Average positive equilibrium displacements (nm) | 11.6 | 13.8 | 13.4 | 11.5 | 10.4 |
| Average negative equilibrium displacements (nm) | −12.1 | −12.7 | −14.0 | −13.5 | −8.6 |
| Events with motor strokes | 634 (94%) | 45 (94%) | 137 (93%) | 246 (97%) | 206 (91%) |
| Events with minus-end directed strokes | 418 (62%) | 29 (60%) | 89 (61%) | 162 (64%) | 138 (61%) |
| Events with plus-end directed strokes | 216 (32%) | 16 (33%) | 48 (33%) | 84 (33%) | 68 (30%) |
| Average of all motor strokes (nm) | 3.1 | 2.4 | 3.1 | 3.4 | 3.0 |
| Average of minus-end directed strokes (nm) | 8.1 | 7.3 | 8.4 | 8.6 | 7.4 |
| Average of plus-end directed strokes (nm) | 6.4 | 6.3 | 6.5 | 6.7 | 6.0 |
In the second approach, before the estimation of the motor-head displacements, data were ensemble-averaged. As in the previous step, attachment events were grouped using the outcome of the syntactic classification and the averaging was carried out separately for different groups. The averaging reduced the influence of thermal and measurement noises, which obscure the exact temporal structure of the events. A more aggressively tuned Kalman filter was then applied to the less noisy averaged measurements. The identified xAT is shown later in Fig. 5, and the corresponding motor stroke amplitudes (Table S2) likely give the more accurate estimates because of the reduced influence of noise.
Figure 5.
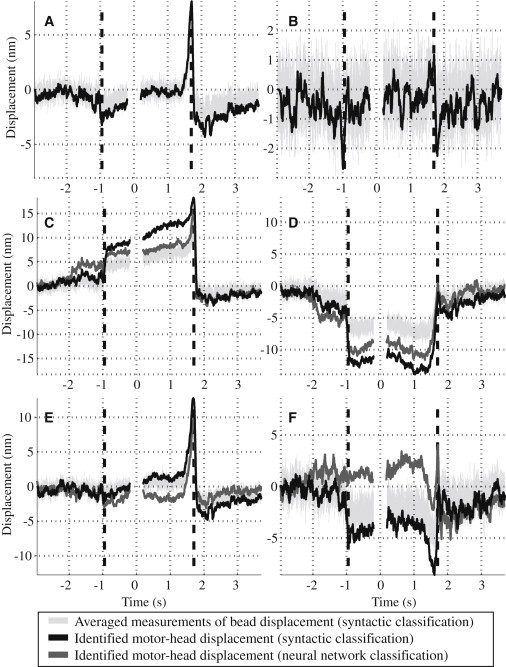
Results of ensemble averaging. (A) Average of all 675 detected motor events. (B) All 675 events in the y axis. (C) All 322 events with a positive equilibrium displacement (333 events based on NN classification). (D) All 353 events with a negative equilibrium displacement (286 events based on NN classification). (E) All 418 events with a positive (minus-end directed) terminal motor action (414 events based on NN classification). (F) All 216 events with a negative (plus-end directed) terminal motor action (205 events based on NN classification). (Dashed vertical lines) Event start and stop times.
The described event segmentation and classification depend on the model-based Kalman filtering of xR measurements and model-based identification of motor head displacements, xAT. A model-independent, confirmatory method that uses neural network (NN) classification of motor events was also implemented (see the Supporting Material). Because NN classification does not use a priori information about a mechanical model of ncd-MT interactions, it provides a general consistency check (last column, Table S2).
Results
Kalman filtering of raw data
Fig. 3 shows the Kalman filtering results for several ncd-MT events. The range of axial thermal motion of the MTs during the experiments was ∼80 nm. The ncd could attach to the MT anywhere within this range. Assuming the ncd-MT orientation of Fig. 1 A, Fig. 3 A shows an event during which the motor attached to a MT that was thermally shifted by ∼30 nm to the right of its mean equilibrium position. The changed equilibrium position of the ncd-MT complex led to a noticeable shift in the mean x position of the right bead. We call this an equilibrium displacement, xeq, to distinguish it from the displacement caused by the power stroke. Because the location of the attachment point is an unknown and not directly modeled, the equilibrium displacement of the right bead leads to a change in the identified motor head position, xAT, (Fig. 3). Therefore, the product KATxAT at the beginning of the event models the force introduced by the addition of the ncd-MT link.
Figure 3.
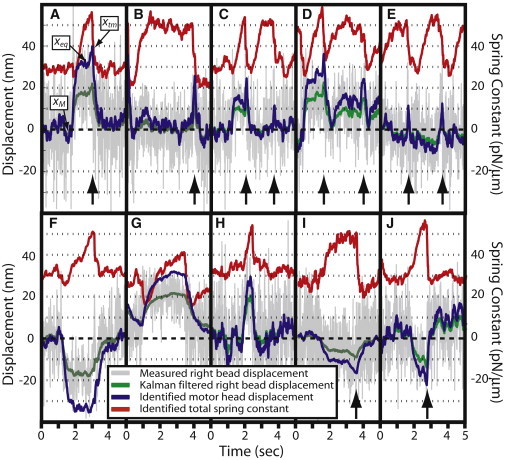
Examples of ncd-MT events. (Vertical arrows) Peak motor head displacements due to terminal motor action. (A–D) Minus-end power strokes against a loading force due to attachment displacement, xeq. (E) Power stroke toward the minus-end starts with assisting force, due to small negative xeq, ending with loading force. (F) Event with a stroke-assisting force due to binding location. (G and H) Events without detected stroke. (I and J) Events with the power stroke toward MT's plus-end and a loading force due to equilibrium displacement.
According to published models (20,23), the ncd motor produces its power stroke when ATP binds, near the end of an ncd-MT attachment period. We refer to the shift in the motor head just before detachment as the terminal displacement, xtm, and assume that it is caused by the power stroke. With the MT orientation of Fig. 1 A, the power stroke in the expected direction (minus-end) will displace the measurement bead in the positive x-direction (positive xtm). During the power stroke, the terminal and equilibrium displacements (and the corresponding forces) superimpose. The size of the power stroke (xtm) is estimated as the difference between the identified average xAT before the stroke (xeq) and the peak in the identified xAT during the stroke, before release.
Events in Fig. 3, A–D, agree with the established model:
-
1.
Ncd attaches to the MT, causing an equilibrium motor-head displacement, and an increase in Ktotal.
-
2.
At the end of the attachment event, the motor produces a minus-end directed stroke, resulting in a positive terminal displacement.
-
3.
Ncd detaches from the MT, causing the return of the motor head, the MT, and the measurement bead to their original mean positions and a return of Ktotal to its value before attachment.
All events in Fig. 3, A–D, had positive equilibrium displacements, which led to a loading force against the power stroke. Approximately the same number of events had negative equilibrium displacements, resulting in a small assisting force (Fig. 3, E and F). When the negative equilibrium displacement is small, the power stroke can start with a small assisting force and end with a loading force (Fig. 3 E). With large negative equilibrium displacements, the power stroke causes a MT displacement in the same (+x) direction as the MT's return to its original mean position after detachment. As a result, a positive terminal displacement is not visually apparent when equilibrium displacement is negative (Fig. 3 F). Such events, however, are readily detected by the syntactic and neural network characterization methods.
Fig. 3, G and H, shows infrequent attachment events that did not terminate in a detectable power stroke. Such events indicate that ncd could also detach from the MT without producing a power stroke.
Even more unexpected events are shown in Fig. 3, I and J. Here, the motor attached and, at the end of the attachment event, produced a stroke toward the plus-end of the MT, shifting it and the right bead in the negative x direction—a negative terminal motor action in our terminology.
The average of the results of syntactic characterization of all detected events is summarized in Table 1. The direction of the predominant power stroke in each data set was used to determine the orientation of the MT. The motor events were broken down in terms of their equilibrium displacements and the direction of the terminal motor action.
The probability of positive and negative equilibrium displacements is expected to be equal. The results of Table 1 indicate a slight preference for negative equilibrium displacements (52% vs. 48%). This bias is attributed to negative drift in the measurements, which was not completely removed by the detrending procedure. Fig. 4 A shows that the distribution of equilibrium displacements is approximately normal with a zero mean, as expected.
Figure 4.
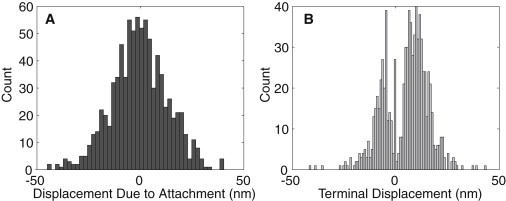
(A) Distribution of equilibrium displacements, xeq, due to binding location. (B) Distribution of the identified terminal displacements, xtm, due to motor action.
An ∼60–30% split between the positive and negative terminal displacements was consistently seen in all four data sets (Table 1). The average of minus-end directed strokes is ∼8.1 nm, compared with 9 nm reported in deCastro et al. (20). The previously unidentified plus-end directed strokes are, on average, −6.4 nm.
The distributions of terminal displacements for minus- and plus-end directed power strokes (Fig. 4 B) are clearly distinct. The spike at the origin corresponds to ∼6% of the ncd-MT attachment events that did not terminate in a detectable stroke. Such events correspond to the case when the identified motor head position is segmented into a single (equilibrium) displacement. We assume that, due to reversibility of ncd-MT attachments, some attachments terminate before ncd completes its kinetic cycle. It is also possible that:
-
1.
Some of the attachment-pull-detachment events occur too rapidly for the Kalman filter, used to identify xAT, to react.
-
2.
The difference between the equilibrium and terminal displacements is less than the 2-nm threshold, used in automatic event classification to conclude that a terminal displacement has occurred.
Kalman filtering of ensemble averaged data
The single-realization filtering and subsequent analysis allowed us to resolve individual motor events and then classify events into different types. After classification, the ensemble averaging of the events of each type can be used to further reduce thermal noise and resolve more detail. Attachment events have different durations, due to random ATP arrival and hydrolysis. Therefore, all events were time-normalized and aligned using an automated procedure.
First, only the data adjacent to the event start (ncd attachment) and stop (detachment) times were retained. The data were then aligned by refined attachment/detachment times (Fig. 5).
The ensemble-averaged measurements of xR (Fig. 5) were obtained by averaging within different event types, as classified by the syntactic method. The averaged measurements of 418 and 216 events, respectively, classified to have positive and negative terminal motor actions (Fig. 5, E and F), confirm the presence of power strokes directed toward minus- and plus-ends of the MT.
To further quantify events, the averaged measurements were used as input to an aggressively-tuned (higher bandwidth) two-bead Kalman filter, which produced the estimate of the right bead position and identified the motor head displacement, xAT (t) (Fig. 5). A different set of averaged measurements (not shown) was obtained by averaging events assigned into different types by NN classifiers and used as the input to the same aggressively tuned filter.
Fig. 5 A shows the ensemble-averaged right bead position (x axis) for all detected events without distinguishing event types. A similar procedure was used in deCastro et al. (20). The method of this article identified a much larger number of events than previously found. Fig. 5 A shows that the events terminate, on average, in an 8-nm positive motor head displacement, which is consistent with the result of deCastro et al. (20) and approximately equal to the length of a tubulin unit. Note the approximately zero average equilibrium displacement, as expected.
The y component of the average power stroke is close to the noise level (Fig. 5 B). A slight, ∼1.75-nm displacement is seen at the initiation and termination of the averaged events which may be attributed to imprecise motor-MT alignment in the x-z plane. If the MT lies in the x-z plane of Fig. 1 and the motor on the stationary bead is located off this plane, then attachment to the MT will create a force with a y-axis component.
Fig. 5, C and D, shows the results for the events with positive and negative equilibrium displacements, averaged separately. Both groups include events with positive and negative terminal motor actions. Fig. 5 C shows an average positive equilibrium displacement of ∼11 nm, followed by a terminal motor action of ∼7 nm, a quick release, and return to the origin. In Fig. 5 D, the negative equilibrium displacement is ∼12 nm, followed by a return to the origin. The power stroke is obscured in Fig. 5 D by the motion of the measurement bead, returning to its unattached equilibrium position in the same direction as the displacement caused by the power stroke. Examination of the detachment segments in Fig. 5, C and E, shows the presence of either a positive or negative drift in the averaged measurements before detachment. This drift is caused by short (<2 s) ncd attachments, which contribute preattachment data to the detachment segment, thus bringing the average closer to the origin in the −t direction.
Fig. 5, E and F, show ensemble-averaged events with positive and negative terminal motor actions, respectively. The identified terminal displacement for the events ending with a stroke toward the minus-end of the MT is ∼12 nm, which is significantly larger than a tubulin dimer length and the value of the stroke reported in deCastro et al. (20). For a nonprocessive motor, there is no reason for a motor stroke to be a multiple of the distance between motor binding sites, which in the case of MTs is 8 nm. Comparison with Fig. 5 A indicates that ensemble averaging over all events, positive and negative, reduces the estimated terminal motor action by ∼4 nm. The minus-end directed stroke notably peaks at essentially the same time as the end of the event, suggesting an immediate ncd-MT detachment after the power stroke, which agrees with the previously proposed model.
Plus-end events (Fig. 5 F) were clearly different from minus-end events. The average size of the plus-end strokes is smaller, ∼7 nm. The peak displacement occurred ∼100 ms before the motor-MT release, suggesting that the end of the power stroke toward the plus-end of the MT does not coincide with the ncd-MT detachment. An alternative explanation is that the motor does not produce a net negative displacement before detaching. Instead, it moves the MT temporarily in the negative direction, then returns it back, and releases. Finally, a plus-end stroke took ∼500 ms to complete, or 1.5 times longer than a minus-end power stroke, indicating either:
-
1.
A slower stroke;
-
2.
A stroke with a broader distribution of the ncd-MT detachments after the motor action.
-
3.
A longer time taken to move the MT back and forth without net displacement before release.
Although the exact mechanism is unknown, the totality of observations indicates that the kinetics of the plus-end strokes differ from the previously reported kinetics of ncd-MT interactions.
Note that the identified average power strokes for the events classified by the neural networks (dark shaded lines) are 1–3 nm shorter for different cases of Fig. 5, but otherwise consistent with the results obtained with the syntactic classification method of Fig. S1.
Summary of the results
The results obtained using raw and ensemble-averaged data, though generally consistent, give different estimates of the size of the power stroke (Table S2). Note the minus-end directed stroke of 12 nm in Fig. 5 E (Table S2 for the two classification methods) vs. 8 nm in Table 1 (also Table S2), and the plus-end strokes of −7 nm vs. −6 nm (Table 1). The source of these discrepancies is the difference in how the classified motor events were used to identify xAT. In all cases, the detection of ncd-MT attachments and determination of attachment and detachment times were identical. The terminal motor head displacements of Table 1 were obtained by averaging time-normalized segments of xAT produced by the two-bead Kalman filter with raw measurements as its input. In contrast, the identified xAT(t) in Fig. 5 is based on the averaged measurements used as the input to an aggressively tuned two-bead Kalman filter. This aggressive filter was designed to function with reduced fluctuation intensity of averaged measurements, and has higher gain and bandwidth. Because of the faster response of a more aggressive Kalman filter, it is likely that Fig. 5 is a more accurate characterization of average motor events of different types than Table 1. Sources of uncertainty and sensitivity to model parameters are discussed in more detail in the Supporting Material.
Discussion
The data obtained from the type of the experiments discussed here is very noisy. A standard method of analysis uses ensemble averaging of selected data segments. When all events are averaged indiscriminately, only the predominant motor action remains evident, and less frequent events are obscured. The alternative approach described in this article started with model-based Kalman filtering of the data (Fig. 3). This approach suggested the presence of ncd events that deviate from the previously proposed model (20). The identified time-dependent event characteristics—such as the filtered bead position, xR, the motor-head displacement, xAT, and the overall spring constant, Ktotal—were used to form a hypothesis about different types of motor events. Events were then classified using automatic event classification procedures. Ensemble averaging was then carried out separately for the different event types, producing the results of Table 1 and Fig. 5. If the noise in the original data had been a lot lower, one might, of course, have been able to detect different types of events by eye and classify them manually. The strength of the method introduced here lies exactly in the fact that even in very noisy data, which are common in single-molecule experiments, different types of events can be detected without observer bias.
Our approach showed that the majority of ncd motor events were consistent with the established model. However, approximately one-third of events terminated with an apparent plus-end stroke, whereas in ∼6% of the events, the motor detached without an apparent stroke.
Ensemble averaging within the same event type confirmed the existence of plus- and minus-end power strokes and showed that the two types of power strokes have different sizes and occur at different instants within the ncd-MT attachment sequence. A minus-end power stroke can take place essentially immediately before motor detachment, whereas plus-end strokes most likely occur ∼100 ms before motor detachment.
The average duration of both types of attachment events depended on ATP concentration (Fig. 6) as was reported before for all events, without segregation into different event types (20), suggesting that both types of power strokes are dependent on ATP hydrolysis.
Figure 6.
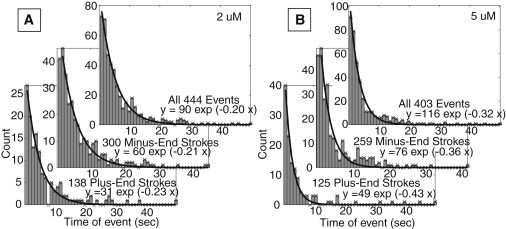
ATP dependence of the duration of positive and negative terminal displacements. (A) Histograms and exponential fits for 2 μM ATP concentration. (B) The same for 5 μM ATP concentration.
Bidirectionality in ncd's movement is not entirely unexpected. It was reported that even slight (single amino acid) modification of the neck region can lead to a change in kinesin's stroke direction and speed of motion (27,28). Evidence that some kinesin motors may occasionally step in the direction opposite to their normal step was presented in Nishiyama et al. (29). Note, however, that it is unlikely that reverse of directionality is observable in MT gliding assays on motor-coated surfaces, even if driven by minimal numbers of motors. If reversal of direction were random, it would be exponentially rare to observe enough reverse steps in a row (i.e., hundreds) to be able to resolve the motion in fluorescence microscopy. Furthermore, loading and assisting forces may play a role in directionality reversal, as has already been shown for individual processive kinesins, which change step direction under certain loads (10). A systematic load-dependence study for nonprocessing motors will be more difficult to complete, and will require real-time detection of the attachment events, followed by feedback control of optical traps to adjust the loading or assisting force.
Acknowledgments
The work of A.E.B. and M.S. was supported in part by the National Science Foundation grant No. CTS-0117300. C.F.S. was supported by the Center for the Molecular Biology of the Brain and by the Sonderforschungsbereich grant No. SFB 755, funded by the Deutsche Forschungsgemeinschaft.
Contributor Information
Anthony E. Butterfield, Email: tony3.1416@gmail.com.
Mikhail Skliar, Email: mikhail.skliar@utah.edu.
Supporting Material
References
- 1.Sablin E.P. Kinesins and microtubules: their structures and motor mechanisms. Curr. Opin. Cell Biol. 2000;12:35–41. doi: 10.1016/s0955-0674(99)00054-x. [DOI] [PubMed] [Google Scholar]
- 2.Schroer T.A., Schnapp B.J., Sheetz M.P. The role of kinesin and other soluble factors in organelle movement along microtubules. J. Cell Biol. 1988;107:1785–1792. doi: 10.1083/jcb.107.5.1785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Vallee R.B., Shpetner H.S. Motor proteins of cytoplasmic microtubules. Annu. Rev. Biochem. 1990;59:909–932. doi: 10.1146/annurev.bi.59.070190.004401. [DOI] [PubMed] [Google Scholar]
- 4.Moore J.D., Endow S.A. Kinesin proteins: a phylum of motors for microtubule-based motility. Bioessays. 1996;18:207–219. doi: 10.1002/bies.950180308. [DOI] [PubMed] [Google Scholar]
- 5.Khan S., Sheetz M.P. Force effects on biochemical kinetics. Annu. Rev. Biochem. 1997;66:785–805. doi: 10.1146/annurev.biochem.66.1.785. [DOI] [PubMed] [Google Scholar]
- 6.Hunt A.J., Gittes F., Howard J. The force exerted by a single kinesin molecule against a viscous load. Biophys. J. 1994;67:766–781. doi: 10.1016/S0006-3495(94)80537-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Meyhöfer E., Howard J. The force generated by a single kinesin molecule against an elastic load. Proc. Natl. Acad. Sci. USA. 1995;92:574–578. doi: 10.1073/pnas.92.2.574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Visscher K., Schnitzer M.J., Block S.M. Single kinesin molecules studied with a molecular force clamp. Nature. 1999;400:184–189. doi: 10.1038/22146. [DOI] [PubMed] [Google Scholar]
- 9.Coppin C.M., Pierce D.W., Vale R.D. The load dependence of kinesin's mechanical cycle. Proc. Natl. Acad. Sci. USA. 1997;94:8539–8544. doi: 10.1073/pnas.94.16.8539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Carter N.J., Cross R.A. Mechanics of the kinesin step. Nature. 2005;435:308–312. doi: 10.1038/nature03528. [DOI] [PubMed] [Google Scholar]
- 11.Svoboda K., Schmidt C.F., Block S.M. Direct observation of kinesin stepping by optical trapping interferometry. Nature. 1993;365:721–727. doi: 10.1038/365721a0. [DOI] [PubMed] [Google Scholar]
- 12.Block S.M., Goldstein L.S., Schnapp B.J. Bead movement by single kinesin molecules studied with optical tweezers. Nature. 1990;348:348–352. doi: 10.1038/348348a0. [DOI] [PubMed] [Google Scholar]
- 13.Vale R.D., Funatsu T., Yanagida T. Direct observation of single kinesin molecules moving along microtubules. Nature. 1996;380:451–453. doi: 10.1038/380451a0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nishiyama M., Muto E., Higuchi H. Substeps within the 8-nm step of the ATPase cycle of single kinesin molecules. Nat. Cell Biol. 2001;3:425–428. doi: 10.1038/35070116. [DOI] [PubMed] [Google Scholar]
- 15.Veigel C., Bartoo M.L., Molloy J.E. The stiffness of rabbit skeletal actomyosin cross-bridges determined with an optical tweezers transducer. Biophys. J. 1998;75:1424–1438. doi: 10.1016/S0006-3495(98)74061-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stewart R.J., Semerjian J., Schmidt C.F. Highly processive motility is not a general feature of the kinesins. Eur. Biophys. J. 1998;27:353–360. doi: 10.1007/s002490050142. [DOI] [PubMed] [Google Scholar]
- 17.deCastro M.J., Ho C.H., Stewart R.J. Motility of dimeric ncd on a metal-chelating surfactant: evidence that ncd is not processive. Biochemistry. 1999;38:5076–5081. doi: 10.1021/bi9829175. [DOI] [PubMed] [Google Scholar]
- 18.Finer J.T., Simmons R.M., Spudich J.A. Single myosin molecule mechanics: picoNewton forces and nanometer steps. Nature. 1994;368:113–119. doi: 10.1038/368113a0. [DOI] [PubMed] [Google Scholar]
- 19.Molloy J.E., Burns J.E., White D.C. Movement and force produced by a single myosin head. Nature. 1995;378:209–212. doi: 10.1038/378209a0. [DOI] [PubMed] [Google Scholar]
- 20.deCastro M.J., Fondecave R.M., Stewart R.J. Working strokes by single molecules of the kinesin-related microtubule motor ncd. Nat. Cell Biol. 2000;2:724–729. doi: 10.1038/35036357. [DOI] [PubMed] [Google Scholar]
- 21.Veigel C., Coluccio L.M., Molloy J.E. The motor protein myosin-I produces its working stroke in two steps. Nature. 1999;398:530–533. doi: 10.1038/19104. [DOI] [PubMed] [Google Scholar]
- 22.Walker R.A., Salmon E.D., Endow S.A. The Drosophila claret segregation protein is a minus-end directed motor molecule. Nature. 1990;347:780–782. doi: 10.1038/347780a0. [DOI] [PubMed] [Google Scholar]
- 23.Endres N.F., Yoshioka C., Vale R.D. A lever-arm rotation drives motility of the minus-end-directed kinesin ncd. Nature. 2006;439:875–878. doi: 10.1038/nature04320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sosa H., Dias D.P., Milligan R.A. A model for the microtubule-ncd motor protein complex obtained by cryo-electron microscopy and image analysis. Cell. 1997;90:217–224. doi: 10.1016/s0092-8674(00)80330-x. [DOI] [PubMed] [Google Scholar]
- 25.Sablin E.P., Case R.B., Fletterick R.J. Direction determination in the minus-end-directed kinesin motor ncd. Nature. 1998;395:813–816. doi: 10.1038/27463. [DOI] [PubMed] [Google Scholar]
- 26.Kozielski F., De Bonis S., Wade R.H. The crystal structure of the minus-end-directed microtubule motor protein ncd reveals variable dimer conformations. Structure. 1999;7:1407–1416. doi: 10.1016/s0969-2126(00)80030-1. [DOI] [PubMed] [Google Scholar]
- 27.Endow S.A., Higuchi H. A mutant of the motor protein kinesin that moves in both directions on microtubules. Nature. 2000;406:913–916. doi: 10.1038/35022617. [DOI] [PubMed] [Google Scholar]
- 28.Endow S.A., Waligora K.W. Determinants of kinesin motor polarity. Science. 1998;281:1200–1202. doi: 10.1126/science.281.5380.1200. [DOI] [PubMed] [Google Scholar]
- 29.Nishiyama M., Higuchi H., Yanagida T. Chemomechanical coupling of the forward and backward steps of single kinesin molecules. Nat. Cell Biol. 2002;4:790–797. doi: 10.1038/ncb857. [DOI] [PubMed] [Google Scholar]
- 30.Finer J.T., Mehta A.D., Spudich J.A. Characterization of single actin-myosin interactions. Biophys. J. 1995;68(Suppl):291S–297S. [PMC free article] [PubMed] [Google Scholar]
- 31.Allersma M.W., Gittes F., Schmidt C.F. Two-dimensional tracking of ncd motility by back focal plane interferometry. Biophys. J. 1998;74:1074–1085. doi: 10.1016/S0006-3495(98)74031-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gittes F., Schmidt C.F. Interference model for back-focal-plane displacement detection in optical tweezers. Opt. Lett. 1998;23:7–9. doi: 10.1364/ol.23.000007. [DOI] [PubMed] [Google Scholar]
- 33.Chandrasekhar S. Stochastic problems in physics and astronomy. Rev. Mod. Phys. 1943;15:1–89. [Google Scholar]
- 34.van Mameren J., Vermeulen K.C., Schmidt C.F. Leveraging single protein polymers to measure flexural rigidity. J. Phys. Chem. B. 2009;113:3837–3844. doi: 10.1021/jp808328a. [DOI] [PubMed] [Google Scholar]
- 35.Kalman R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960;82:35–45. [Google Scholar]
- 36.Kalman R.E., Bucy R.S. New results in linear filtering and prediction theory. J. Basic Eng. 1961;83:95–108. [Google Scholar]
- 37.Jazwinski A.H. Academic Press, New York; New York: 1970. Stochastic Processes and Filtering Theory. [Google Scholar]
- 38.Li A., Ahmadi G. Dispersion and deposition of spherical particles from point source in a turbulent channel flow. Aerosol Sci. Technol. 1992;16:209–226. [Google Scholar]
- 39.Shewhart W.A. Van Nostrand Reinhold; Princeton, NJ: 1931. Economic Control of Quality Manufactured Product. [Google Scholar]
- 40.Roberts S.W. A comparison of some control chart procedures. Technometrics. 1966;8:411–430. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


