Lower-Level Stimulus Features Strongly Influence Responses in the Fusiform Face Area

Abstract

An intriguing region of human visual cortex (the fusiform face area; FFA) responds selectively to faces as a general higher-order stimulus category. However, the potential role of lower-order stimulus properties in FFA remains incompletely understood. To clarify those lower-level influences, we measured FFA responses to independent variation in 4 lower-level stimulus dimensions using standardized face stimuli and functional Magnetic Resonance Imaging (fMRI). These dimensions were size, position, contrast, and rotation in depth (viewpoint). We found that FFA responses were strongly influenced by variations in each of these image dimensions; that is, FFA responses were not “invariant” to any of them. Moreover, all FFA response functions were highly correlated with V1 responses (r = 0.95–0.99). As in V1, FFA responses could be accurately modeled as a combination of responses to 1) local contrast plus 2) the cortical magnification factor. In some measurements (e.g., face size or a combinations of multiple cues), the lower-level variations dominated the range of FFA responses. Manipulation of lower-level stimulus parameters could even change the category preference of FFA from “face selective” to “object selective.” Altogether, these results emphasize that a significant portion of the FFA response reflects lower-level visual responses.

Introduction

Previous fMRI (Puce et al. 1995; Kanwisher et al. 1997; Grill-Spector et al. 1999; Halgren et al. 1999; Haxby et al. 1999; Hasson et al. 2001) and neuropsychology studies (McCarthy et al. 1997; Marotta et al. 2001) have identified an area in human inferior temporal cortex that responds selectively to images of faces, relative to a wide range of control stimuli. This has often been called the “fusiform face area” (FFA). Additional functional specializations have also been described in this cortical region (Haxby et al. 1999; Gauthier et al. 2000a; Kriegeskorte et al. 2008), and additional face-selective areas have also been reported (Gauthier et al. 2000b; Hooker et al. 2003; Moeller et al. 2008).

Empirically, this face selectivity is well established in FFA, but the neural mechanisms producing this remarkable specificity are not fully known. Computationally, face processing is quite challenging (e.g., Sinha 2002). How would such computations be accomplished in FFA within a few synaptic steps from those in lower visual cortical areas—which respond best to simple local edges in the visual field?

A fundamental challenge to face computation is posed by the endless variation in real-life lower-level features. For instance, an ideal detector must correctly signal “face versus nonface” (face detection) or “face A versus face B” (face recognition) in response to either a small face viewed in profile or a large face facing forward, in isolation or embedded among many other objects, in twilight or in direct sunlight, either young or old, and so forth. For this reason, strictly invariant responses to lower-level stimulus dimensions are an important goal in computational models (Hummel and Biederman 1992; Wallis and Rolls 1997; Riesenhuber and Poggio 1999). Analogously, some fMRI (Grill-Spector et al. 1999; Andrews and Ewbank 2004; Sawamura et al. 2005; Murray and He 2006; Kovacs et al. 2008) and single-unit (Rolls and Baylis 1986; Ito et al. 1995) studies have emphasized stimulus invariance in inferotemporal cortex and in FFA in specific. To what extent does FFA respond invariantly to faces, despite the wide variation in lower-level features?

Other studies have instead observed variation in FFA activity when lower-level cues are varied (Avidan et al. 2002; Yue et al. 2006; Schwarzlose et al. 2008; Andresen et al. 2009; Carlson et al. 2009; Xu et al. 2009). To clarify the situation, here we systematically tested the effects of 4 basic cues that are known to challenge visual object processing, including face computation: size, position, contrast level, and viewpoint (rotation in depth). Do these stimulus variables influence activity in FFA, as they do in lower-level visual areas, such as V1?

Despite the higher-order face selectivity that defines FFA, we found that FFA also responded strongly to all 4 lower-level image variations, and the FFA response variations correlated highly with those in V1. Accordingly, FFA responses could be accurately modeled by a combination of stimulus contrast and the cortical magnification factor (CMF). Each of these lower-level influences was quite strong, accounting for up to 55% of the response to optimized faces. Combinations of these stimulus dimensions were even more influential. Manipulation of lower-level cues could even reverse the defining category selectivity in FFA, such that FFA responded better to nonface objects compared with faces.

Materials and Methods

Visual Stimuli

The face/head 3D meshes were generated by FaceGen (Singular Inversions) and then imported into Matlab (The MathWorks) by customized Matlab programs. All stimulus images were rendered in Matlab with precise controls of lighting, viewpoint, rotation, and so forth. Stimuli were presented in the scanner via LCD projector (Sharp XG-P25, 1024 × 768 pixels) using PsychToolbox (Brainard 1997; Pelli 1997).

In different experiments, faces were varied in either size, position, viewpoint (rotation in depth), contrast level, or a combination thereof (contrast × size). All stimulus sets included a common subset of reference faces (frontal view and gaze, centered in the visual field, 8 identities, 4 males/females, neutral expression).

Stimulus conditions were organized into a block design. Blocks (16-s duration) were presented in semi-random order (8 different faces/block, 1 face/s), along with control blocks of uniform gray, of equal mean luminance.

Task

A fixation dot was present on the center of all face stimuli and the baseline (uniform gray) images. Subjects performed a dot detection task during central fixation throughout the functional scanning using a button box in the scanner. The probe dot appeared at unpredictable times (100 ms random shift from each stimulus onset), distributed randomly across the display with equal spatial probability. The detectability of the probe dot was manipulated by varying its cyan/white ratio (decreased saturation = decreased detection). Threshold was modulated by the staircase method, converging on 75% correct. To reduce response variability, the dot size varied with eccentricity.

Subjects

All 17 subjects gave written consent. The experimental protocol was approved by the Institutional Review Board of Massachusetts General Hospital. All subjects had normal or corrected-to-normal vision.

Imaging

All scanning were done in a 3T Siemens Trio. Functional scans used a gradient echo EPI sequence (repetition time = 2s, voxel size 3 mm isotropic). Over all experiments, we analyzed 51 910 functional volumes. An additional 1840 functional volumes were excluded from analysis due to excessive head motion. For each subject, high-resolution anatomical scans were also collected for cortical surface reconstruction.

Analysis

Each individual brain was inflated using FreeSurfer (http://surfer.nmr.mgh.harvard.edu). Statistical analysis of the functional data was performed with FS-FAST. All functional images were motion corrected, spatially smoothed with a 5-mm Gaussian kernel, and normalized across sessions individually. Average signal intensity maps were calculated for each condition for each subject. Voxel-by-voxel statistical tests were conducted by computing contrasts based on a General Linear Model (GLM). For averaging across subjects, each subject’s functional and anatomical data were spatially normalized by using the spherical transformation (Fischl et al. 1999). Data from both hemispheres were averaged together unless otherwise noted.

In each subject, areas FFA and parahippocampal place area (PPA) were localized using an independent set of stimuli: groups of faces and indoor scenes, respectively (Supplementary Fig. 1). Subsequent region-of-interest (ROI) analyses were based on these individually localized areas. ROIs for V1 were based on the Montreal Neurological Institute standard inflated brain at group level. Activations for all conditions (all vs. fixation) in each experiment were compared using random effects analyses with a threshold of P < 0.01. Then, the group-averaged data were extracted from that ROI for each condition.

All statistics were performed in SPSS. All error bars are standard error of the mean.

The Lower-Order Model

We modeled the lower-order (e.g., V1) visual responses as follows. Each image was filtered with a Gabor function composed of one spatial frequency at 8 equally spaced orientations (i.e., 45 ° difference in angle). The Gabor filter was modified from the model in Lades et al. (1993): 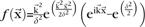, where k is orientation. The filter approximates the response of complex cells in V1. Then, the filtered response was weighted with a Gaussian: 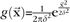. The final output of the model is the sum of all responses across all 8 orientations.

Results

Overall Hypotheses

In response to variations in each parameter, several possible outcomes were possible in FFA.

First, responses to a given parameter could reflect apparent “face processing in FFA.” For instance, variations in a parameter that is known to affect face perception could produce a corresponding effect in FFA but not in lower-level cortical areas, such as V1.

Second, a given parameter might be “irrelevant for FFA.” In such cases, FFA would respond equivalently, no matter how this parameter was varied. We defined this type of fMRI response as feature invariance (see also DiCarlo and Maunsell 2003).

Third, a given parameter could affect FFA activity in a way “unrelated to face processing.” For instance, variation of a given stimulus parameter might produce response covariations in FFA—as well as in V1 and other visual cortical areas. Such a correlated response would suggest a passive transmission of visual activity through V1 into FFA.

In a larger parametric study, we found examples of each of these 3 response types in FFA. Here, we describe the effect of the 4 parameters that fell under outcome 3.

Attention Task

Typically, subject performance on the dot detection task converged quickly to threshold levels (see Supplementary Fig. 2). Thus, the attentional load was relatively stabilized during the functional scans.

Experiment 1: Size

Hypotheses

Computationally, it is useful if a face detector responds in a way that does not vary with face size (Hummel and Biederman 1992; Wallis and Rolls 1997; Riesenhuber and Poggio 1999). Accordingly, size invariance has been reported in fMRI studies of FFA and the Lateral Occipital complex (LO) (Grill-Spector et al. 1999; Andrews and Ewbank 2004; Sawamura et al. 2005).

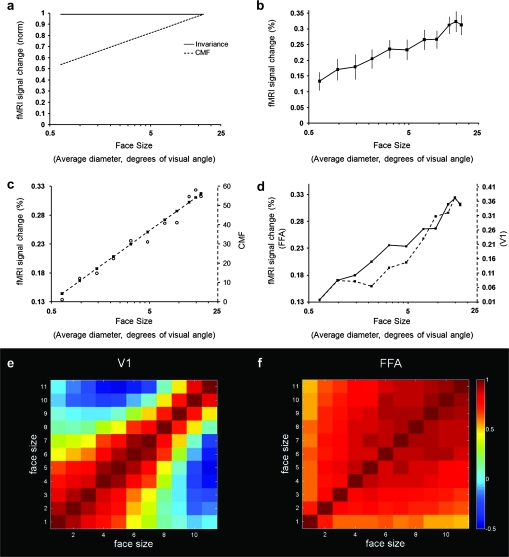
Figure 1a shows 2 predictions of FFA activity in response to variations in face size. The hypothesis of size invariance is shown as a solid line. The alternative prediction (dashed line) is based on the response of lower-level visual areas in which population activity increases with stimulus size. That second function is described by the well-known CMF. Typically, the CMF has been used to map variations in receptive field center location. Here, we instead used the CMF to predict variations in population activity (measured as fMRI amplitude over the entire ROI-defined area) in response to a given face presented at different sizes. The CMF prediction (Fig. 1c) was based on measurements from V1 (Sereno et al. 1995; Engel et al. 1997).

Figure 1.

Responses to variations in face size. (a) The hypothesis of size invariance is shown as a solid line. In the alternative hypothesis (dashed line), a population response based on the CMF produces increasing responses as face size is increased as a linear function on a logarithmic scale. (b) Results in FFA. The FFA response is consistent with the CMF hypothesis but not with the size invariance hypothesis. (c) The FFA response correlated highly with the CMF. The CMF function is (log(x)/0.063 + 11.36), where x is size in averaged diameter. (d) The FFA and V1 responses correlated highly. Two y-axes are displayed showing the absolute percent changes in both FFA (left y-axis) and V1 (right y-axis) and their amplitude-normalized correlation. (e) Correlation in individual voxels in V1. Voxels in V1 showed clear retinotopic correlations. (f) Correlation in individual voxels in FFA. Voxels were largely devoid of this retinotopic effect. For voxel-wise correlation analysis, each voxel’s activity within the ROI was extracted based on GLM for each condition and converted to a percent signal change. The correlation was done for each individual subject and each hemisphere.

Stimuli and Data Set

All faces were presented upright in frontal view. Except for the variable of interest (size), all faces were identical to the reference face in other experiments. Test sizes (average of vertical and horizontal diameters) varied from 0.64 to 16.80 ° in 11 steps. All stimuli were clearly recognized as faces based on subject report. Faces can be accurately recognized even at very small sizes (Yip and Sinha 2002; Lindsay et al. 2008) comparable with the smallest size tested here. The data set included 18 720 functional volumes from 15 subjects.

Results

Figure 1b shows the resultant face size function in FFA. Responses were not invariant over any portion of the curve (F_10,140 = 5.8, P < 0.001). Instead, we found a linear increase in the FFA responses with logarithmic increases in face size throughout the tested range. The function correlated very highly (r = 0.986, P < 0.001) with the prediction derived from the CMF (Fig. 1c). Thus, the face size function in FFA also correlated well with that measured empirically in V1 (r = 0.956, P < 0.001) (Fig. 1d). Although our analysis focused on V1 and FFA, the activity maps showed a clear increase in activity with increasing size throughout many areas of visual cortex (Supplementary Fig. 3).

If cortical area FFA has an explicit retinotopic map, this influence of the CMF would be unsurprising—as in V1. However, previous studies have reported that FFA does not have an explicit retinotopic map (Haxby et al. 2001). Are retinotopic variations from lower areas instead distributed nonretinotopically in FFA?

We tested this by performing a voxel-wise correlation. For each subject, BOLD signal changes were estimated with a GLM model for every single voxel for each face size. Then, the BOLD signal change of each voxel within each ROI was extracted, which yielded a single vector for each face size. The correlation between conditions was calculated, which generated an 11 × 11 matrix. From these data, the final correction matrix was averaged across all subjects. This procedure produced a correlation matrix for both V1 and FFA.

In V1, we found a strong positive correlation between the activity produced by similar face sizes, especially for small face sizes (Fig. 1e). Faces of dissimilar size were uncorrelated or negatively correlated. All these results are consistent with a well-ordered retinotopic map based on small receptive fields—the hallmark of V1 organization.

However, in FFA, all correlations were positive (Fig. 1f). This suggests that bottom-up retinotopic information is largely intermixed within FFA at least at this voxel size. Correlations were slightly higher for large faces compared with small faces in FFA; this pattern was the reverse of the V1 pattern. This evidence is consistent with the presence of larger receptive fields in FFA.

The PPA is a discrete cortical area located immediately adjacent to FFA, which does not respond well to faces (Epstein and Kanwisher 1998). In response to these nonoptimal stimuli, would PPA nevertheless show a size dependence in its fMRI responses? Here, we found that the smaller faces (less than 10°) produced little or no response. However, in response to progressively larger faces, PPA activity increased systematically and significantly (F_10,140 = 5.8, P < 0.001) (Supplementary Fig. 4). This suggests that an activity threshold (“floor”) exists for smaller faces in PPA, yielding response amplitudes near zero. Above 10°, the PPA size gain function increased even more steeply than that in FFA (interaction between FFA_PPA vs. size: F_2,28 = 6.621, P < 0.01). The steeper slope in PPA indicates that the PPA response is not simply “spillover” from FFA. The steeper slope is also consistent with reports of a peripheral bias in PPA responses (Levy et al. 2001) (see Discussion).

Experiment 2: Visual Field Position

Hypotheses

Next, we measured the effect of variations in visual field position. Many computational models (Hummel and Biederman 1992; Wallis and Rolls 1997; Riesenhuber and Poggio 1999) assume invariance for face/object position in the visual field (“position invariance”) for reasons similar to those for size invariance. Size and position specificity are linked by common receptive field mechanisms, at least at lower levels of the visual system (Hubel and Wiesel 1974).

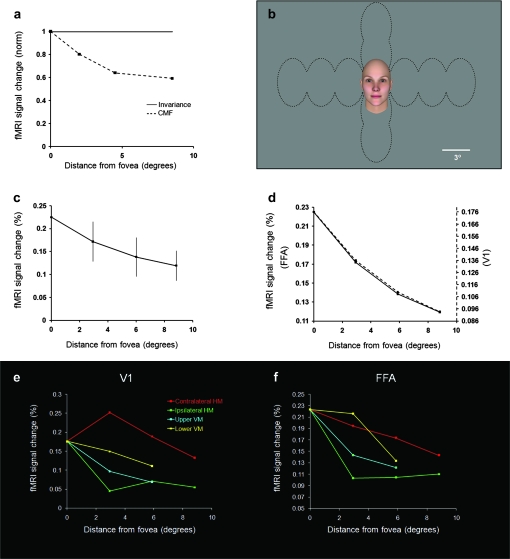
The invariance hypothesis for position (Fig. 2a) predicts that FFA responses to a given face will be equivalent to each other, irrespective of where that face is positioned in the visual field. However, the hypothesis of position invariance is biologically problematic because neural mechanisms vary profoundly with visual field eccentricity (see Discussion). Accordingly, visual perception also varies a great deal across the visual field. Previous fMRI tests of position invariance have yielded mixed results in FFA (Grill-Spector et al. 1999; Hemond et al. 2007; Kovacs et al. 2008; Schwarzlose et al. 2008).

Figure 2.

Responses to variations in visual field position of face stimuli. (a) The hypothesis of position invariance (solid line) predicts an equivalent response in FFA irrespective of visual field position. Alternatively, the CMF hypothesis (dashed line) predicts a response that decreases according to the CMF variation (e.g., Figure 1). (b) Stimulus configuration. Within a given block, faces were presented in one of the visual field locations outlined by dashed black lines. (c) Results from FFA combined across all 4 axes. FFA activity decreases systematically with increasing stimulus eccentricity consistent with the CMF hypothesis. (d) The FFA response curve (solid line) was near-identical to that in V1 (dashed line). (e) FMRI variations in V1 due to variations in position along 4 major visual field axes. As expected, the steepest decrease resulted from moving the face into the ipsilateral visual field by the most direct path along the horizontal meridian (green). Movement in the opposite direction (contralateral visual field, red) produced the highest overall activity. The slope of these 2 curves was a nonmonotonic function reflecting 2 competing factors: 1) activity decreased with increasing face eccentricity, as in the other measurements, but: 2) activity increased/decreased more at the first offset from zero as the face shifted from half-viewed in a given hemisphere (central position) to whole viewed (all other positions). As expected, activity along the vertical meridian (yellow and cyan) decreased with a slope intermediate to those along the horizontal meridian. (f) Variations in FFA activity as a function of position, otherwise as in panel (e). The changes in activity are qualitatively similar to those in V1 (see e) except for a single point. However, the range of response difference is compressed relative to that in V1, as one would expect from larger receptive fields in FFA.

Given this evidence and our size results (Fig. 1b), a specific alternative to the hypothesis of position invariance was based on the CMF. This hypothesis (Fig. 2a) predicts that FFA responses will decrease as a given face is viewed at progressively greater distance from the center of gaze in accordance with the CMF.

Stimuli and Data Set

Faces (frontal view, 4.6° diameter) were presented in 5 × 7 equally spaced positions (vertical × horizontal, respectively, in 2.9° steps) on the display screen using one position per block (Fig. 2b). The data set included 8320 functional volumes from 8 subjects.

Results

We did not find invariance for position in FFA (F_3,21 = 7.3, P < 0.01); instead our data again matched the CMF prediction (Fig. 2a). In fact, the face position function in FFA matched that in V1 near perfectly (r = 0.999, P < 0.001; Fig. 2d).

In V1, the known retinotopic organization predicts a specific response variation to the 4 axes tested (Fig. 2e). As predicted, we found that the largest fMRI differences occurred along the horizontal meridian: Contralateral face positions produced the highest activity, whereas ipsilateral face positions produced the least. This was expected because essentially all V1 activity is driven by contralateral stimuli (Tootell et al. 1988). In contrast, test positions along the vertical meridian straddled each hemifield equally. Correspondingly, V1 activity along the vertical meridian was similar along the dorsal and ventral axes, and intermediate to activity produced along the ipsilateral/contralateral extremes (i.e., along the horizontal meridian).

A weaker version of the same variation was found in FFA (Fig. 2f). The weaker difference is consistent with the decreased retinotopy and larger receptive fields in FFA compared with V1. Overall, the face position results were fully consistent with a CMF influence in FFA.

Experiment 3: Contrast Level

Hypotheses

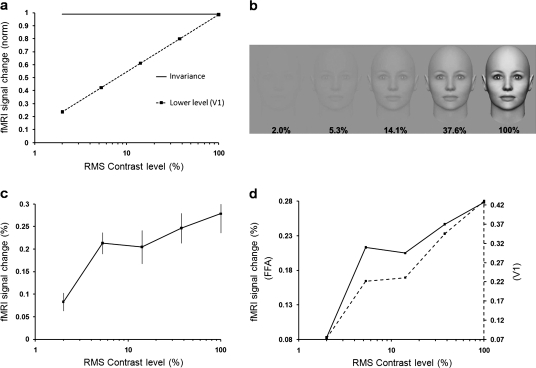
Next, we tested the effects of varying contrast level. Figure 3a illustrates the hypotheses tested for contrast level in FFA. The contrast invariance hypothesis (solid line in Fig. 3a) predicts an equivalent response to each contrast level across the visible range (e.g., Rolls and Baylis 1986). In an alternative hypothesis, FFA responses increase with increasing contrast. Such contrast gain functions are the rule in lower-tier visual areas in response to simple geometrical stimuli, such as gratings and checkerboards (Kaplan et al. 1987; Tootell et al. 1988, 1995; Sclar et al. 1990; Boynton et al. 1996). For example, the dashed line in Figure 3a shows the contrast gain function produced by grating stimuli in V1, based on fMRI (Tootell et al. 1995).

Figure 3.

Responses to variations in facial contrast. (a) Hypotheses for changes in FFA activity due to variations in contrast level of face stimuli. The “contrast invariance” hypothesis is shown as a solid line. Alternatively, FFA responses might increase with increasing contrast, as in the V1 prediction (dashed line), based on grating stimuli (from Tootell et al. 1995). (b) Stimulus examples. (c) FFA activity to faces increases at progressively higher contrast (relative to the uniform gray baseline stimuli), similar to the V1 prediction based on gratings (dashed line in panel a). (d) Based on the face stimuli, the contrast gain response in FFA (solid line) was similar to that in V1 (dashed line). The contrast levels shown here are not exact due to lack of control over publication displays.

Stimuli and Data Set

Figure 3b shows examples of the stimuli. The face size was 12.7°. The mean luminance of the face was identical to the mean luminance of the uniform gray background. Contrast levels were defined as the root-mean-square (RMS) contrast across the entire face in equal logarithmic steps ranging from 2% to 100%. Contrast detection is improved when based on RMS compared with other measures (Bex and Makous 2002). Corresponding Michelson contrast value varied between 2.44% and 94.09%. Psychophysically, visual objects are reliably detected at Michelson contrasts more than 1.5% (Murray and He 2006).

The data set for this experiment included 9360 functional volumes from 8 subjects.

Results

Figure 3c shows the results. Averaged FFA responses increased monotonically with increasing contrast level (F_4,28 = 36.91, P < 0.001); thus, the hypothesis of contrast invariance was ruled out. Instead, the FFA data closely matched the contrast gain curve from V1 in response to grating stimuli (see Fig. 3a). In V1, the contrast gain for these face stimuli (Fig. 3d) was also similar to that in earlier V1 measurements using gratings. Based on face stimuli, the contrast gain in V1 also correlated highly with that in FFA (r = 0.957, P < 0.05 [P = 0.011]) (Fig. 3d).

Experiment 4: Viewpoint (Rotation in Depth)

Hypotheses

The image of the face/head changes as it rotates in 3 dimensions—often fundamentally. This image change occurs during all axes of rotation, except in the single case of rotation exactly in plane. To measure the effect of these ubiquitous changes in viewpoint, we measured fMRI responses in response to face/head views following systematic rotations in depth.

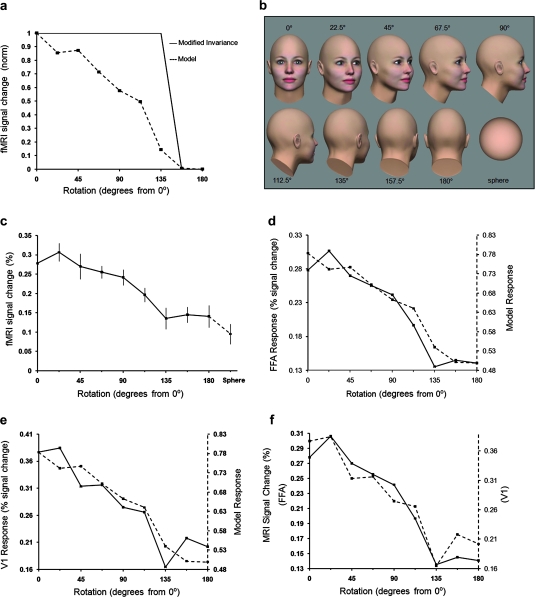
Figure 4a,b shows the predictions and stimuli. During rotation in depth, the face is occluded by the remainder of the head over an appreciable portion of the rotation range. In our stimuli (Fig. 4b), the eyes and nose cannot be seen beyond 112.5°. Thus, the generic invariance hypothesis (i.e., that responses to any face will be equivalent) is here restricted to the rotation range within which the face is visible.

Figure 4.

Response to variations in face viewpoint (rotation in depth). (a) Two hypotheses for FFA activity. The solid line shows the rotation-limited invariance hypothesis. Since the face is occluded beyond 0 ± 135°, a baseline response is predicted to those stimuli. The second hypothesis (dashed line) is the prediction from the lower-order model incorporating the contrast and CMF influence in FFA. (b) Stimulus examples. Half of the tested rotations are illustrated; the remaining stimuli are mirror symmetrical. We also tested the responses to a sphere similar in size to the back of the head (bottom right). (c) fMRI responses in FFA. Results from left and right rotation angles have been combined. Normalized responses to the sphere are shown in dashed line. (d) The variation in FFA response (solid line) correlated well with the variation produced by the model (dashed line). (e) An analogous result was found in V1. (f) Responses from FFA (solid line) and V1 (dashed line) correlated highly.

Instead, the results in experiments 1–3 predict that a face that is barely visible (e.g., 112.5° in Fig. 4b) will produce much less activity, compared with the frontal (0°) view of that same face. Multiple factors contribute to this prediction. First, as the viewpoint changes from frontal through the profile view, and beyond (to 112.5°), the visible portion of the face becomes smaller, and it is positioned more peripherally in the visual field. Thus, the CMF influence (experiments 1 and 2) predicts progressively lower responses to facial viewpoints further from frontal.

Variations in contrast also influence this prediction. As it rotates, the average RMS contrast level of our face/head decreases from frontal view through the back-of-the-head view (180°). Since FFA responses decrease with decreasing contrast (experiment 3), this factor thus predicts smaller responses to faces at viewpoints rotated further from frontal.

We formalized this prediction using a “lower-order” model (see Materials and Methods) based on the well-known response properties of V1. This model’s prediction for the rotation experiments is illustrated in Figure 4a.

Stimuli and Data Set

We tested the full range of rotations in 22.5° increments in semi-randomized order. To save space, only half of this rotation range is shown in Figure 4b. All the heads were 12.7° in diameter in frontal view. A constant virtual head “distance” from the viewer was maintained across rotation angles.

This data set included 11 200 functional volumes from 7 subjects.

Results

The FFA response function (Fig. 4c) did not match the restricted invariance hypothesis. Instead, it closely matched the prediction of the lower-order model (r = 0.961, P < 0.001) (Fig. 4d). Thus, the FFA response decreased progressively at rotation angles further from the frontal view to a minimum at the back of the head.

Our model predicted that V1 would show a similar response function. Figure 4e confirms that the V1 function did match the lower-order model prediction quite closely. Hence, the FFA and V1 functions were highly correlated with each other (r = 0.957, P < 0.001) (Fig. 4f). Again, the FFA responses were indistinguishable from a passive reflection of lower-level activity in V1.

FFA responded fairly well (roughly half-maximum) to the “back” of the head, although no part of the face was visible from that viewpoint. Did that result represent a response to an inferred face based on prior knowledge of heads and faces (Cox et al. 2004; Wild and Busey 2004)—or simply a visually nonselective component in the aggregate FFA response?

To address this, we conducted an additional control experiment measuring FFA responses to a sphere compared with the back (180°) view of these bald heads. FFA responded nearly (76%) as well to the sphere compared with the 180° head view (Fig. 4c). Considering that the sphere had even less local contrast than the back of the head, there may be no higher-order advantage to the head compared with the sphere. In fact, the lower-order model predicts the sphere result within the error of measurement (model prediction = 63% decrease to the sphere, relative to the back-of-the-head view). Overall, this supports previous evidence that a generalized (non-face-selective) component contributes to the FFA responses (Grill-Spector et al. 1999; Gauthier et al. 2000a; Tong et al. 2000; Tsao et al. 2003, 2006; Caldara et al. 2006; Yue et al. 2006; Tootell et al. 2008)—in addition to any components that are face selective.

Above, we combined data from both hemispheres. However, differences between the hemispheres were also expected (and confirmed) from these stimuli in V1. Responses were relatively higher when the face was rotated further into the contralateral hemispheres, and lower when the face was rotated into the ipsilateral hemisphere (F_1,13 = 12.2, P < 0.01). This hemispheric bias was expected because V1 responds to local contrast in the contralateral hemifield, and in our stimuli, the face had more local contrast compared with the back of the head.

This contralateral bias was also observed in FFA (F_1,13 = 13.6, P < 0.01). This is consistent with the idea that FFA responds in part to local contrast, as in V1. Additionally, this result confirms that contralateral dominance is retained through cortical levels at least as high as FFA (Hemond et al. 2007)

Experiment 5: Interactions

Hypotheses

Above, we varied only one stimulus dimension at a time. From those data, can we predict the response to changes in multiple dimensions? Do the response functions to each dimension combine linearly? That would be computationally convenient, and it would ease the translation of our present results from the laboratory to real-world faces.

This assumption of linear summation predicts exceptionally low responses to face stimuli in FFA when multiple low-level stimulus dimensions are nonoptimal. For instance, in the single-dimension experiments in FFA (Fig. 1b), smaller (nonoptimized) faces produced ∼45% of the activity, compared with that produced by the larger (optimized) faces. Similarly, lower contrast faces produced much lower activity than faces at higher contrast. When these 2 dimensions are combined (a small low-contrast face), would those decreases also combine? Alternatively, does the response to a given face have a lower limit, as long as the visual stimulus is a face? The latter is an extension of the category model.

Depending on the stimuli used, the FFA responses predicted for such nonoptimal faces might be even lower than the responses to specific nonface objects.

Stimuli and Data set

These predictions were tested by presenting 1) relatively “optimized” faces (12.7° diameter, 100% RMS contrast, frontal viewpoint) versus 2) “nonoptimized” faces (1.02° diameter, 14.14% RMS contrast). Assuming a linear combination of our single-dimension results, these nonoptimized faces should produce 42.8% of the activity (i.e., 55% for size, x 77.8% for contrast) compared with the optimized faces.

Several considerations ensured that both sets of stimuli were readily perceived as faces. First, we made only 2 features nonoptimal: size and contrast level. The 2 remaining features (position and rotation) remained optimized. Second, we chose “nonoptimal” values that were well above perceptual threshold. As expected, subjects confirmed that all experimental faces were readily visible and perceived as faces.

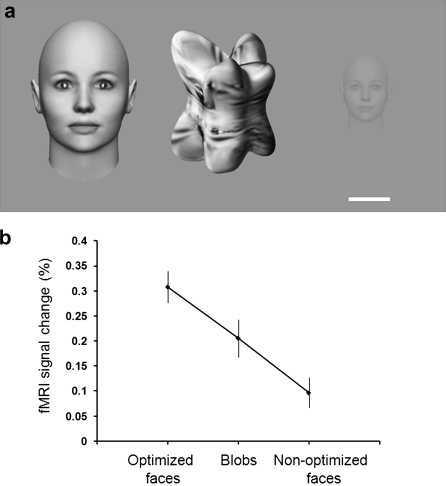
To test whether nonface objects could produce more activity than nonoptimized faces, we also tested a third condition: computer-generated nonface objects (“blobs”; Fig. 5a). These blobs were otherwise similar to the optimized faces in terms of the lower-level properties size, contrast, and position (rotation values are moot in these shapes). The blob texture was generated from images of faces using an algorithm that markedly altered the higher-order structures while preserving image statistics (Portilla and Simoncelli 2000). The shape of the blobs approximated facial concavities and convexities (e.g., nose, cheekbone) (Yue et al. 2006; Nederhouser et al. 2007).

Figure 5.

Sensitivity to stimulus category and parameters. (a) Examples of the stimuli from left to right: 1) optimized faces (12.7° diameter, 100% contrast); 2) computer-generated objects (“blobs”), with lower-level features matched to the optimized faces; 3) nonoptimized faces (1.02° diameter; 14.14% contrast). The white scale bar represents 1° for the nonoptimized face and 6.3° for the blob and optimized face. (b) Average FFA response to each stimulus type.

This data set included 4400 functional volumes from 5 subjects.

Results

The results (Fig. 5b) confirmed that the “preferred” stimulus category in FFA could be fully reversed from faces to objects by using 2 nonoptimal parameters for the face stimuli, and presumably optimized parameters for unfamiliar blob-shaped objects. The response to these objects was more than double (increase = 113%) that of the nonoptimized faces. This difference was significant (t₄ = 9.3, P < 0.001).

Post hoc calculations revealed that this stimulus category reversal could have been achieved by changing only a single parameter. Based on our data (Figs 1 and 3), FFA activity in response to the blob stimuli should be equivalent to that produced by a face of maximum (100%) contrast and a larger (2.14°) diameter. Thus, any face that is smaller, and/or lower in contrast, would instead produce less activity compared with these particular blob stimuli.

Within our measurement limits, the fMRI effects of multiple facial parameters combined near-linearly in FFA. The nonoptimized faces produced 30.0% as much activity compared with the optimized faces. This result was statistically indistinguishable (t₄ = 1.8, P = 0.14) from the linear prediction for this combination (42.8%).

Parahippocampal Place Area

Despite the expected small response amplitudes to face stimuli, we found that PPA response functions were generally consistent with those in FFA and V1 (e.g., Fig. 3c,d)—except for the small peripheral bias described previously in PPA (Supplementary Fig. 4a,b). Again, this emphasized the widespread influence of these lower-level influences (e.g., Supplementary Fig. 3).

Discussion

FFA Activity Is Correlated with V1 Activity

In many reports, face selectivity is the defining feature of the FFA (Puce et al. 1995; Kanwisher et al. 1997; Grill-Spector et al. 1999; Halgren et al. 1999; Haxby et al. 1999; Hasson et al. 2001, but see Gautier et al. 2000; Haxby et al. 2001). Computationally, face selectivity is much easier to achieve if it is not confounded by response variation to lower-order image components. Reflecting this expectation, invariant responses to several lower-level properties have been reported previously from FFA and nearby regions of visual cortex (Rolls and Baylis 1986; Ito et al. 1995; Grill-Spector et al. 1999; Andrews and Ewbank 2004; Sawamura et al. 2005; Murray and He 2006; Kovacs et al. 2008).

Instead, here, we found that at least 4 lower-order image dimensions produced systematic variation in FFA responses. Moreover, this response variation was highly correlated with that in V1. Those V1–FFA correlations were as follows: r = 0.956 for size, 0.999 for position, 0.957 for contrast gain, and 0.957 for rotation in depth. Accordingly, all these results in FFA were closely fit by a model based on V1 function. The model assumed only a response to local contrast corrected by the CMF; it did not include any additional face-selective component.

In the hierarchy of primate visual cortical areas, V1 is the information bottleneck (Van Essen et al. 1992; Distler et al. 1993); most or all the input to higher-tier cortical areas (presumably including FFA) passes through V1. For simplicity, we measured lower-level visual cortical activity in V1. Although we did not systematically analyze data from other visual areas (e.g., V2, etc.), our activity maps (e.g., Supplementary Fig. 3) revealed that many additional lower-level visual cortical areas responded similarly to V1 and FFA. This eased the burden of proof for our lower-level influences in FFA, and it eased certain technical constraints. For instance, if our “V1” ROI encroached slightly into neighboring V2, this presumably had little effect on our data; both V1 and V2 are lower-level visual cortical areas, functionally similar at the level of fMRI.

Facial Size

Variations in face size (e.g., in degrees of visual angle) strongly affected responses in FFA. In fact, size was the strongest lower-level influence that we found in FFA, given the experimental ranges tested here. This size-driven response variation was relatively surprising because several previous fMRI (Grill-Spector et al. 1999; Andrews and Ewbank 2004; Sawamura et al. 2005) and single-unit (Rolls and Baylis 1986; Ito et al. 1995) studies have reported size invariance in inferior temporal cortex. Instead, our results are more consistent with psychophysical studies (Kolers et al. 1985; Fiser et al. 2001) showing significantly longer reaction time when sequentially matching faces of dissimilar size compared with faces of same size. A recent fMRI study using fast event-related adaptation also showed a significant size effect in right FFA (Xu et al. 2009).

What accounts for this apparent discrepancy between results in the present data, relative to some previous reports? One factor may arise from differences in the stimulus ranges tested. Specifically, some previous studies tested relatively limited ranges of stimulus size (e.g., 2- or 4-fold in diameter). By comparison, here, we tested a 26-fold range of face sizes. These differences in sampling range could account for the different conclusions in those studies: Analogous 2- or 4-fold size variation in our own data also produced statistically insignificant differences (i.e., size invariance). Here, the wider range of stimulus sizes revealed the size tuning function in FFA; this would not have been uncovered by tests using more limited test ranges.

Foveal Bias in FFA

It has been reported (Levy et al. 2001; Hasson et al. 2003) that FFA responds more to foveal stimuli, relative to adjacent area PPA, which responds relatively more to peripheral stimuli. However, that information alone is ambiguous. Relative to classically retinotopic visual cortical areas such as V1, does this FFA/PPA comparison reflect a foveal bias in FFA, or a peripheral bias in PPA, or both?

The present data suggest that FFA is not biased for foveal stimuli relative to V1 because FFA and V1 share a common CMF. However, FFA could be biased for foveal stimuli relative to PPA if we assume that PPA has a peripheral bias. Evidence for such a peripheral bias can be seen in Supplementary Figure 4a: The size gain function shows a steeper slope in PPA compared with that in FFA and V1, when all responses exceeded baseline. Thus, in PPA, our evidence is broadly compatible with previous reports (Levy et al. 2001; Hasson et al. 2003; Schwarzlose et al. 2008).

Facial Position

Retinal mechanisms vary profoundly with respect to eccentricity. Such neural mechanisms include the rod/cone ratio (Andrade da Costa and Hokoc 2000), photoreceptor packing (Roorda et al. 2001), cone photoreceptor type (Knau et al. 2001), morphology and arborization (Callaway and Wiser 1996), preretinal absorbance (Yolton et al. 1974), and so forth. Variation in some of these retinal mechanisms contributes to the CMF (Perry and Cowey 1985).

Accordingly, visual perception also varies enormously with eccentricity. These perceptual variations include acuity (Waugh and Levi 1993), color vision (Martin 1998), spatial frequency sensitivity (Rovamo et al. 1992), and crowding (Pelli et al. 2007). Even face perception itself varies with eccentricity (Melmoth et al. 2000; Afraz and Cavanagh 2008).

Given these visual field variations, and the CMF influence in FFA (e.g., Fig. 1c), it would be surprising if otherwise-equal faces did not produce decreased activity at progressively greater visual field eccentricities. Although the converse conclusion (position invariance) has also been reported in posterior Fusiform gyrus (pFs) (analogous to FFA) (Grill-Spector et al. 1999), the stimuli in that study varied over a narrower visual field range (5.6°) compared with the stimuli used here (17.6°). Thus, again, testing a smaller range of stimulus variation may explain a conclusion of stimulus invariance. In fact, the CMF influence predicts that one could deliberately create an even more dramatic “position invariance” by comparing only the responses with faces that are positioned far apart in the visual field, equidistant from the center of gaze, along the vertical meridian (e.g., Fig. 2e,f).

Schwarzlose et al. (2008) reported that foveal stimuli produced slightly larger responses compared with peripheral stimuli in FFA even when stimulus size was corrected by a CMF. If the CMF completely explained the variations in FFA response, then the CMF-corrected stimuli should have produced equal responses in FFA. However, the CMF in Schwarzlose et al. (2008) was extrapolated from values in the literature; concurrent measurements were not analyzed from V1 to confirm the CMF values in that specific subject pool. If there is a discrepancy between our data and those of Schwarzlose et al. (2008), this raises an interesting question: Is size versus position information encoded along different (vs. equal) “CMF” functions? From single-unit recordings in macaque V1, either conclusion is possible (e.g., Van Essen et al. 1984, but see Hubel and Wiesel 1974).

Facial Contrast Level (Gain)

Responses to a range of contrast levels (i.e., contrast gain functions) have been extensively studied using gratings based on psychophysics (Legge 1981), event-related potentials (DiRusso et al. 2001), single units (Kaplan et al. 1987; Sclar et al. 1990), and fMRI from the retina through mid-level visual cortex (Tootell et al. 1995; Boynton et al. 1999; Olman et al. 2004; Gardner et al. 2005). Here, we extended such measurements to face stimuli in FFA based on RMS contrast.

The contrast gain function imposes significant constraints for the computation of face/object processing. Most importantly, does contrast invariance exist in FFA? One fMRI study (Avidan et al. 2002) concluded that pFs (FFA) showed an “increasing tendency toward contrast invariance” in LO (and pFs, the FFA equivalent) relative to V1. However, when those earlier data are replotted on a conventional logarithmic scale, it also showed a near-linear increase in pFs (FFA) similar to that presented here. The similarity between contrast gain functions in these 2 studies is notable, considering the many technical differences between them. For instance, the earlier fMRI study was based on-responses to luminance variations of line drawings on a constant luminance background, rather than the equal-luminance contrast variations in the gray-level faces tested here. Another fMRI study also reported contrast-varying responses in nearby region “LO” (Murray and He 2006). Overall, these results suggest that contrast invariance cannot be assumed in FFA nor likely in other ventral stream areas.

Facial Viewpoint (Rotation in Depth)

Several changes occur as the head rotates in depth (e.g., Fig. 4). The size and averaged eccentricity of the face increases and decreases during the head rotation, like the waxing and waning of the bright side of the moon during the lunar cycle. In our head stimuli, the averaged local contrast also covaried with these size/eccentricity variations because local contrast was concentrated on the face. Thus, all 3 stimulus variables (size, eccentricity, and contrast) predicted higher responses to frontal views of a face and minimum responses to the back of the head in both FFA and V1. This prediction was formalized in our lower-order model.

Our results closely matched the model predictions in both FFA and V1 (Fig. 5b,c). The model even accounted for the slightly decreased FFA response to a sphere compared with the back of the head. Again, a face-selective component was not required to account for the FFA activity variation.

Several fMRI studies (Grill-Spector et al. 1999; Fang et al. 2007; Xu et al. 2009) have tested the effects of rotation in depth in FFA, using sparser sampling compared with the present study. Xu et al. (2009) showed that FFA was sensitive to rotation angle as small as 20°. One study (Tong et al. 2000) also tested responses to the back of the head including hair. In general, those studies showed FFA results similar to ours: Overall, activity decreased as viewpoint diverged progressively from frontal views. However, previous studies did not measure the rotation in as much detail in FFA nor V1 responses in comparison with those in FFA. The V1 measurement especially shaped our ultimate conclusion.

Conceivably, head stimuli with hair might yield a different result because hair adds a fine-grained contrast. However, hairless faces (as used here) are commonly used in studies of face perception because such stimuli avoid confounding cues due to hair (e.g., gender, race, culture, and age).

The Overall Role of Lower-Level Influences in FFA

Why would FFA show such a strong lower-level influence in these experiments? First (and simplest), many previous studies have not compared activity in FFA with that occurring in V1; thus, some close V1–FFA correlations may have remained undetected.

Second, our experimental task was deliberately designed to minimize attention to higher-order facial characteristics (e.g., identity, gender, etc.) by requiring subjects to attend to a competing lower-level feature (dot detection). Thus, lower-level influences may have been relatively uncovered in FFA compared with other possible tasks that elicit higher-order influences (e.g., Grill-Spector et al. 2004). In any event, FFA has been historically defined and localized based on its sensory (face) selectivity (Puce et al. 1995; Kanwisher et al. 1997; Halgren et al. 1999)—not on its higher-order properties (but see Gautier et al. 2000a).

Third, our measurements spanned a greater stimulus range compared with previous studies, for all 4 stimulus dimensions tested. Such extended test ranges increased our statistical power to uncover variations in responses function, which could have gone undetected with a more restricted test range.

A fourth possible explanation arises from the position of FFA in the cortical visual hierarchy. Based on monkey data (Van Essen et al. 1992; Distler et al. 1993; Nakamura et al. 1993; Rajimehr et al. 2009), information could presumably get from human V1 to FFA via as few as 1 or 2 intervening areas (e.g., V1 > V4 > FFA, or V1 > V4 > TEO [temporo-occipital] > FFA). This suggests that FFA occupies a middle (not an upper) tier in the visual cortical hierarchy (e.g., higher than V1 but lower than anterior TE). Thus, FFA should show some residual generalized influence from lower-tier areas.

This perspective implies that face selectivity is not yet complete at the level of FFA. This idea is supported by the moderate FFA responses to stimuli that are only loosely similar to natural faces—or not face-like at all (Grill-Spector et al. 1999; Gauthier et al. 2000; Tong et al. 2000; Tsao et al. 2003, 2006; Caldara et al. 2006; Yue et al. 2006; Tootell et al. 2008).

Lack of Stimulus Invariance

A common view is that FFA responds selectively to faces as a distinct category (reviewed in Kanwisher and Yovel 2006). However, faces vary infinitely in detail: Does FFA respond invariantly to all faces, despite this variation in individual face images? Here, we documented that FFA activity varies a great deal in response to 4 important face parameters: size, position, contrast, and viewpoint.

The relative strength of each lower-level parameter cannot be easily reduced to a single number because the strength of that variation depends on the range of variation tested. For instance, in our measurements, variations of face size amounted to more than half of the FFA response to the most effective face; in that case, the lower-level influence dominated the response of the test faces relative to uniform gray baseline. By comparison, the influence of face position was weaker in our position data. However, if we had been technically able to test faces at a wider range of visual field positions, presumably this would have produced a correspondingly larger influence of position in FFA in accord with a CMF-like function.

In a further experiment (e.g., Fig. 5), a combination of 2 parameters was influential enough to wholly reverse the category selectivity of FFA from faces to objects. At least in that case, the lower-order influences were even stronger when combined. Our data (Figs 1 and 3) also suggest that a similar (though smaller) “preference” for the “blob” (nonface) stimuli could have been achieved by manipulating only one parameter (size).

This emphasizes that face selectivity in FFA is parameter dependent, not absolute. This has implications at the level of a population code: Cortical neurons at higher levels cannot simply respond according to a face/nonface threshold because the response range to faces overlaps the response range to nonface objects. At most activity levels, some object-driven activity will be above a given threshold and some face-driven activity will be below it.

Implications for Neural Models of Face Processing

Studies of FFA have influenced neural models of high-level face processing (Sinha et al. 2006). Our data, and previous observations (Avidan et al. 2002; Murray and He 2006; Yue et al. 2006; Hemond et al. 2007; Schwarzlose et al. 2008; Andresen et al. 2009; Carlson et al. 2009; Xu et al. 2009), emphasize that biologically plausible models cannot assume response invariance for size, position, and contrast nor viewpoint at a level corresponding to FFA. Our data are more consistent with the idea that FFA corresponds to the structural encoding stage in the proposal by Bruce and Young (1986). At such a stage, FFA could encode faces while also preserving low-level information (Biederman and Kalocsai 1997; Yue et al. 2006; Yue 2007).

Limitations

To minimize parameter explosion across our many stimulus conditions, we tested only a single dependent measure of the BOLD response. Given that constraint, we focused on the amplitude of the classic on-response rather than fMRI adaptation, nonlinear classifier, or other measurement. This allowed more direct comparisons between our results relative to the on-responses in the single-unit literature and in the original fMRI reports.

Using different approaches, other studies may come to different conclusions. For instance, single-unit techniques may reveal functional distinctions that cannot be distinguished using fMRI. Evolutionary differences between humans and macaques may also temper the current conclusions. Variations in the nature of the attention task might change the shape of the response curves (e.g., Murray and He 2006; Li et al. 2008; Castelo-Branco et al. 2009). Further fMRI analyses (e.g., based on adaptation, multivoxel pattern analysis, and/or event-related approaches) may yield additional insights compared with the direct on-responses measured here.

As described above, the relative strength of each stimulus dimension also depends crucially on the range of stimulus parameters tested.

Though V1 and FFA activity correlated highly in all the amplitude-normalized comparisons (e.g., Figs 1d, 2d, 3d, and 4f), the slope of the gain functions was sometimes higher in V1 compared with FFA, when based on raw fMRI signal levels (e.g., Figs 1d, 2d, and 3d). Multiple unknown factors could underlie this difference in slope, including 1) larger receptive fields in FFA, 2) the significant residual response to nonface stimuli in FFA (e.g., Fig. 4b; Grill-Spector et al. 1999; Gauthier et al. 2000; Tong et al. 2000; Tsao et al. 2003, 2006; Caldara et al. 2006; Yue et al. 2006; Tootell et al. 2008), and 3) known differences in the physiology and anatomy of V1 relative to extrastriate cortex (e.g., a higher cell packing density and denser vasculature [Perry and Cowey 1985], a specialized laminar structure, and high spontaneous and driven single-unit activity). It is possible that a lower slope in FFA could indicate “an increasing tendency toward invariance,” in LO or FFA, relative to V1, as described by Avidan et al. 2002. However, only a strict invariance (not an “increasing tendency toward” invariance) for a given variable will aid the computation of faces/objects by allowing the computation to ignore that variable; whether the slope is higher or lower is relatively moot for the computation. The fact that we were able to reverse FFA selectivity for faces versus objects by manipulating only lower-level properties (Fig. 5) strongly suggests that any “tendency toward invariance” remains incomplete at the level of FFA.

Conclusions

These results emphasize that FFA activity can be strongly affected by lower-level stimulus parameters. Receptive field properties similar to those known in V1 can account for essentially all the response variation we found in FFA. Given the strength of these effects, it is possible that previous controversies about function in FFA were inadvertently complicated by lower-level stimulus differences. At least, our results reemphasize the importance of specifying and standardizing stimulus parameters, and of acquiring control measurements in V1, in studies of higher-order function.

These results do not rule out the presence of an apparently face-selective component in the FFA response. Although we were able to systematically reverse the normal category selectivity in FFA by manipulating lower-level parameters, relatively atypical parameters were used for those nonoptimal faces. Moreover, the face-driven activity in FFA was always much higher than that in adjacent area PPA, as expected. Thus, overall, our results are consistent with some face selectivity in FFA in addition to the sensitivity to lower-level features emphasized here.

Funding

National Institutes of Health (EY017081 to R.B.H.T., MH076054 to D.J.H.); the National Alliance for Research on Schizophrenia and Depression (NARSAD) (R.B.H.T., D.J.H.); the Sidney J. Bear Trust (D.J.H.); Martinos Center for Biomedical Imaging, National Center for Research Resources (NCRR) (P41RR14075).

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/